随着被动声呐检测性能的不断提高,声呐的作用距离得到有效提高,在声呐作用距离内可检测到的目标数大大增加,多目标轨迹分布情况越来越复杂,同时背景杂波数目也随之增多,如何在多目标复杂的情况下对感兴趣的威胁目标进行有效跟踪具有迫切需求。
传统的被动声呐跟踪方法,适用于目标较少且方位间隔较大的情况,对于目标较多且轨迹变化比较复杂的情况,例如目标交叉、邻近、新目标出现、已有目标突然消失等情形,往往会出现失跟、漏跟以及错跟等情况。例如多假设跟踪[1]和联合概率数据关联算法[2]等基于数据关联技术的多目标跟踪方法,在目标数较少、多目标情况不复杂的条件下,可以获得一定的有效跟踪效果,但是在目标数目增加或者目标情况复杂的情况下,容易在计算复杂度增大的同时导致跟踪效果较差。这是由于这些算法的中心思想是将多目标跟踪问题解析成多个单目标问题,再对各个单目标分别进行滤波处理,最后通过数据关联的方法融合每个单目标处理后的结果。
针对传统多目标跟踪算法面对强干扰或多目标轨迹情况复杂时跟踪效果较差的问题,Mahler教授提出了基于随机有限集理论(RFS)的概率假设密度滤波[3](PHD)的多目标跟踪算法,实现了集函数的积分运算到单个变量积分运算的转化,避免了数据关联问题,解决了计算复杂度“爆炸”的问题,适用于较复杂背景下的多目标跟踪。Vo教授的研究小组为了解决PHD滤波器不存在一般意义上解析解的问题,分别提出了能提供闭合解的高斯混合PHD(GM-PHD)滤波器和粒子PHD(P-PHD)滤波器[4]。其中,GM-PHD滤波器既可以提供PHD的解析解,又避免了粒子采样和聚类等复杂操作,具有运算效率高、计算量较小的优点,已在雷达的多目标领域得到应用[5]。
本文针对多目标干扰情况下被动声呐的多目标中威胁目标方位的自动跟踪进行研究,提出一种基于GM-PHD滤波器的威胁目标方位的自动跟踪算法。首先利用GM-PHD滤波器对多目标时间方位历程图进行处理,得到观测区域内所有存在目标的方位信息,对这些存在目标的方位进行功率谱估计,再利用GM-PHD滤波器对观测区域内所有目标的线谱进行跟踪,通过提取不同频段线谱能量区分干扰目标和威胁目标,有效地找出多目标中威胁目标的轨迹及方位信息。最后,利用试验数据对所提算法的有效性进行了验证。
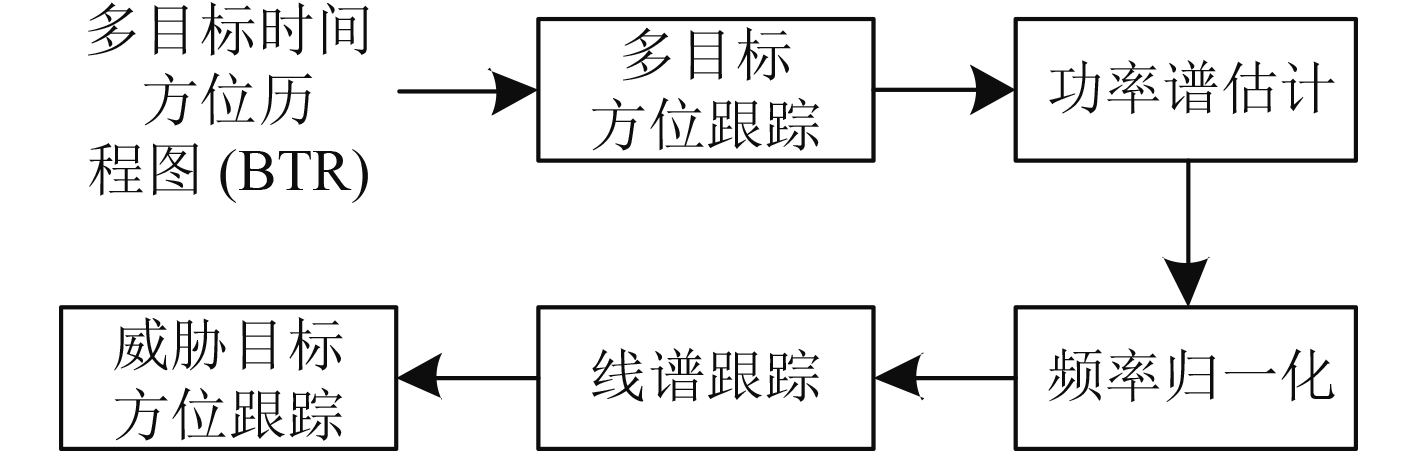
1 算法原理为了精确地找到感兴趣的威胁目标的方位,首先对多目标的时间方位历程图(BTR)进行多目标方位跟踪处理,本文使用GM-PHD滤波的算法进行多目标的跟踪处理,得到观测区域内所有存在目标的方位,并对每一个存在目标的方位进行功率谱估计和频率归一化,得到每个目标的线谱信息,再使用GM-PHD滤波算法对目标线谱进行跟踪,通过分析不同频段线谱的能量特征,找出感兴趣的威胁目标并给出威胁目标的方位信息。
|
图 1 多目标中威胁目标方位的自动跟踪流程图 Fig. 1 Flow chart of automatic tracking of threat target position in multiple targets |
假设在
可以将
| ${X_k} = \left[ {\bigcup\limits_{x \in {X_{k - 1}}} {{S_{k|k - 1}}\left( x \right)} } \right] \cup \left[ {\bigcup\limits_{x \in {X_{k - 1}}} {{B_{k|k - 1}}\left( x \right)} } \right] \cup {{\rm{\varGamma }}_k}{\text{。}}$ | (1) |
其中,
以此类推,观测集
| ${Z_k} = {K_k} \cup \left[ {\bigcup\limits_{x \in {X_k}} {{{\rm{\Theta }}_k}\left( x \right)} } \right]{\text{,}}$ | (2) |
其中,
多目标系统需要满足以下3个假设条件[3]:
1)每个目标运动过程与其产生的观测彼此相互独立;
2)由先验概率预测获得的多目标随机有限集(RFS)遵循泊松分布;
3)杂波的随机有限集遵循泊松分布,并且与目标所产生的观测的随机有限集相互独立。
PHD滤波的基本递归方程如下:
| $ \begin{split} {v_{k|k - 1}}\left( x \right) =& \mathop \smallint \nolimits {P_{S,k}}\left( \xi \right){f_{k|k - 1}}\left( {x|\xi } \right){v_{k - 1}}\left( \xi \right)d\xi +\\ & \mathop \smallint \nolimits {\beta _{k|k - 1}}\left( {x|\xi } \right){v_{k - 1}}\left( \xi \right)d\xi + {\gamma _k}\left( x \right){\text{,}} \end{split} $ | (3) |
| $ \begin{split} {v_k}\left( x \right) =& \left[ {1 - {P_{D,k}}\left( x \right)} \right]{v_{k|k - 1}}\left( x \right) +\\ & \mathop \sum \limits_{z \in {Z_k}} \frac{{{P_{D,k}}\left( x \right){g_k}\left( {z|x} \right){v_{k|k - 1}}\left( x \right)}}{{{\kappa _k}\left( z \right) + \mathop \smallint \nolimits {P_{D,k}}\left( \xi \right){g_k}\left( {z|\xi } \right){v_{k|k - 1}}\left( \xi \right)d\xi }}{\text{。}} \end{split} $ | (4) |
式中:
将GM-PHD滤波器应用于被动声呐的目标跟踪,除了要遵循PHD滤波器的假设外,多目标的线性高斯模型应包括新生目标、消失目标、一直存在目标的3种情况。
被动声呐的观测范围为[0°,180°],目标状态变量用
在多目标的跟踪系统中,目标的运动状态模型遵循下式的线性高斯条件:
| ${f_{k|k - 1}}\left( {x|\xi } \right) = N\left( {x;{{{F}}_{k - 1}}\left( \xi \right),{Q_{k - 1}}} \right){\text{。}}$ | (5) |
其中:
目标的运动方程为:
| ${x_k} = {{{F}}_{k|k - 1}}{x_{k - 1}} + {w_{k - 1}}{\text{,}}$ | (6) |
其中,目标的状态转移矩阵
| $ {F_k} = \left[ {\begin{array}{*{20}{c}} 1&T \\ 0&1 \end{array}} \right],\;{{{Q}}_k} = \left[ {\begin{array}{*{20}{c}} {\dfrac{{{T^2}}}{2}} \\ T \end{array}} \right]{\sigma ^2}{\text{。}} $ |
其中,取
目标观测模型服从下式的线性高斯条件:
| ${g_k}\left( {z|x} \right) = N\left( {z;{H_k}x,{R_k}} \right){\text{,}}$ | (7) |
其中,
目标的观测方程为:
| ${z_k} = {H_k}{x_k} + {n_k}{\text{,}}$ | (8) |
其中,观测向量
假设每个目标的运动模型和观测模型都符合线性高斯模型,各目标的存活概率
1)预测
假设在
| ${v_{k - 1}}\left( x \right) = \sum\limits_{i = 1}^{{J_{k - 1}}} {w_{k - 1}^{\left( i \right)}} N\left( {x;m_{k - 1}^{\left( i \right)},P_{k - 1}^{\left( i \right)}} \right){\text{,}}$ | (9) |
在
| $\begin{split} {v_{k|k - 1}}\left( x \right) =& {v_{S,k|k - 1}}\left( x \right) + {v_{\beta ,k|k - 1}}\left( x \right) + {\gamma _k}\left( x \right) =\\ &{P_{S,k}}\mathop \sum \limits_{j = 1}^{{J_{k - 1}}} w_{k - 1}^{\left( j \right)}N\left( {x;m_{S,k|k - 1}^{\left( j \right)},P_{S,k|k - 1}^{\left( j \right)}} \right) +\\ &\mathop \sum \limits_{j = 1}^{{J_{k - 1}}} \mathop \sum \limits_{l = 1}^{{J_{\beta ,k}}} w_{k - 1}^{\left( j \right)}w_{\beta ,k}^{\left( l \right)}N\left( {x;m_{\beta ,k|k - 1}^{\left( {j,l} \right)},P_{\beta ,k|k - 1}^{\left( {j,l} \right)}} \right) +\\ &\mathop \sum \limits_{i = 1}^{{J_{\gamma ,k}}} w_{\gamma ,k}^{\left( i \right)}N\left( {x;m_{\gamma ,k}^{\left( i \right)},P_{\gamma ,k}^{\left( i \right)}} \right){\text{,}} \end{split}$ | (10) |
其中,可以利用卡尔曼滤波分别推导得到存活目标和衍生目标的高斯分量的预测均值和协方差:
| $m_{S,k|k - 1}^{\left( j \right)} = {F_{k - 1}}m_{k - 1}^{\left( j \right)}{\text{,}}$ | (11) |
| $P_{S,k|k - 1}^{\left( j \right)} = {Q_{k - 1}} + {F_{k - 1}}P_{k - 1}^{\left( j \right)}F_{k - 1}^{\rm{T}}{\text{,}}$ | (12) |
| $m_{\beta ,k|k - 1}^{\left( {j,l} \right)} = F_{\beta ,k|k - 1}^{\left( l \right)}m_{k - 1}^{\left( j \right)} + d_{\beta ,k|k - 1}^{\left( i \right)}{\text{,}}$ | (13) |
| $P_{\beta ,k|k - 1}^{\left( {j,l} \right)} = Q_{\beta ,k|k - 1}^{\left( l \right)} + F_{\beta ,k|k - 1}^{\left( l \right)}P_{\beta ,k|k - 1}^{\left( j \right)}{\left( {F_{\beta ,k|k - 1}^{\left( l \right)}} \right)^{\rm{T}}{\text{。}}}$ | (14) |
2)更新
根据卡尔曼滤波得到更新后的多目标概率假设密度(PHD)的高斯分量的特征参数如下:
| $q_k^{\left( j \right)}\left( z \right) = N\left( {z;{H_k}m_{k|k - 1}^{\left( j \right)},{R_k} + {H_k}P_{k|k - 1}^{\left( j \right)}H_k^{\rm{T}}} \right){\text{,}}$ | (15) |
| $m_{k|k}^{\left( j \right)}\left( z \right) = m_{k|k - 1}^{\left( j \right)} + K_k^{\left( j \right)}\left( {z - {H_k}m_{k|k - 1}^{\left( j \right)}} \right){\text{,}}$ | (16) |
| $P_{k|k}^{\left( j \right)} = \left[ {I - K_k^{\left( j \right)}{H_k}} \right]P_{k|k - 1}^{\left( j \right)}{\text{,}}$ | (17) |
| $K_k^{\left( j \right)} = P_{k|k - 1}^{\left( j \right)}H_k^T{\left( {{H_k}P_{k|k}^{\left( j \right)}H_k^T + {R_k}} \right)^{ - 1}}{\text{,}}$ | (18) |
由式(4)可得更新后的多目标概率假设密度(PHD)为:
| ${v_k}\left( x \right) = \left( {1 - {P_{D,k}}} \right){v_{k|k - 1}}\left( x \right) + \mathop \sum \limits_{z \in {Z_k}} {v_{D,k}}\left( {x;z} \right){\text{,}}$ | (19) |
其中:
| ${v_{D,k}}\left( {x;z} \right) = \mathop \sum \limits_{j = 1}^{{J_{k|k - 1}}} w_k^{\left( j \right)}\left( z \right)N\left( {x;m_{k|k}^{\left( j \right)},P_{k|k}^{\left( i \right)}} \right){\text{,}}$ | (20) |
| $w_k^{\left( j \right)}\left( z \right) = \frac{{{P_{D,k}}w_{k|k - 1}^{\left( j \right)}q_k^{\left( j \right)}\left( z \right)}}{{{\kappa _k}\left( z \right) + {P_{D,k}} \displaystyle\sum \nolimits_{l = 1}^{{J_{k|k - 1}}} \omega _{k|k - 1}^{\left( l \right)}q_k^{\left( l \right)}\left( z \right)}}{\text{。}}$ | (21) |
3)合并与裁剪
在GM-PHD滤波实现的过程中,随着时间的增加,后验概率的高斯项的数目会不断增多,所以需要通过对滤波后的高斯分量进行合并和裁剪来达到控制高斯项数目的目的[6]。可以通过设置合并阈值
经过对高斯混合分量的合并与裁剪,可以估计目标的数目为分量的权值之和
通过对多目标进行方位跟踪得到各个目标的方位信息后,对其进行功率谱估计,并进行频率归一化的计算,将标准化的频谱通过基于GM-PHD滤波的线谱跟踪器进行线谱跟踪。
基于GM-PHD滤波的线谱跟踪与2.2节中方位跟踪的区别在于,将目标的状态变量用
海试数据由拖曳式48元均匀线列阵采样获得,试验过程中合作目标包含丰富的线谱成分,方向由68°向57°变化,同时存在约15个干扰目标。图2为宽带能量检测检测图,图中包含给出个多个目标的轨迹,在实际应用中很难快速找出感兴趣的窄带线谱目标。

|
图 2 真实海试数据的宽带能量检测图 Fig. 2 Broadband energy detection map of real sea trial data |
|
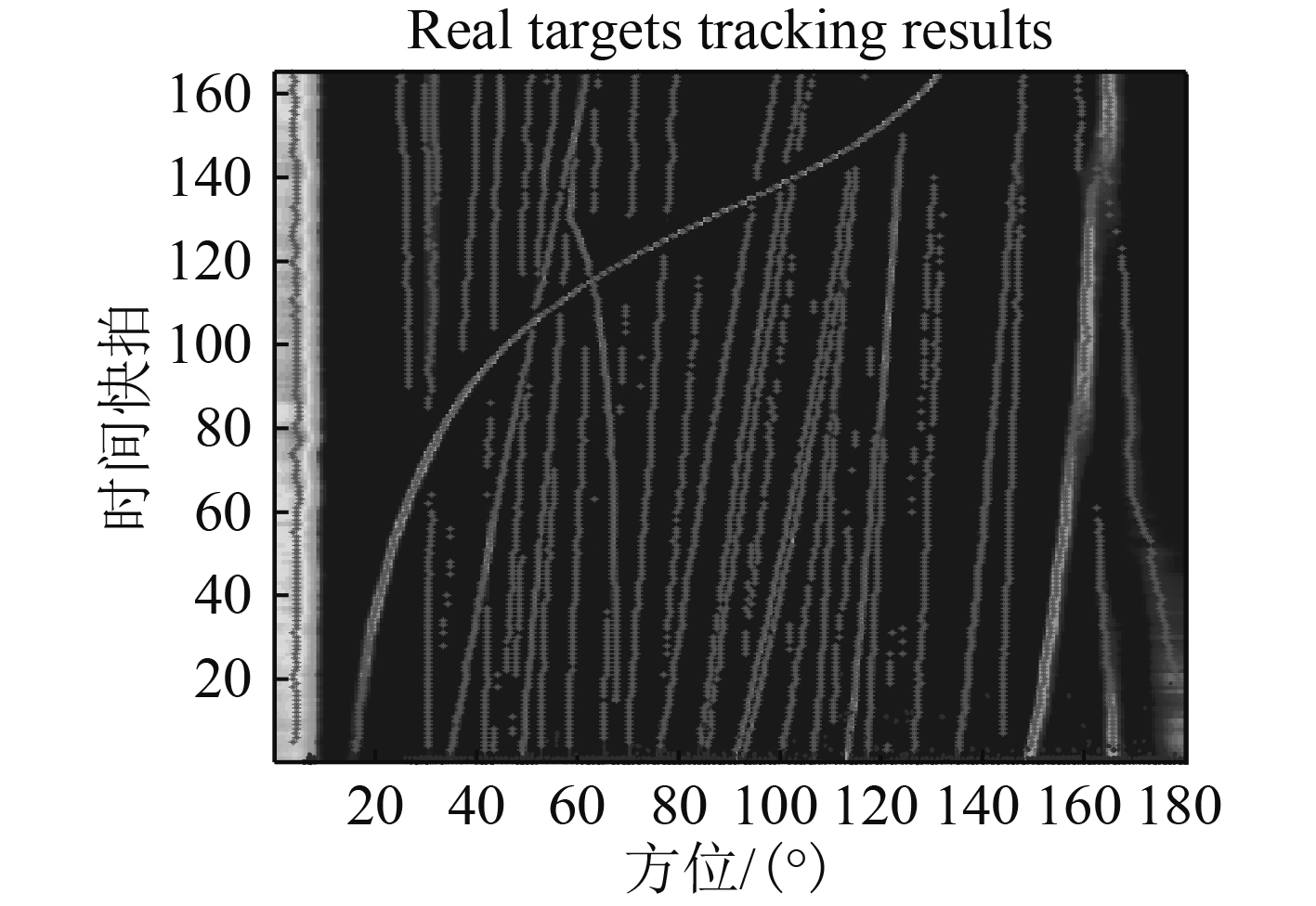
图 3 基于GM-PHD滤波器的真实海试数据的跟踪结果 Fig. 3 Tracking results of real sea trial data based on GM-PHD filter |
通过对所选区域所有存在目标的方位进行线谱特征分析,可以找出感兴趣的威胁目标,其时间方位历程图如图4所示。

|
图 4 威胁目标的时间方位历程图 Fig. 4 Time-bearing gragh of the threat target |
本文利用GM-PHD滤波算法在复杂情况下的被动声呐的多目标跟踪时的良好性能,建立目标运动与观测的随机有限集模型,有效地跟踪了多目标的方位轨迹,验证了高斯混合概率密度假设滤波跟踪算法可以在强杂波的条件下,对多目标交叉邻近、新目标衍生或新生、目标突然消失的多目标复杂情况进行有效跟踪。
本文基于此实现了复杂情况下多目标中威胁目标方位的自动跟踪,成功获取了威胁目标的时间方位历程图,有望在被动声呐中得到工程实用。
| [1] |
WILLETT P, LUGINBUHL T. MHT tracking for crossing sonar targets[C]. SPIE conference on Signal and Data Processing of Small Targets, 2007, 6(2): 66991C-66991C-12.
|
| [2] |
BAR-SHALOM Y, LI X R. Multitarget–multisensor tracking: principles and techniques[M]. Storrs, CT: YBS Publishing. 1995.
|
| [3] |
MAHLER R. Multitarget Bayes filtering via first-order multi–target moments[J]. IEEE Transactions on Aerospace and Electronic Systems, 2003, 39(4): 1152-1178. DOI:10.1109/TAES.2003.1261119 |
| [4] |
VOBN, MAWK. The Gaussian mixture probability hypothesis density filter[J]. IEEE Transactions on Signal Processing, 2006, 54(11): 4091-4104. DOI:10.1109/TSP.2006.881190 |
| [5] |
CLARK D, VOBN, BELL J. GM-PHD filter multi-target tracking in sonar images[C]. Defense and Security Symposium, 2006: 6235.
|
| [6] |
孟凡彬. 基于随机集理论的多目标跟踪技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2010. MENG F B. Research on the multi-target tracking techniques based on random set theory[D]. Harbin: Harbin Engineering University, 2010. |
| [7] |
朱宗斌, 陶剑锋, 葛辉良, 等. 一种基于GM-PHD滤波的纯方位多目标跟踪方法研究[J]. 声学技术, 2016, 490-495. ZHU Z B, TAO J F, GE H L, MENG Y Q, SHI C X. A bearings-only multi-targets tracking method based on GM-PHD filtering[J]. Editor Office of Technical Acoustics, 2016, 490-495. |
| [8] |
WAITE A D, 王德石(译). 实用声纳工程(第三版)[M]. 北京: 电子工业出版社, 2004.
|
| [9] |
蒋小勇, 谭君红, 周胜增. 分裂阵宽带相关检测在圆阵中应用[J]. 舰船科学技术, 2017, 39(8): 160-163. JIANG X Y, TAN J H, ZHOU S Z. An application of split-array broadband correlation detection in circular array[J]. Ship Science and Technology, 2017, 39(8): 160-163. DOI:10.3404/j.issn.1672-7649.2017.08.034 |
 2021, Vol. 43
2021, Vol. 43
