船用二冲程柴油机由于其高功率输出、对油品要求低、可靠性相对较高,在最近数十年的海运事业发展过程中成为大部分商用船舶的主要动力装置。据统计超过99%的大型商用船舶采用柴油机作为发动机[1],二冲程大缸径涡轮增压柴油发动机在海运船舶中占据主导地位。作为船舶的动力心脏,柴油机的运行状态决定着船舶是否能安全运行。船舶柴油机结构复杂,工作条件恶劣,在实际运营中时常发生故障。基于统计资料[2],船舶动力系统引发的故障占总体的85%。一旦柴油机发生故障,不仅会导致船舶动力装置无法正常工作,造成巨大的经济损失,甚至可能危及人身安全,造成重大事故。据日本船级社对220余艘船舶10年故障统计分析表明,船用柴油机的故障率大约是每小时0.4×10−3次。因此,船用柴油机的可靠性管理、监测和诊断技术的研究是船舶工程领域内的一项重要课题[3]。
裴大茗等[4]总结了近年来国内外船舶状态监测技术的进展情况,其中詹玉龙等[5]提出基于支持向量机的船舶柴油机故障诊断技术,牛晓晓等[6]提出基于神经网络的柴油机性能预测模型。以上方法均可以实现柴油机的状态监测以及故障诊断,但存在的普遍问题是:1)支持向量机或神经网络模型均需要大量数据训练并且需要不同方法调参或寻找合适的核函数,难以实现在线故障诊断;2)需要使用故障数据对模型进行训练。对于船用大型二冲程低速柴油机代价高昂,无法在实验室中使用试错法取得故障数据[7]。
为此提出基于自联想核回归(Auto Associative Kernel Regression,以下简称AAKR)模型的船舶柴油机运行状态监测方法。该方法是基于相似性建模方法中的一种,属于非参数建模技术,它利用记忆向量(memory vector)和样本向量之间的相似性来修正当前样本中出现的偏差,具有无需故障数据,只利用正常状态下的检测参数作为建模数据即可实现柴油机的状态监测,具有快捷高效的特点。
对于造价高昂且难以取得故障数据的大型二冲程低速柴油机,建立无需故障数据的柴油机状态监测方法十分必要。本文基于柴油机实验台架实验数据,对柴油机进行建模分析,并使用AAKR方法对柴油机模型进行状态监测。通过为模型设置不同的故障,测试AAKR监测方法的有效性,以期实现对柴油机性能的稳定监测,从而为船用低速柴油机状态监测和实时在线故障诊断探讨一种新的方法。
1 柴油机特性模拟本文以MAN B&W 6S35ME-B9型船用二冲程柴油机为研究对象,该机型的基本技术参数如表1所示。
|
|
表 1 MAN B&W 6S35ME-B9型机基本技术参数 Tab.1 Basic technical parameters of MAN B&W 6S35ME-B9 |
以柴油机参数为基础,柴油机实际运行数据为参考,对柴油机模型进行有效性判定。
1.1 柴油机建模柴油机的燃烧同时进行复杂的物理、化学、传质等反应,其工作过程十分复杂而又不可逆。因此,首先需要对实际工作过程进行简化,使之成为理想的热力循环,才能进行模拟计算。具体过程如下[8]:
1)气缸内工质状态均匀,忽略同一瞬间气缸内各点的压力、温度和工质浓度的差异。
2)工质为理想气体,其比热、内能仅与气体温度和气体成分相关。
3)将燃油的蒸发吸热与缸内的辐射传热等都放在传热系数中统一考虑。
4)空燃比的减少从燃烧开始到燃烧结束是逐渐进行的。
本文根据文献[9-13]所述方法并结合一维仿真软件GT-Power对柴油机进行建模。
1.2 模型有效性验证本文通过对MAN B&W 6S35ME-B9柴油机进行实机实验。在主机负荷为75%,单缸循环喷油量为10.285 g,转速为129 r/min的工况下,取得相应实验参数。随后与模型计算出的相应参数以及示功图进行对比,结果如表2和图1所示。其中曲轴转角的相对误差计算方法为绝对误差除以360°。
|
|
表 2 柴油机模拟计算值与实验实测数据对比 Tab.2 Comparison of simulated calculation values of diesel engine and experimental measured data |
|
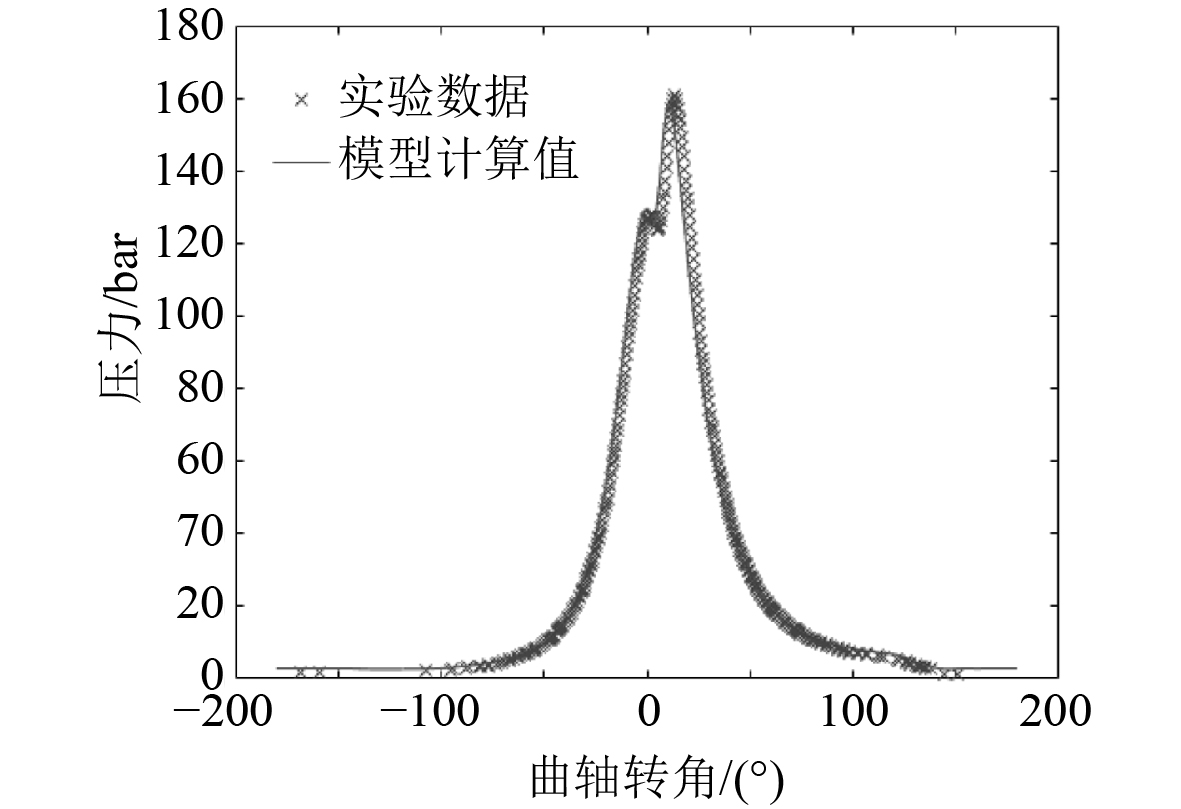
图 1 柴油机模拟计算值与实验实测数据缸压曲线对比图 Fig. 1 Comparison of simulated and calculated values of diesel engine and experimental measured data |
可见,模型计算值与实验台架实际测试数据对比结果误差均较小,总体看来模型十分理想。模型数据与实验数据相差不大,适用于本文实验研究。
2 自联想核回归算法(AAKR)AAKR是一种非参数的经验建模技术,它使用历史的无故障观测数据重构当前观测数据来校正其中出现的误差。用于开发经验模型的记忆向量存储在矩阵X中,其中xi,j是第i个观测数据中的第j个观测值。对于有nm个观测点的p个观测值数据,该记忆矩阵可写为:
| ${{X}} = \left[ {\begin{array}{*{20}{c}} {x_{1,1}^{}}&{x_{1,2}^{}}&{...}&{x_{1,p}^{}} \\ {x_{2,1}^{}}&{x_{2,2}^{}}&{...}&{x_{2,p}^{}} \\ \vdots & \vdots & \ddots & \vdots \\ {x_{n_m^{},1}^{}}&{x_{n_m^{},2}^{}}&{...}&{x_{n_m^{},p}^{}} \end{array}} \right]\text{,}$ | (1) |
由此可得,当前观测数据可以用1×p的向量来表示:
| ${{x}} = \left[ {\begin{array}{*{20}{c}} {x_{\rm{1}}^{}}&{x_2^{}}& \ldots &{x_p^{}} \end{array}} \right]\text{。}$ | (2) |
经验模型是根据记忆矩阵的加权平均值计算出当前观测值的重构向量,具体计算方法分为3步:
1)计算当前观测数据与记忆矩阵中每个记忆向量Xi的距离,并将计算结果记录在nm×1的距离向量d中。此处有多种距离函数可供选择,而最常用的欧氏距离为:
| $d_i^{}(X_i^{},{\rm{x}}) = \sqrt {(X_{i,1}^{} - x_{\rm{1}}^{})_{}^2 + (X_{i,2}^{} - x_{\rm{2}}^{})_{}^2 + \cdots + (X_{i,p}^{} - x_p^{})_{}^2}{\text{。}}$ | (3) |
2)将距离向量dn×1中的距离参数代入高斯核函数计算出相应权值,并得出nm×1的权值向量为:
| $w_i^{} = K_h^{}(d_i^{}) = \frac{1}{{\sqrt {2\text{π} } h}}e_{}^{\frac{{ - d_i^2}}{{2h_{}^2}}}{\text{。}}$ | (4) |
3)模型通过相似性系数(即权值wi)构造出记忆向量的加权平均值从而得出观测数据的预测向量,公式为:
| ${\bf{\hat x}} = \frac{{\displaystyle\sum\limits_{i = 1}^{n_m^{}} {(w_i^{} \cdot X_i^{})} }}{{\displaystyle\sum\limits_{i = 1}^{n_m^{}} {w_i^{}} }}\text{。}$ | (5) |
应该指出,AAKR模型是经验模型。不同的观测点和带宽h决定了模型的准确性,观测点的选择和带宽的确定将在下面讨论。记忆矩阵X中应尽可能多的包含柴油机当前工况下的正常情况观测值作为记忆向量。柴油机工况发生变化后,若记忆矩阵中未包含当前工况下的任何观测值,则模型失效,应该用新的观测值填充记忆矩阵X或使用新的记忆矩阵X' 替换X。
当前观测值与模型重构向量的差异反映了柴油机的正常程度,均方误差(mean-square error,MSE)是反映估计量与被估计量之间差异程度的一种度量。对单一变量给出方差:
| $MSE = \frac{1}{{n_m^{}}}\sum\limits_{i = 1}^{n_m^{}} {(\hat x_i^{} - x_i^{})_{}^{\rm{2}}}\text{,} $ | (6) |
式中x为当前观测值向量。该指标越大表明当前柴油机运行状态越差,该指标越接近于0表明柴油机运行状态越接近正常。当前观测值与模型重构向量的均方误差在控制限σlim内,即MSE<σlim时,监测模型判定当前状态为正常。若超过了控制限,即MSE>=σlim时,监测模型判定当前柴油机处于异常状态或产生报警,控制限σlim的取值通过经验或模型的性能来确定。
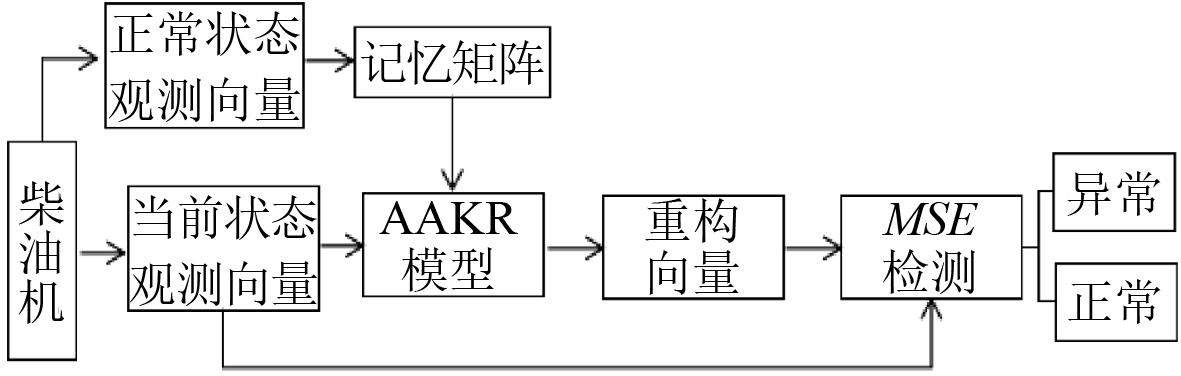
3 柴油机状态监测 3.1 AAKR状态监测方法利用正常状态下的观测向量组成记忆矩阵X建立AAKR经验模型,通过不断监测当前观测值向量与模型重构向量的均方误差,判断其是否超过正常状态控制限σlim从而判定柴油机当前运行状态是否正常,以此达到对柴油机进行状态监测的目的。AAKR状态监测方法流程图如图2所示,其中正常状态观测向量的测取和记忆矩阵的生成应在状态监测前完成。
|
图 2 AAKR状态监测流程图 Fig. 2 AAKR status monitoring flow chart |
记忆矩阵X决定了AAKR模型的可用性,而测点的多少决定了记忆矩阵X的观测范围。测点过少会导致模型不准确,某些故障无法得到反映,导致模型可信度下降。测点过多导致记忆矩阵过大,计算负荷过高,降低模型实时性与实用性。对柴油机进行状态监测可以广泛选用各种数据。本文主要验证AAKR状态监测模型的有效性,通过监测柴油机缸压曲线图对柴油机运行状态进行判断,通过对比不同测点数量的记忆矩阵所对应AAKR模型的优劣,从而将测点确定在最佳范围内。
带宽的选择会影响模型的连续性,合适的带宽可以使模型产生连续的重构向量。而某些带宽下模型无法对观测向量进行重构。带宽的选择需要一定的经验,本文采用0.02,0.05,0.1,0.2,0.5,1.0不同的带宽进行实验。
AAKR模型对当前柴油机运行状态的反映通过均方误差体现。本文通过对正常状态下的柴油机进行观测,取其观测量的偏差值σmax上限增加10%作为均方误差控制限σlim。超过控制限的观测值则会触发异常报警。
3.3 故障设置通过设置不同的故障,检测AAKR模型的有效性。本文设置供油不足、中冷器温度高、喷油角提前、喷油角延迟、排气系数低5种常见柴油机故障,具体故障参数如表3所示。
|
|
表 3 柴油机故障设置表 Tab.3 Diesel engine fault setting table |
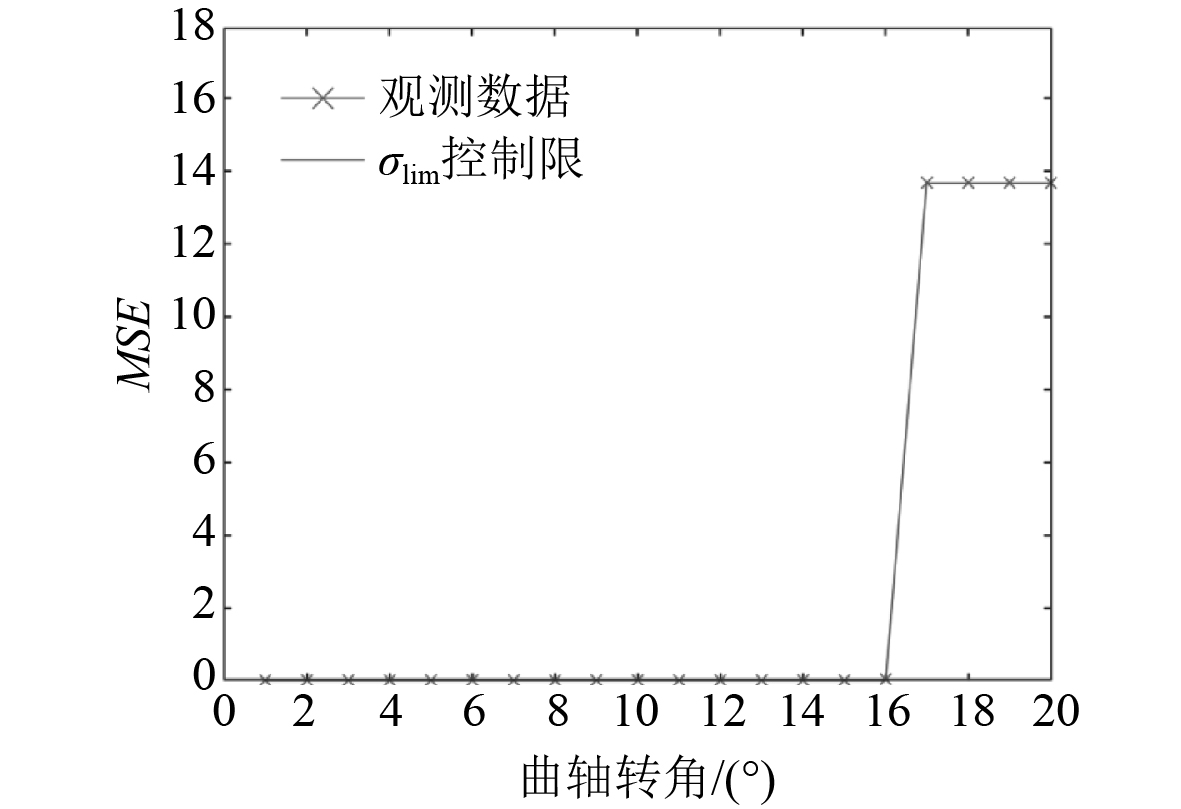
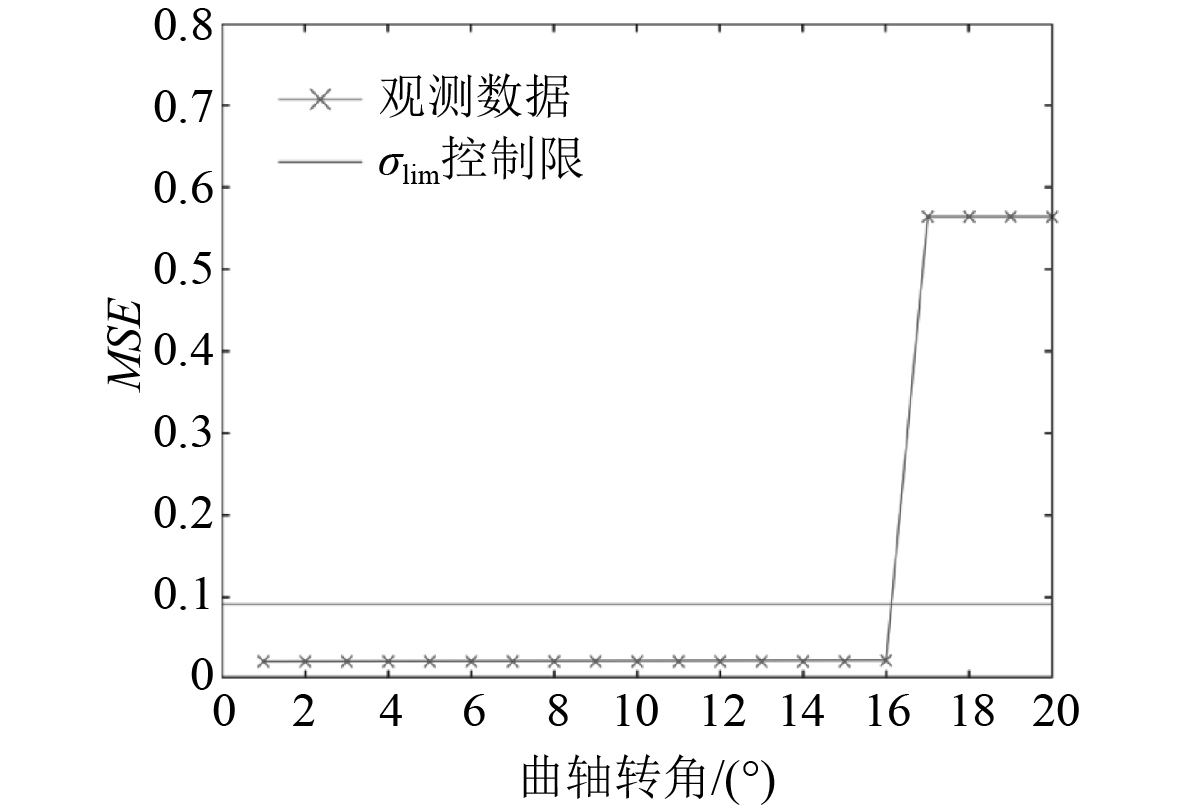
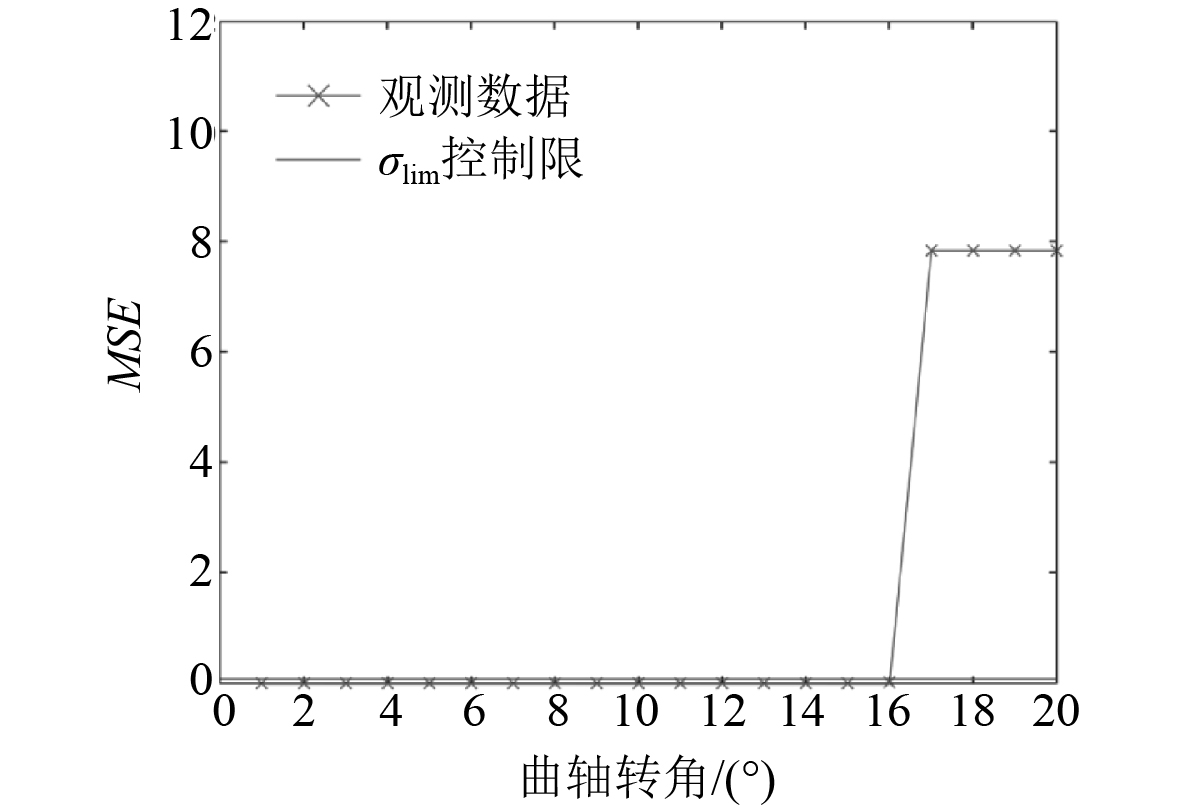
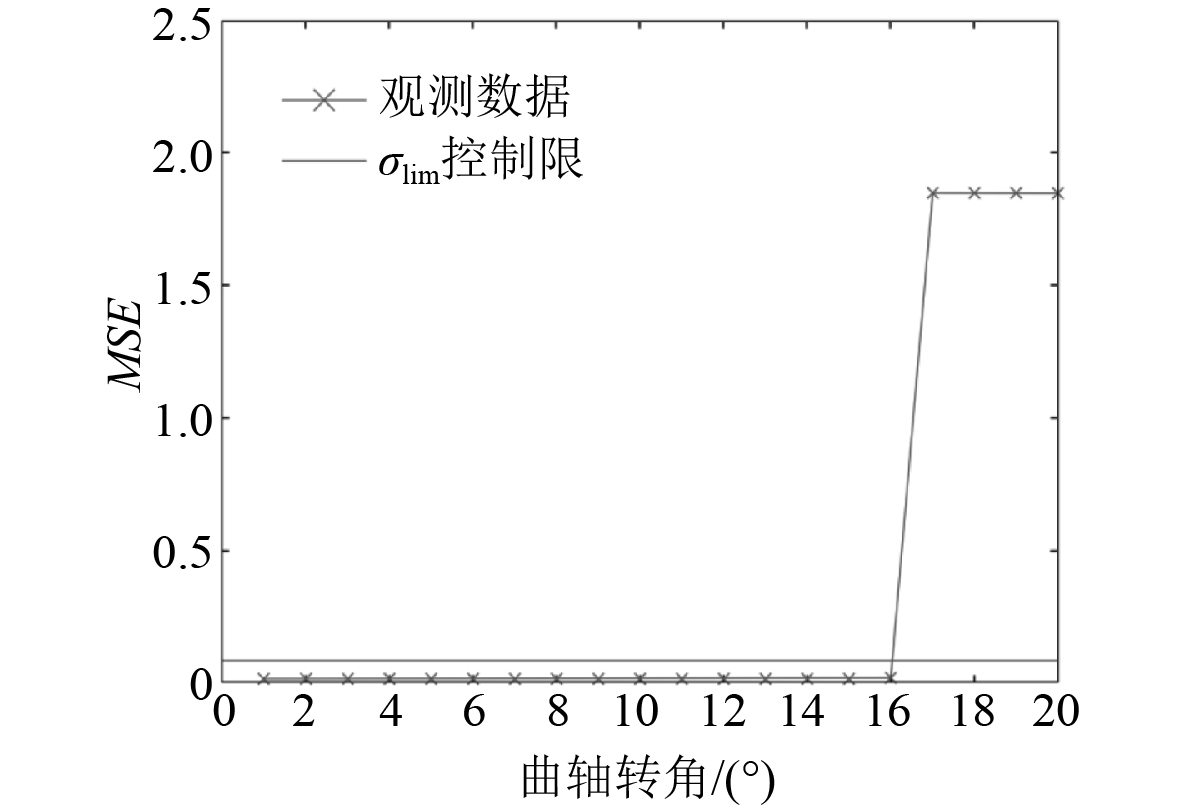
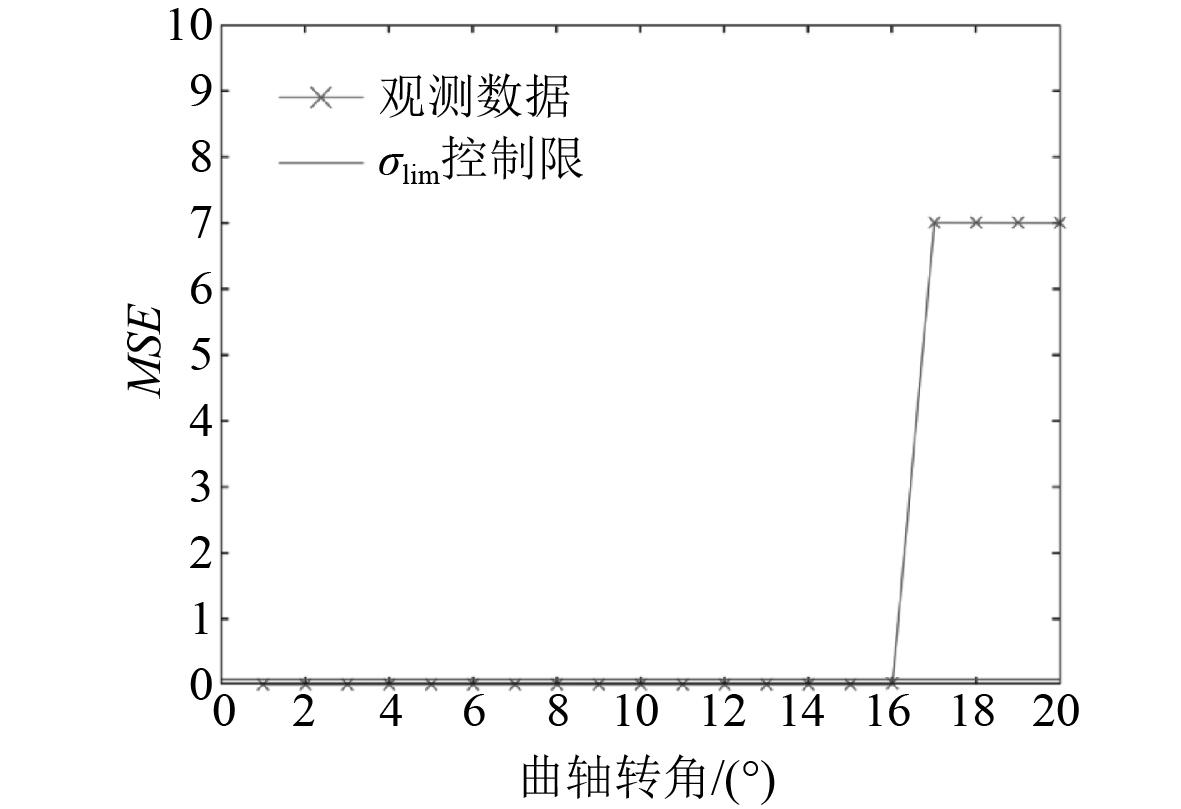
本文利用计算机对前面建立的柴油机模型进行状态监测模拟,在模型以正常状态运转后进行随机故障模型,测试AAKR状态监测模型的有效性。设置监测时长为20 s,每隔1s进行一次监测。为了方便观测,设置故障出现时间为17 s。带宽h设置为0.05,监测曲轴转角−180°CA到180°CA范围内缸内压力,步长为1,监测点数为360。监测结果如图3~图7所示。结果显示,采油机正常状态下的MSE值均较低,最大值仅为0.0833。控制限设置为0.0913。故障状态下的MSE值除故障2外其余均较大,由于故障2中冷器温度变化不大,所以故障状态并不明显,其MSE为0.5599。图中可见,各种故障条件下,柴油机观测值MSE远超控制限σlim,均触发异常报警,证明AAKR状态监测模型可有效对柴油机进行状态监测。
|
图 3 供油不足故障监测结果 Fig. 3 Insufficient oil supply failure monitoring result |
|
图 4 中冷器温度高故障监测结果 Fig. 4 Inter cooler temperature high fault monitoring results |
|
图 5 喷油提前故障监测结果 Fig. 5 Fuel injection timing advance fault monitoring result |
|
图 6 喷油延迟故障监测结果 Fig. 6 Fuel injection delay fault monitoring result |
|
图 7 排气系数低故障监测结果 Fig. 7 Low exhaust coefficient fault monitoring result |
不同的带宽可以影响AAKR观测模型的性能,较大的带宽模型灵敏度较高,但容易出现超限错误导致模型无法正常产生重构向量。太小的带宽会导致模型监测不准确,导致错误报警或检测不到异常。本文选择不同步长下的10组正常状态观测值和5个故障状态下的观测值进行探究,通过比较其MSE的变化讨论带宽h的取值范围,结果如表4所示。
|
|
表 4 不同带宽下MSE结果对比 Tab.4 Comparison MSE results under different bandwidths |
可以看出,带宽越大异常与正常状态的MSE差值越大,AAKR监测到的异常也越明显。说明提高带宽可以提高模型的灵敏度。但是从表中可以看出,在带宽h=0.5时正常状态下的MSE已经很小,此时模型已经可以对实验对象进行有效的状态监测。当带宽h=1时出现了AAKR无法正常对异常状态观测值进行向量重构的问题,说明过高的灵敏度会导致AAKR模型失效。当带宽h小于0.2时MSE变化不明显,说明过小的带宽对应的模型灵明度太低,无法正常对实验对象进行状态监测。通过测试说明,带宽选择在0.5左右比较合适。在不确定AAKR模型性能的情况下,带宽应选择一个较小的值。只有模型灵敏度无法满足监测要求时再适当增大带宽值。
4 结 语对仿真模型进行模拟状态监测的实验证明,AAKR模型可以在无故障数据的前提下对柴油机进行状态监测,克服了其他智能算法需要对模型调参和使用故障数据训练模型的问题。在不确定AAKR模型性能的情况下,初始带宽应选择一个较小的值。如果模型灵敏度无法满足监测要求可适当增大带宽值。在对不同带宽进行测试后发现,带宽选取在0.5左右时本文模型状态较佳。
本文通过实验表明,AAKR是一种行之有效的柴油机状态监测方法,其无需故障数据的特性使其有更强的广泛性。该方法简便快捷的特点使之可以应用于船舶的在线状态监测和预警中。
| [1] |
LAMARIS V T, HOUNTALAS D T. A general purpose diagnostic technique for marine diesel engines–Application on the main propulsion and auxiliary diesel units of a marine vessel[J]. Energy Conversion and Management, 2010, 51(4): 740-753. DOI:10.1016/j.enconman.2009.10.031 |
| [2] |
李伟峰, 王磊. 船舶机械设备的常见故障及状态监测与诊断技术研究[J]. 自动化与仪器仪表, 2018(6): 32-34. |
| [3] |
王洪锋. 船用智能化柴油机热力参数监测与诊断技术研究[D]. 武汉: 武汉理工大学, 2008.
|
| [4] |
裴大茗, 王建峰, 周鹏太, 等. 船舶PHM技术综述[J]. 电子测量与仪器学报, 2016, 30(9): 1289-1297. |
| [5] |
关文锦, 杜群贵, 刘丕群. 橡胶O形圈密封性能的有限元分析[J]. 润滑与密封, 2012, 37(6): 60-64. DOI:10.3969/j.issn.0254-0150.2012.06.014 |
| [6] |
PERL M. Steiner M. 3-D stress intensity factors due to full autofrettage for inner radial or coplanar crack arrays and ring cracks in a spherical pressure vessel[J]. Engineering Fracture Mechanics, 2015, 138: 233-249. DOI:10.1016/j.engfracmech.2015.03.007 |
| [7] |
周赛群. 全断面硬岩掘进机(TBM)驱动系统的研究[D]. 杭州: 浙江大学, 2008.
|
| [8] |
肖宏, 杨霞, 陈泽军, 等. 赫兹接触理论在采用边界元法分析轧机轴承载荷中的应用[J]. 中国机械工程, 2010, 21(21): 2532-2535. |
| [9] |
高耀东. Ansys机械工程应用精华50例(第3版)[M]. 北京: 电子工业出版社, 2011: 20−30.
|
| [10] |
郦正能, 关志东, 张纪奎, 等. 应用断裂力学[M]. 北京: 北京航空航天大学出版社, 2012: 30−40.
|
| [11] |
刘学平, 庞祖富, 向东. 废旧塑封芯片分层裂纹仿真[J]. 中国机械工程, 2015, 26(2): 143-146. DOI:10.3969/j.issn.1004-132X.2015.02.001 |
| [12] |
ERIKSSON A, NORDMARK A. Non-unique response of mooney-rivlin model in bi-axial membrane stress[J]. Computers & Structures, 2014, 144: 12-22. |
| [13] |
MORRELL P R, PATEL M, SKINNER A R. Accelerated thermal ageing studies on nitrile rubber O-rings[J]. Polymer Testing, 2003, 22(6): 651-656. DOI:10.1016/S0142-9418(02)00171-X |
 2021, Vol. 43
2021, Vol. 43
