2. 海军工程大学 动力工程学院,湖北 武汉 430033
2. College of Power Engineering, Naval University of Engineering, Wuhan 430033, China
船舶柴油机气缸套的内表面因直接受到高温燃气的冲击,会承受极高的热负荷;同时,内表面是活塞组往复运动的接触面,其在工作过程中除受到高温燃气的爆炸压力外,还受到缸盖螺栓的预载荷和活塞的侧向推力。因此,缸套在运行期间同时承受热负荷和机械负荷。如果单独计算热负荷或机械负荷,则不能很好地反映缸套的实际负荷情况。利用有限元分析软件,耦合计算缸套在温度场、应力场综合作用下的应力和变型,有利于更加精确分析缸套的疲劳寿命,为缸套的结构设计、制造、强度校核及疲劳寿命分析提供参考依据[1]。
1 气缸套有限元模型与网格根据某型柴油机缸套几何模型的计算特点,删除部分圆角、倒角和小圆孔等对计算结果影响很小却影响网格划分的细节特征[2],对简化后的几何模型进行分区处理,将缸套内表面及外表面按照不同的边界条件加载要求分成不同的求解区域[3],然后进行自动四面体网格划分,最终划分的网格节点757557个、单元496543个、最大单元尺寸14.069 mm,最小单元尺寸2.8139 mm,如图1和图2所示。

|
图 1 缸套几何实体 Fig. 1 Cylinder liner geometry |

|
图 2 缸套网格 Fig. 2 Cylinder liner grid |
在三维传热问题中,稳态温度场应满足没有内部热源的笛卡尔坐标系中的微分方程:
| $\frac{{{\partial ^{\rm{2}}}{\rm{t}}}}{{\partial {x^2}}} + \frac{{{\partial ^2}t}}{{\partial {y^2}}} + \frac{{{\partial ^2}t}}{{\partial {z^2}}} = 0 {\text{。}}$ | (1) |
其中:t是温度场中的点的温度值;(x,y,z)是三维笛卡尔坐标系中的点的坐标值。方程(1)必须在相应的边界条件下才能求解。在本文中,第3种边界条件用于边界面的传热计算,如下式:
| ${\rm{ - }}{\lambda _{\rm{s}}}{(\frac{{\partial t}}{{\partial n}})_w} = h({t_w} - {t_f}){\text{。}}$ | (2) |
式中:tf为外界流体温度;tw为固体的壁面温度;λs为固体的热导率;h为边界面的对流换热系数。
设置单元属性为SOLID70热分析单元。缸套本体材料为球墨铸铁,压紧环、止推环及水套环的材料为合金钢,设置材料属性见表1,各装配体的接触关系设置为BOUNDED。
|
|
表 1 缸套本体材料属性 Tab.1 Material properties of cylinder liner body |
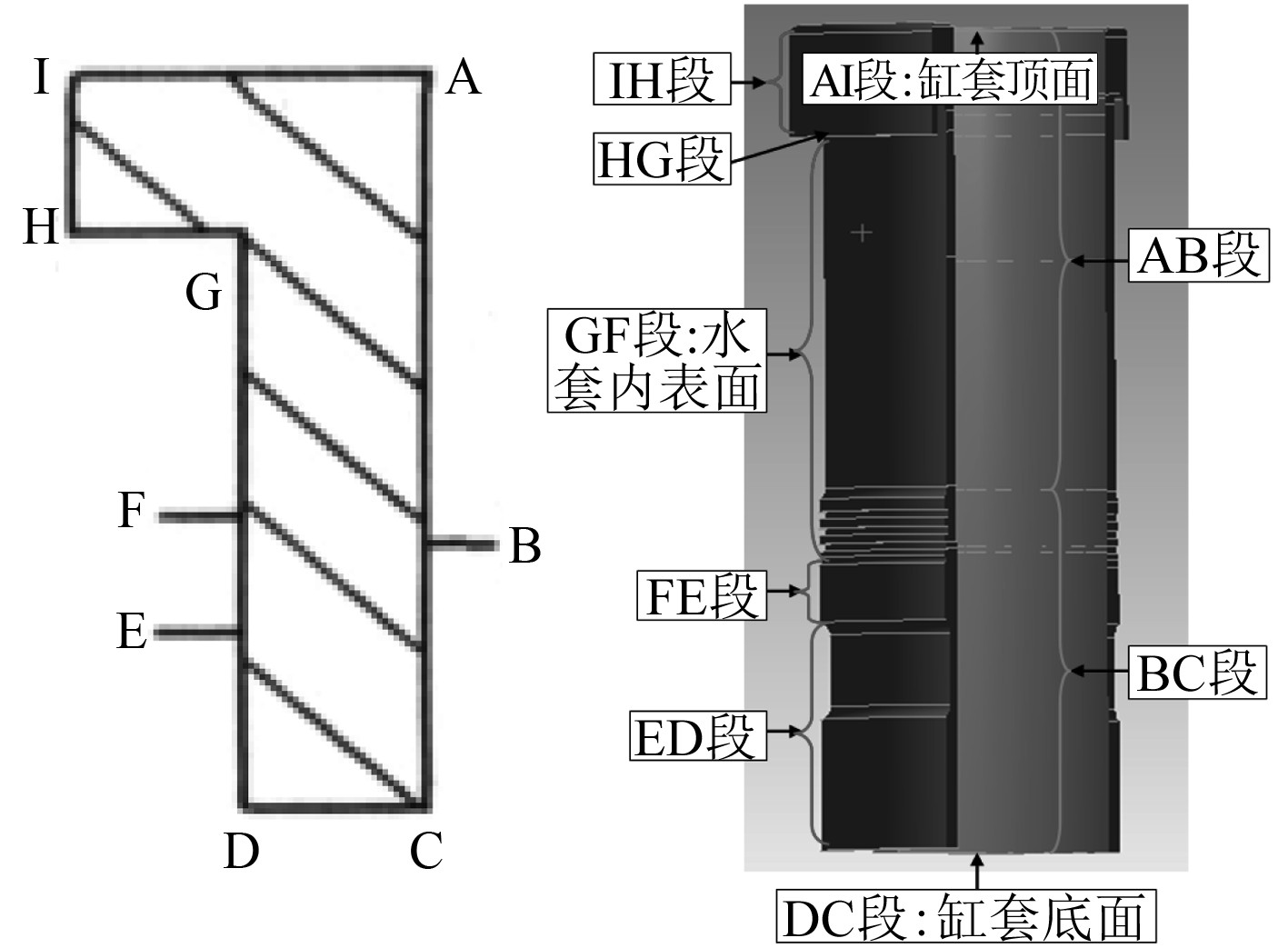
|
图 3 缸套本体分区图和示意图 Fig. 3 Block block diagram and schematic diagram of cylinder liner body |
1)AB段的边界条件(活塞上死点到下死点)
计算燃气换热系数αg与曲轴转角的对应关系,如下式:
| ${\alpha _{\rm{g}}} = {k_0} \cdot \sqrt {{C_m}} \cdot \sqrt {{P_g} \cdot {T_g}} {\text{。}}$ | (3) |
其中,修正系数k0由机型确定,取值1.95;活塞平均速度Cm=9.5 m/s,缸内气体瞬时压力为Pg,缸内气体瞬时温度为Tg。将AVL BOOST软件用于计算气缸中的一维工作过程[2],得到了缸内一个工作循环的曲柄角压力、温度和对流换热系数的变化,具体工况如表2所示。缸内压力、温度和对流换热系数随曲轴转角变化情况见文献[2]。
|
|
表 2 工况列表 Tab.2 Working condition list |
为满足第三类边界条件,必须获得稳态温度场,这就需要对瞬态过程的燃气温度和对流换热系数进行加权平均。因此,使用等式(4),气缸中的温度和对流传热系数分别取加权平均值[6]:
| ${f_m} = \frac{1}{{4\text{π} }}\int_0^{4\text{π} } {f(\theta )} \cdot {\rm{d}}\varphi {\text{。}}$ | (4) |
其中:f(θ)代表一个瞬时值,它可以是缸内温度,也可以是对流换热系数;fm为各自的循环平均值,燃气的加权平均温度为744 K,对流换热系数562 W/(m2·K)。最后,AB段的传热系数和介质温度由柴油机缸套内表面在轴向高度处的稳态传热边界条件的分布规律确定,如下式:
| $ {\alpha _m}(h) = {\alpha _m}(0) \cdot (1 + {K_1}\beta ) \cdot {e^{\sqrt[{ - 3}]{\beta }}} \text{,} $ | (5) |
| $ {T_{res}}(h) = {T_{res}}(0) \cdot (1 + {K_2}\beta ) \cdot {e^{\sqrt[3]{\beta }}} \text{。} $ | (6) |
式中:β=h/S,
2)BC段边界条件
在活塞的下死点下方,由于它不与燃气接触,因此热交换量很小,采用第一种边界条件,固定温度为380 K。
3)IH,HG段边界条件
IH,HG两段互相接触,所以截面的传热系数由缸套和机体热阻共同决定,参考同型号机,IH段的换热系数取1000 W/(m2·K),HG段换热系数取4000 W/(m2·K)。机架温度Tf可由实验测量或按经验公式
4)GF段边界条件
GF段被冷却水包围,机体水套和缸盖水套接触面的换热系数aw由循环水的流动特性、缸套的表面特性共同决定。由宗涅肯公式计算:
| ${a_w} = 300 + 1\;800\sqrt {{W_m}} \text{。} $ | (7) |
式中:Wm为冷却水的流速,m/s;冷却水的温度为358.15 K。
5)FE,ED段边界条件
FE及ED段与机体分别为接触配合和间隙配合,换热量均较小,参考同类机型,分取换热系数115 W/(m2·K)和100 W/(m2·K),机体温度取380 K。
6)CD,AI段边界条件
CD部分和AI部分分别是缸套本体的上表面和下表面,其中与介质的热交换很小,因此它们被认为是绝热。
7)其他表面边界条件
水套的传热分为4个区域,与冷却水接触的表面的传热边界与缸套主体的GF部分的值相同;水套环的外表面与缸套主体的ED段取值相同;入口孔表面的传热边界与缸套主体的GF部分相同; 其他零部件的外表面作绝热处理,与机体接触的内表面按接触热阻处理。
|
|
表 3 热分析的边界条件 Tab.3 Boundary conditions for thermal analysis |
将表3的热边界条件加载到热分析模型中,获得缸套的温度场,如图4所示。缸套最高温度为533.89 K(260 ℃),最低温度为354.71 K(82 ℃),最高温度出现在缸套内表面与燃烧室和上表面接触的边缘且远离上水孔的区域,此处因受高温燃气的不断加热,故温度最高;最低温度出现在与水腔位于同一高度的水套环外表面,此处由于水腔的存在,热量不能传递,但冷却水充分冷却,因此温度最低。缸套温度分布规律大致为内表面沿轴向从上到下逐渐降低,缸套上部沿径向从内表面到外表面逐渐降低;缸套组件中离水腔较近的外表面由于得到冷却水的充分冷却,温度普遍低于外表面的其他区域。

|
图 4 缸套温度场 Fig. 4 Cylinder liner temperature field |
转换分析单元,缸套最大热应力为231.43 MPa,分布在气缸螺栓孔的上部,从顶部到底部,缸套的热应力逐渐减小,如图5所示。

|
图 5 缸套热应力结果 Fig. 5 Thermal stress result of cylinder liner |
缸套热变形量在热负荷下的分析结果如图6所示,缸套的最大热变形为0.64188 mm。最大变形量位于缸套顶面上的两螺栓孔之间,此处离燃烧室内壁面较近,且没有上水孔进行冷却,因此温度最高,热变形量最大。从整体来看,缸套热变形量最大的区域主要集中在温度较高的缸套顶部的小片区域,汽缸套的变形大致以轴对称的方式分布。变形量在轴向上从顶部到底部增加。最小热变形量区域位于缸套中间的入口孔高度的环形区域中。此区域远离燃烧室,受高温气体的影响较小,已被衬里的冷却水完全冷却,故热变形量最小。

|
图 6 缸套的热变形结果 Fig. 6 Thermal deformation result of cylinder liner |
将软件的单位类型从SOLID70热分析单元转换为SOLID185结构分析单元。其中,机械负荷的主要成分为缸盖预压和气压。
1)缸套内壁燃气作用
首环以上部位为Pz;对应于第1环的气缸壁的气体压力为0.76Pz;气体压力可以从第1环下方的部分到第2环的相应部分近似为0.20Pz;第2环下方到最后一个气环的气缸套部分可近似为0.076Pz;最后一个气环基本上不受燃烧气体压力的影响。
2)螺栓预紧力
螺栓预紧力作用于柴油机缸套上每个预紧力矩为0.15 kN·m的7个固定螺栓上,按照式(8)计算单个螺栓的预紧力:
| ${M_t} = k \cdot {p_0} \cdot d \cdot 0.001 \text{。}$ | (8) |
其中:Mt为预紧力矩,k为拧紧力系数,p0为预紧力,螺纹公称直径d=21 mm,对于无摩擦的一般机加工表面,k的取值一般为0.18~0.21,最后将计算的7倍预载荷加载在汽缸套的上表面上。
3.2 机械应力计算结果将缸套内壁面的燃气压力及螺栓预紧力施加于缸套有限元模型,得出缸套的机械应力场。在纯机械载荷作用下,缸套的应力值相对较小,最大应力为50.074 MPa。最大机械应力均分布在缸套内表面和上表面的交界处以及螺栓孔壁面上,如图7所示。

|
图 7 缸套机械应力计算结果 Fig. 7 Mechanical stress calculation of cylinder liner |
机械载荷几乎不会使缸套发生变形,缸套在机械载荷下的最大变形量为0.0047458 mm,最大变形幅度均分布于缸套内表面的第一道环槽以上部分以及缸套内壁面与螺栓孔之间的薄壁部分,原因是缸套内表面对应于第一道环槽以上部分所承受的缸内压力最大,壁面与螺栓孔壁面所围成的部分壁厚更薄,抵抗变形能力更差,如图8所示。

|
图 8 缸套的机械变形 Fig. 8 Mechanical deformation of cylinder liner |
根据计算结果,气压随气缸内工作循环中曲柄转角的变化而变化。将气缸温度场计算结果作为温度负载加载到气缸套有限元模型中,在缸套上表面加载螺栓预紧力以及在缸套内表面沿轴向分区加载燃气压力,如图9所示。气缸套在热-机械耦合下的最大应力为383.47 MPa,最大热-机耦合应力分布于缸套内表面与上表面的交界处。缸套螺栓孔的根部区域由于应力集中,热-机耦合应力值也比较大。气缸套整体耦合应力最大值不超过材料的极限应力(球墨铸铁的抗拉强度约为446~551 MPa,合金钢的屈服强度约为800 MPa)。

|
图 9 缸套热-机耦合应力 Fig. 9 Thermal-mechanical coupling stress of cylinder liner |
缸套在热机耦合下的整体变形趋势与每个方向的变形趋势基本相同,最大变形为0.6824 mm,最大变形量位于缸套顶面上的两螺栓孔之间,此处离燃烧室内壁面较近且没有冷却水,因此温度最高,变形量最大。从变形的方向来看,缸套主要沿轴向变形并沿轴线分布。Y方向的变形量主要集中在气缸套的顶部,最大轴向变形量为0.51168 mm。缸套沿 X,Y向的变形量均比较小,变形区域主要集中在缸套温度最高的一小片区域,缸套的径向变形量为0.47737 mm,活塞的最大变形为0.41813 mm,最大相对变形量为0.05924 mm,远小于活塞和气缸套之间的匹配间隙,因此活塞环不会卡住或折断;缸套和活塞的轴向相对变形为0.00643 mm。相对变形量非常小,且轴向相对变形对缸套和活塞的装配关系影响不大,缸套和活塞的配合满足要求,如图10所示。

|
图 10 缸套的热-机耦合变形结果 Fig. 10 Thermal-mechanical coupling deformation results of cylinder liner |
利用DANG VAN疲劳理论对气缸套的疲劳安全系数进行计算,最有可能疲劳破坏的部位位于缸套上部螺栓孔根部所处高度的平面、水套最底面以及缸套上表面外沿部分。原因是螺栓孔根部的应力集中比较严重、水套根部温度梯度较大、缸套上表面外沿部分受热膨胀的预应力较大以及循环载荷作用下产生拉伸,相比其他部位,上述3个部位疲劳安全系数较小。计算结果表明,缸套的最小疲劳安全系数为2.653,大于1,符合设计要求,如图11所示。

|
图 11 缸套结构的疲劳安全系数云图 Fig. 11 Fatigue safety factor nephogram of cylinder liner structure |
1)在某指定工况下,缸套组件最高温度出现在缸套与燃烧室接触的内表面与上表面接触边缘,且远离上水孔的区域;缸套本体的最高温度约为261 ℃,未超过球墨铸铁的蠕变温度(约540 ℃),冷却水环的最高温度约为186 ℃,低于合金钢的蠕变温度(约400 ℃)。缸套组件在温度载荷下安全。
2)最大热应力分布于气缸螺栓孔的上部,大小为231.43 MPa,远低于缸套材料的抗拉强度(446~551 MPa);缸套的最大热变形为0.64188 mm,位于气缸套顶面上的2个螺栓孔之间。主要变形为轴向变形,热变形对缸套与活塞环组的装配关系影响不大。
3)缸套在纯机械载荷作用下具有较小的应力值,最大应力为50.074 MPa,最大机械应力分布在气缸套内表面和上表面与螺栓孔壁面之间的边界处;气缸套在机械载荷作用下的变形很小,最大变形量为0.0047458 mm。
4)热-机械耦合下缸套的最大应力为383.47 MPa,分布于缸套内表面与上表面交界处,缸套螺栓孔的根部区域应力较为集中,耦合应力的最大值不超过材料的极限应力。
5)缸套的最小疲劳安全系数为2.653,满足设计要求,最有可能发生疲劳破坏的部位位于缸套上部螺栓孔根部所处的高度平面、水套最底面所处平面及缸套上表面外沿部分。
计算结果如表4所示。
|
|
表 4 计算结果汇总 Tab.4 Summary of calculation results |
| [1] |
胡祝昌. 基于多场耦合分析的柴油机气缸盖结构仿真研究及疲劳寿命预测[D]. 太原: 中北大学, 2012.
|
| [2] |
伍鹏, 赵建华, 刘琦, 等. 基于热-机耦合的柴油机气缸盖强度研究[J]. 兵器装备 工程学报, 2016, 37(10): 158-163. |
| [3] |
曹海滨, 王家宏. 船用6300柴油机缸套热负荷的有限元分析[J]. 浙江海洋学院学报(自然科学版), 2006(4): 414-416. DOI:10.3969/j.issn.1008-830X.2006.04.012 |
| [4] |
付月磊, 苏铁熊, 张丽强, 等. 150型柴油机气缸套温度场有限元分析[J]. 内燃机车, 2010(1): 22−24+54. FU.
|
| [5] |
张国成. 温度对柴油机曲轴—连杆—活塞的力学性能影响研究[D]. 沈阳: 东北大学, 2012.
|
| [6] |
吕建明, 欧阳光耀, 张萍. 某高功率密度柴油机气缸套热-结构耦合分析[J]. 船海工程, 2011, 40(5): 73−75. LV.
|
 2021, Vol. 43
2021, Vol. 43

