2. 高新船舶与深海开发装备协同创新中心,上海 200240;
3. 船舶与海工程水动力湖北省重点实验室,湖北 武汉 430074
2. Collaboration Innovation Center for Advanced Ship and Deep-Sea Exploration, Shanghai 200240, China;
3. Hubei Key Laboratory of Naval Architecture and Ocean Engineering Hydrodynamics, Wuhan 430074, China
在船舶设计过程中船机桨能否良好的匹配取决于主机功率的选择和航速的预报,而能否恰当地选择主机功率并准确地预报航速关键在于有效功率的预报是否准确。
在船舶主机功率估算方面通常有2种做法:一是参考与研究船舶具有相似船型、尺寸和载重吨的船舶主机功率进行近似地选取; 二是基于船舶阻力的估算方法进行计算[1]。基于船舶阻力的估算方法通常通过模型试验或是CFD(computational fluid dynamics)计算得到船舶的阻力[2-3]。两种方法各有特点:模型试验方法得到的阻力更加准确,但需要制作模型、专门的实验设备及场地等,需要大量的人力物力;CFD计算则更加方便快捷,但采取不同的软件进行计算所得的结果会有差异,工作量和工作效率也略有不同。因此为了提高船舶有效功率预报的效率并保证其准确性,本文以某船为研究对象,采用Star-CCM+软件对其缩比模型进行了阻力计算,再通过换算得到其实船阻力及有效功率,并与模型试验的结果进行对比验证其准确性,为船舶有效功率的计算提供一定的参考。
1 计算对象 1.1 计算对象介绍本文对某LPG运输船在指定航速下的有效功率进行了研究,该船的主要要素如表1所示。
|
|
表 1 船舶主尺度 Tab.1 Principal dimensions |
由于所需的计算模型为薄壁曲面结构,所以在三维建模软件CATIA中根据所提供的某LPG运输船型线图及型值表建立几何模型。以横剖面为基准建立模型。首先,在各站位的位置建立平面,然后将各站位的型线图依次导入;然后导入首尾及舭部等曲率变化较大部位的水线面图;再根据型线图建立型值点,通过样条曲线连接各型值点形成船舶模型框架;最后,通过填充拉伸等操作生成多块曲面,并将曲面合并成整体,得到整个船体的曲面模型。船舶模型如图1所示。

|
图 1 船舶几何模型 Fig. 1 Ship geometry model |
本文主要对某LPG运输船在设计载平浮状态下,航速为12 kn,13 kn,14 kn,15 kn时的阻力及有效功率预报。仿真过程中将实船按照1∶25.178进行缩比计算,计算工况如表2所示。
|
|
表 2 模型计算工况 Tab.2 The calculation condition of model |
运输船的CFD仿真是运用STAR-CCM+ 软件实现[4-6]。
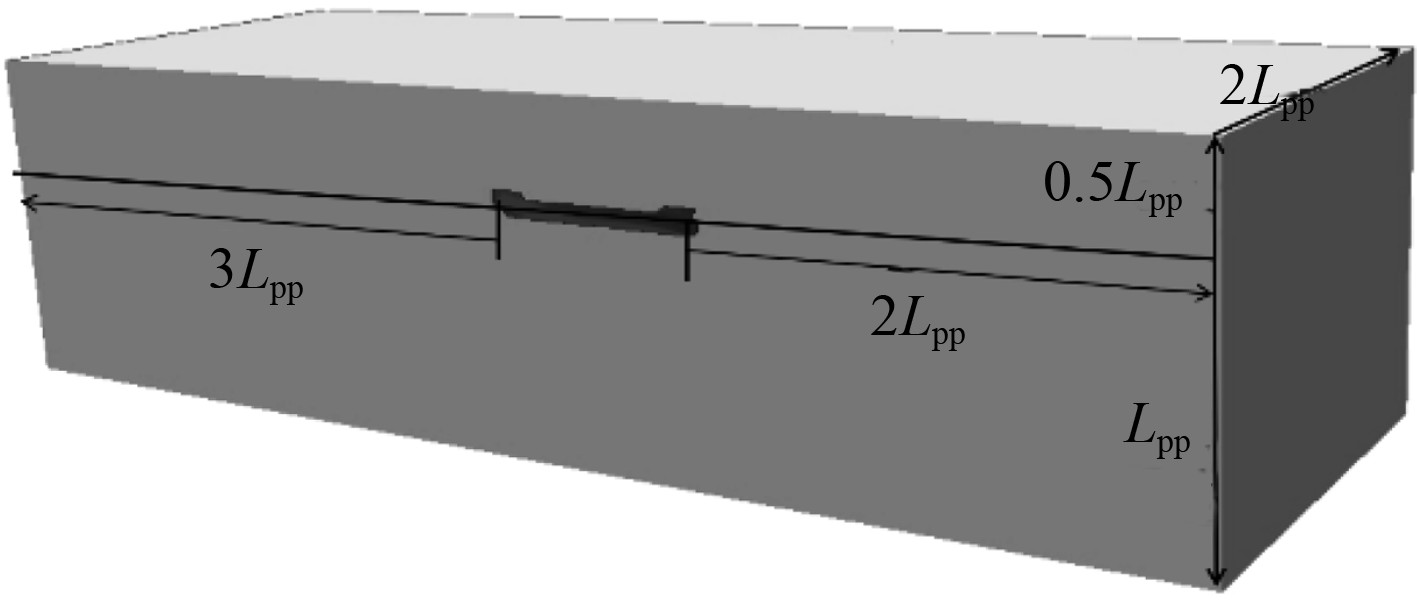
2.2.1 计算区域划分由于船体模型为半船对称模型,且在试验中船模以匀速直航运动,即对称问题[7-9],因此只取一半流域建立计算域以此减少网格数量、减少计算量。计算时以船体中纵剖面做为对称面。数值模拟计算域长度约为6倍船长,其中进流段约2倍船长,出流段取约3倍船长;宽度沿右舷方向取约2倍船长;自由页面位于设计水线处,水深取约1倍船长,空气高度取0.5倍船长。计算区域如图2所示。
|
图 2 仿真计算区域 Fig. 2 Simulation calculation area |
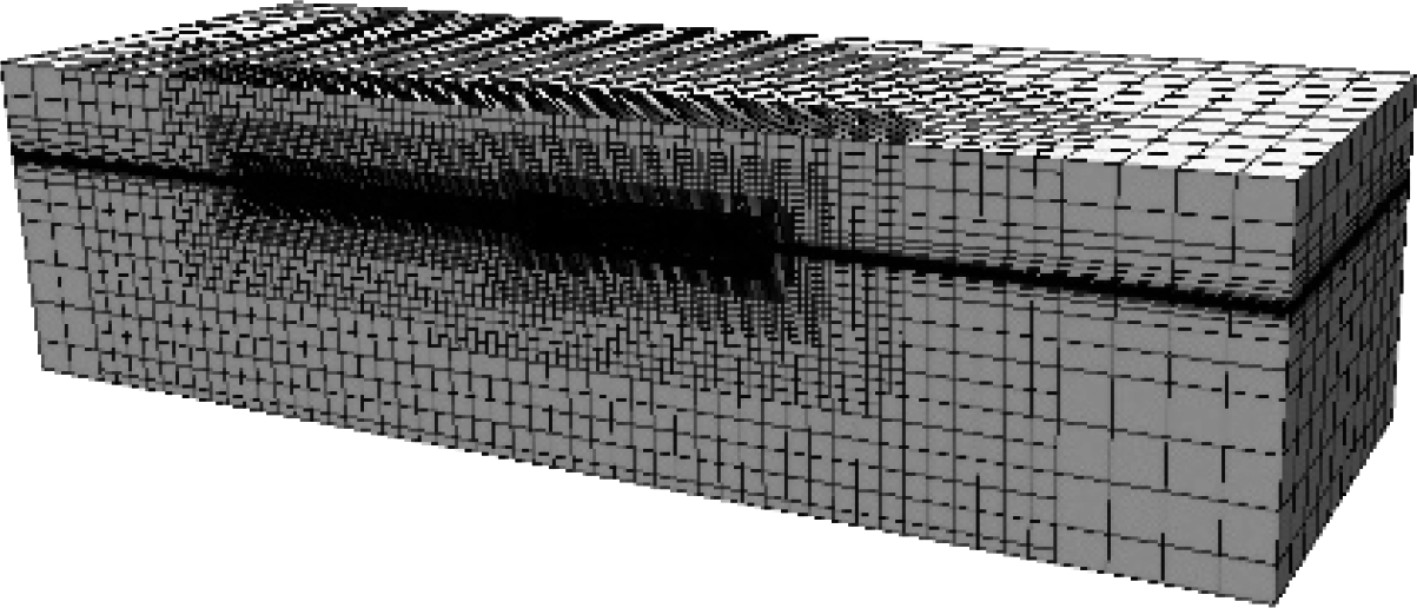
STAR-CCM+软件搭载了CD-adapco独创的最新网格生成技术,能够根据船舶外形,快速生成满足计算要求的多面体网格[6]。为了提高计算精度,保证计算的可靠性,在船舶周围、船舶首部、船舶尾部、水线面以及船行波区域对网格进行加密[10-13]。网格基础尺寸为0.14 m,经过加密后的网格数量约为230万,网格图如图3所示。
|
图 3 计算域网格 Fig. 3 Computational domain grid |
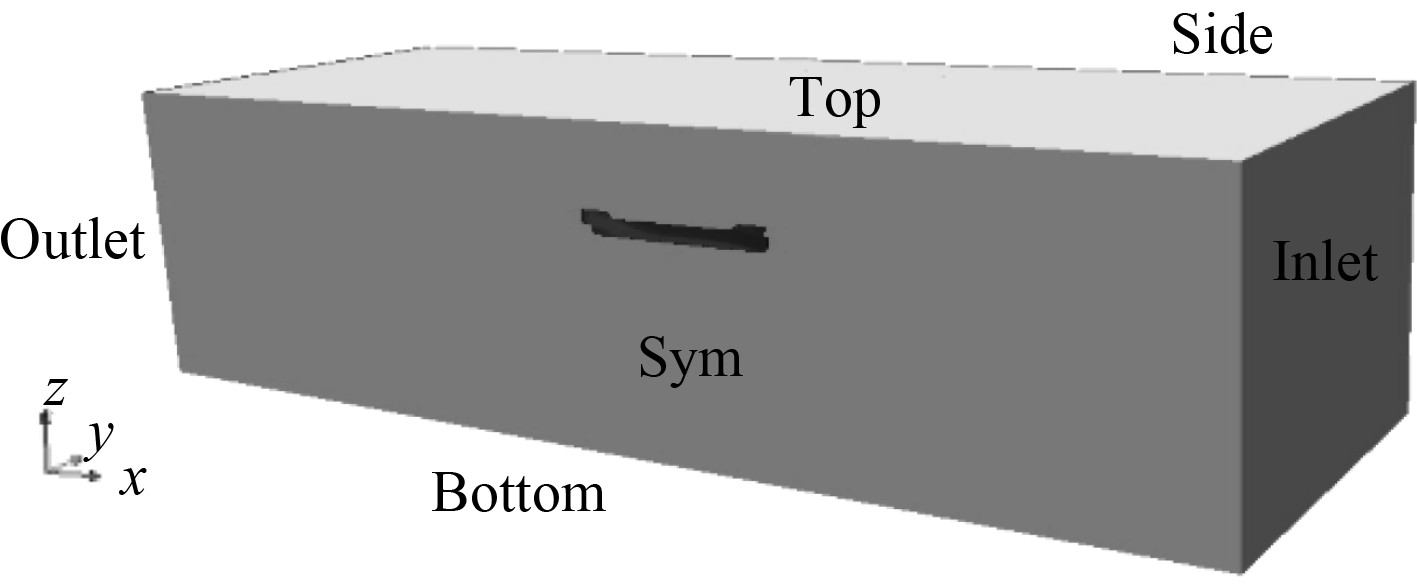
计算区域初步创建后,进行区域划分。将船体设置为固定壁面,其他边界条件按照位置依次设定为对称面(sym)、速度入口(inlet)、压力出口(outlet)、流域顶部(top)、流域底部(bottom),边界(side)等[9]。仿真计算时,除压力出口和对称面外,其他平面均设置为速度进口,计算的时间步长设为0.1 s计算模型边界条件如图4所示。
|
图 4 计算域边界条件 Fig. 4 Calculate domain boundary conditions |
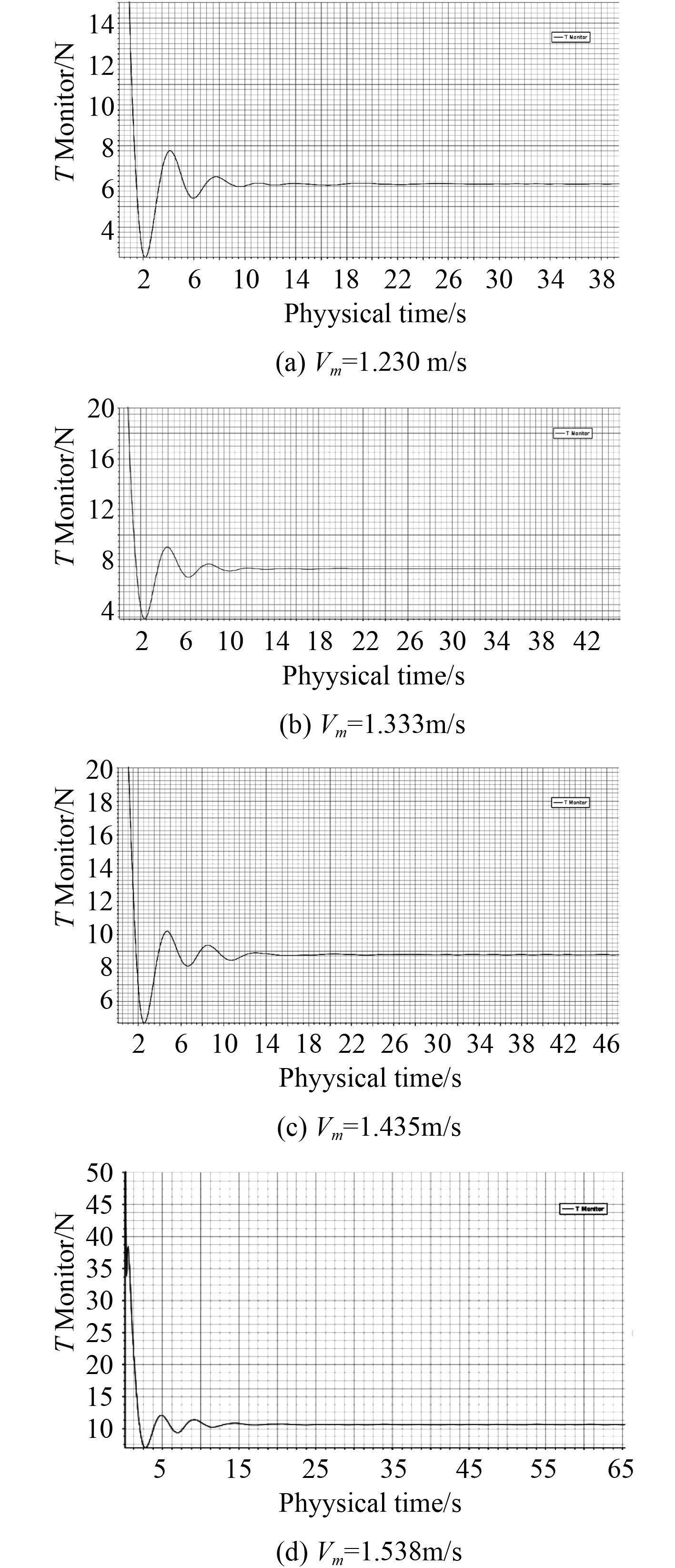
船舶在设计吃水平浮状态下,计算所得的模型阻力值如表3所示。各航速对应的半船模阻力历时曲线如图5所示,船舶兴波如图6所示。
|
|
表 3 不同航速下船模阻力值 Tab.3 Ship model resistance at different speeds |
|
图 5 半船模阻力历史曲线 Fig. 5 Half ship model resistance duration curve |

|
图 6 各航速下船模波形图 Fig. 6 Ship model waveform at each speed |
由模型阻力换算至实船阻力时采用傅汝德法(Froude’s Method),摩擦阻力系数计算采用1957-ITTC公式,其表达式为[14-15]:
| ${C_f} = \frac{{0.075}}{{{{(\log {R_N} - 2)}^2}}} \text{。}$ | (1) |
所计算船舶的摩擦阻力补贴系数取
同时,为了验证计算结果的准确性,在水池对该船进行模型实验,数值计算与模型实验2种方法所得的结果如表4和表5所示。为了更直观反映2种方法的差异,将数值计算结果与模型实验结果进行对比,如表6所示。绘制实船总阻力系数、实船总阻力及有效功率随傅汝德数变化的曲线,如图7所示。
|
|
表 4 设计载模型阻力计算结果及实船阻力换算 Tab.4 The resistance calculation results and real ship resistance conversion on design load |
|
|
表 5 设计载模型阻力试验结果及实船阻力换算 Tab.5 The model test results and real ship resistance conversion on design load |
|
|
表 6 模型实验与数值计算结果对比 Tab.6 The comparison between model test and numerical calculation results |
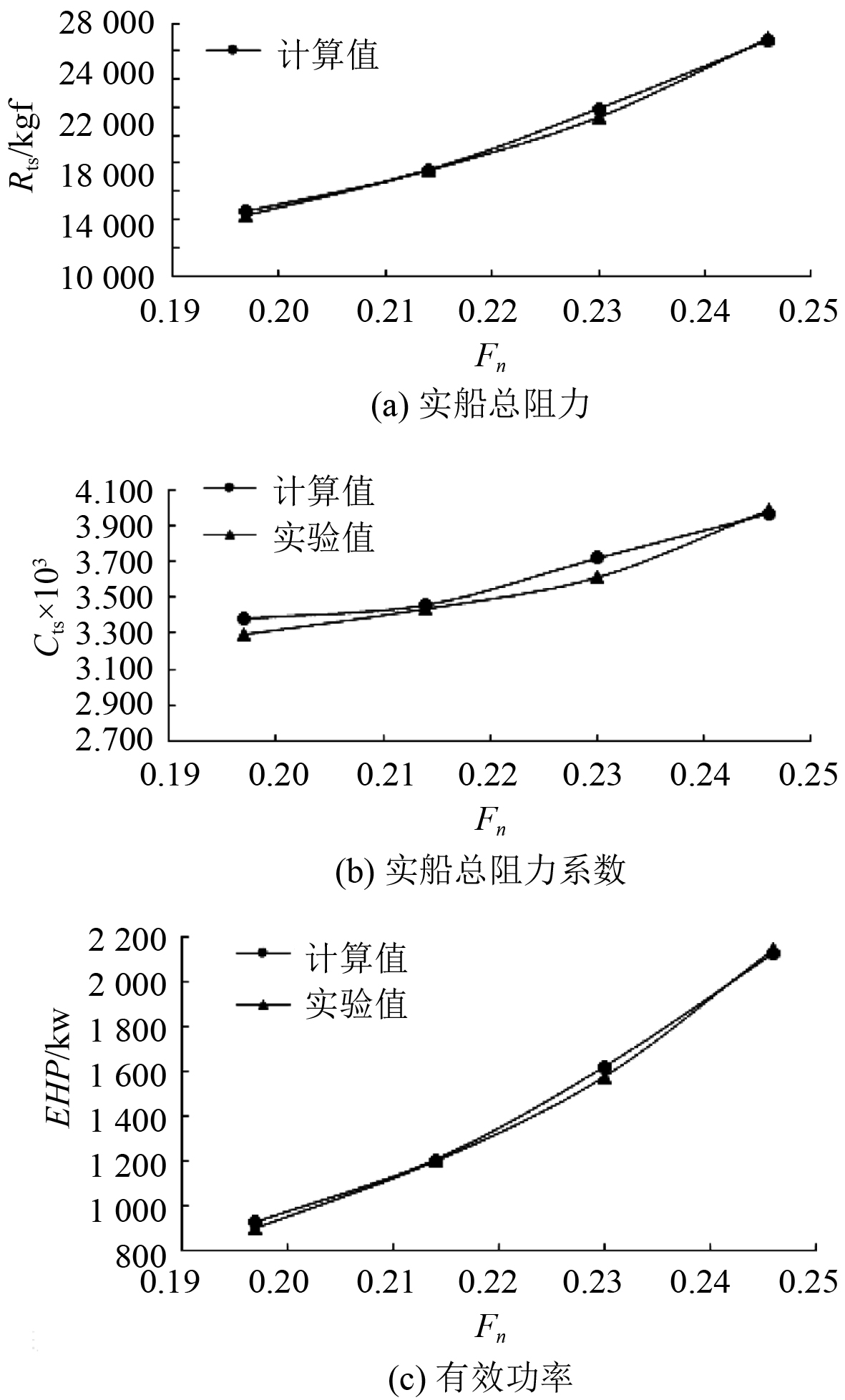
|
图 7 各参数随Fn变化曲线图 Fig. 7 Curve of each parameter as a function of Fn |
由表6可看出,2种方法所得结果的误差大部分在2%左右,最大的误差也小于5%。由图7可看出,对于实船总阻力以及有效马力来说,2种方法所得的结果随傅汝德数的变化趋势一致,证明本文采取的数值计算方法来预测船舶有效功率是可行的而总阻力系数略有差异是由于数值计算与模型实验的水温及环境因素不同,导致模型的雷诺数不同进而影响了模型的摩擦阻力系数,使得所得的剩余阻力系数不同,最终使实船总阻力系数不同。
4 结 语针对某LPG运输船,本文采用Star-CCM+软件,选取设计载下航速分别为12,13,14,15 kn的状态进行缩比模型的仿真计算,通过二因次法将计算结果换算至实船,并对其主机有效功率进行了预报。同时,将数值计算模型实验所得的结果进行了对比,验证了数值计算的准确性,证明通过数值计算预报主机功率的方法是可行的。
| [1] |
周春辉, 黄弘逊, 周玲, 等. 基于大数据的内河船舶主机功率估算方法[J]. 大连海事大学学报, 2019, 45(2). |
| [2] |
郑小龙, 黄胜, 尚秀敏. 基于CFD的船舶阻力预报方法研宄[J]. 江苏科技大学学报(自然科学版), 2014, 28(2): 109-113. |
| [3] |
王诗洋, 王超, 常欣, 等. CFD技术在船舶阻力性能预报中的应用[J]. 武汉理工大学学报, 2010(21). DOI:10.3963/j.issn.1671-4431.2010.21.044 |
| [4] |
魏可可, 高霄鹏. 基于STAR-CCM+对5415船模的阻力预报[J]. 兵器装备工程学报, 2016(9). DOI:10.11809/scbgxb2016.09.001 |
| [5] |
吴乘胜, 赵峰, 张志荣, 等. 基于CFD模拟的水面船功率性能预报研究[J]. 中国造船, 2013(1). DOI:10.3969/j.issn.1000-4882.2013.01.003 |
| [6] |
李晓文, 林壮, 郭志群, 等. 基于Star-CCM+的滑行艇水动力性能模拟计算[J]. 中南大学学报(自然科学版), 2013(S2). |
| [7] |
倪崇本. 基于CFD的船舶阻力性能综合研究[D]. 上海: 上海交通大学, 2011.
|
| [8] |
CS WU, L YANG, Z R ZHANG, etc. CFD simulation of ship model free to sinkage and trim advancing in calm water. Proceedings Vol. II, Gothenburg 2010- A Workshop on Numerical Hydrodynamics. 2010.
|
| [9] |
LARSSON L, ZOU L. Evaluation of resistance, sinkage and trim, self propulsion and wave pattern predictions. Gothenburg 2010-A Workshop on Numerical Hydro- dynamics. Proceedings.
|
| [10] |
张健, 王凯民, 许俊华, 等. 基于数值仿真与经验公式的船舶破冰阻力预报[J]. 舰船科学技术, 2019, 41(15): 1-6. |
| [11] |
高现娇, 孙江龙, 黄本燊, 等. 基于纵倾优化的油船节能研究[J]. 舰船科学技术, 2017, 39(15): 70-74. |
| [12] |
苏绍娟, 介推, 王天霖, 等. 基于CFD与三因次法结合的低速多用途船的阻力预报[J]. 舰船科学技术, 2017, 39(7): 59-63. |
| [13] |
宋磊, 涂海文, 谢文雄, 等. 散货船纵倾阻力研究[J]. 舰船科学技术, 2016, 38(23): 48-52. |
| [14] |
张艳, 阙晓辉. 基于CFD的船舶船体总阻力预报方法[J]. 舰船科学技术, 2015, 37(3): 139-142. DOI:10.3404/j.issn.1672-7649.2015.03.030 |
| [15] |
盛振邦, 刘应中. 船舶原理[M]. 上海: 上海交通大学出版社, 2003.
|
 2021, Vol. 43
2021, Vol. 43
