建立浅水浮式海洋平台作为多用途海上综合保障平台,可为军民生产生活、海洋科学考察探测、渔业捕捞等提供保障。
由于浮式海洋平台与系泊系统耦合动力响应的计算结果精度对平台安全性及可靠性影响显著,因此系泊系统与浮式结构运动分析是浮式海洋平台设计与建造方面研究的重点和难点,在进行浮式结构-系泊系统运动分析时,根据应用水深不同,可以大致分为深水浮式结构物耦合动力响应分析方法与浅水浮式结构物耦合动力响应分析方法两大类。
对于深水浮式结构物耦合动力响应分析方法,童波等[1]采用时域耦合分析方法探讨系泊缆直径、长度和预张力角度对系泊缆动力特性的影响。嵇春艳等[2-4]针对深水半潜式海洋平台采用时域全耦合分析法探讨了新型系泊系统的水动力性能。Yang等[5]采用全时域方法对系泊状态下的桁架浮筒式平台进行耦合分析。
由于当前研究主要关注深水条件下的结构水动力问题,浅水浮体耐波性的研究相对于深水水动力来说非常有限[6]。但近年来,大型浮体在浅水中的水动力特性由于实际工程需要,也引起了众多学者的研究兴趣。杨建民等[7]对FPSO在渤海浅水不规则波浪中六自由度运动和碰底情况进行了试验研究分析。丁军等[8]针对近岛礁浅水环境下浮式海洋平台提出一种新型桩柱式系泊系统。国外对于大型结构物浅水水动力性能研究相对较少。Buchner 等[9]通过模型试验研究了一浮式接收终端和LNG船之间起辅助作用拖船的运动特性,发现即使一般的波浪也会引起拖船的显著运动。
浅水浮式海洋平台一般布置在水深不超过20 m的浅水区,波浪条件易发生改变;平台结构接近海底,造成平台的水动力系数发生改变;系泊系统往往为非对称式,从而造成系泊与平台、平台与波浪之间耦合作用更为复杂。本文所研究两类典型非对称系泊系统为左右非对称和前后非对称系泊系统,基于TMA浅水波浪谱对2种非对称系泊系统作用下浮式平台的动力响应以及张力分布进行数值计算,计算结果与对称式系泊作用下结果进行对比分析,获得非对称系泊系统作用下平台运动特点和变化规律。
1 基本理论 1.1 TMA浅水波浪谱理论波浪传入近海浅水区,波浪谱将发生明显变化,Kitaigorodoskii等根据研究结果将浅水波浪谱表示为深水波浪谱与无因次水深
| $S(\omega ) = \varPhi (kd){S_0}(\omega )\text{。}$ | (1) |
式中,
| $\varPhi ({\omega _d}) = \left\{ {\begin{array}{*{20}{c}} {0.5\omega _d^2},&{{\omega _d} < 1},\\ {1 - 0.5{{(2 - {\omega _d})}^2}},&{1 \text{≤} {\omega _d} \text{≤} 2},\\ 1,&{{\omega _d} > 2}\text{。} \end{array}} \right.$ | (2) |
式中无因次量为:
| ${\omega _d} = \omega {\left( {\frac{d}{g}} \right)^{1/2}} = 2{\text{π}} f{\left( {\frac{d}{g}} \right)^{1/2}}\text{。}$ | (3) |
上述理论随后被实测资料所证实并发展为浅水波浪谱TMA谱。
| $S(f) = \varPhi (kd){S_j}(f)\text{。}$ | (4) |
式中:
| $\varPhi (kd) \!=\! \frac{{{{\tanh }^3}kd}}{{\tan kd \!+\! kd \!-\! kd{{\tanh }^2}kd}} \!=\! \frac{{{{\tanh }^2}kd}}{{1 \!+\! 2kd/\sinh 2kd}}\text{。}$ | (5) |
式中:
时域运动方程分为高频与低频2个部分。1阶高频运动方程为:
| $\begin{split} ( {{{M}}_{ij}} +&{{{\mu}} _{ij}} )\ddot x_j^{\left( 1 \right)} + \int\nolimits_0^\infty {{{{K}}_{ij}}\left( \tau \right)\dot x_j^{\left( 1 \right)}\left( {t - \tau } \right){\rm d}\tau } + {{{C}}_{ij}}x_j^{\left( 1 \right)} = \\ & F_i^{moor} + F_i^{wave\left( 1 \right)}\text{。}\end{split}$ | (6) |
其中:M为结构物惯量矩阵;
2阶低频运动方程为:
| $\left\{ {\begin{array}{*{20}{c}} \left( {m + {\mu _{11}}} \right)\ddot x_1^{\left( 2 \right)} + {\mu _{12}}\ddot x_2^{\left( 2 \right)} + {\mu _{16}}\ddot x_6^{\left( 2 \right)} + \left( {{B_{11}} + {B_{wdd}}} \right)\dot x_1^{\left( 2 \right)} = \\ F_1^{wind} + F_1^{current} + F_1^{wave\left( 2 \right)} + F_1^{moor} ,\\ {\mu _{21}}\ddot x_1^{\left( 2 \right)} + \left( {m + {\mu _{22}}} \right)\ddot x_2^{\left( 2 \right)} + {\mu _{26}}\ddot x_6^{\left( 2 \right)} + {B_{22}}\dot x_1^{\left( 2 \right)} = \\ F_2^{wind} + F_2^{current} + F_2^{wave\left( 2 \right)} + F_2^{moor} ,\\ {\mu _{61}}\ddot x_1^{\left( 2 \right)} + {\mu _{62}}\ddot x_2^{\left( 2 \right)} + \left( {I + {\mu _{66}}} \right)\ddot x_6^{\left( 2 \right)} + {B_{66}}\dot x_6^{\left( 2 \right)} = \\ F_6^{wind} + F_6^{current} + F_6^{wave\left( 2 \right)} + F_6^{moor} \text{。}\end{array}} \right.$ | (7) |
式中:m为结构物质量;
本文所分析浅水浮式海洋平台如图1所示。

|
图 1 浅水浮式海洋平台 Fig. 1 Shallow Water Floating Offshore Platform |
其主体结构由浮体、立柱、横撑与主甲板组成,具体特征参数见表1[10]。
|
|
表 1 浅水浮式平台主要特征参数 Tab.1 Main parameters of shallow water floating platform |
本文采用张紧式系泊方式,8根系泊缆分为4组,每组由2根组成,每组系泊缆夹角为15°,仰角为45°,选取3段组合缆形式,即上下2段为锚链,中间为聚酯缆,具体参数如表2所示。前后非对称与左右非对称系泊布置方式如图2和图3所示,地形坡度设为45°,系泊缆布置于岛礁地形中间,预张力均设为1500 kN。
|
|
表 2 系泊缆主要参数 Tab.2 Main parameters of mooring lines |
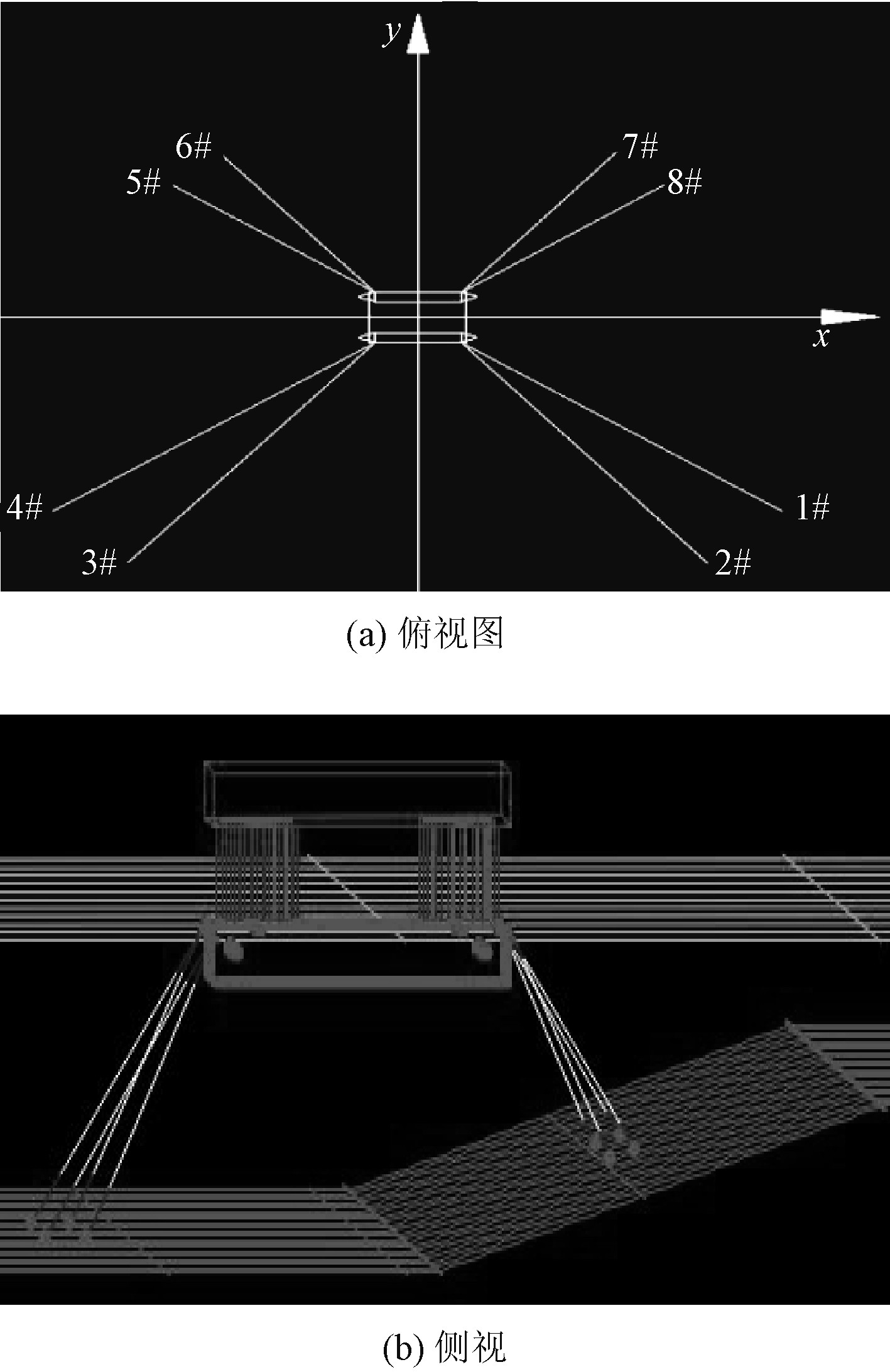
|
图 2 前后非对称系泊系统 Fig. 2 Forward and backward asymmetric mooring system |
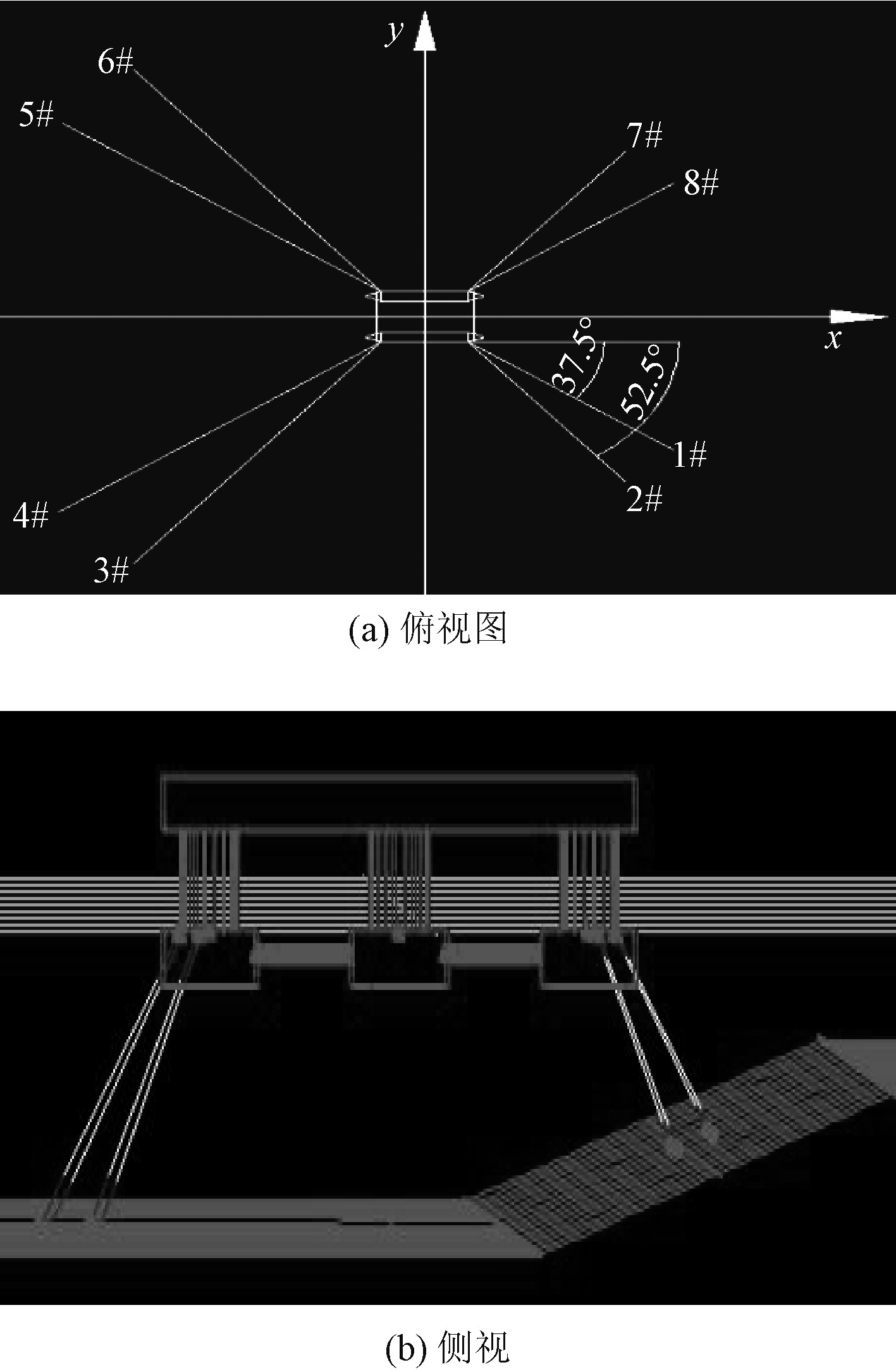
|
图 3 左右非对称系泊系统 Fig. 3 Left and right asymmetric mooring system |
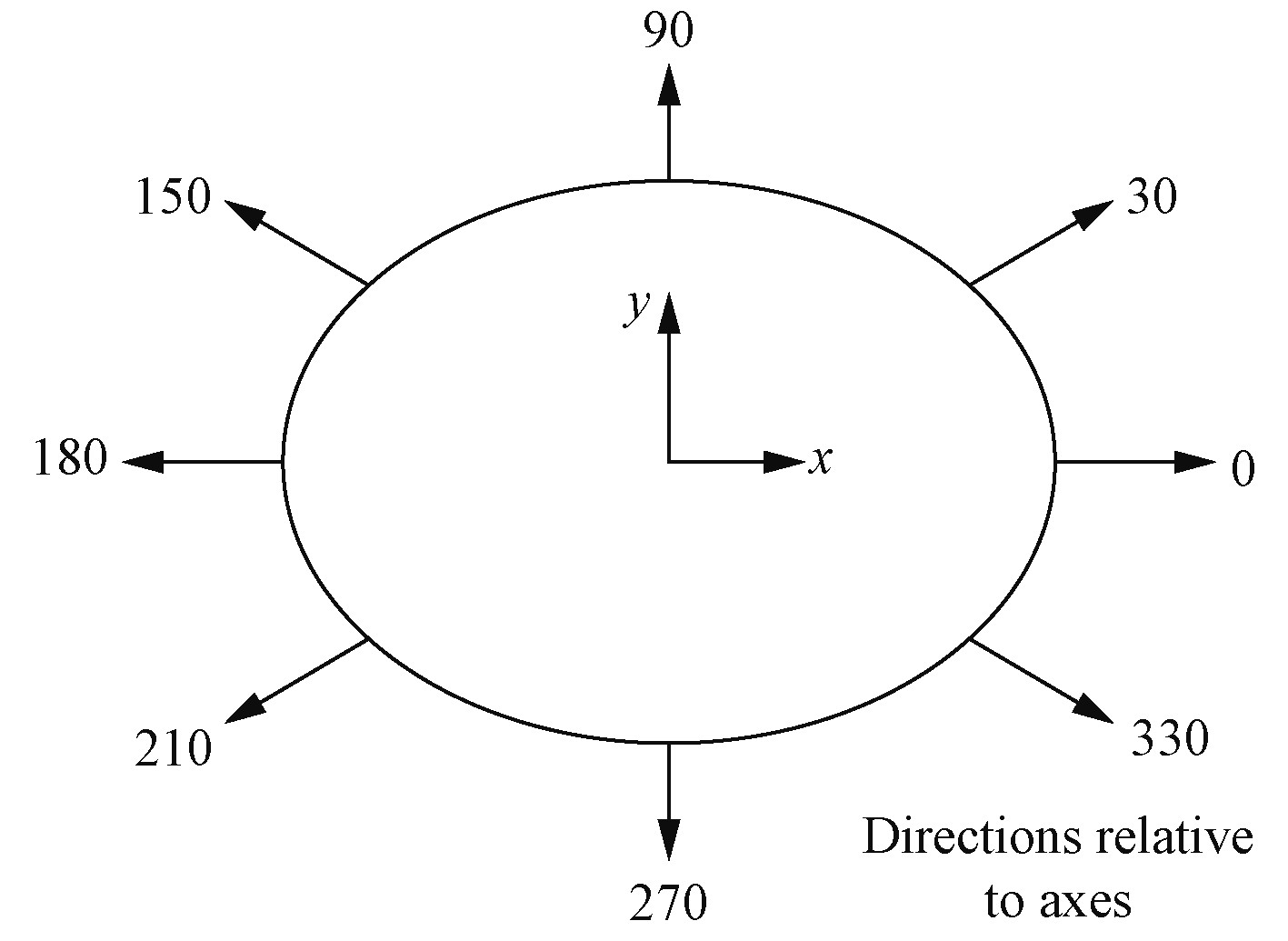
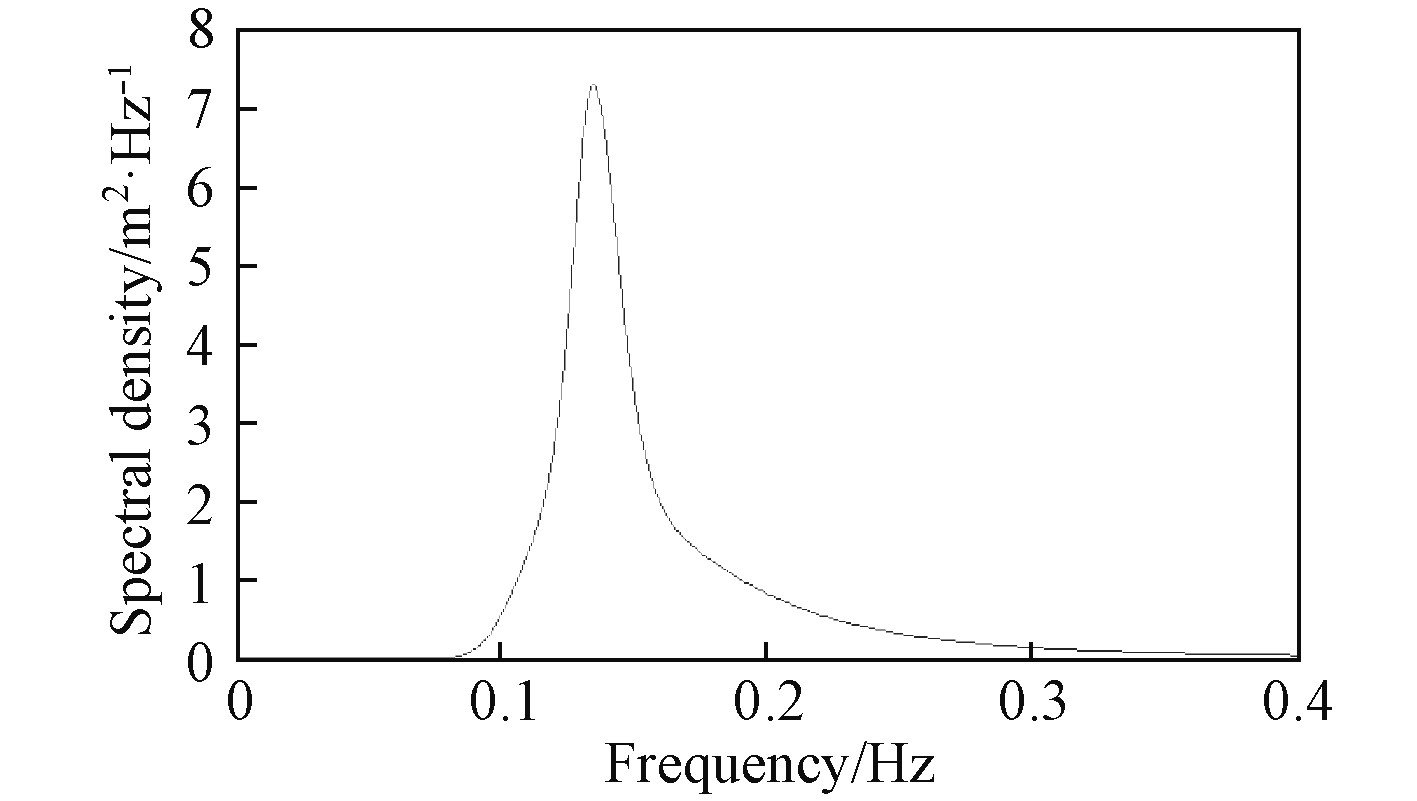
为模拟南海浅水区生存海况下平台运动情况,本文所选环境工况如表3所示[3]。研究90°典型浪向,浪向角坐标系定义如图4所示,波浪谱选用TMA浅水波浪谱,如图5所示。风谱选用NPD风谱,风速为40 m/s;由于平台布置在20 m水深的岛礁浅水区,海流流速较小,计算时暂不予考虑。
|
|
表 3 环境参数 Tab.3 Environment parameters |
|
图 4 坐标系定义 Fig. 4 Coordinate system definition |
|
图 5 TMA浅水波浪谱 Fig. 5 TMA shallow water wave spectrum |
90°浪向角下,平台运动响应结果统计如表4所示。在所给环境力条件下,2种非对称系泊系统作用下平台运动响应虽较大,但均在API规范允许的范围内。
|
|
表 4 90°浪向角下平台运动响应结果 Tab.4 Results of motion response of platform at 90°wave angle |
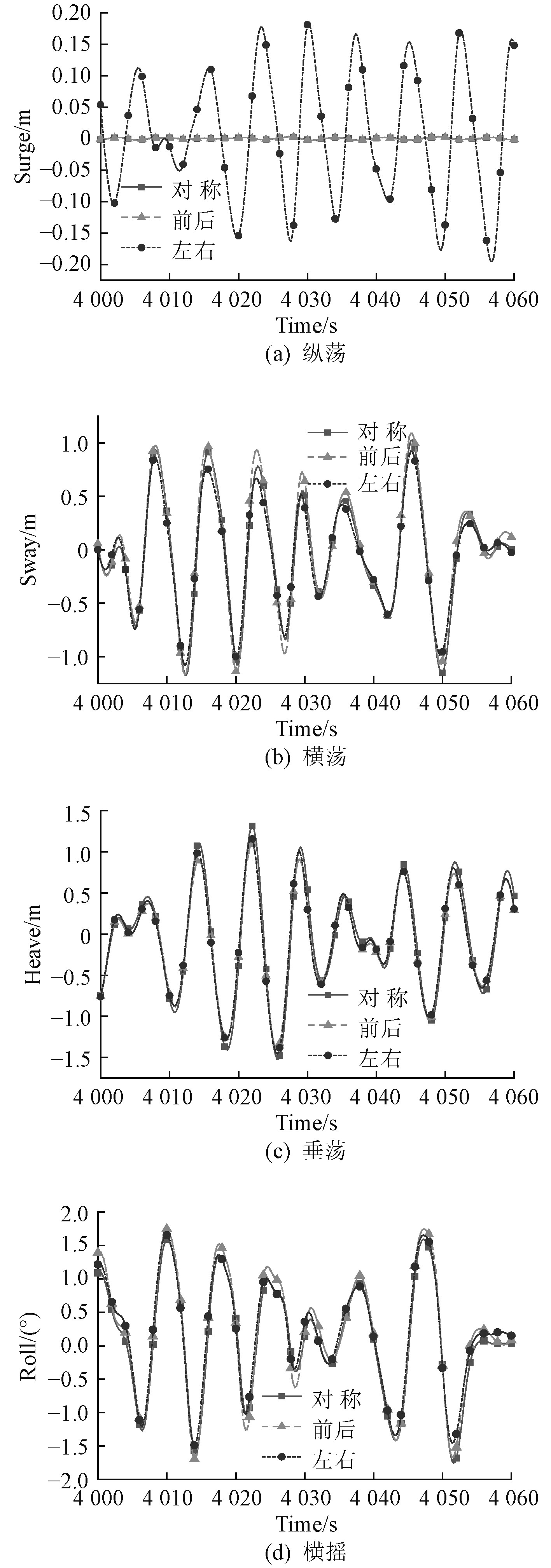
取系统稳定后的4000~4060 s这60 s之间平台的运动时间历程图进行对比分析,如图6所示。
|
图 6 90°浪向角下平台运动响应 Fig. 6 Platform motion response at 90°wave angle |
结合平台六自由度时历曲线及表4可以看出,当浪向角为90°时,3种系泊方式作用下平台运动响应都主要表现为横荡、垂荡与横摇运动。
相比对称系泊系统,前后非对称系泊系统作用下平台纵荡、纵摇与首摇运动响应几乎不变,横荡、垂荡与横摇运动均有不同程度改善。横荡最大值由3.348 m减小到3.26 m,减小了2.63%;垂荡最大值由3.418 m减小到3.31 m,减小了3.16%;横摇最大值由4.521°减小到4.322°,减小了4.4%。
相比对称系泊系统,左右非对称系泊系统作用下平台纵荡、纵摇与首摇运动均有所增大,但运动幅度在规范允许范围内。纵荡最大值由0.006 m增大到0.339 m,纵摇最大值由0.004°增大到0.377°,首摇最大值由0.01°增大到0.705°。横荡、垂荡与横摇运动均有所减小。横荡最大值由3.348 m减小到3.211 m,减小了4.09%,垂荡最大值由3.418 m减小到3.292 m,减小了3.69%,横摇最大值由4.521°减小到4.224°,减小了6.57%。
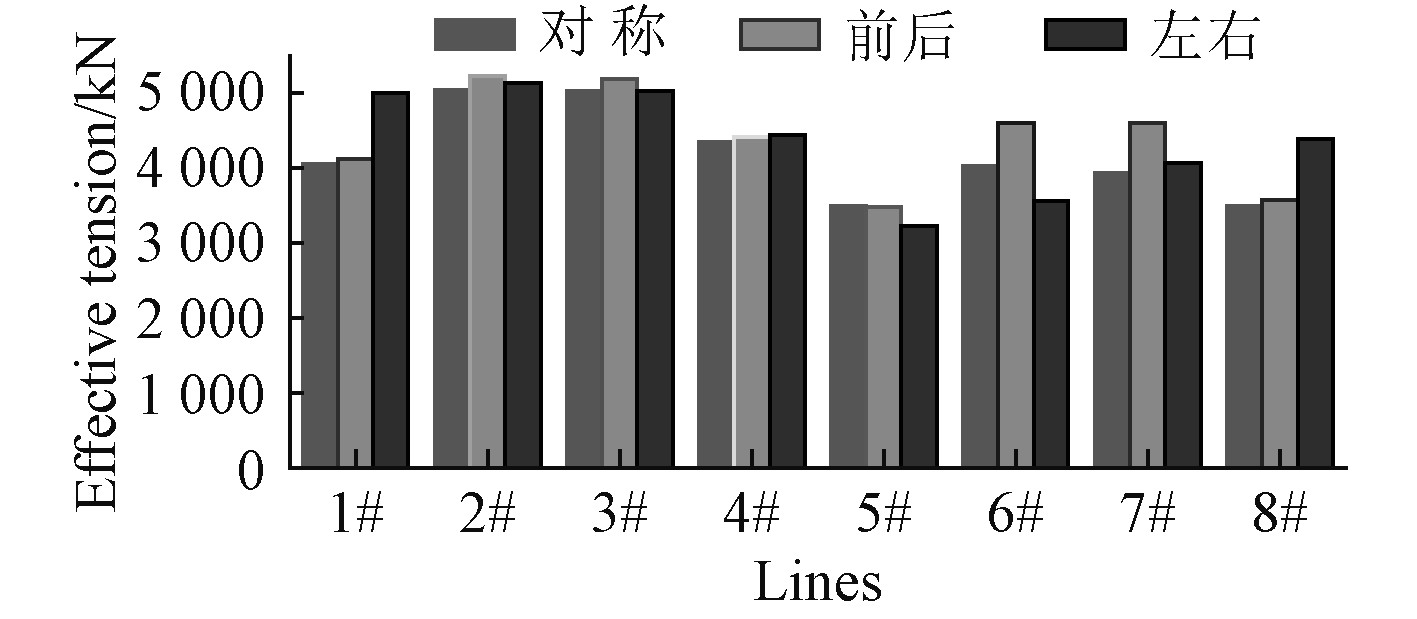
3.2 系泊缆张力计算结果及分析为验证2种非对称系泊方式的可行性,还需校核系泊缆张力,3种系泊方式下8根系泊缆最大张力如图7所示。
|
图 7 最大张力统计结果对比 Fig. 7 Comparison of statistic results of maximum tension |
可以看出,3种系泊方式下受力最大系泊缆均为2号缆绳,并且2种非对称系泊方式下缆绳最大张力相比对称系泊均有不同程度增大。前后非对称系泊方式作用下系泊缆最大张力由5040 kN增大到5223 kN,增加了3.63%;左右非对称系泊方式作用下系泊缆最大张力由5040 kN增大到5131 kN,增加了1.81%。
前后非对称系泊系统作用下受力最大系泊缆安全系数为1.71,大于1.67,满足API规范要求,系泊于岛礁地形上的5#,6#,7#和8#系泊缆最大受力均比对称系泊作用下有所增大。左右非对称系泊系统作用下受力最大系泊缆安全系数为1.74,大于1.67,满足规范要求,并且系泊于岛礁地形上的1#,2#,7#和8#系泊缆最大受力相比对称系泊作用下也有不同程度的增大。
2种非对称系泊方式作用下系泊缆最大张力安全系数虽然大于1.67,但均存在破断风险,因此在设计系泊缆时,考虑到浅水浮式平台处于变化的海况中,系泊缆时刻受到动力的作用,而每根系泊缆受力不均匀,容易发生疲劳断裂,应进行强度校核。
4 结 语根据研究目标平台特点,考虑岛礁地形变化,本文设计了2种典型非对称式系泊系统布置方案,基于TMA浅水波浪谱理论,考虑平台与系泊系统的耦合作用,对2种非对称系泊系统作用下浮式平台的动力响应以及张力分布进行数值计算,计算结果与对称式系泊系统作用下结果进行对比分析,得到以下结论:
1)在所给环境力条件下,2种非对称系泊系统作用下,浅水浮式平台可以在岛礁地形中较好地定位,由于浅水效应,平台整体运动响应虽然较大,但根据API规范要求,均在自存海况规范允许的范围内;系泊缆张力虽然较大,但满足自存海况的破断要求,证明这2种非对称系泊方式应用于浅水岛礁地形下平台的定位是安全可行的。
2)相比对称系泊系统,2种非对称系泊系统作用下,平台横荡、垂荡及横摇运动均有所减小,降低了平台的触底风险。
3)相比对称系泊系统,2种非对称系泊系统作用下,各环境工况下受力最大系泊缆均相同,但最大张力均有所增大,系泊于岛礁地形上的缆绳最大张力大多有不同程度的增大,可能存在破断风险,因此在设计系泊缆时有必要进行强度校核。
| [1] |
童波, 杨建民, 李欣. 深水半潜平台悬链线式系泊系统耦合动力分析[J]. 中国海洋平台, 2008, 23(6): 1-7. DOI:10.3969/j.issn.1001-4500.2008.06.001 |
| [2] |
JI Chunyan, YUAN Zhinming, CHEN Minglu. Study on a new mooring system integrating catenary with taut mooring[J]. China Ocean Engineering, 2011, 25(3), 427−440.
|
| [3] |
YUAN, Z. M., JI, C. Y, CHEN, M. L., ZHANG, Y. Coupled analysis of floating structures with a new mooring system, Proceedings of the ASME 2011[C]. 30th International Conference on Ocean, Offshore and Arctic Engineering, 2011.
|
| [4] |
元志明, 嵇春艳, 陈明璐. 半潜式平台完全时域耦合分析[J]. 海洋技术, 2010, 29(4): 81-87. |
| [5] |
YANG M, TENG B, NING D, et al. Coupled dynamic analysis for wave interaction with a truss spar and its mooring line/riser system in time domain[J]. Ocean Engineering. 2012, 39: 72-87.
|
| [6] |
李淑一. 浅水软钢臂系泊FPSO水动力性能和运动响应数值研究[D]. 青岛: 中国海洋大学, 2011.
|
| [7] |
杨建民, 肖龙飞, 彭涛, 等. 浅水不规则波浪中油轮运动研究[J]. 海洋工程, 2000, 18(3): 25-29. |
| [8] |
丁军. 近岛礁浅水环境下浮式平台系泊系统设计研究[J]. 船舶力学, 2015, 19(7): 782-790. DOI:10.3969/j.issn.1007-7294.2015.07.004 |
| [9] |
BUCHNER B., DIERX P., WAALS O., 2005. The behaviour of tugs in waves assisting LNG carriers during berthing along offshore LNG terminals[J]. Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, OMAE 2005, 2, 983−991.
|
| [10] |
王永恒, 王磊, 汪学锋, 等. 南海岛礁极浅水下半潜平台锚泊系统数值模拟探究[J]. 舰船科学技术, 2017, 39(1): 68-73. |
 2021, Vol. 43
2021, Vol. 43
