随着国家新能源战略的不断推进,国内海上风电场的开发建设速度明显加快,市场对自升式风电安装船的需求也越来越迫切。支撑桩腿作为自升式风电安装船的重要组成部分,与主船体构成了一个相对运动和约束变形的整体,在负责将船体提升到离开水面一定高度后,还承载着各类施工可变载荷,为船舶施工提供了一个稳定的作业平台,避免了涌浪颠簸和海流影响,其强度、刚度和稳定性对于风电安装船的性能发挥至关重要。
桩腿的设计是自升式风电安装船的关键技术难点之一。桩腿设计与船体尺度、设计环境条件、作业水深、可变载荷等参数密切相关,是风电安装船升降系统能力校核分析的基础,也是影响作业安全性的关键环节。为确保风电安装船的设计性能得以实现,需要充分研究桩腿工作环境和边界条件,结合过往经验,不断优化其结构设计和强度校核方法。
桩腿强度分析和优化主要包括载荷确定与计算、约束条件与模型简化、边界条件与应力衡准、强度评估与优化等内容。
1 桩腿结构型式与特点自升式风电安装船的升降系统起降频次较大,其作业特点要求桩腿不仅要有良好的整体刚度和举升能力,还要有良好的使用寿命和水动力性能。自升平台的桩腿结构一般分为桁架式和板壳式两大类[1]。由于齿轮齿条桁架桩腿的使用寿命存在局限性,且圆柱形桩腿各方面综合性能较好,因此目前的主流设计一般选用四腿板壳式圆柱形桩腿和液压插销式升降机构,如图1所示。

|
图 1 桩腿结构和布置示意图 Fig. 1 Sketch map of spud leg structure and arrangement |
在设计桩腿板厚时,不仅需要考虑桩腿整体屈曲强度问题,还要兼顾插销孔局部强度问题。
2 计算工况与载荷根据自升式风电船的作业模式,对桩腿强度的分析应至少包括作业、航行、抗风自存、升降和静载5种工况条件,而且还应将不同工况下的载荷按各种最不利方向进行组合加载。
主要载荷内容包括重量载荷、环境载荷、动力惯性载荷、P-Delta效应载荷等。
2.1 重量载荷重量载荷包括固定载荷和可变载荷。固定载荷指本船自有的结构、设备等的自重,取恒定值,但由于作业功能的需求,各工况的重量重心是有所差别的;可变载荷是指在各工况中不同操作工艺下的大钩载荷、甲板风机部件载荷及其他可变载荷,如压载水及燃油等。
重量载荷一般通过调整船体材料的密度或施加质量点将固定载荷转换为船体的重量施加到整个船体上,并调整使得重量达到空船重量、重心与操作手册中空船重量重心的一致。
2.2 环境载荷环境载荷主要是指作业时受到的风、浪及流的影响,载荷方向定义如图2所示。
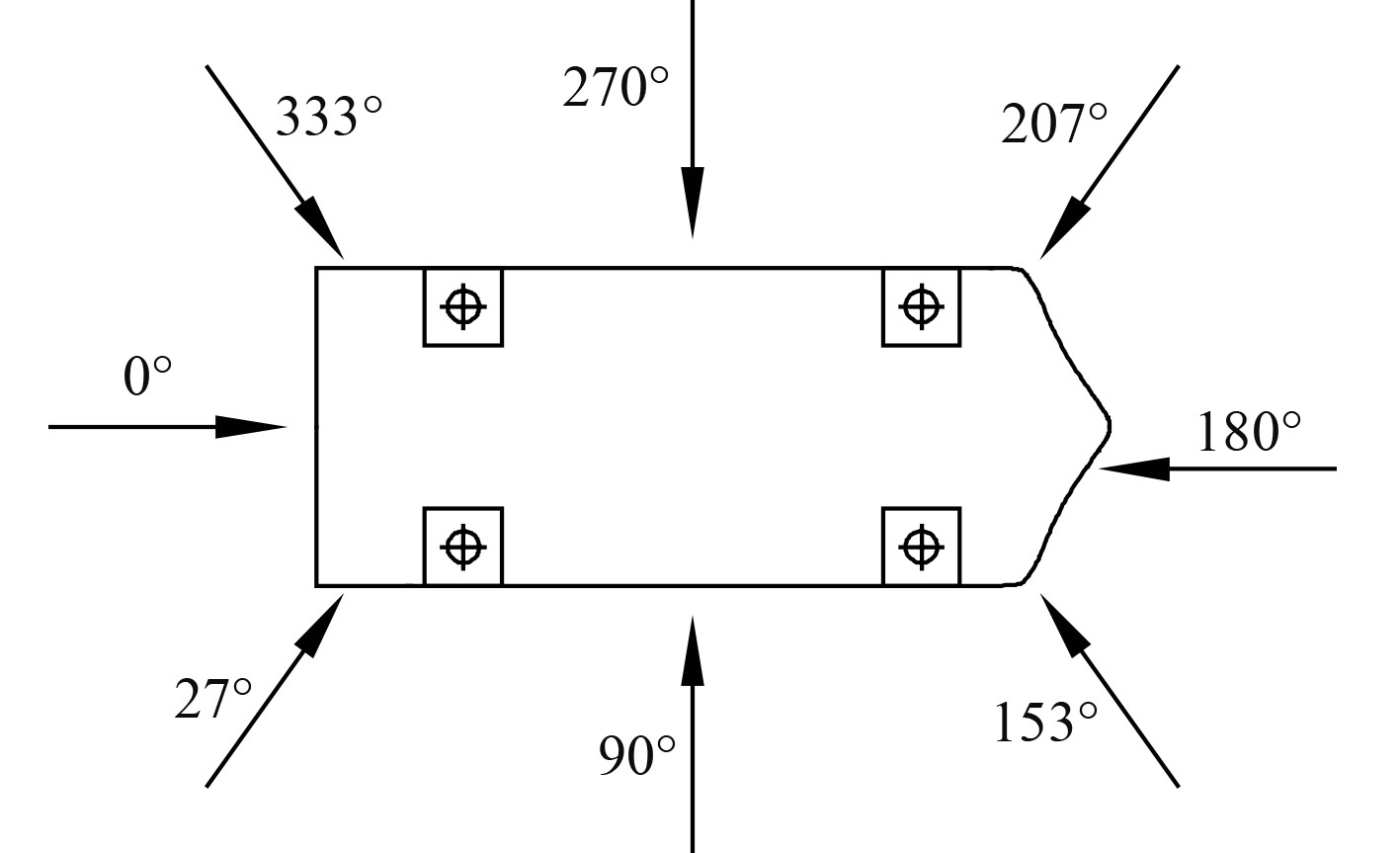
|
图 2 环境载荷方向示意图 Fig. 2 Sketch map of environmental load direction |
风载荷主要作用在上船体结构(包括甲板上的可变载荷、起重机、固桩室等)及其露天设备和水线面以上的桩腿上,基于风电安装船的特殊作业环境,风载荷成为各工况下需要考虑的主要载荷[2]。风压P及风力F的计算公式为:
| $P = f{V_k}^2{C_h}{C_s}(N/{m^2})\text{,}$ |
| $F = P \times A(N)\text{。}$ |
其中:f=0.611;Vk为风速;Ch为高度系数;Cs为形状系数;A为受风面积。
按波浪理论,圆形桩腿对波浪而言属于小尺度圆形构件,其波流水动力载荷计算可采用Morison 公式,当
| $\Delta F = \Delta {F_{{\rm{drage}}}} + \Delta {F_{inertial}} = {C_D}\rho \frac{D}{2}u\left| u \right| + {C_M}\rho \frac{{\text{π} {D^2}}}{4}\dot u\text{。}$ |
式中:ρ为海水密度,kg/m3;CD为曳力系数,CM=惯性力系数,CD,CM由试验确定,当实验资料不足时,可以按照经验数据选取;D=柱型桩腿直径;L=柱型桩腿长度;u=垂直于桩腿轴线的水质点相对于桩腿的速度分量,用Stokes五阶波理论计算;
风电安装船的作业海况较差,船体在洋流和涌浪的周期作用下而产生的结构振动动力响应必须重点分析[3]。在CCS《海上移动平台入级规范》[4]中对此以动力放大系数(DAF)值为标准进行了详细规定,动力放大系数计算公式如下:
| $DAF = \dfrac{1}{{\sqrt {{{\left\{ {1 - \left. {{{\left( {\dfrac{{{T_n}}}{T}} \right)}^2}} \right\}} \right.}^2} + {{\left( {2\varsigma \dfrac{{{T_n}}}{T}} \right)}^2}} }}\text{。}$ |
式中:ζ为临界阻尼百分比(取为7%);
惯性力通过SDOF方法计算得到:
| ${F_i} = (DAF - 1) \times \frac{{{F_{\max }} - {F_{\min }}}}{2}\text{。}$ |
式中:
P−Δ效应载荷是指风电安装船在作业时因受到风浪等载荷影响而产生横向位移时,由船体的自身重力对桩腿产生的二次弯矩。二次弯矩MΔ可以通过公式计算得出结果后施加到计算模型中。
3 模型简化实际工程计算中,可以利用梁单元模拟主船体结构,在建模过程中应确保船体模型的刚度以保证桩腿结构变形的一致性。其他如桩腿刚度、船体刚度、桩腿-船体连接刚度,也都应进行适当的模拟。模型质量分布和载荷施加按照操船手册船体重量和载荷重量重心数据进行实际模拟,以便能够准确的反映实际结构的质量分布[5]。
4 固桩室与桩腿的连接约束所有约束通过单元结点自由度的释放或约束来模拟。导向装置和插销自由度的约束如表1所示。在上下导向处采用虚拟单元将船体与桩腿连接,将虚拟单元的自由度进行释放,只传递水平载荷;在插销处采用虚拟单元将船体与桩腿连接,将虚拟单元的自由度进行释放,只传递垂向载荷。
|
|
表 1 导向装置和插销自由度的约束 Tab.1 Constraints to degrees of freedom of guide and sledge pin connection |
风电安装船作业水深一般按桩腿入泥3~5 m计算,因此桩腿模型的边界条件可按在泥面下3 m处的铰支来进行模拟。国内大部分沿海地区的实际作业插桩深度超过10 m以上,边界条件更为宽松。
由于按照铰支点进行计算时,分析结果过于保守,不利于平台空船重量的控制。实际应用中,还需要考虑土壤的非线性特性、桩靴结构等因素的影响。主要参照 IMO《海上移动式钻井平台构造和设备规则》[6]中的规定,计算得出土壤转动刚度的最大值。在实际计算中,一般采用20%的极限转动刚度值作为弹性约束。
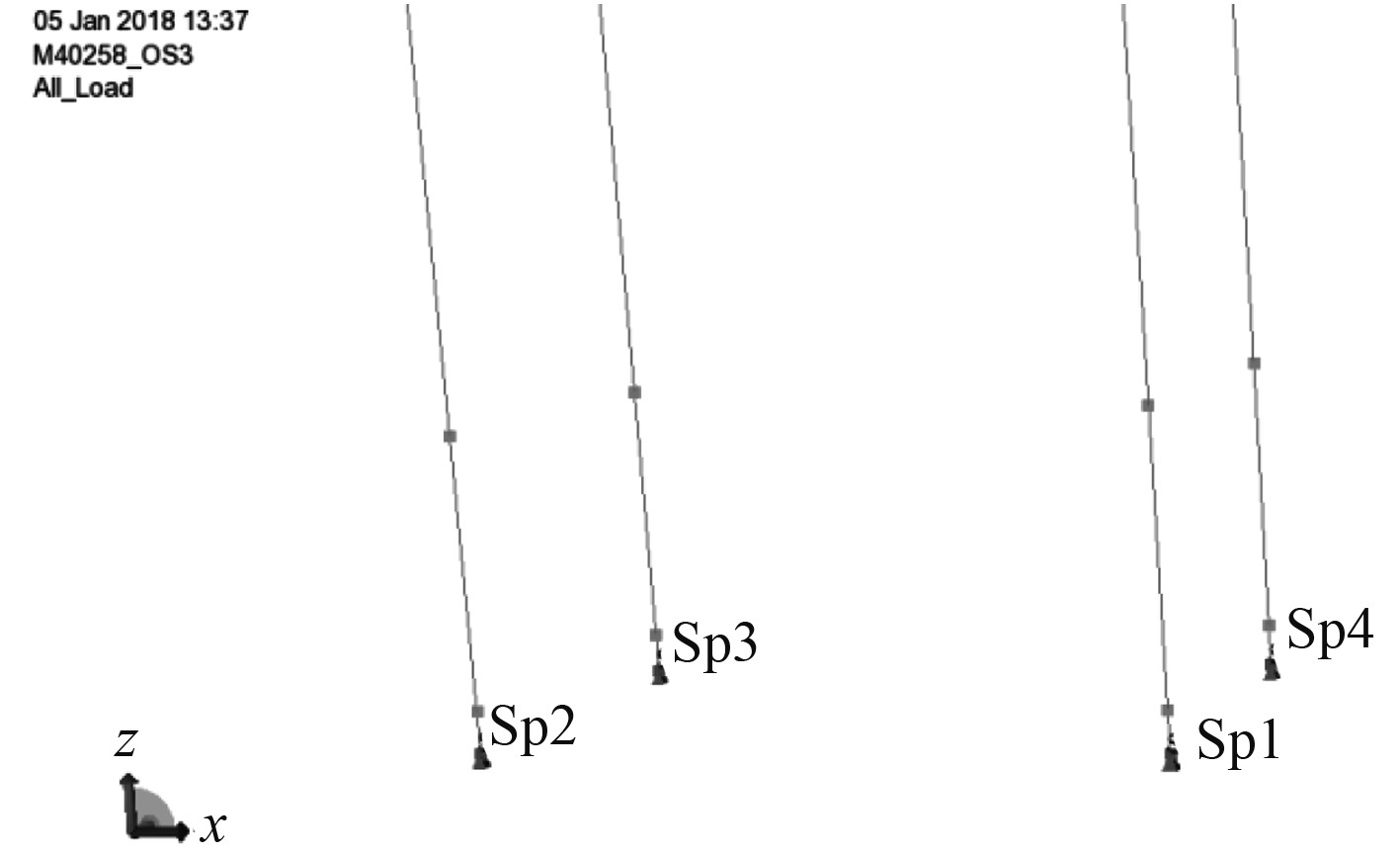
|
图 3 边界条件示意图 Fig. 3 Sketch map of boundary conditions |
另外,对于预压载工况则需要对桩腿进行强迫约束,使得单腿所受支持载荷接近升降系统的支持能力(计算中通过读取计算支反力来核算是否达到支持负荷这一目标值)[8]。四桩腿平台预压载工况下边界条件设置如表2所示。
|
|
表 2 预压载工况桩腿强迫约束 Tab.2 Forced restraint of spud leg in preballast condition |
对于板壳式柱型桩腿,不仅要考虑屈服强度,更重要的是屈曲强度。桩腿屈曲强度主要包括板格屈曲、局部板架屈曲、整体板架屈曲及整体柱型屈曲4个层次,其中桩腿柱型屈曲则是柱型桩腿整体强度的核心,计算长度及有效长度系数K是分析的关键。一般在铰支约束时,计算长度取边界铰支点距下导向的距离;在弹性约束时,计算长度取弹性约束下桩腿反弯矩点距下导向的距离。
7 桩腿强度优化设计按上述桩腿校核流程,根据船体装载工况下的各种平台工况下最极端的重量分布建立有限元模型,结合优化软件Optimus完成桩腿厚度优化,在桩腿实现最大能力的同时降低桩腿厚度[9]。
Optimus为挪威开发的一款用于工程优化的软件,内部集成多种优化设计算法。首先建立优化工作流程见图4。
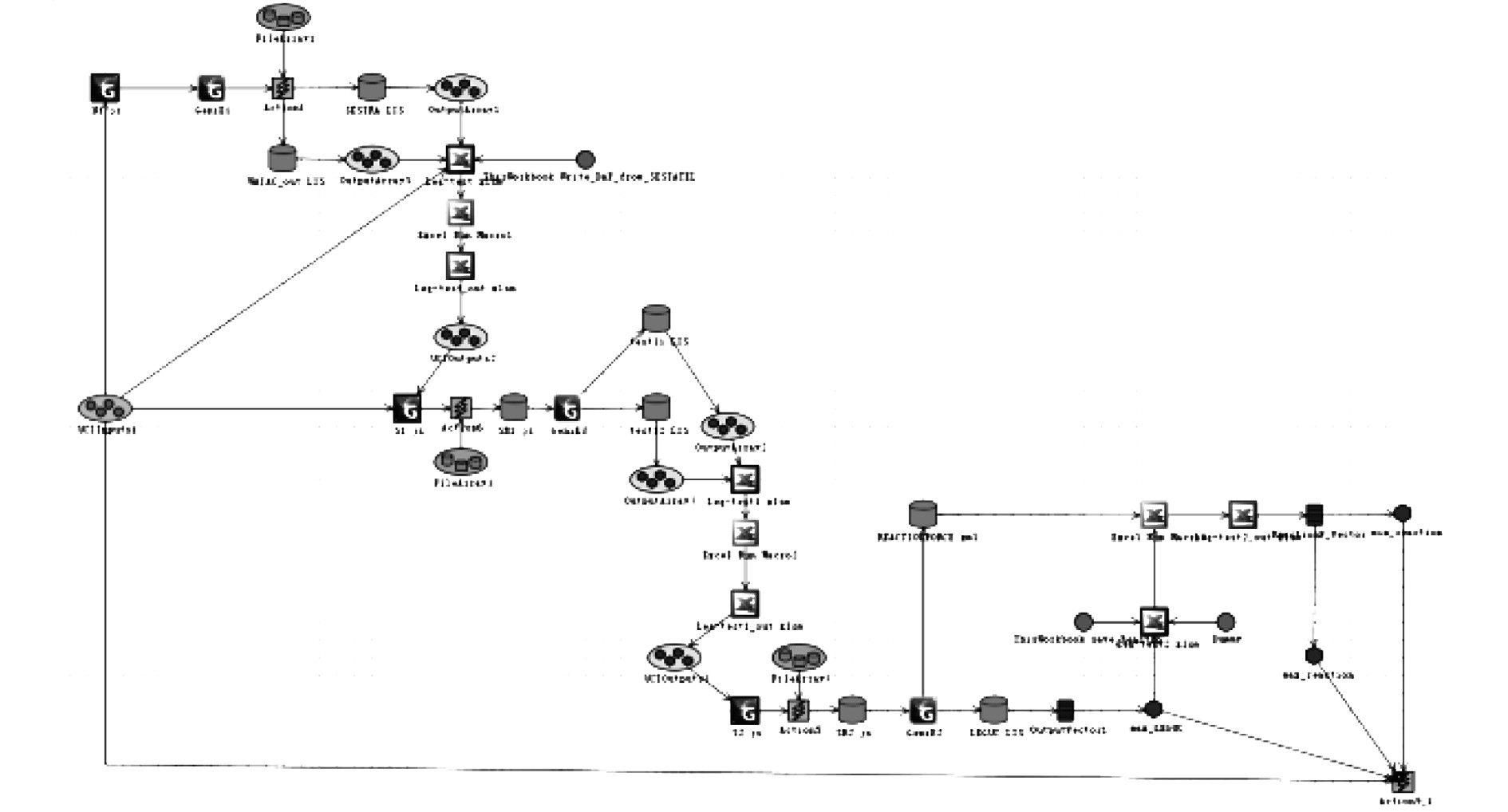
|
图 4 优化设计流程 Fig. 4 Optimization design process |
将模型、载荷、约束条件及优化目标定义在工作流中,详见表3。
|
|
表 3 优化设计工作流说明 Tab.3 Optimization design workflow description |
按上述要求制定好工作流后,选取适当的优化算法,缩短优化时间,得到UC无限接近于0.95的各种桩腿厚度试算,选取最优值。
8 插销孔设计及强度评估液压插销式升降机构通过在桩腿上开孔实现平台顶升,开孔后在桩腿强度评估过程中需要重点考虑板厚折减问题及插销孔设计及其本身结构强度问题。
桩腿插销孔处局部强度的有限元分析方法主要有2种:一是由总强度模型读出插销孔处的总载荷,假设载荷在插销开孔处的种分布型式,如余弦分布等,在线性范围内直接计算桩腿插销开孔处的应力分布;二是对插销进行直接建模,设置适当的参数,在非线性范围内进行接触分析。下面主要对直接建模分析方法进阐述,并分析桩腿直径、开孔大小等对桩腿插销孔局部强度的影响。
对插销的直接建模基于Abaqus软件的接触分析方法[10]。接触是随着时间不断变化的一个过程,这个过程同时也包含着材料以及几何的非线性。
作为接触界面,必须满足法向接触的2个条件:接触面之间不允许相互贯入;接触面之间的法向接触力只可能是压力。在切向接触条件方面,还要考虑接触面之间是否存在摩擦。
因为由上述条件所给出的约束都是不等式单边约束,而且接触面上的作用区域和动力模型也是不确定的,所以在进行接触分析时,一般使用试探、校核、循环迭代的增量方式进行求解。
依据前一步的计算结果,以及本增量步所设定的载荷条件,对接触条件再次进行判定,确定本增量步的第1个迭代步中,接触面的范围和状态,由此得出运动学及动力学的等式约束,并引入方程组,然后对接触面上的所有点进行求解。
检查接触面的计算结果是否满足运动学及动力学的不等式约束条件。若接触面上的所有点都满足校核的要求,本增量步计算结束,转入下一步的计算。如果不满足校核的要求,需返回第1步重新开始计算,直到所有点的计算结果都满足校核的要求,再进行下一个增量步的计算。以上接触分析迭代流程如图5所示。
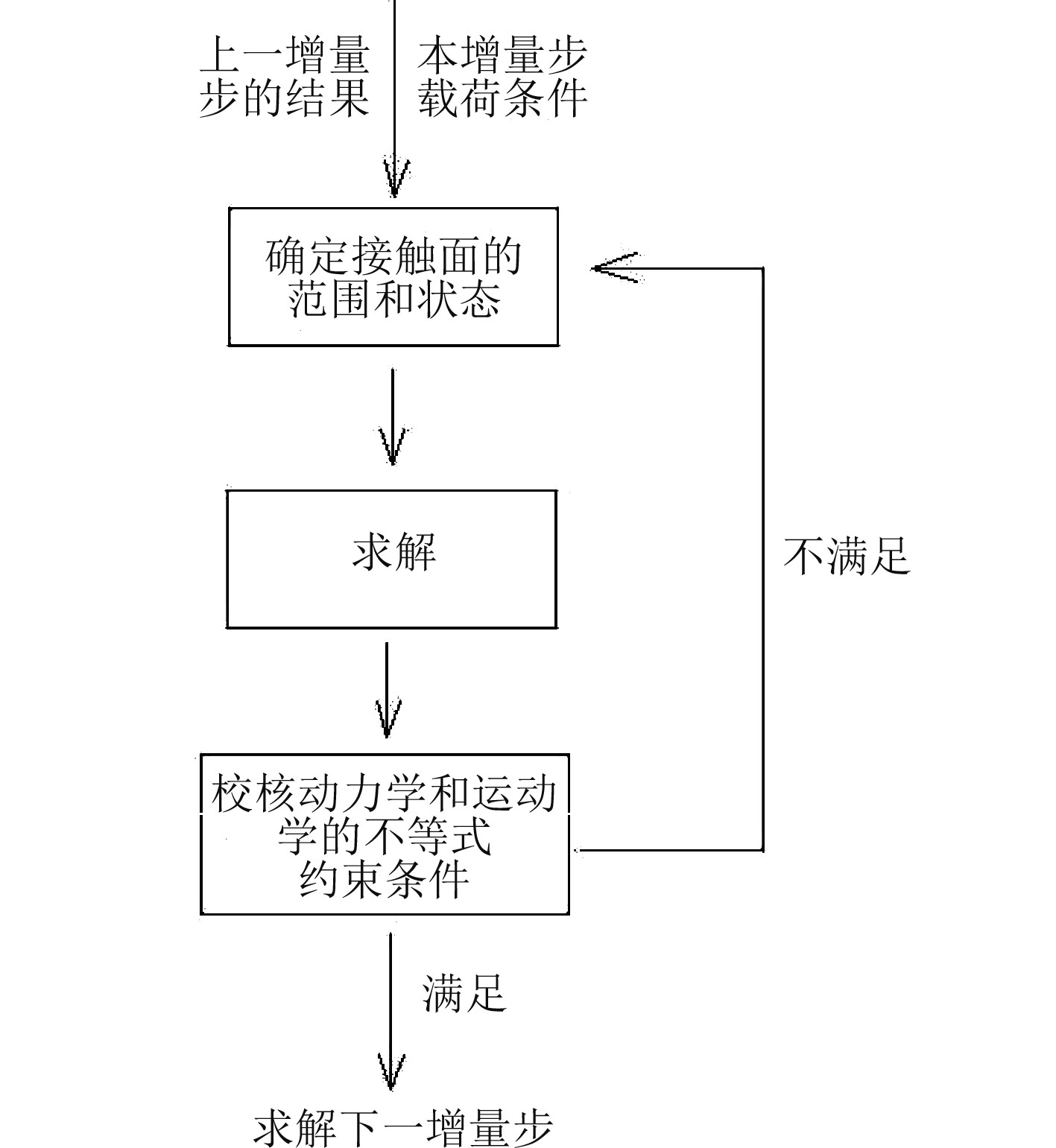
|
图 5 接触分析迭代过程 Fig. 5 Contact analysis iterative process |
插销孔区域局部强度分析是典型的接触强度问题,并且船级社规范规定对于桩腿插销孔强度分析还应考虑一个插销失效之后的极端工况。接触强度分析模型和结果如图6和图7所示。
|
图 6 总装分析模型示意图 Fig. 6 Sketch map of assembly analysis modle |

|
图 7 插销孔区域结构等效应力分布图 Fig. 7 Distribution map of structural equivalent stress in bolt hole area |
插销孔对桩腿强度的影响主要体现在桩腿的总强度(主要包括轴向和弯曲刚度,截面剖面模数)及桩腿局部屈曲强度两方面。在计算桩腿总强度时,如果直接扣除插销孔的开孔面积的方式对桩腿截面面积去折减,则会由于桩腿计算截面面积损失较大导致桩腿设计过于保守,大大增加了建造成本,降低了经济性。
为了合理评估插销孔对桩腿强度的影响,最终确认折减后的计算板厚,可以通过对比带销孔的桩腿与折减板厚桩腿在同等载荷(包括弯矩及轴向压力载荷)及约束下整体变形一致即可,通常板厚折减约12%。对比如图8所示,桩腿局部屈曲强度也可采取同样方式通过对比板壳屈曲模态来进行折减。

|
图 8 板厚折减前后桩腿变形对比云图 Fig. 8 Comparative stress nephogram of spud leg deformation before and after plate thickness reduction |
通过对自升式风电安装船桩腿的结构型式及强度进行分析和论证的过程,研究桩腿设计和优化过程中的关键技术和步骤,形成较为系统的设计理念,能够在确保安全的前提下实现结构合理减重,提高了设计经济性,从而为自升式风电安装船的桩腿设计与校核提供了可供借鉴的方法。
| [1] |
丁金鸿, 谭家华. 近海专用风电安装船概述[J]. 中国海洋平台, 2009, 5. DING Jin-hong, TAN Jia-hua. Offshore dedicated wind power installation ship overview[J]. China Offshore Platform, 2009, 5. |
| [2] |
魏可可, 高霄鹏. 水面舰船风载荷系数研究[J]. 舰船科学技术, 2018, 17: 27-31+38. WEI Ke-ke, GAO Xiao-peng. Research on wind load factor of a surface ship[J]. Ship Science and Technology, 2018, 17: 27-31+38. DOI:10.3404/j.issn.1672-7649.2018.09.005 |
| [3] |
林岳, 曹代利. 波浪作用下高桩墩式结构时程动力分析[J]. 水运工程, 2019, 8: 74-77. LIN Yue, CAO Dai-li. Dynamic analysis of pile structure under wave action[J]. Port&Waterway Engineering, 2019, 8: 74-77. DOI:10.3969/j.issn.1002-4972.2019.08.014 |
| [4] |
中国船级社, 海上移动平台入级规范[S]. 北京, 2016 : 2−63. CCS, Rules for classification of offshore mobile platforms[S]. Beijing, 2016: 2−63. |
| [5] |
冼敏元. 自升式平台“踩脚印”试验系统研制[J]. 船海工程, 2019, 05: 116-119. XIAN Min-yuan. Development of a model test system for jack-up unit reinstallation near a footprint[J]. Ship&Ocean Engineering, 2019, 05: 116-119. DOI:10.3963/j.issn.1671-7953.2019.05.029 |
| [6] |
国际海事组织, 海上移动式钻井平台构造和设备规则[S]. 2009. IMO, Mobile drilling platform construction and equipment rules[S]. 2009.
|
| [7] |
高耀东.ANSYS机械工程应用精华50例(第3版) [M]. 北京: 电子工业出版社, 2011: 20−30.
|
| [8] |
何伟, 徐志军. 考虑桩底沉渣的摩擦桩竖向承载力可靠度研究[J]. 铁道建筑技术, 2018, 10: 22-25. HE Wei, XU Zhijun. Study on reliability of vertical bearing capacity of friction pile considering bottom sediment[J]. Railway Construction Technology, 2018, 10: 22-25. DOI:10.3969/j.issn.1009-4539.2018.10.005 |
| [9] |
刘玉坤. 自升式服务平台桩靴结构优化设计[J]. 船舶与海洋工程, 2017, 3: 23-24. LIU Yukun. Structural optimization design of jack-up platform pile boots[J]. Naval Architecture and Ocean Engineering, 2017, 3: 23-24. |
| [10] |
肖宏, 杨霞, 陈泽军, 等. 赫兹接触理论在采用边界元法分析轧机轴承载荷中的应用[J]. 中国机械工程, 2010, 21(21): 2532-2535. XIAO Hong, YANG Xia, CHEN Ze-jun, et al. Application of Hertz contact theory in analyzing load distribution of Mill Roller bearing with boundary element method[J]. China Mechanical Engineering, 2010, 21(21): 2532-2535. |
 2021, Vol. 43
2021, Vol. 43

