2. 中国海洋大学 工程学院,山东 青岛 266100
2. Ocean University of China, College of Engineering, Qingdao 266100, China
随着海洋浮式结构的广泛应用,Spar海洋平台、Spar型浮式风电基础等所包含的立柱式结构,在一定流速下发生涡激振动的现象。为了区别,将这种长径比比较低、漂浮于水面的刚性结构物的涡激振动现象称为涡激运动。涡激运动涉及诸多科目,如流体力学、计算流体力学、振动学、结构力学和统计学等[1]。
海洋结构物涡激运动(Vortex induced motion,VIM)这一热点问题越来越受到深海工程技术人员和研究人员的关注,它是典型钝体绕流中升力和拖曳力所导致的直接后果[2]。目前国际上已有一些学者对涡激运动进行了研究,其中包含对海洋平台等结构物进行涡激运动集体预报等[3-5]。深水Spar平台、浮筒等均具有特殊的深吃水立柱式结构,当水流经过时,圆柱体后方发生周期性涡旋分离,致使结构受到沿流向的拖曳力以及垂直于流向的升力[6]。
本文重点研究的是低质量比圆柱与浮式圆柱涡激运动特性之间的关系。将运动系统简化为质量(m)-弹簧(k)-阻尼(ζ)系统,分析浮式圆柱运动的控制方程并通过4阶Runge-Kutta法离散,得到一段时间内步长的速度和位移。通过软件的自定义功能编程并嵌入到Fluent软件中,可以实现圆柱体的运动以及流场的更新,流场更新后再次反作用于圆柱,实现圆柱与流体的流固耦合。这已成为安全性及运动性能评估方面必须考虑的重要原因[7]。
1 数值计算模型 1.1 涡激运动的主要研究方法随着计算机技术的发展,计算流体力学(CFD)方法逐渐应用到研究浮式海洋平台涡激振动的问题中[8],采用数值模拟方法弥补了模型试验对于一些多参数的敏感性分析和流场捕捉方面成本太高的不足。为了保证有限元仿真的可靠性,在建模时需要考虑模型的力学性质,采用合理的单元类型和应变方程去模拟实际的结构[9]。
涡激运动的研究在于规定流体的参数,因为它与许多参数有关,这些参数都会直接或者间接影响这个流体力。
1.2 涡激运动的相关参数1)雷诺数:
2)斯托哈尔数:
3)约化速度:
4)无量纲振幅:
5)质量比:
式中:
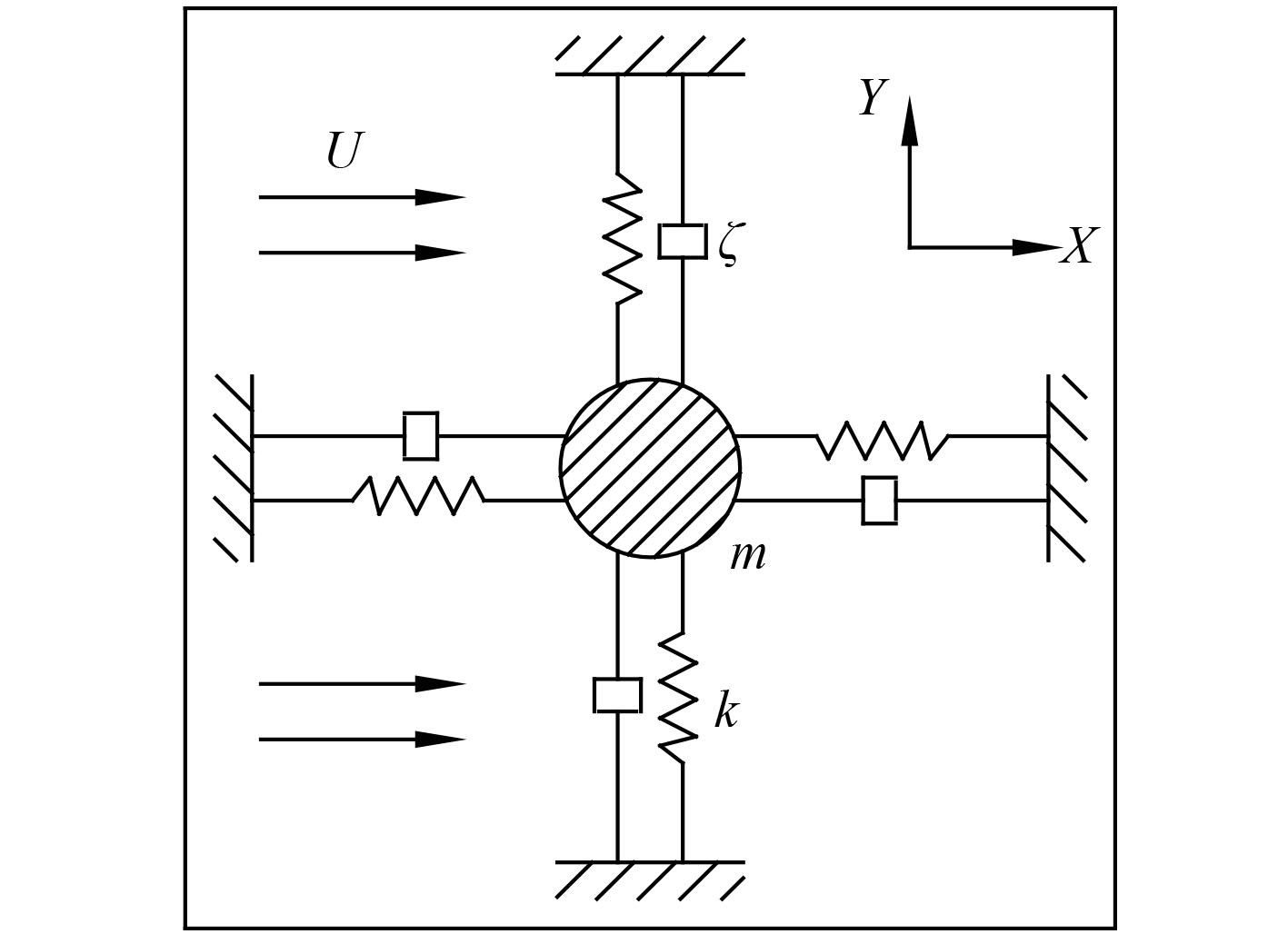
本文将弹性支撑圆柱的涡激运动系统简化为质量-弹簧-阻尼系统,如图1所示。
|
图 1 弹性支撑圆柱涡激运动模型 Fig. 1 Vortex-induced motions model of elastically supported cylinder |
均匀流中,圆柱涡激运动控制方程为:
| $ m\frac{{{{\rm{d}}^2}x}}{{{\rm{d}}{t^2}}} + {C_x}\frac{{{\rm{d}}x}}{{{\rm{d}}t}} + {K_x}x = {F_d}\left( t \right)\text{,} $ | (1) |
| $ m\frac{{{{\rm{d}}^2}y}}{{{\rm{d}}{t^2}}} + {C_y}\frac{{{\rm{d}}y}}{{{\rm{d}}t}} + {K_y}y = {F_l}\left( t \right)\text{。} $ | (2) |
式中:
本文计算区域与流场网格划分情况采用圆柱直径
网格划分既要保证足够的计算精确程度,又要兼顾运算的时间成本。在正式计算之前需要测试网格的密度,以获得最佳效果。由于在数值模拟中采用了动网格技术,所以单纯的测试圆柱绕流并不能获得计算精度与时间的最优方案。本文在质量比
|
|
表 1 网格测试结果 Tab.1 Grid test results |
为了验证数值模拟方法的可靠性,选择质量比为2.6的工况与Jauvtis和Williamson[10]实验结果进行对比。后期对质量比2.6的圆柱与质量比为1的浮式圆柱进行涡激运动特性研究比较,具体工况信息如表2所示。
|
|
表 2 计算工况表 Tab.2 Calculation condition table |
图2为不同响应分支所对应的涡旋泄放模式:左侧方为数值模拟结果,右侧方为Jauvtis和Williamson的实验结果。
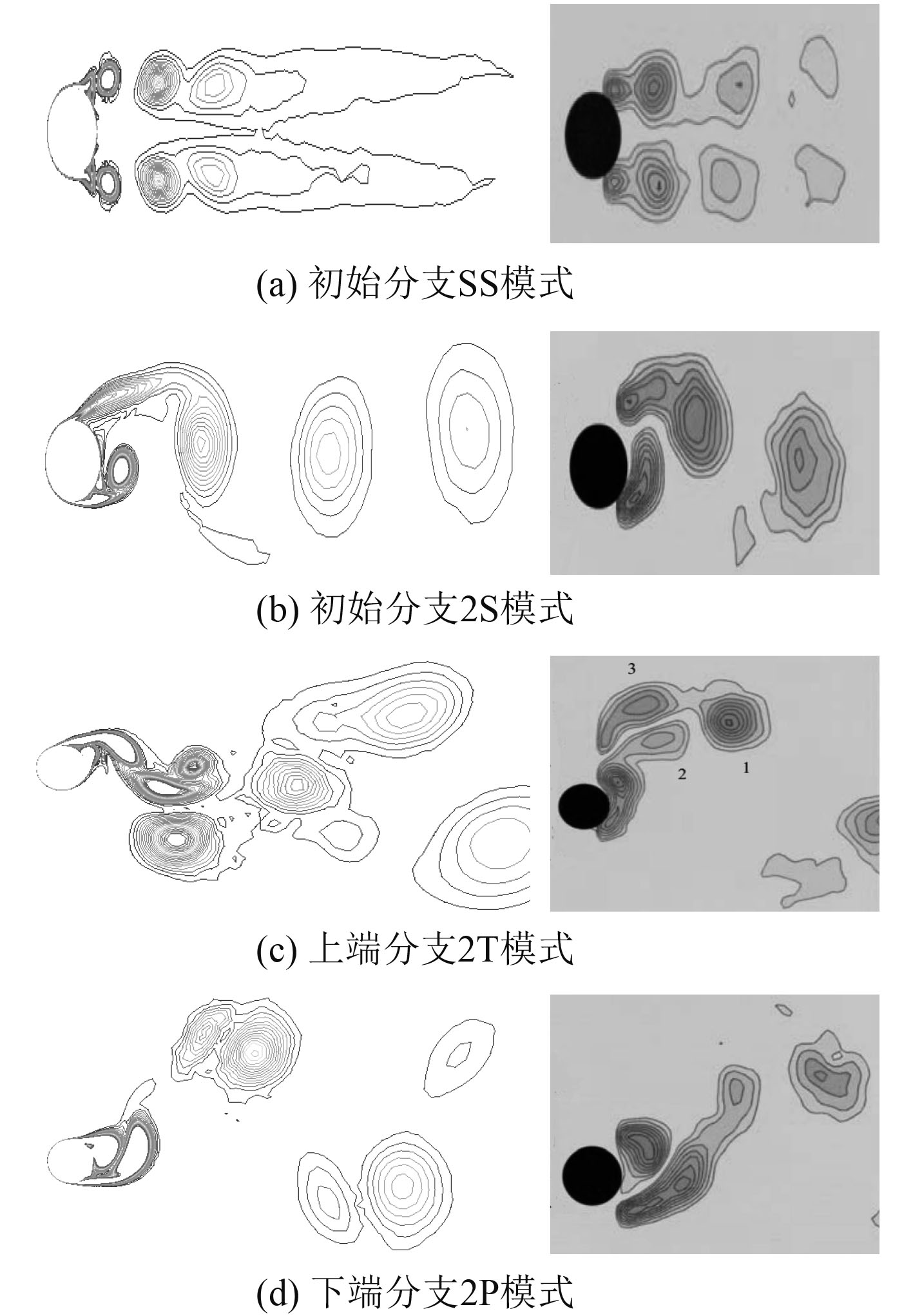
|
图 2 不同响应分支对应的涡泄模式 Fig. 2 Vortex release modes corresponding to different response branches |
在初始涡旋泄放模式有2种,分别为
在上端分支,当横向振幅达到最大值时,旋涡泄放出现了
在下端分支,涡旋泄放表示为
图3给出了

|
图 3 2T涡泄模式1个周期内的涡旋图 Fig. 3 2T Vortex diagram within one cycle of vortex release mode |
图4给出了不同约化速度下无量纲振幅与实验结果的对比。由图4(a)可见,数值模拟与实验所得的无量纲横流向振幅
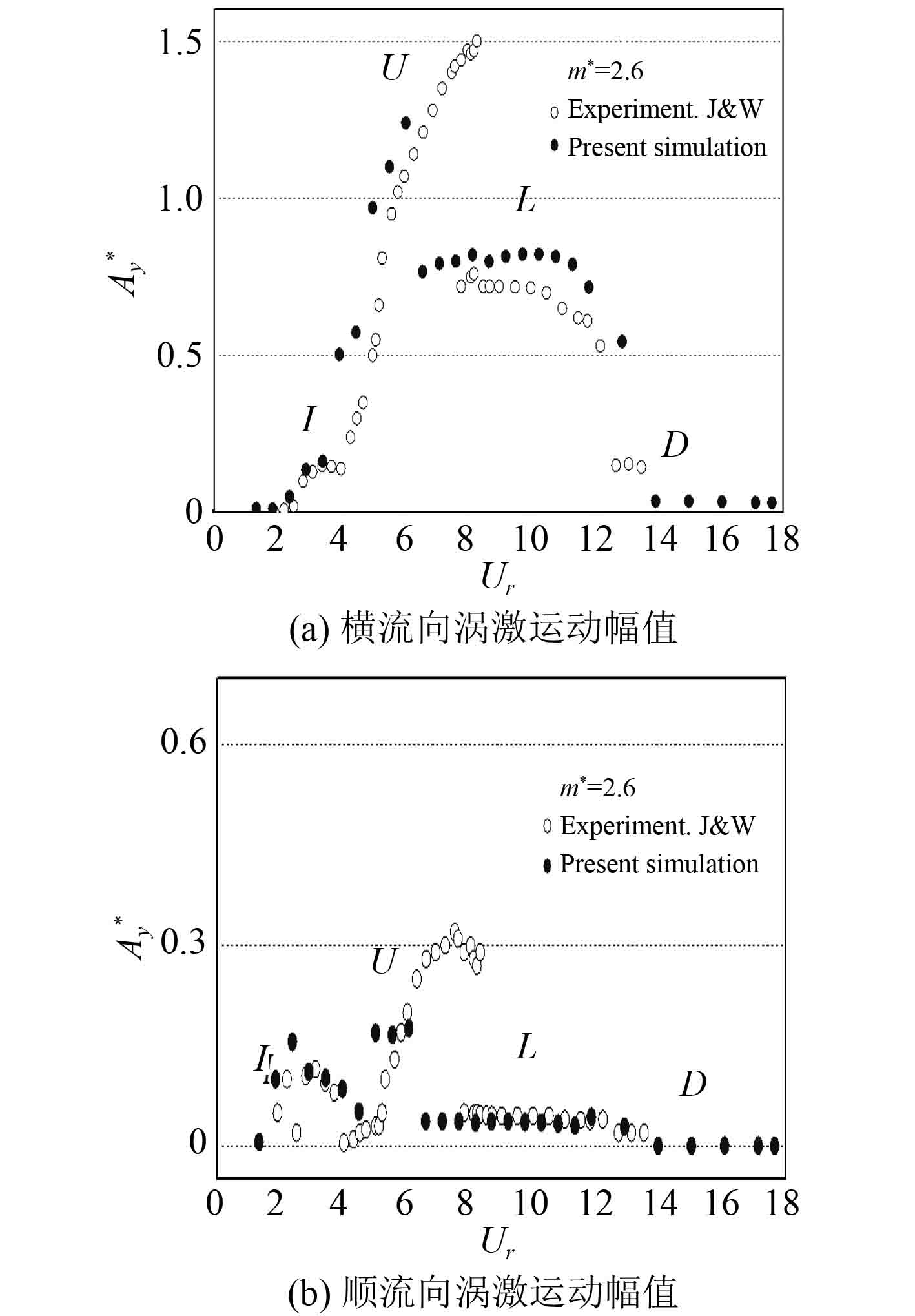
|
图 4 不同约化速度下无量纲振幅与实验结果的对比 Fig. 4 Comparison of dimensionless amplitude and experimental results at different reduction speeds |
图5给出了不同约化速度下,数值模拟与Jauvtis和Williamson实验所得的运动轨迹比较。数值模拟所得到的初始分支、上端分支和下端分支的圆柱运动轨迹与实验结果基本相似,再次验证了数值模拟方法的可靠。

|
图 5 不同约化速度下圆柱运动轨迹 Fig. 5 Cylindrical trajectory under different reduced speeds |
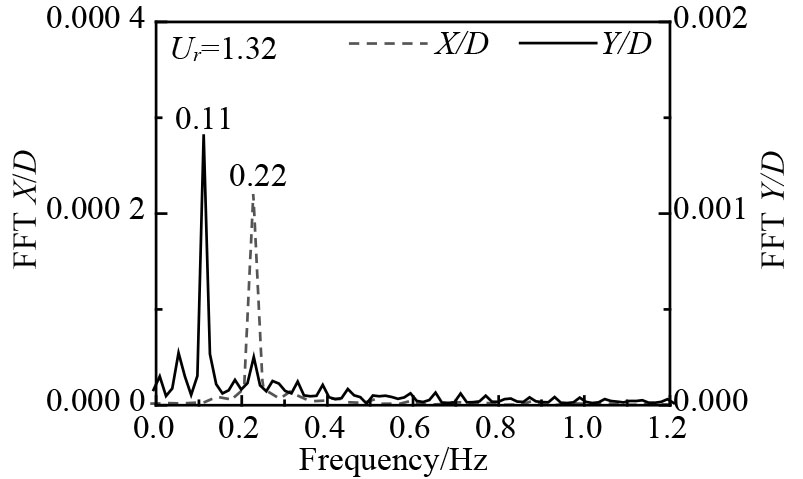
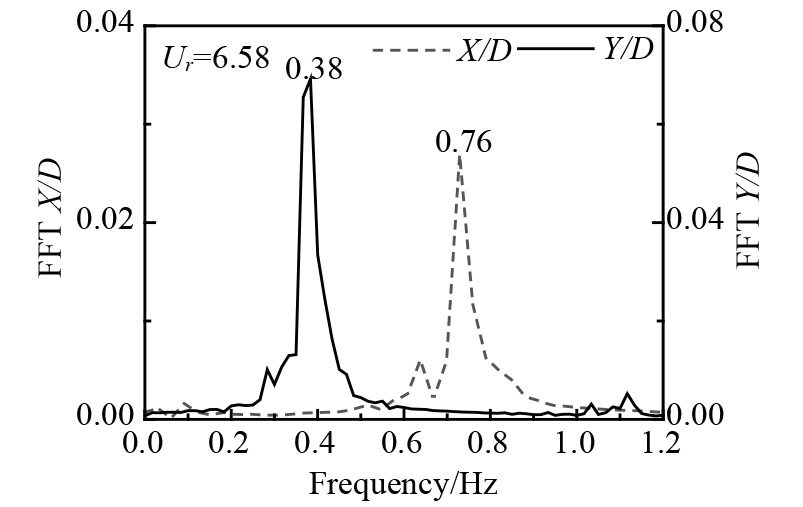
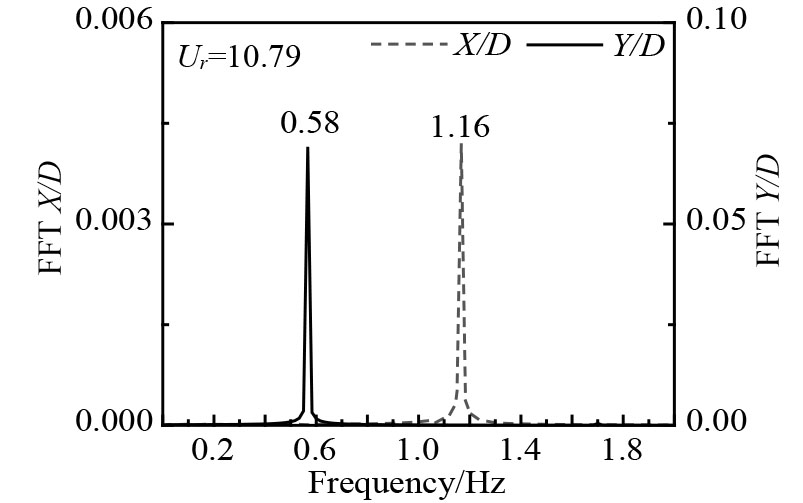
随着约化速度的不断增加,顺流向涡激运动频率均为横流向涡激运动频率的2倍关系。

|
图 6
浮式圆柱涡激运动在
|
表3给出了质量比为1的浮式圆柱横流向、顺流向涡激运动响应谱,图7给出了各自对应的涡泄图。顺流向与横流向频率比为2倍关系,初始分支和去同步化分支涡泄模式为
|
|
表 3 浮式圆柱X/D、Y/D涡激运动响应频谱图(m*=1) Tab.3 Spectral diagram of X/D and Y/D vortex induced motion of floating cylinder(m*=1) |
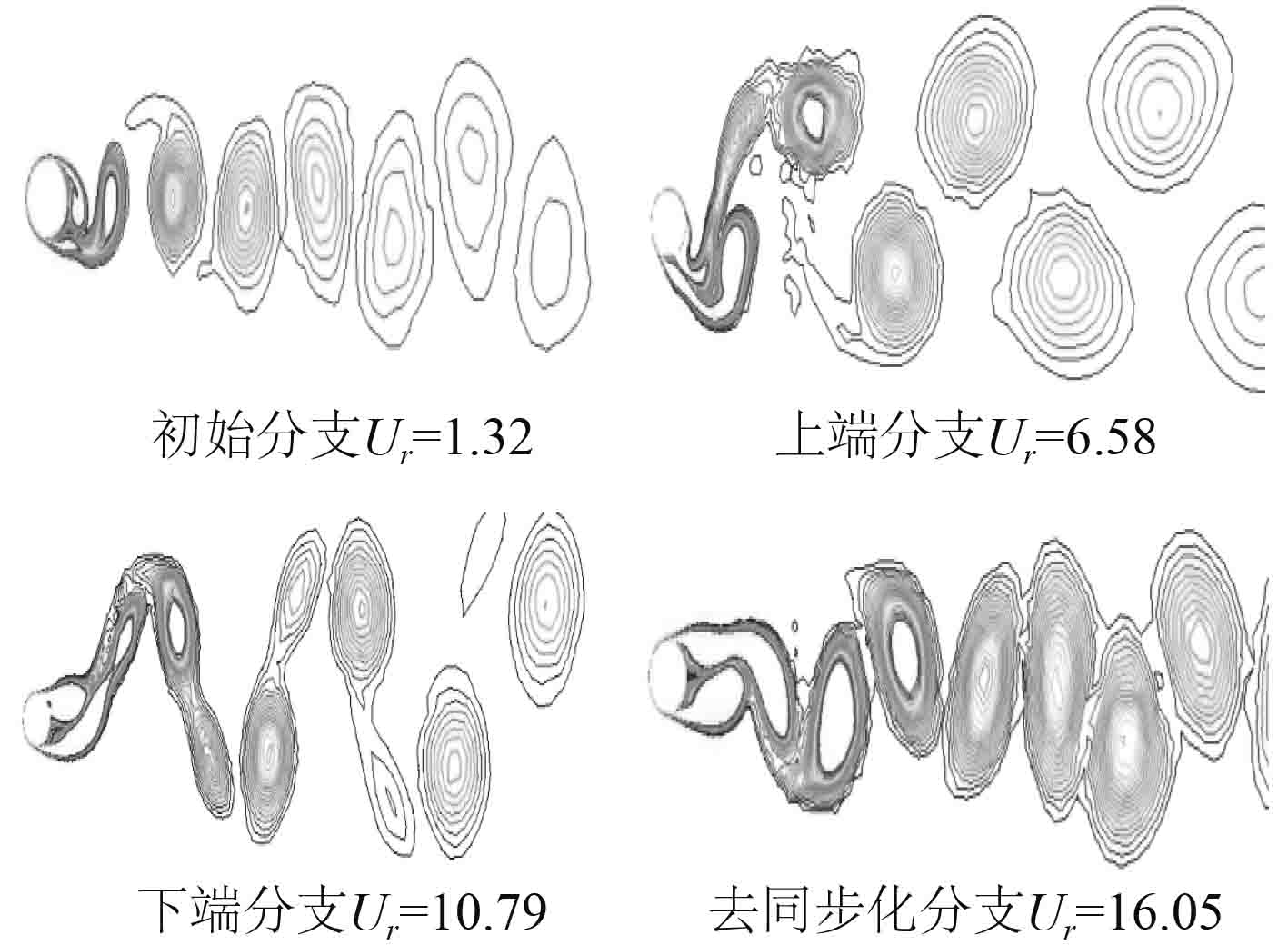
|
图 7 浮式圆柱X/D,Y/D涡激运动涡泄图 Fig. 7 Vortex-exhaust diagram of floating cylinder X/D and Y/D vortex-induced motion |
可以看出它的上端分支的范围很小,与初始分支难以区分,所以上端分支中的
本文应用CFD数值模拟方法对二维圆柱在不同流速下的涡激运动问题进行研究。
1)通过与Jauvtis&Williamson在2004年的经典实验结果的对比,数值计算可以较好模拟圆柱涡激运动,但在最大振幅方面有所低估。初始分支、上端分支和下端分支的运动轨迹与实验结果基本相似。数值模拟再现了实验中的
2)浮式圆柱涡激运动的初始分支,表现为2种不同的涡泄模式,分别为
| [1] |
渠基顺, 管义锋. 柱体涡激运动研究概述[J]. 中外船舶科技, 2013(3): 12-16. |
| [2] |
刘为民, 谷家扬, 陶延武, 等. 低质量比圆形四立柱涡激运动特性研究[J]. 振动与冲击, 2015, 34(19): 175-180. |
| [3] |
VAN DIJK R R T, MAGEE A, PERRYMAN S, et al. Model test experience on vortex induced vibrations of truss spars[C]. Offshore Technology Conference, 2003.
|
| [4] |
IRANI M, FINN L. Model testing for vortex induced motions of spar platforms[C]. Proceedings of the 23rd International Conference on Offshore Mechanics and Arctic Engineering, OMAE Conference, 2004: 605−611.
|
| [5] |
VAN DIJK R R T, FOURCHY P, VOOGT A J, et al. The effect of mooring system and sheared currents on vortex induced motions of truss spars[C]. Proceeding of the 22nd International Conference on Offshore Mechanics and Arctic Engineer-ing, OM AE Conference, 2003.
|
| [6] |
周 阳, 黄维平. 大直径浮式结构涡激振动的数值模拟[J]. 中国海洋大学学报(自然科学版), 2014, 44(9): 98-103. ZHOU Yang, HUANG Wei-ping. Numerical simulation of the vortex-induced motion of spar platform considering the coupling effect[J]. Periodical of Ocean University of China, 2014, 44(9): 98-103. |
| [7] |
王 颖, 杨建民, 李欣, 等. 均匀来流中浮式圆柱的涡激运动研究[J]. 中国海洋平台, 2010, 25(1): 8-15. DOI:10.3969/j.issn.1001-4500.2010.01.002 |
| [8] |
许鑫, 王春升, 陈国龙, 等. SDPSO设计关键技术及其在西非海域应用研究[J]. 中国造船, 2019, 060(z1): 379-391. DOI:10.3969/j.issn.1000-4882.2019.z1.052 |
| [9] |
李坤宏, 陈峥. 有限元分析在船舶复杂结构强度计算与优 化中的应用[J]. 舰船科学技术, 2020, 42(20): 4-6. |
| [10] |
JAUVTIS N, WILLIAMSON C H K. The effect of two degrees of freedom on vortex-induced vibration at low mass and damping[J]. Journal of Fluid Mechanics, 2004, 509: 23-62. DOI:10.1017/S0022112004008778 |
| [11] |
李 芬, 邹早建. 浮式海洋结构物研究现状及发展趋势[J]. 武汉理工大学学报(交通科学与工程版), 2003, 27(5): 682-686. |
| [12] |
PAN Z Y, CUI W C, MIAO Q M. Numerical simulation of vortex-induced vibration of a circular cylinder at low mass-damping using RANS code[J]. Journal of Fluids and Structures, 2007, 23(1): 23-37. DOI:10.1016/j.jfluidstructs.2006.07.007 |
 2021, Vol. 43
2021, Vol. 43