2. 上海交通大学,船舶海洋与建筑工程学院,上海 200240
2. School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiaotong University, Shanghai 200240, China
海上风电行业从20世纪80年代开始发展,并且自2000年以来发展迅速。截至2017年12月底,全球累计风电装机容量为5.4亿 kW。近年来,我国也加快了海上风电建设的步伐,截至2017年底,我国海上风电累计装机容量已达279万 kW。与陆上风机基础相比,海上风机基础面临的环境更为严峻。此外,海上风机比陆上风机安装更加困难,并且安装与维护成本也更高,据统计海上风机基础设施的成本占风机总投资的34%。因此,安全经济的基础设计也是海上风机能够正常长久运行的可靠保障[1]。海上风机基础作为风机支撑基础的重要部分,用来承担风机系统所受到的复杂荷载其稳定性直接关系到整个海上风机系统的安全运行。因此海上风机基础的稳定性成为海上风电场设计的重要考虑因素[2]。
不论是海洋平台还是海上风机,其在海洋环境中所受荷载均由其下部支撑基础承担。与海洋平台相比,海上风机受到的水平荷载较大,这些水平荷载主要是由风、波浪和冰引起的,基础受到的竖向荷载较小,其主要来源于结构的自重[3]。在极端条件下,海上风机基础受到的水平载荷会达到所受竖向载荷的约60%[4]。当基础受到外界荷载时,会发生沉降和转动,从而影响上部风机结构的正常工作,因此对其承载力进行研究对确定基础的稳定性至关重要[5]。
海上风机固定式支撑基础因其所适用环境和地质条件的不同,目前主要有单桩基础、承台基础、导管架基础、吸力式桶形基础等主要结构类型。吸力式桶形基础是近年来从海洋平台基础中逐渐发展起来的一种新型的海上风机基础,该基础由于其安装简单和可重复利用等优点,在海洋平台基础中得到了广泛应用,并逐步被应用于海上风机基础中。但由于海上风机与海洋平台在海洋环境中的荷载工况有一定的差别,仍需要通过对其承载特性研究现状进行全面认识,以实现吸力式桶形基础在海上风机基础中的可靠应用。
目前,国内外有学者通过试验、数值模拟或者理论分析的方法研究了吸力式桶形基础在竖向荷载下的承载特性。Liu等[6]通过试验研究了海上风机吸力式桶形基础与软土地基的相互作用机理,并且研究了软土地基中桶形基础在竖向荷载作用下的承载力特性。Vulpe[7]通过数值模拟研究了不排水条件下土体不排水抗剪强度对桶形基础的竖向承载力的影响。武科[8]、Hung&Kim[9]、Mehravar等[10]、代恒军[11]等通过数值模拟的方法对粘土中吸力式桶形基础的竖向承载力进行了研究并提出了计算公式。但这些研究的关注点多为大长径比桶形基础的承载特性,且对桶形基础在饱和黏土中的数值分析多是基于假设桶土接触面为不分离的情况进行,而实际桶土接触可能产生分离情况。同时,对适用于海上风机基础的小长径比宽浅桶形基础的分析较为有限,且现有的研究结果存在结论不一致的问题。因此对海上风机吸力式桶形基础的承载特性仍缺乏完整统一的认识,也因此对该类风机基础缺乏相应的行业设计规范和统一标准。为了使吸力式桶形基础未来在海上风机基础中得到良好的应用,仍需要进行全面的较为完善的研究。
本文将通过三维有限元数值分析对海上风机吸力式桶形基础的竖向承载力及其影响因素进行研究。以饱和黏土地基中的海上风机吸力式桶形基础为研究对象,通过大量的模拟计算,给出不同单向荷载作用下桶形基础的荷载位移曲线和土体破坏模式,重点考察了桶土接触面分离方式、桶体长径比、土体重度和土体不排水抗剪强度分布等因素对桶形基础竖向承载特性的影响。
1 计算模型为了模拟地基土的不排水条件,土体采用基于Tresca破坏准则的理想弹塑性模型,模型中的土体单元类型设置为C3D8RH[10]。土体不排水抗剪强度
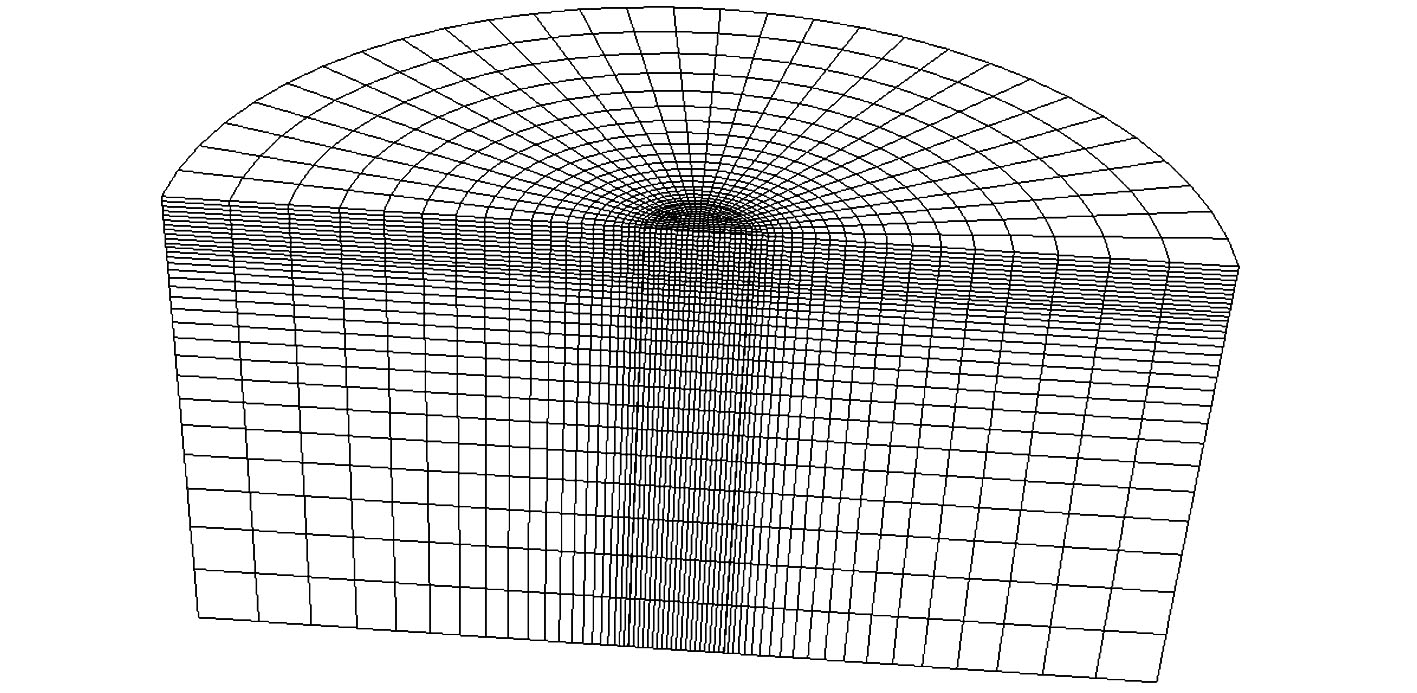
考虑到模型的对称性,文中取1/2模型进行建模,如图1所示。为了达到一定的计算精度,降低计算成本,通过网格分析后选择了较为合理的有限元尺寸。靠近桶形基础的区域网格划分较细,远离桶形基础的区域网格较大。通过研究发现,当土体直径为桶体直径的10倍、土体高度为桶体高度的5倍时,边界效应对计算结果的影响较小,可以忽略不计。本研究中有限元模型各边界的约束条件为:土体底部3个方向(x,y,z)的位移全部约束,土体侧向边界径向约束,对称面边界法向约束。
|
图 1 吸力式桶形基础有限元模型 Fig. 1 Finite element model of suction bucket foundation |
正确处理土体和桶形基础的接触关系是数值分析的关键。在Abaqus中,采用主从接触对算法定义该接触[12]。由于桶体材料的刚度和强度显著高于土体材料,因此,可将桶体表面选作主动面,对应的土体表面选作被动面。对于桶土接触面法向接触关系,因实际桶土分离情况难以确定,现有多数研究采用了不允许分离假设,但实际桶土接触面分离情况应介于二者之间。因此,本文分别采用了允许桶土接触面分离和不分离的假设进行了计算,以探讨接触面分离模式对承载特性的影响。
本文采用位移控制法逐步施加竖向位移,确定相应的荷载,由此得到地基的荷载-位移关系曲线[13]。通常,试验和计算得到的荷载-位移曲线,有2种典型情况,即陡变型和缓变型。在陡变型曲线中,存在明显的第二拐点,可将其对应的荷载作为极限承载力。在缓变型曲线中,没有明显的第二拐点,这时需根据沉降量来确定极限承载力[14]。对竖向极限承载力,Vesic[15]通过对饱和软黏土的沉降研究指出,浅基础地基破坏时的沉降
在本文研究中,竖向位移增量
吸力式桶形基础的长径比
在土体和桶形基础允许分离与不允许分离2种接触条件下,分别对长径比L/D为0,0.25,0.5,0.75,1.0的海上风机吸力式桶形基础进行有限元数值模拟,计算其竖向极限承载力,并分析不同参数对桶形基础极限承载力的影响。
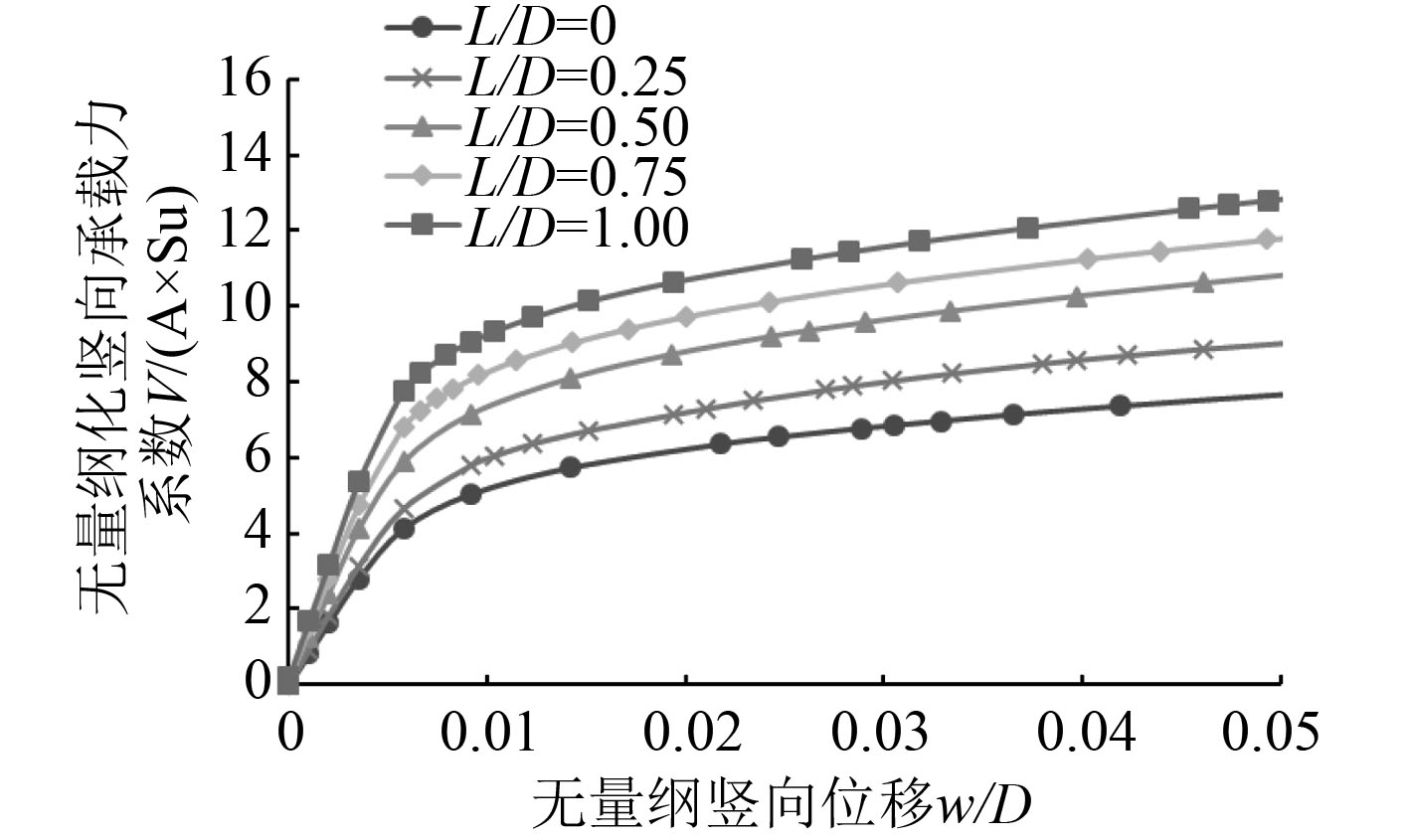
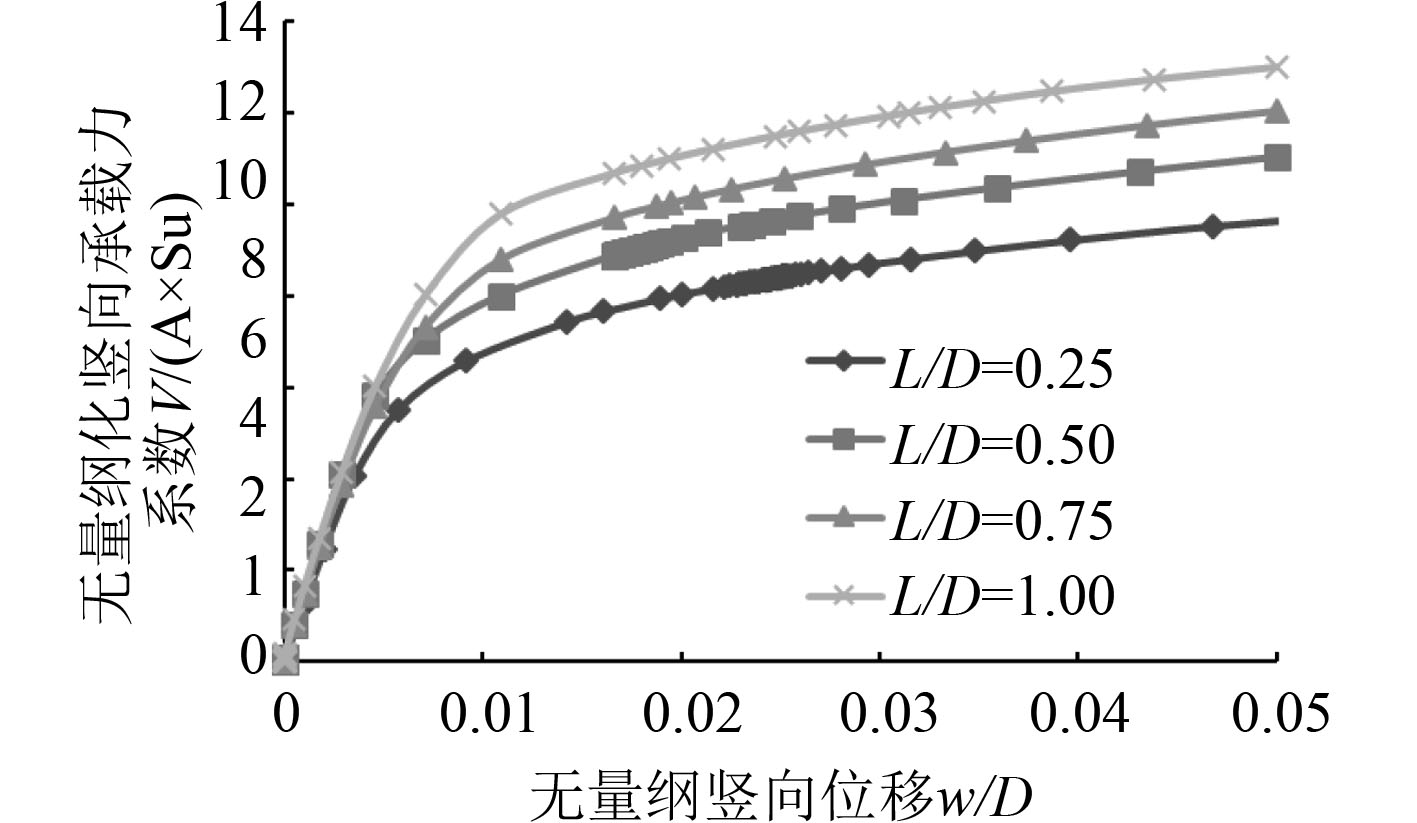
2.1 海上风机吸力式桶形基础的竖向极限承载力通过对桶形基础施加一定的竖向位移,考察不同长径比的桶形基础的竖向极限承载力。对有限元数值模拟得到的结果进行了无量纲处理,结果如图2和图3所示。图2和图3分别给出了桶土接触面允许分离与不允许分离这2种接触条件下,桶形基础的无量纲竖向荷载-位移曲线。根据前文所述,取竖向位移0.05
|
图 2 无量纲竖向荷载-位移曲线(不允许分离) Fig. 2 Normalized vertical load-displacement curve(fully bonded) |
|
图 3 无量纲竖向荷载-位移曲线(允许分离) Fig. 3 Normalized vertical load-displacement curve(allow separation) |
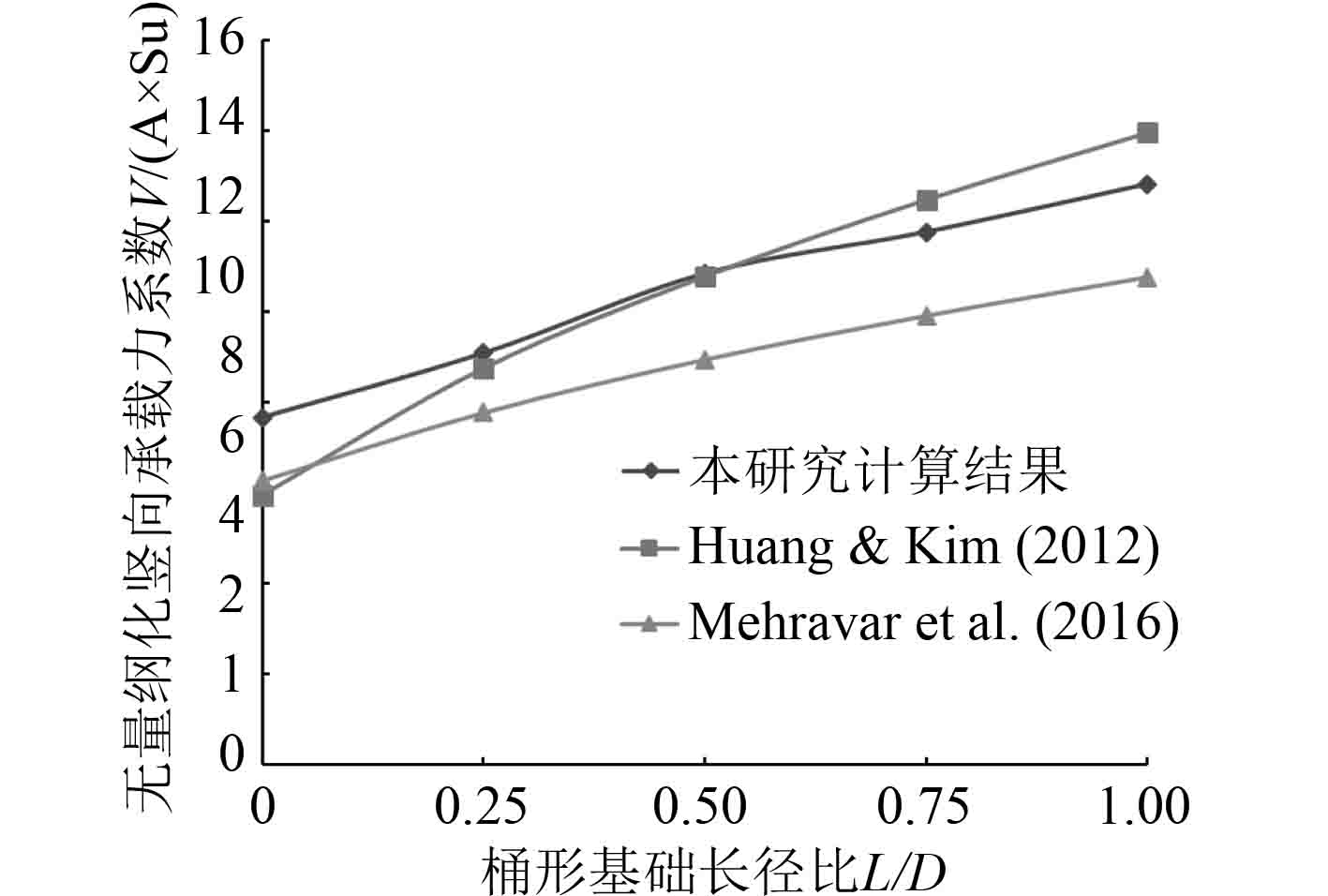
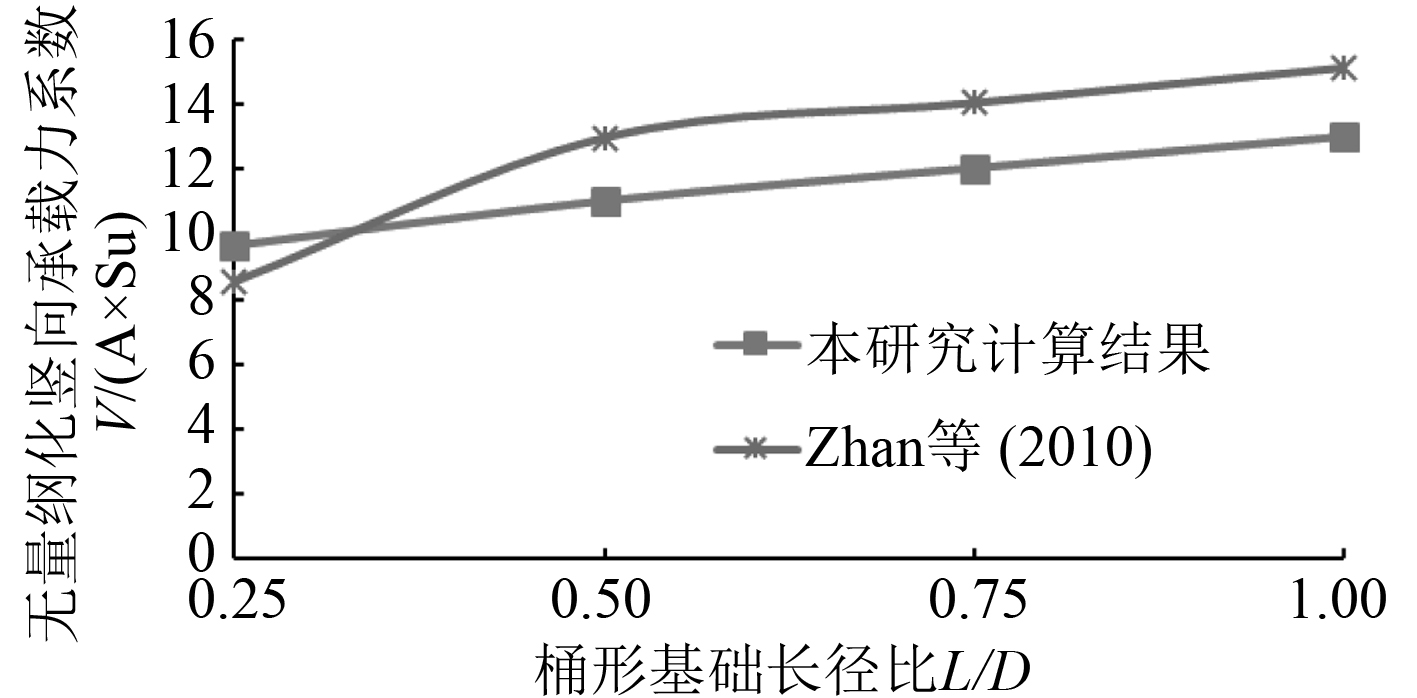
本文与其他研究中的模拟结果进行了对比,对比结果如图4和图5所示。Hung & Kim [9]通过数值模拟研究了桶土不允许分离时,长径比为0~1的吸力式桶形基础的竖向极限承载力,其土体和桶形基础参数的选择与本研究参数一致。Mehravar等[10]通过数值模拟研究了土桶不允许分离时,长径比为0~1的吸力式桶形基础的竖向极限承载力,其土体和桶形基础的参数与本文研究参数一致。Zhan等[18]通过数值模拟研究了桶土允许分离时,长径比为0.25~1的吸力式桶形基础的竖向极限承载力,其土体和桶形基础参数的选择与本研究参数一致。其中,图4为土体和桶形基础不允许分离的条件下,吸力式桶形基础的竖向承载力系数与基础长径比之间的非线性关系曲线对比图。通过与其他研究进行对比可以发现,当土体和桶形基础不允许发生分离时,本文的计算结果与文献[17]的模拟计算最大误差不超过8%,可以认为二者的结果是接近的。而Mehravar等[10]的模拟计算结果整体偏小,这可能是由于在其有限元计算的过程中考虑了桶体重力的作用而造成的。图5为土体和桶形基础允许分离的条件下,吸力式桶形基础的竖向承载力系数与基础长径比之间的非线性关系曲线对比图。当土体和桶形基础允许发生分离时,本文的计算结果与文献[18]的模拟结果最大误差不超过15%,认为本文研究的计算结果可靠。Zhan等[18]的计算结果偏大,可能是由于网格的划分密度造成的。
|
图 4 桶形基础竖向承载力与基础长径比关系曲线(不允许分离) Fig. 4 Vertical bearing capacity according to embedment ratios(fully bonded) |
|
图 5 桶形基础竖向承载力与基础长径比关系曲线(允许分离) Fig. 5 Vertical bearing capacity according to embedment ratios(allow separation) |
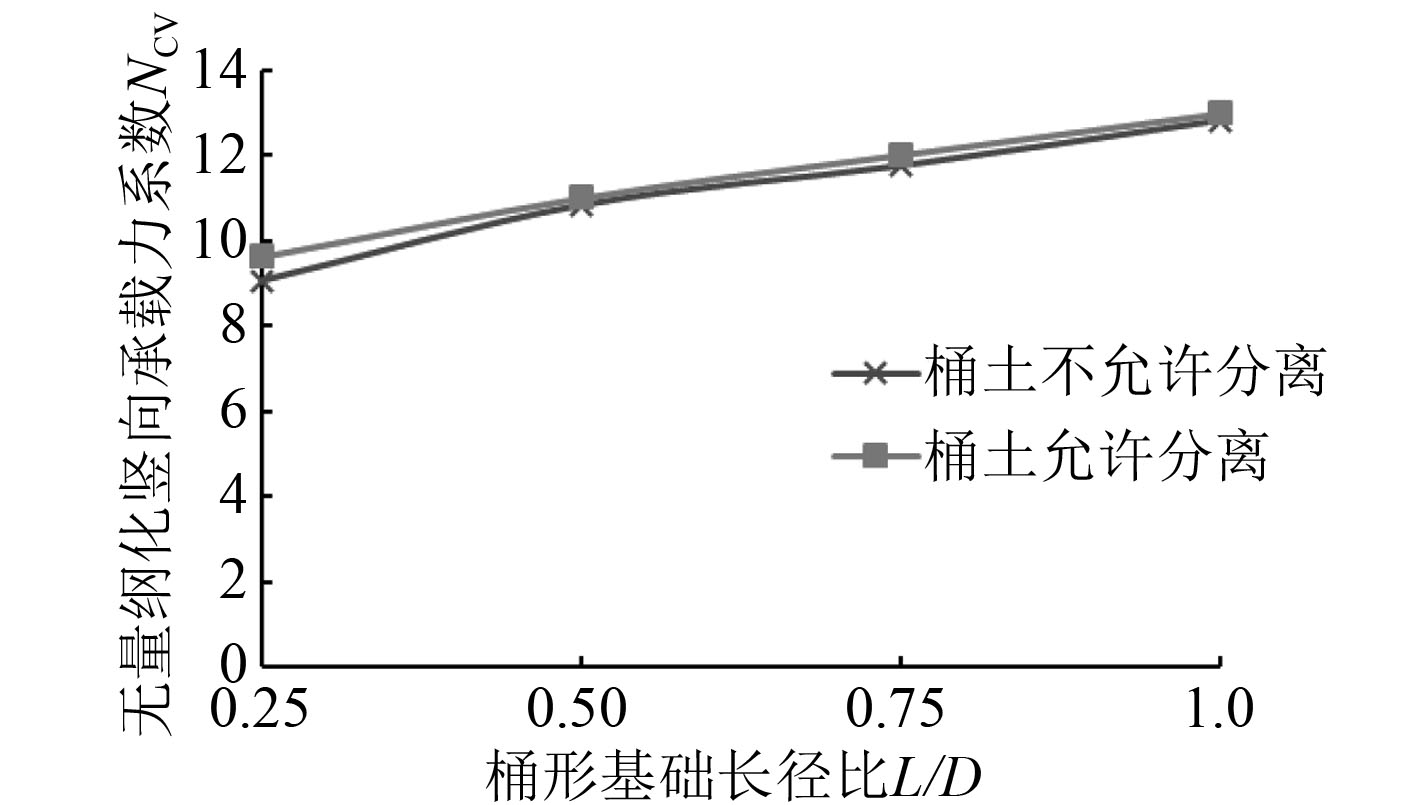
图6为桶形基础在桶土允许分离和不允许分离这2种接触条件下,桶形基础竖向承载力系数曲线对比图。可以看出,桶土的接触条件基本对桶形基础的竖向承载力没有影响。当桶土不允许分离时,基础的竖向承载力系数随着桶形基础长径比的增加而增加,二者的关系是非线性的。当桶形基础的长径比
|
图 6 桶形基础竖向承载力关系曲线对比图 Fig. 6 Comparison of the vertical bearing capacity |
|
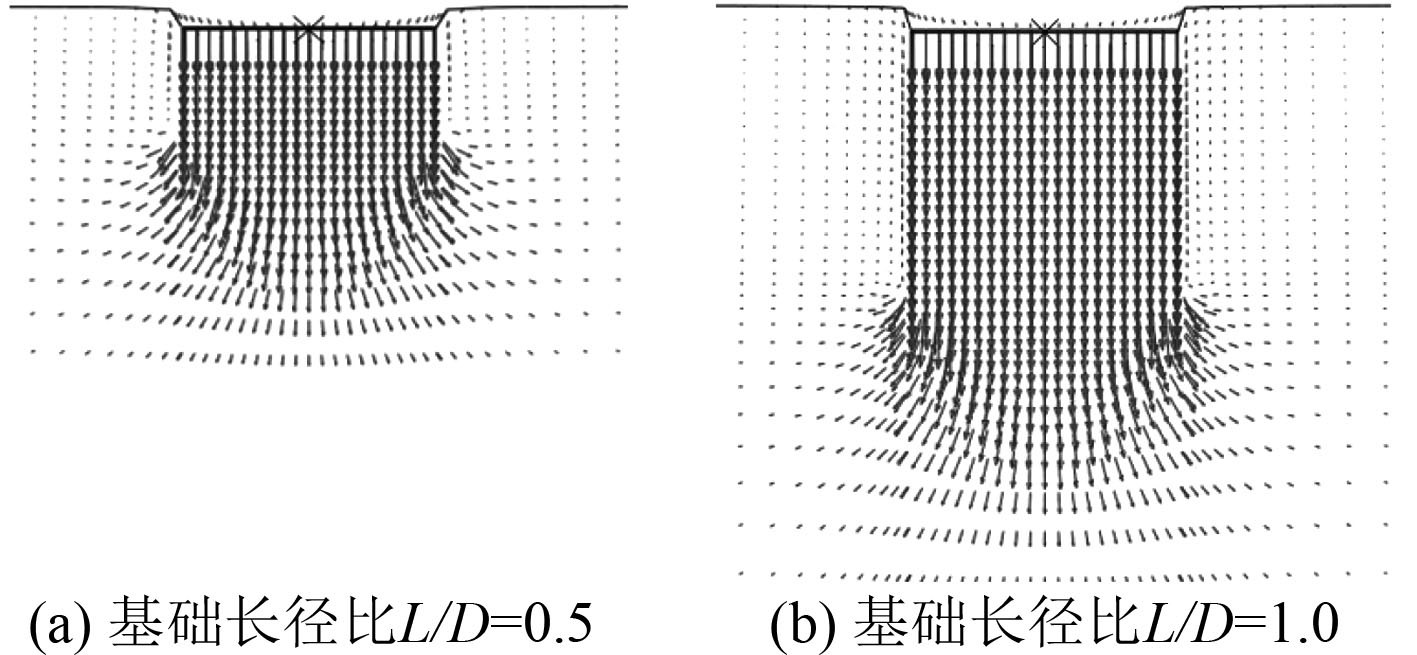
图 7 桶形基础在竖向荷载作用下的破坏模式图(不允许分离) Fig. 7 Failure mechanism under vertical load(fully bonded) |
|
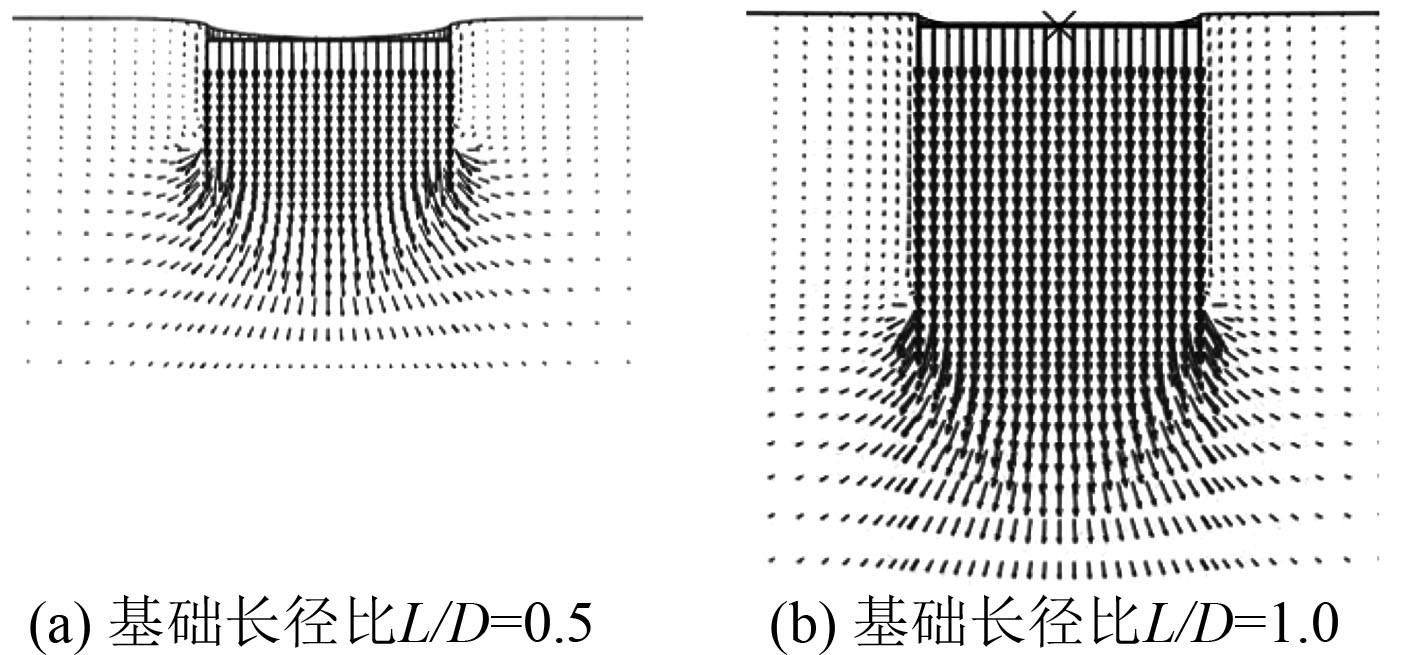
图 8 桶形基础在竖向荷载作用下的破坏模式图(允许分离) Fig. 8 Failure mechanism under vertical load(allow separation) |
针对长径比为0.25,0.5,0.75和1.0的桶形基础,变化土体的有效重度
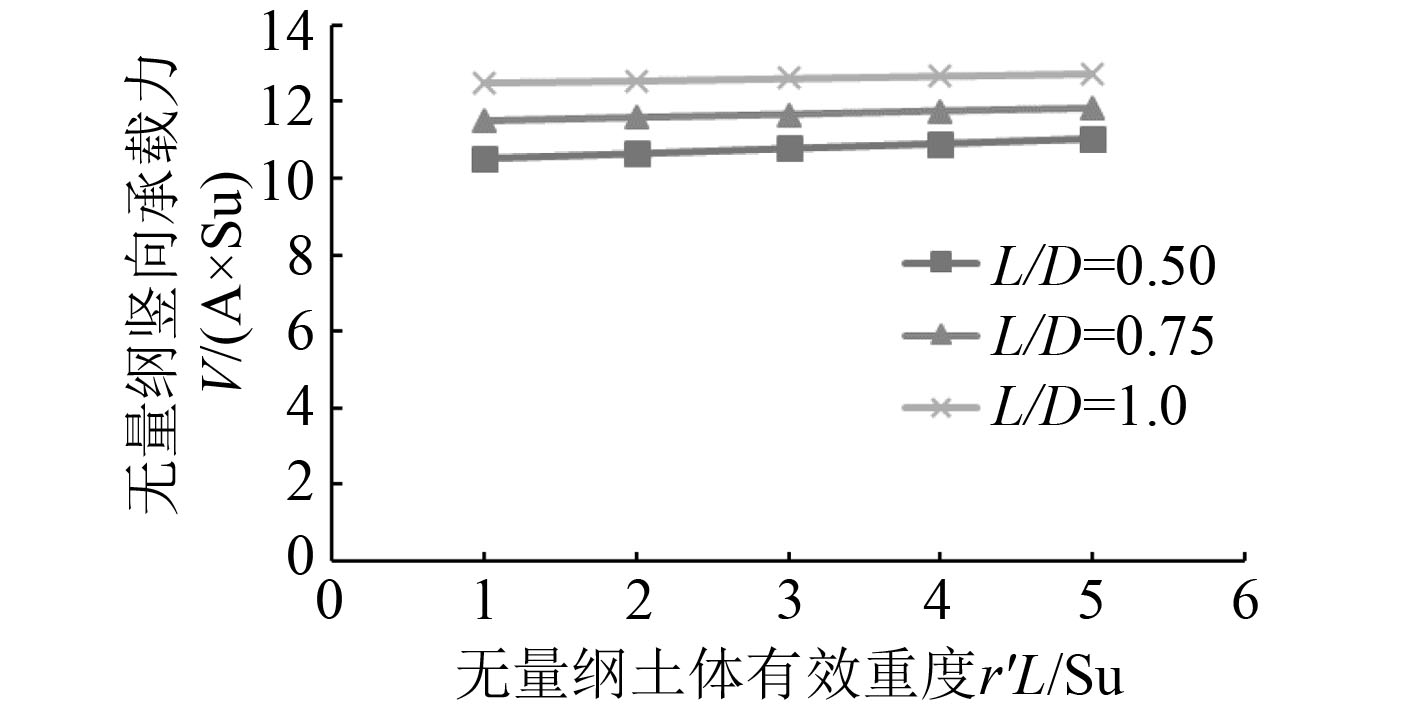
本文计算了在土体和桶形基础不允许分离和允许分离2种接触条件下,土体的有效重度的变化对桶形基础竖向极限承载力的影响,选取土体的有效重度的无量纲参数
|
图 9
土体有效重度对桶形基础竖向承载力的影响(不允许分离)
Fig. 9
Vertical bearing capacity with
|
|
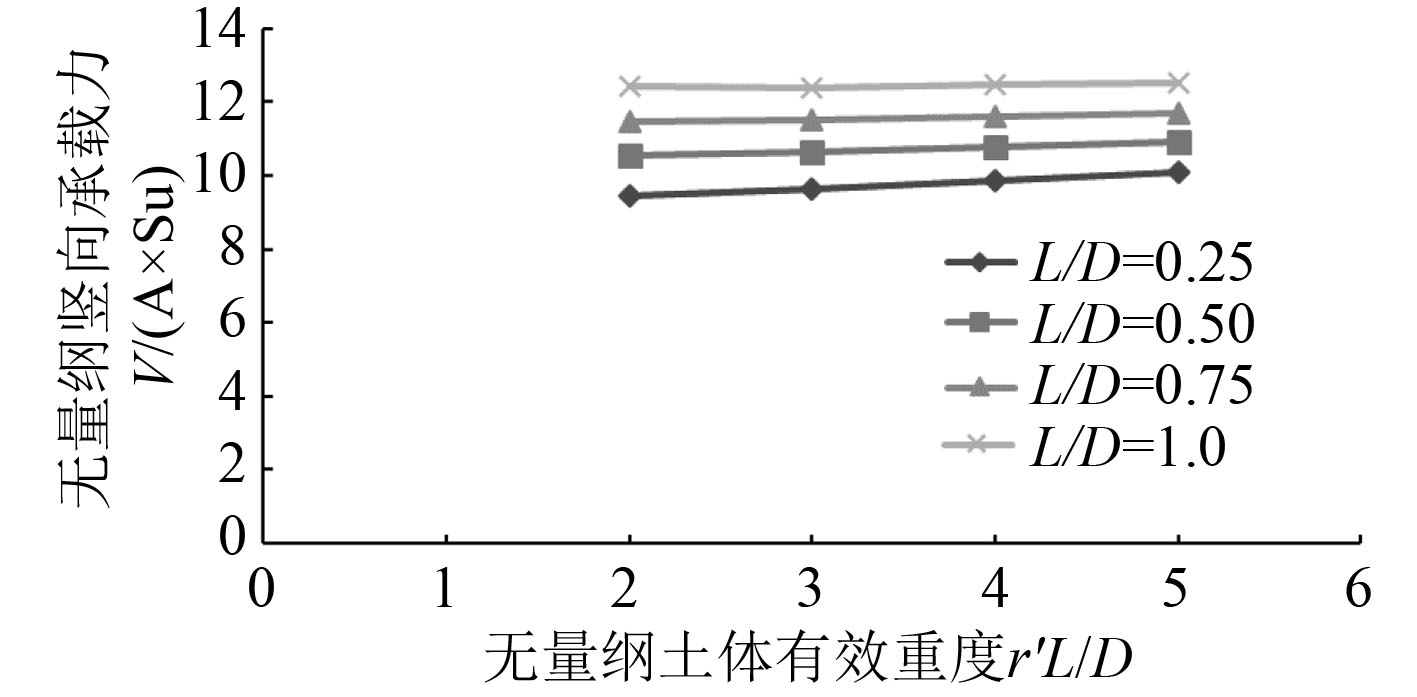
图 10
土体有效重度对桶形基础竖向承载力的影响(允许分离)
Fig. 10
Vertical bearing capacity with
|
由图9可知,对于长径比在0.5~1.0范围内的吸力式桶形基础,当土体和桶形基础不允许分离时,软土地基中桶形基础的竖向极限承载力几乎不会随着土体的有效重度的变化而变化。当土体的有效重度无量纲参数
由图10可知,对于长径比小于1的桶形基础,当土体和桶形基础允许发生分离时,软土地基中桶形基础的竖向极限承载力随着土体的有效重度的增加而近似呈线性增长的趋势,且随着桶形基础长径比的增加,曲线的增长率逐渐降低。当土体有效重度的无量纲参数
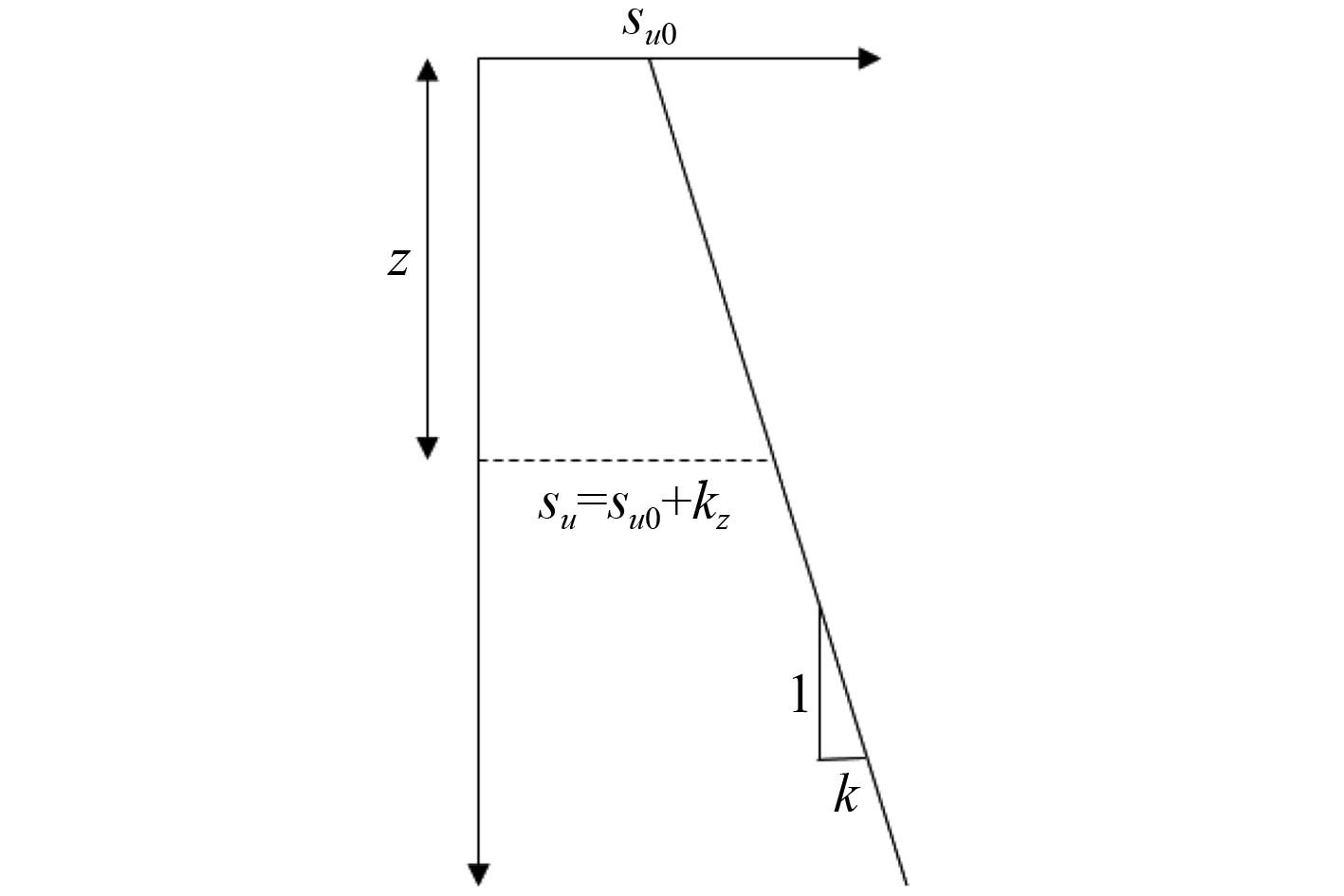
根据已有的现场原位测试经验可知[19],对于大部分的正常固结土及超固结土而言,其不排水抗剪强度随埋深的增加而呈近似的线性增长趋势,如图11所示。其中
|
图 11 土体不排水抗剪强度的竖向分布 Fig. 11 Undrained shear strength distribution in the direction of z |
Yun等[20]提出基础的承载力系数不会受到单个系数
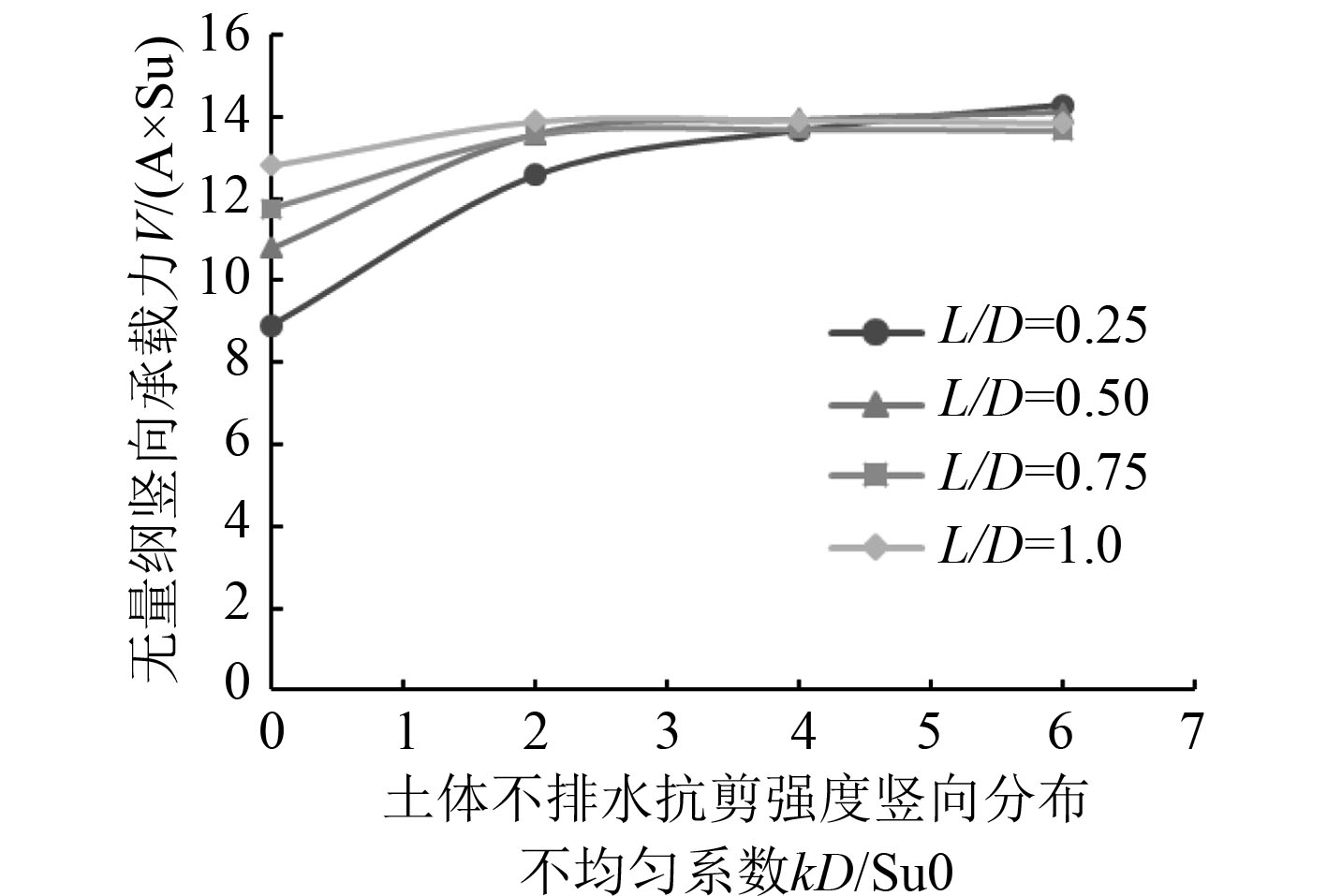
图12为不同长径比的桶形基础的竖向极限承载力与土体不排水抗剪强度竖向不均匀分布的关系曲线。可以得出,桶形基础的竖向承载力系数随着土体不排水抗剪强度竖向分布不均匀系数
|
图 12
土体不排水抗剪强度竖向不均匀分布对桶形基础竖向承载力的影响
Fig. 12
Vertical bearing capacity with
|
本文通过Abaqus三维有限元计算,分析讨论了桶形基础的长径比、土体有效重度和土体不排水抗剪强度分布等因素对黏土中海上风机吸力式桶形基础的竖向极限承载力的影响,得到以下结论:
海上风机吸力式桶形基础的长径比会影响基础的竖向极限承载力,随着基础长径比的增加,基础的极限承载力呈线非线性增长的趋势。土体和桶形基础之间是否允许分离基本不会对桶形基础在竖向荷载作用下的破坏模式产生影响。
土体重度对海上风机吸力式桶形基础的极限承载力影响较小。在桶土不允许分离的条件下,当土体的有效重度无量纲参数
土体不排水抗剪强度的竖向不均匀分布对海上风机吸力式桶形基础的影响较大。桶形基础的竖向承载力系数随着土体不排水抗剪强度竖向分布不均匀系数
| [1] |
CARTER J M F. North Hoyle offshore wind farm: design and build[J]. Energy, 2007, 160(1): 21-29. |
| [2] |
彭耀, 张笑通, 万德成, 等. 海上固定式风机基础的波流载荷数值计算分析[J]. 水动力学研究与进展, 2017, 32(1): 1-10. |
| [3] |
YU H, ZENG X, LI B, et al. Centrifuge modeling of offshore wind foundations under earthquake loading[J]. Soil Dynamics & Earthquake Engineering, 2015, 77: 402-415. |
| [4] |
WANG H, CHENG X. Undrained bearing capacity of suction caissons for offshore wind turbine foundations by numerical limit analysis[J]. Marine Geotechnology, 2016, 34(3): 252-264. DOI:10.1080/1064119X.2015.1004766 |
| [5] |
鲁晓兵, 郑哲敏, 张金来. 海洋平台吸力式基础的研究与进展[J]. 力学进展, 2003, 33(1): 27-40. DOI:10.3321/j.issn:1000-0992.2003.01.005 |
| [6] |
LIU R, CHEN G, LIAN J, et al. Vertical bearing behaviour of the composite bucket shallow foundation of offshore wind turbines[J]. Journal of Renewable and Sustainable Energy, 2015, 7(1): 013123. DOI:10.1063/1.4907598 |
| [7] |
VULPE C. Design method for the undrained capacity of skirted circular foundations under combined loading: effect of deformable soil plug[J]. Géotechnique, 2015, 65(8): 669-683. DOI:10.1680/geot.14.P.200 |
| [8] |
武科. 滩海吸力式桶形基础承载力特性研究[D]. 大连: 大连理工大学, 2007.
|
| [9] |
HUNG L C, KIM S R. Evaluation of vertical and horizontal bearing capacities of bucket foundations in clay[J]. Ocean Engineering, 2012, 52: 75-82. DOI:10.1016/j.oceaneng.2012.06.001 |
| [10] |
MEHRAVAR M, HARIRECHE O, FARAMARZI A. Evaluation of undrained failure envelopes of caisson foundations under combined loading[J]. Applied Ocean Research, 2016, 59: 129-137. DOI:10.1016/j.apor.2016.05.001 |
| [11] |
代恒军. 软土中吸力锚承载力分析[D]. 杭州: 浙江大学, 2008.
|
| [12] |
齐威. ABAQUS 6.14超级学习手册[M]. 2016.
|
| [13] |
刘振纹. 软土地基上桶形基础的稳定性研究[D]. 天津: 天津大学, 2002.
|
| [14] |
李驰. 软土地基桶形基础循环承载力研究[D]. 天津: 天津大学, 2006.
|
| [15] |
VESIC A S. Analysis of ultimate loads of shallow foundations[J]. Jsm & F Divprocasce, 1973, 99(11): 45-73. |
| [16] |
周景星. 基础工程[M]. 北京: 清华大学出版社有限公司, 1996.
|
| [17] |
HUNG L C, KIM S-R. Evaluation of undrained bearing capacities of bucket foundations under combined loads[J]. Marine Georesources & Geotechnology, 2014, 32(1): 76-92. |
| [18] |
ZHAN Y, LIU F. Numerical analysis of bearing capacity of suction bucket foundation for offshore wind turbines[J]. Electronic Journal of Geotechnical Engineering, 2010, 15: 633-644. |
| [19] |
ANDERSEN K H, JOSTAD H P. Foundation design of skirted foundations and anchors in clay[C]// proceedings of the Offshore technology conference, 1999. Offshore Technology Conference.
|
| [20] |
YUN G, BRANSBY M F. The horizontal-moment capacity of embedded foundations in undrained soil[J]. Revue Canadienne De Géotechnique, 2007, 44(4): 409-424(416). DOI:10.1139/t06-126 |
 2021, Vol. 43
2021, Vol. 43
