2. 中国石油大学(华东),山东 青岛 266580
2. China University of Petroleum, Qingdao 266580, China
近年来,陆地常规油气资源在逐年减少,合理地开发和利用海洋资源才能缓解未来可能面临的能源危机。一般用于开采海洋资源的海上平台、海洋管道等都包含一些圆柱体结构,往往这些圆柱体结构是平台或管道的重要支撑和组成部件,一旦其发生破坏,后果将难以预想。所以研究圆柱结构在海水中绕流时的瞬时流场分布和受力特性情况将有助于更好更安全地开采海洋资源。
目前已经有许多国内外的学者对圆柱绕流和卡门涡街进行过研究和模拟,李霖等[1]建立了二维圆柱体绕流模型,通过大涡模拟的方法对模型做仿真模拟,得到在低雷诺数时卡门涡街的漩涡脱落规律。苏铭德等[2]采用大涡模拟法,得到非正交曲线坐标系下N-S方程的表达式,求出平均阻力系数与平均升力系数。Zdrabkobich[3]及Igarash[4]在试验中发现两串列圆柱周围的流场与圆心距之间密切相关。麻伟巍等[5]建立了双圆柱绕流三维数值模型,并利用Fluent软件对模型进行仿真模拟。刘娟等[6]建立了四圆柱绕流模型,将 Fluent大涡模拟方法应用于这种多圆柱绕流模型的数值模拟,所得结果与其他研究结果比较,可以很好地吻合。陈斌等[7] 模拟出多圆柱绕流流场的势流解,得到多圆柱模型流场的流体分布图。
本文在前人研究的基础上采用大涡模拟的方法对海上平台支撑柱单圆柱绕流和双圆柱绕流模型进行数值仿真模拟,通过改变雷诺数和双圆柱绕流排列方式模拟分析流体瞬时流场和圆柱表面的升力系数和阻力系数随时间的变化关系曲线,根据速度云图和力系数曲线图分析流场和圆柱体受力的变化规律。
1 基本理论与物理模型 1.1 大涡模拟控制方程1)傅里叶截断滤波函数
其滤波速度如下式:
| $ G\left( x \right) = \frac{1}{{\sqrt {2\text{π} } }}\int {_{ - \infty }^{ + \infty }} \widehat G\left( k \right){e^{ - ikx}}{\rm{d}}k\text{;} $ | (2) |
2)高斯型滤波速度
其滤波速度如下式:
| $ G(|x - x'|) = {\prod\limits_{i = 1}^3 {\left( {\frac{6}{{\text{π} {\Delta ^3}}}} \right)} ^{1/2}}e\frac{{6{{\left( {{x_i} - x'} \right)}^2}}}{{{\Delta ^2}}}\text{。} $ | (3) |
高斯滤波器性能最好,但计算量大,傅氏滤波器应用较广。
1.2 Smagorinsky模型Smagorinsky动力模型能较好地贴合大涡模拟方法中常用的涡粘模型,其表达式如下式:
| $ {\tau _{ij}} - \frac{1}{3}{\sigma _{ij}}{\tau _{kk}} = - 2{v_t}\overline {{S_{ij}}} \text{,} $ | (4) |
在二维坐标系中,不可压缩粘性流体的运动规律可以用N-S方程来描述,LES中滤波速度的表达式如下式:
| $\overline {{u_i}} \left( {x,t} \right) = \int {G\left( {x,x',\Delta } \right)} {u_i}\left( {x',t} \right){\rm{d}}x'\text{,}$ | (5) |
不可压缩粘性流体的运动遵循连续性方程:
| $ \frac{{\partial u}}{{\partial x}} + \frac{{\partial v}}{{\partial y}} + \frac{{\partial w}}{{\partial z}} + \frac{{\partial \rho }}{{\partial t}} = 0\text{。} $ | (6) |
式中:u,v,w 为速度矢量;ρ为不可压缩流体的密度,kg/m3。
1.3 三种圆柱绕流物理模型1)单圆柱绕流
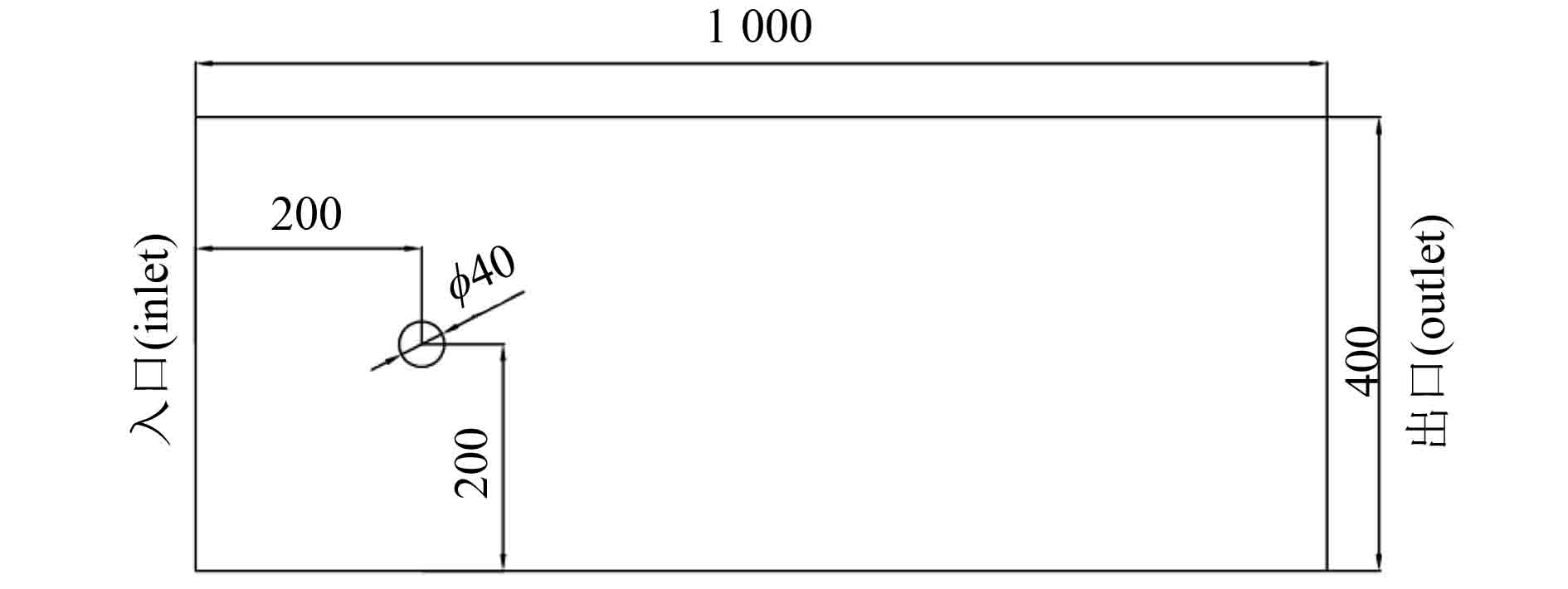
将海上平台支撑柱简化为图1所示的计算域,圆柱直径为D=40 mm。区域长×宽为1000×400 mm,圆心离入口和下边界的距离均为200 mm。
|
图 1 单圆柱绕流物理模型 Fig. 1 Physical model of flow around a single cylinder |
2)串列双圆柱绕流
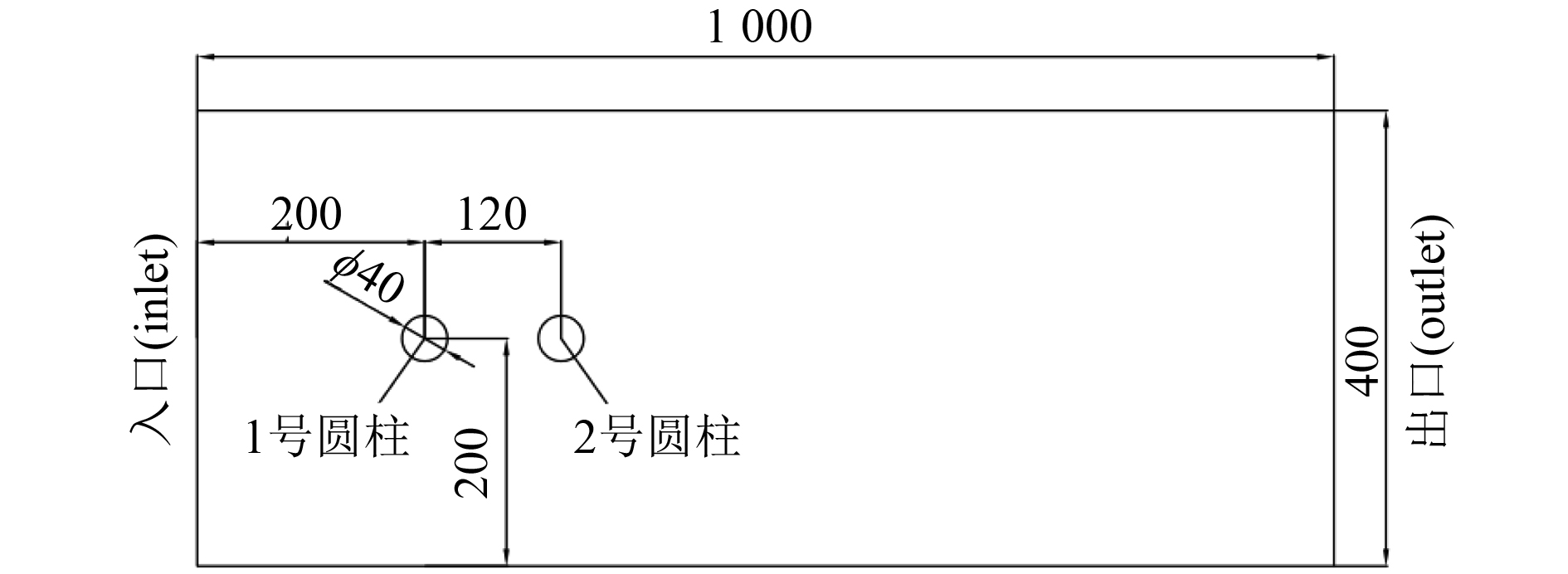
模拟海上平台支撑柱串列绕流时的物理模型如图2所示。以第1个圆柱的圆心为坐标原点,距离上下壁为200 mm,距离入口处为200 mm。
|
图 2 串列双圆柱绕流物理模型 Fig. 2 Physical model of the flow around a tandem double cylinder |
3)并列双圆柱绕流
模拟海上平台支撑柱并列绕流时的物理模型如图3所示。以2个圆柱的圆心连线的中心点为坐标原点,入口处距离圆柱为200 mm。

|
图 3 并列双圆柱绕流物理模型 Fig. 3 Physical model of flow around parallel double cylinders |
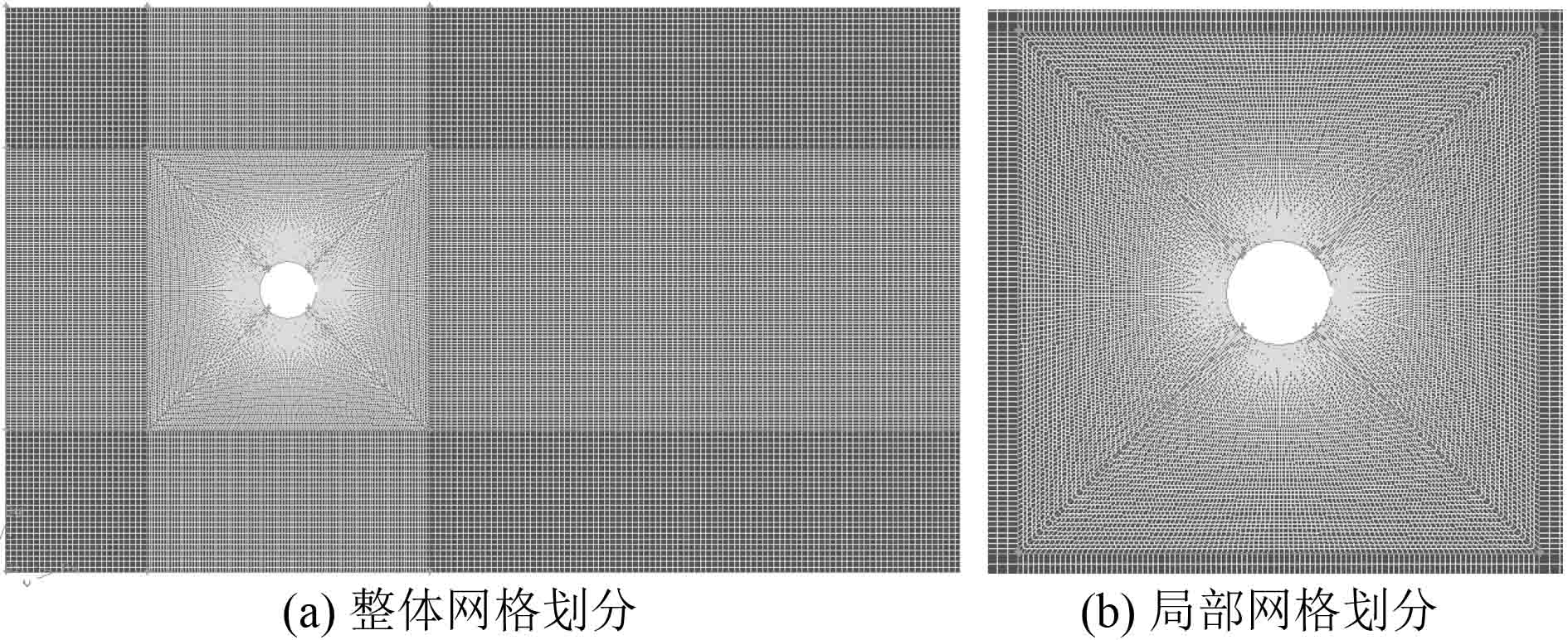
本文采用mesh对流域进行结构化网格划分,参考文献[8]可知,将整个流场域分为9个模块,柱体所在的模块根据对角线可划分为4个小区域。将这4个小区域的网格加密,可以得到合理的计算网格,具体网格划分情况如图4所示。
|
图 4 网格划分详图 Fig. 4 Mesh division |
串列和并列双圆柱绕流网格划分方法与单圆柱绕流类似,均需要在柱体附件流域进行网格加密。
2.2 边界条件雷诺数是可以描述粘性流体流动情况的一个无量纲物理量,即
| $ {\rm{Re}} = \frac{{\rho UL}}{\mu }\text{。} $ | (7) |
式中:ρ为流体的密度,kg/m3;U为流体的特征速度,m/s;L为刚体特征长度,m;μ为流体的粘度系数,Pa•S。
边界条件:来流方向选取为速度入口,出口则为自由出流,上下表面以及圆柱表面为壁面,瞬态时间步长则取5×10−5 s。选取200,2000,200000 三种雷诺数进行模拟。
3 数值模拟结果与分析 3.1 圆柱绕流瞬时流场模拟结果利用大涡模拟计算出在3种雷诺数下t=15 s时单圆柱绕流的瞬时流场结果,如图5所示。

|
图 5 不同雷诺数下单圆柱绕流瞬时流场 Fig. 5 Instantaneous flow field around a single cylinder under different Reynolds numbers |
流体的速度越大其压力就越小,从图5可以看出,3种雷诺数下由于流体遇到柱体时会发生绕流现象,使柱体上下两侧流速较大,而柱体后面的流体速度较小,在Re=2000时,虽然流体为层流,但由于圆柱绕流产生的漩涡使流场发生变化,漩涡的产生具有周期性,形成明显的卡门涡街。
3.2 圆柱表面受力特性圆柱尾部旋涡形成到脱落的过程中,流体作用在圆柱上的力是与流向平行和垂直的两组力,即阻力和升力,阻力系数和升力系数的计算公式为:
| $ {C_d} = \dfrac{{{F_d}}}{{\dfrac{1}{2} \times \rho {u_\infty }HD}}\text{,} $ | (8) |
| $ {C_L} = \dfrac{{{F_L}}}{{\dfrac{1}{2} \times \rho {u_\infty }HD}}\text{。} $ | (9) |
式中:FL和Fd分别为圆柱体的升力和阻力,N;H为展向高度,m;u∞为无穷远处的流速,m/s。
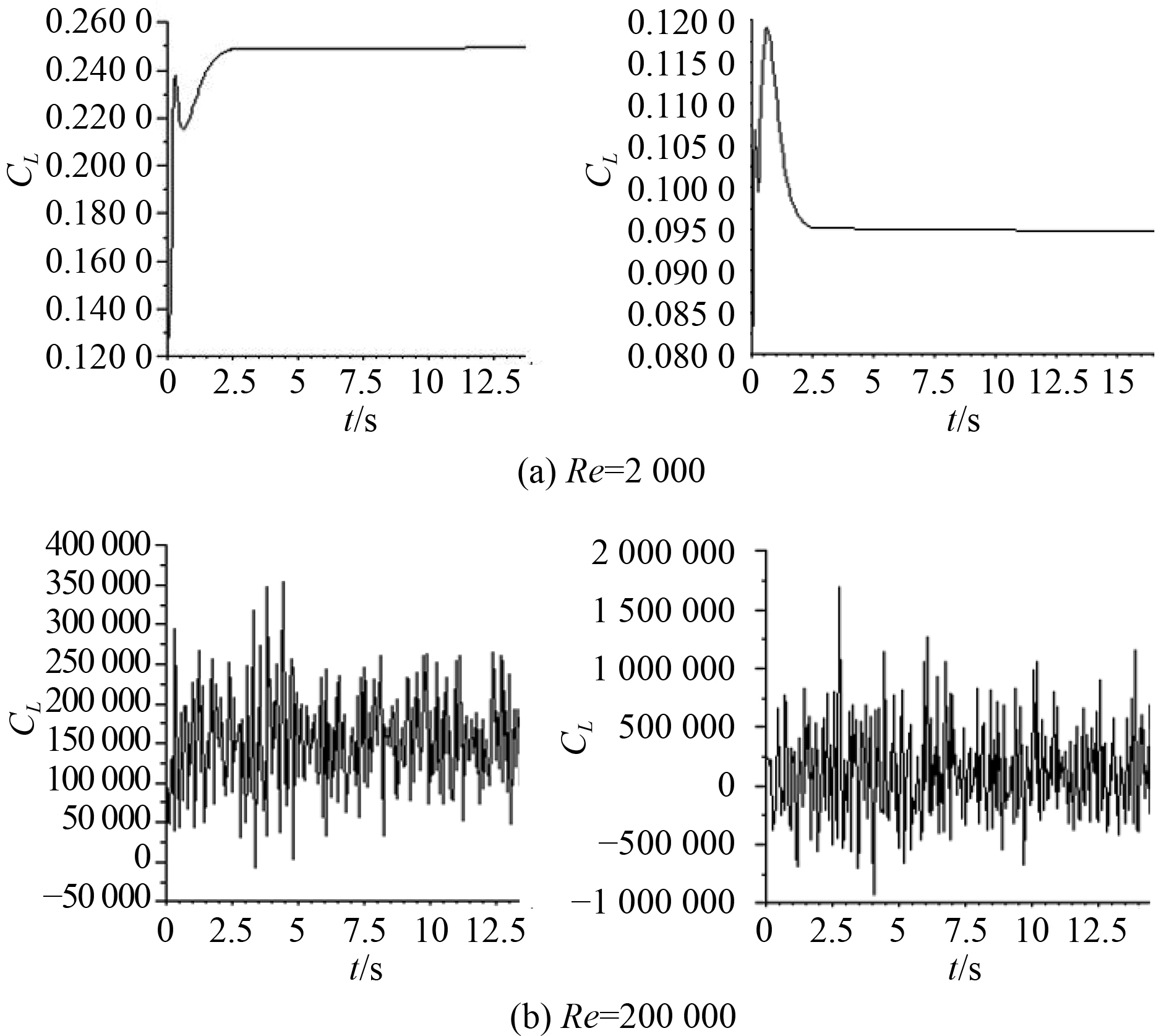
从图6可以看出,层流时,圆柱体的升力系数和阻力系数随着时间增加波动较小,很快趋于平稳;湍流时,圆柱体升力系数和阻力系数随着时间增加波动明显,不断发生变化,说明圆柱体受到流体的不均匀作用力。
|
图 6 圆柱表面受力特性随时间变化 Fig. 6 The force characteristics of the cylindrical surface change with time under different Reynolds numbers |
漩涡脱落及尾流摆动情况是影响圆柱绕流流场特性的主要因素,从速度云图可以看出圆柱体漩涡脱落及尾流摆动的情况。
在Re=2000,t=15 s串列和并列双圆柱绕流的瞬时流场结果如图7所示。
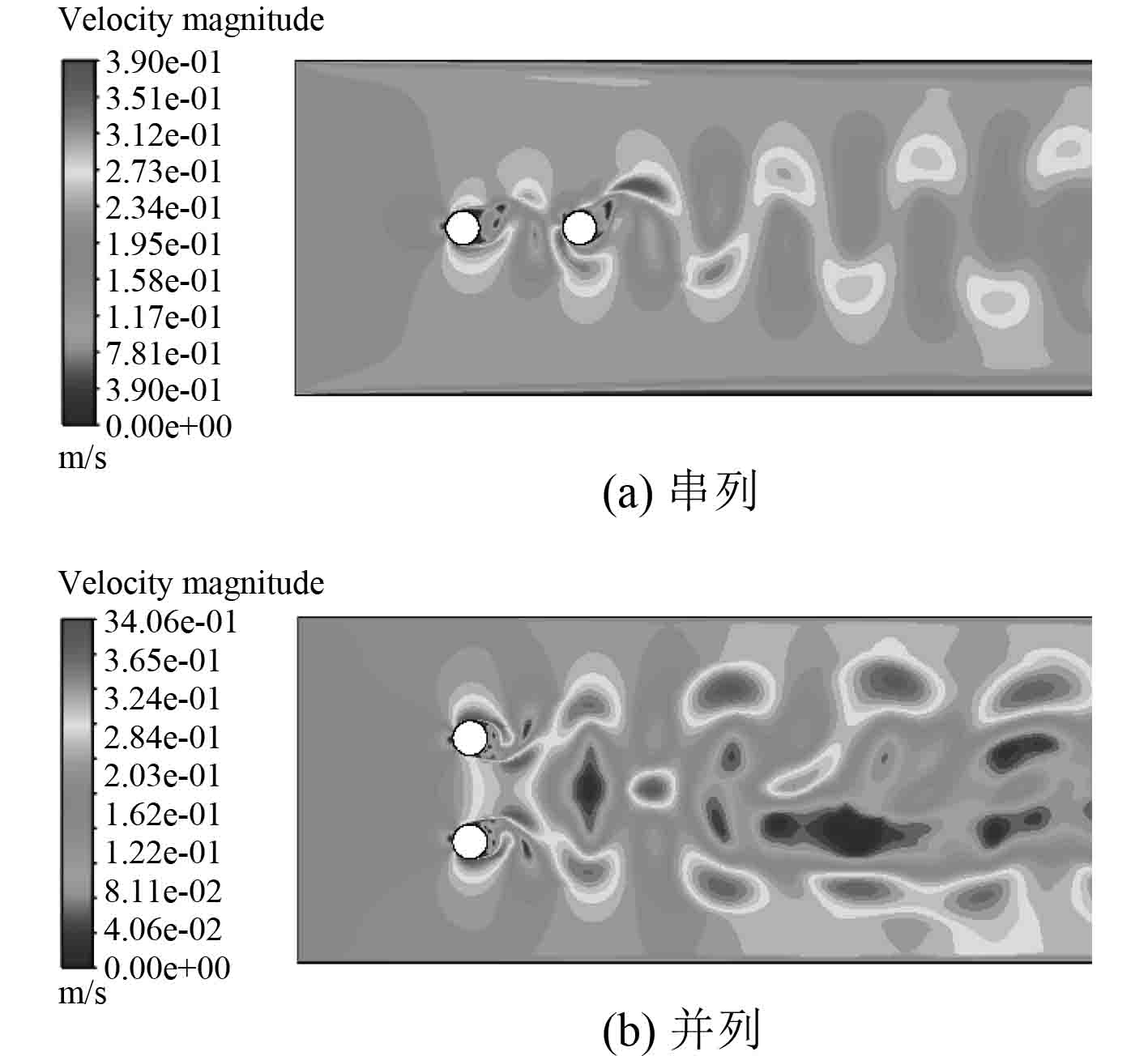
|
图 7 串列和并列双圆柱瞬时流场云图 Fig. 7 Instantaneous flow field cloud diagram of double cylinders in series and in parallel |
从图7可以看出,串列双圆柱绕流时,由于圆柱体之间存在负压区,导致流体速度增大,压力减小,圆柱体发生漩涡脱落,且尾流对称有序;并列双圆柱绕流时,上下2个圆柱体的漩涡脱落和尾流流动规律相似,两侧漩涡脱落和尾流明显,在一定程度上呈对称分布。
3.4 双圆柱绕流表面受力特性1)串列双圆柱
通过计算得到串列双圆柱绕流中不同圆柱体表面受力特性图,如图8所示。
将图8和图6比较可以看出,在串列双圆柱绕流中后柱所受到的力与前柱有关,前柱先产生卡门涡街,使流场发生变化,在后柱的两侧形成明显压力差,导致后柱受到流体的不均匀作用力,使得后柱受前柱的力随着时间呈周期性变化。
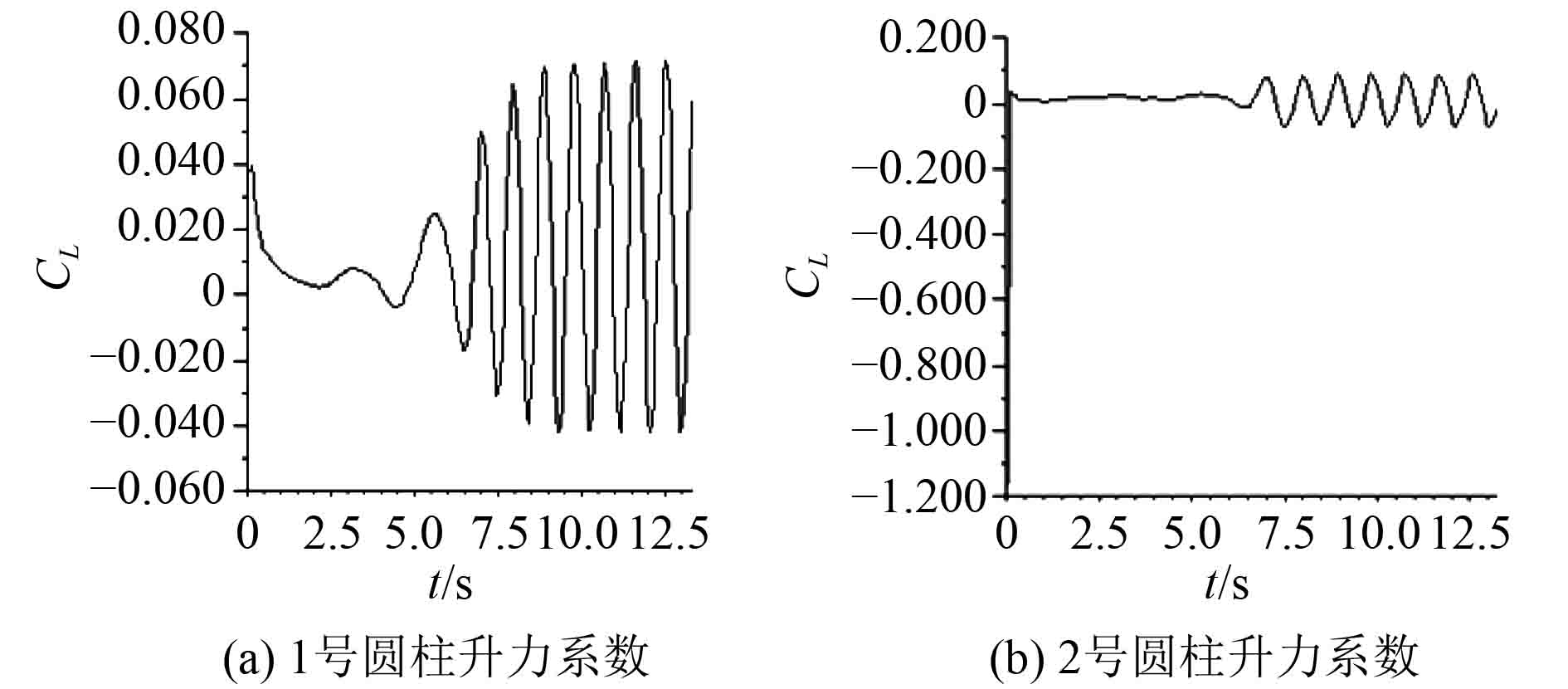
|
图 8 串列双圆柱绕流中圆柱体升力系数 Fig. 8 Lift coefficient of double cylinders in series |
2)并列双圆柱
通过计算得到并列双圆柱绕流中不同圆柱体表面受力特性图,如图9所示。

|
图 9 并列双圆柱绕流中圆柱体升力系数 Fig. 9 Lift coefficient of double cylinders in parallel |
从图9可以看出,上下2个圆柱的升力系数在数值上随时间增加均在零点上下波动,说明上下2个圆柱体有相反的相位,与串列相比,并列双圆柱体相互之间的影响较小。
4 结 语本文基于海上平台支撑柱在海水中绕流和受力情况建立了单圆柱绕流和双圆柱绕流模型,采用大涡模拟的方法进行数值仿真,通过改变雷诺数和双圆柱排列方式模拟计算出相应的瞬时流场云图和水动力系数曲线图,并对模拟结果进行分析,得到如下结论:
1)单圆柱绕流
对3种雷诺数下的单圆柱绕流流场进行数值模拟,Re=2000时可以看的明显的卡门涡街;当流体为层流时,柱体受到流体的稳定作用力,当流体为湍流时,柱体受到流体的不均匀作用力。
2)串列双圆柱绕流
串列时后柱发生漩涡脱落,尾流对称有序;前柱先产生漩涡,改变流场,使后柱上下两侧产生压力差,并受到流体不同方向的力。
3)并列双圆柱绕流
并列时上下2个圆柱体的漩涡脱落和尾流流动规律相似;柱体的升力系数变化趋势相似,上下2个圆柱体相位相反,相互之间影响较小。
| [1] |
李霖, 张志国, 王先洲, 等. 低雷诺数圆柱绕流的大涡模拟分析[J]. 舰船科学技术, 2013, 35(1): 22-26. DOI:10.3404/j.issn.1672-7649.2013.1.004 |
| [2] |
苏铭德, 康钦军. 亚临界雷诺数下圆柱绕流的大涡模拟[J]. 力学学报, 1999, 31(1): 100-105. DOI:10.3321/j.issn:0459-1879.1999.01.012 |
| [3] |
ZDRAVKOVICH M M. Flow around circular cylinders: Vol 1: fundamentals[J]. Journal of Fluids Engineering, 1997, 120(1): 216. |
| [4] |
BRADHAM D M, IGARASHI A, POTTER R L, et al. Connective tissue growth factor: a cysteine-rich mitogen secreted by human vascular endothelial cells is related to the SRC-induced immediate early gene product CEF-10[J]. Journal of Cell Biology, 1991, 114(6): 1285-1294. DOI:10.1083/jcb.114.6.1285 |
| [5] |
麻伟巍, 蒋运幸, 余宇轩. 双圆柱绕流的数值模拟[J]. 复旦学报: 自然科学版, 2013, 52(5): 592-600. |
| [6] |
刘娟, 董启明. 大涡模拟方法下的四圆柱绕流数值模拟[J]. 低温建筑技术, 2013, 35(12): 86-87. DOI:10.3969/j.issn.1001-6864.2013.12.034 |
| [7] |
陈斌, 郭烈锦, 杨晓刚. 圆柱绕流的离散涡数值模拟[J]. 自然科学进展, 2002, 12(9). DOI:10.3321/j.issn:1002-008X.2002.09.013 |
| [8] |
崔宜梁, 王海峰, 李蒙, 等. 相同雷诺数下串列双圆柱绕流的仿真分析[J]. 应用力学学报, 2018, 35(5): 1164-1169. |
 2021, Vol. 43
2021, Vol. 43
