船舶作为水上可移动的载物平台,舱室内设备越来越多,设备之间更加紧凑,舱内的电缆发热、设备正常运行期间会向周围空气释放大量的热量,高温环境下容易引发火灾,统计数据显示火灾已成为船舶安全的主要威胁之一[1-2]。因此国内外学者对船舶舱室火灾进行了不少仿真和试验研究,Gouutk[3]实验研究了全尺寸舱室回燃现象,探讨了回燃的主控参数;Rocket[4]对美国海军舰船火灾增长模型和烟气蔓延模型进行了研究和评价。邹高万等[5]对船舶机舱火灾热流场特性进行了数值仿真研究,用耗氧原理测量并得到不同通风因子下轰燃临界释热速率;董华等[6]对密闭舱室的火灾发展过程进行了数值研究,胡隆华[7]对隧道火灾烟气蔓延的热物理特性研究。狭长舱室火灾会有一些独有特征,若能较好把握狭长空间的火灾特性,有利于火灾初期的准确自动探测报警。本文使用流体仿真软件通过计算机建模以仿真形式再现舰船狭长舱室火灾场景,得到狭长空间火灾发生后烟气蔓延特性规律,舱内温度场分布以及随时间的变化,不同位置的火灾特征参数变化的差异性,以及典型工况下特征参数的阈值,探讨设备发热对火灾热流场的影响。通过分析火灾流场特性变化规律,为狭长空间火灾探测设计提供参考,对于其他场所狭长空间火灾规律研究也有重要意义。
1 数学模型 1.1 控制方程组狭长舱室内的火灾热流场主要为热浮力驱动的低马赫数流动过程,对于此类受重力作用的多组分理想气体的通用控制方程组,根据火灾流场特性和计算求解速度的需要,对方程组进行一些处理,具体过程在文献[8-9]中已有详细推导与论述。通过对控制方程组中速度散度项
| $\frac{{\partial \rho }}{{\partial t}} + \nabla \cdot \left( {\rho {{V}}} \right) = 0\text{,}$ | (1) |
| $\frac{{\partial \left( {\rho {Y_l}} \right)}}{{\partial t}} + {{V}} \cdot \left( {\nabla \rho {Y_l}} \right) = - \rho {Y_l}\nabla \cdot {{V}} + \nabla \cdot \left( {\rho {D_l}\nabla {Y_l}} \right) + {\dot m'''_l}\text{,}$ | (2) |
| $\frac{{\partial {{V}}}}{{\partial t}} - {{V}} \times {{\varOmega }} + \nabla H = \frac{1}{\rho }\left[ {(\rho - {\rho _\infty }){{g}} + \nabla \cdot {\bf{\tau }}} \right] - \left( {\frac{1}{\rho } - \frac{1}{{{\rho _\infty }}}} \right)\nabla \tilde P\text{,}$ | (3) |
| $\begin{split} \nabla \cdot {{V}} =& \frac{1}{{\rho {C_P}T}}\left[ {\dot q + \nabla \cdot \left( {k\nabla T} \right) + \nabla \cdot \left( {\sum\limits_l {{h_{s,l}}\rho {D_l}\nabla {Y_l}} } \right) - \nabla \cdot {{{q}}_r}} \right. - \\ & \left. { \sum\limits_l {{h_l}{{\dot m'''}_l} - \sum\limits_l {{h_l}\nabla \cdot \left( {\rho {D_l}\nabla {Y_l}} \right)} } } \right] +\\ &\frac{{\bar M}}{\rho }\sum\limits_l {\nabla \cdot \rho {D_l}\nabla \left( {{{{Y_l}} / {{M_l}}}} \right)} + \\ & \frac{1}{\rho }\sum\limits_l {\left( {\frac{{\bar M}}{{{M_l}}} - \frac{{{h_l}}}{{{C_P}T}}} \right){{\dot m'''}_l}} + \left( {\frac{1}{{\rho {C_p}T}} - \frac{1}{{{P_0}}}} \right)\frac{{D{P_0}}}{{Dt}} \text{,} \\[-15pt] \end{split} $ | (4) |
| ${P_0}\left( t \right) = \rho TR\sum\limits_l {\frac{{{Y_l}}}{{{M_l}}}} \text{,}$ | (5) |
| $ \begin{split}&{\nabla }^{2}H=-\frac{\partial \left(\nabla \cdot {{V}}\right)}{\partial t}-\nabla \cdot {{F}};\\ &{{F}}=-{{V}}\times {{\varOmega}} +\left(\frac{\rm{1}}{\rho }-\frac{1}{{\rho }_{\infty }}\right)\nabla \tilde{P}-\frac{1}{\rho }\left[\left(\rho -{\rho }_{\infty }\right){{g}}+\nabla \cdot {\bf{\tau}} \right]\text{。}\end{split}$ | (6) |
为了得到大涡模拟技术处理的控制方程组,需要对与时间相关的N-S方程组在傅里叶空间或物理空间进行滤波。对任意一个流动变量
| $\phi \left( x \right) = \overline \phi \left( x \right) + \phi '\left( x \right)\text{。}$ | (7) |
目前常用的滤波函数有高斯滤波、盒式滤波(又称顶盖滤波)和傅里叶阶段滤波。其中比较常用的盒式滤波可以表示为:
| $G(x) = \frac{1}{\Delta }H\left( {\frac{1}{2}\Delta - \left| x \right|} \right)\text{。}$ | (8) |
计算中将燃烧过程简化处理,认为燃料和氧气混合燃烧速率无限快,燃烧过程仅和二者混合分数有关,可以简化计算量,适用于较大空间内火灾的模拟,其对于单步瞬时反应假设燃料与氧气混合后按如下化学反应进行:
| $\begin{split}{{\rm{C}}_{\rm{x}}}{{\rm{H}}_{\rm{y}}}{{\rm{O}}_{\rm{z}}}{{\rm{N}}_{\rm{v}}} +& {v_{{{\rm{O}}_{\rm{2}}}}}{{\rm{O}}_{\rm{2}}} \to {v_{{\rm{C}}{{\rm{O}}_{\rm{2}}}}}{\rm{C}}{{\rm{O}}_{\rm{2}}} + {v_{{{\rm{H}}_{\rm{2}}}{\rm{O}}}}{{\rm{H}}_{\rm{2}}}{\rm{O}} +\\ &{v_{{\rm{co}}}}{\rm{CO}} + {v_{\rm{s}}}{\rm{Soot}} + {v_{{{\rm{N}}_{\rm{2}}}}}{{\rm{N}}_{\rm{2}}}\text{。}\end{split}$ | (9) |
热辐射在火灾流场计算中对计算结果有较大影响,考虑到热辐射的复杂性,要完全模拟难度较大,一般对模型合理简化处理。辐射控制方程为:
| $ {{s}} \cdot \nabla I({{x}}, {{s}})=\kappa({{x}})\left[I_{b}({{x}})-I({{x}}, {{s}})\right] \text{。}$ | (10) |
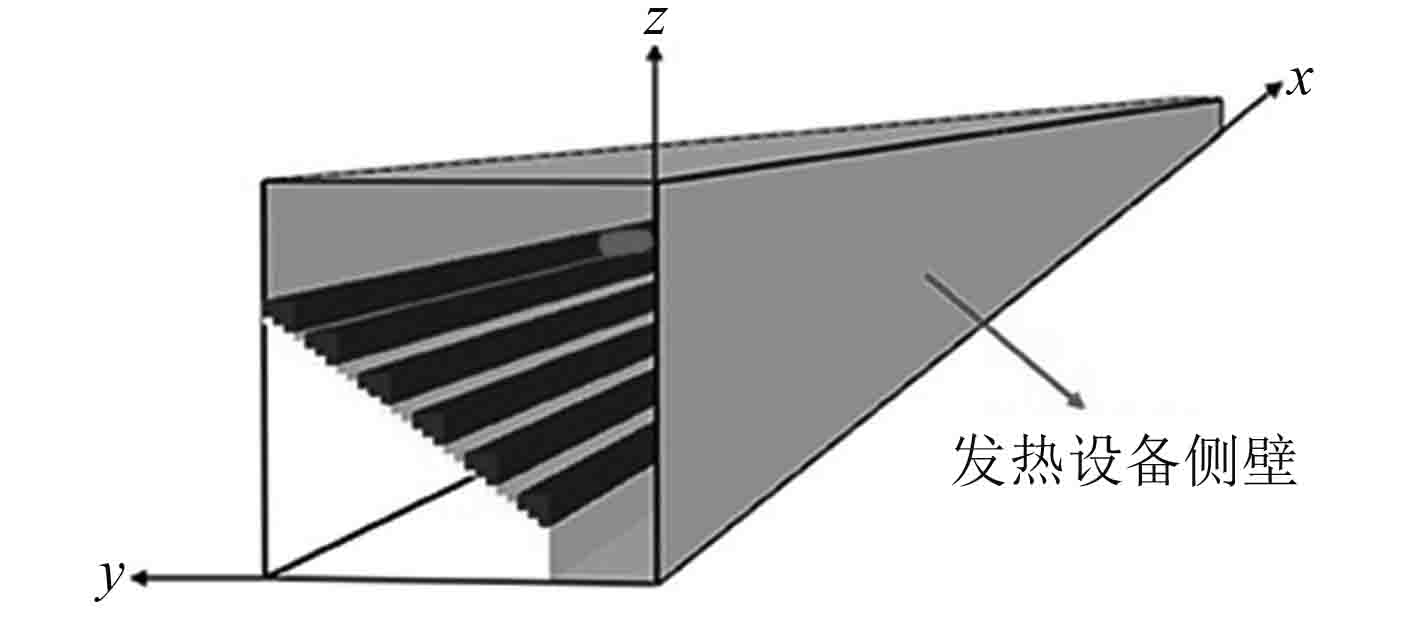
舰船舱室狭长空间设备较多,结构比较复杂,图1为仿真计算时简化的狭长舱室空间。简化后纵切面为半梯形结构,右侧壁为发热设备,左侧为V型空间,上甲板整体尺寸(长×宽)为:36 m×1.6 m,下底板整体尺寸(长×宽)为:36 m×0.4 m,高为1.5 m,舱内其他设备进行同样简化,简化后计算网格如图2所示。为准确捕捉火场信息,火源及其附近区域网格尺寸为0.02 m,其他区域采用边长不大于0.03 m的网格进行划分,整个计算空间的总体网格数约为350万,舱室表面固体均假设为绝热边界,没有热量向外散失。
|
图 1 舱室狭长空间三维模型 Fig. 1 Three-dimensional model of ship's long-narrow space |
计算过程中,基于Deardorff亚格子模型的大涡模拟(LES)技术求解湍流模型,用有限体积法(FVM)计算热辐射,以显性二阶预测/校正机制迭代变量的时间微分离散,用CFL条件保证迭代的稳定。
2.2 火源位置和大小根据狭长舱室内设备实际情况,结合相关文献中记录的电缆火灾发生的原因[8-9],同时考虑不同火源位置对探测报警装置的影响,分别模拟火源位于狭长舱室边缘上部、边缘下部2个典型位置发生火灾时的热流场,火源设置在距离端面4 m处,具体位置如图1所示。
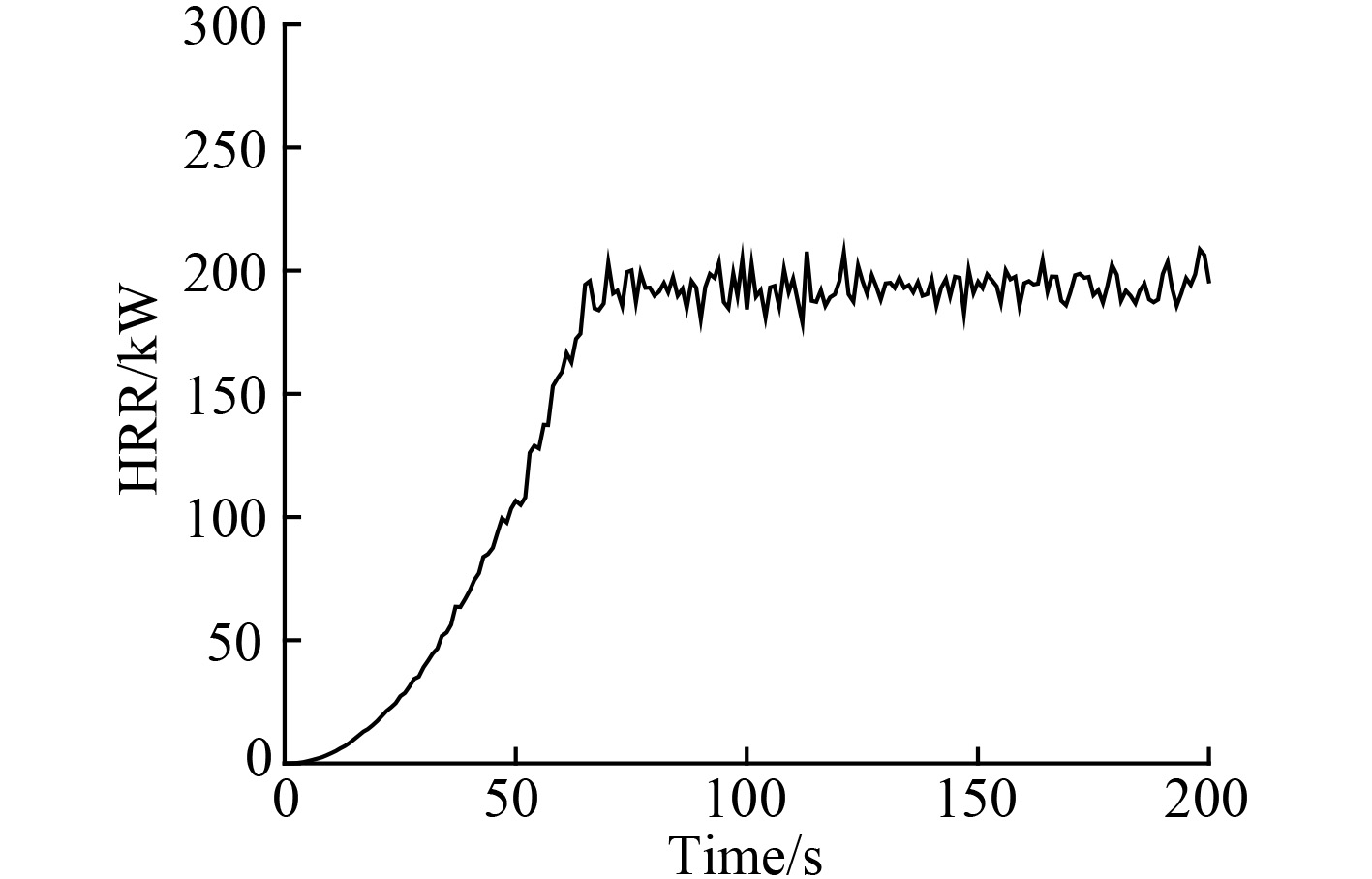
实际的火源情况非常复杂,在尽可能真实地反映燃烧过程基础上,将火源抽象并简化,结合国际标准ISO/TS16733,最普遍使用的
|
图 2 热释放速率曲线 Fig. 2 Heat release rate curve |
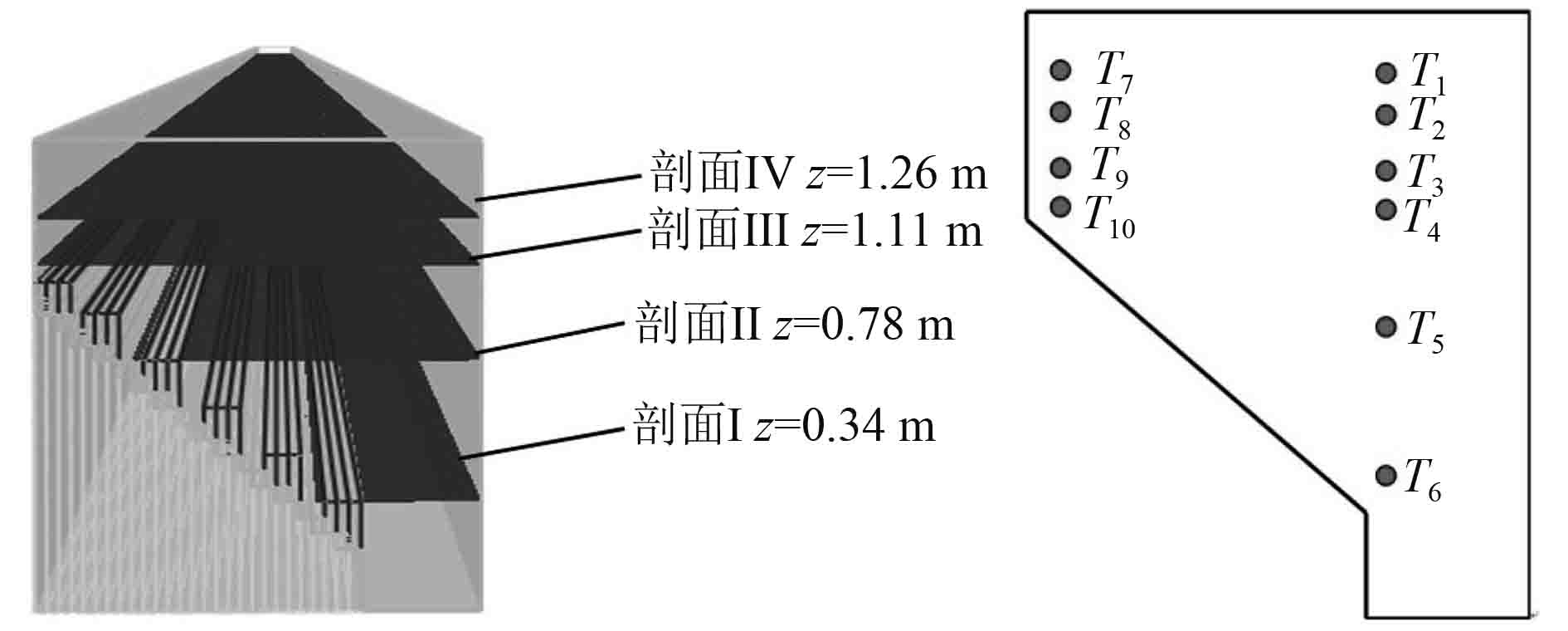
为分析各种工况下温度变化规律,在计算过程中对特征参数进行记录,在火源中心截面平面上布置温度测点,具体测点位置如图3所示。采样周期为0.2 s,频率为5 Hz。
|
图 3 截面和监测点位置示意图 Fig. 3 Diagram of sections and monitor points |
本文采用CFD数值模拟方法,根据狭长舱室火灾流场特性,计算过程描述如下:1)设置舱室初始环境条件包括时间步和各变量值和;2)计算下一时刻的参数预测值;3)根据速度预测值求与第2步得到的速度值判定收敛与否;4)结合CFL判定是否稳定;5)求解参数校正值;6)与在第5步中求得的速度散度值比较,判定收敛与否;7)返回第2步继续计算;8)反复迭代完成计算。
2.5 计算工况假设狭长舱室内电缆因为高温形成火灾,在电缆保持发热的前提下,分别考虑甲板69 ℃高温和发热设备以80 ℃温度发热独立和耦合作用时,以电缆(固体)蔓延火为火源,模拟火源位于狭长舱室舱边缘上部典型位置发生火灾时的热流场。计算时间为1000 s,其中800 s为舱内环境达到稳态的时间,200 s为火灾发生初期所形成的热流场。通过模拟结果判断在火源工况下狭长舱室内各测点处的温度随火灾发展的变化情况。模拟设备发热和不发热2种工况,如表1所示。
|
|
表 1 计算工况 Tab.1 Conditions of calculation |
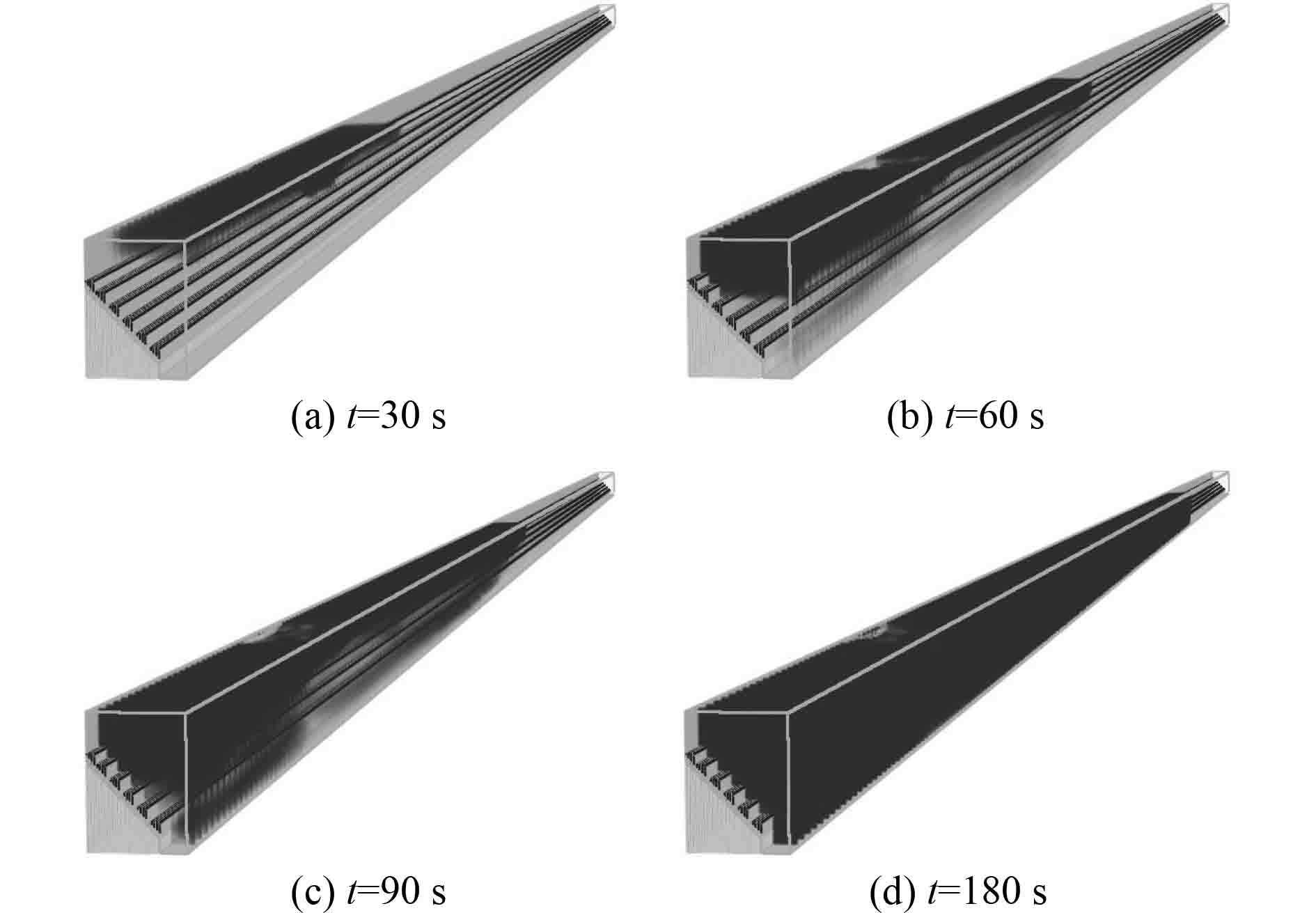
图4为火源位于舱室边缘上层时不同时刻烟气蔓延分布。在t=30 s时位于舱室边缘处火源产生的烟气在火源处向上运动,撞击到舱室上壁面后开始向周围横向蔓延,但由于舱室一端是封闭状态,因此左端壁面对火灾烟气的扩散蔓延起到了一定的影响,表现在火灾发生90 s时烟气碰到左端壁面时烟气向舱室内下部蔓延,在火灾发生180 s时舱室左侧下部边缘处空间已基本都被火灾烟气覆盖,而舱室另一端基本未受烟气侵扰(烟气长度约25 m,有11 m左右没有被烟气蔓延),这是由于狭长空间结构导致烟气在水平方向阻力大于向下的浮力阻力,烟气不足以继续向前运动而改为向下运动。而普通空间的火灾一般烟气在整个空间的顶部完全弥散后才向空间下部蔓延。
|
图 4 火源位于舱室边缘上层时不同时刻烟气蔓延 Fig. 4 Smoke spread over time when fire is on the edge of upper layer |
图5为 z=0.34 m时平均剖面温度在35 ℃~55 ℃范围内的变化。t=30 s时,温度差异并不明显,整体温度在47 ℃左右,t=60 s时,火源下方处的温度明显升高,并逐步向两侧延伸,由于烟气在舱室边缘处聚集,在火灾发生180 s时,高温区域扩大,而且高温烟气分布不均匀导致温度分布出现较大差异。z=0.78 m处平均剖面温度在35 ℃~65 ℃,高于舱室下部截面z=0.34 m,在t=30 s时剖面温度在53 ℃,比z=0.34 m温度高6 K,在火灾发生180 s时,在CD舱长度方向上温度分布不再是连续升高,而是局部区域出现温度降低又升高现象,这是由于在该位置处烟气发生沉降而发生局部温度较高。z=1.11m处平均剖面温度在35 ℃~111 ℃范围内变化,t=30 s时,火源上方靠侧壁局部温度远高于其他区域,温度分布很不均匀,t=180 s时,以火源位置为对称轴到舱室左右两侧温度值均在111 ℃,沿舱室延伸方向温度逐渐降低。

|
图 5 上边电缆着火时不同时刻不同高度截面的温度场分布 Fig. 5 Temperature field distribution at different heights and time |
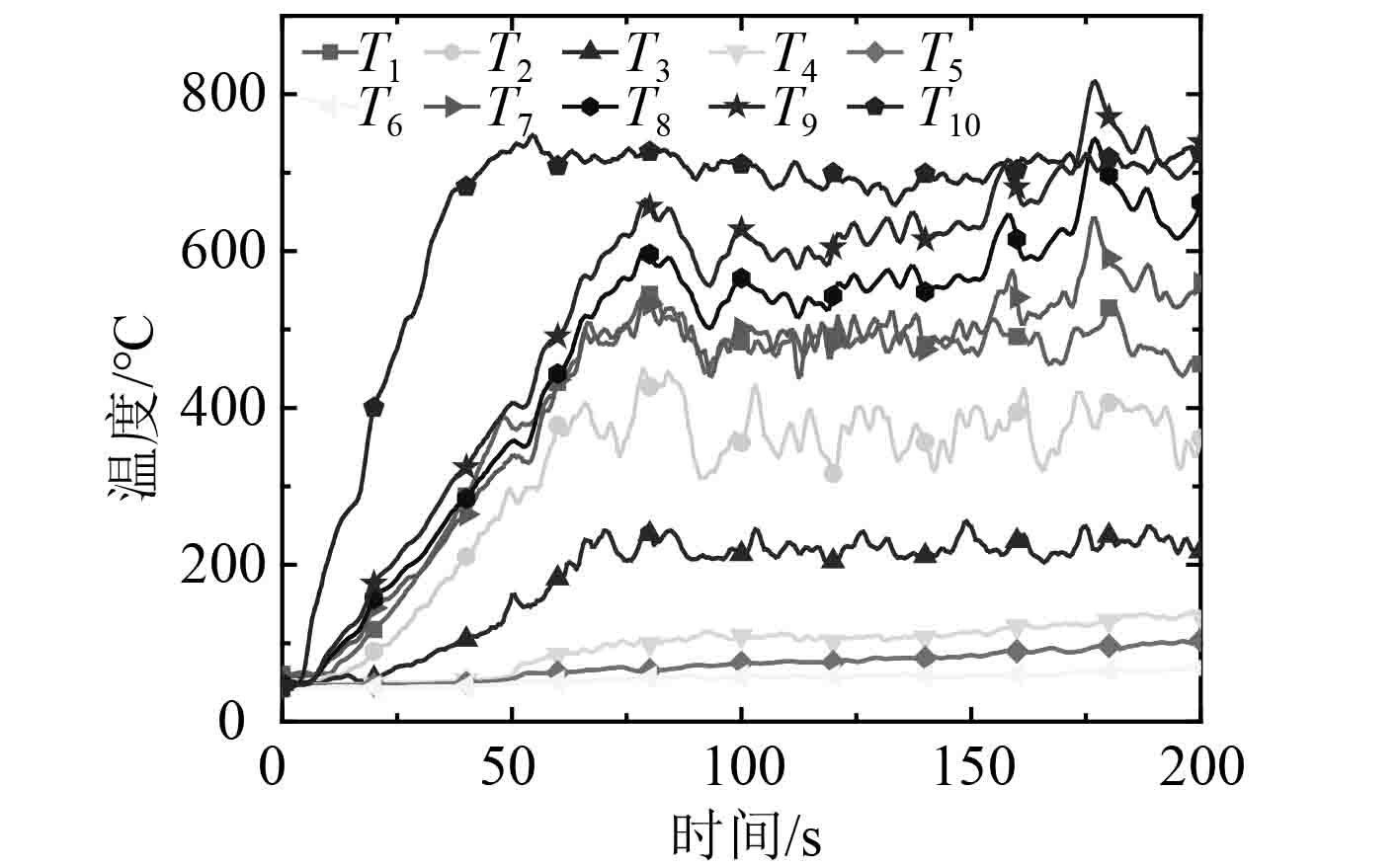
图6为火灾发生后10个温度探测器T1~T10温度随时间变化结果。靠火源附近T10测点最先开始升温,其余测点变化趋势相同。在火源正上方T7~T10,随着高度的增加温度变小,而在远离火源的T1~T6随着高度的增大,温度变大。其中远离火源且处于下层测点的T4~T6的温度变化幅度小,火源上方的测点T7~T10温度整体高于远离火源的测点T1~T6温度。在40 s后上层测点T1和T7温度曲线基本一致,随着烟气的蔓延在160 s后上层测点T1温度又低于火源上方测点T7的温度。整个火灾过程在t=55 s时达到火源上方距离最近的T10温度最高达到747 ℃,而此时靠近舱室下层的T6只有62 ℃。
|
图 6 各测点测点温度随时间的变化 Fig. 6 The variation in monitor points' temperature over time |
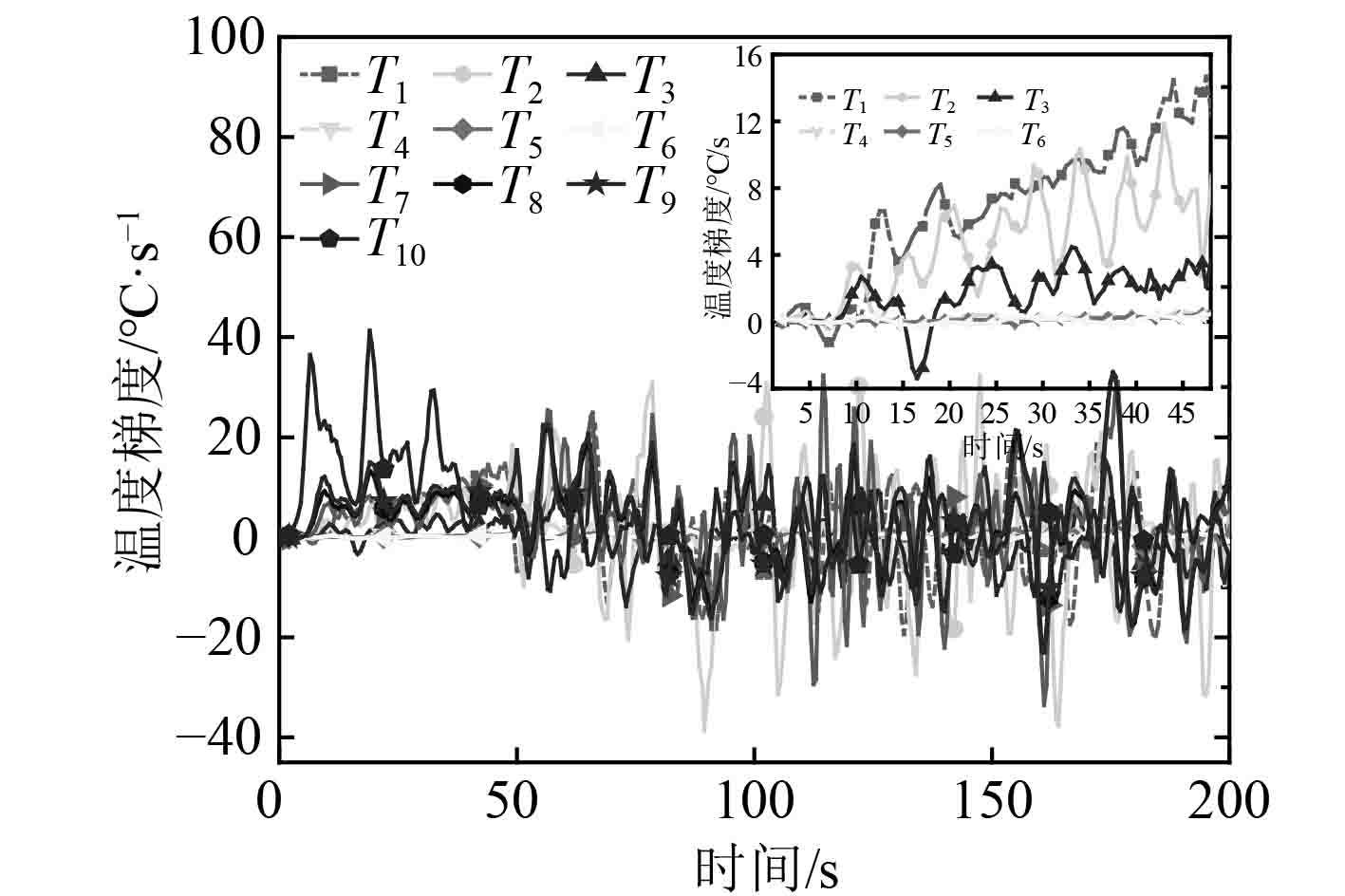
图7为温度梯度。在火灾充分发展之前,也即前50 s T10~T7温度梯度逐渐变小,T6~T1温度梯度逐渐增大。50 s之后温度梯度变化最大的是T2测点,最大梯度达到了40 ℃/s,这是由于在T2位置烟气涡旋运动更剧烈导致。
|
图 7 各测点温度梯度随时间的变化 Fig. 7 Monitor points′ temperature gradient over time |
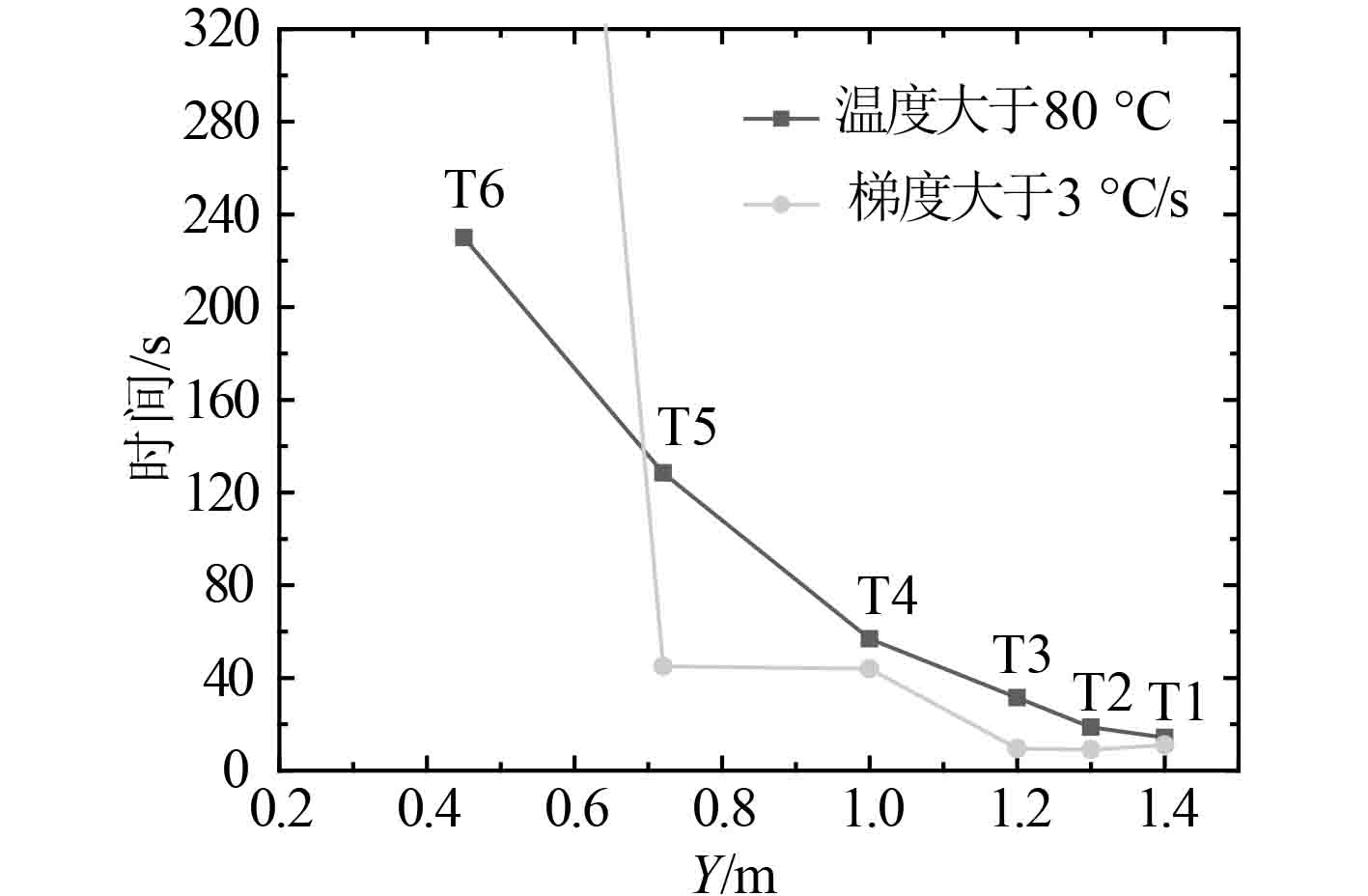
实际工程中,火灾发生有一定的随机性,探测器不在火源正上方是大概率事件,探测要尽早尽准,因此重点分析非火源正上方的T1~T6测点在火灾发生初期的温度和温度梯度随时间变化。一般来说探测器达到某一设定的阈值温度或者温度梯度时开始报警,或者同时达到温度值和温度梯度时开始报警。本次仿真温度阈值取80 ℃,温度梯度取3 ℃/s时。T1~T6测点安温度和温度梯度达到阈值的时间如图8所示。
|
图 8 温度和温度梯度达到阈值的时间 Fig. 8 Time for temperature and temperature gradient to reach threshold |
图8显示T1~T5五个测点的温度阈值达到80 ℃时间都大于温度梯度达到3 ℃/s所需时间。而T6测点在240 s达到温度阈值,整个火灾过程温度梯度都没有达到阈值。T1~T2无论是温度还是温度梯度达到阈值的时间均在15 s以下,温度梯度综合考虑了温度和时间2个因素,可以实现及早报警。当然无论是温度还是温度梯度只要阈值设置的足够低,就能实现及早报警。当阈值足够低时,可能不是火灾却达到了报警阈值,从而错误报警。因此无论是温度还是温度梯度结合火灾特性都要设置一个合理的阈值。探测器布置在顶层附近,对舱室其他设备的干涉影响较小,此外也能实现较早的报警。
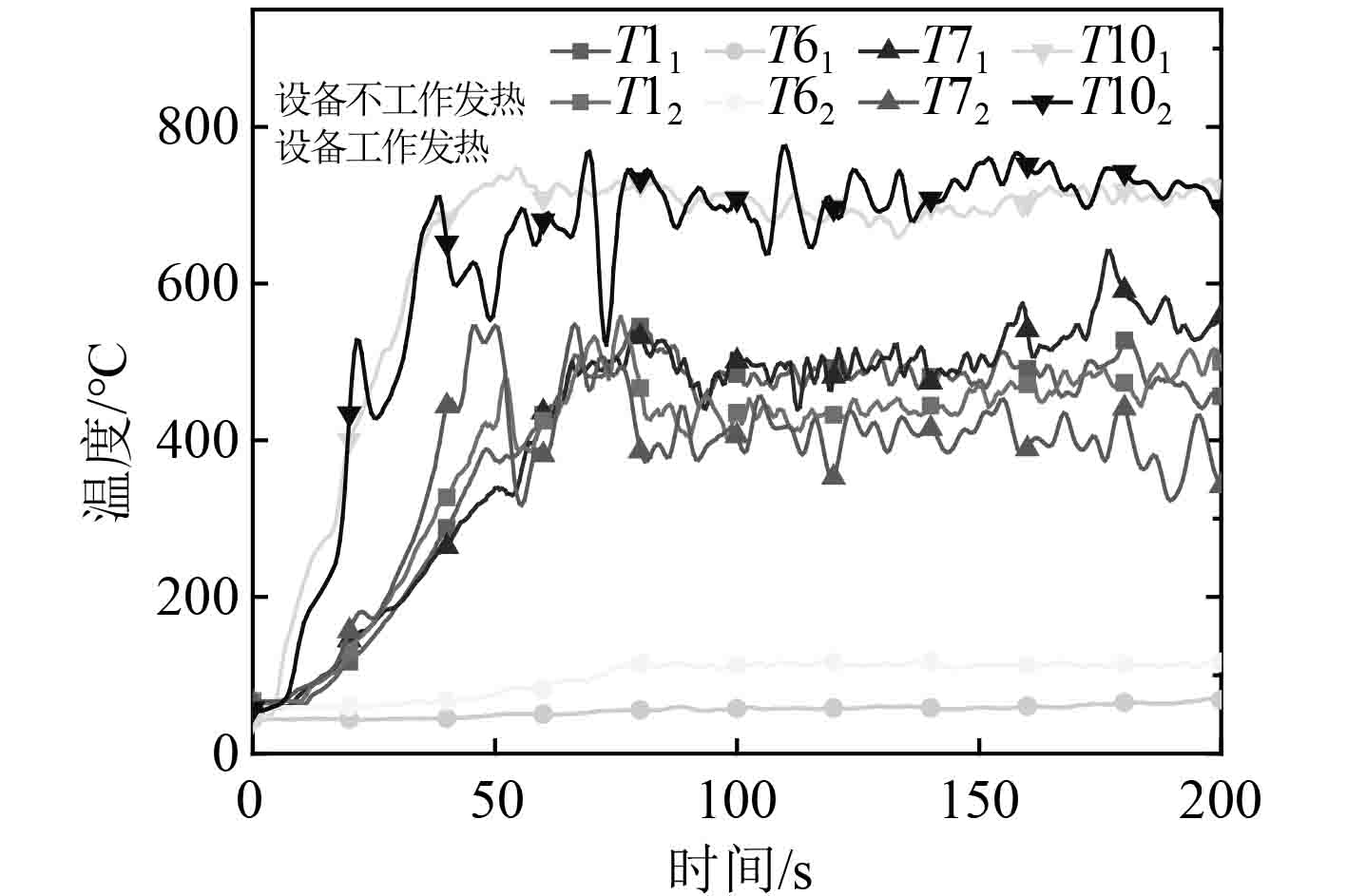
从图9可以看出,在火灾发生初期,有设备发热时,T1,T6,T7和T10升温速度更快。而在火灾充分发展阶段,设备发热对T1,T7和T10三个测点的温度的升高作用不明显,由于新的热源加入,高温烟气的运动更紊乱,3个测点温度的波动范围更大。而下层测点T6温度变化显示,有设备发热时温升速率更快,温升更大。
|
图 9 有/无发热设备对火灾各测点温度的影响 Fig. 9 Influence of heating equipment on measuring points′ temperature |
通过以上计算和分析得出以下结论:
1)对于狭长空间,烟气在火源处向上运动,漂浮至上壁面后开始向周围横向蔓延,不同于普通空间烟气在顶部完全弥散,在180 s舱室一端被烟气完全覆盖,另一端未受烟气侵扰,这是由于狭长空间结构导致烟气在水平方向阻力持续增大,直至大于向下的阻力导致。
2)当温度阈值80 ℃,温度梯度阈值为3 ℃/s的时间,上层测点T1和T2,无论温度还是温度梯度达到阈值的时间均在15s之内。
3)当设备发热时,上层测点温升不明显,温度波动范围更大;下层测点温升速率更快,温升更大。
| [1] |
谢晓勇. 船舶封闭空间火灾模型研究[J]. 舰船科学技术, 2017, 39(2A): 181-183. |
| [2] |
李志辉, 李其修, 刘辉, 等. 船舶火灾监控报警系统中的视觉传感器应用[J]. 舰船科学技术, 2017, 39(9A): 148-150. |
| [3] |
GOTTUK D T, PEATROSS M J, FARLEY J P, et al. The development and mitigation of back draft: a real-scale shipboard study[J]. Fire Safety Journal, 1999, 33(4): 261-282. DOI:10.1016/S0379-7112(99)00033-8 |
| [4] |
NBSIR 86-3451, Fire growth in combat ships[S].
|
| [5] |
邹高万. 船舶机舱火灾热流场特性研究[D]. 哈尔滨: 哈尔滨工程大学, 2005.
|
| [6] |
董华, 范维澄, 等. 船舶密闭舱室火灾过程及其模拟计算[J]. 计算力学学报, 1998, 15(1): 80-85. |
| [7] |
胡隆华. 隧道火灾烟气蔓延的热物理特性研究[D]. 合肥: 中国科学技术大学, 2006.
|
| [8] |
帕坦卡(著), 张政(译), 等. 流场的计算[M]. 北京: 科学出版社, 1984: 130-160.
|
| [9] |
WANG H Y. Numerical study of under-ventilated fire in medium-scale enclosure[J]. Building and Environment, 2009, 44(6): 1215-1227. DOI:10.1016/j.buildenv.2008.09.011 |
 2021, Vol. 43
2021, Vol. 43
