2. 中国科学院机器人与智能制造创新研究院,辽宁 沈阳 110169;
3. 中国科学院大学,北京 100049
2. Institutes for Robotics and Intelligent Manufacturing, Chinese Academy of Sciences, Shenyang 110169, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China
近年来自主水下航行器(Autonomous Under-water Vehicle,AUV)在海洋资源勘探、羽流追踪、海底地形测绘等方面都发挥着重要的作用[1]。但由于AUV自身硬件的局限性和作业环境的特殊性,单个AUV已经无法满足日益增加的快速大规模海洋探测任务的需求。相比之下Multi-AUV系统不仅具有作业效率高、运行成本低等特点,还可以增加系统的冗余性和鲁棒性。因此许多机构对海洋资源勘探的Multi-AUV协同探测系统进行了研究,如美国的Ocean Infinity公司[2]、日本的Zipangu项目[3-4]、欧盟的MORPH项目[5-6]以及XPRIZE比赛中的SEA-KIT项目[7]等。
Multi-AUV系统的编队控制是AUV协同作业的关键技术。许多研究人员将无人车或无人机系统中使用的编队控制方法应用到Multi-AUV系统[8]。如通过将AUV编队控制分解为队形形成、队形保持、避障等一系列行为组合的基于行为法[9-10];将AUV编队视为刚性结构,AUV视为节点,参照虚拟结构几何中心移动的虚拟结构法[11];分别对目标及障碍物构建虚拟势场,通过计算AUV在势场中受到的合力导出编队控制律,从而实现编队航行的人工势场法[12-13];以及通过指定编队中1台AUV作为领航者,其余AUV作为跟随者按期望距离进行跟随从而实现编队航行的领航-跟随方法[14-16]。
但上述的方法均假设AUV编队处于同一水平面内航行,并未考虑到AUV实际的作业场景与运行环境。调查海域海底地形的起伏变化,甚至存在悬崖、海沟等复杂地形,为取得更好的勘探效果还需要维持AUV距离海底在一定的高度,因此在执行勘探任务时AUV编队可能不处于同一平面。
本文结合AUV编队实际的深海作业场景,将AUV的编队控制解耦到水平面和垂直面2个方向分别进行控制。水平面内采用基于领航跟随和反馈线性化的方法,提出编队控制律并使用李雅普诺夫稳定性理论进行证明;垂直面内对采集到的地形高度数据采用最小二乘法对海底地形高度进行拟合并估计的高度控制,并对可能存在的极端地形提出相应的避障策略。同时,针对AUV编队在作业过程中行驶的梳状路径提出编队优化策略。最后,采用“潜龙一号”AUV作为研究对象,对所提出的协同控制策略进行仿真和验证。
1 问题描述Multi-AUV与水面无人艇(Unmanned Surface Vehicle, USV)组成的异构海洋勘探作业系统应用场景如图1所示。由多台AUV组成的同构Multi-AUV编队在上方USV搭载的超短基线(Ultra Short Baseline,USBL)提供的定位支持下,按预先规划的作业路径进行巡航,使用所搭载的传感器或声学设备对待探测区域进行扫描。为实现探测区域的全覆盖扫描,需要保持编队中各AUV在水平方向上的相对位置。此外,为设备取得较好的探测效果,还需要维持AUV的距底高度。考虑到海底地形的复杂变化,各AUV将不再处于同一水平面内,因此引入AUV距海底的高度控制。
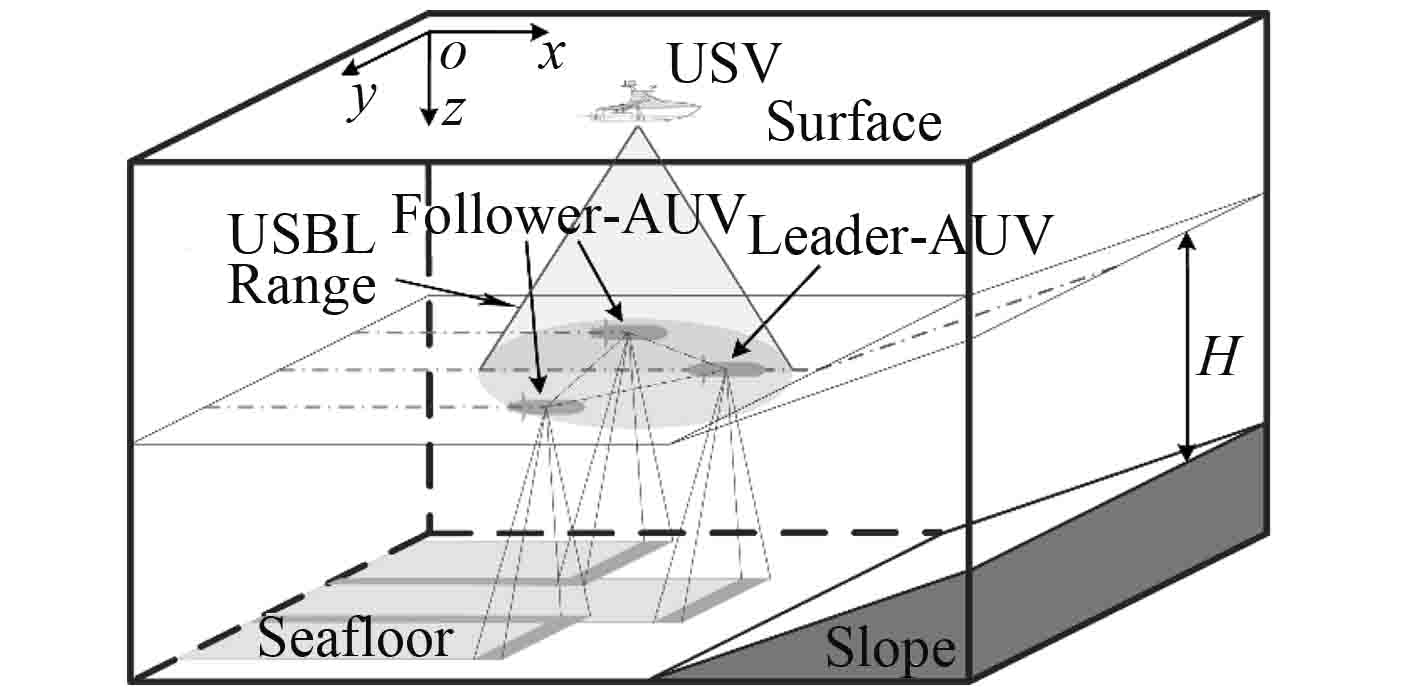
|
图 1 异构海洋勘探系统应用场景 Fig. 1 Application scenarios of heterogeneous oceanographic exploration system |
如图1所示,建立北东坐标系
| $\left[ {\begin{array}{*{20}{c}} {\dot x(t)} \\ {\dot y(t)} \\ {\dot \varphi (t)} \end{array}} \right]{\rm{ = }}\left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\cos \varphi (t)} \\ {\sin \varphi (t)} \\ 0 \end{array}}&{\begin{array}{*{20}{c}} 0 \\ 0 \\ 1 \end{array}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {v(t)} \\ {\omega (t)} \end{array}} \right]\text{。}$ | (1) |
其中:
同时根据AUV实际的水下作业环境与需求,假设编队中各AUV均装备超短基线、多普勒速度计程仪、电子罗盘、深高度计以及水声通信机等,以保证AUV可以获得自身的状态信息的同时并保持整个异构系统之间的良好通信。
在以上的条件下设定Multi-AUV编队的控制目标,即在
| $\mathop {\lim }\limits_{t \to \infty } \left| {\left[ {\begin{array}{*{20}{c}} {x(t) - {x_r}(t)} \\ {y(t) - {y_r}(t)} \\ {\varphi (t) - {\varphi _r}(t)} \\ {h(t) - H} \end{array}} \right]} \right| = 0\text{。}$ | (2) |
其中:
Multi-AUV系统的协同编队控制策略由基于领航跟随和反馈线性化的编队控制器、基于最小二乘估计的高度控制与避障策略以及路径优化编队策略3个部分组成。
2.1 编队控制器结合AUV在水下的实际作业应用场景,采用领航跟随思想与反馈线性化的编队控制方法。如图2所示,由3台AUV组成的同构Multi-AUV编队,预先指定编队中1台AUV作为整个编队的全局领航者,编队中其余AUV分解为领航-跟随者子系统。引入领航者信息和跟随者信息分别生成参考AUV和离轴点P,离轴点P以参考AUV为目标进行跟踪,从而保持跟随者与领航者之间的相对位置、以及偏航角和速度的一致,从而实现Multi-AUV系统的编队控制。
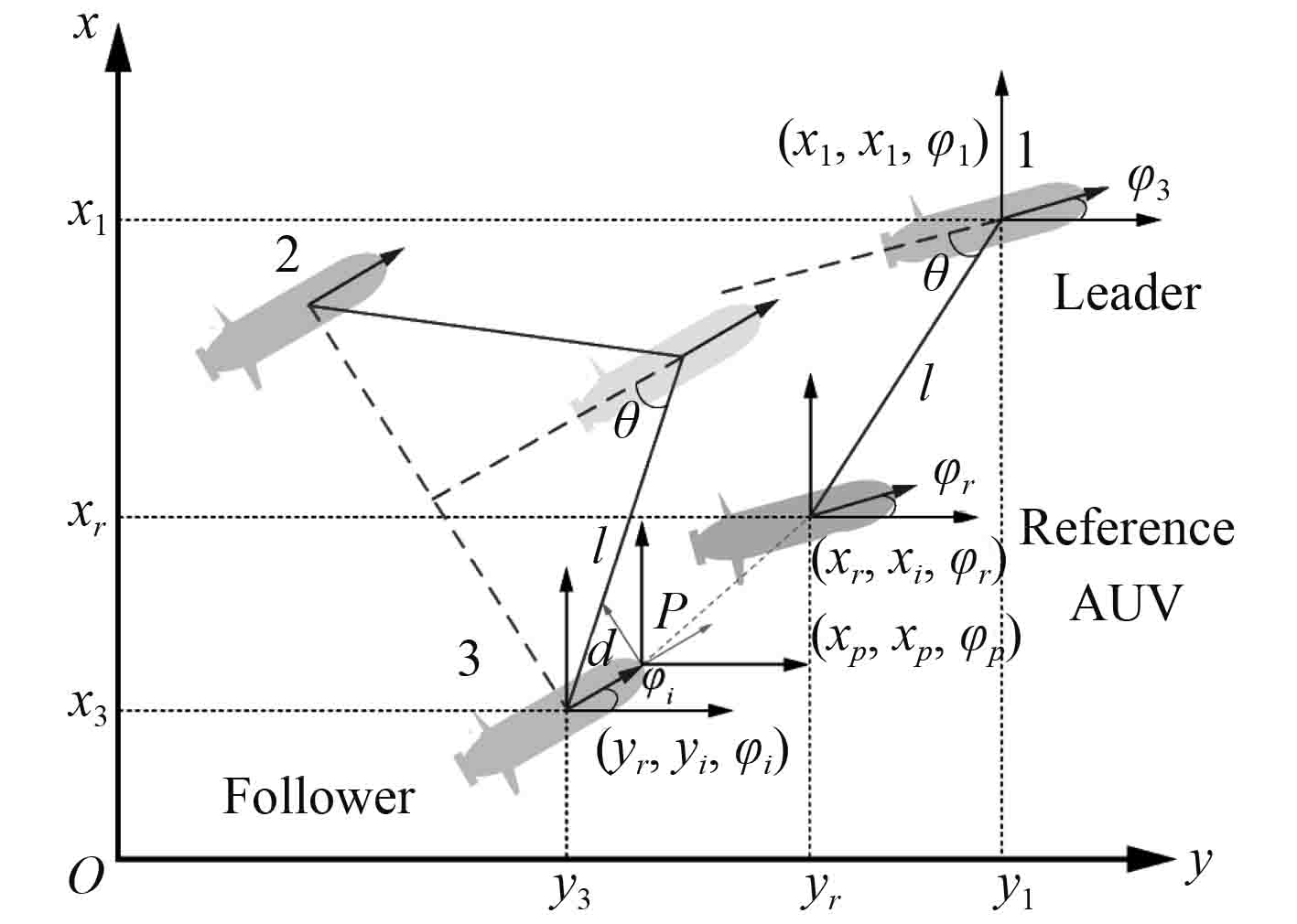
|
图 2 领航跟随与反馈线性化编队控制 Fig. 2 Leader-follower and input-output feedback linearization formation control |
如图2所示,选取领航AUV与跟随AUV-3子系统为例。领航和跟随AUV的位置和航向信息在北东惯性坐标系下分别表示为
以领航AUV信息生成的参考AUV的位置和航向信息
| $\left[ {\begin{array}{*{20}{c}} {{x_r}(t)} \\ {{y_r}(t)} \\ {{\varphi _r}(t)} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{x_l}(t) - l\cos ({\varphi _l}(t) + \theta )} \\ {{y_l}(t) - l\sin ({\varphi _l}(t) + \theta )} \\ {{\varphi _l}(t)} \end{array}} \right]\text{,}$ | (3) |
以跟随AUV信息为参考,定义位于AUV艏部,相对质心偏移量为d的点为离轴点P。则离轴点P的位置信息和航向信息可以表示为:
| $\left[ {\begin{array}{*{20}{c}} {{x_p}(t)} \\ {{y_p}(t)} \\ {{\varphi _p}(t)} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{x_i}(t) + d\cos {\varphi _i}(t)} \\ {{y_i}(t) + d\sin {\varphi _i}(t)} \\ {{\varphi _i}(t)} \end{array}} \right]\text{,}$ | (4) |
则离轴点
| $\left[ {\begin{array}{*{20}{c}} {{e_x}} \\ {{e_y}} \\ {{e_\varphi }} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{x_l} - l\cos ({\varphi _l} + \theta ) - {x_i} - d\cos {\varphi _i}} \\ {{y_l} - l\sin ({\varphi _l} + \theta ) - {y_i} - d\sin {\varphi _i}} \\ {{\varphi _l}(t) - {\varphi _i}(t)} \end{array}} \right]\text{,}$ | (5) |
其中,
| $\left\{ \begin{array}{l} {{\dot e}_x}{\rm{ = }}{v_l}\cos {\varphi _l} - {v_i}\cos {\varphi _i} + l\sin ({\varphi _l} + \theta ) \cdot {\omega _l}+ \\ \quad\;\; d\sin {\varphi _i} \cdot {\omega _i} \text{,}\\ {{\dot e}_y}{\rm{ = }}{v_l}\sin {\varphi _l} - {v_i}\sin {\varphi _i} - l\cos ({\varphi _l} + \theta ) \cdot {\omega _l} -\\ \quad\;\; d\cos {\varphi _i} \cdot {\omega _i}\text{,} \\ {{\dot e}_\varphi } = {\omega _l} - {\omega _i} \text{。}\end{array} \right.$ | (6) |
将系统误差
| $\left[ {\begin{array}{*{20}{c}} {{z_1}(t)} \\ {{z_2}(t)} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\cos {\varphi _i}(t)}&{\sin {\varphi _i}(t)} \end{array}} \\ {\begin{array}{*{20}{c}} {\sin {\varphi _i}(t)}&{ - \cos {\varphi _i}(t)} \end{array}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{e_x}(t)} \\ {{e_y}(t)} \end{array}} \right]\text{,}$ | (7) |
将位置误差式(5)代入式(7)中,位置误差在载体坐标系下可以表示为:
| $\left\{ \begin{array}{l} {z_1} = \cos {\varphi _i} \cdot {e_x} + \sin {\varphi _i} \cdot {e_y} - d - l\cos ({e_\varphi } + \theta ) \text{,} \\ {z_2} = \sin {\varphi _i} \cdot {e_x} + \cos {\varphi _i} \cdot {e_y} + l\sin ({e_\varphi } + \theta ) \text{,} \end{array} \right.$ | (8) |
对式(8)进行求导,跟踪误差在载体坐标系式(7)下可以表示为:
| $\left\{ \begin{array}{l} {{\dot z}_1} = {v_l}\cos {e_\varphi } - {v_i} - {z_2}{\omega _i} + l\sin ({e_\varphi } + \theta ) \cdot {\omega _l}\text{,} \\ {{\dot z}_2} = - {v_l}\sin {e_\varphi } + l\cos ({e_\varphi } + \theta ) \cdot {\omega _l} + d{\omega _i} + {z_1}{\omega _i} \text{,} \\ {{\dot e}_\varphi } = {\omega _l} - {\omega _i}\text{,} \end{array} \right.$ | (9) |
为使得误差达到最小且系统达到稳定,选用以下控制律
| $\left\{ \begin{array}{l} {v_i} = {v_l}\cos {e_\varphi } + {k_1}{z_1} + l\sin ({e_\varphi } + \theta ) \cdot {\omega _l}\text{,} \\ {\omega _i} = \dfrac{1}{d}[{v_l}\sin {e_\varphi } - {k_2}{z_2} - l\cos ({e_\varphi } + \theta ) \cdot {\omega _l}]\text{,} \end{array} \right.$ | (10) |
控制律
| $\left\{ \begin{array}{l} {{\dot z}_1} = - {k_1}{z_1} - {z_2}{\omega _i} \text{,} \\ {{\dot z}_2} = - {k_2}{z_2} + {z_1}{\omega _i}\text{,} \\ {{\dot e}_\varphi } = {\omega _l} - \dfrac{1}{d}[{v_l}\sin {e_\varphi } - {k_2}{z_2} - l\cos ({e_\varphi } + \theta ) \cdot {\omega _l}] \text{。} \end{array} \right.$ | (11) |
选取李雅普诺夫函数:
| $V = \dfrac{1}{2}(z_1^2 + z_2^2)\text{,}$ | (12) |
对所选取的李雅普诺夫函数进行求导,并将(11)式代入式(12)中可得:
| $\begin{split} \dot V= &{z_1}{{\dot z}_1} + {z_2}{{\dot z}_2}=\\ &- {k_1}z_1^2 - {k_2}z_2^2\text{。} \end{split} $ | (13) |
由式(12)和式(13)易知
其次证明AUV之间航向角误差
| $\begin{split} {{\dot e}_\varphi } = & - \dfrac{1}{d}{v_l}\sin {e_\varphi } + \dfrac{1}{d}{k_2}{z_2} + \dfrac{l}{d}\cos ({e_\varphi } + \theta ) \cdot {\omega _l} + {\omega _l}= \\ & - \dfrac{1}{d}{v_l}\sin {e_\varphi } + \delta ({z_2},{e_\varphi })\text{,} \end{split} $ | (14) |
其中考虑到实际情况
| ${\dot e_\varphi } = - \dfrac{1}{d}{v_l}\sin {e_\varphi }\text{,}$ | (15) |
可知式(15)渐进稳定,对于
| $\delta ({z_2},{e_\varphi }){\rm{ = }}\frac{1}{d}{k_2}{z_2} + \frac{l}{d}\cos ({e_\varphi } + \theta ) \cdot {\omega _l} + {\omega _l}\text{。}$ | (16) |
当
不同于Multi-AUV系统的围捕与追击任务,需要对动态障碍物进行规避,海洋探测任务中的避障任务主要针对静态的地形避障。与路径规划中的绕行避障不同的是,为实现探测区域的全覆盖扫描要保证AUV水平之间的相对位置,需要对极端地形进行跨越式避障。因此引入AUV在垂直方向上的高度控制与避障策略。
考虑到实际的探测需求与作业环境,AUV通常需要搭载侧扫声呐等声学设备对海底指定区域进行全覆盖扫描,为获得更佳的探测效果,需要保持AUV的距底高度。将动态滑动采样和最小二乘法引入到AUV的高度控制中。
最小二乘法是经典的参数估计方法,具有计算简单、运算速度快等特点。选取采用滑动采样获得的高度数据,使用基于最小二乘拟合的多项式模型逼近实际的海底地形高度,并对下一时刻海底地形高度进行预测。
如图3所示,
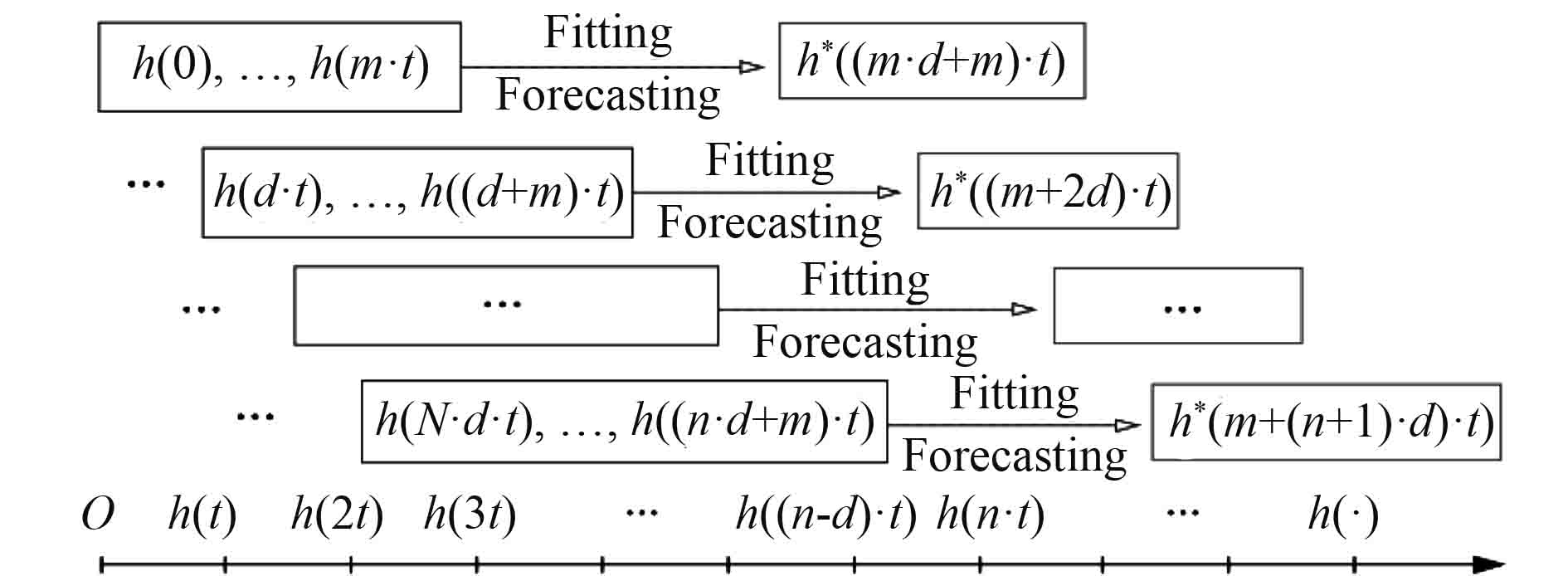
|
图 3 动态滑动采样与最小二乘拟合 Fig. 3 Dynamic sliding sampling and least square fitting |
| $\begin{split} P =& {a_0} + {a_1}t + {a_2}{t^2} + \cdot \cdot \cdot + {a_p}{t^p} =\\ &\sum\limits_{{\rm{i}} = 0}^p {{a_i}{t^i}} (p < m)\text{,} \end{split} $ | (17) |
式(17)可以表示为矩阵形式
| $\begin{split} {h^ * }(m + d) =& {a_0} + {a_1}(m + d) + \cdots + {a_p}{(m + d)^p} =\\ &\sum\limits_{{\rm{i}} = 0}^p {{a_i}{{(m + d)}^i}} \text{,} \end{split} $ | (18) |
同时设定AUV期望的距底高度为
| $\begin{split} {{Height}} =& {h^ * }(m + d) + H =\\ &\sum\limits_{{\rm{i}} = 0}^p {{a_i}{{(m + d)}^i}} + H\text{。} \end{split} $ | (19) |
其中采样周期t、决策周期d、用于数据拟合的采样点个数m以及多项式阶次p可结合实际进行调整。高度控制的输出Height作为AUV在垂直运动底层控制的输入,底层采用PID控制实现AUV在垂直方向上运动的控制。
此外海底地形起伏变化复杂,当AUV遇到地形高度落差极大的极端海底地形如海底悬崖、海沟等,则需要AUV越过障碍,为此提出相应的避障策略。
如图4所示,当AUV前方出现海底悬崖时,设定AUV避障的安全距离为
| ${v_{AUV}} = \left\{ {\begin{array}{*{20}{l}} {\begin{array}{*{20}{c}} 0\text{,} \\ {\dfrac{1}{p} \cdot {v_{cruise}}({R_d} - {R_a})}\text{,} \\ {{v_{cruise}}}\text{,} \end{array}}&{\begin{array}{*{20}{c}} {{R_d} < {R_a}} \text{,}\\ {{R_a} < {R_d} < {R_b}}\text{,} \\ {{R_d} > {R_a}}\text{。} \end{array}} \end{array}} \right.$ | (20) |
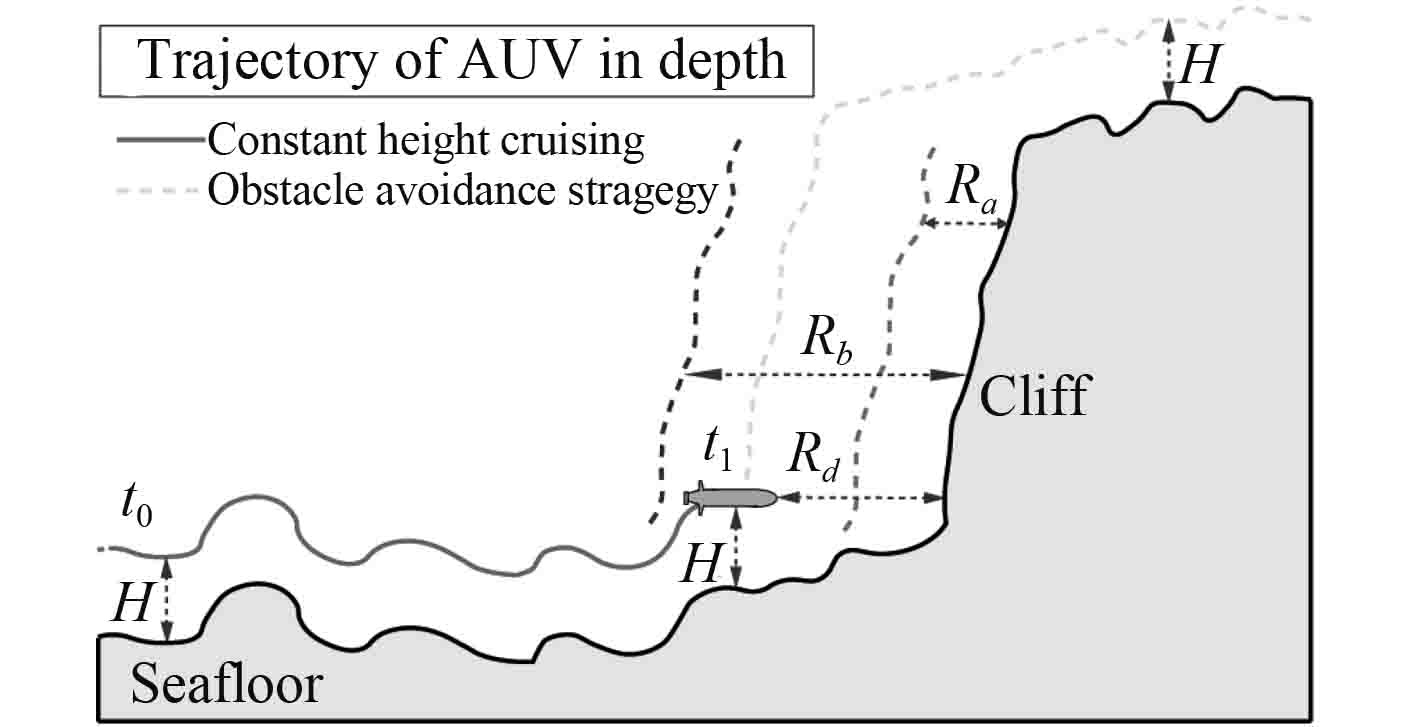
|
图 4 避障策略 Fig. 4 Obstacle-avoidance strategy |
当AUV与障碍物之间的距离
Multi-AUV的编队控制与高度控制如图5所示。控制器的控制目标在于编队中跟随AUV的状态
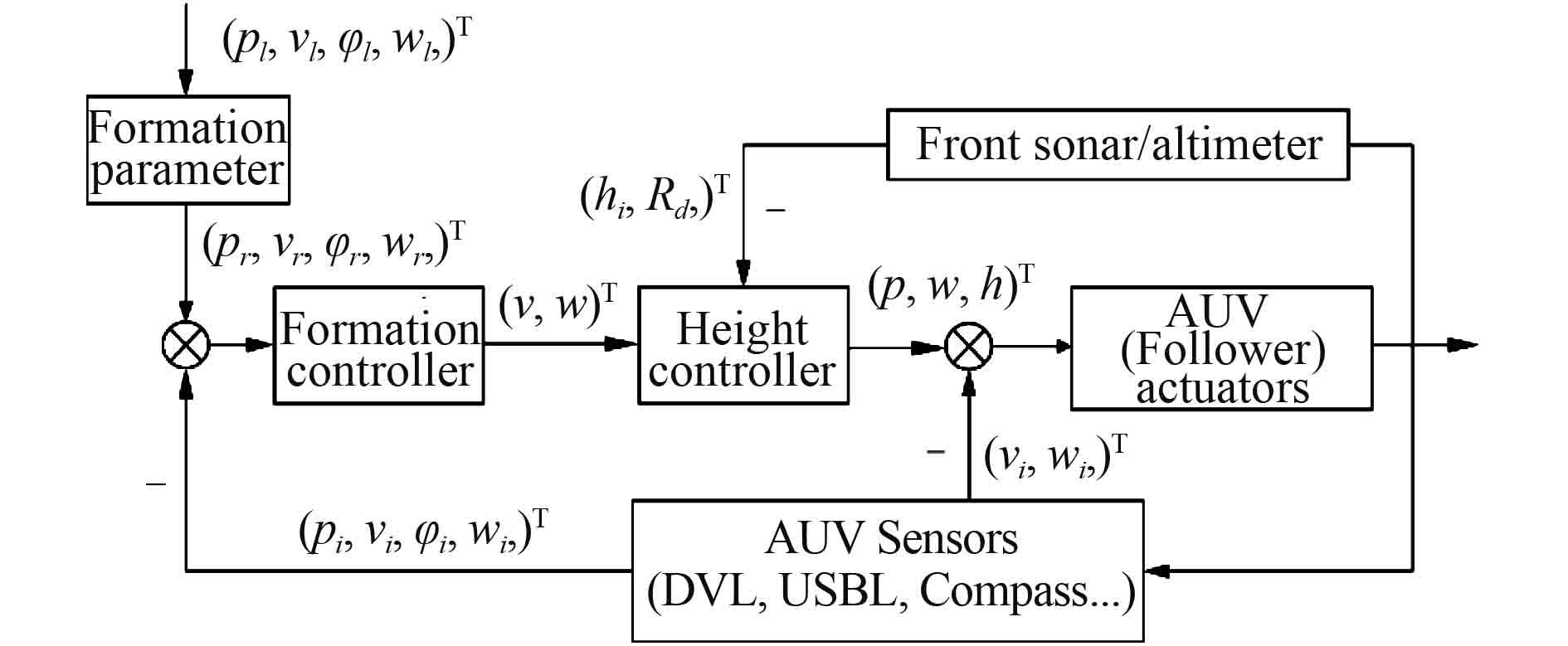
|
图 5 Multi-AUV编队与高度控制示意图 Fig. 5 Schematic of horizontal and perpendicular controller for the Multi-AUV |
编队中各AUV的状态信息可以通过自身搭载的设备进行获取。通过USBL和航迹推算可以获得AUV自身的位置信息,多普勒速度计程仪(DVL)获取AUV的航行速度,电子罗盘获得AUV航向角和角速度,而安装在AUV首部的高度计可以用于探测AUV据前方障碍物的距离以确定是否执行避障进程。
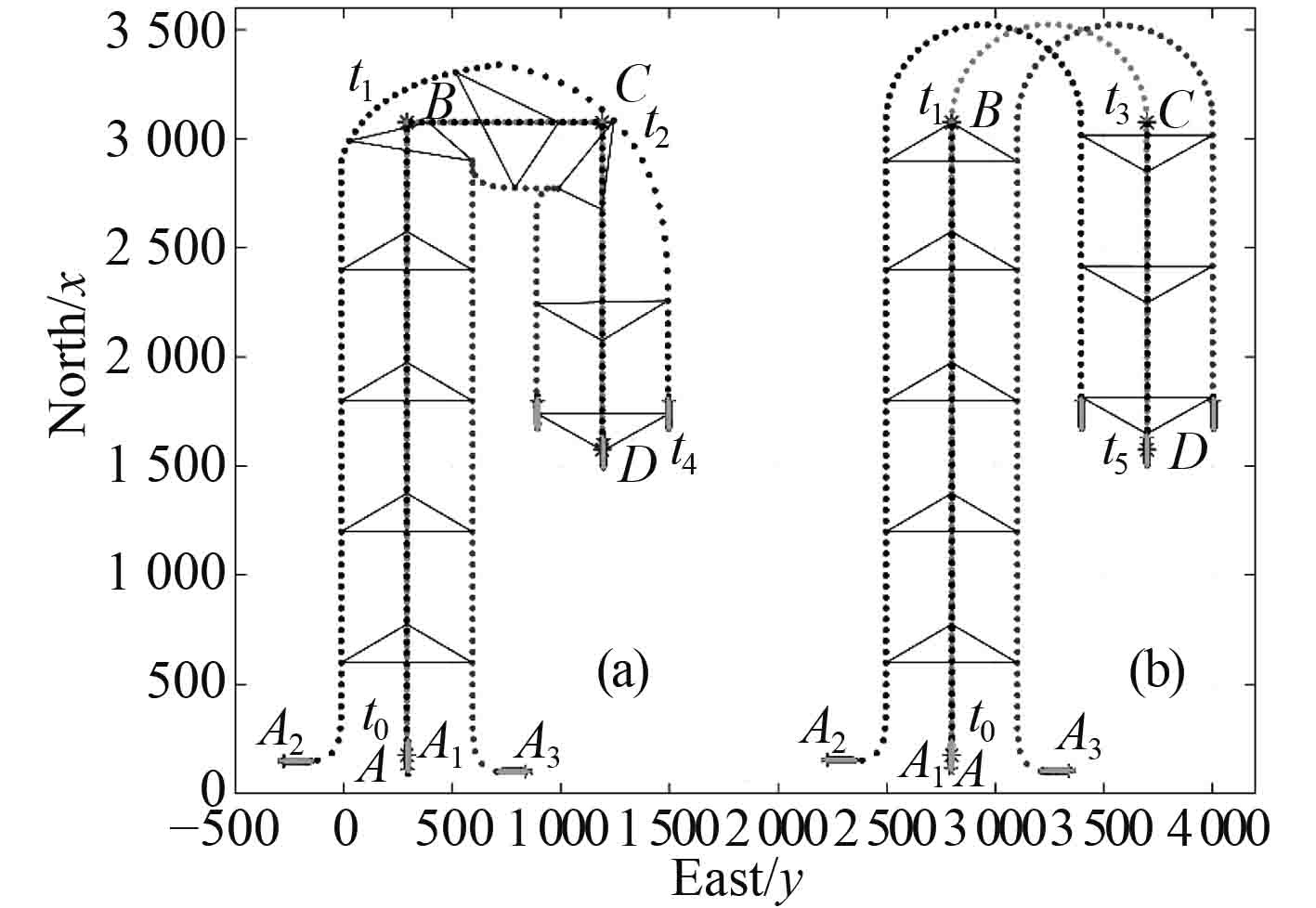
2.3 路径变换优化策略梳状扫描路径是AUV海洋探测任务中最常见的作业路径。如图6所示,折线为“潜龙一号”AUV在执行探测作业时行驶的梳状扫描路径[17]。
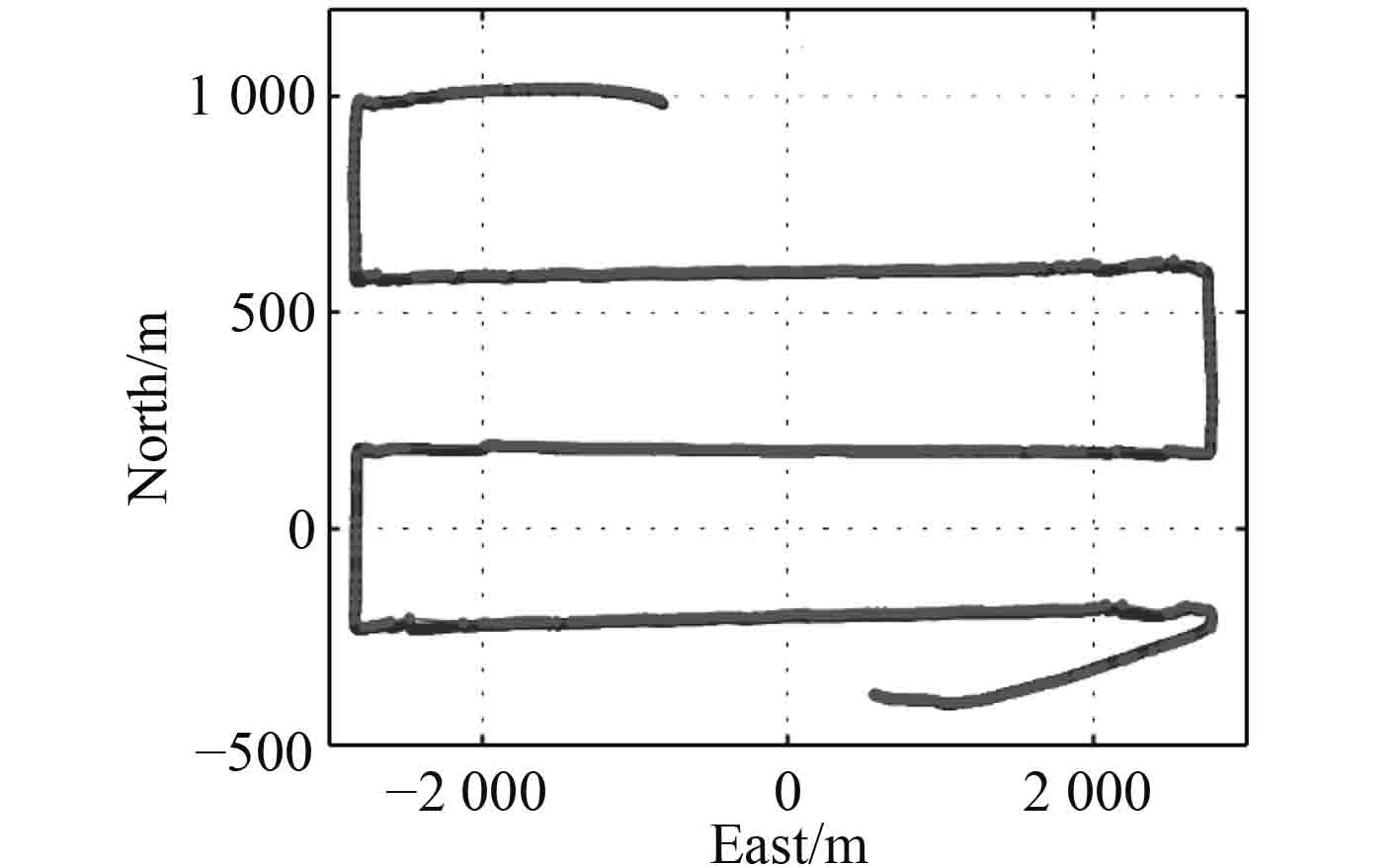
|
图 6 梳状搜索路径 Fig. 6 Lawnmower searching path |
图6所示的梳状扫描路径,当AUV编队完成当前一列扫描路径变换到下一列扫描路径的过程中存在路径变换的问题。图7左侧所示的折线路径,AUV编队沿
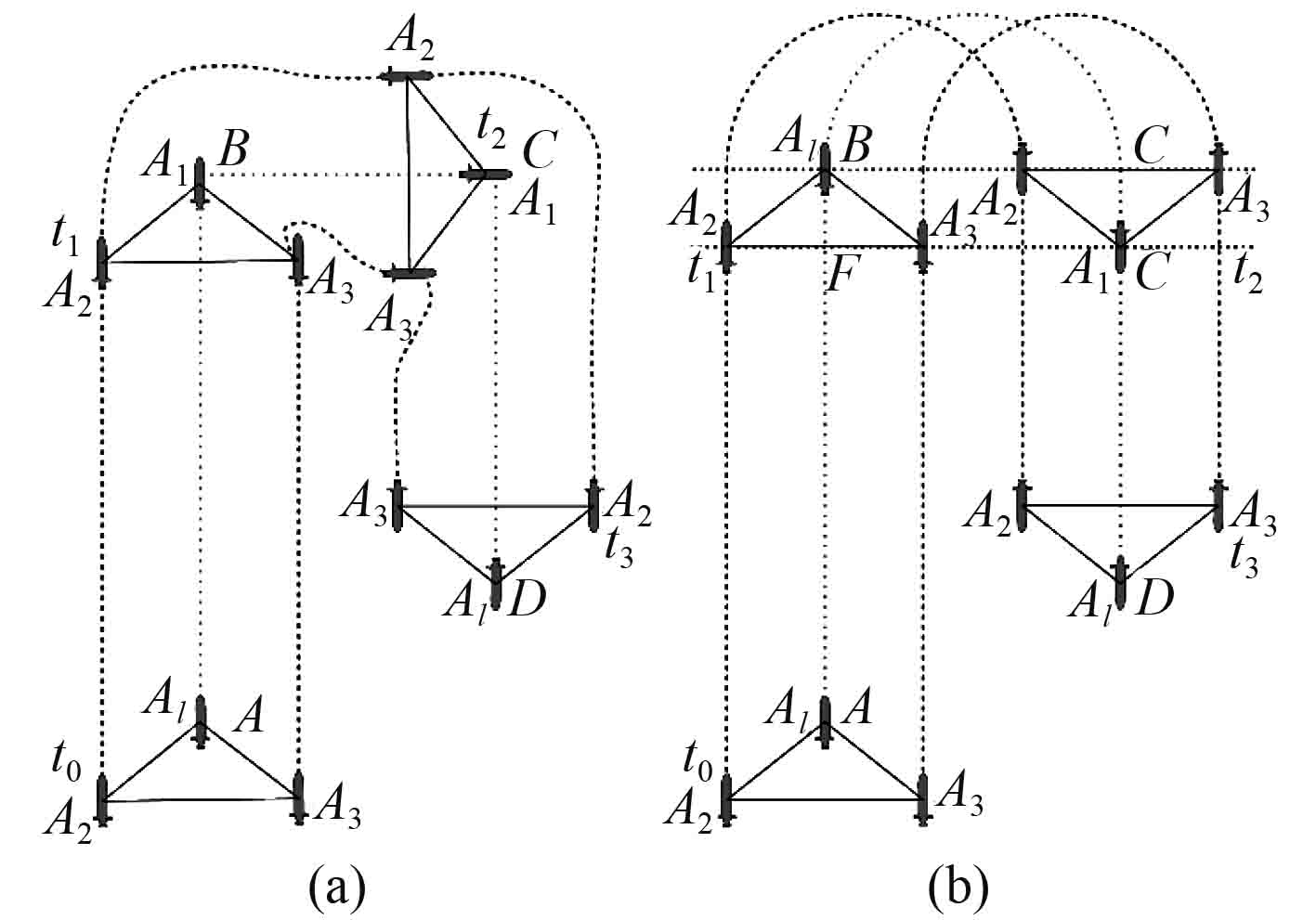
|
图 7 路径变换优化策略 Fig. 7 Route switching optimized formation strategy |
为消除路径变换对AUV编队造成的不良影响,采用圆弧
虽然优化策略消除了路径变换对AUV编队造成的不良影响,但编队中AUV的相对位置发生了改变。为更加直观展示编队中AUV之间关系的变化,引入图论中有向图的邻接矩阵
| $\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} \qquad\qquad\quad{{A_1}}&{{A_2}}&{{A_3}} \end{array}} \\ {{{{G}}_a} = \begin{array}{*{20}{c}} {{A_1}} \\ {{A_2}} \\ {{A_3}} \end{array}}\;\;{\left[ {\begin{array}{*{20}{c}} 0&0&0 \\ 1&0&0 \\ 1&0&0 \end{array}} \right]}\text{,} \end{array}}{\begin{array}{*{20}{c}} \qquad\qquad\;{\begin{array}{*{20}{c}} l&\;\;\theta \end{array}} \\ {{{{G}}_p} = \begin{array}{*{20}{c}} {{A_1}} \\ {{A_2}} \\ {{A_3}} \end{array}}\;\;{\left[\!\!\! {\begin{array}{c} {\begin{array}{*{20}{c}} 0 \\ l \\ l \end{array}}{\begin{array}{*{20}{c}} 0 \\ { - \theta } \\ \theta \end{array}} \end{array}} \!\!\!\right]} \text{。} \end{array}} \end{array}$ | (21) |
邻接矩阵
| ${{\rm{g}}_{ij}} = \left\{ {\begin{array}{*{20}{l}} {\begin{array}{*{20}{c}} 1\text{,}&{}&{\begin{array}{*{20}{c}} {\rm{if}}&{{g_{ij}} \in {\rm E}}\text{,} \end{array}} \end{array}} \\ {\begin{array}{*{20}{c}} 0\text{,}&{}&{\rm{otherwise}}\text{。} \end{array}} \end{array}} \right.$ | (22) |
编队参数矩阵
如图7右侧所示,当AUV编队采用路径优化的策略后,AUV编队可以平滑的完成扫描路径的变换,完成变换后AUV编队依然可以保持编队的外形和航向速度,可以无需进行调整继续进行全覆盖扫描。而编队内部位置关系的改变可以通过编队的参数矩阵
| $\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} \qquad l&\theta \end{array}} \\ {\begin{array}{*{20}{c}} {{A_1}} \\ {{A_2}} \\ {{A_3}} \end{array}}{\left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} 0 \\ l \\ l \end{array}}{\begin{array}{*{20}{c}} 0 \\ { - \theta } \\ \theta \end{array}} \end{array}} \right]} \end{array}\begin{array}{*{20}{c}} \to \end{array}\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} \qquad l&\theta \end{array}} \\ {\begin{array}{*{20}{c}} {{A_1}} \\ {{A_2}} \\ {{A_3}} \end{array}}{\left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} 0 \\ l \\ l \end{array}}{\begin{array}{*{20}{c}} 0 \\ \theta \\ { - \theta } \end{array}} \end{array}} \right]} \text{。} \end{array}$ | (23) |
采用这种优化的路径变换策略,可使得编队在路径变换的过程中各AUV所航行的路程以及航行的速度保持相同,同时在完成路径变换后不需要对编队进行调整缓冲即可立即进行作业,可以避免因路径变换造成不利影响。
3 仿真分析为验证所提出的Multi-AUV系统编队控制与策略的有效性,采用“潜龙一号”AUV作为研究对象(见图8)。“潜龙一号”在尾部配置有4台矢量布置的推进器,前部分别配置有垂直方向和水平方向的槽道桨,首部装备有高度计用作前方障碍物检测,同时装备有USBL、DVL、IMU、电子罗经、深高度计、侧扫声呐等,满足本文对AUV的假设。仿真案例为由3台AUV组成的Multi-AUV编队,在复杂海底环境中执行全覆盖探测扫描探测的任务。执行任务的过程中,要保持AUV编队在执行任务时的队形,以及各AUV的距底高度。采用Matlab软件对所提出的编队与高度控制以及避障与路径变换优化策略进行数值仿真。

|
图 8 “潜龙一号”AUV Fig. 8 Qian Long I AUV |
设定AUV作业航行时的速度为2 kn,小于AUV的最大续航速度3 kn;按顺序设定AUV的起始位置分别为
图9为Multi-AUV编队控制器的仿真过程,Multi-AUV编队中各AUV可以迅速对参考AUV状态进行跟随形成期望队形并对队形进行维持。但当领航AUV进行转向时,由于左右两侧跟随AUV转弯半径的不同导致两侧AUV的速度和航向发生变化对队形的维持产生不良影响。
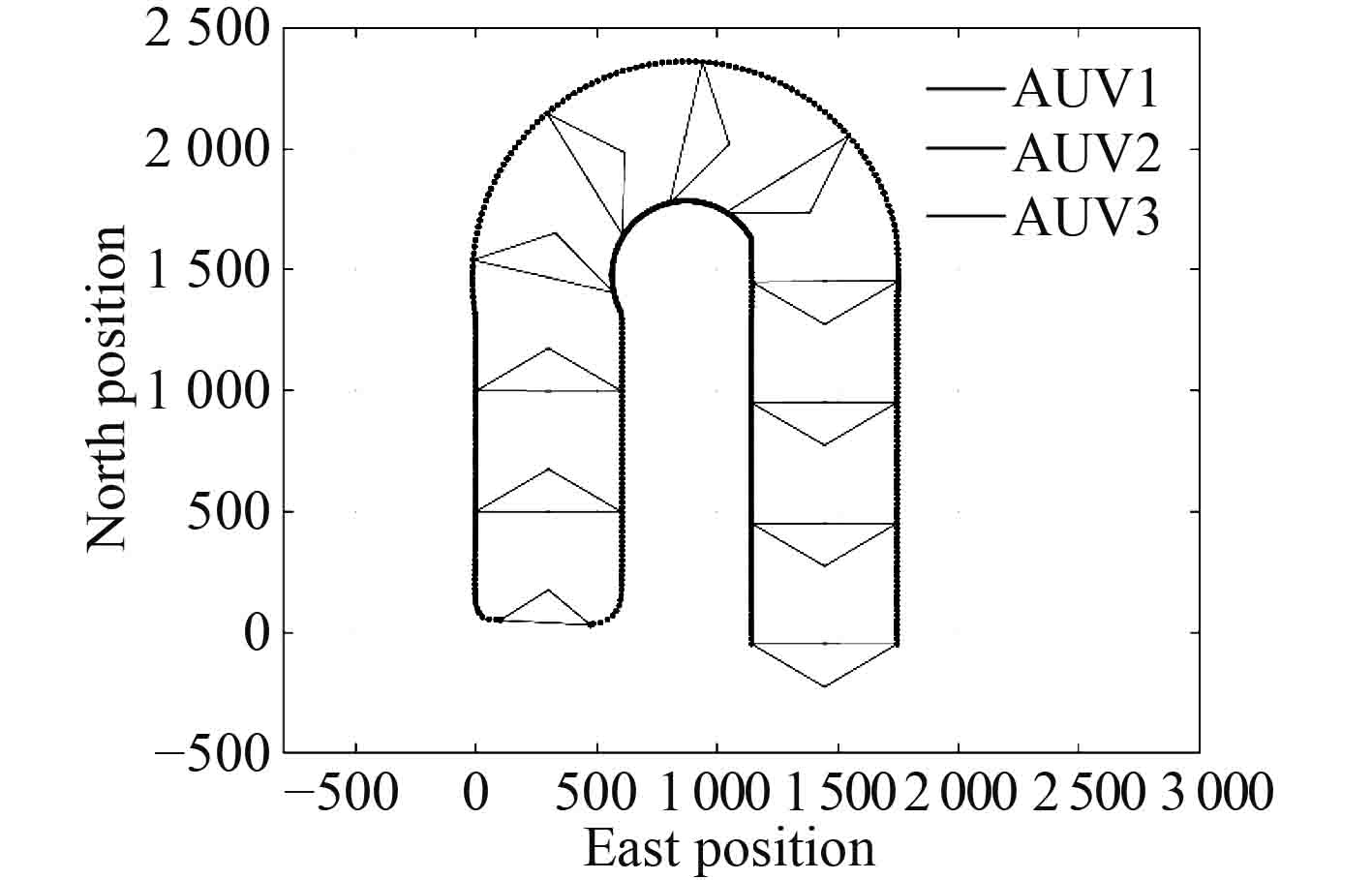
|
图 9 Multi-AUV编队航行过程 Fig. 9 Simulation result of Multi-AUV formation control |
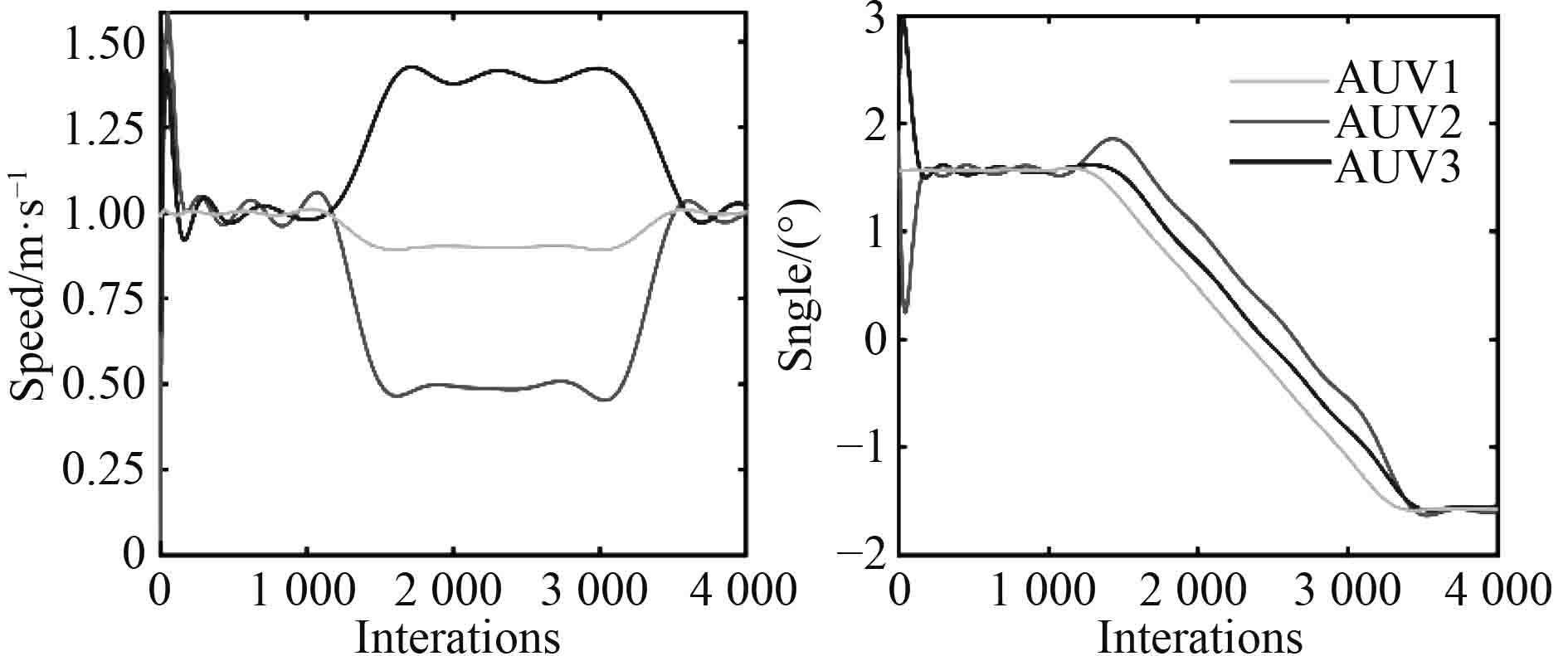
图10和图11分别表示仿真过程中Multi-AUV编队位置误差和编队中各AUV速度与航向的变化。

|
图 10 Multi-AUV编队位置误差变化 Fig. 10 Position error of the Multi-AUV formation |
|
图 11 Multi-AUV编队中个体速度与航向 Fig. 11 Speed and angle variation during the simulation |
如图10与图11所示,开始阶段AUV可以迅速收敛到参考AUV的位置并对生成的参考AUV的速度和航行进行跟踪。当领航AUV进行转向时,转弯半径不同导致两侧AUV的速度和航向发生变化,队形发生畸变,AUV的位置误差也相应增大;当领航AUV完成转向时,AUV的速度和航向再次收敛到领航AUV的状态,位置误差同样需要调整时间重新收敛队形;当领航AUV转弯半径减小时,队形将发生更严重的畸变。
图12为水平面内Multi-AUV编队路径优化策略的仿真对比结果,图12(a)和图12(b)分别为未采用优化策略以及采用优化策略后AUV编队的轨迹。采用优化策略的AUV编队航行轨迹明显更加平滑,且在完成路径变换后无需对编队位置和状态进行调整即可继续进行扫描作业,相比之下未采用优化策略的AUV编队在进入下一列扫描路径后需要对AUV编队进行调整才可继续进行全覆盖扫描作业。
|
图 12 Multi-AUV编队路径变换优化策略 Fig. 12 Multi-AUV route switching optimized strategy |
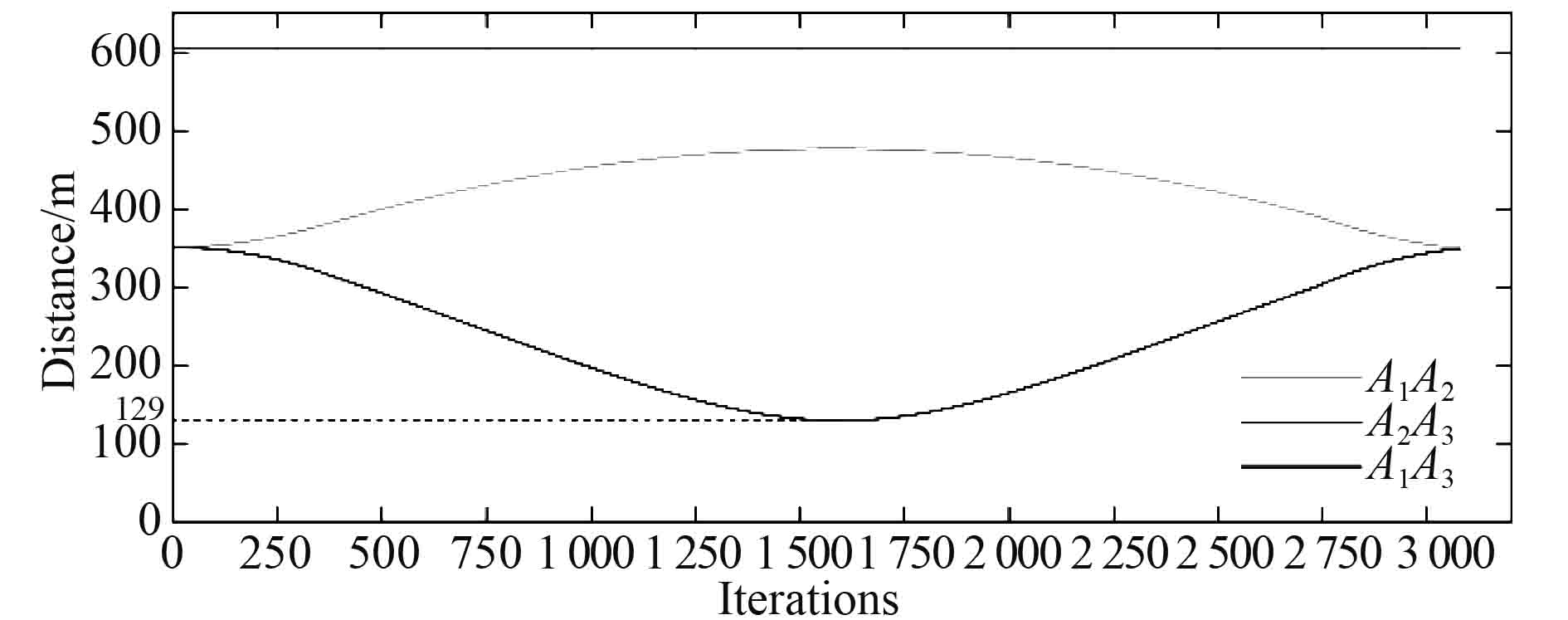
如图12仿真结果俯视图所示,AUV编队在执行路径变换策略的过程中轨迹存在交叉,因此在仿真过程中对编队各AUV之间的距离进行监测。如图13所示,在执行路径变换时AUV之间的最小距离大于所设定的安全距离R,因此编队中AUV无碰撞风险。
|
图 13 Multi-AUV编队中各AUV间距离变化 Fig. 13 Distance between each AUV in the formation |
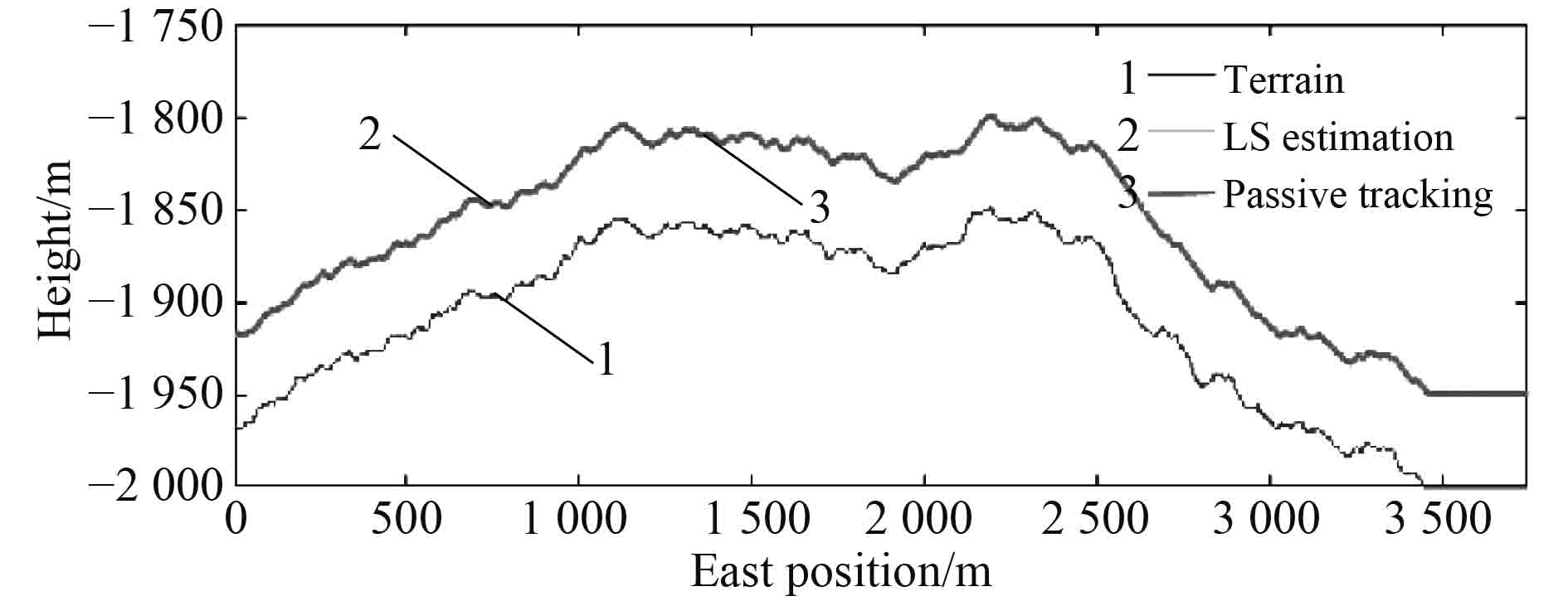
对于AUV的高度控制,设定AUV距离海底的期望高度H为50 m;用于地形拟合的采样点个数 与多项式阶次p分别选取为10与2;避障策略的安全距离
|
图 14 AUV高度控制仿真 Fig. 14 Simulation result of AUV height control |
|
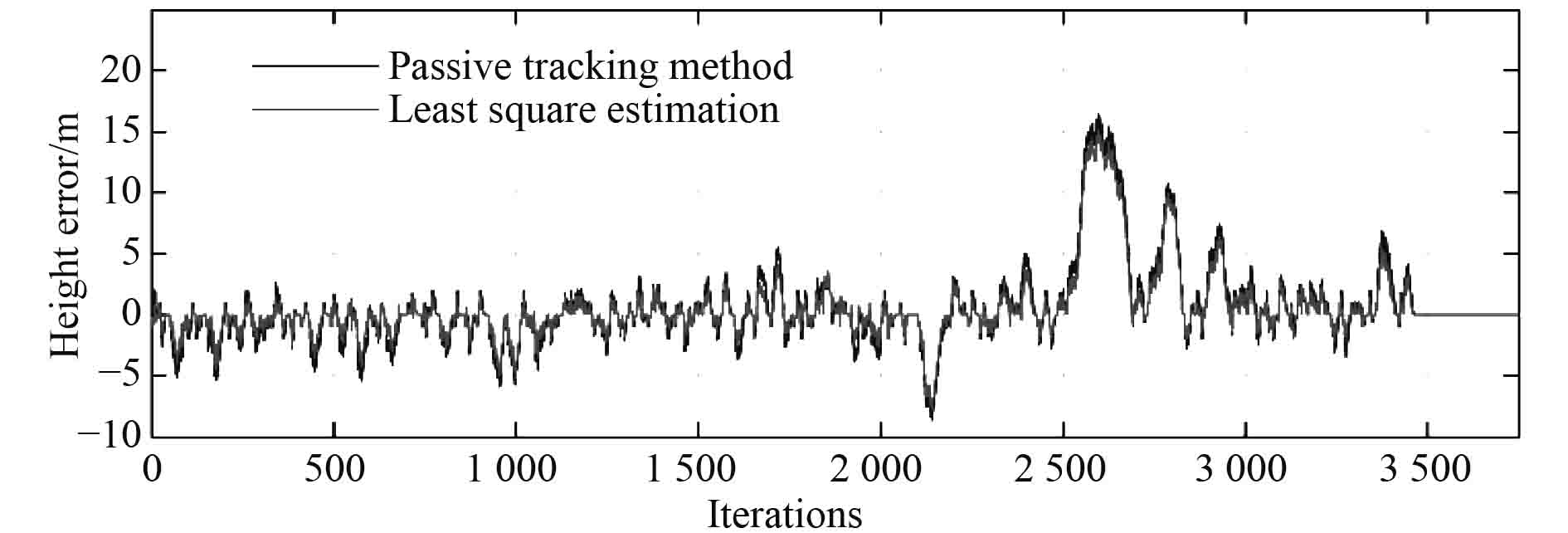
图 15 AUV定高航行误差变化 Fig. 15 Height error of AUV with fixed height |
图14中线1为实际地形;线2和线3分别表示基于提出的最小二乘估计与未采用估计的被动高度控制的仿真结果。可以看出,两者均可以对地形进行有效的跟踪。图15为2种方法对地形进行定高跟踪时的误差变化,其中基于最小二乘估计方法的高度误差的标准差为2.59 m小于不采用估计的被动跟踪方法的3.06 m。所提出的高度控制方法可以有效的进行定高航行。
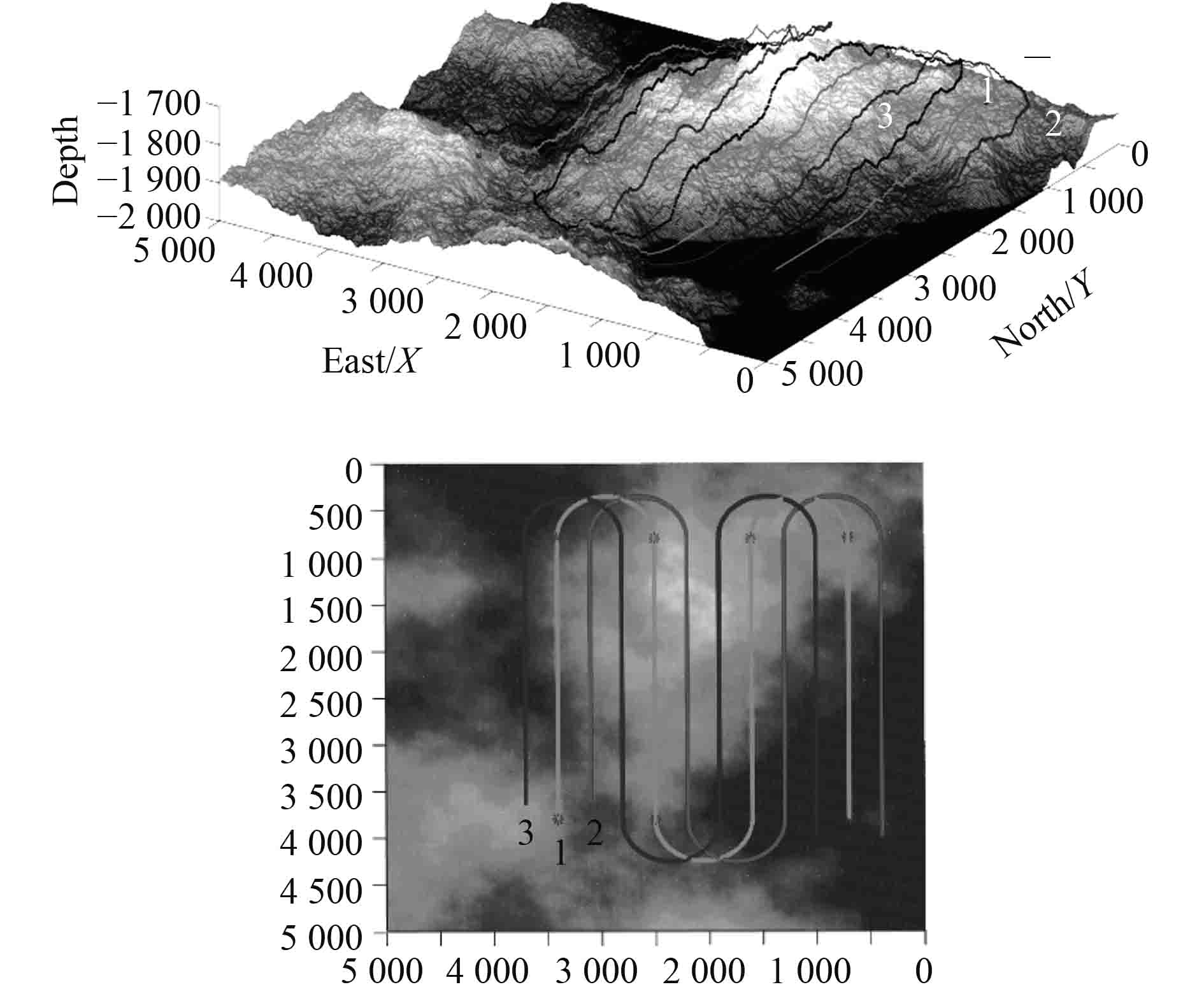
图16左侧为三维视图下Multi-AUV编队执行复杂地形海洋探测任务仿真结果,右侧为仿真结果的俯视图。图中线1表示领航AUV的航行轨迹,线2与线3为跟随AUV的航行轨迹。通过仿真结果可以看出Multi-AUV编队执行任务时,在水平方向上可以有效维持编队的几何构型,在垂直方向上可以独立的维持AUV的距底高度,并实现探测区域的全覆盖。
|
图 16 Multi-AUV编队海洋勘探任务过程 Fig. 16 Simulation result of Multi-AUV oceanographic exploration in three dimensions and top view |
从以上的仿真实验结果可以看出,本文提出的Multi-AUV协同编队控制方法和策略可以有效实现Multi-AUV系统的编队航行和高度控制,满足复杂地形海洋勘探任务要求。
4 结 语本文针对现在Multi-AUV编队执行复杂海底地形勘探任务的实际需求与问题,提出了基于领航-跟随思想和反馈线性化的系统编队控制方法、基于滑动采样与最小二乘估计的高度控制以及避障与路径优化策略,最后建立3-AUV编队作业场景,通过计算机仿真验证了本文提出的协同编队控制与策略在执行海底复杂地形探测任务中的有效性。
| [1] |
RUSSELL B. WYNN, VEERLE A. I. HUVENNE, TIMOTHY P, et al. Autonomous underwater vehicles (AUVs): Their past, present and future contributions to the advancement of marine geoscience[J]. Marine Geology, 2014, 352. |
| [2] |
CHRIST B, KLARA J. A new approach to wide area survey multiple AUV application[C]//OCEANS Monterey 2016, 1−6.
|
| [3] |
URABE T, URA T, TSUJIMOTO T, et al. Next-generation technology for ocean resources exploration (Zipangu in the Ocean) project in Japan[C]//OCEANS 2015 Genova. 2015, 1−5.
|
| [4] |
KIM, K. AND TAMURA, K. The Zipangu of the sea project overview: Focusing on the R&D for simultaneous de-ployment and operation of multiple AUVs[C]//Offshore Technology Conference 2016, Kuala Lumpur, Malaysia.
|
| [5] |
ABREU P C, BAYAT M, BOTELHO J, et al. Cooperative for-mation control in the scope of the EC MORPH project: Theory and experiments[C]//OCEANS Genova 2015, 1−7.
|
| [6] |
SOARES J M, AGUIAR A P, ANTÓNIO M. PASCOAL, et al. Joint ASV/AUV Range-Based formation control: Theory and experimental results[C]//Robotics and Automation (ICRA), 2013 IEEE International Conference on. IEEE, 2013.
|
| [7] |
ZWOLAK K, SIMPSON B, ANDERSON B, et al. An unmanned seafloor mapping system: The concept of an AUV inte-grated with the newly designed USV SEA-KIT[C]// OCEANS 2017. Aberdeen, United Kingdom.
|
| [8] |
严浙平, 刘祥玲. 多UUV协调控制技术研究现状及发展趋势[J]. 水下无人系统学报, 2019, 27(3): 226-231. |
| [9] |
BALCH T, ARKIN R C. Behaviour-based formation control for multirobot teams[J]. IEEE Transactions on Robotics and Automation, 1998, 14(6): 926-939. DOI:10.1109/70.736776 |
| [10] |
MONTEIRO, S. AND BICHO, E. A dynamical systems approach to behaviour-based formation control[C]//IEEE Int. Conf. on Robotics and Automation. Washington, DC. 2002 2606−2611.
|
| [11] |
LEWIS M A, TAN K H. High precision formation control of mobile robots using virtual structures[J]. Autonomous Robots, 1997, 4(4): 387-403. DOI:10.1023/A:1008814708459 |
| [12] |
LEONARD N E, FIORELLI E. Virtual leaders, artificial poten-tials and coordinated control of groups[C]//Proceedings of the 40th IEEE Conference on Decision and Control 2001, 3: 2968−2973.
|
| [13] |
JIA Q, LI G. Formation control and obstacle avoidance algorithm of multiple autonomous underwater vehicles (AUVs) based on potential function and behaviour rules[C]// IEEE International Conference on Automation & Logistics, 2007.
|
| [14] |
CUI, R. GE, S. S., et al. Leader–follower formation control of underactuated autonomous underwater vehicles[J]. Ocean Engineering 2010, 37(17): 1491−1502.
|
| [15] |
SHAO, J., XIE, G., WANG, L.. Leader-following formation control of multiple mobile vehicles[J]. IET Control The-ory & Applications, 2007, 1(2): 545-552. |
| [16] |
YAN Z, XU D, CHEN T, et al. Leader-Follower formation control of UUVs with model uncertainties, Current Disturbances, and Unstable Communication[J]. Sensors, 2018, 18(2): 662. DOI:10.3390/s18020662 |
| [17] |
李硕, 刘健, 徐会希, 等. 我国深海自主水下机器人的研究现状[J]. SCIENCE CHINA Information Sciences, 2018, 48(9): 1152-1164. |
 2021, Vol. 43
2021, Vol. 43

