0 引　言

水下滑翔机（Autonomous Underwater Glider，AUG）^[1-4]作为一种新型的水下航行器，具有能源需求量小、航行效率高、航行时间长、成本和维护费用低等优点，在大范围海洋探索和监测中发挥出越来越重要的作用。水下滑翔机的基本工作原理是将水翼所产生的升力转化为推动其向前的动力，故水动力性能的优劣对水下滑翔机的总体性能和航行距离具有重要影响。水下滑翔机外形优化设计可提高水下滑翔机的水动力性能，已成为水下滑翔机的热点研究方向^[5]。

外形参数化是水下滑翔机外形优化设计的重要内容，其主要通过一定的函数关系，用一组设计参数（也被称为设计变量）对水下滑翔机的几何形状进行定义和表示，从而将水下滑翔机外形的优化设计过程转化为对这组设计变量的寻优过程。因此，从降低优化计算量和提高优化结果两方面考虑，既要求采用的参数化方法能够采用较少的参数对几何外形进行定义，又要保证一定精度，同时提供充分的设计空间，能够描述尽可能丰富的外形变化。

相较于由回转体、水翼和操纵面组成的传统布局水下滑翔机，翼身融合（Blended-Wing-Body，BWB）水下滑翔机^[5-6]具有剖面形状的身，且水翼平滑地与机身融合在一起，具有更高的升阻比，水动力性能更好。但翼身融合水下滑翔机的外形曲面也更为复杂，机身与机翼连接处运用了大量的曲线、曲面平滑过渡，很难用简单的外形参数化方法进行描述。

CAD（Computer Aided Design）参数化方法^[7]是一种基于计算机辅助设计软件的参数化方法。这一类方法依赖如UG，CATIA 等商业CAD软件，可通过建立特征树进行外形的自动生成，并且支持二次开发，具备一定的拓展性。但CAD参数化方法无法直接操作水动力计算所需的CFD（Computational Fluid Dynamics）网格，需要将CAD的外形变化映射到CFD表面网格上，进而依据网格变形方法重新生成CFD空间网格。此外，CAD参数化方法在构建特征树时，很难既保持部件间的特征，又满足根据物理意义直观地改变外形的设计要求。

B样条方法和非均匀有理B样条方法^[8]（Non-uniform Rational B-spline，NURBS）主要通过移动控制点的位置实现水下滑翔机外形的参数化，能够对曲面外形进行局部控制和光滑处理，具有很强的灵活性和良好的可微性。此外，该2种方法可通过将表面网格投影至曲面上^[9-10]，求解出每个网格点的局部坐标值，进而对表面网格直接进行操控，克服CAD参数化方法的缺点。但该2种方法首先需要将外形曲面划分为一系列的拼接曲面，要求外形具有结构化的拓扑结构；然后要求不同曲面在拼接处具有连续可微性，实现起来较为繁琐和困难。总的来说，在复杂外形的应用中灵活性不足。

近年来，自由变形方法（Free-form Deformation，FFD）^[11]以其简单灵活、易于保持外形的拓扑结构和光滑性等优点，被广泛应用于外形的优化设计过程中。FFD方法主要基于弹性物体受力变形的思想，将欲变形的几何外形控制点或者CFD表面网格包络在一个FFD控制体当中，变形时改变控制体的形状，则控制体内的几何外形控制点或者CFD表面网格同时发生相应的改变。该过程无需生成几何外形，不需要具备很强的几何知识储备，也不需要将几何变形映射到CFD表面网格中，操作简单并具备较好的局部变形能力。但对于翼身融合水下滑翔机，外形比较复杂，若把FFD控制体的每一个控制点都作为优化变量，则会导致优化设计变量过多、计算量大、效率低、收敛慢等问题。

针对上述问题，本文首先建立翼身融合水下滑翔机外形的FFD参数化模型，实现翼身融合水下滑翔机的自由变形；然后在FFD控制体内建立参考轴，提出一种翼身融合水下滑翔机外形的轴变形参数化方法，减少优化变量的数目及计算量；最后通过实例验证所提方法的有效性。

1 FFD参数化模型

FFD方法为Sederberg 和Parry在1986年提出^[12]。该方法基于弹性物体受力变形的思想，如果将研究对象放置于弹性体内，给弹性体施加外力后，则弹性体内部的空间会发生形变，嵌入其中的研究对象也会根据某种映射关系发生变化。对于翼身融合水下滑翔机来说，可以采用其CFD表面网格（即为物面网格边界）来表达几何外形，将表面网格导入到FFD控制体中，通过FFD控制体变化可实现优化过程中的水下滑翔机外形变化。

为了采用FFD方法对CFD表面网格进行参数化，首先，需要在表面网格周围建立FFD控制体。Bernstein多项式、B样条函数或NURBS函数等均可作为基函数来创建FFD控制体，但考虑到Bernstein多项式的局部变形性能不佳，实际中常采用B样条函数或者NURBS函数创建FFD控制体。

曲线节点矢量 $U$ 上的 $p$ 阶B样条基函数 ${N_{i,p}}(u)$ 可表述如下：

${N_{i,0}}(u) = \left\{ \begin{array}{l} 1 \text{,}\;\;\;{u_i} \leqslant u \leqslant {u_{i + 1}} \text{，} \\ 0 \text{，}\;\;\;{\rm{else}} \text{，}\\ \end{array} \right.{\rm{ }}$

(1)

$\begin{split} {N_{i,p}}(u) =& \frac{{u - {u_i}}}{{{u_{i + p}} - {u_i}}}{N_{i,p - 1}}(u) + \\ & \frac{{{u_{i + p + 1}} - u}}{{{u_{i + p + 1}} - {u_{i + 1}}}}{N_{i + 1,p - 1}}(u) \text{，} \end{split} $

(2)

由B样条基函数创建的控制体方程可表述如下形式：

$K(u,v,w) = \sum\limits_{i = 0}^l {\sum\limits_{j = 0}^m {\sum\limits_{k = 0}^n {{N_{i,p}}} } } (u){N_{j,p}}(v){N_{k,p}}(w){P_{i,j,k}} \text{。}$

(3)

式中： ${P_{i,j,k}}$ 为FFD控制体上的控制点在原始笛卡尔坐标系中的坐标值； ${N_{i,p}}(u)$ 、 ${N_{j,p}}(v)$ 和 ${N_{k,p}}(w)$ 分别为参数化空间 $(u,v,w)$ 上的 $p$ 阶B样条基函数。

然后，计算待变形的各个网格点在FFD控制体中的局部坐标 $(u,v,w)$ ，其中局部坐标的3个分量均位于[0，1]之间，通过逆向求解式（3）确定。需注意的是，每个网格点的局部坐标只需计算一次，不需要在每次CFD网格变形的过程中重复计算。

接着，改变FFD控制点的位置，产生位移量 $\Delta {P_{i,j,k}}$ ，则任一个局部坐标为 $(u,v,w)$ 的网格点的位移 $\Delta K$ 可由下式确定：

$\Delta K(u,v,w) = \sum\limits_{i = 0}^l {\sum\limits_{j = 0}^m {\sum\limits_{k = 0}^n {{N_{i,p}}} } } (u){N_{j,p}}(v){N_{k,p}}(w)\Delta {P_{i,j,k}} \text{,}$

(4)

最后，可得到变形后表面网格上每一个网格点的位置 $\hat K(u,v,w)$ 为：

$\hat K(u,v,w) = K(u,v,w) + \Delta K(u,v,w) \text{。}$

(5)

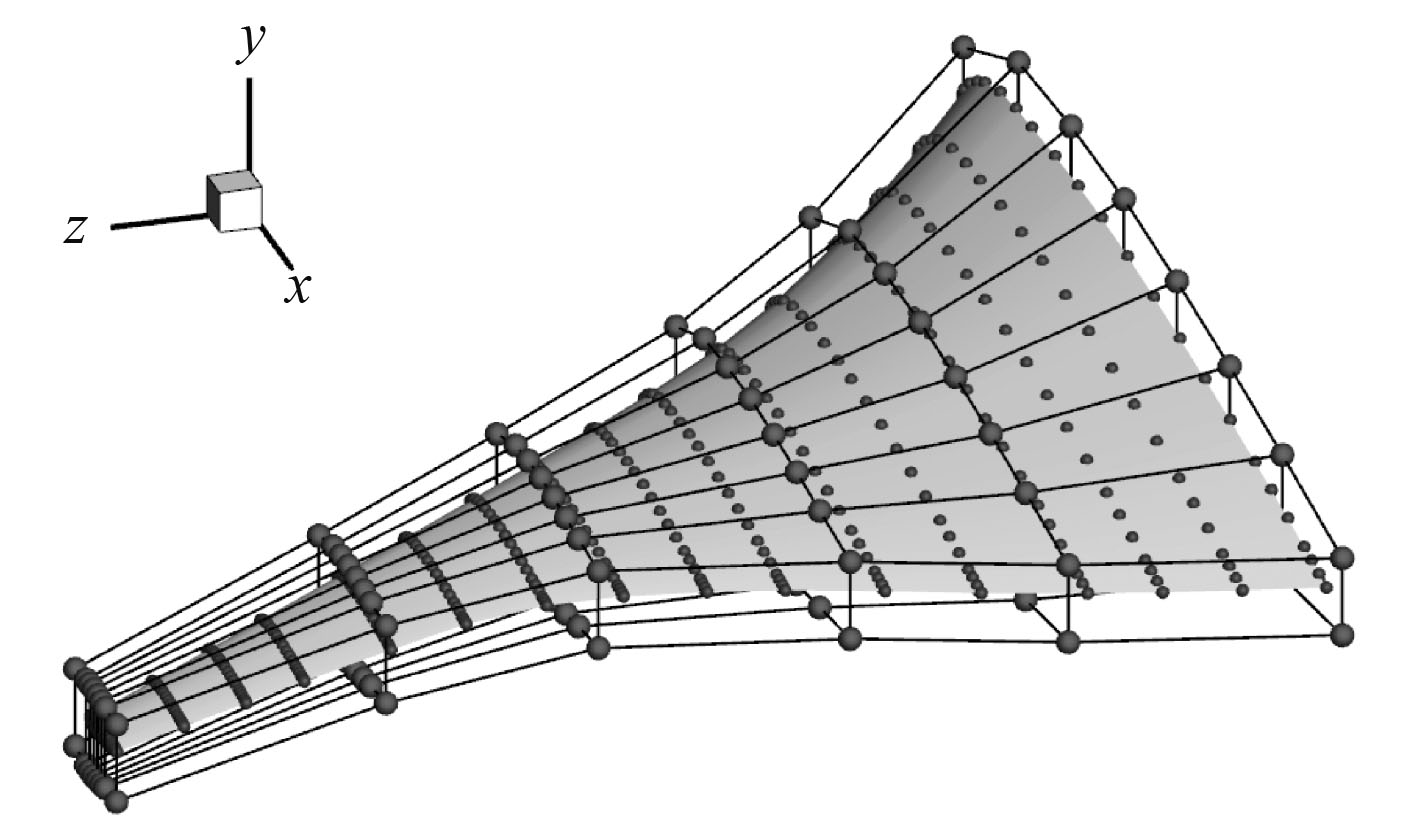
考虑到翼身融合水下滑翔机外形常常左右对称，故取其一半建立相应的FFD控制体，如图1所示。其中，大点为FFD控制体的控制点，小点为嵌入的水下滑翔机表面网格，通过改变控制点的位置，可间接实现翼身融合水下滑翔机外形的变形控制。

2 轴变形参数化方法

尽管FFD参数化方法具有不依赖外形拓扑结构、可保持初始外形连续光滑、变形简单灵活等优点，但若把每一个FFD控制体的控制点都作为优化变量，对于复杂外形，则会导致优化设计变量规模过大，进而造成优化设计计算量大、效率低、收敛慢等问题。

对于翼身融合水下滑翔机外形，如何既能充分利用FFD参数化方法的优点，又合理控制优化设计变量的规模，是一个亟需解决的问题。本文提出一种基于轴变形的全局FFD参数化方法，在FFD控制体内引入一条参考轴，并将FFD的所有控制点关联到该参考轴上，通过设置全局变量对参考轴进行变形控制，进而实现对FFD控制点的分组集中控制，减少优化设计变量的规模。该方法详细阐述如下：

1）使用如下的 $p$ 阶B样条曲线定义一条参考轴：

$ C(s) = \sum\limits_{i = 0}^N {{N_{i,p}}(s){Q_i}} ,\;\;{\rm{0}} \leqslant u \leqslant {\rm{1}} $

(6)

式中： ${Q_i}(i = 1, \cdots ,N)$ 是曲线的 $N$ 个控制点； ${N_{i,p}}(s)$ 是曲线节点矢量 $S$ 上的 $p$ 阶B样条基函数。

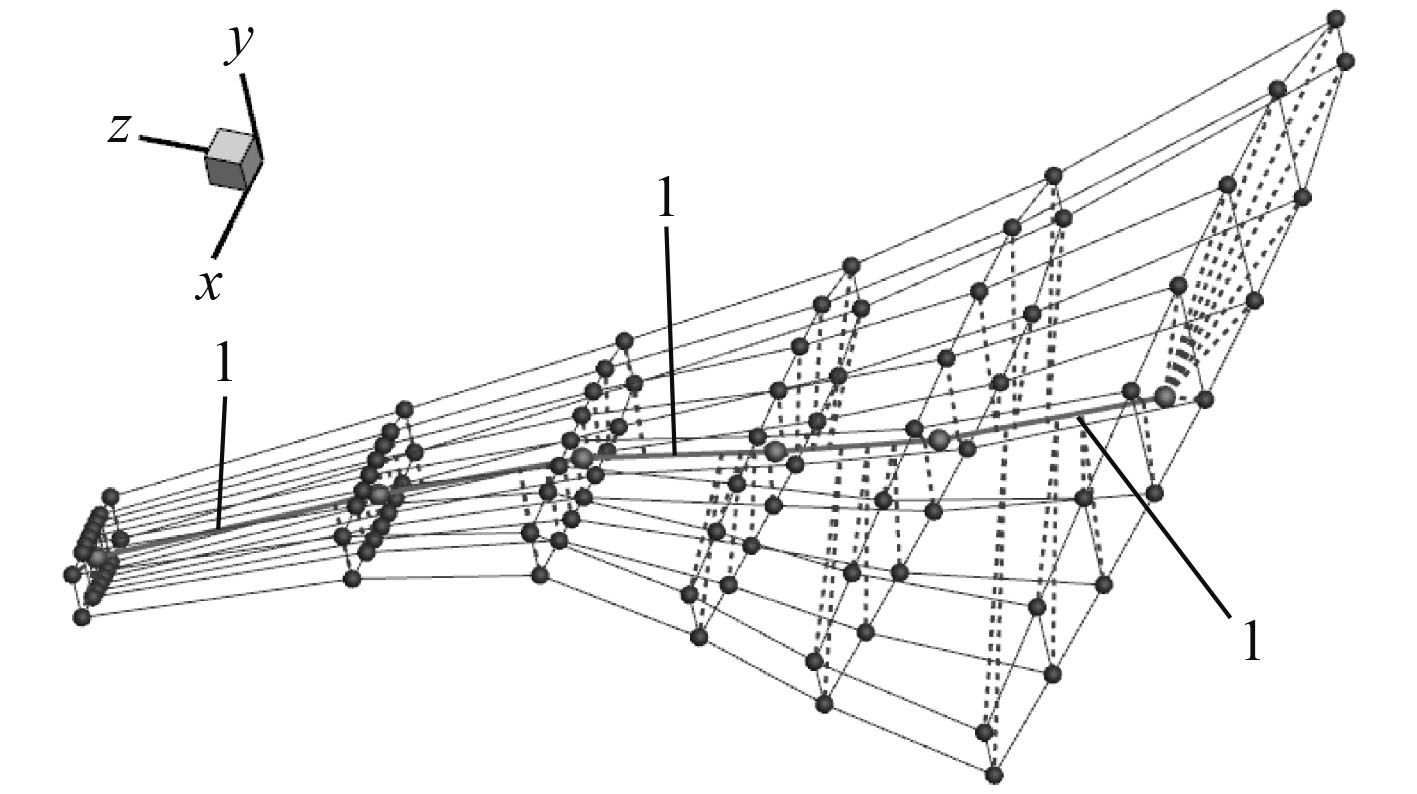
2）将FFD控制点映射到参考轴上。映射的主要思路为：对于每个FFD控制点 ${P_{i,j,k}}$ ，分别求出参考轴上与其距离最近的点，则该点为相应FFD控制点在参考轴上的映射点，并计算出其在参考轴上的参数化坐标值为 ${\tilde s_{i,j,k}}$ 。该映射方法保证每个FFD控制点与相应映射点的直线与参考轴在映射点处的切线具有垂直关系。求出映射点后，计算每个FFD控制点到映射点的向量 ${\vec R_{i,j,k}} = {P_{i,j,k}} - C({\tilde s_{i,j,k}}){\kern 1pt} {\kern 1pt} $ ，以备后续步骤使用。图2为翼身融合水下滑翔机的FFD控制点到参考轴的映射图，图中，曲线1表示参考轴，黑色点表示FFD控制点，虚线表示映射向量 ${\vec R_{i,j,k}}$ 。

3）基于参考轴，设置弦长、展长、厚度、后掠角、上反角、几何扭转角等具有实际物理意义的全局变量，控制参考轴的变化，进而控制映射在参考轴上的FFD控制点的变化。根据操控参考轴的方式不同，全局变量主要被分为两类：一类通过改变参考轴在笛卡尔坐标系中的长度、角度等形状参数，进而实现映射在参考轴上的FFD控制点沿轴向变化，如展长、后掠角及上反角等全局变量，统称为轴向全局变量；另一类不需要改变参考轴在空间中的形状，只需在参考轴任一参数化坐标 $s$ 处给定具体的变量值，并根据变量值操控映射在参考轴上的FFD控制点，进而改变任一参数化坐标 $s$ 处截面的形状，如弦长、厚度和几何扭转角等全局变量，统称为截面全局变量。

对于轴向全局变量，本文主要借助于其变量值移动参考轴的控制点 ${Q_i}$ ，实现参考轴的形状变化。假设该变量改变后将参考轴的控制点改变为 ${T_i}$ ，则形状改变后的FFD控制点 ${\hat P_{i,j,k}}$ ，可改变公式（6）中的控制点，由下式计算：

${\hat P_{i,j,k}} = \sum\limits_{i = 0}^N {{N_{i,p}}({{\tilde s}_{i,j,k}}){T_i}} (X) + {\vec R_{i,j,k}} \text{。}$

(7)

式中： $X$ 表示弦长、厚度和扭转角等全局变量； ${T_i}(X)$ 表示控制点改变后的位置关于全局变量 $X$ 的函数。

对于截面全局变量，本文主要借助于给定其在典型翼型剖面处的变量值 ${X_i}{\kern 1pt} $ ，并使用 $p$ 阶B样条曲线对其进行拟合，计算出参考轴任一参数化坐标 $s$ 处的相应变量值 $V(s)$ ，具体形式描述如下：

$ V(s) = \sum\limits_{i = 0}^N {{N_{i,p}}(s){X_i}} ,\;\;{\rm{0}} \leqslant u \leqslant {\rm{1}} \text{,} $

(8)

再通过 $V(s)$ 改变映射在参考轴上的FFD控制点 ${P_{i,j,k}}$ ，并采用式（9）计算改变后的FFD控制点 ${\hat P_{i,j,k}}$ ：

${\hat P_{i,j,k}} = C({\tilde s_{i,j,k}}) + M(V({\tilde s_{i,j,k}})){\vec R_{i,j,k}} \text{。}$

(9)

式中， $V({\tilde s_{i,j,k}})$ 表示在FFD控制点映射参数化坐标处的变量值， $M$ 为由 $V({\tilde s_{i,j,k}})$ 确定的平移、缩放和旋转矩阵。

4）根据FFD控制点的新坐标 ${\hat P_{i,j,k}}$ ，可通过式（4）和式（5）求得嵌入FFD控制体中的表面网格的新坐标 $\hat K$ 。

3 参数化实例

以一型左右对称，轴长1.5 m、展长3 m的翼型融合水下滑翔机为例，验证所提参数化方法的可行性。

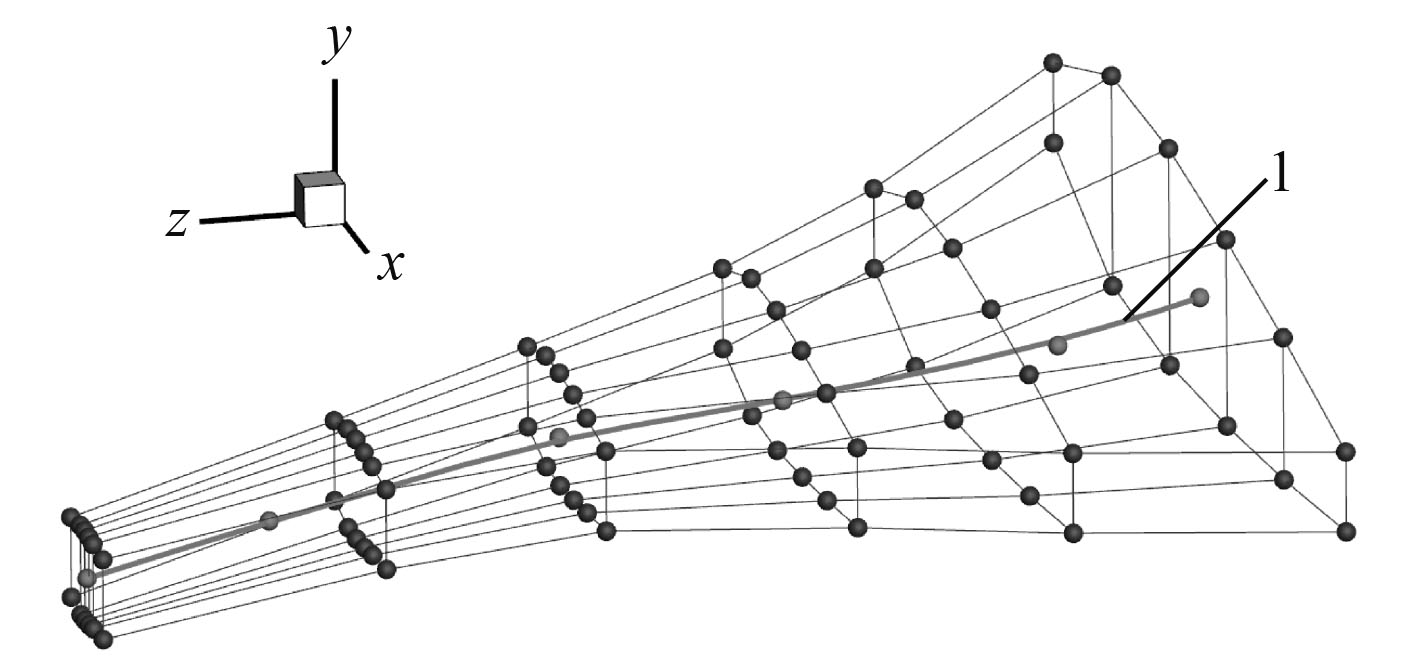
1）取滑翔机的左半边，基于B样条基函数，在参数化空间 $(u,v,w)$ 上分别沿弦长方向布置6个控制点，垂直方向布置2个控制点、展长方向布置6个控制点，建立该型翼身融合水下滑翔机的FFD控制体，其总共具有72（ ${\rm{6}} \times {\rm{6}} \times {\rm{2}}$ ）个控制点，并以FFD控制体在展长方向的每个剖面的中点作为控制点建立参考轴，如图3所示。其中，黑色点表示FFD的控制点，曲线1表示建立的参考轴。

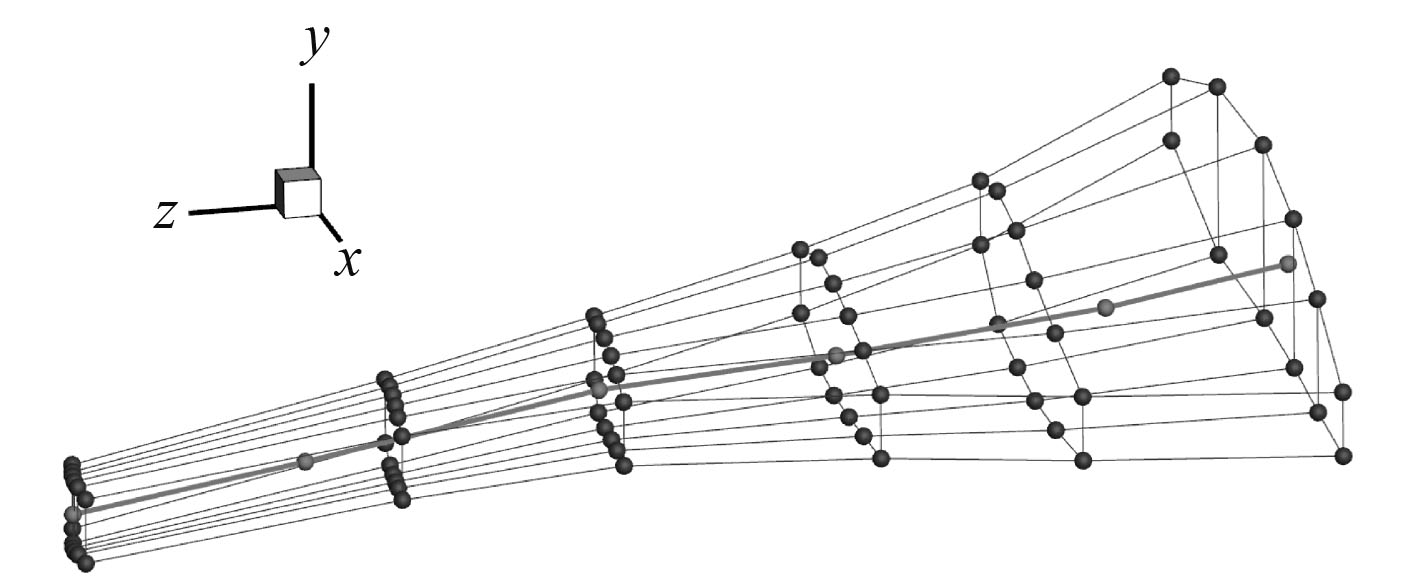
2）设置展长全局变量，将参考轴沿展长方向增加0.50 m，可得到改变后的参考轴和FFD控制体，如图4所示。

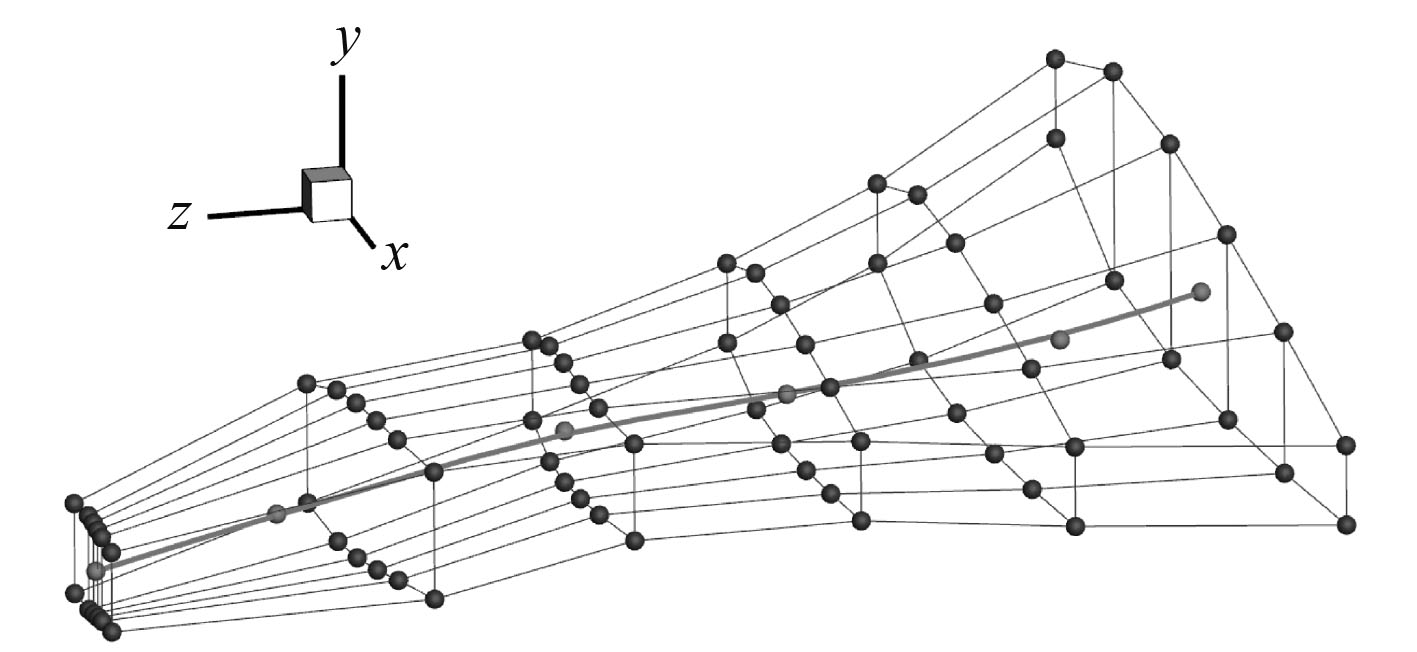
3）设置弦长和厚度全局变量，将第5个剖面处的展长和弦长同时增大到2倍，可得到改变后的参考轴和FFD控制体，如图5所示。

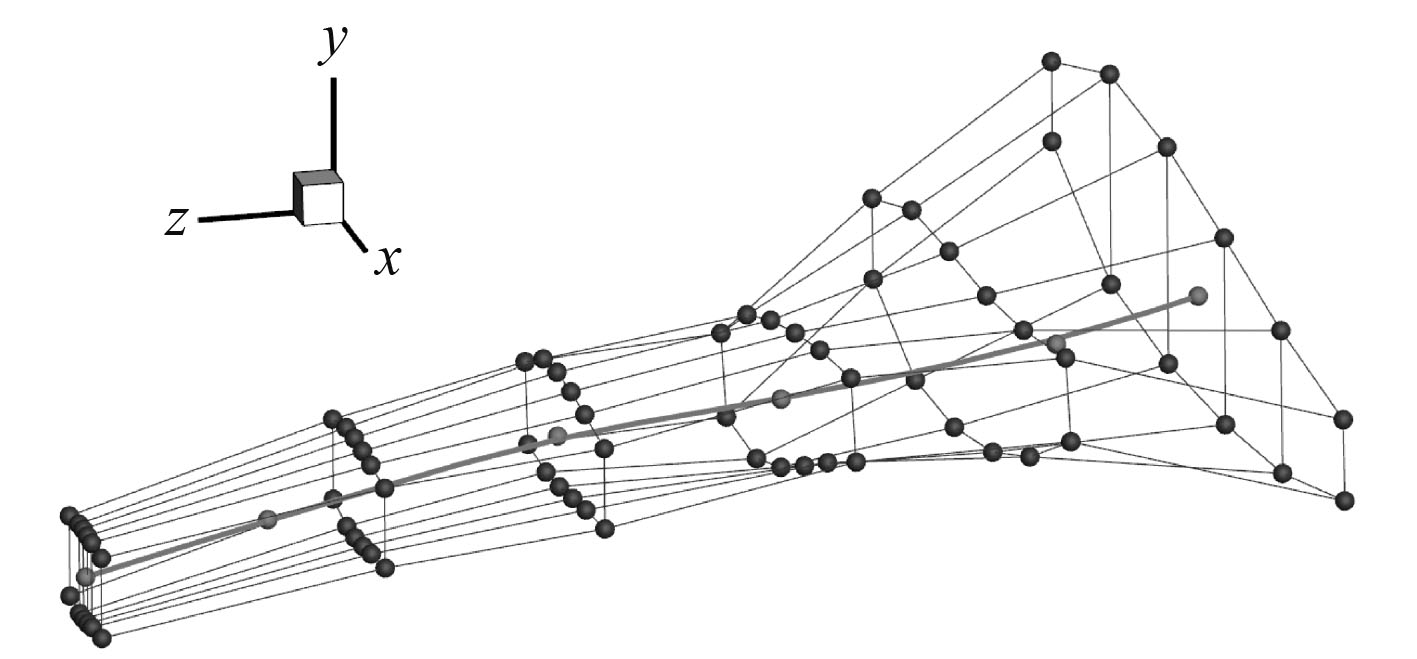
4）设置扭转角全局变量，将第3个剖面处的FFD控制点旋转20°，则可得到图6中所示的参考轴和FFD控制体。

分析对比图3～图6可以发现：通过参考轴，设置全局变量对FFD控制点进行分组集中控制，既可根据物理意义直观地改变外形的形状，又可克服FFD方法带来的优化变量过多的不足，减少优化设计变量的个数。

4 结　语

外形参数化是翼身融合水下滑翔机外形优化设计的重要内容，针对CAD、B样条、非均匀有理B样条等参数化方法在翼身融合水下滑翔机外形参数化建模中存在的问题，本文提出一种基于FFD和轴变形方法的翼身融合水下滑翔机外形参数化建模方法，该方法具有以下特征：

1）采用B样条基函数建立翼身融合水下滑翔机外形的FFD控制体，通过改变FFD控制体的形状，对嵌入的几何外形或CFD表面网格实现自由变形。

2）在FFD控制体内引入一条参考轴，并将FFD控制体上的所有控制点关联到该参考轴，通过设置全局变量对参考轴进行变形控制，进而实现对FFD控制点的集体控制，减少优化变量的数目。