2. 船舶和海洋水动力湖北省重点实验室,湖北 武汉 430074;
3. 高新船舶与深海开发装备协同创新中心,上海 200240
2. Hubei Key Laboratory of Naval Architecture and Ocean Engineering Hydrodynamics, Wuhan 430074, China;
3. Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration, Shanghai 200240, China
船舶大型化的趋势使得船舶主机功率越来越大、传动轴系长度越来越长以及随之而来的振动噪声问题。在这种情况下,轮缘推进的概念得以提出[1]。
轮缘推进器是一种依靠轮缘驱动桨叶旋转的新型推进器。由于不依靠桨毂的驱动,因此不需要布置过长的轴系,同时减少了因为轴系旋转产生的噪声和振动问题,更减小了推进系统在船舶上的占用空间。轮缘推进器采用吊舱式结构安装在船尾,增强了船舶的操纵性[2]。
美国通用动力电船公司最早在20世纪90年代提出了轮缘推进器新概念,但在设计时仍保留桨毂的结构,故又称作梢部驱动推进器。进入 21 世纪后,轮缘推进技术取得了较大发展,取消了桨毂结构。目前,国外已能够在千吨级的船舶上运用轮缘推进,且最大功率可达到 1000 kW [3]。
Schilling Robitics 公司在2004年开发出5叶的轮缘推进器,在转速为1000 r/min的时候能够产生大约2 kN的推力,同时没有水密性方面的要求,海水在通过推进器电机时,还能够起到给电机降温的作用。2005年,位于挪威的 Brun-voll 公司开发出了4叶的轮缘推进器,与 Schilling Robitics 公司相比,其产品更侧重于操纵性和耐用性[4]。
除了对轮缘推进器原理样机的研究不断取得突破,国内外学者开始对轮缘推进器的水动力性能展开研究。Yakovlev等[5]为轮缘推进器设计了一套桨叶,并进行了简要的强度分析,同时估算了空化性能。为了验证设计,制造了一种简易的推进器桨叶试验模型,并在Krylov造船研究所的深水拖曳水箱中进行了测试。韦喜忠等[6]研究了在考虑压差情况与无压差情况下轮缘推进器驱动环之间的间隙流动对推进器水动力的影响,分析了径向间隙比、轴向间隙比等参数变化对间隙流动和水动力的影响,得到了轴向、径向间隙变化对摩擦扭矩的变化规律。Bao-wei Song等[7]基于CFD比较了有轴与无轴2种轮缘推进器的敞水性能,并证明无轴的轮缘推进器敞水性能优于有轴的轮缘推进器敞水性能。
此外也有不少国内外学者从电机结构、制造工艺等角度研究轮缘推进器的散热性能、噪声及振动方面的性能[8-9]。
本文基于STAR-CCM+软件,计算在SST k-ω湍流模型下轮缘推进器的水动力性能,并从三维模型的简化,桨叶形状多方面分析轮缘推进器的水动力性能。
1 数值计算方法及理论 1.1 控制方程 1.1.1 连续性方程所有关于流动的问题都必须满足质量守恒这一基本定律。该定律可表述为:单位时间内流体微元体中质量的增加,等于同一时间间隔内流入该微元体的净质量。连续性方程描述的是流动过程中流体质量守恒的性质。质量守恒方程的数学描述为[10]:
| $ \frac{\partial \rho }{\partial t}+\frac{\partial \left(\rho u\right)}{\partial x}+\frac{\partial \left(\rho v\right)}{\partial y}+\frac{\partial \left(\rho w\right)}{\partial z}=0 \text{。}$ |
式中:ρ为流体密度,kg/m3;u,v,w分别为速度矢量在x,y,z方向的分量。
1.1.2 动量守恒方程动量守恒定律也是任何流动系统都必须满足的基本定律,实际上是牛顿第二定律在流体运动中的一种表达形式。可表述为:微元体中流体的动量对时间的变化率等于外界作用在此微元体上的各力之和。1827年Navier提出了不可压缩的黏性流体运动方程。Stokes在1845年提出了黏性系数为常数的形式,称为Navier-Stokes方程,简称N-S方程。方程较准确地描述了实际流体在黏性流动状态下的流动。N-S方程是进行流体力学计算的最基本公式。流体的黏性系数和流体的密度均是常数条件下的矢量形式:
| $ \rho \frac{{\rm d}\overrightarrow{v}}{{\rm d}t}=\rho \overrightarrow{F}-grad\rho +\mu {\nabla }^{2}\overrightarrow{v}\text{。} $ |
式中:p为流体微元体上的压力;
湍流流动是自然环境中最普遍的流动形式,而在模拟螺旋桨所在的实际流场时,首先遇到的问题就是湍流问题。湍流的一个很重要的特点是物理量的脉动,为了描述湍流运动的强弱,定义湍流脉动速度与平均速度的比值为湍流强度。
如果在湍流尺度的网格尺寸内求解瞬态三维方程,此时湍流问题不需引入任何模型,但由于计算机容量和速度的限制,这种方法还难以应用在实际的工程计算上。一般工程上采用的是由雷诺时均方程出发的模拟方法,基于某些假设,用低阶关联项或时均量表达雷诺时均方程或湍流特征量的输运方程中高阶的未知关联项,以使雷诺时均方程封闭[11]。
2 水动力性能计算 2.1 研究对象轮缘推进器是永磁电机在船舶推进领域上的一种全新的应用,主要由转子轴承、固定轴承、多磁极定子、外壳等组成[12],电机原理图如图1所示。
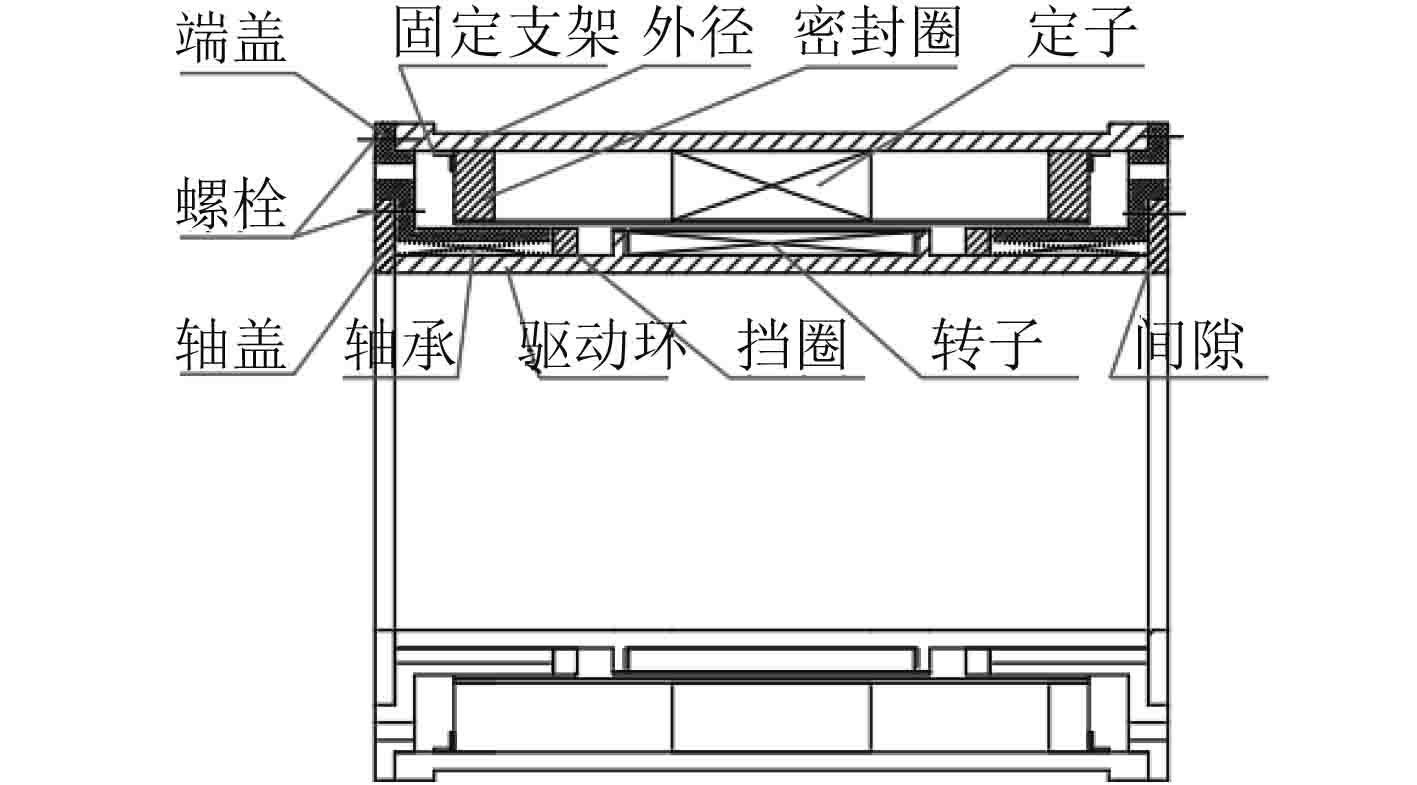
|
图 1 电机原理图[13] Fig. 1 Motor schematic |
实际应用中,推进器导管部分的设计需要考虑阻力影响。本文选No.19A型导管作为轮缘推进器的导管外形,在导管中封装电机部分,在研究轮缘推进器水动力性能的时候,不考虑推进器内部结构。导管外部尺寸如表1所示。
|
|
表 1 导管尺寸表 Tab.1 Pipe size chart |
选用的叶型均为梭型切面的Ka4-70螺旋桨,螺旋桨叶厚分布重新设计。假定其叶厚分布如表2所示[14]。
|
|
表 2 叶厚分布表(P/D=1.2) Tab.2 Thickness distribution(P/D=1.2) |
轮缘推进器其他参数如表3所示。
|
|
表 3 轮缘推进器参数表 Tab.3 Rim thruster parameter |

|
图 2 轮缘推进器外观 Fig. 2 Rim thruster appearance |

|
图 3 导管轴向截面图 Fig. 3 Pipe axial section |
将推进器模型文件导入STAR-CCM+软件进行修复,建立圆柱体的流场区域,直径为推进器直径的10倍,轴向长度为推进器轴向长度的10倍,为使尾流充分发展,减少数值模拟中流场边界对其的影响,设置推进器与流场出口的距离为7倍推进器轴向长度,流场进口设置为速度入口,出口设置为压力出口,如图4所示。
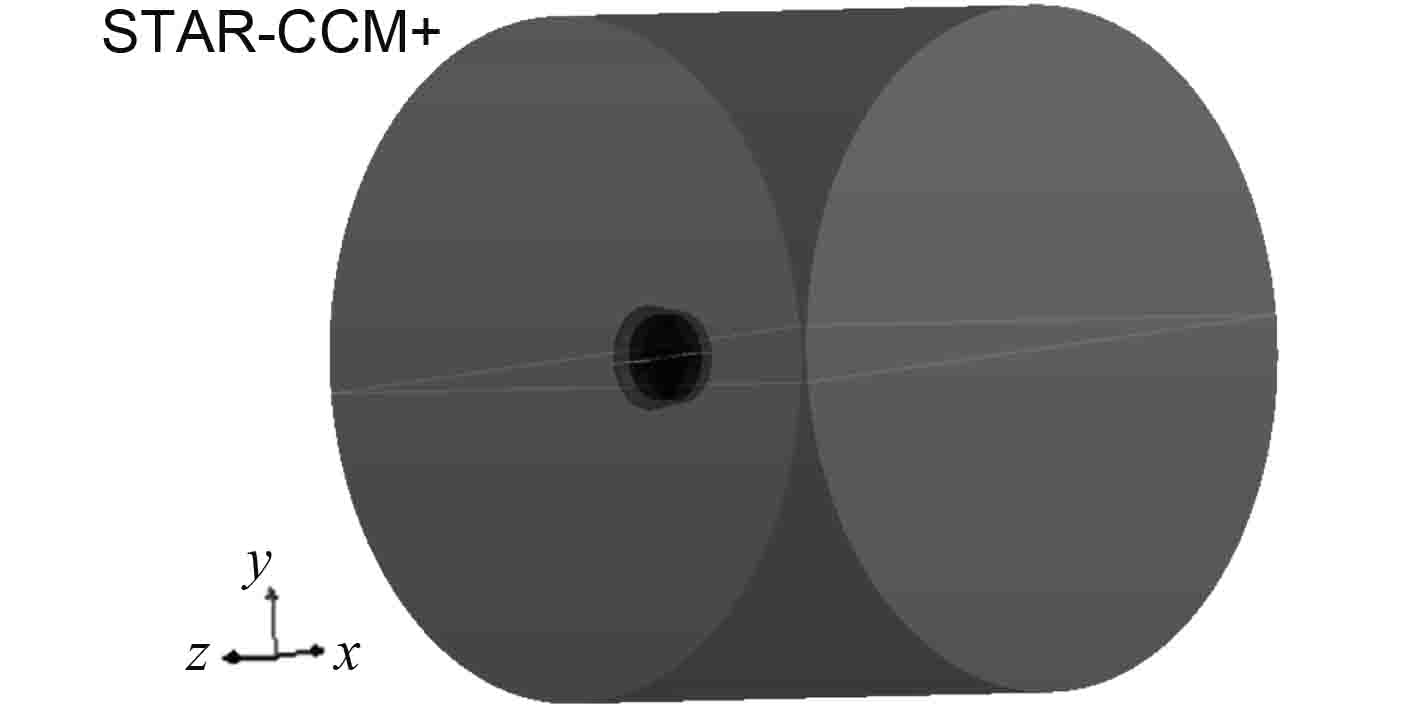
|
图 4 流场图 Fig. 4 Flow field diagram |
选择SST k-ω湍流模型,推进器表面采用壁面无滑移条件。推进器内部流场设置为旋转坐标系,推进器内、外流场连接处设置为交界面,设置推进器桨叶转速为10 r/s。
2.3 网格划分与计算设置内部流场域网格基础尺寸为0.03 m,设置外部流场网格基础尺寸为0.3 m,完成对网格尺寸的基本设置后生成网格图,如图5所示。

|
图 5 总体网格图 Fig. 5 Overall grid diagram |
对轮缘推进器叶片边缘曲率变化过大的区域以及叶片与推进器的连接区域进行局部加密,如图6所示。

|
图 6 网格加密图 Fig. 6 Mesh encryption diagram |
在推进器尾部选择局部加密,推进器所在内部流场区域网格加密,同时,为了保证推进器内部流场与外部流场网格大小的平稳过渡,需要适当调整推进器桨叶紧前方和紧后方的网格尺寸,如图7所示。

|
图 7 网格轴向截面图 Fig. 7 Grid axial section diagram |
调整完网格,设置好计算条件进行计算。设导管发出的推力为TP、桨叶发出的推力为TN,两者总推力为T,桨叶扭矩为Q。
故定义轮缘推进器总推力系数为:
| $ {K}_{T}=\frac{T}{\rho {n}^{2}{D}^{4}}=\frac{{T}_{P}+{T}_{N}}{\rho {n}^{2}{D}^{4}} \text{,}$ |
桨叶转矩系数:
| $ {K}_{Q}=\frac{Q}{\rho {n}^{2}{D}^{5}} \text{,}$ |
进速系数:
| $ J=\frac{{V}_{A}}{nD} \text{,}$ |
轮缘推进器效率:
| ${{\rm{\eta }}_0} = \frac{{{K_T}}}{{{K_Q}}}\frac{J}{{2\text{π} }}\text{。}$ |
根据计算结果及公式计算敞水效率,如表4所示。
|
|
表 4 计算数据表 Tab.4 Calculation data table |
将计算数据绘制成敞水性征曲线,如图8所示。
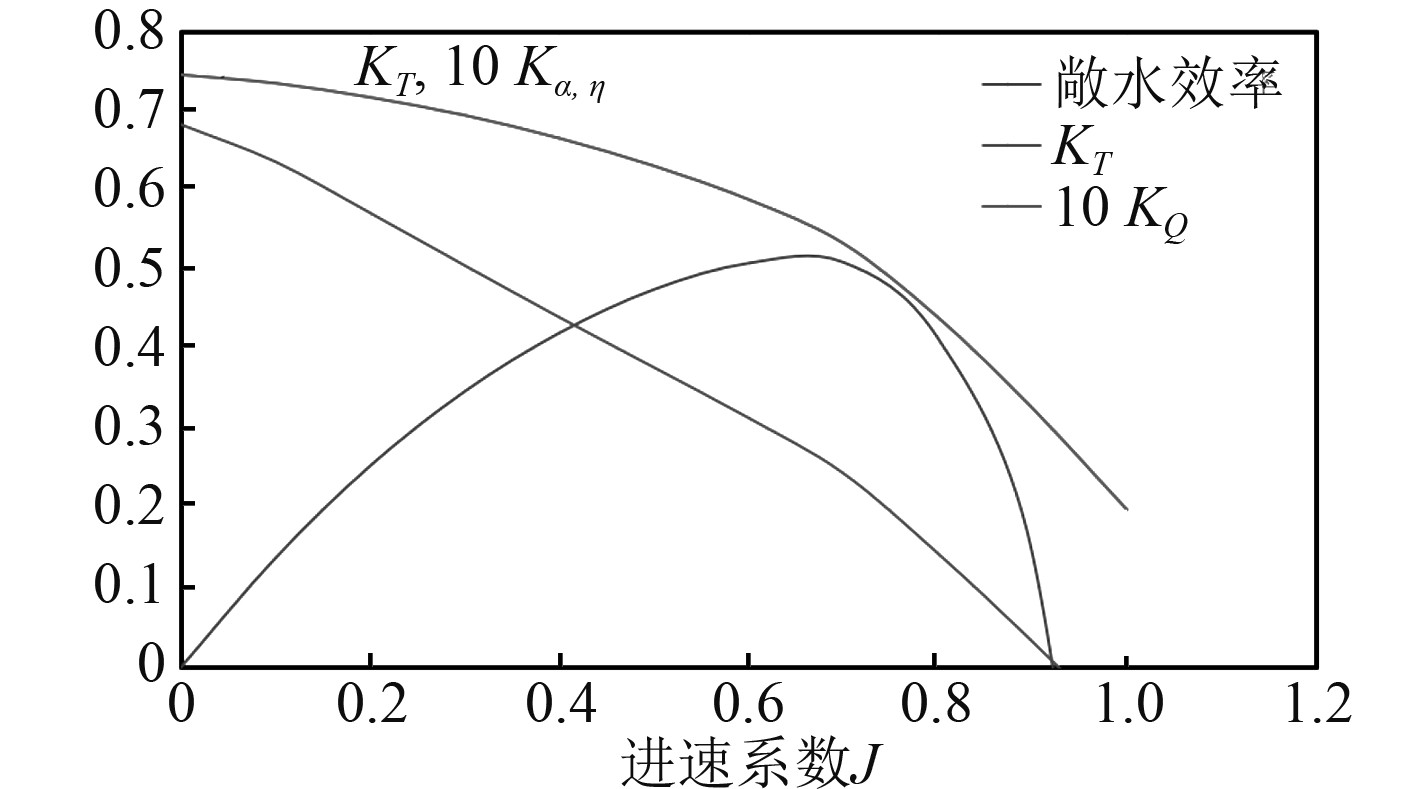
|
图 8 敞水性征曲线 Fig. 8 Open water curve |
此时效率计算结果与文献[14]中同叶型、同导管形状的结算结果大致吻合,最大误差不超过8%,对比结果验证了本文研究方法的正确性。对比结果如图9所示。
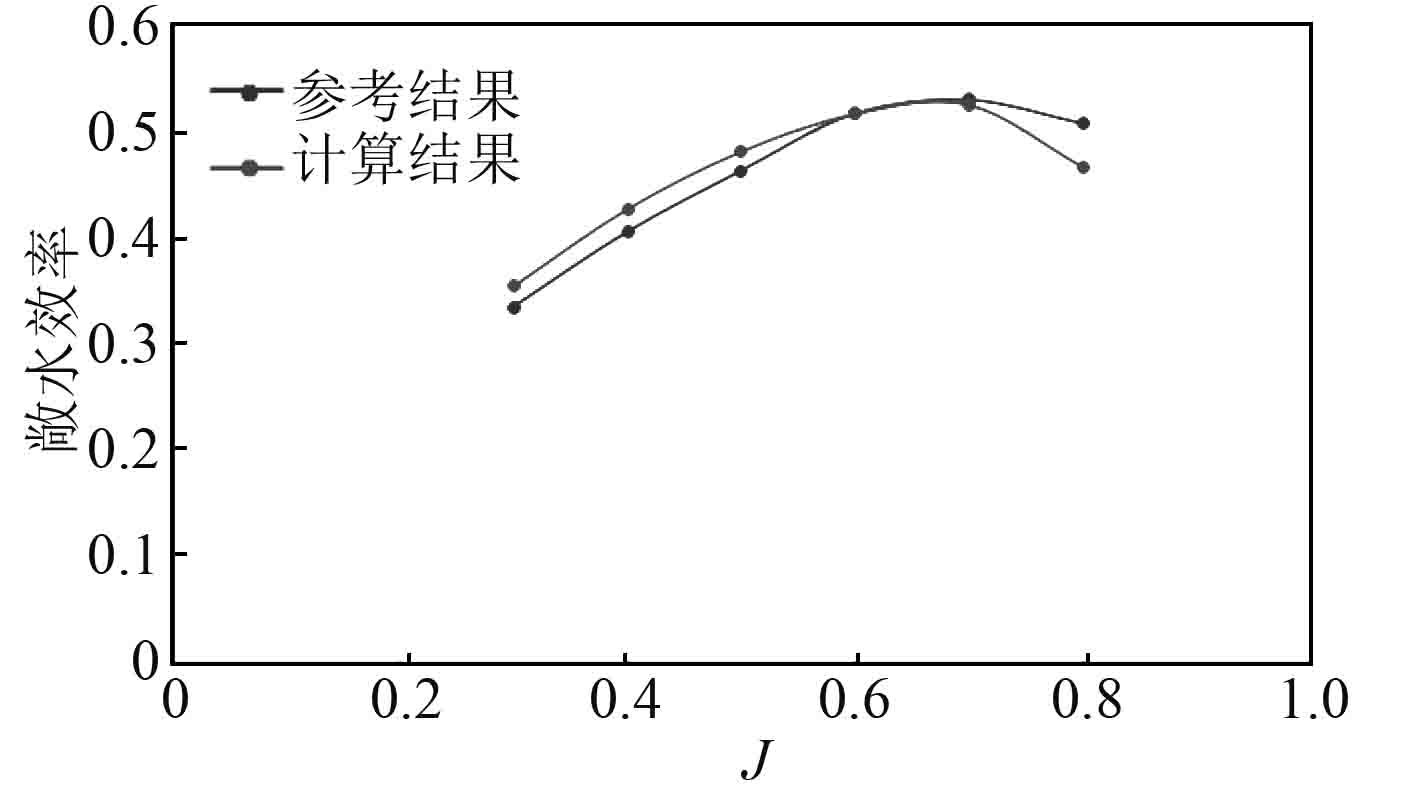
|
图 9 计算对比结果图 Fig. 9 Comparison of calculation results |
轮缘推进器是由布置于导管内部的电磁铁驱动内部的桨叶旋转,桨叶固连在驱动环上,通过轴承与导管相连,在推进器工作的时候,驱动环周围的间隙允许水流通过,然而尺寸较小,在数值模拟中为了详细表达出间隙的存在,对物理模型的建立和网格的划分提出了更高要求。为验证建模时简化间隙对推进器整体的敞水效率的影响,设计对比算例,即保持导管和桨叶外形不变,一个在建模过程中保留间隙,并设计为凹形槽形式,另一个则填充间隙,如图10所示。即默认间隙内部不允许水流经过,进行对比计算。
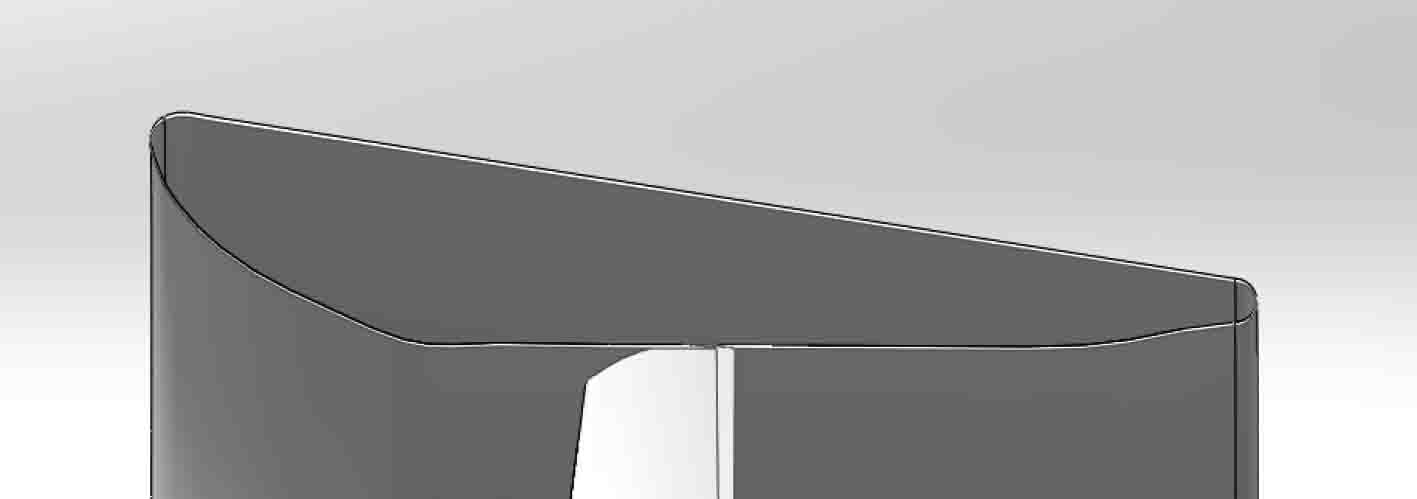
|
图 10 间隙封闭模型轴向截面 Fig. 10 Clearance closure model axial section |
计算过程中,保证其余参数相同,简化间隙的计算结果如表5所示。敞水性征曲线如图11所示。
|
|
表 5 简化间隙计算数据表 Tab.5 Calculation data table ignoring clearance |
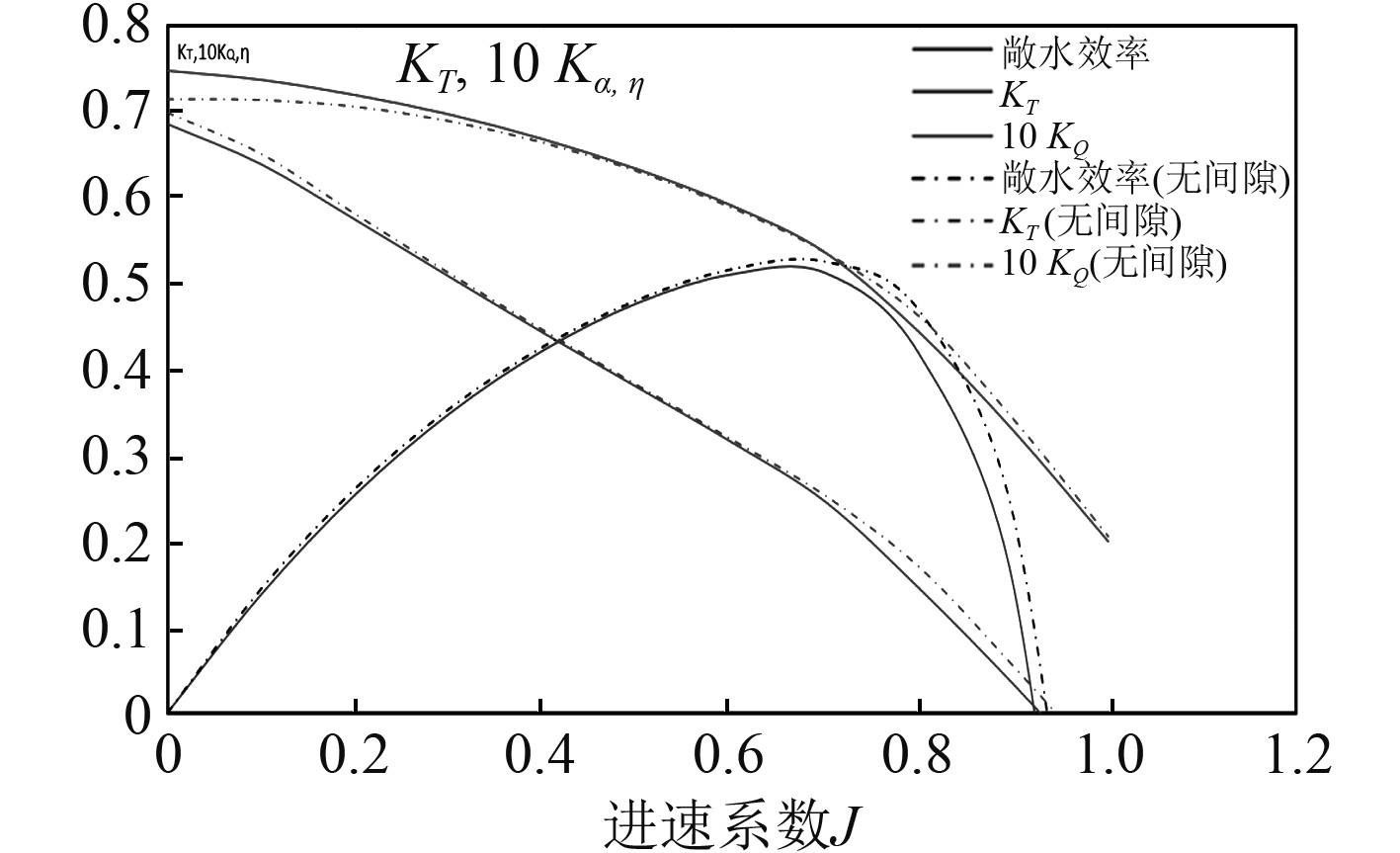
|
图 11 建模忽略间隙的敞水性征曲线 Fig. 11 Open water curve ignoring clearnance |
比较结果显示,建模时封闭间隙的模型敞水曲线与考虑间隙的模型的最大敞水效率接近,计算结果相差1%~2%。说明当前尺度下,在建模过程中是否简化间隙带来的效率方面的影响可以忽略不计。因此,在研究敞水性能的时候,为了简化模型,提高计算效率,可以选择对间隙进行简化,即做封闭填充处理。
3.2 叶切面弦长研究在传统的Ka4-70叶型中,桨叶切面弦长沿径向向外增加,而在实际流动中,靠近轮缘侧的桨叶,将产生更大的扭矩,从而降低了轮缘推进器的水动力性能。通过调整桨叶的切面弦长沿径向的分布,提升轮缘推进器的水动力性能。
逐渐减小靠近轮缘处的桨叶切面弦长,设置10种不同弦长分布的桨叶,使用相同的导管外形,计算时,保持其他条件不变,确定10种计算方案,如图12所示。
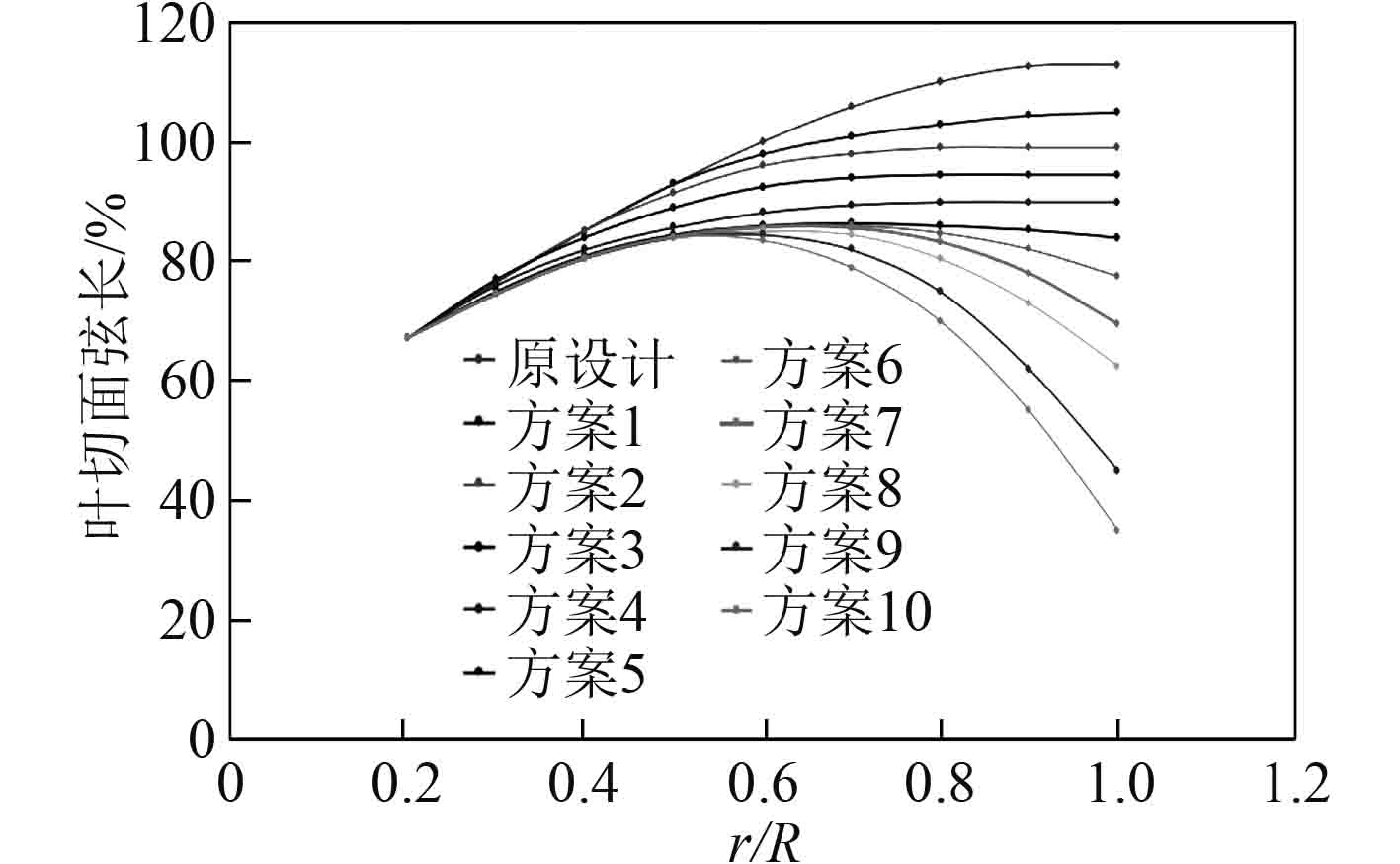
|
图 12 叶切面弦长计算方案 Fig. 12 section chord length calculation scheme |
图13展示了在10种设计方案中,靠近轮缘处的桨叶切面弦长逐渐减小的趋势。

|
图 13 设计方案三维模型对比图 Fig. 13 Design scheme 3D model comparison chart |
在仿真计算时,为了节省计算时间,对桨叶轮缘处的驱动环采取简化处理,保证模型整体内部的全封闭。将10组方案的计算结果绘制在同一张敞水效率曲线中,进行对比分析,如图14所示。
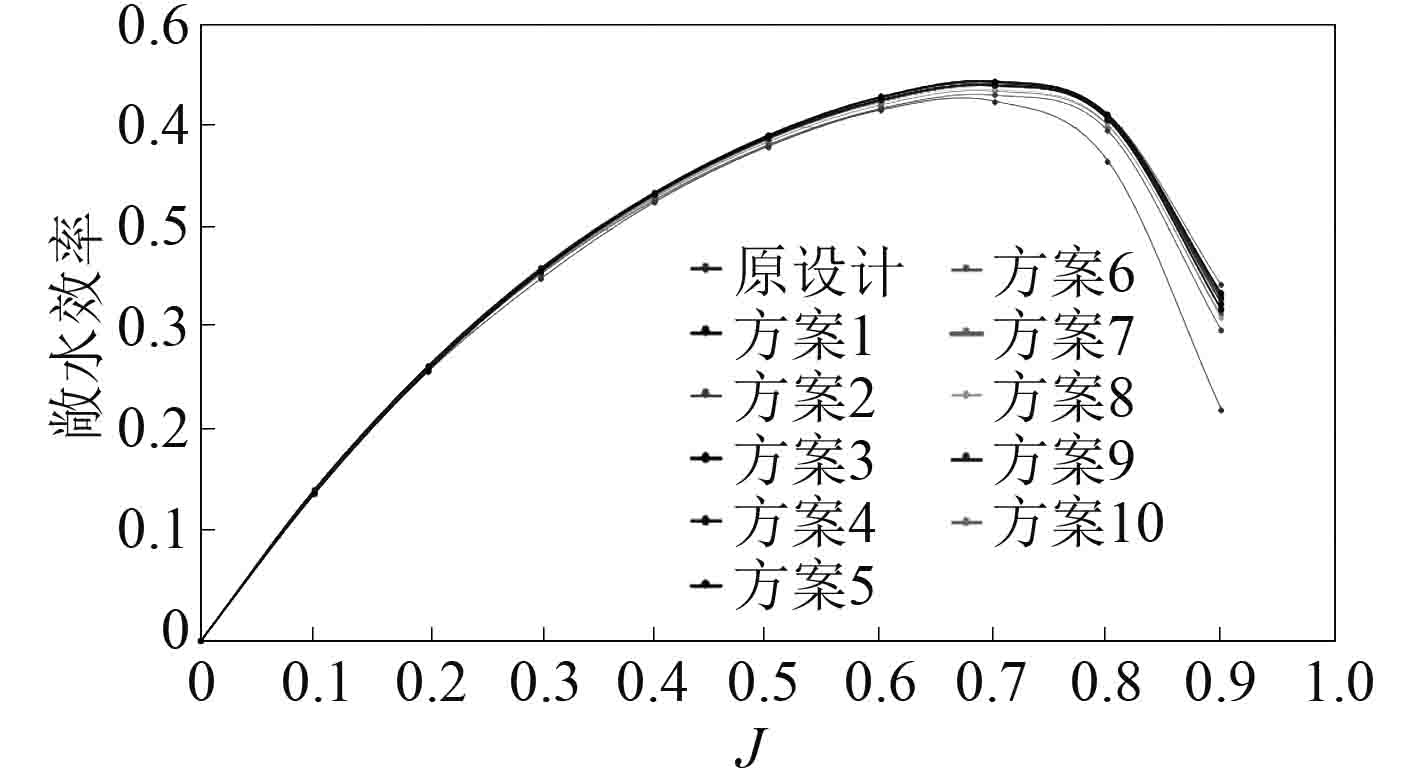
|
图 14 不同弦长方案的敞水效率曲线 Fig. 14 Open water efficiency curve for different chord length schemes |
从计算结果可以发现,不断修改叶切面弦长,使得靠近轮缘处的切面弦长逐渐减小,在最初的几组计算中,敞水效率提升效果明显,在效率最高点,提升了2%左右。但随着轮缘处桨叶弦长的进一步减小,推进器敞水效率的提升很小,同时由于桨叶面积的大幅减小,桨叶推力下降明显,降低了推进器的实用性。
3.3 螺距比研究为了进一步提升轮缘推进器的敞水效率,在上一节研究桨叶切面弦长对水动力性能的影响的基础上,研究桨叶螺距比对推进器水动力性能的影响。以上一组试验方案中敞水效率最高的方案10中的桨叶弦长分布作为本次研究中的桨叶弦长,通过调整桨叶螺距比来设计研究方案,如表6所示。
|
|
表 6 调整螺距比计算方案表 Tab.6 Adjusting the pitch ratio calculation schemes |
仍然使用对推进器模型的简化处理,并保持其他计算条件不变,通过计算得到10条敞水效率曲线,如图15所示。

|
图 15 不同螺距比方案的敞水效率曲线 Fig. 15 Open water efficiency curve for different pitch ratio schemes |
由计算结果可知,当螺距比增加的时候,螺旋桨的最大敞水效率在增加,同时最高效率呈现向高进速系数方向移动的趋势。同时在计算结果中发现,当螺距比增大到P/D=1.3之后,在低进速下,螺旋桨受周期震荡力,不断提高进速,在高进速下才趋于平稳。且螺距比越大,振荡力影响的低进速系数范围越大。
4 结 语本文基于STAR-CCM+软件,针对轮缘推进器的水动力性能进行了数值模拟计算及分析,得到以下结论:
1)轮缘推进器是一种复杂的旋转机械,其最大结构特点在于允许水流通过电机内部,然而在研究整体的水动力性能时,可以简化计算模型,水流进入电机内部带来的影响可以忽略不计。
2)在整体的水动力性能研究上,建模时间隙的影响可以忽略,但是当问题细化,开始考虑如何降低扭矩,以及桨叶设计等问题的时候,间隙的结构对计算结果的影响不可忽视,必须考虑,同时应该尽量保证计算模型的精度,对网格的要求也将更加严格。
3)通过减小靠近轮缘处的桨叶切面弦长可以提升推进器的敞水效率,但是桨叶弦长太小,会降低推进器产生的推力。
4)通过增加桨叶螺距比可以提升推进器的最大敞水效率,但是螺距比越大,推进器收到震荡力影响的低进速范围就越大。同时在低进速下,不同螺距比的推进器敞水效率变化很小。
| [1] |
GRAY A, SHAHRESTANI N, FRANK D, et al. Propagator 2013: UF autonomous surface vehicle[J]. AUVSI Foundation’s 6th Annual RoboBoat Competition, Virginia Beach, VA, 2013. |
| [2] |
汪勇, 李庆. 新型集成电机推进器设计研究[J]. 中国舰船研究, 2011, 6(1): 82-85. WANG Yong, LI Qing. Design of a new integrated motor propulsion system[J]. Chinese Journal of Ship Research, 2011, 6(1): 82-85. DOI:10.3969/j.issn.1673-3185.2011.01.016 |
| [3] |
王汉刚. 美国核潜艇推进系统减振降噪技术发展分析[J]. 舰船科学技术, 2013, 35(7): 149-153. WANG Han-gang. Study of vibration isolation and noise reduction technology in US nuclear submarine propulsion system[J]. Ship Science And Technology, 2013, 35(7): 149-153. DOI:10.3404/j.issn.1672-7649.2013.07.031 |
| [4] |
WU Y. Design and fabrication of a maneuverable robot for in-pipe leak detection[D]. Massachusetts: Massachusetts Institute of Technology, 2014.
|
| [5] |
YAKOVLEV A Y, SOKOLOV M A, MARINICH N V. Numerical design and experimental verification of a rim-driven thruster[C]// Second International Symposium on Marine Propulsors, Hamburg, Germany. 2011: 396−403.
|
| [6] |
曹庆明, 韦喜忠, 唐登海, 等. 有/无压差的间隙流动对轮缘推进器水动力的影响研究[J]. 水动力学研究与进展, 2015, 30(5): 485-494. CAO Qing-ming, WEI Xi-zhong, TANG Deng-hai, et al. Study of gap flow effects on hydrodynamic performance of rim driver thrusters with/without pressure difference[J]. Chinese Journal of Hudrodynamics, 2015, 30(5): 485-494. |
| [7] |
Bao-wei SONG, You-jiang WANG, Wen-long TIAN. Open water performance comparison between hub-type and hubless rim driven thrusters based on CFD method[J]. Ocean Engineering, 2015, 103. |
| [8] |
赵文峰, 曹庆明, 许影博, 等. 轮缘推进器噪声特征分析研究[J]. 中国造船, 2016, 57(4): 98-108. ZHAO Wenfeng, CAO Qingming, XU Yingbo, et al. Study on noise characteristics of rim driving thrusters[J]. Shipbuilding of CHINA, 2016, 57(4): 98-108. DOI:10.3969/j.issn.1000-4882.2016.04.011 |
| [9] |
胡鹏飞, 靳栓宝, 沈洋, 等. 轮缘驱动无轴推进器冷却方案设计与多物理场耦合计算[J]. 船电技术, 2016, 36(3): 28-31. HU Pengfei, JIN Shuanbao, SHEN Yang, et al. Design and multifield coupled analysis of cooling system for PM motor in rim driven propulsor[J]. Marine Electric, 2016, 36(3): 28-31. DOI:10.3969/j.issn.1003-4862.2016.03.008 |
| [10] |
付颐鑫. 船舶螺旋桨敞水性能CFD模拟[D]. 大连: 大连海事大学, 2012. FU Yixin. CFD Simulation of marine propeller open water performance[D]. Dalian: Dalian Maritime University, 2012. |
| [11] |
高飞飞. 基于CFD技术的螺旋桨非定常流场数值模拟[J]. 科学技术与工程, 2011, 11(30): 7564-7569. GAO Feifei. Numerical simulation of unsteady flow around propeller based on CFD technology[J]. Science Technology and Engineering, 2011, 11(30): 7564-7569. DOI:10.3969/j.issn.1671-1815.2011.30.054 |
| [12] |
谈微中, 严新平, 刘正林, 等. 无轴轮缘推进系统的研究现状与展望[J]. 武汉理工大学学报(交通科学与工程版), 2015, 39(3): 601-605. TAN Wei-zhong, YAN Xin-ping, LIU Zheng-lin, et al. Technology development and prospect of shaftless rim-driven propulsion system[J]. Journal of Wuhan University of Technology(Transportation Science& Engineering), 2015, 39(3): 601-605. DOI:10.3963/j.issn.2095-3844.2015.03.033 |
| [13] |
孔斌, 熊立众, 陈林, 等. 轮缘推进器模型试验装置设计研究[J]. 舰船科学技术, 2017, 39(23): 163-166. KONG Bin, XIONG Li-zhong, CHEN Lin, et al. Esearch of the model test device design for rim-driven propulsor[J]. Ship Science And Technology, 2017, 39(23): 163-166. |
| [14] |
CAI M, YANG C, WU S, et al. Hydrodynamic analysis of a rim-driven thruster based on RANS method[C]. OCEANS 2015-MTS.
|
 2021, Vol. 43
2021, Vol. 43
