2. 船舶振动噪声重点实验室,湖北 武汉 430033
2. National Key Laboratory on Ship Vibration and Noise, Wuhan 430033, China
穿孔管消声器较扩张腔消声器有更小的流动阻力损失和良好的消声性能而被广泛应用。Sullivan[1]和Ross[2]分别基于一维解析方法和三维有限元法,推导出穿孔管消声器的传递损失理论计算公式并进行试验,结果显示在低频区间理论计算值与实验值吻合良好。Ji和Selamet[3]通过对穿孔管消声器的研究,提出一种多域边界元法,与实验值吻合良好,被广泛用于阻性消声器的声学性能预测。国内也对穿孔管消声器做了大量研究,季振林[4]所采用的三维边界元法可以在整个频率范围预测穿孔管消声器的传递损失,并且讨论了吸声材料参数对传递损失的影响。郑晗[5]对多腔室穿孔管消声器进行了研究,并给出了腔室划分方式、连接方式、数目和间距对传递损失的影响规律。尹佳玮[6]研究了穿孔管消声器在水介质中的应用,并且增加环状膜来改善消声性能。
目前研究的穿孔管消声器将背腔视为刚性,为研究如何提高穿孔管消声器的消声性能,本文将用于水介质的弹性壁穿孔管消声器作为研究对象,探究弹性背腔与水介质的耦合作用对消声性能的影响。首先介绍基础理论与有限元仿真边界条件,然后对此弹性背腔穿孔管消声器进行有限元仿真,并分析了背腔参数以及在消声器等容积、等长度条件下弧形背腔的弧形半径对声学性能的影响。
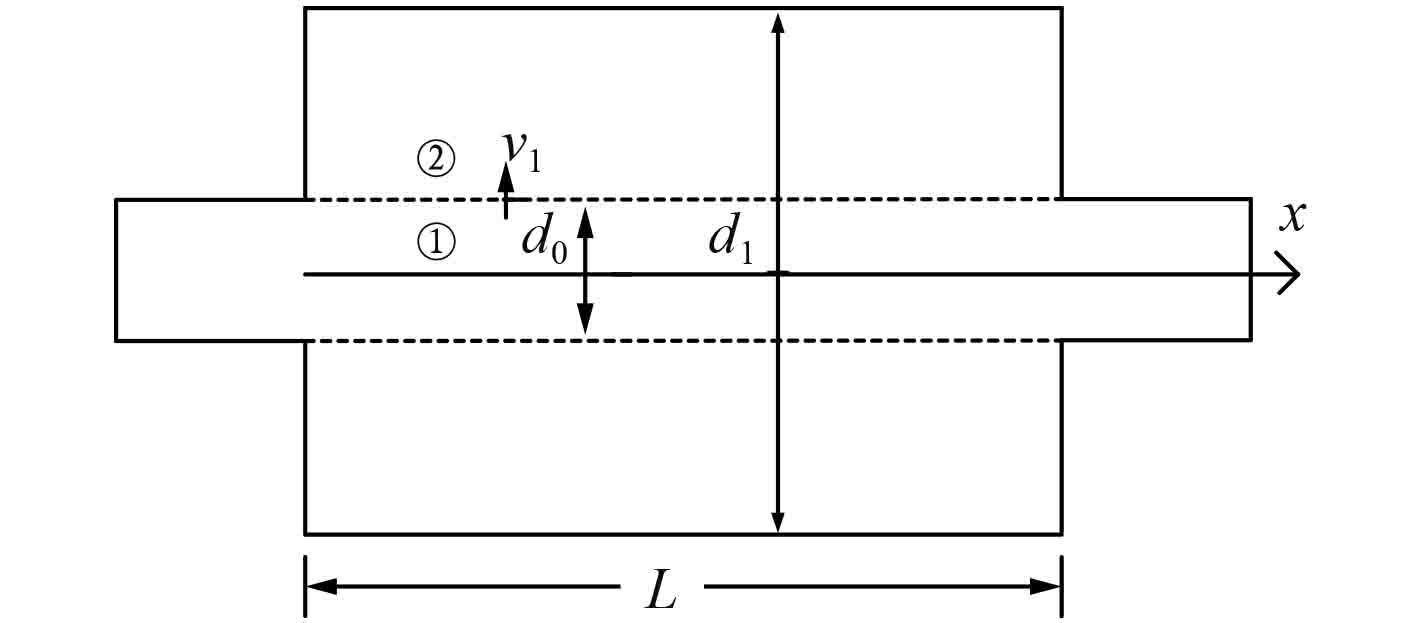
1 穿孔管声阻抗穿孔管消声器模型如图1所示,取轴线方向为坐标轴x,其中
|
图 1 穿孔管消声器结构模型 Fig. 1 Structural model of the perforated tube muffler |
在研究穿孔管消声器传递损失时,穿孔管声阻抗率可以定义为:
| ${Z_t} = \frac{{{p_1} - {p_2}}}{{{\rho _0}{c_0}{v_1}}} = {R_p} + {\rm{j}}{X_p}{\text{。}}$ | (1) |
其中:
根据经验公式[7],穿孔板的声阻率表达式为:
| ${R_p} = \frac{{\sqrt {8{\rho _0}\mu \omega } (1 + {t_w}/{d_h})/{z_0}}}{\phi }{\text{。}}$ | (2) |
其中:
声抗率为:
| ${X_P} = \frac{{k({t_w} + \alpha {d_h})}}{\phi }\text{。}$ | (3) |
其中:
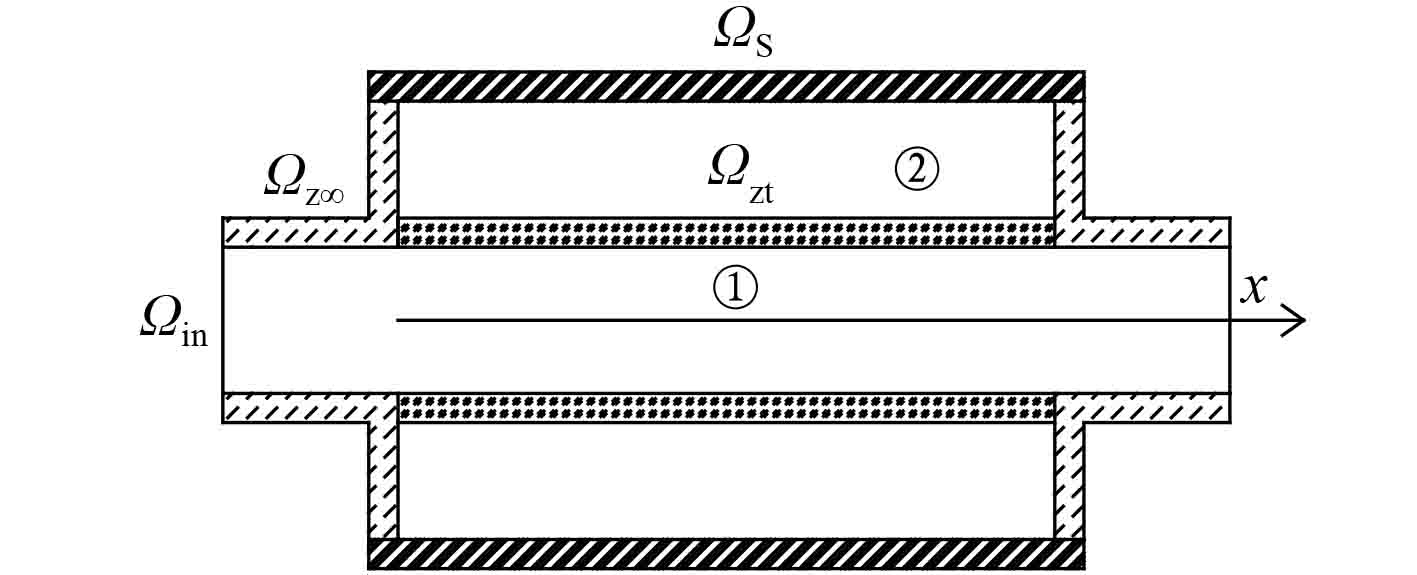
以下4种边界条件用于图1所示消声器结构的仿真模型,如图2所示。
|
图 2 穿孔管消声器边界条件模型 Fig. 2 Boundary condition model of the perforated tube muffler |
1)外部声压激励(
| ${\left. p \right|_{{\Omega _{in}}}} = 1\ {\rm{Pa}}\text{。}$ | (4) |
2)声学硬边界条件(
| ${\left. u \right|_{{\varOmega _{{Z_\infty }}}}} = 0\text{。}$ | (5) |
3)声阻抗边界条件(
| ${\left. {\frac{{{p_1} - {p_2}}}{{{\rho _0}{c_0}{v_1}}}} \right|_{{\varOmega _{{Z_t}}}}} = {Z_t}\text{。}$ | (6) |
其中
4)声固耦合边界条件(
| ${\left. {{u_{(r,x)}}} \right|_{{\varOmega _S}}} = \frac{{{\rm{d}}w(r,x)}}{{{\rm{d}}t}} = {\rm{j}}\omega w(r,x)\text{。}$ | (7) |
在消声器内部声场域满足Helmholtz方程:
| $\left({\nabla ^2} - \frac{1}{{{c_0}^2}}\frac{{{\partial ^2}}}{{\partial {t^2}}}\right)\phi = 0\text{。}$ | (8) |
其中
| $p = - {\rho _0}\frac{{\partial \phi }}{{\partial t}},{v_1} = \nabla \phi \text{。}$ | (9) |
在有限元分析中表示有限元模型的方程组采用以下形式:
| $\begin{split} & \left\{ {\left[ {\begin{array}{*{20}{c}} {{K_s}}&{{K_c}} \\ 0&{{K_a}} \end{array}} \right] + {\rm{j}}\omega \left[ {\begin{array}{*{20}{c}} {{C_s}}&0 \\ 0&{{C_a}} \end{array}} \right] - {\omega ^2}\left[ {\begin{array}{*{20}{c}} {{M_s}}&0 \\ {{M_c}}&{{M_a}} \end{array}} \right]} \right\} \times \\ &\qquad\qquad\qquad \left\{ {\begin{array}{*{20}{c}} {{w_u}} \\ {{p_u}} \end{array}} \right\} = \left\{ {\begin{array}{*{20}{c}} {{F_{si}}} \\ {{F_{ai}}} \end{array}} \right\} \text{。}\\[-15pt]\end{split}$ | (10) |
其中:
通过求解式(10)可以得到整个系统的响应,进而求得系统传递损失。
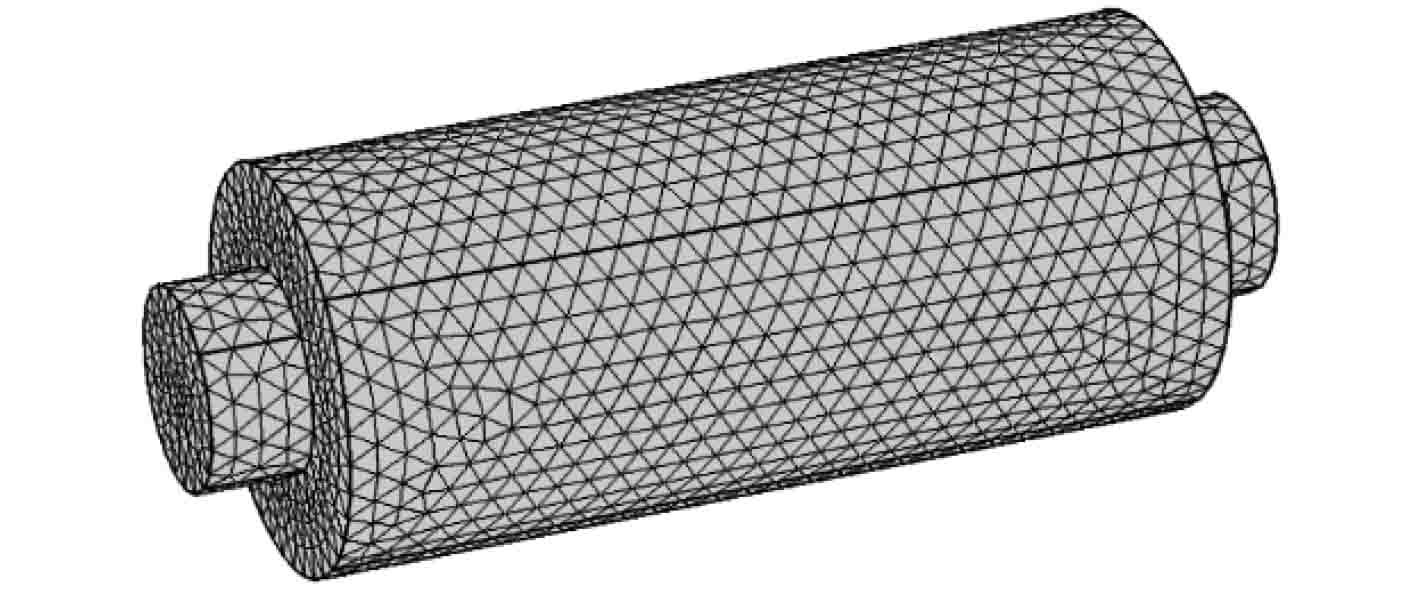
3 仿真分析 3.1 模型建立用于数值模拟的穿孔管水消声器的有限元模型如图3所示,结构简图见图1。
|
图 3 消声器有限元模型 Fig. 3 Finite element model of the muffler |
穿孔管消声器模型具体尺寸见表1,其中
|
|
表 1 穿孔管消声器结构参数 Tab.1 Structural parameters of the perforated tube muffler |
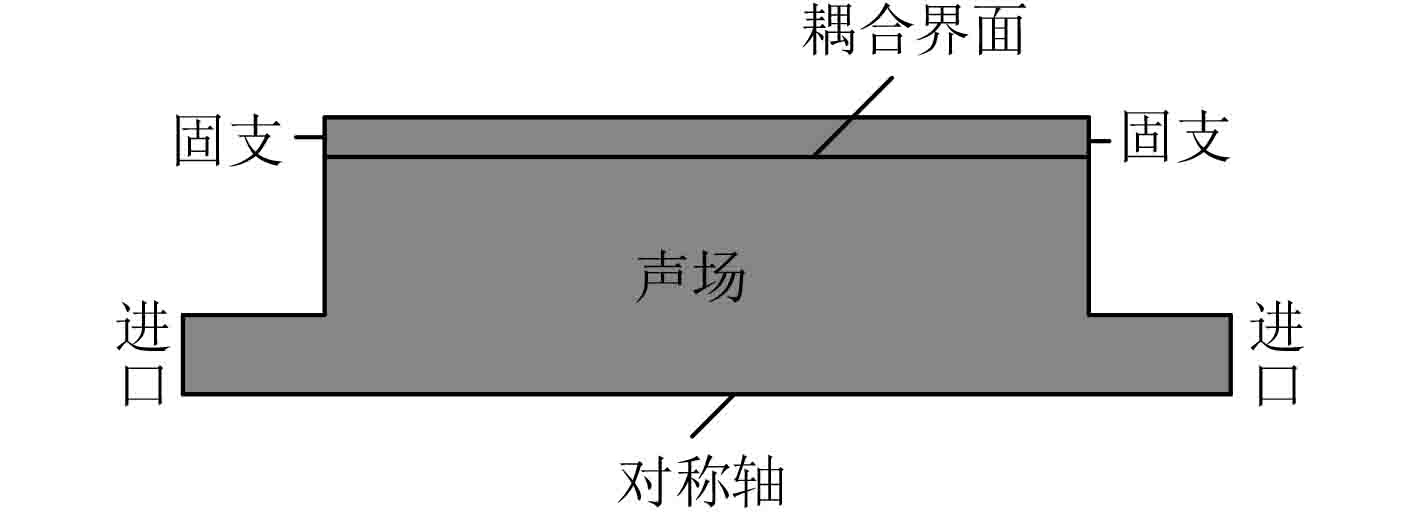
采用多物理场软件COMSOL进行仿真模拟。由于所研究的消声器模型尺寸与边界条件均具有轴对称性,故采用二维轴对称性模型进行建模分析,同时简化计算过程,提高计算速度[8],二维轴对称简图如图4所示。消声器弹性背腔材料为橡胶,密度
|
图 4 消声器二维轴对称模型 Fig. 4 Two-dimensional axisymmetric model of muffler |
在评价消声器的消声性能时,常采用传递损失这一指标,其计算公式为:
| $TL = 10\log \left( {\frac{{{P_{in}}}}{{{P_{out}}}}} \right)\text{。}$ | (11) |
式中:
| ${P_{in}} = \int_A {\frac{{{p_i}^2}}{{2{\rho _f}{c_f}}}} {\rm{d}}s\text{。}$ | (12) |
| ${P_{in}} = \int_A {\frac{{{{\left| {{p_o}} \right|}^2}}}{{2{\rho _f}{c_f}}}} {\rm{d}}s\text{。}$ | (13) |
式中:
为了验证仿真的准确性,将刚性壁穿孔管消声器传递损失理论计算得到的结果和有限元计算结果进行对比。Matlab计算数据和Comsol仿真得到的传递损失对比曲线如图5所示。
|
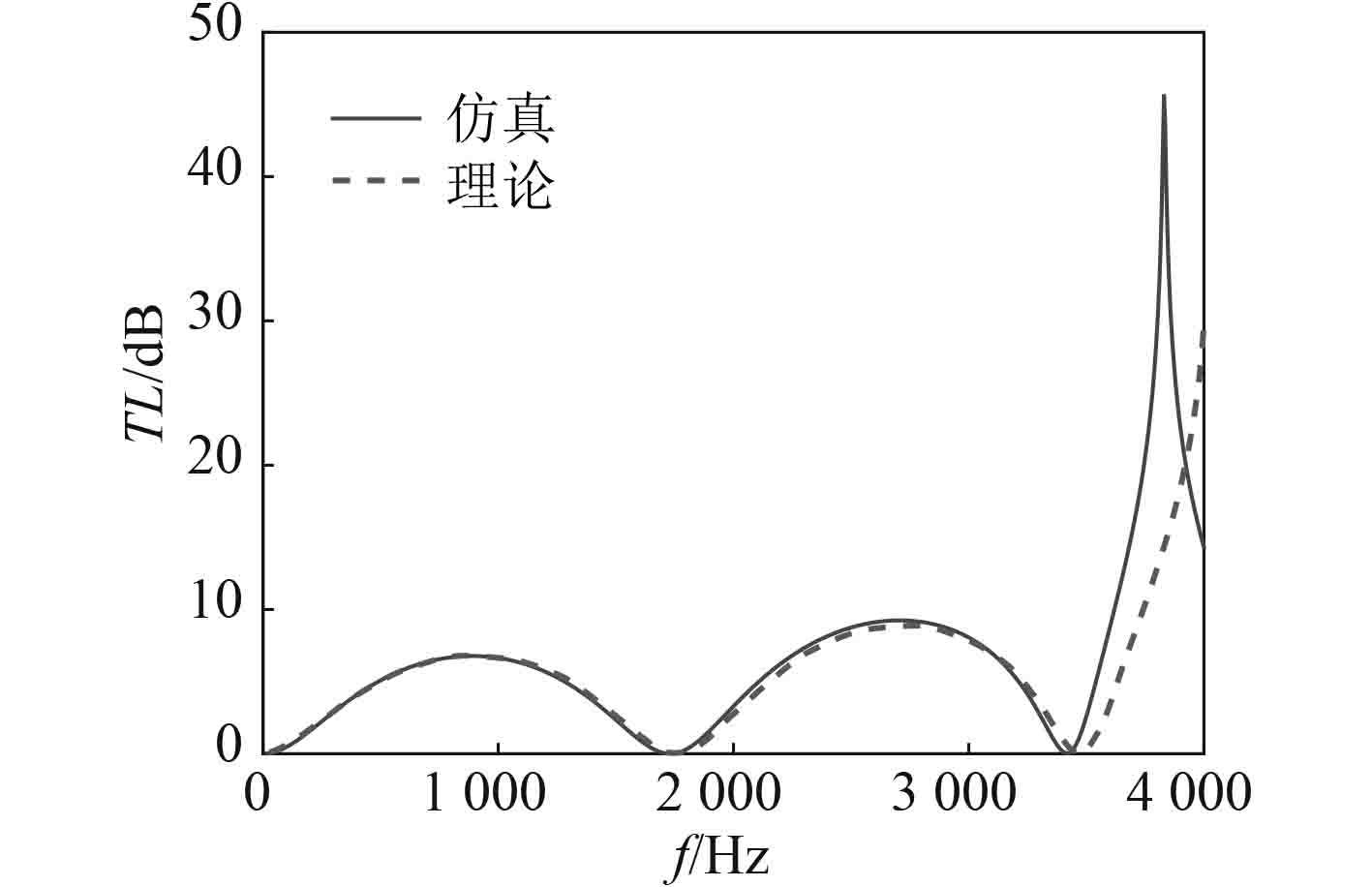
图 5 有限元仿真与理论计算的比较 Fig. 5 Comparison of calculated values with FEM results |
图中,实线为Comsol仿真结果,虚线为根据文献[1]中理论计算所得传递损失值。对比结果显示2种计算方法在截止频率3450 Hz以下吻合良好,高于此频率时出现高次波传播,误差增大,此时平面波理论已不在适用。
为改善穿孔管消声器低频吸声性能,将消声器刚性壁改用弹性壁后的传递损失曲线如图6所示。
|
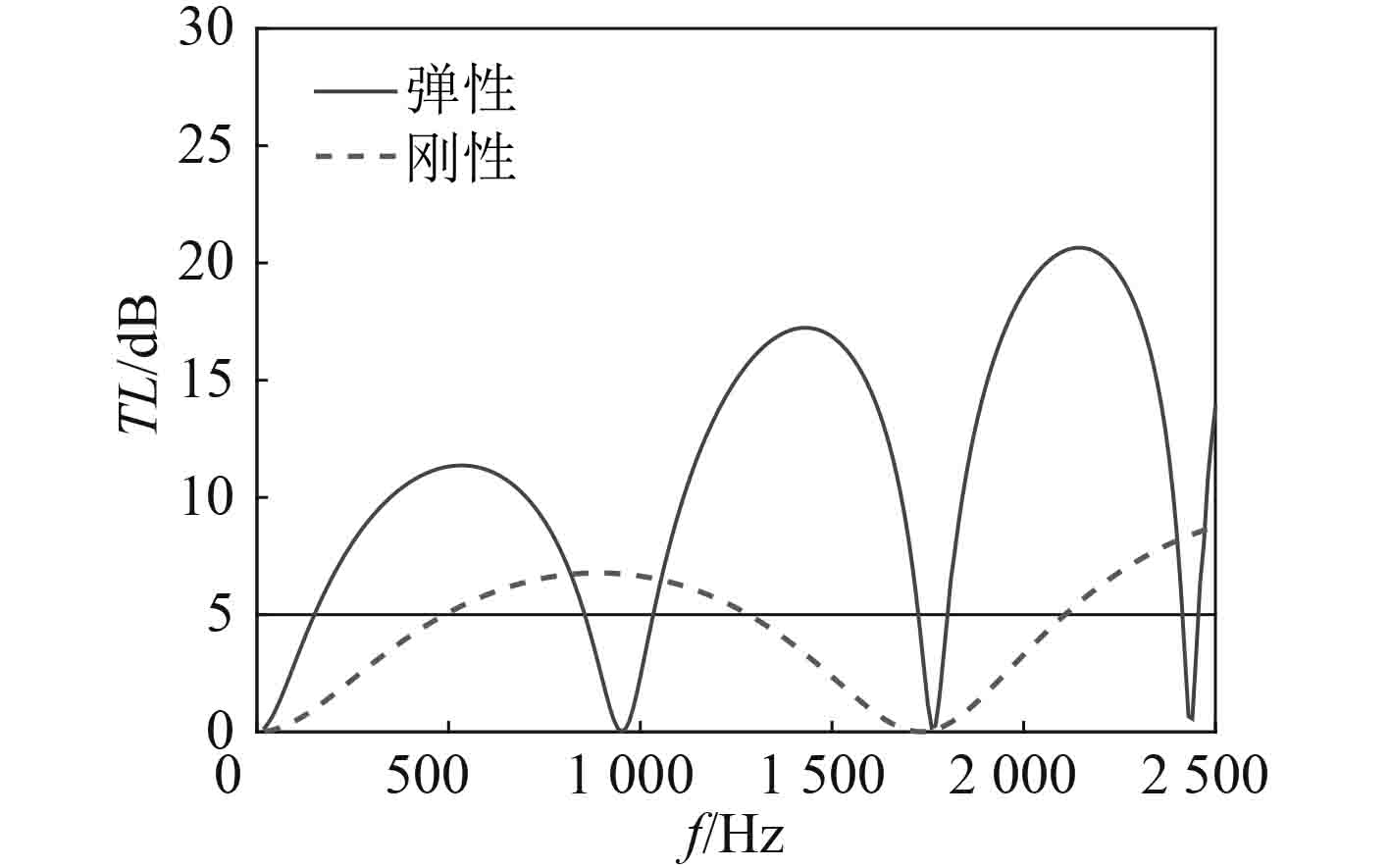
图 6 刚性与弹性背腔传递损失的比较 Fig. 6 Comparison of transmission losses in rigid and flexible dorsal cavities |
发现改为弹性背腔后,传递损失曲线向低频移动,新增2个峰值,且各峰值均提高7 dB左右,有效改善消声器的吸声特性。
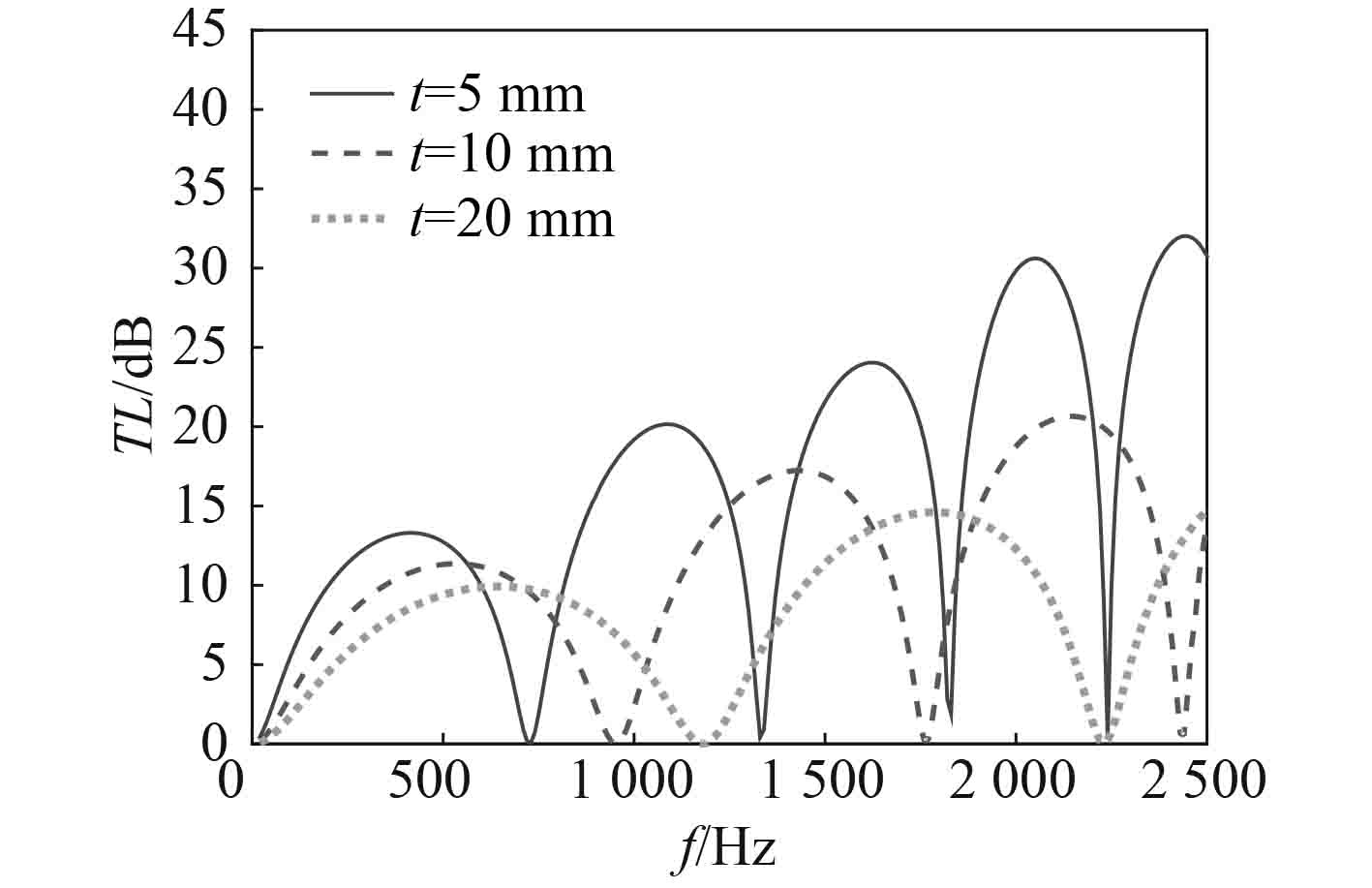
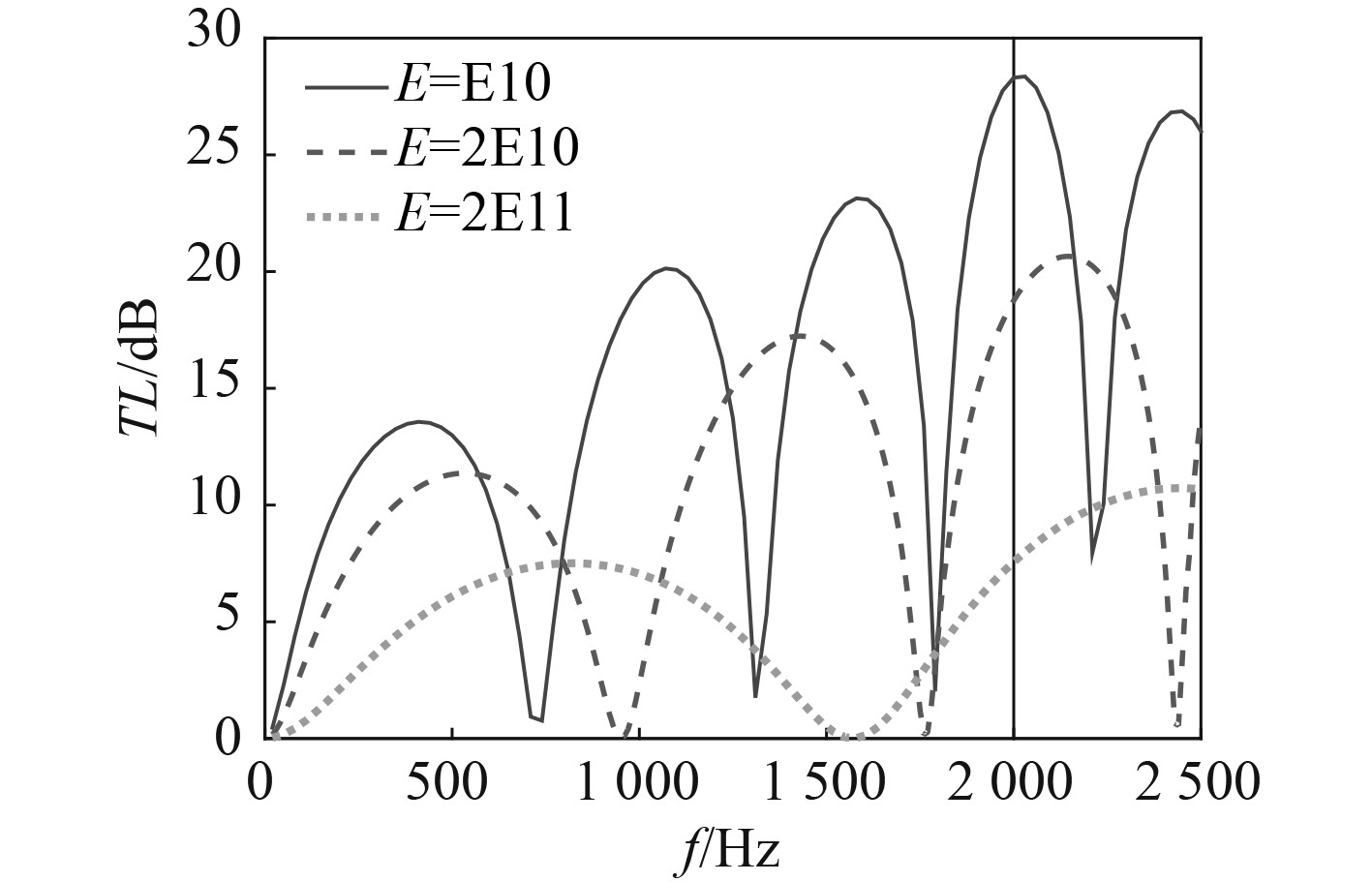
4 弹性背腔参数对传递损失的影响为进一步探究弹性背腔参数对传递损失的影响,对背腔的厚度t以及背腔材料弹性模量E进行分析,不同厚度t的传递损失曲线如图7所示,不同弹性模量E的传递损失曲线如图8所示。分析发现,减小背腔厚度或采用更小弹性模量的背腔材料所取得的效果类似,都能增加传递损失峰值个数,增大传递损失,并且低频消声性能更优。
|
图 7 厚度对传递损失的影响 Fig. 7 The effect of thickness on transmission loss |
|
图 8 弹性模量对传递损失的影响 Fig. 8 The effect of modulus of elasticity on transmission loss |
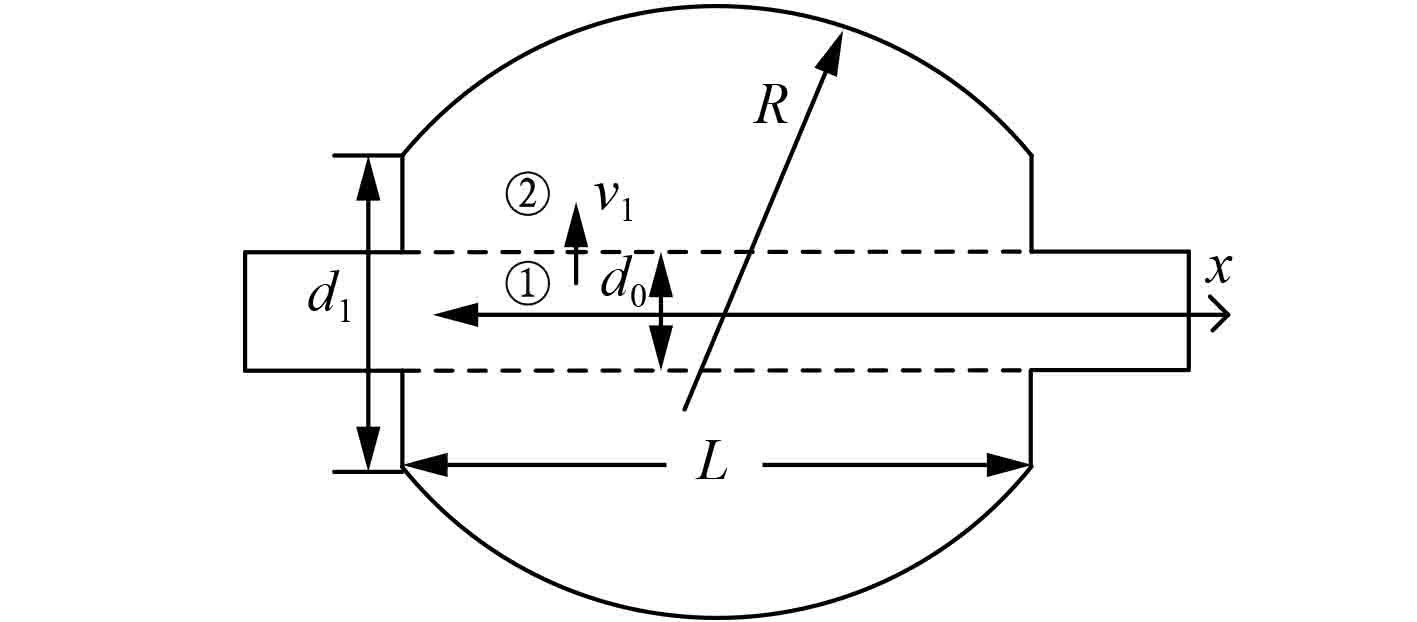
继而改用弧形体背腔,比较上述圆柱形背腔消声器,在等容积、等长度的条件下,构造如图9所示的弧形体消声器模型,弧形背腔半径为
|
图 9 弧形体背腔穿孔管消声器 Fig. 9 Perforated tube muffler with arc-shaped flexible dorsal cavity |
|
|
表 2 弧形体背腔穿孔管消声器结构参数 Tab.2 Structural parameters of the perforated tube muffler with arc-shaped dorsal cavity |
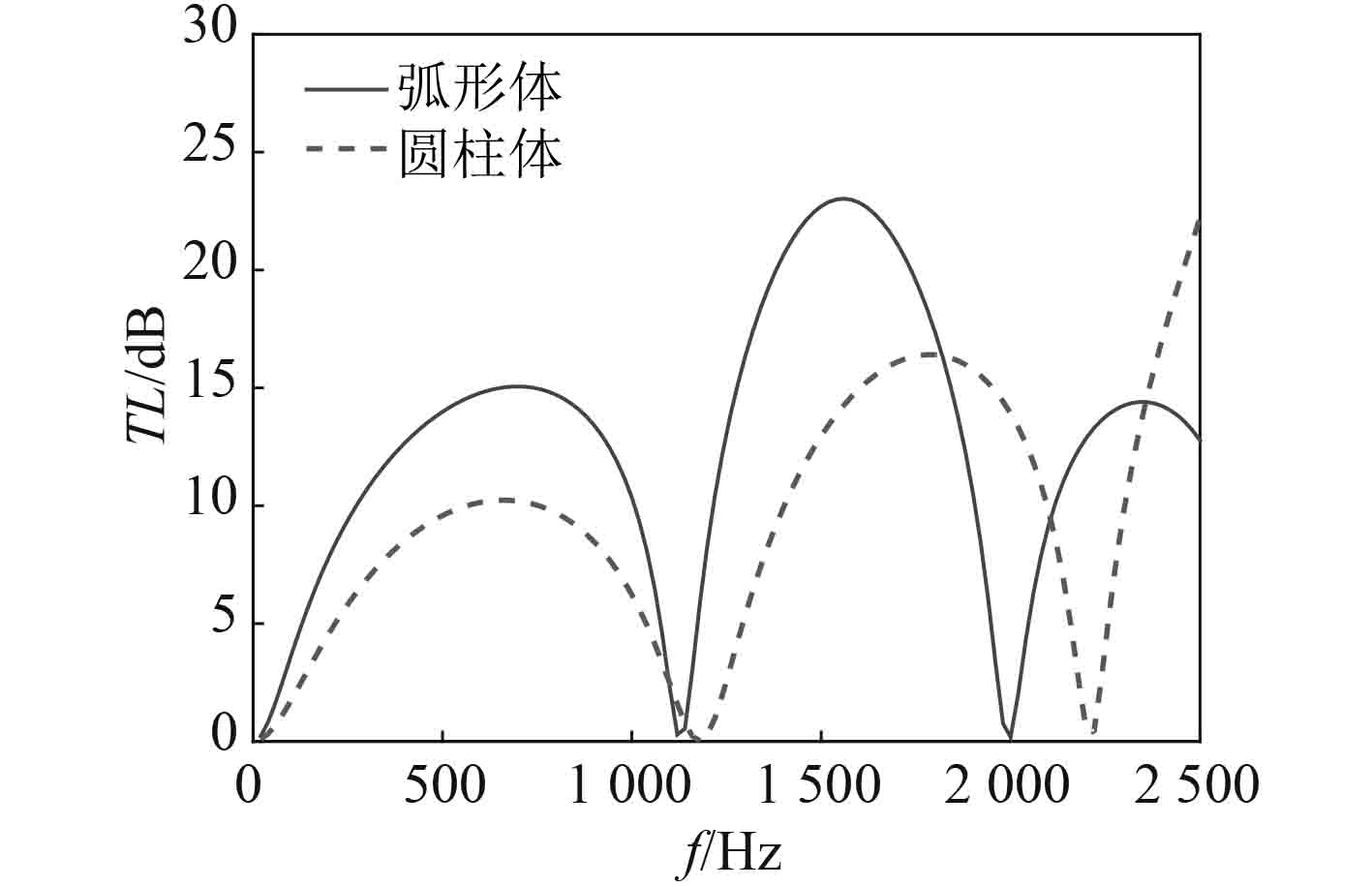
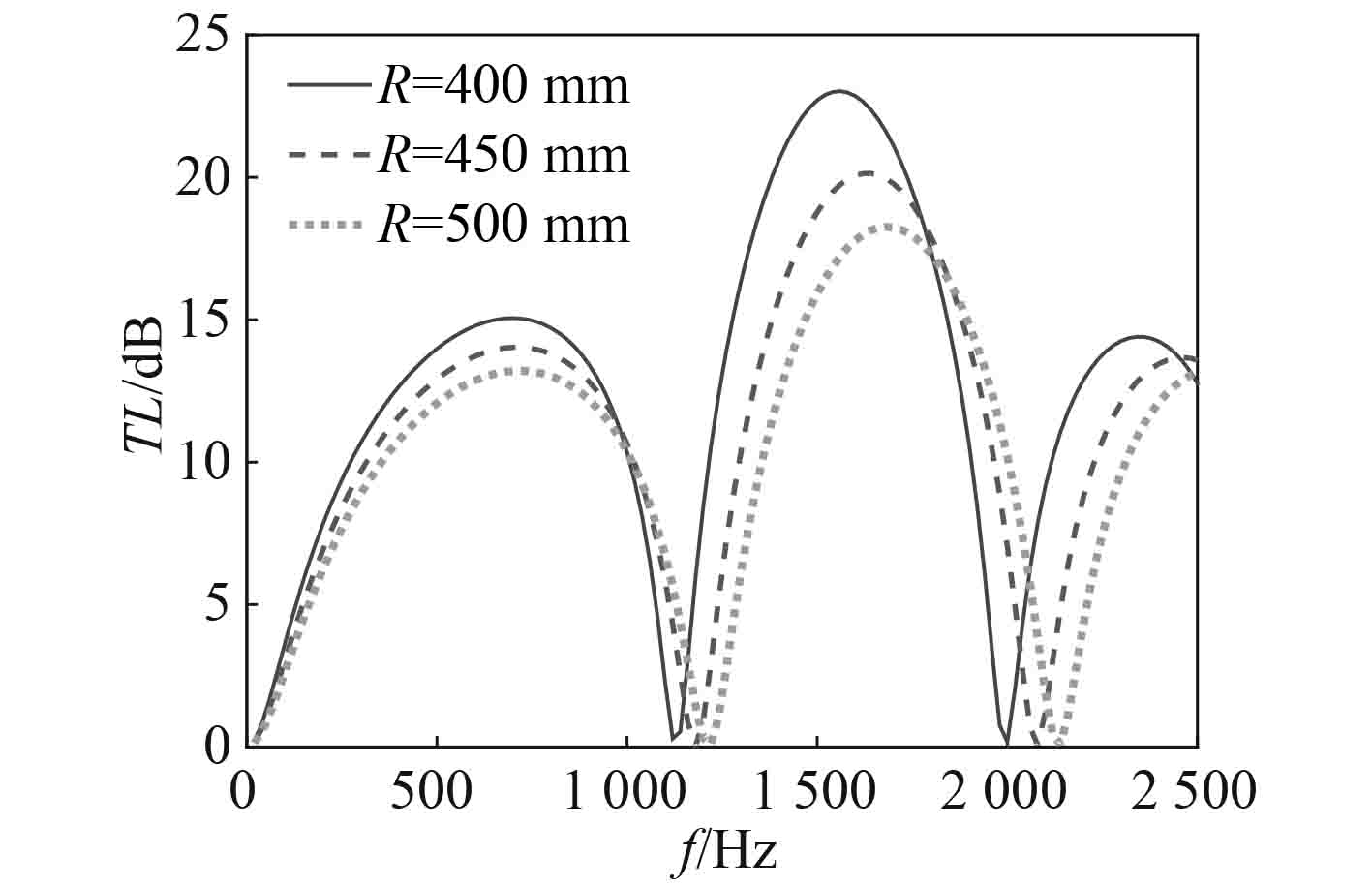
圆柱形背腔与弧形体背腔传递损失对比如图10所示。传递损失曲线向低频移动,并且在低频部分有更好的消声性能。不同弧形半径
|
图 10 弧形体背腔与圆柱体背腔的比较 Fig. 10 Comparison of the arc-shaped dorsal cavity and the cylindrical dorsal cavity |
|
图 11 弧形半径对传递损失的影响 Fig. 11 Influence of radius on transmission loss |
本文研究了弹性背腔穿孔管消声器的传声特性,并对弹性背腔参数以及等容积、等长度的条件下弧形背腔半径对传递损失的影响进行仿真,得出以下结论:
1)仿真结果与根据文献中理论[1]得到的穿孔管消声器的传递损失值与在中低频吻合较好。
2)弹性背腔可以使传递损失曲线向低频移动,并且传递损失值有所增大,消声性能得到提高。
3)一定范围内,减小弹性背腔的厚度和选用弹性模量较小的背腔材料,都能使传递损失峰值数目增多,且传递损失增大、低频消声量增大,消声效果更好,采用较小弧形半径的弧形弹性背腔同样可以提高低频消声性能。
| [1] |
SULLIVAN J W, CROCKER M J. Analysis of concentric tube resonators having unpartitioned cavities[J]. Journal of the Acoustical Society of American, 1978, 64(1): 207-215. DOI:10.1121/1.381963 |
| [2] |
ROSS D F. A finite element analysis of perforated component acoustic systems[J]. Journal of Sound and Vibration, 1981, 79: 133-143. DOI:10.1016/0022-460X(81)90333-3 |
| [3] |
JI Z L, SELAMET A. Boundary element analysis of three-pass perforated duct mufflers[J]. Noisy Control Engineering Journal, 2000, 48: 151-156. DOI:10.3397/1.2827962 |
| [4] |
季振林. 穿孔管阻性消声器声学性能计算及分析[J]. 哈尔滨工程大学学报, 2005(4): 453-457. |
| [5] |
郑晗, 周其斗, 毛艳蕾. 多腔室穿孔管消声器声学特性分析[J]. 武汉理工大学学报(交通科学与工程版), 2015, 39(4): 778-783. DOI:10.3963/j.issn.2095-3844.2015.04.023 |
| [6] |
尹佳玮. 环状膜水管路消声器研究[D]. 哈尔滨: 哈尔滨工程大学, 2015.
|
| [7] |
BAUER A B. Impedance theory and measurements on porous acoustic lines[J]. Journal of Aircraft, 1977, 14(8): 1037-1061. |
| [8] |
龚京风, 宣领宽, 周健. 结构声耦合对膨胀腔水消声器声学性能的影响[J]. 哈尔滨工业大学学报, 2018, 50(10): 195-199. |
 2021, Vol. 43
2021, Vol. 43
