小水线面双体船(Small Waterplane Area Twin Hull,SWATH)是从20世纪70年代开始投入试验并逐渐得到各国重视的一种排水型的高性能船舶。从第1艘SWATH船建成至今,经过40余年的发展,已经有多个国家开发出了有着国防与军事背景的高性能SWATH船[1],并且SWATH船逐渐在民用领域得到了应用,如作为观光游览、客渡和娱乐艇等。
SWATH船由船体的水下部分(也称下体、潜体、主体)、水上平台(也称上体、箱体)、支柱和附加的稳定鳍等4部分组成。与排水量相当的常规单体船和双体船相比,SWATH船具有较小的水线面,使得它在航行的时候所受干扰力较小,因而具有更加优异的快速性、耐波性以及稳性等特点,但SWATH船同时也存在摩擦阻力较大、回转直径较大,浮态对船舶载重量敏感等不足[2-4]。特别是在中高速时,作用在船舶上的MUNK力矩,容易使船舶发生纵向运动失稳[5-7]。
针对SWATH船纵向运动稳定性这一问题,众多学者进行了研究。邬婷[7]通过参照高速水翼艇纵向运动方程建立了SWATH船的纵向运动方程,采用Hurwitz-Routh方法对SWATH船的纵向运动稳定性进行了分析,并对某SWATH船的光体做出了纵向运动稳定性的预报分析。高占胜[8]进行了控制鳍的安装位置、鳍面积等参数变化对某型SWATH船纵向运动稳定性影响的分析。邓磊[9]采用粘性CFD方法对某型SWATH船在顶浪规则波中的纵向运动响应特性进行了数值研究,并较为系统地分析了SWATH船片体间相互干扰对其在波浪中运动响应的影响规律。熊文海[10]在SWATH船的MMG运动数学模型的基础上,同时充分考虑了SWATH船的结构特点和双体、双桨、双舵之间水动力的相互影响,对某型SWATH船的操纵性能进行了预报分析。此外,一些学者也对SWATH船的自动控制系统设计出了不同控制方法下的控制器。王虎军[11]将ESO与终端滑模控制相结合进行了某型SWATH船在随机海浪作用下的运动控制。梁利华[12]针对带有海浪干扰和参数不确定的SWATH船运动控制问题,进行了基于NDO技术的SWATH船运动非线性预测控制。叶志州[13]利用ADRC实时估计SWATH船控制对象的模型摄动和外扰,设计出了一种多变量解耦的鲁棒镇定控制器。周鑫华[14]对SWATH船的纵向运动进行了区域极点配置LQ最优控制器设计。张显库[4]在熊文海[10]的基础上获得了SWATH船的Nomoto模型,在考虑舵机特性后进行了鲁棒控制器设计。
近年来,一些研究人员已经将分数阶PIλDμ控制方法应用于航海领域,如船舶航向控制[15]、船舶横摇控制[16]、船舶电站柴油机调速系统控制[17]和水下潜器姿态角控制[18],并取得了较为良好的控制效果。
本文针对SWATH船纵向运动的稳定性问题,在考虑舵机特性和风浪干扰对系统影响的情况下进行分数阶PIλDμ控制器设计。同时为了证明所设计控制器的良好性能,同时选取一种最优PID控制器作为比对对象,对最优PID控制器与分数阶PIλDμ控制器的控制性能进行仿真实验对比,探讨了2种控制器的控制性能及能量消耗情况。
1 分数阶微积分及分数阶PIλDμ控制器 1.1 分数阶微积分分数阶微积分是传统整数阶微积分的直接拓展,但它比整数阶微积分具有更广泛的适用性。所谓的分数阶微积分是指阶次为非整数的微积分,它可以实现任意阶次的微积分。分数阶微积分的算子可以由整数阶微积分的算子直接扩展得到,它的定义如下[19-20]:
| ${}_aD_t^\alpha = \left\{ {\begin{array}{*{20}{c}} {\dfrac{{{{\rm{d}}^\alpha }}}{{{\rm{d}}{t^\alpha }}},{\rm{Re}} \left( \alpha \right) > 0} \text{,}\\ {1,{\rm{Re}} \left( \alpha \right) = 0}\text{,} \\ {\displaystyle\int_a^t {{{\left( {{\rm{d}}\tau } \right)}^{ - \alpha }},{\rm{Re}} \left( \alpha \right) < 0} } \text{。} \end{array}} \right.$ | (1) |
式中:
目前,在分数阶微积分理论中较为常用的定义有以下4种[19-20]:
1)Cauchy定义下的表达式
| ${}_aD_t^\alpha f\left( t \right) = \frac{{\Gamma \left( {\alpha + 1} \right)}}{{2{\text{π}\rm{ j}}}}\int_C {\frac{{f\left( \tau \right)}}{{{{\left( {\tau - t} \right)}^{\alpha + 1}}}}{\rm{d}}\tau }\text{,} $ | (2) |
式中:
2)Grunwald-Letnikov定义下的表达式
| ${}_a^{GL}D_t^\alpha f\left( t \right) = \mathop {\lim }\limits_{h \to 0} \frac{1}{{{h^\alpha }}}\sum\limits_{j = 0}^{\left[ {{{\left( {t - a} \right)} / h}} \right]} {{{\left( { - 1} \right)}^j}\left( {\begin{array}{*{20}{c}} \alpha \\ j \end{array}} \right)} f\left( {t - jh} \right)\text{。}$ | (3) |
式中:
3)Riemann-Liouville定义下的表达式
| ${}_a^{RL}D_t^\alpha f\left( t \right) = \frac{1}{{\Gamma \left( {n - \alpha } \right)}}\frac{{{{\rm{d}}^n}}}{{{\rm{d}}{t^n}}}\left[ {\int_a^t {\frac{{f\left( \tau \right)}}{{{{\left( {t - \tau } \right)}^{\alpha - n + 1}}}}} {\rm{d}}\tau } \right]\text{,}$ | (4) |
式中:
4)Caputo定义下的表达式
| ${}_0D_t^\alpha f\left( t \right) = \frac{1}{{\Gamma \left( { - \alpha } \right)}}\int_0^t {\frac{{f\left( \tau \right)}}{{{{\left( {t - \tau } \right)}^{1 + \alpha }}}}} {\rm{d}}\tau\text{。} $ | (5) |
式中:
分数阶PIλDμ控制器的概念是由Podlubny在1997年时提出的[21]。分数阶PIλDμ控制器除了兼具常规PID控制器的优点外,由于分数阶微积分自身的特性,分数阶控制器还具有许多整数阶控制器无法实现的优越性,其微分阶次μ和积分阶次λ可以进行实数范围内的任意设置,这使得分数阶PIλDμ控制器具有比常规PID控制器更灵活的控制结构。分数阶PIλDμ控制器的传递函数模型为:
| ${G_c}\left( s \right) = {k_p} + \frac{{{k_i}}}{{{s^\lambda }}} + {k_d}{s^\mu }\text{。}$ | (6) |
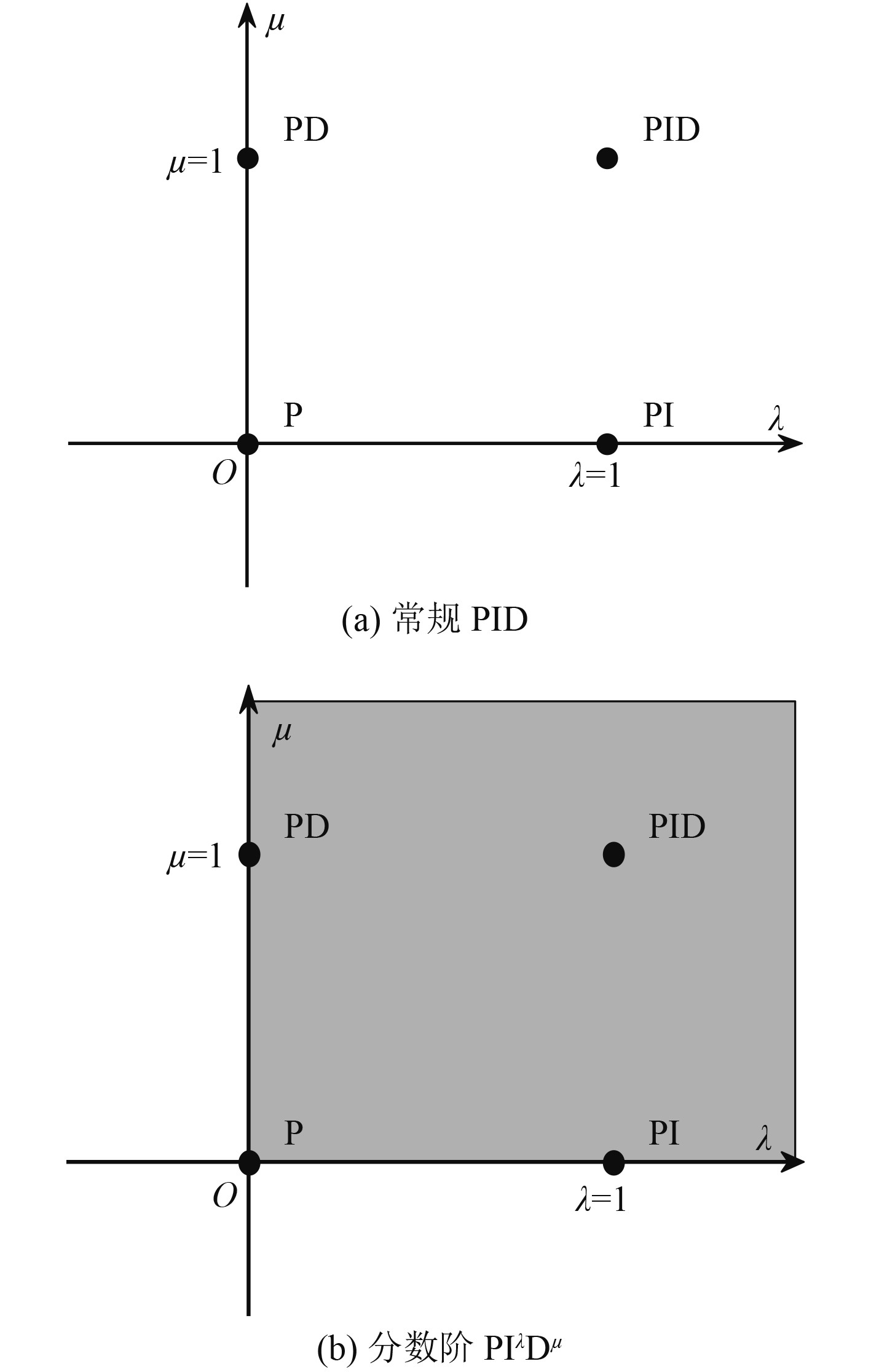
分数阶PIλDμ控制器的示意图如图1所示。其中,横轴代表分数阶PIλDμ控制器的积分阶次λ,纵轴代表分数阶PIλDμ控制器的微分阶次μ。常规的PI控制器、PD控制器和PID控制器均为分数阶PIλDμ控制器平面内的一个点。
|
图 1 分数阶PIλDμ控制器示意图 Fig. 1 Diagram of fractional-order PIλDμ controller |
通过对比可知,常规PID的积分阶次λ与微分阶次μ的值均为1,是一种特例分数阶PIλDμ;与此类似,当λ=1,μ=0则对应常规PI控制器;当λ=0,μ=1则对应常规PD控制器。此外,由于分数阶PIλDμ的积分阶次λ与微分阶次μ可以是任意实数,这使得分数阶PIλDμ控制器与整数阶PID控制器相比,具有更灵活的控制结构与优越的性能。
2 SWATH船纵向运动的分数阶PIλDμ控制器设计 2.1 SWATH船纵向运动的传递函数模型|
|
表 1 某SWATH具体参数 Tab.1 Particulars of a SWATH ship |
假设舵角δ作为输入信号,首向角ψ作为输出信号,可以获得该SWATH实船从舵角δ到首向角ψ的等效Nomoto模型[4]为:
| ${G_\psi }_\delta = \frac{{{\rm{0}}{\rm{.05}}}}{{{\rm{s(6s + 1)}}}}\text{。}$ | (7) |
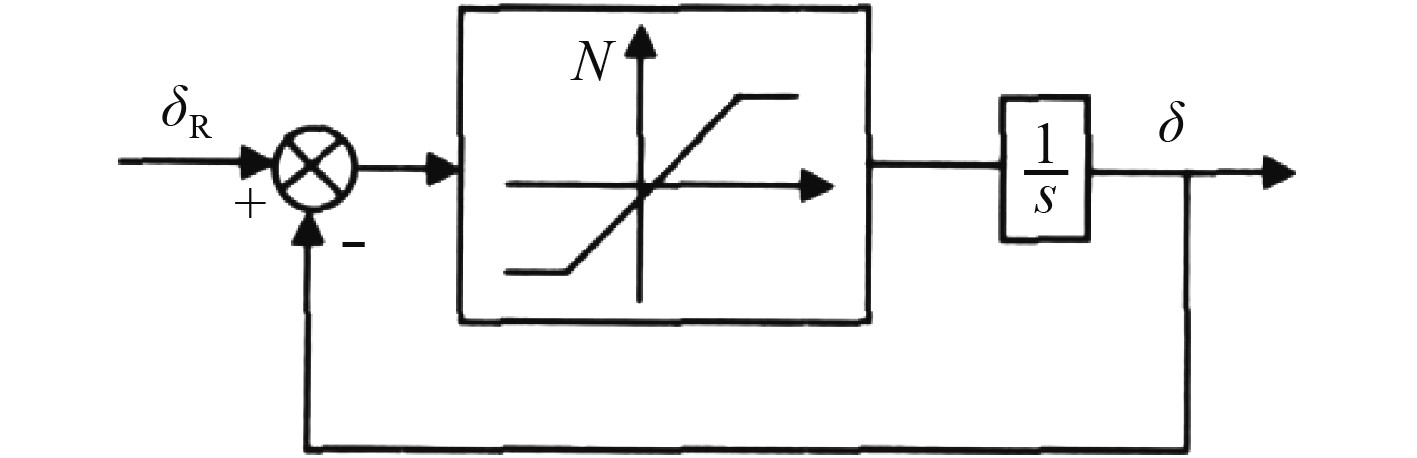
在设计分数阶PIλDμ控制器时,以等效Nomoto模型为控制对象,并在设计过程中考虑舵机伺服系统,如图2所示。
|
图 2 舵伺服系统 Fig. 2 Rudder servo system |
为了能快速获得分数阶PIλDμ控制器的优化参数,提高控制器的控制性能,本文在分数阶PIλDμ控制器设计时引入ITAE准则如下式:
| ${J_{ITAE}} = \int_0^\infty {t\left| {e\left( t \right)} \right|} {\rm{d}}t\text{。}$ | (8) |
通过数值方法对ITAE准则指标进行优化,则可以得到优化后的分数阶PIλDμ控制器参数,kp=0.95,ki=0.0,kd=0.1,λ=0.8,μ=0.1(实际优化得到的ki为极小的非零正量,实际仿真时将ki设为0),即优化参数的分数阶PDμ控制器为:
| ${G_1} = 0.95 + 0.1{s^{0.1}}\text{,}$ | (9) |
此外,采用最优PID控制器的设计方法[22],可得到最优PID控制器参数,kp=1.2,ki=0.0,kd=3.0(实际优化得到的ki也依然为极小的非零正量,仿真时将ki设为0),最终可获得最优PD控制器如下:
| ${G_2} = 1.2 + 3s\text{。}$ | (10) |
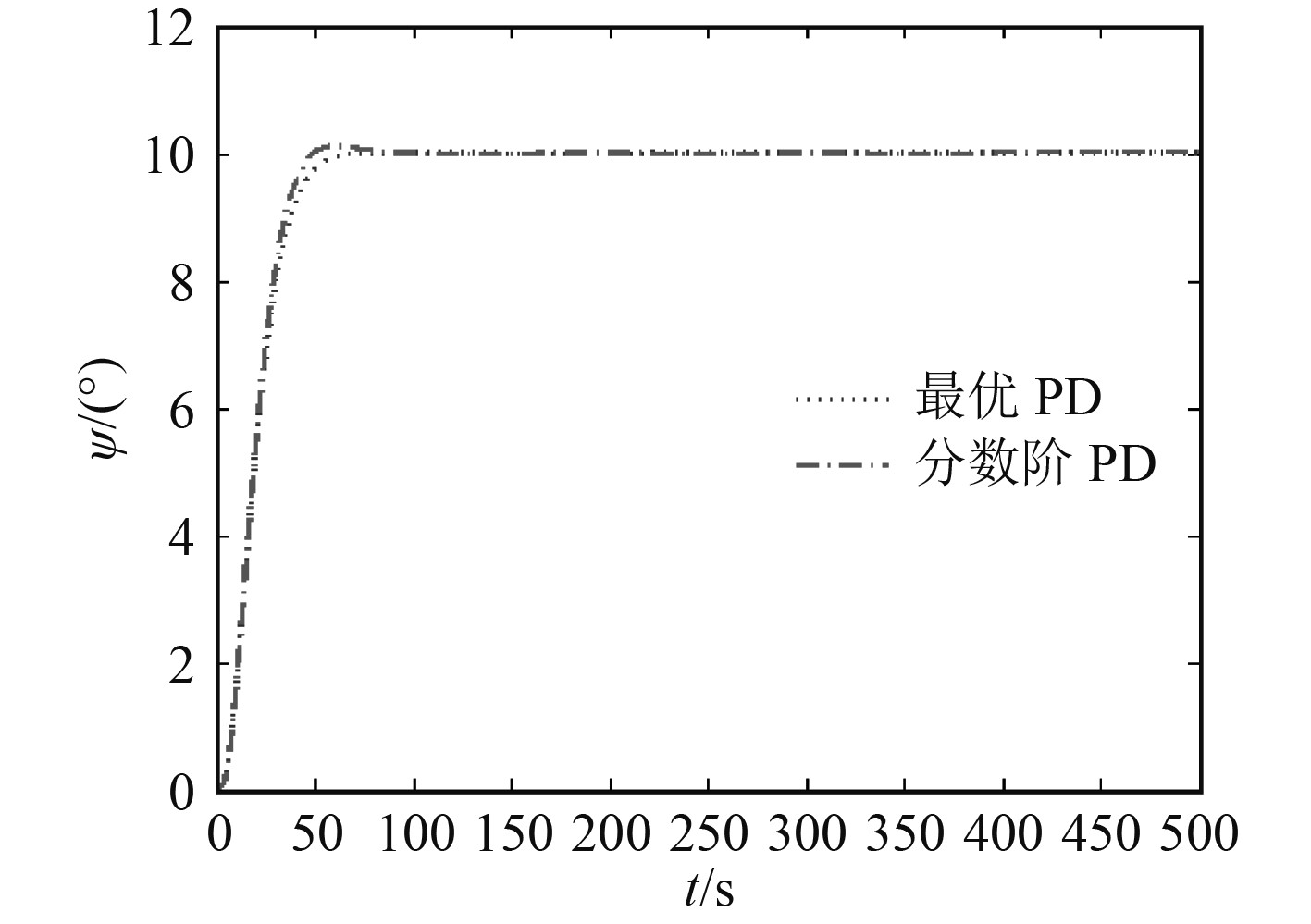
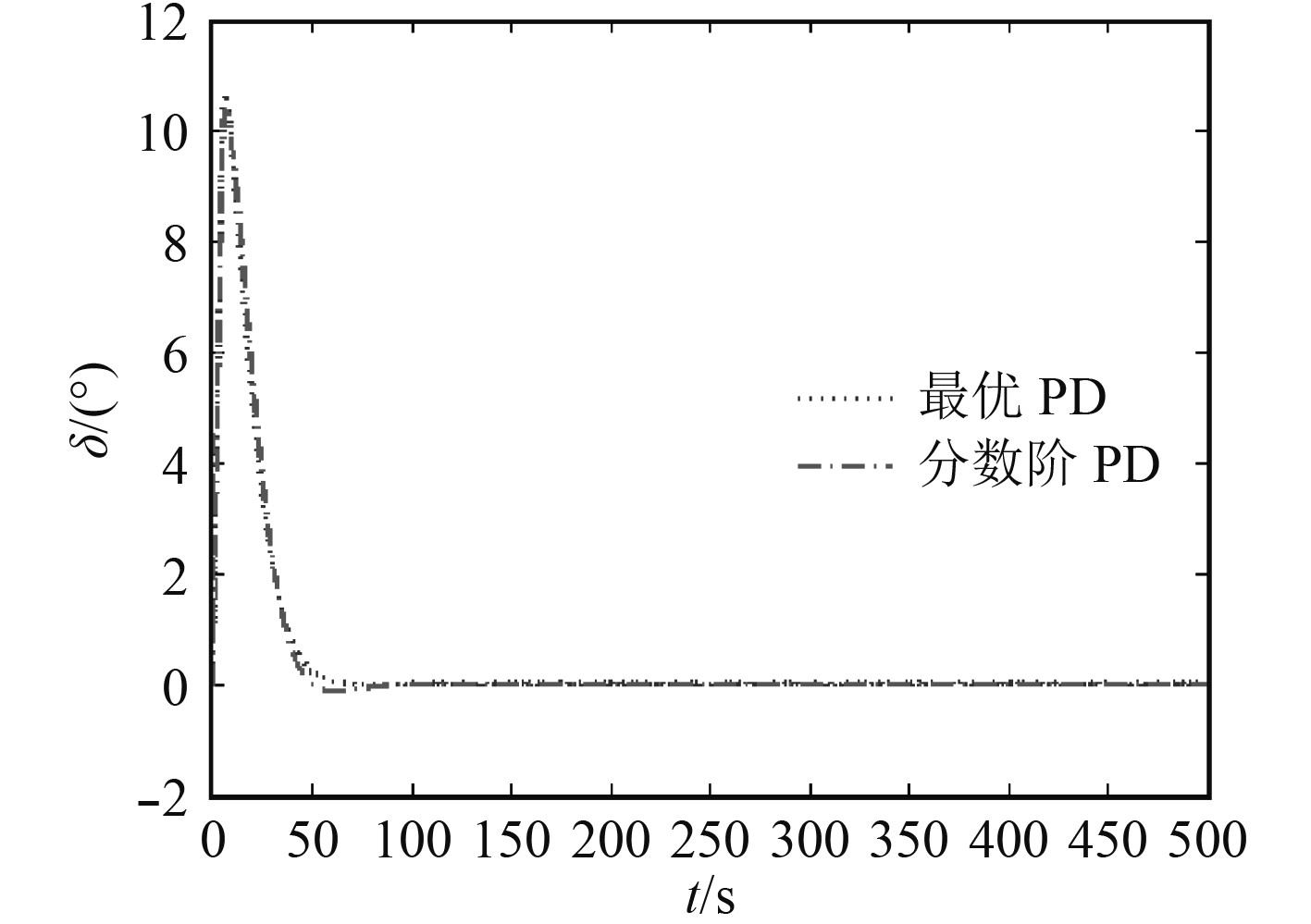
首先,对仅考虑舵机特性(由最大舵角饱和限制、最大舵速限制与积分环节3部分组成)的SWATH船纵向运动的等效Nomoto模型行仿真比对试验(参照文献[4]进行航向自0°转到10°的仿真实验),因为本文中所采用的2种控制器的的控制效果均优于一般参数整定方法所得到的常规PID控制器的控制效果,故在接下来的比对中不给出其仿真结果曲线。等效Nomoto模型的首向角ψ仿真结果如图3所示,舵角δ仿真结果如图4所示。
|
图 3 等效Nomoto模型的艏向角ψ仿真结果 Fig. 3 Equivalent Nomoto model simulation result of course ψ |
|
图 4 等效Nomoto的舵角δ仿真结果 Fig. 4 Equivalent Nomoto model simulation result of rudder angle δ |
其中,最优PD控制器的调节时间为ts=44.04 s(5%),ts=51.48 s(2%),上升时间为tr=29.61 s,峰值时间tp=80.42 s,超调量σ%=0.076%。分数阶PDμ控制器的调节时间为ts=39.35 s(5%),ts=43.65 s(2%),上升时间为tr=26.75 s,峰值时间tp=60.04 s,超调量σ%=1.177%。从以上数据可知,2种控制器的超调都较小,舵角几近相同,但是分数阶PDμ控制器呈现出更快速的响应性能与更良好的综合性能。
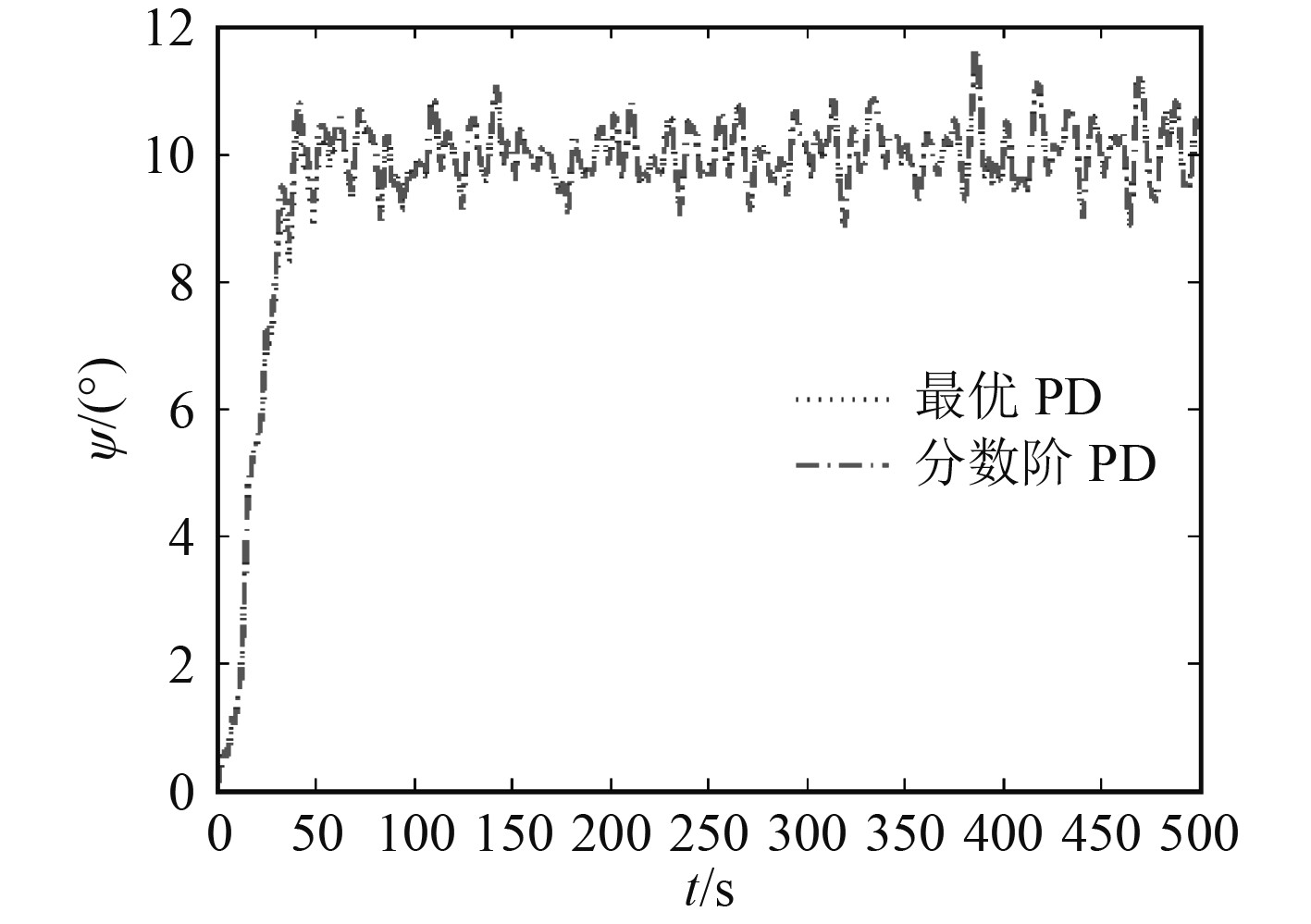
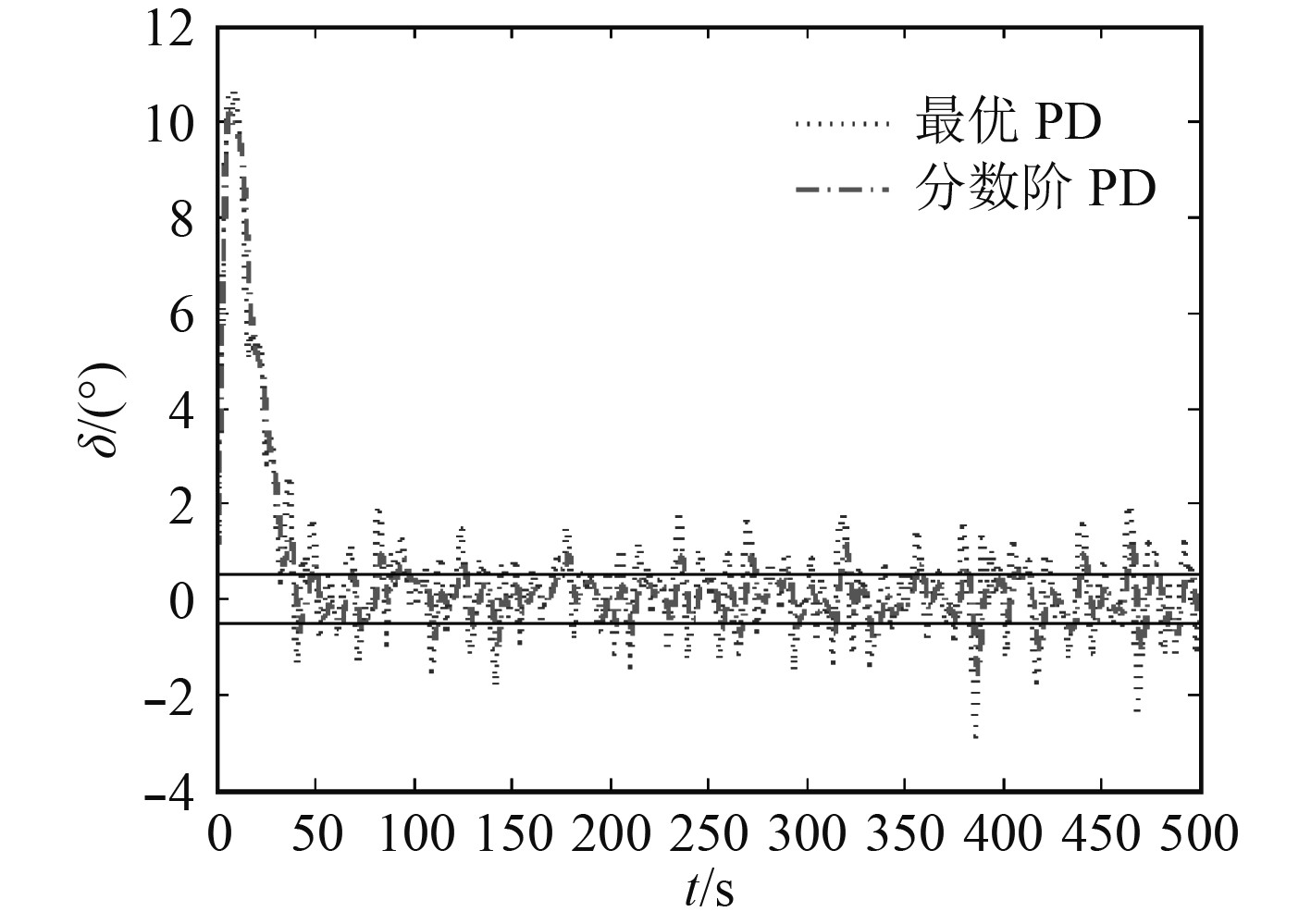
其次,在进行2种控制器性能的仿真比对实验时,为使结果更接近航海实践,在仿真过程中考虑了风浪对船舶操纵性能的影响[23]。其中,6级海浪的干扰选用国际ITTC认可的白噪声驱动的2阶震荡环节描述[11-12, 23]。考虑风浪干扰后的首向角ψ仿真结果如图5所示,舵角δ仿真结果如图6所示(图中黑色水平线代表动舵±0.5°)。
|
图 5 考虑风浪干扰后的艏向角ψ仿真结果 Fig. 5 Simulation result of course ψ after considering wind and wave interferences |
|
图 6 考虑风浪干扰后的舵角δ仿真结果 Fig. 6 Simulation result of rudder angle δ after considering wind and wave interferences |
张显库[23]指出:1)舵的能耗体现在操舵平稳性、动舵(0.5°以上)次数、作用时间和舵叶转动幅度等几个方面;2)平均舵角小,说明操舵平稳性好,舵叶平均转动幅度小,可达到减少舵机系统磨损和转舵时推力损耗的效果;3)从控制界代表能量性能指标函数J=∫δ2dt来衡量耗能,其离散化后为J=∑δ2(k)。
从以上3个方面对考虑风浪干扰后的模型的控制效果进行分析。从仿真结果可以看出,分数阶PDμ控制器动舵幅度较小,且动舵频率较低,比较节能。其中,采样时,等效Nomoto模型仿真实验中,最优PD控制器的J=1351.9,分数阶PDμ控制器J=1426.9(两者耗能相近)。考虑风浪干扰后的模型仿真实验中,最优PD控制器的J=1670.9,分数阶PDμ控制器的J=1530.3。最优PD控制器耗能增加23.6%,分数阶PDμ控制器耗能增加7.25%,考虑风浪干扰后的分数阶PDμ控制器相比最优PD控制器节能约8.41%;不采样时,等效Nomoto模型仿真实验中,最优PD控制器的J=41007,分数阶PDμ控制器的J=43338(两者耗能相近)。考虑风浪干扰后的模型仿真实验中,最优PD控制器的J=52695,分数阶PDμ控制器的J=48282。最优PD控制器耗能增加28.50%,分数阶PDμ控制器耗能增加11.41%,考虑风浪干扰后的分数阶PDμ相比最优PD控制器节能约8.37%。
此外,为了进一步比对控制器的性能,分别进行了20°~80°的转向仿真实验。仿真结果表明,最优PD控制器会出现一定的静差,而且舵角输出呈现较为频繁的抖动。而分数阶PDμ控制器则未出现上述现象,依旧呈现了如10°仿真实验时的良好效果。
对比以上的仿真结果可知,本文所设计的分数阶PDμ控制器的控制效果明显优于最优PD控制器,并具有更为快速的响应性能与更加良好的综合性能,且分数阶PDμ控制器在经受外界风浪干扰时,体现出了更加节能的控制性能,同时也展现出了更强的鲁棒性能。分数阶PDμ控制器能很好地克服SWATH船由于外界因素干扰而导致的模型不确定性的影响。本文所设计的分数阶PDμ控制器具有鲁棒性强、控制性能好、更节能等优点。
4 结 语本文针对小水线面双体船的纵向运动稳定性问题,设计了一种分数阶PIλDμ控制器,并在控制器设计时引入ITAE准则对分数阶PIλDμ的参数进行快速优化,并以类似方式得到优化参数的最优PID控制器。对某SWATH实船的等效Nomoto模型和考虑风浪干扰后的模型分别进行了仿真实验,结果表明,本文所设计的分数阶PIλDμ控制器可用于小水线面双体船的纵向运动控制,且该控制器具有鲁棒性强、控制性能好、更节能等优点。
| [1] |
林伟国, 朱云翔, 范井峰, 等. 小水线面双体船的发展及在海军舰船领域中的应用前景[J]. 船舶, 2007, 19(3): 1-5. LIN Wei-guo, ZHU Yun-xiang, FAN Jing-feng, et al. Development of smallwaterplane area tw in hull and its application prospect in navy[J]. Ship and Boat, 2007, 19(3): 1-5. DOI:10.3969/j.issn.1001-9855.2007.03.001 |
| [2] |
马建文, 张安西, 周兆欣, 等. 小水线面双体船五自由度运动建模与仿真[J]. 中国舰船研究, 2017, 12(2): 133-150. MA Jian-wen, ZHANG An-xi, ZHOU Zhao-xin, et al. Modeling and simulation of five DOF motions for SWATH ships[J]. Chinese Journal of Ship Research, 2017, 12(2): 133-150. DOI:10.3969/j.issn.1673-3185.2017.02.017 |
| [3] |
孙小帅, 姚朝帮, 叶青. 小水线面双体船波浪中纵向运动性能模型试验研究[J]. 国防科技大学学报, 2017, 39(4): 161-167. SUN Xiao-shuai, YAO Chao-bang, YE Qing. Experimental investigation on the seakeeping performance of small waterplane area twin hull in head waves[J]. Journal of National University of Defense Technology, 2017, 39(4): 161-167. DOI:10.11887/j.cn.201704025 |
| [4] |
张显库. 船舶控制系统[M]. 大连: 大连海事大学出版社, 2010.
|
| [5] |
何懋华, 孙树民. 小水线面双体船纵向运动稳定性研究进展[J]. 广东造船, 2012, 31(5): 55-59. DOI:10.3969/j.issn.2095-6622.2012.05.011 |
| [6] |
林政, 毛筱菲. 小水线面双体船的纵向运动稳定性研究[J]. 船海工程, 2010, 39(2): 54-57. DOI:10.3963/j.issn.1671-7953.2010.02.0015 |
| [7] |
邬婷, 程红蓉, 苗飞, 等. SWATH 纵向运动稳定性分析与航行姿态控制研究[J]. 中国造船, 2017, 58(4): 91-99. WU Ting, CHENG Hong-rong, MIAO Fei, et al. Stability of longitudinal motion and control of voyage gesture of SWATH[J]. Shipbuilding of China, 2017, 58(4): 91-99. DOI:10.3969/j.issn.1000-4882.2017.04.011 |
| [8] |
高占胜, 蔡烽, 侯建军. 鳍参数对某型SWATH船纵向运动稳定性的影响分析[J]. 船舶工程, 2014, 36(2): 30-33. |
| [9] |
邓磊, 董文才, 姚朝帮. 顶浪规则波中小水线面双体船纵向运动特性数值分析[J]. 舰船科学技术, 2016, 38(8): 5-10. DENG Lei, DONG Wen-cai, YAO Chao-bang. Numerical study on characteristics of SWATH ship longitudinal motions in regular head waves[J]. Ship Science and Technology, 2016, 38(8): 5-10. |
| [10] |
熊文海, 周振路, 陈力. 基于细长体理论的小水线面双体船操纵性预报[J]. 中国航海, 2007(4): 9-12. DOI:10.3969/j.issn.1000-4653.2007.04.003 |
| [11] |
王虎军, 贾鹤鸣. 基于扩张状态观测器的小水线面双体船终端滑模控制[J]. 船舶工程, 2014, 36(5): 81-85. |
| [12] |
梁利华, 王保华, 贾鹤鸣. 基于干扰观测器的SWATH船运动非线性预测控制[J]. 控制与决策, 2014, 29(3): 431-436. |
| [13] |
叶志洲, 姚华利, 孙洪飞. 基于自抗扰控制的SWATH船纵向运动控制[J]. 厦门大学学报(自然科学版), 2014, 53(2): 190-195. |
| [14] |
周鑫华, 邱贝贝. SWATH船纵向运动的区域极点配置LQ最优控制研究[J]. 淮海工学院学报 (自然科学版), 2019, 28(1): 37-40. |
| [15] |
李光宇, 郭晨, 李延新. 基于改进粒子群算法的USV航向分数阶控制[J]. 系统工程与电子技术, 2014, 36(6): 1146-1151. DOI:10.3969/j.issn.1001-506X.2014.06.20 |
| [16] |
FAIEGHI M R, NADERI M, JALALI A A. Design of Fractional-Order PID for ship roll motion control using chaos embedded PSO algorithm[C]// 2nd International Conference on Control, Instrumentation and Automation (ICCIA). IEEE, 2011: 606−610.
|
| [17] |
李志民, 孙其振, 孙勇, 等. 基于BF-PSO的船舶电站柴油机分数阶控制器[J]. 控制工程, 2012, 19(3): 515-518. DOI:10.3969/j.issn.1671-7848.2012.03.036 |
| [18] |
赵健, 白春江, 章文俊. 水下潜器姿态角的分数阶 PID 控制研究[J]. 舰船科学技术, 2016, 38(21): 129-132. |
| [19] |
Concepción A. MONJE, YangQuan CHEN, Blas M. VINAGRE, et al. Fractional-order systems and controls fundamentals and applications[M]. New York: Springer Press, 2010.
|
| [20] |
薛定宇. 分数阶微积分学与分数阶控制[M]. 北京: 科学出版社, 2018.
|
| [21] |
I. PODLUBNY, L. DORCAK, I. KOSTIAL. On fractional derivatives, Fractional-Order dynamic systems and PIλDμ controllers[C]// 36th Conference on Decision & Control, San Diego, USA, 1997.
|
| [22] |
薛定宇. 控制系统计算机辅助设计−Matlab语言与应用(第3版)[M]. 北京: 清华大学出版社, 2012.
|
| [23] |
张显库, 杨光平, 张强. 一种双极性S函数修饰的非线性船舶航向保持算法[J]. 大连海事大学学报, 2016, 42(3): 15-19. |
 2021, Vol. 43
2021, Vol. 43
