2. 河南省水下智能装备重点实验室,河南 郑州 450015
2. Henan Key laboratory of Underwater Intelligent Equipment, Zhengzhou 450015, China
本文研究对象为水下航行器环肋圆柱壳耐压结构。在静水压力作用下,圆柱壳耐压结构将产生均匀收缩变形,肋间壳体产生弯曲,若壳体超过临界应力,材料进入塑性状态,甚至在载荷不变的情况下壳体的变形还将继续急剧增大直到使壳体破坏为止,威胁结构安全与可靠性。此外,耐压结构在制造加工过程中不可避免地存在着一些初始裂纹缺陷,并且在服役过程中将受到海水的严重腐蚀。这些因素都将对水下耐压结构的疲劳强度和稳定性造成巨大影响。
针对以上影响因素,本文利用结构裂纹扩展软件Franc3D建立基于裂纹扩展试验的非线性裂纹仿真模型,通过与试验比对校验仿真方法的合理性。随后建立无缺陷状态下的耐压结构强度分析模型,对其强度与稳定性进行校核,在此基础上进一步加入裂纹缺陷因素,建立了耐压结构非线性有限元模型,研究不同缺陷参数对于结构的敏感性分析,提出多失效模式下结构强度与稳定性评估方法。
1 Franc3D断裂力学理论Franc3D是美国FAC公司开发的裂纹分析软件,用来计算工程结构在任意复杂的几何形状、载荷条件和裂纹形态下的三维裂纹扩展,它结合有限元软件进行断裂力学计算。
1.1 应力强度因子计算Franc3D使用M积分来计算应力强度因子,M积分能量表达式为:
| $\begin{split} {\overline M ^{(1,2)}} = &\displaystyle\int\limits_\Gamma {\left( {\sigma _{ij}^{\left( 1 \right)}\dfrac{{\partial u_i^{\left( 2 \right)}}}{{\partial {x_1}}} + \sigma _{ij}^{\left( 2 \right)}\dfrac{{\partial u_i^{\left( 1 \right)}}}{{\partial {x_1}}}} \right)} \dfrac{{\partial q}}{{\partial {x_j}}}{\rm{d}}s -\\ &\displaystyle\int\limits_\Gamma {\left( {{W^{1,2}}{\delta _{1j}}} \right)} \dfrac{{\partial q}}{{\partial {x_j}}}{\rm{d}}s \text{,} \end{split} $ | (1) |
式中,
| ${W^{\left( {1,2} \right)}} = \sigma _{ij}^{\left( 1 \right)}\varepsilon _{ij}^{\left( 2 \right)} = \sigma _{ij}^{\left( 2 \right)}\varepsilon _{ij}^{\left( 1 \right)}\text{,}$ | (2) |
M积分与应力强度因子关系为:
| $\begin{split} {\overline M ^{(1,2)}} = &\frac{{1 - {\nu ^2}}}{E}K_I^{\left( 1 \right)}K_I^{\left( 2 \right)} + \frac{{1 - {\nu ^2}}}{E}K_{II}^{\left( 1 \right)}K_{II}^{\left( 2 \right)} + \\ &\frac{{1 - {\nu ^2}}}{E}K_{III}^{\left( 1 \right)}K_{III}^{\left( 2 \right)} \text{。} \end{split}$ | (3) |
式中:KI,KII,KIII为3种基本裂纹形式对应的应力强度因子。
1.2 裂纹扩展计算Franc3D通过指定载荷的循环次数,基于裂纹扩展速率公式直接计算裂纹前缘所有节点的扩展距离:
| $\Delta {a_j} = \Delta NC{\left( {\Delta {K_j}} \right)^n}\text{。}$ | (4) |
再利用Paris公式(
|
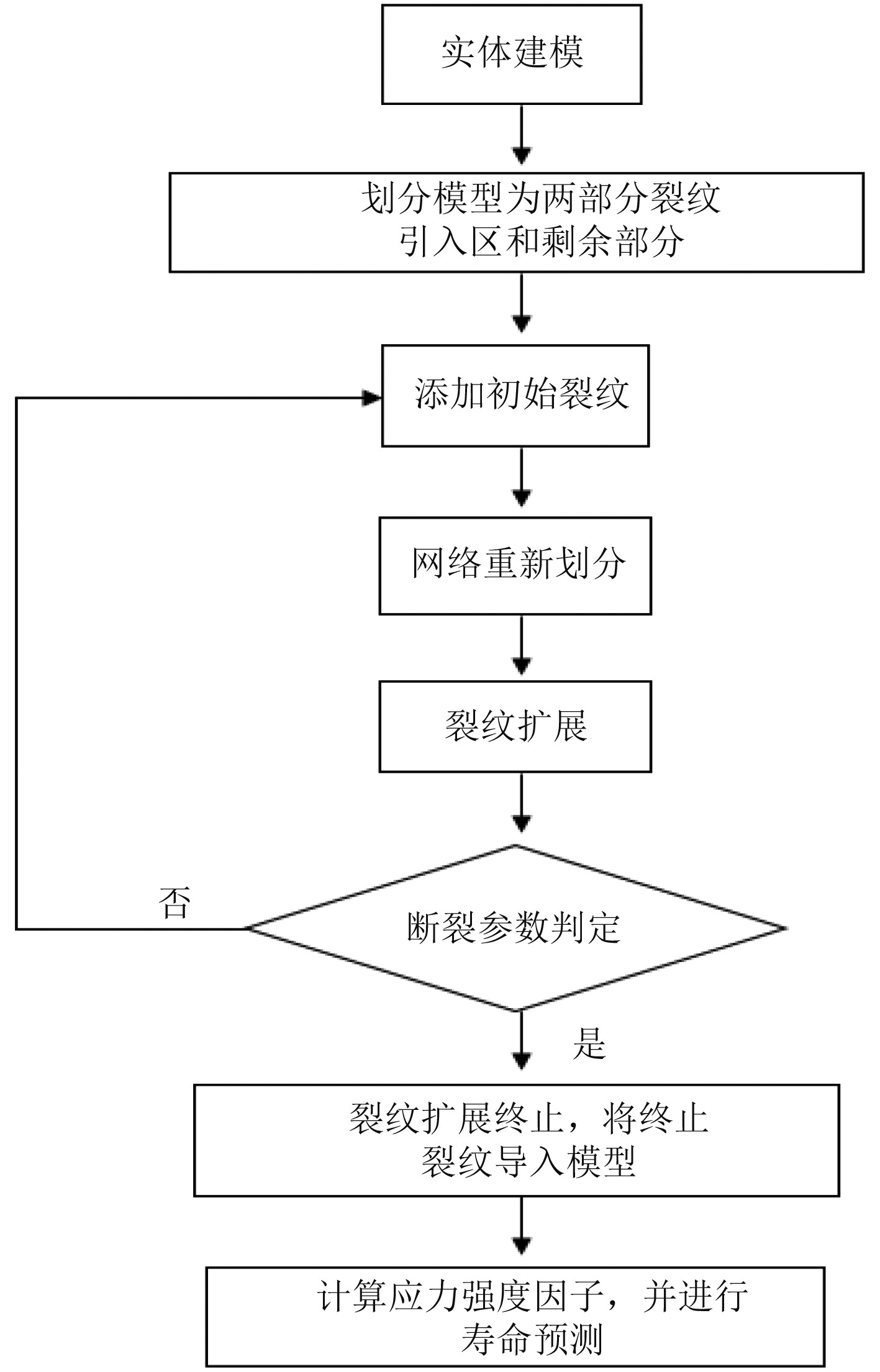
图 1 结构裂纹扩展分析流程 Fig. 1 Analysis process of structural crack growth |
使用Franc 3D模拟标准CT样件的疲劳裂纹扩展试验,可预先了解该材料在不同交变载荷作用下裂纹的扩展、失稳及断裂的规律,为结构设计选材,预估零件剩余寿命提供参考。
2.1 CT试件建模按照紧凑拉伸试样设计中的尺寸要求,建立CT样件的模型。由于预制裂纹的存在,可以将模型尖端简化,如图2所示。

|
图 2 CT试样仿真模型 Fig. 2 CT sample simulation model |
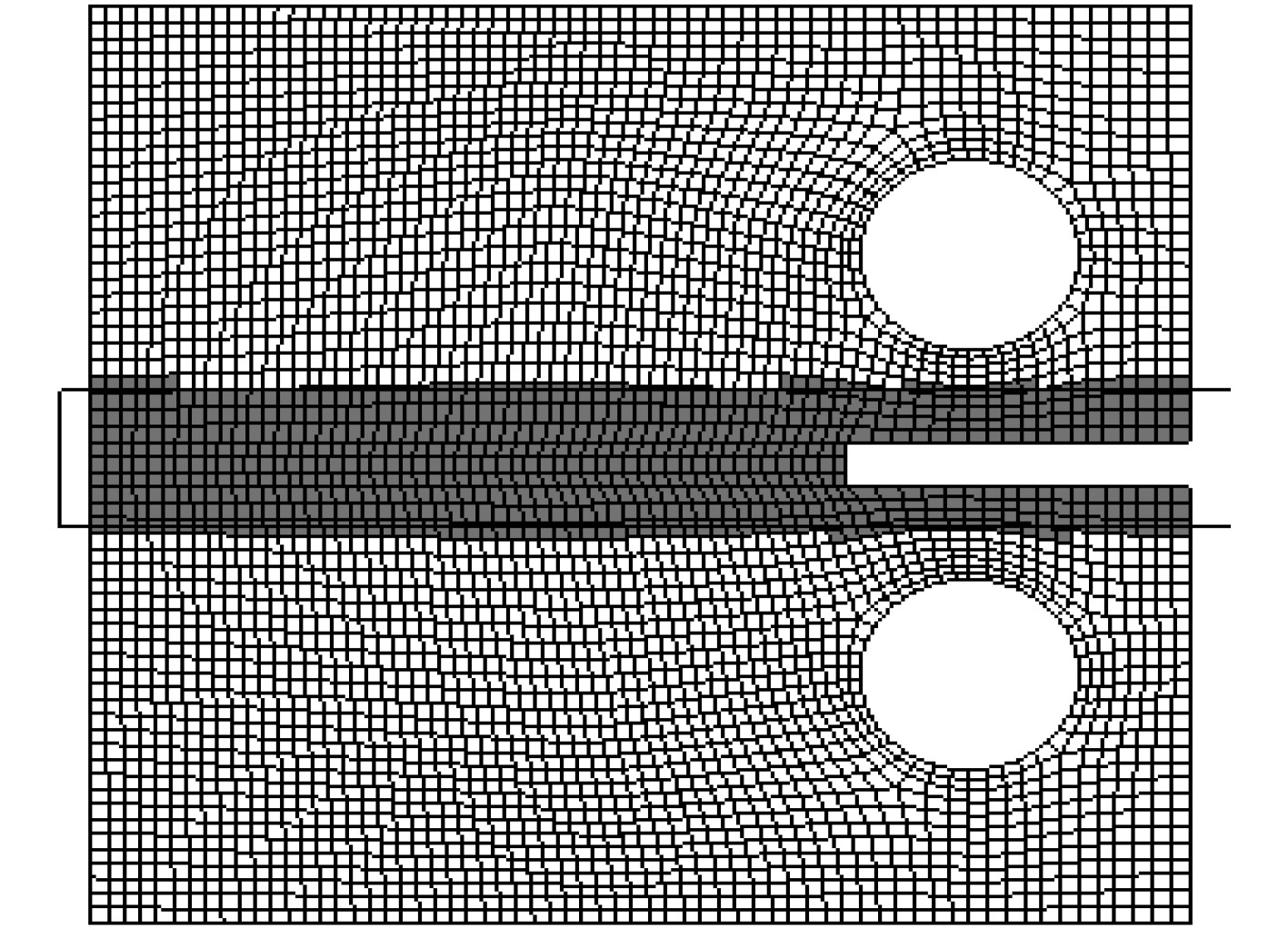
将模型划分为如图3所示,裂纹引入区(红色部分)和剩余部分(白色部分)。引入矩形片裂纹,设置裂纹自动扩展。
|
图 3 CT试样仿真模型网格划分 Fig. 3 CT sample simulation model grids |
1)计算裂纹尖端应力强度因子
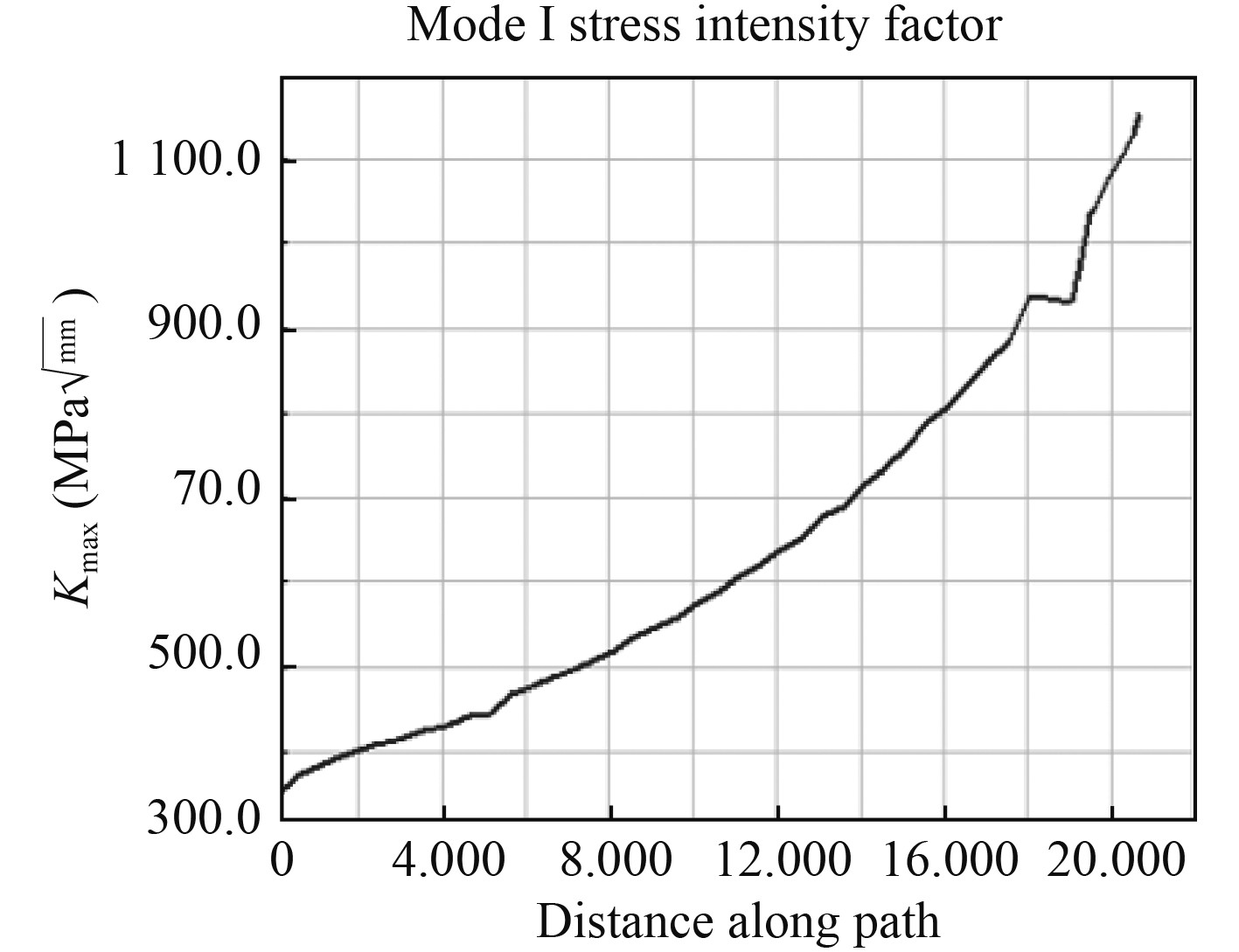
本仿真中,裂纹尖端应力强度因子的数值取得是裂纹扩展路径的中点处应力强度因子的数值,如图4所示。

|
图 4 裂纹扩展路径 Fig. 4 Crack growth path |
|
图 5 沿裂纹扩展路径的应力强度因子 Fig. 5 Stress intensity factor along the crack propagation path |
2)计算剩余寿命
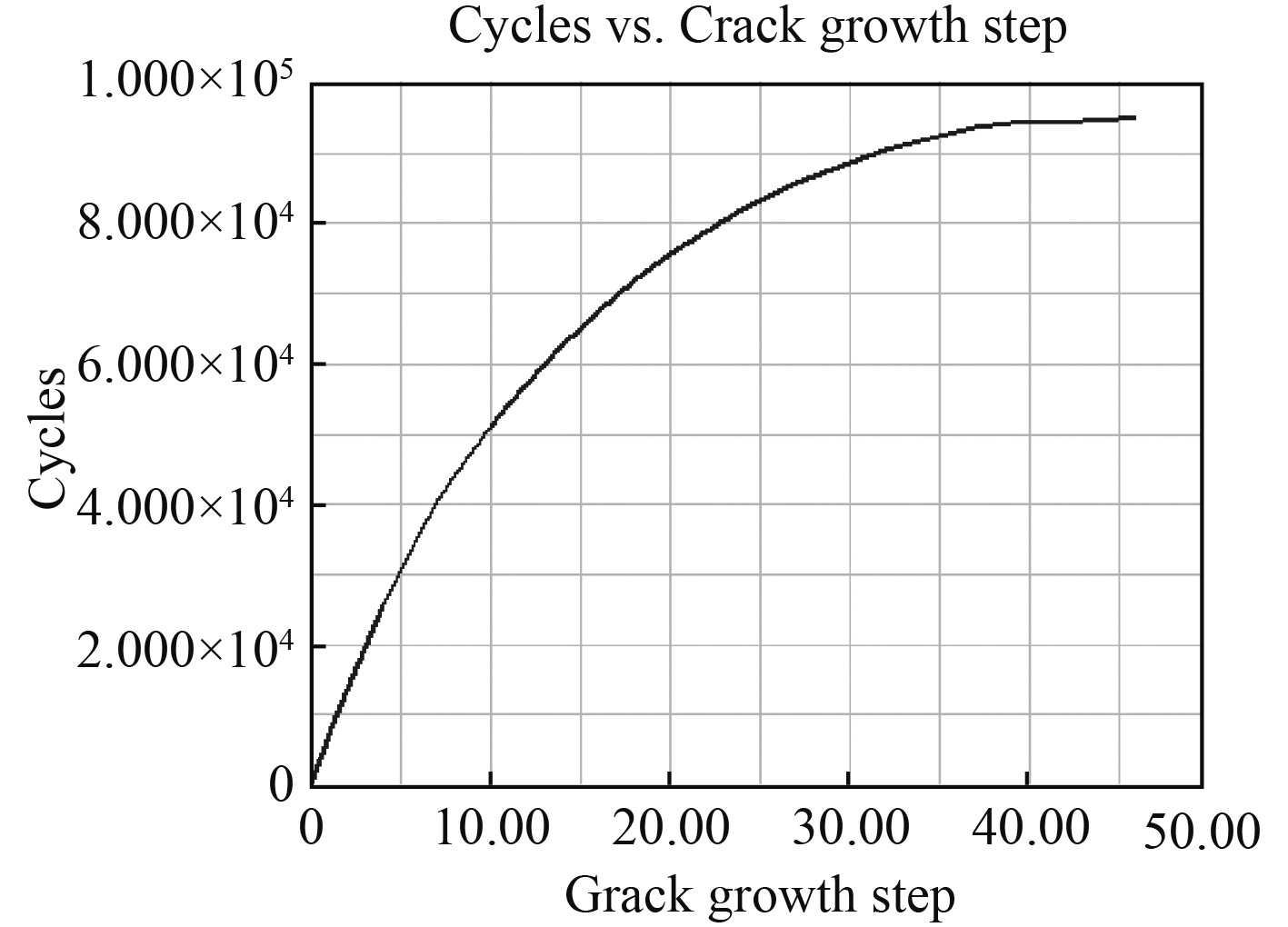
根据1.2节进行剩余寿命预测,如图6所示。
|
图 6 最大载荷为1.5 kN的裂纹扩展剩余寿命 Fig. 6 Remaining life of crack propagation with the maximum load of 1.5 KN |
3)裂纹扩展规律分析
裂纹扩展共计46步,选取其中6步结果进行展示(a为裂纹扩展长度),如图7所示。

|
图 7 CT试件裂纹扩展过程 Fig. 7 Crack propagation process of CT sample |
4)仿真与试验结果对比
完成CT样件裂纹扩展试验后,使用上述仿真进行验证,结果如表1所示。
|
|
表 1 裂纹扩展寿命对比 Tab.1 Crack growth life comparison |
通过与试验结果进行比对校验,试验与仿真相对误差可达15%,满足工程计算要求,验证裂纹扩展有限元仿真方法的有效性,为研究耐压结构损伤安全研究提供有力支撑。
3 裂纹初始缺陷的结构强度与稳定性分析 3.1 无缺陷模型分析在不影响仿真结果准确性的情况下需要对水下奈叶结构进行简化处理。对模型封堵螺栓孔,切除左端和右端阶梯结构之后,得到最终用于仿真分析的简化模型如图8所示。

|
图 8 耐压结构物理模型 Fig. 8 Physical model of pressure-resistant structure |
结构材料为2A-12铝合金,载荷为1.5 MPa水下静压力,沿外表面径向均匀分布于部件外表面。

|
图 9 无缺陷模型应变云图 Fig. 9 Strain cloud diagram of flawless model |

|
图 10 无缺陷模型应力云图 Fig. 10 Stress cloud diagram of flawless model |
由无缺陷模型的计算结果可知,在壳体端部楔环连接区域应力较大,主要由于该处结构无肋骨支撑且具有较多的凸起、凹陷结构,易出现应力集中效应,在横、纵肋骨支撑处刚性较强,变形小,在缺少肋骨支撑位置变形较大。耐压结构在工作深度下最大应力为52.67 MPa,远小于材料屈服强度(>280 MPa),满足强度要求。
3.2 裂纹缺陷模型分析1)裂纹缺陷对结构强度影响
首先进行完好模型的静力分析,分别引入矩形片裂纹(裂纹方向与轴向垂直),矩形片裂纹(裂纹方向与轴向交45°)探究不同的裂纹方向、大小对结构强度的影响(参数见表2),进行裂纹扩展、寿命计算。
|
|
表 2 不同裂纹参数 Tab.2 Different crack parameters |

|
图 11 预置裂纹方式 Fig. 11 Preset crack form |
不同裂纹缺陷下的应力云图如图12所示。

|
图 12 不同裂纹下结构应力云图(4×1,垂直) Fig. 12 Structural stress cloud diagram under different cracks (4×1, vertical) |
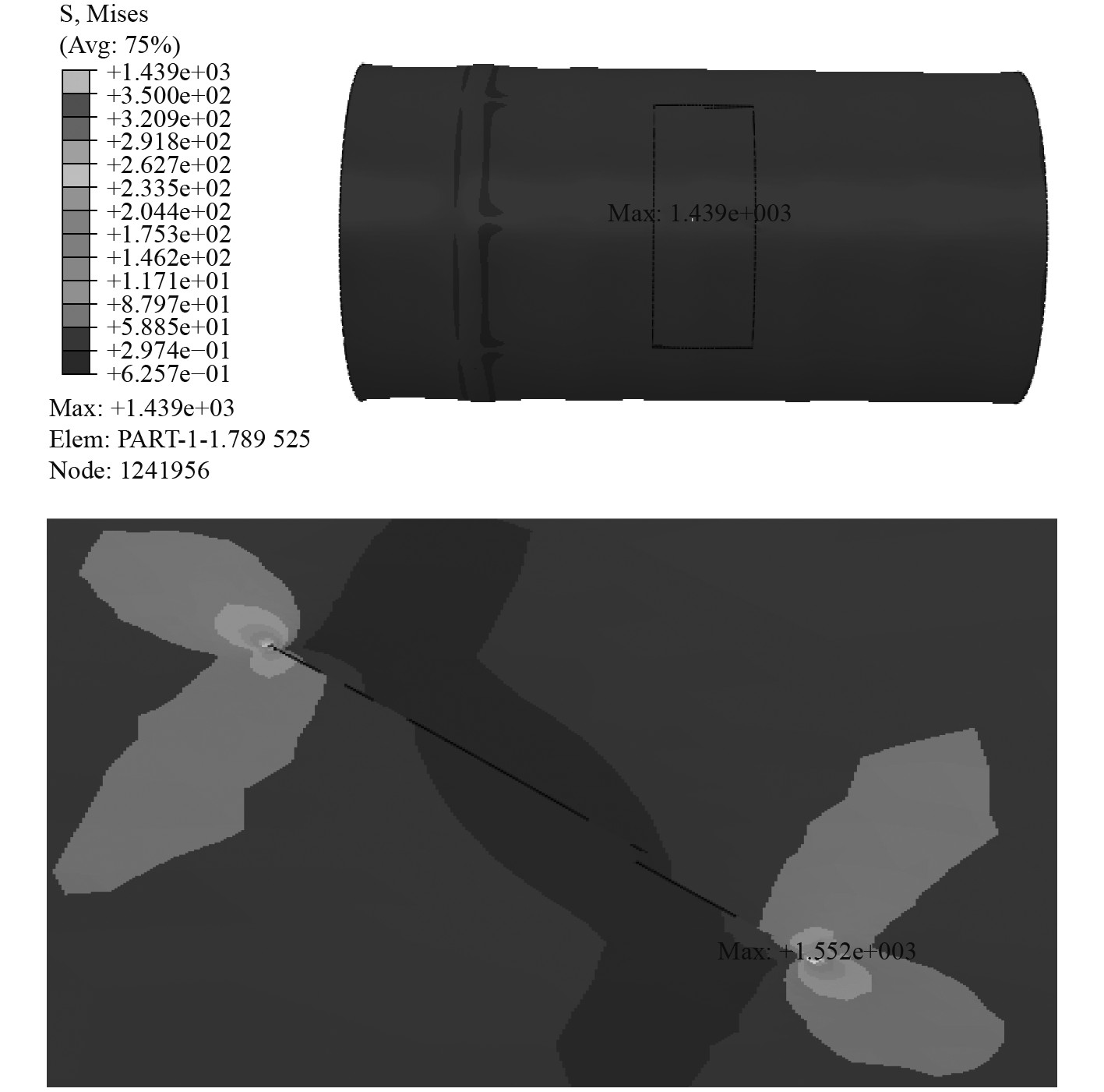
|
图 13 不同裂纹下结构应力云图(4×3,45°夹角) Fig. 13 Structural stress cloud diagram under different cracks (4×3, 45° angle) |
|
|
表 3 不同裂纹扩展尖端应力结果分析 Tab.3 Analysis of peak stress under different crack growth |
①当裂纹方向一致时(垂向方向),相同裂纹深度,裂纹越短应力越大,应力集中现象越明显;
②当裂纹方向与轴向45°夹角时,裂纹处于闭合状态,裂纹越长,应力集中程度越大。裂纹越深,应力集中程度越小。与轴向45°夹角时应力集中程度最大,与轴向垂直时应力集中程度最小。因此45°夹角裂纹工况对结构强度的影响最为严峻,应当尽量避免该情况的出现。
2)裂纹缺陷对稳定性的影响
在研究裂纹缺陷对结构稳定性分析时,选取了较危险的交叉肋板处作为缺陷施加位置,选取长度4 mm、深度1 mm与长度4 mm、深度3 mm两组裂纹参数(45°夹角)建立非线性屈曲分析模型,校核结构稳定性。
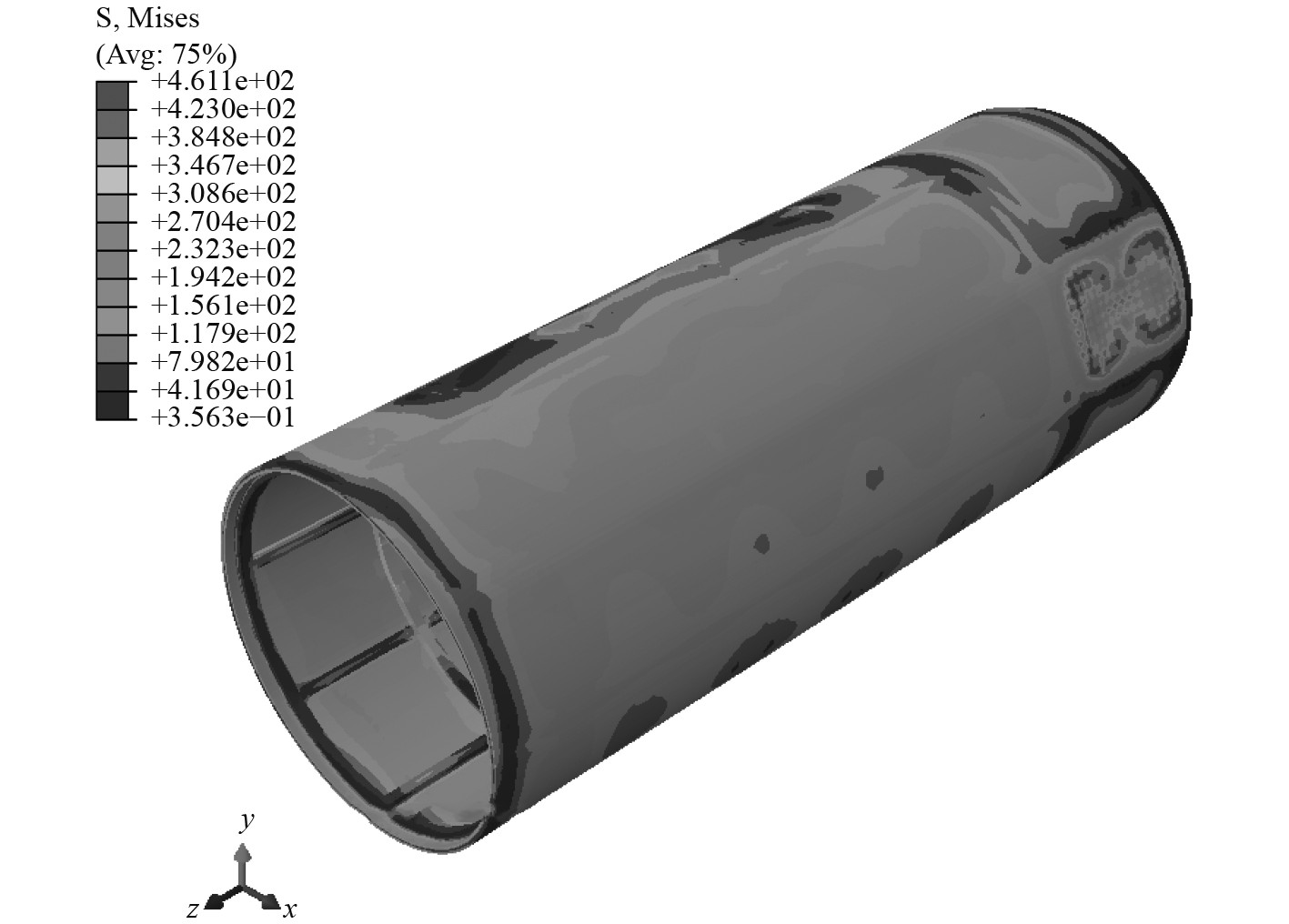
|
图 14 不同裂纹下结构屈曲应力云图(4×1) Fig. 14 Structural buckling stress cloud diagram under different cracks (4×1) |

|
图 15 不同裂纹下结构屈曲应力云图(4×3) Fig. 15 Structural buckling stress cloud diagram under different cracks (4×3) |
由计算结果可知,当裂纹方向一致时,相同裂纹深度,裂纹越短应力越大,应力集中现象越明显,临界屈曲载荷越小,结果越容易失稳。
4 结 语本文针对裂纹缺陷的水下耐压结构建立非线性有限元模型,研究不同裂纹缺陷下的结构强度与稳定性问题,得出以下结论:
1)基于Franc3D软件建立裂纹缺陷仿真模型预示疲劳寿命与试验结果具有良好的吻合性,验证仿真方法的有效性,为后续裂纹仿真分析提供技术支撑;
2)不同的裂纹缺陷对于结构强度影响效果不同,其中当裂纹与轴向呈45°夹角时,结构应力集中情况较严重,结构出现局部强度破坏;当裂纹长度越短时,结构临界屈曲载荷越小,易出现结构失稳问题;
3)建立的结构裂纹仿真分析方法可为水下发射装置结构、水下智能装备等领域的结构强度与稳定性评估提供合理的研究手段。
| [1] |
靖海宏. 潜水器耐压壳结构稳定性分析与研究[D]. 武汉: 武汉理工大学, 2011.
|
| [2] |
何雪浤, 李燕燕, 郭珍珍. 潜水器耐压壳强度分析方法研究[J]. 机械设计与制造, 2014(2): 8-10. DOI:10.3969/j.issn.1001-3997.2014.02.003 |
| [3] |
刘文成, 李朋波, 任少飞. 瞬态外压载荷时间特性对网格加筋圆柱壳动力屈曲影响[J]. 舰船科学技术, 2018, 40(19): 22-27. |
| [4] |
程靳, 赵树山. 断裂力学[M]. 北京: 科学出版社, 2006: 93.
|
| [5] |
陈传尧, 高大兴. 表面裂纹的应力强度因子[J]. 机械强度, 1984(1): 9. |
 2021, Vol. 43
2021, Vol. 43
