在水下航行器的初步设计阶段,对其主要组成的圆柱壳结构进行声振响应预报,可以为结构的声学优化设计提供理论基础[1-2]。
在实际工程中,为了对结构振动数据进行采样,需要在结构表面布置相关传感器,但在整个结构上均布置传感器实施难度大、不现实。所以,通过一种好的测点布置方法,实现较少数目的传感器对结构声振响应的准确预报就显得非常重要。目前,国内研究人员基本是采用均匀布置方法[3-7],这种方法简单易行,但测点数目及位置的选择存在较大的主观性和盲目性,且需借助大量的数值分析算例。
几十年来,学者们根据自然界中的生物进化或物理演变过程,提出了很多基于概率变换来实现最优组合的随机类算法,如遗传算法等[8]。这类算法可在全域内进行搜索,不易陷入局部最优解,比较适合解决组合优化类的问题,但也存在收敛速度慢、迭代次数多、计算效率有待改善等缺点。
针对圆柱壳结构的测点布置问题,本文提出一种改进方法—均匀子集随机选取测点方法:将所有待选测点分成相互独立的均匀子集,子集数量与测点数量保持一致,测点从各个子集中随机选取,再利用设定的目标函数对随机选取的测点组进行评价,从而选择出好的测点布置方案。这种测点布置改进方法不仅具有均匀布置方法中取样全面、操作简单等优点,同时通过划分子集进行随机选择,可避免选择范围广、收敛速度慢、迭代次数多等缺点。
根据模态叠加原理,可将结构振速展开为模态叠加的形式,再利用均匀子集随机选取方法得到的测点布置方案,与均匀布置方法对比。通过上述不同测点布置方案得到的水下圆柱壳振动声辐射预报结果对比表明,均匀子集随机选取测点方法是一种优秀的测点布置方法。
1 基本理论 1.1 模态叠加理论水下弹性结构振动响应方程如下:
| ${{M}}\ddot x(t) + {{C}}\dot x(t) + {{K}}x(t) = f(t) + p(t)\text{,}$ | (1) |
其中:M为质量矩阵;C为阻尼矩阵;K为刚度矩阵;
经拉普拉斯变换可得:
| $ - {\omega ^2}{{M}}X + j\omega {{C}}X + {{K}}X = F + P\text{,}$ | (2) |
将结构振速展开为如下形式:
| $V = \sum\limits_{r = 1}^\infty {{\phi _r}{q_r}}\text{,} $ | (3) |
式中:
速度与位移的关系如下:
| $X = \frac{1}{{j\omega }}V\text{,}$ | (4) |
结合式(2)~式(4)可得:
| $j\omega {m_s}{q_s} + {c_s}{q_s} + \frac{1}{{j\omega }}{k_s}{q_s} = {\phi _s}^{\rm{T}}(F + P)\text{,}$ | (5) |
式中:
由此,可得第
| ${q_s} = \dfrac{{{\phi _s}^{\rm{T}}(F + P)}}{{j\omega {m_s} + {c_s} + \,\dfrac{1}{{j\omega }}{k_s}}}\text{,}$ | (6) |
当阻尼及外部激励均为0时,式(5)可表示如下:
| $ - {\omega _r}^2{m_s}{q_s} + {k_s}{q_s} = 0\text{,}$ | (7) |
式中:
| ${k_s} = {\omega _r}^2{m_s} = {\omega _r}^2\text{,}$ | (8) |
根据式(7),当结构处于流体介质中时,其对结构振动影响可表示成附加质量的形式:
| $ - {\omega _s}^2({m_s} + \Delta {m_s}){q_s} + {k_s}{q_s} = 0\text{,}$ | (9) |
式中:
结合式(7)~式(9),可得:
| $\frac{{\omega _r^2}}{{\omega _s^2}} = 1 + \Delta {m_s}\text{。}$ | (10) |
即可通过式(10),对结构空气和水中的振动固有频率进行转换。
1.2 均匀子集随机选取测点方法均匀子集随机选取测点包含以下3个方面内容:
1)子集划分
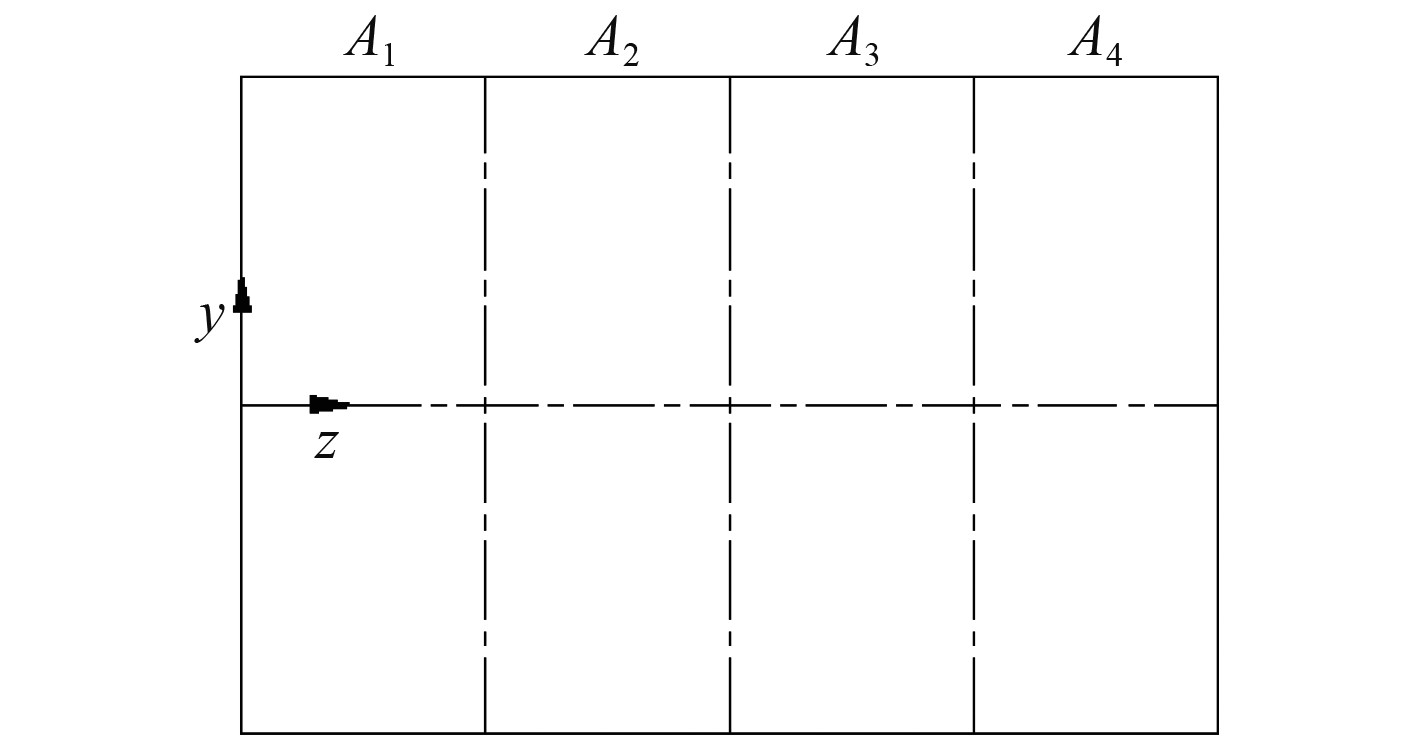
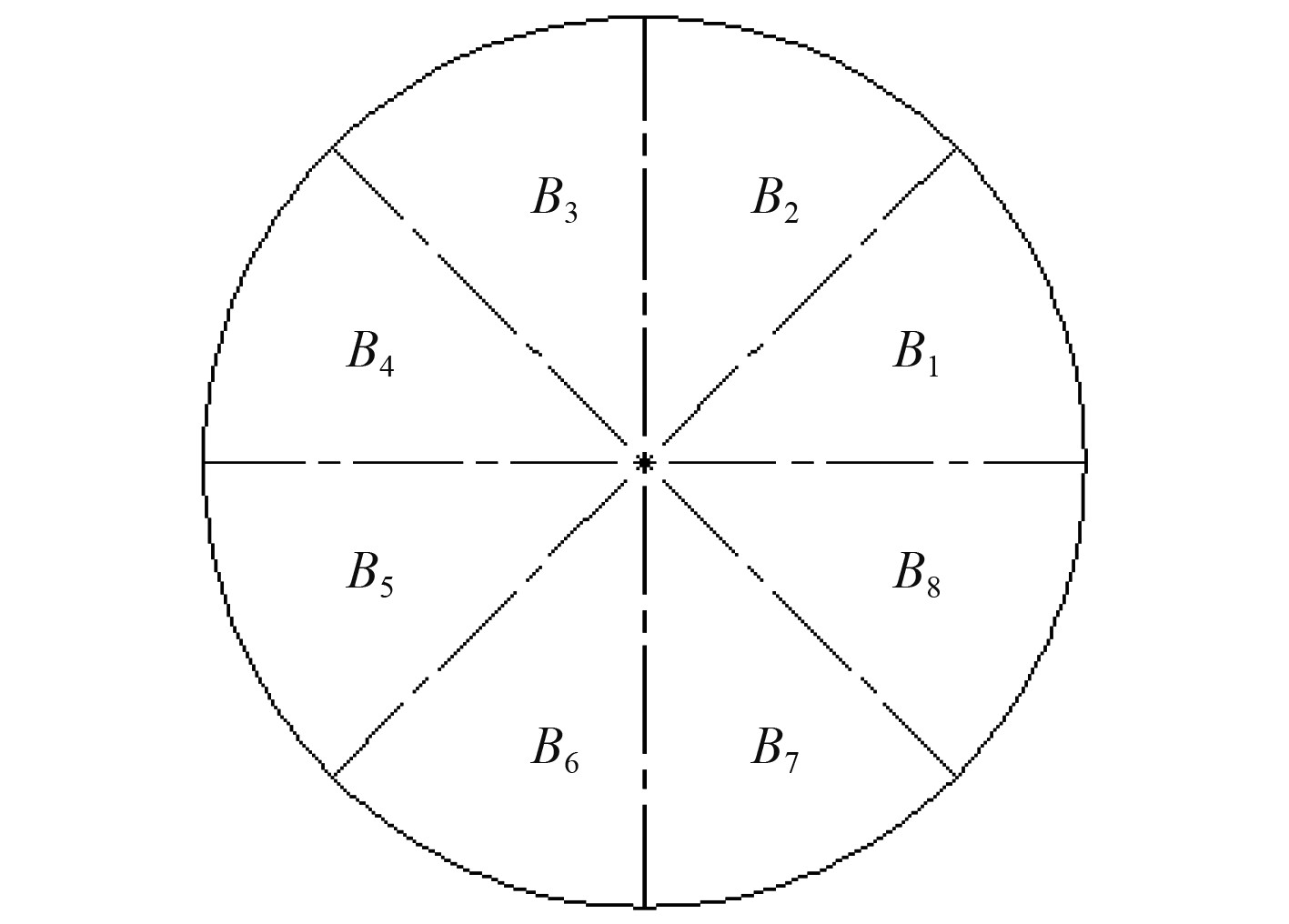
将所有待选测点划分成相互独立的均匀子集,子集数量与测点数量保持一致。并且可根据结构形状选择合适的子集划分方式,针对本文中的单层圆柱壳结构,可沿轴向和周向进行划分,图1所示将圆柱壳沿轴向分成了4个子集,图2所示将圆柱壳沿周向分成了8个子集,子集的表示方式为
|
图 1 沿轴向划分子集示意图 Fig. 1 The axial subset |
|
图 2 沿周向划分子集示意图 Fig. 2 The circumferential subset |
2)测点选取
从每个子集中随机选择一个测点形成测点组合,并且引入循环策略,循环选择的次数应足够多,以保证能够大概率的选到子集中每一个待选测点。
3)目标函数设定
由于每个测点均是从对应子集中随机选取,所以通过设定目标函数,对选取的测点组合进行评判。可根据实际情况设定合适的目标函数,本文将测点组模态矩阵的MAC值[9-10]作为目标函数,如下式:
| $MA{C_{ij}} = \frac{{{{({\phi _i}^{\rm{T}}{\phi _j})}^2}}}{{{\phi _i}^{\rm{T}}{\phi _i}{\phi _j}^{\rm{T}}{\phi _j}}}\text{。}$ | (11) |
式中:
本文通过计算不同测点组的模态矩阵MAC值,从而选择MAC值最小的测点组,再对水下单层圆柱壳结构的振动声辐射进行预报,以验证本文方法的准确性。
1.3 振动声辐射预报基本理论假设模态阶数为
| ${\left[ V \right]_{n \times 1}} = {\left[ \varPhi \right]_{n \times N}}{\left[ q \right]_{N \times 1}}\text{,}$ | (12) |
根据式(12),若测点数为
| ${\left[ V \right]_{M \times 1}} = {\left[ \varPhi \right]_{M \times N}}{\left[ q \right]_{N \times 1}}\text{,}$ | (13) |
已知测点振速
| ${p_a} = \left[ {ATV} \right] \cdot \left[ V \right]\text{。}$ | (14) |
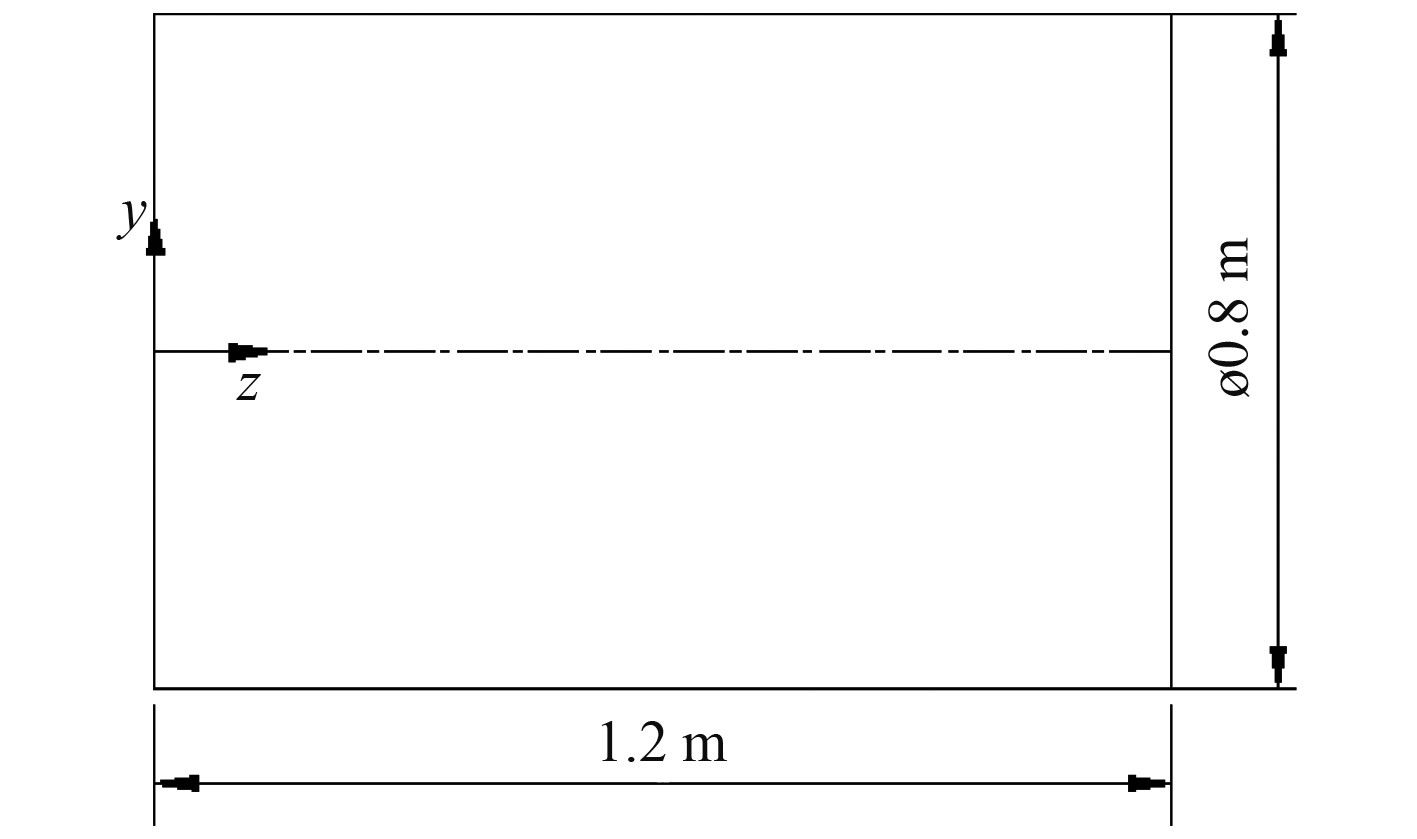
本文中的单层圆柱壳结构相关参数如下:
总长
|
图 3 结构尺寸示意图 Fig. 3 The structure size |
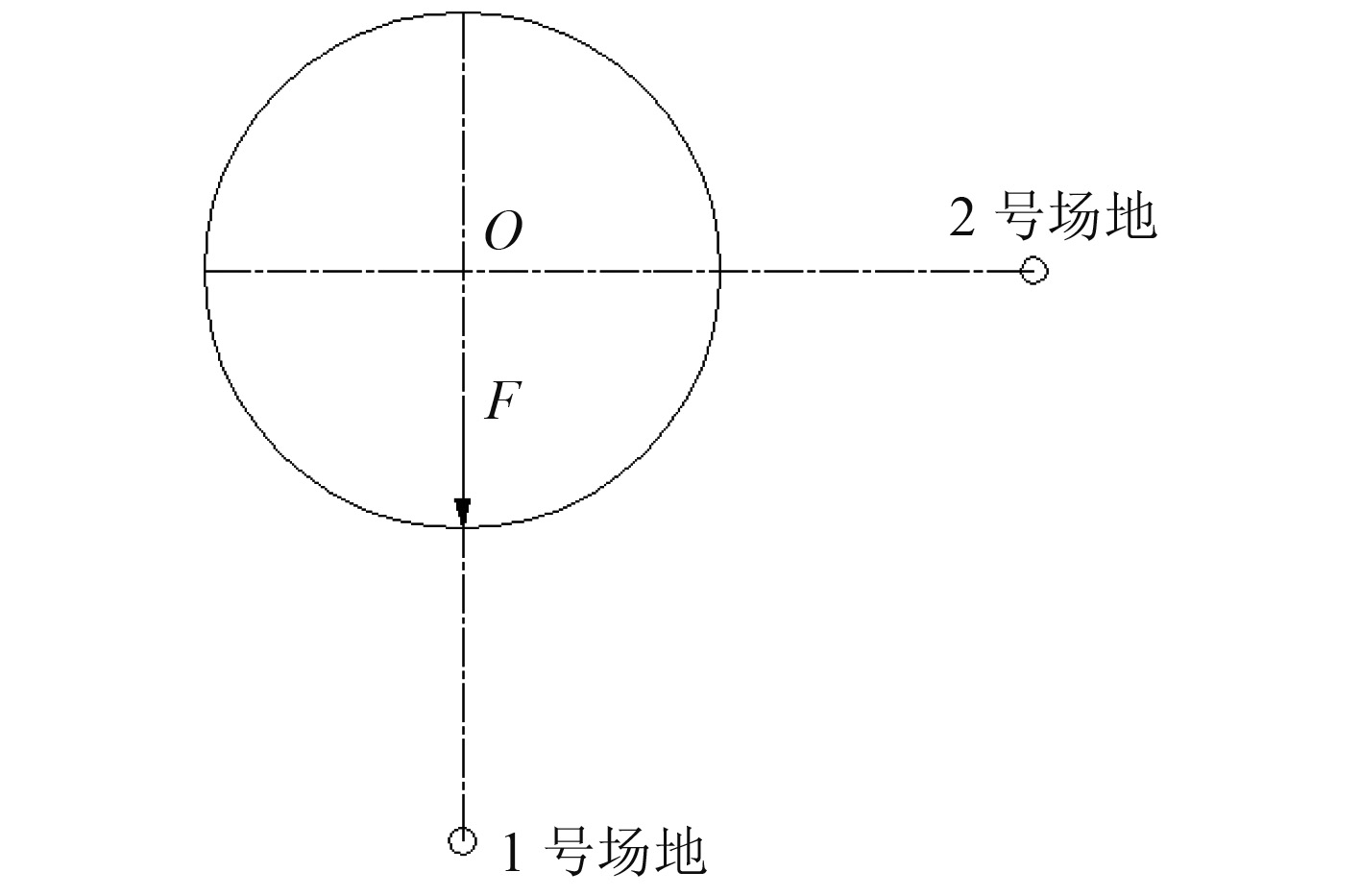
对结构两端面上的节点约束横向和垂向位移,在结构中间正下方作用一垂向单位力。同时在距离结构100 m处,与激励力相同方向和垂直方向分别布置1个声压场点,如图4所示。
|
图 4 声压场点位置示意图 Fig. 4 The sound pressure field point |
采用Ansys软件对结构进行有限元建模,在轴向和周向分别划分24和48个网格,频率分析范围由2~1000 Hz,间隔2 Hz。有限元模型如图5所示。
|
图 5 结构有限元模型 Fig. 5 The structural finite element model |
根据上述理论分析,结合有限元软件,可得到结构的模态分析结果如表1所示。
|
|
表 1 固有频率换算表 Tab.1 Natural frequency conversion table |
根据上表分析结果,第47阶空气振动模态对应的水中频率已达1000 Hz以上。为了避免频率范围内的模态遗漏,本文选取了空气中前100阶模态进行分析。
2.3 振动声辐射预报为验证本文方法的准确性,开展对比分析。
1)均匀测点布置
目前,均匀测点布置方法在圆柱壳结构振动采样中应用最为广泛,所以,本文先针对这种方法预报结构振动声辐射开展分析研究。
根据上述建模情况,模型总的节点数目为1200,去除边界节点,其余均可作为待选测点,共计1104个待选测点。按照测点布置的疏密程度不同,本文设计了以下3种方案:方案1的测点总数为264,其中轴向11排,周向24列,测点布置较为密集;方案2相比方案1,将轴向测点减为6排,周向测点不变,测点总数144;方案3相比方案2,轴向测点不变,将周向测点减为12列,测点总数72。
|
|
表 2 三种均匀布置方案对比 Tab.2 Comparison of three uniform layout schemes |
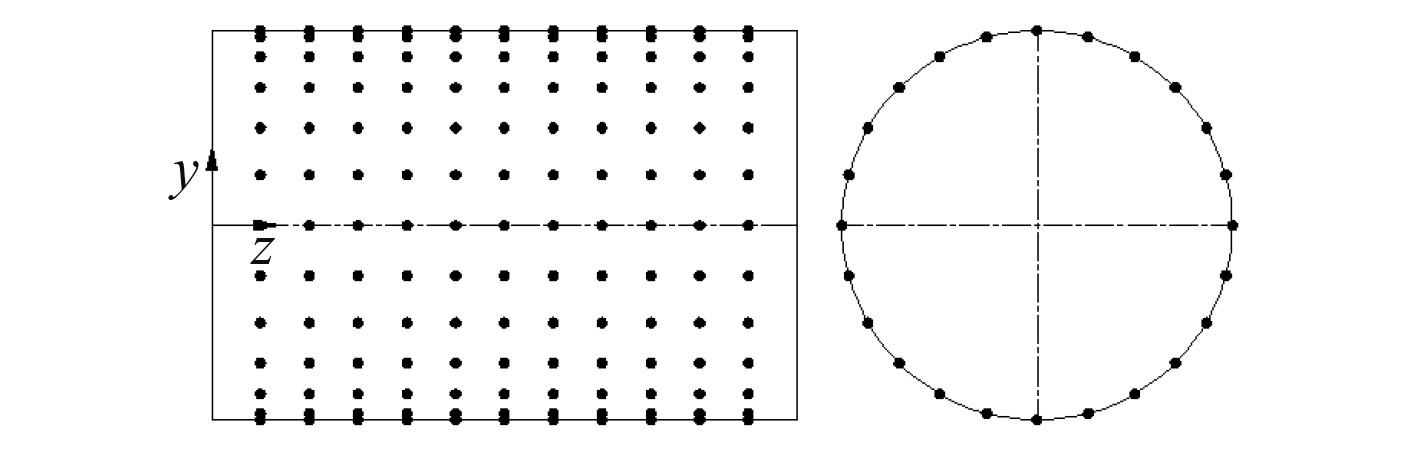
|
图 6 均匀布置方案1 Fig. 6 The first uniform layout scheme |
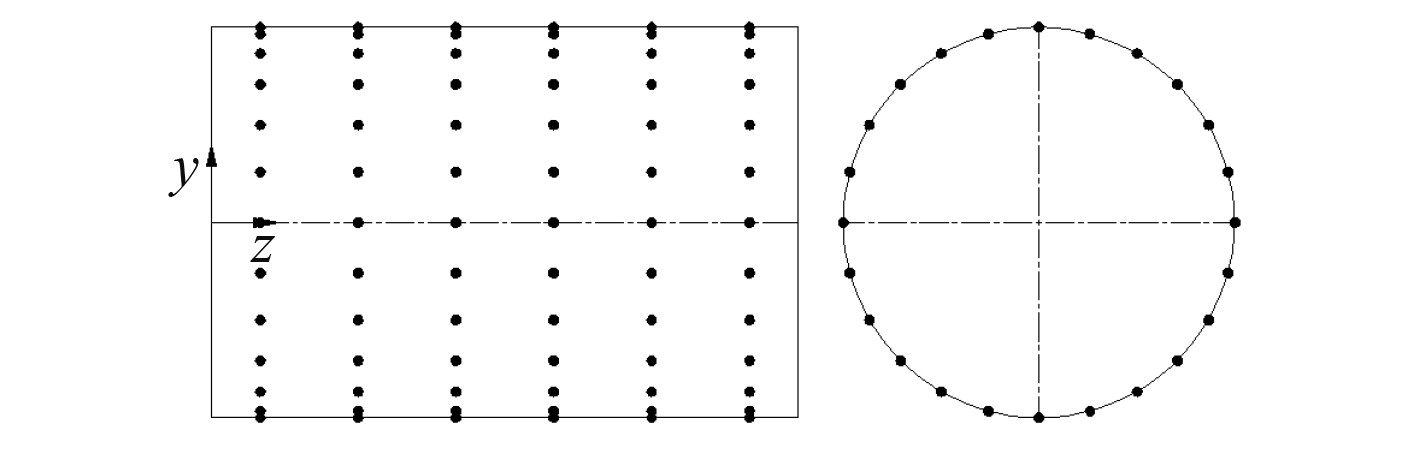
|
图 7 均匀布置方案2 Fig. 7 The second uniform layout scheme |
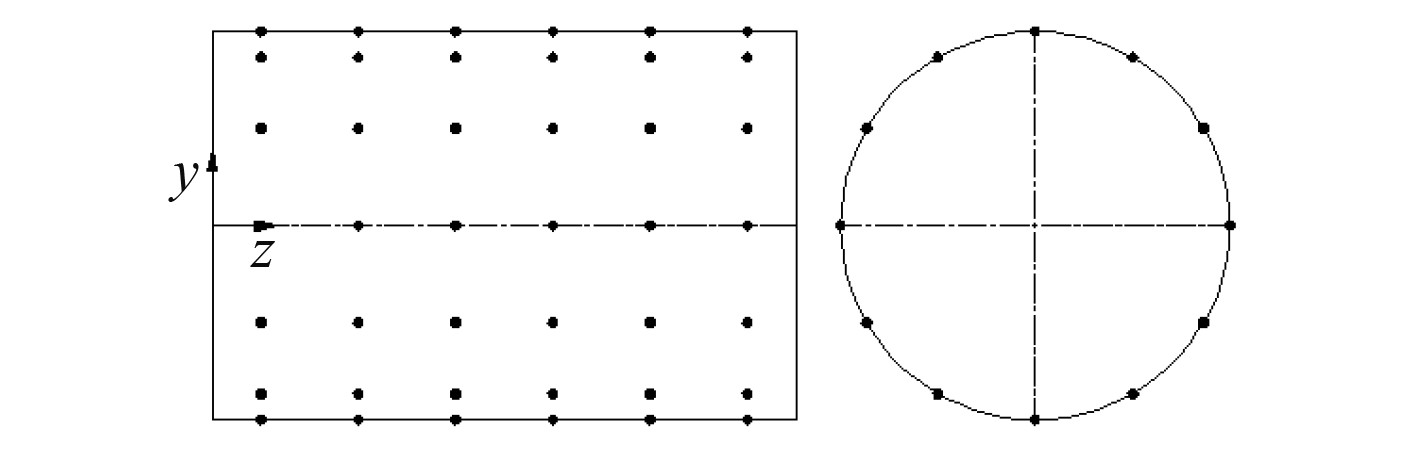
|
图 8 均匀布置方案3 Fig. 8 The third uniform layout scheme |
根据截断的前100阶空气中模态、及上述3种均匀测点布置方案,通过式(13)对结构表面振速场进行重构。其中方案1和方案2的测点数目
|
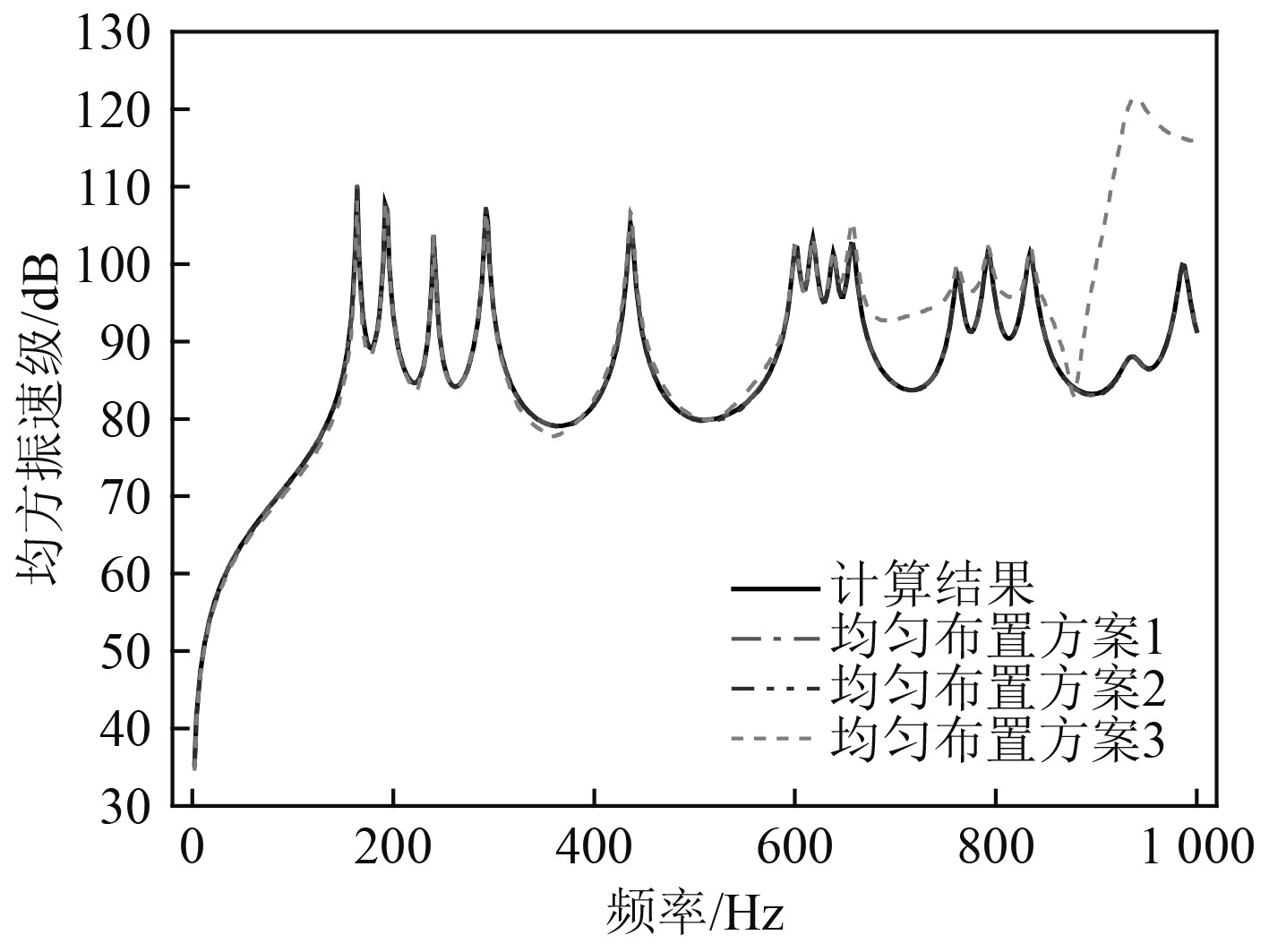
图 9 均方振速对比结果 Fig. 9 The change curve of square vibration velocity |
|
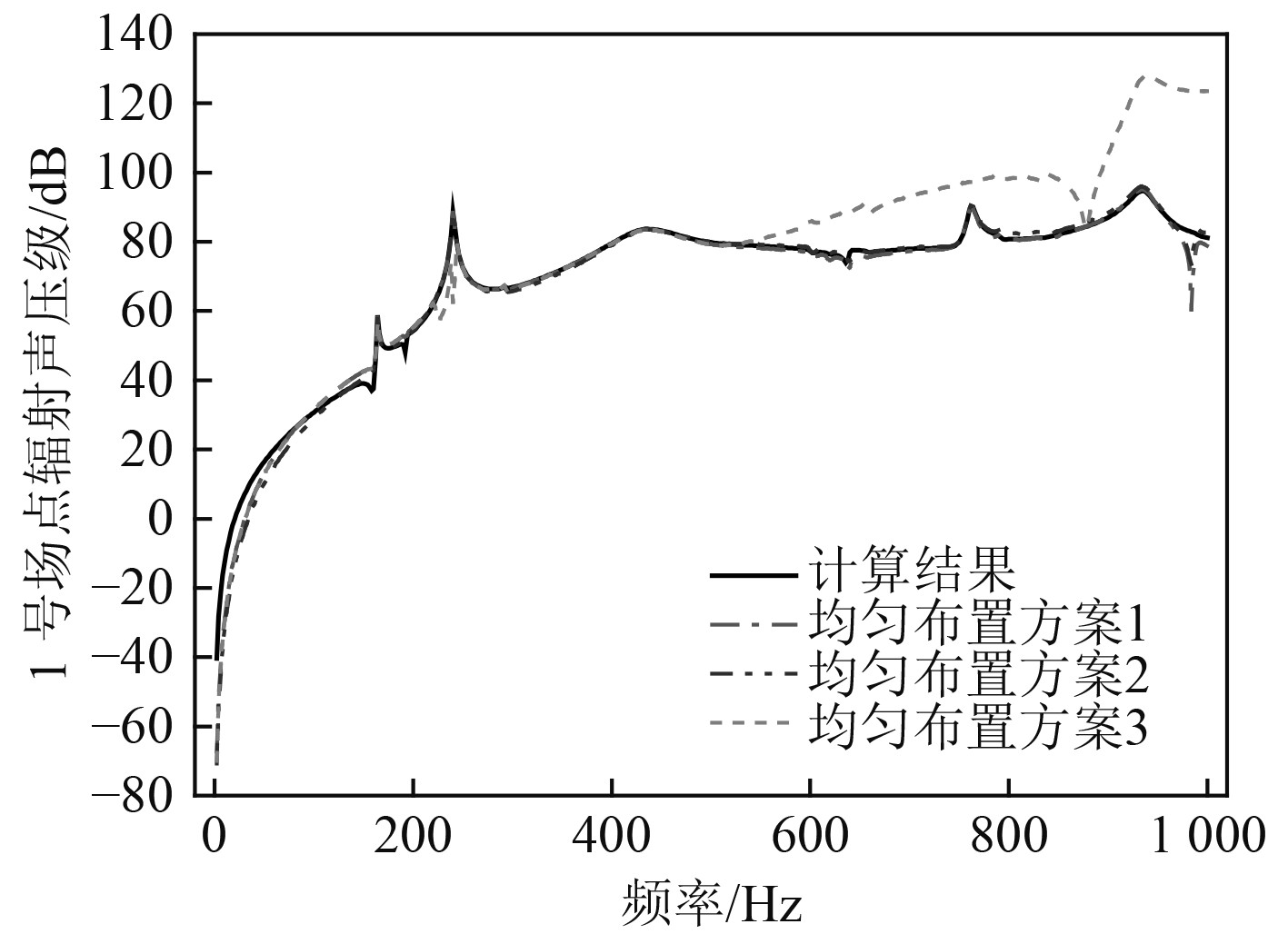
图 10 1号场点辐射声压对比结果 Fig. 10 The radiated sound pressure of field point No.1 |
|
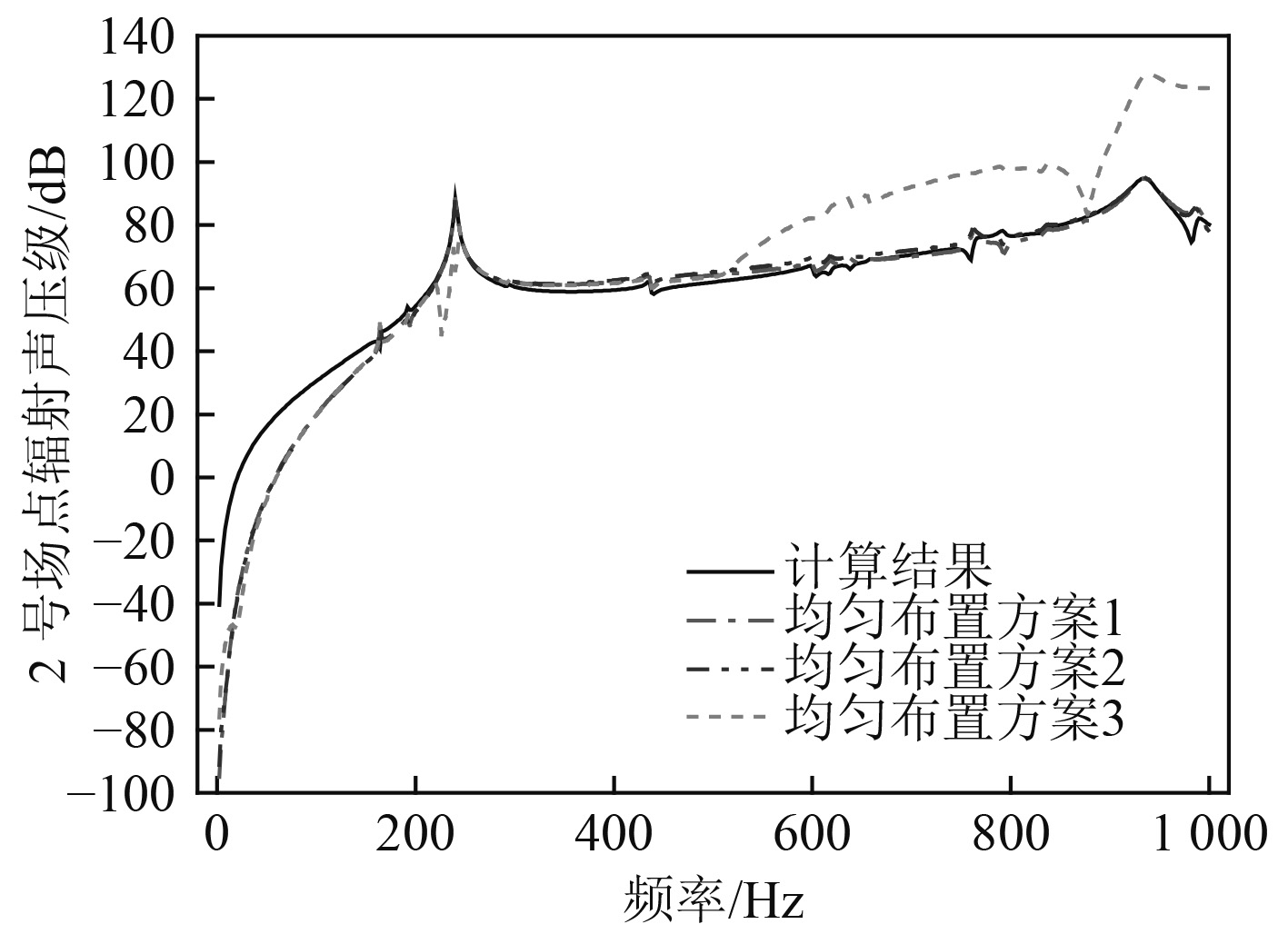
图 11 2号场点辐射声压对比结果 Fig. 11 The radiated sound pressure of field point No.2 |
通过对比上述结果可知,在分析频段内,方案1和方案2的预报结果精度更高,且方案2的预报结果已基本达到收敛,但方案3的预报结果精度明显降低。
2)均匀子集随机选取测点布置
根据上述理论分析,该方法将所有待选测点分成相互独立的均匀子集,子集数量与测点数量保持一致,从每个子集中随机选择一个测点形成测点组合,再通过目标函数对每种测点组合进行评价,从而选择出好的测点布置方案。
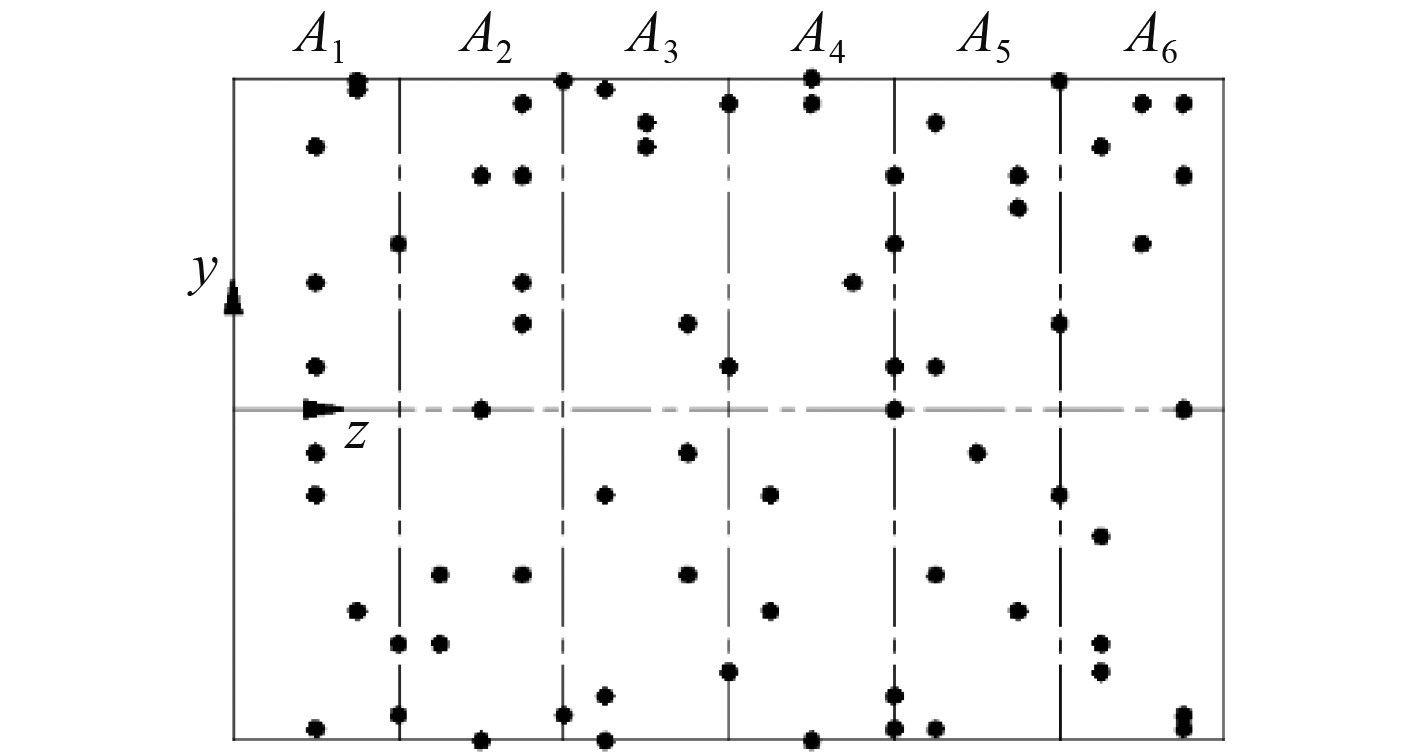
以上述方案3为参照,对应其测点布置方案,本文将结构沿周向划分了12个子集,轴向划分了6个子集,划分的子集总数为72个,如图12和图13所示。在循环策略中,为了尽可能选到每一个待选测点,本文将循环次数定为单个子集中待选测点数目的10倍,考虑单个子集中最多有16个待选测点,相应需进行160次循环操作。再根据式(11)中设定的目标函数,当目标函数MAC值为0.1461时达到最小,其对应的测点布置方案如图12和图13所示。利用该组测点对结构振动声辐射进行预报,得到的预报结果与均匀布置方法对比曲线如图14~图16所示。
|
图 12 轴向测点分布示意图 Fig. 12 The axial measuring point distribution |
|
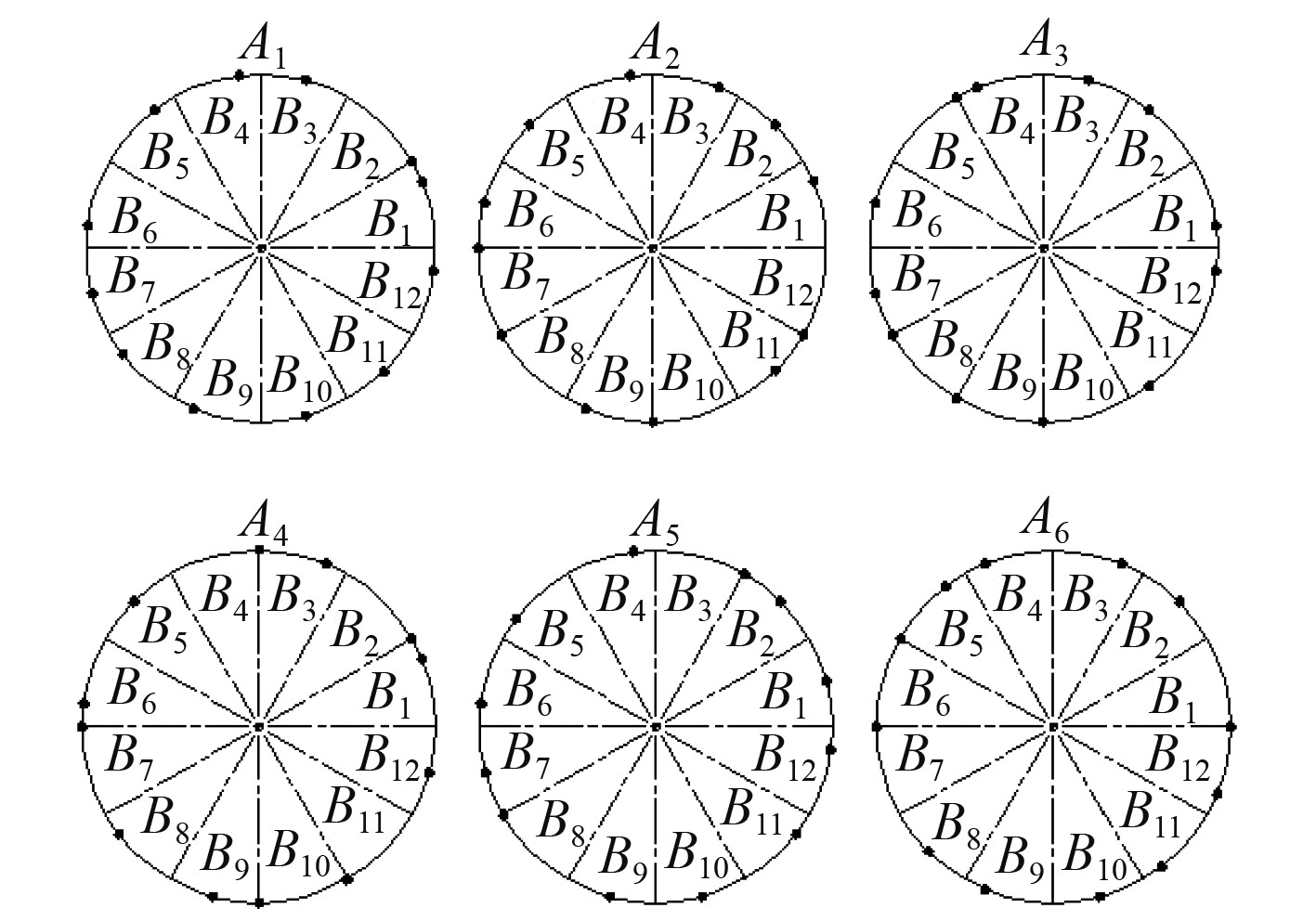
图 13 周向测点分布示意图 Fig. 13 The circumferential measuring point distribution |
|
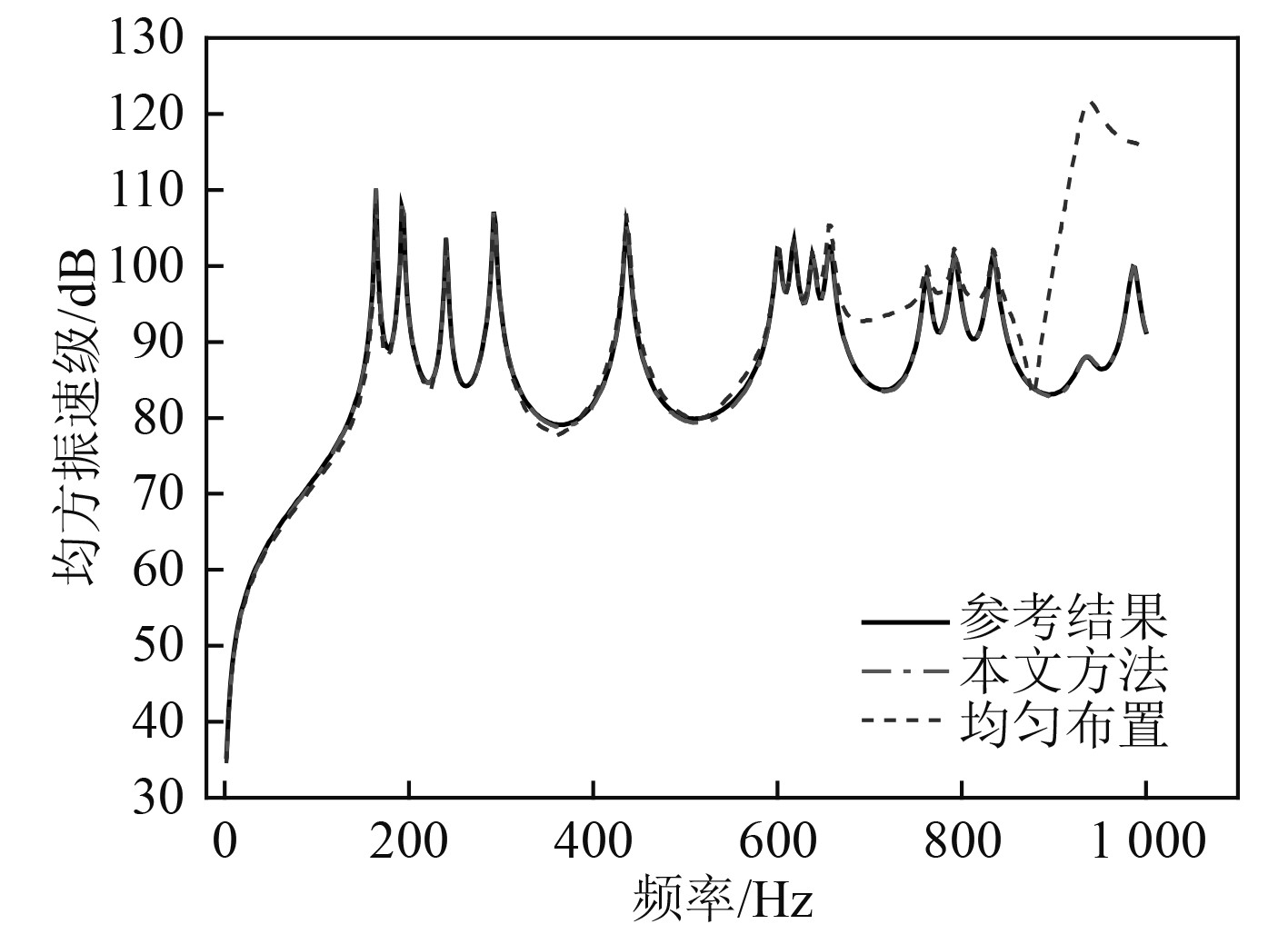
图 14 均方振速对比结果 Fig. 14 The change curve of square vibration velocity |
|
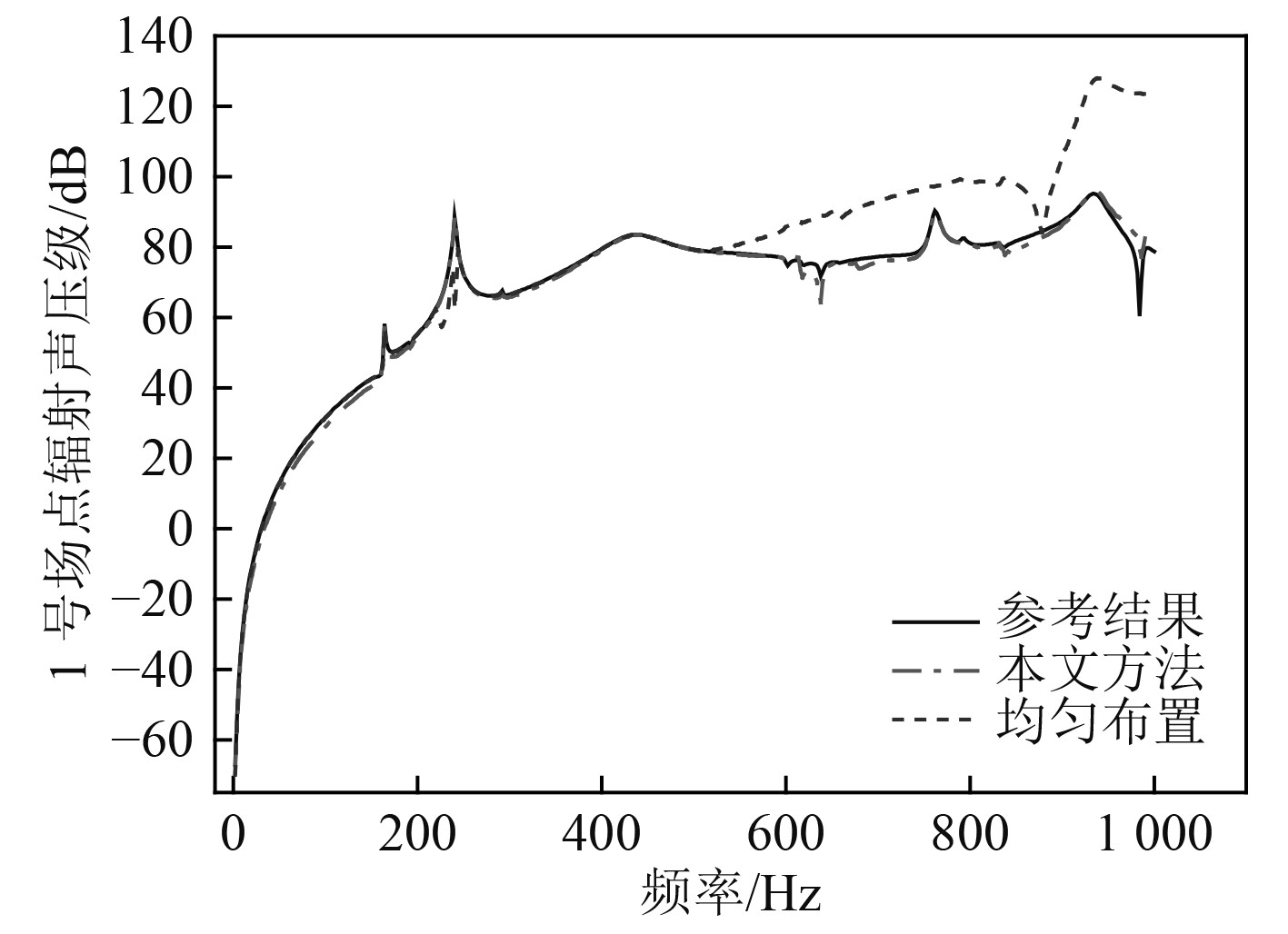
图 15 1号场点辐射声压对比结果 Fig. 15 The radiated sound pressure of field point No.1 |

|
图 16 2号场点辐射声压对比结果 Fig. 16 The radiated sound pressure of field point No.2 |
由图12和图13可知,本文通过划分子集的方式选取测点,使得测点能够覆盖曲面且分布相对均匀。通过设定目标函数MAC值,可保证能够选取到模态向量空间夹角小的测点组合,对应的模态振型更易辨识。最后通过图14~图16中的振动声辐射预报结果对比曲线可知,当其他因素(如分析频段、测点数目、模态截断数目等)相同时,相比均匀测点布置方法,均匀子集随机选取测点方法能够更准确地进行振动声辐射预报,且能与参考结果吻合较好。
3 结 语通过上述分析,可得到以下结论:
1)均匀子集随机选取测点方法测点覆盖曲面、分布均匀,并且测点选取不存在主观性和盲目性。
2)本文以测点组模态矩阵的MAC值作为目标函数,可保证测点组的模态向量间的空间夹角较小,其模态振型相应较易识别。
3)通过数值分析,当分析频段、测点数目、模态截断数目等相同时,该方法对结构振动声辐射预报结果的精度比均匀布置方法更高。
| [1] |
LI T Y, MIAO Y Y, YE W B, et al. Far-field sound radiation of a submerged cylindrical shell at finite depth from the free surface[J]. Journal of the Acoustical Society of America, 2014, 136(3): 1054. DOI:10.1121/1.4890638 |
| [2] |
钱治文, 何元安, 等. 三维浅海下圆柱壳声辐射预报方法研究[J]. 船舶力学, 2019, 23(10): 1266-1276. DOI:10.3969/j.issn.1007-7294.2019.10.013 |
| [3] |
陶襄樊, 陈美霞, 魏建辉. 欠定盲分离方法预报水下双层加筋圆柱壳辐射声场[J]. 舰船科学技术, 2012, 34(11): 8-13. DOI:10.3404/j.issn.1672-7649.2012.11.002 |
| [4] |
阮竹青, 彭伟才. 基于表面响应预报水下圆柱壳声辐射的振动测点布置研究[J]. 中国舰船研究, 2013, 8(1): 80-83. |
| [5] |
王斌, 汤渭霖. 基于辐射声场预报的圆柱壳表面空间采样研究[J]. 船舶力学, 2010, 14(6): 690-698. DOI:10.3969/j.issn.1007-7294.2010.06.013 |
| [6] |
和卫平, 陈美霞. 基于有限测点的单层圆柱壳辐射声功率计算[J]. 船舶力学, 2012, 16(10): 1240-1211. |
| [7] |
叶珍霞, 杜堃. 基于L1范数最小化的水下圆柱壳振动声辐射预报[J]. 中国舰船研究, 2015, 10(3): 70-76. DOI:10.3969/j.issn.1673-3185.2015.03.012 |
| [8] |
HOLLAND J H. Adaptation in natural and artificial system: An introductory analysis with applications to biology, Control and Artificial Intelligence[M]. U Michigan Press, 1975: 123−125.
|
| [9] |
THOMAS G Came, CLARK R Dohmann. A modal test design strategy for modal correlation[C]//Proceedings of 13th International Modal Analysis Conference, New York Union College, 1995: 927−993.
|
| [10] |
BREITFELD T. A method for identification of a set of optimal measurement points for experimental modal analysis[J]. Journal of Analytical and Experimental Modal Analysis, 1996, 11: 254-273. |
 2021, Vol. 43
2021, Vol. 43
