2. 武汉理工大学 交通学院,湖北 武汉 430063
2. Wuhan University of Technology, School of Transportation, Wuhan 430063, China
传统的浮筏隔振系统是将多台设备弹性安装在一个公共筏架上,筏架与基座之间通过下层隔振器弹性连接。浮筏隔振系统能大幅减小动力机械振动和噪声,并能提高设备工作的稳定性。而随着浮筏的大型化、新型化以及其本身的隔振抗冲击性能提高,浮筏结构也被应用于整个舱段,形成舱筏。舱筏主要用作船体的重要舱室,起到保护重要设备和人员的目的[1]。当前的传统板梁形式的筏体结构已无法满足舱筏日益增长的性能需求。对于新型结构形式的浮筏需求也迫在眉睫。本文结合桁架结构能够充分发挥材料强度、节约建造成本等优点,将其应用于传统浮筏,形成可用于舱筏的一种新型桁架箱体浮筏结构。新型桁架箱体舱筏由于其尺寸较大,会面临过多占用总体重量和空间的矛盾。因此,为了降低浮筏隔振装置重量和空间尺寸,对舱筏进行重量优化设计研究具有重要意义。
对于浮筏结构的优化设计,国内外在该方向都有很多研究[2-6],文献[7]结合灵敏度分析结果,对浮筏有限元模型进行多目标优化分析,优化了筏架结构的结构参数,改善了浮筏隔振系统性能,提高了隔振效果;文献[8]研究表明,常规减振动力学优化设计模型存在明显缺陷,应同时考虑振级落差和功率流约束的综合结构优化模型,能获得较好的优化设计效果;文献[9-10]运用优化理论对筏体结构进行了拓扑优化,优化后的模型经过修正,重新建立模型,比较了优化前后筏体的隔振特性,为筏体结构设计提供了依据。
本文的新型浮筏结构由于用途与结构形式的特殊性,拓扑优化的适用性较低。故根据箱体浮筏结构本身的特点,在有限元软件Abaqus中建立桁架箱体浮筏有限元模型,基于模态分析,重力场分析和抗冲击分析,以筏架上、下面板厚度为设计变量,分析面板厚度变化对结构刚度及强度水平的影响,对浮筏结构刚度水平及强度水平进行分析,且在保证足够刚度和强度水平的前提下对浮筏进行重量优化研究。
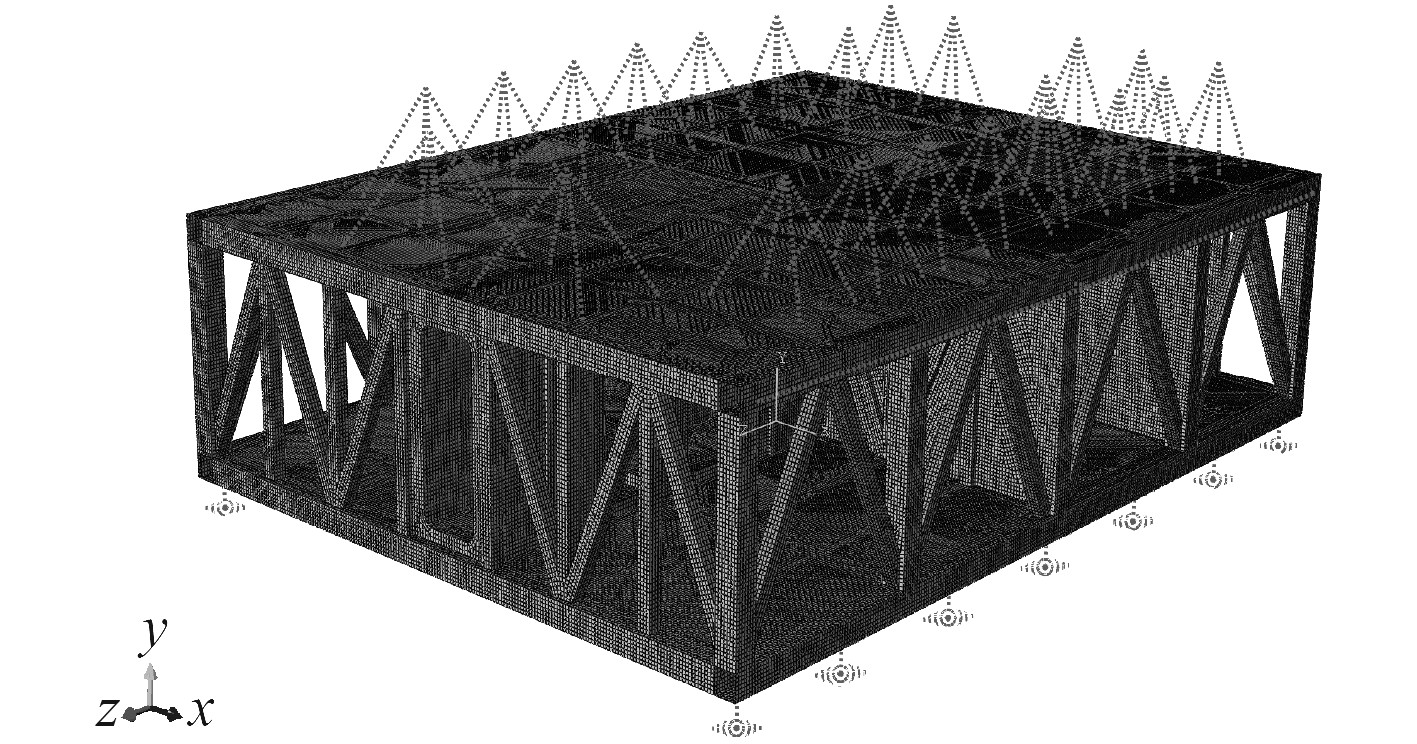
1 桁架箱体浮筏模型分析 1.1 模型建立本文初步设计的桁架式舱段浮筏结构长8 m、宽6.08 m,高2.1 m,桁架结构由上下面板、底板以及中部相互交错的桁架支撑结构组成,其上、下面板的设计初始厚度为20 mm,重量为17.65 t,占筏架总重量比例为58.9%(筏架重29.95 t)。结构材料选取为Q345钢,材料密度为7.85×103kg/m3,弹性模量E=2.06×1011 N/m2,泊松比σ=0.3。对浮筏系统进行1∶1实体建模,模型的坐标系方向为:Z轴正向指向艇体纵向首部,Y轴正向为铅垂向上,X轴正向指向艇体右舷。坐标原点设在筏架下面板几何中心。筏架主要用板单元来进行建模。由于筏架上的设备和人员的重量以及尺度与筏架本身相比要小的多,故采用重量点的方式来模拟设备和人员。上层隔振器采用BE85线性隔振器安装在上层设备的下端,中层隔振器采用KB-1500非线性隔振器安装在筏架舱壁上(左右两侧各3个),下层隔振器采用KB-3000非线性隔振器安装在筏架底部(左右两侧各7个),建模时采用创建Wire Feature的方式模拟上、中、下层隔振器,设备与上层隔振器之间采用MPC(Multi-point constraint,多点约束)进行连接。建立的桁架浮筏结构有限元模型如图1所示。
|
图 1 浮筏有限元模型 Fig. 1 Floating raft finite element model |
对于初步设计的桁架箱体浮筏,在重力场和冲击环境下需具备足够的强度水平。静载荷下强度分析时,考虑设备、人员和筏架自身的重量,对模型施加重力场进行计算分析(重力加速度G=9810 mm/s2)。
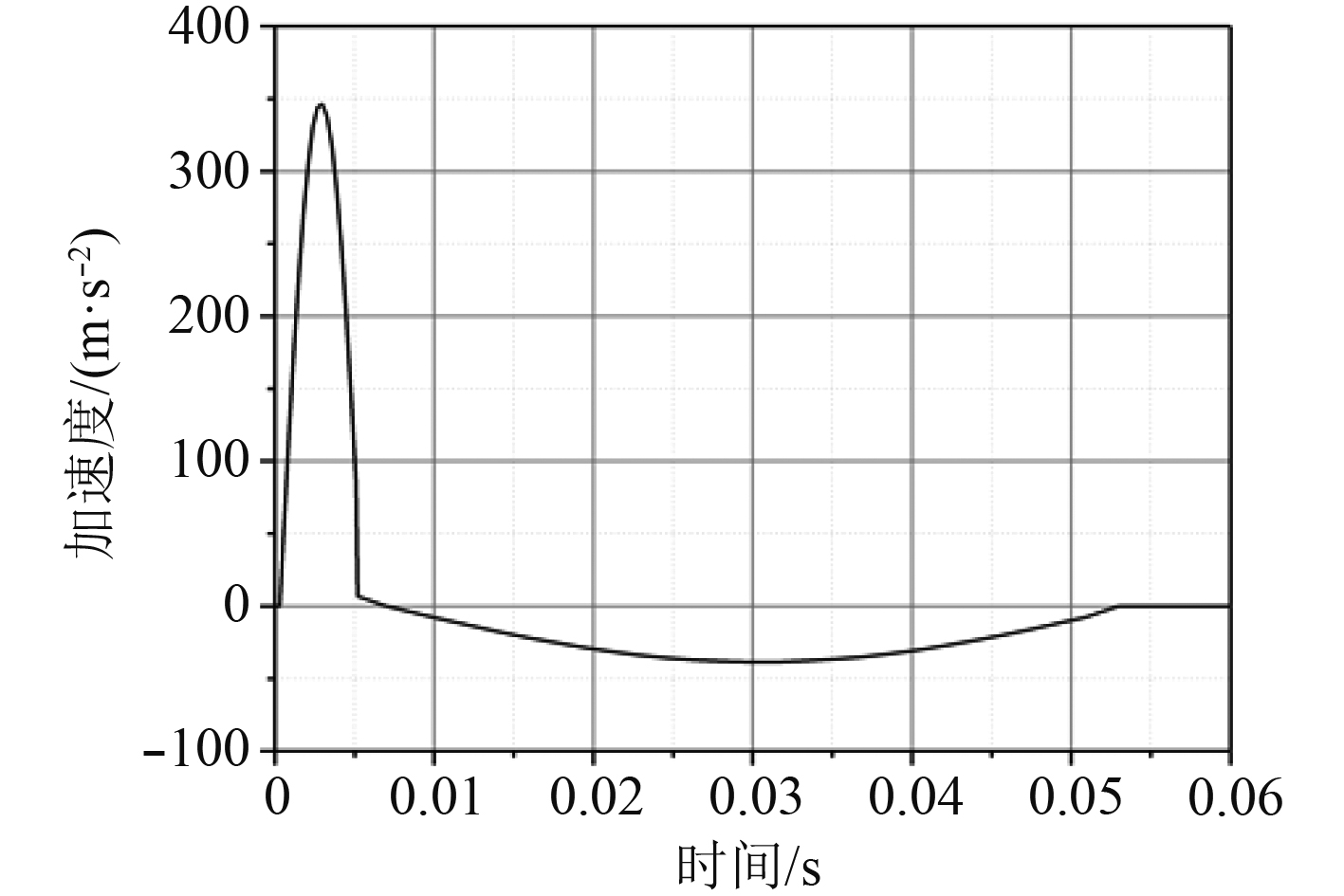
对于冲击动载荷,本文选取GJB1060.1-91[11]中冲击设计输入,根据德国BV043-85标准将浮筏隔振系统的设计冲击响应关于频率的冲击谱等效转化为系统的冲击载荷-时间变化曲线[12]。将设计冲击谱转换成正反半正弦波冲击信号,正反半正弦冲信号的典型波形图如图2所示。
|
图 2 冲击加速度时域曲线 Fig. 2 Impact acceleration time domain curve |
桁架箱体浮筏结构主要由上下面板以及相互交错的桁架支撑结构组成。同时,箱体浮筏的筏架部分作为船体的重要舱室,上、下面板要考虑人员及各种中小型设备,需保留完整的上、下面板,而无法采用常规的拓扑优化分析[9]。由于初始设计的筏架上、下面板的重量占整体筏架总重量的比重较大(58.9%)。因此,可分析上、下面板的厚度变化对筏架结构刚度以及强度的影响,并通过减小板厚对筏架整体结构的重量进行优化,设计工况选取如表1所示。
|
|
表 1 设计工况 Tab.1 Design conditions |
对不同工况下的筏架结构本身进行自由边界条件下的模态分析,分析时去掉设备、人员和上、下层隔振器。工况1前3阶模态振型如图3~图5所示。

|
图 3 第1阶模态振型(41.44 Hz) Fig. 3 First-order mode shape (41.44 Hz) |

|
图 5 第3阶模态振型(68.83 Hz) Fig. 5 Third-order mode shape (68.83 Hz) |

|
图 4 第2阶模态振型(53.46 Hz) Fig. 4 Second-order mode shape (53.46 Hz) |
由于筏架本身为弹性结构,基于固有频率,可由下式得到整体筏架的等效刚度:
| $ K={\left(2\text{π} {f}_{n1}\right)}^{2}M\text{。}$ | (1) |
式中:
|
|
表 2 一阶固有频率、等效刚度计算结果 Tab.2 First-order natural frequency and equivalent stiffness calculation results |
|
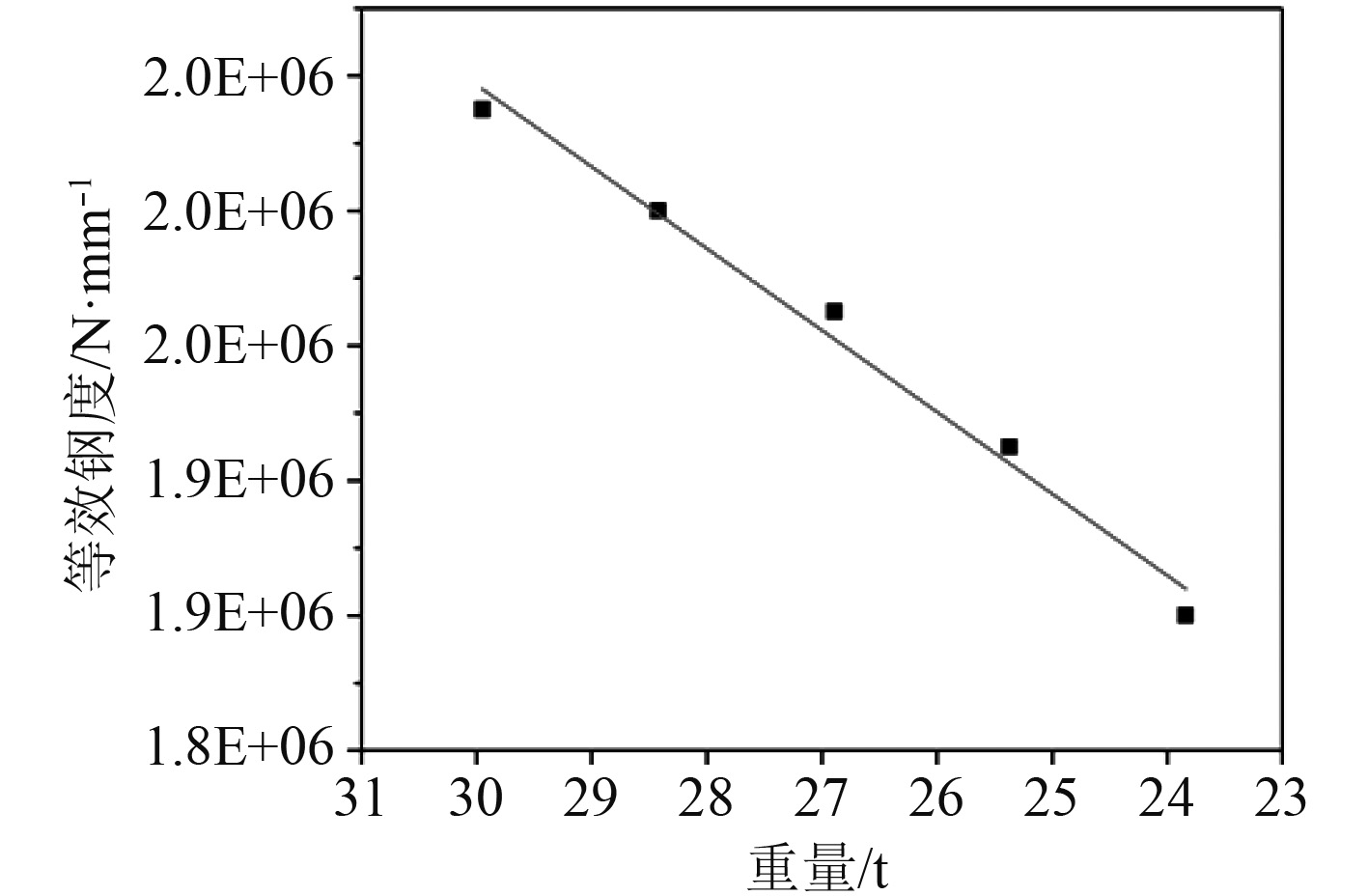
图 6 浮筏等效刚度-重量曲线 Fig. 6 Floating raft equivalent stiffness-weight curve |
| $ K=-24229t+1.31\times {10}^{6}\text{。}$ | (2) |
另外,当面板厚度从20 mm(29.95 t)减小到12 mm(23.84 t)时,重量减小20.4%,而刚度仅减小7.3%。说明在重量优化过程中(板厚减小),总刚度水平没有明显的减弱。基于刚度水平的分析,在浮筏结构刚度水平有一定余量的基础上,减小上下面板板厚是一种有效的重量优化方法。
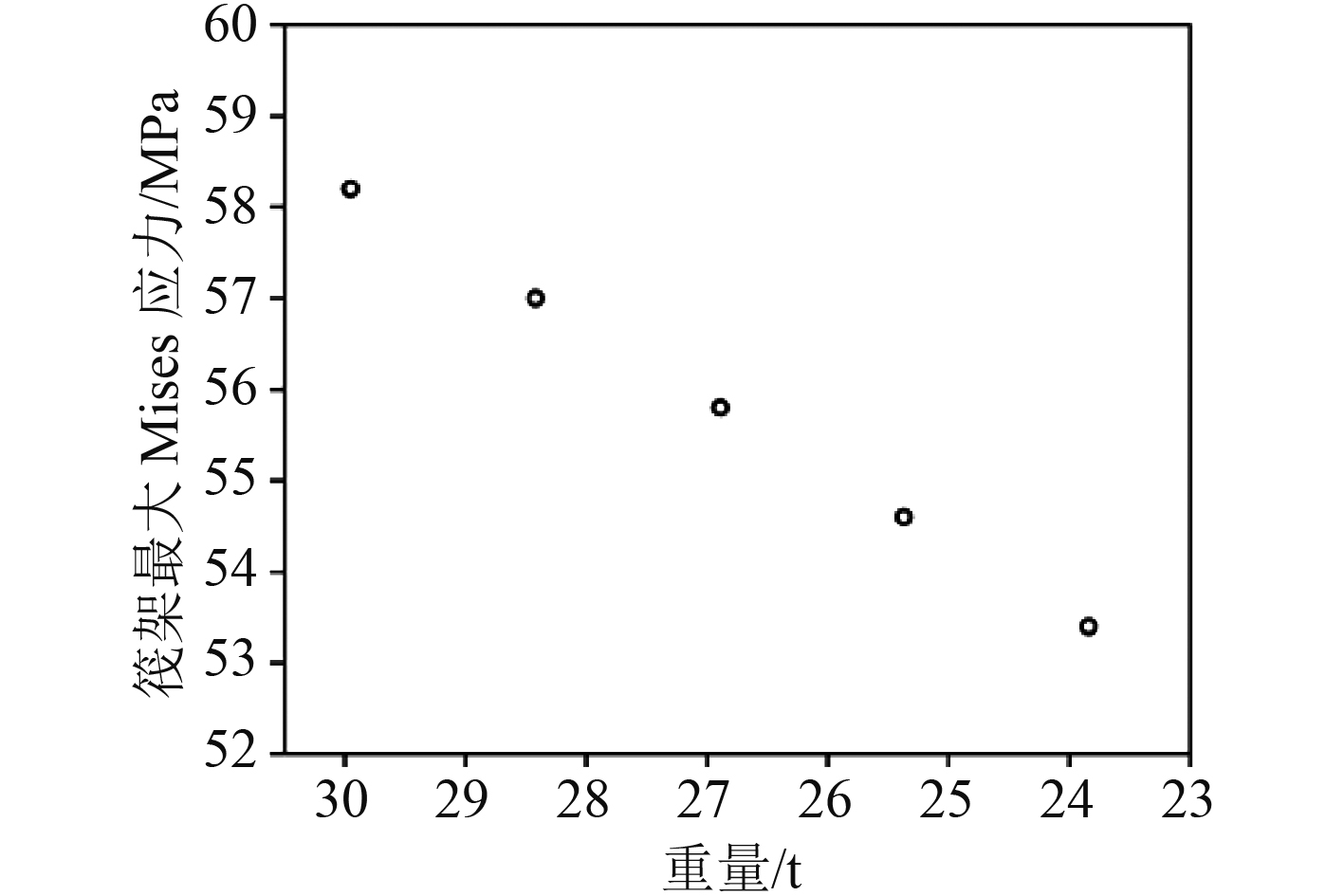
3 基于强度水平重量优化分析根据2.2节,将有限元模型置于重力场中进行静强度分析。将边界约束施加在筏架下底板两侧,限制其在6个方向上的自由度。不同工况下的计算结果如表3所示,筏架最大应力-重量图如图7所示。随着板厚的减小,筏架最大位移变化不大。工况1的最大Mises应力最大,仅为58.2 MPa, 远小于材料的屈服极限350 MPa。最大Mises应力随板厚减小逐渐减小,这是因为面板厚度减小会降低筏架自身重力,使得筏架上下面板之间支撑结构承受的压力减小,且由第3节的分析可知,刚度水平随面板厚度减小只有微弱的降低,从而造成应力减小。从重力场的静强度分析可知,各种工况的强度都满足要求,可减小上、下面板厚度对重量进行优化。
|
|
表 3 浮筏重力场下计算结果 Tab.3 Calculation result of floating raft in gravity field |
|
图 7 重力场下筏架最大应力-重量图 Fig. 7 Maximum stress-weight diagram of a raft in a gravity field |
分析不同工况的筏架结构在垂向冲击载荷下的结构强度,冲击载荷输入曲线如图2所示。在满足冲击载荷设计要求的同时,对结构进行轻量化设计。具体做法为将垂向冲击载荷加载在下层隔振器下端和中层隔振器外端,计算时间设置为1 s。同时,为增强分析对比度,增设工况6,即筏架上、下面板厚度为10 mm,重量为22.31 t。
不同工况的结果如表4所示。随着上、下面板厚度的减小,筏架结构最大Mises应力总体上呈现减小趋势,但变化不大,且均小于材料许用应力350 MPa。由于筏架作为重要舱室,内有各种中小型设备与人员,因此将上、下面板峰值加速度纳入考核标准是十分必要的。由表4可知,上、下面板峰值加速度随着板厚的减小而逐渐增大,即上下面板上人员和受到的加速度冲击增大。当上下面板厚度为10 mm(工况6)时,上、下面板峰值加速度为13.5 g,超过了人体可承受的最大冲击加速度(约为12 g)。因此,工况五为最优方案,即当上、下面板厚度为12 mm时,桁架式浮筏结构在垂向冲击环境下,满足设计要求,且重量最轻。
|
|
表 4 浮筏冲击载荷下计算结果 Tab.4 Calculation results under floating raft impact load |
本文结合桁架结构的优点,将桁架结构应用于传统浮筏形成一种新型桁架箱体浮筏结构,并基于新型桁架浮筏结构特点,对其重量进行优化研究,得出以下主要结论:
1)当上、下面板厚度减小时,浮筏筏架等效刚度随之减小,呈线性相关。且面板厚度减小使筏架重量明显降低(20.4%)的情况下,筏架等效刚度只是轻微减弱(7.3%)。
2)在重力场下,当上、下面板厚度减小时,筏架结构最大位移较小且几乎保持不变,筏架最大应力逐渐降低。
3)在垂向冲击载荷下,当上、下面板厚度减小时,筏架结构最大应力总体上呈现减小趋势,但变化不大,且均小于材料许用应力350 MPa,而上下面板的最大加速度增大。
4)当上、下面板厚度为12 mm时(工况5)时为最优,总重量减重达15.4%。
| [1] |
黄修长. 舱筏隔振系统声学设计及优化、控制[D]. 上海: 上海交通大学, 2011.
|
| [2] |
BONDARYK J E, DYER I, CHIASSON L, et al. Experimental measurements of vibrational energy and acoustic radiation for a 3-D truss[J]. The Journal of the Acoustical Society of America, 1995, 98(5): 2889. |
| [3] |
KOHRS T, PETERSSON B A T. Wave propagation in light weight profiles with truss-like cores: Wavenumber content, forced response and influence of periodicity perturbations[J]. Journal of Sound and Vibration, 2007, 304(3-5): 691-721. DOI:10.1016/j.jsv.2007.03.022 |
| [4] |
李志远, 彭子龙, 等. 浮筏筏体结构改进设计及隔振性能分析[J]. 噪声与振动控制, 2019, 39(5): 245-249. DOI:10.3969/j.issn.1006-1355.2019.05.046 |
| [5] |
刘军伟, 姜节胜. 桁架动力学形状优化的统一设计变量方法[J]. 振动工程学报, 2000(1): 88-92. |
| [6] |
魏燕定, 赖小波, 陈定中, 等. 两级振动隔振系统参数优化设计[J]. 浙江大学学报(工学版), 2006(5): 893-896. DOI:10.3785/j.issn.1008-973X.2006.05.034 |
| [7] |
张辉. 船舶浮筏隔振系统的性能分析及参数优化匹配研究[D]. 武汉: 华中科技大学, 2016.
|
| [8] |
陈静. 结构动力学优化设计模型研究[D]. 上海: 上海交通大学, 2011.
|
| [9] |
彭亮. 浮筏隔振系统的结构优化研究[D]. 武汉: 中国舰船研究院, 2015.
|
| [10] |
余林波. 浮筏隔振系统隔振特性与筏体拓扑优化研究[D], 武汉: 华中科技大学, 2007.
|
| [11] |
GJB1060.1-91, 舰船环境条件要求—机械环境[S]. 北京: 国防科学技术工业委员会, 1991.
|
| [12] |
刘林炜. 浮筏隔振系统静动态响应直接计算法研究[D]. 武汉: 华中科技大学, 2018.
|
 2021, Vol. 43
2021, Vol. 43
