2. 中国船舶科学研究中心,江苏无锡 214082;
3. 上海船舶设计院,上海 201203
2. China Ship Scientific Research Center, Wuxi 214082, China;
3. Shanghai Ship Design Institute, Shanghai 201203, China
随着深海领域的不断开发,深潜器的数量和尺寸随之增加,也使得大壁厚钢结构的焊接在深潜器建造过程中变得越来越重要。Ti80是一种高强度的钛合金,具有耐腐蚀和易于焊接等优质性能,因此被广泛用于深潜器的制造。在焊接过程中,由于不均匀的热循环,焊接接头不可避免地会产生焊接残余应力,这将导致一系列问题,例如强度降低和产生裂纹。因此,必须采取有效的措施来降低焊接残余应力。焊后热处理是减少焊接残余应力的常用方法[1],可以有效提高焊接结构的使用寿命和承载能力。
姜云禄等[2-3]对热处理后TC4钛合金试板表面焊接残余应力进行了测量。Yan等[4-5]对TC4板热处理前后表面焊接残余应力进行了数值模拟和实验验证。李有华等[6]采用X射线衍射法测定了TA15钛合金厚板热处理后残余应力值。金俊龙等[7]对TC17钛合金平板的焊接和焊后热处理的过程进行了数值模拟,研究了热处理前后残余应力演变情况。通过这些文献发现钛合金热处理后的残余应力显著降低,表面残余应力重新分布。
目前,对Ti80钛合金热处理前后残余应力的数值模拟研究较少。因此,本文对Ti80对接焊平板的焊接以及焊后热处理过程的残余应力进行数值模拟研究。
1 基本理论 1.1 焊接温度场对均匀、各向同性的连续介质,其材料特征与温度无关时,在能量守恒的基础上可以得到热传导微分方程为:
| ${\rm{c}}\rho \frac{{\partial T}}{{\partial {\rm{t}}}} = \lambda \left( {\frac{{{\partial ^2}T}}{{\partial {{\rm{x}}^2}}} + \frac{{{\partial ^2}T}}{{\partial {{\rm{y}}^2}}} + \frac{{{\partial ^2}T}}{{\partial {{\rm{z}}^2}}}} \right) + \frac{{\partial Q}}{{\partial {\rm{t}}}}\text{。}$ | (1) |
式中:T为温度场分布函数;λ为材料的热传导系数;t为传热时间;c为材料的质量比热容;ρ为材料的密度;Q为内热源强度。
1.2 焊接应力场焊接应力场弹塑性变形的根本原因是由于温度场的存在,焊接残余应力的本质是由于在焊接过程中产生了不可恢复的塑性变形,因此应力场的本构关系为:
| ${\rm d}\sigma = { D}{\rm d}\varepsilon - C{\rm d}{ T}\text{。}$ | (2) |
式中:
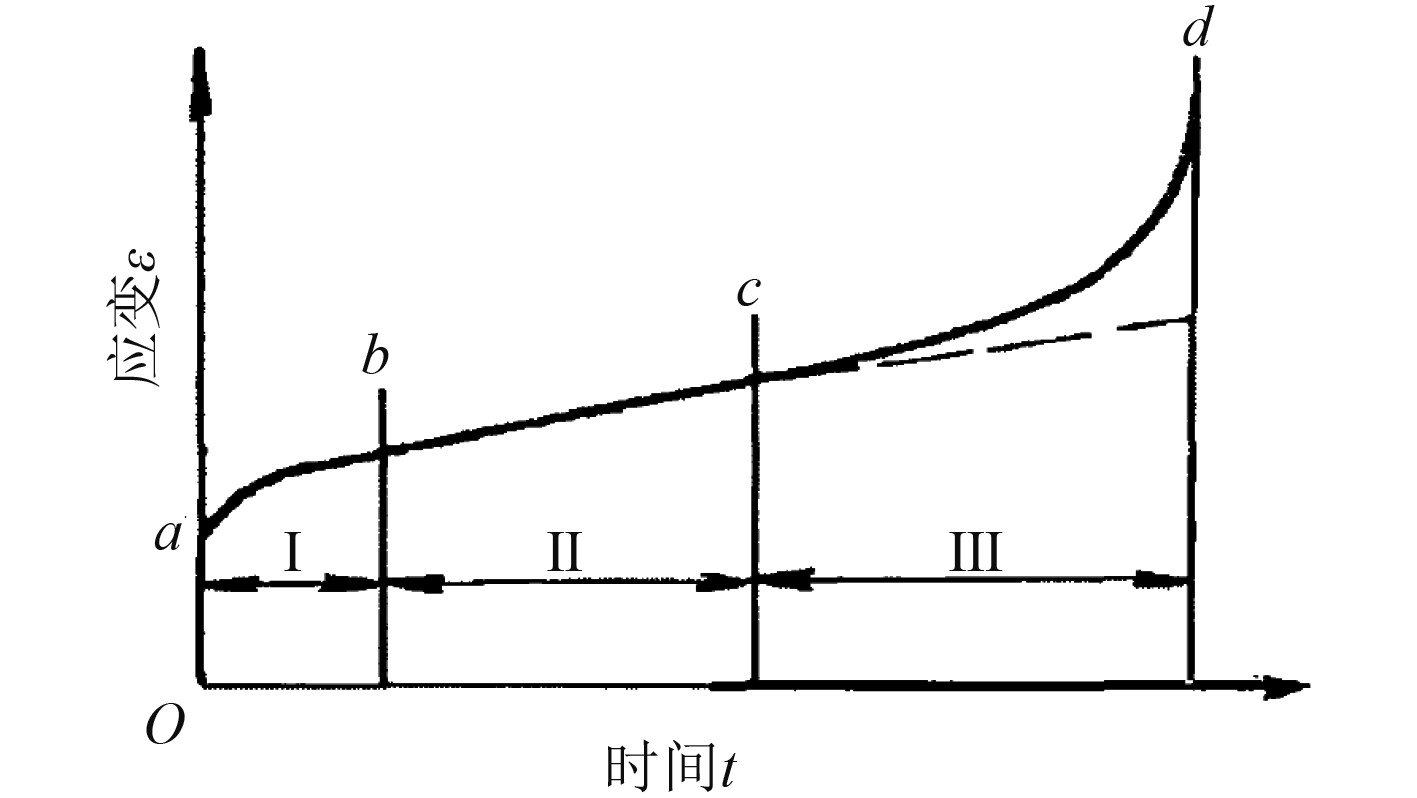
通常,热处理过程中焊接件残余应力的消除可以解释为:1)在热处理过程中,随着温度的升高,金属材料的弹性模量和屈服强度随之降低。当弹性模量和屈服强度低于残余应力时,材料发生塑性变形,焊接件内部残余应力也因此得到减小;2)在高温条件下材料的蠕变导致残余应力进一步降低。蠕变是高温环境下材料承受低于屈服强度载荷作用时发生的缓慢塑性变形行为。Andrade[8]定量地描述了材料的蠕变行为,蠕变曲线如图1所示。由于每个阶段的蠕变率变化规律不同,蠕变曲线通常被分为3个阶段:第Ⅰ阶段蠕变应变率随着蠕变时间的增加而减小,为初始蠕变阶段。第Ⅱ阶段与时间无关,蠕变应变率近似为一常数,为稳态蠕变阶段。第Ⅲ阶段随着蠕变时间的增加,蠕变应变率不断增大,为加速蠕变阶段。
|
图 1 蠕变应变随时间变化 Fig. 1 Creep strain changes with time |
许多模型描述了金属的蠕变,其中有一些比较著名,例如Don模型[9]、Fields模型[10]等。由于温度历史和应力历史对蠕变的影响,目前尚无可以完全描述和解释蠕变中各种现象的理论或模型。为了预测和计算材料在高温下的瞬态蠕变,通常在大量试验的基础上通过统计分析获得一些回归公式。其中,Norton模型的主要理论基础是Norton理论[11],它不考虑时间与应力或材料温度的耦合效应,仅考虑蠕变的第Ⅱ阶段,方程中仅3个拟合参数。orton模型给出的蠕变率的函数表达式为:
| $ \varepsilon _{cr}'={{C}}_1{\sigma ^{{C_2}}}{e^{\left( { - \frac{{{C_3}}}{T}} \right)}}\text{。} $ | (3) |
式中:
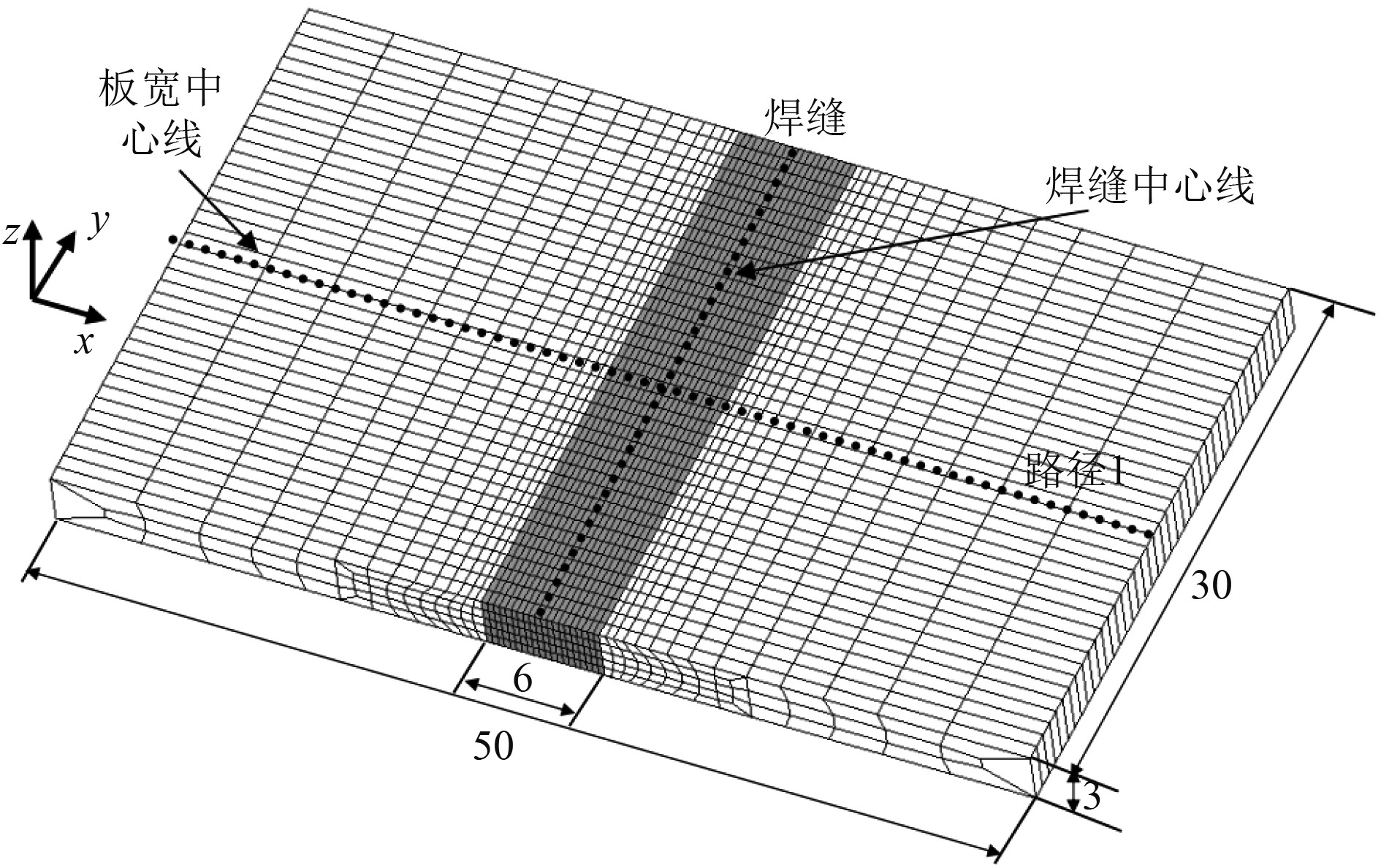
由于Ti80对接焊平板热处理前后残余应力试验研究成本较高,目前缺少相关实验研究,因此,本文首先对文献[4]中TC4对接焊平板焊后热处理进行数值模拟和试验数据验证。文献[4]中TC4对接焊平板是由2块30 mm×22 mm×3 mm的TC4板对接焊而成,TC4的屈服强度为860 MPa[5];焊缝尺寸为30 mm×6 mm×3 mm;在建立有限元模型时,为提高计算效率,焊缝区采用细密网格,远离焊缝区采用较粗网格,如图2所示。其材料、焊接工艺参数及边界条件等相关参数参考文献[4]。
|
图 2 TC4对接焊平板有限元模型(mm) Fig. 2 Finite element model of TC4 butt welding plate (mm) |
设X轴垂直于焊缝中心线,Y轴沿焊缝长度方向,Z轴沿板厚方向;路径1为沿平板表面板宽中心线方向(沿X轴方向)(见图2)。
首先基于热弹塑性理论,利用Ansys的APDL语言编制TC4对接焊平板模型残余应力数值模拟程序,并采用给定温度法[12]和生死单元技术相结合的计算分析方法来模拟板的焊接过程。然后依据文献[4]中热处理工艺方案,以2.5 K/min的速率升温,在973 K保温1 h,然后再以2.5 K/min的速率冷却至常温。
选择Ansys中的Norton模型进行数据拟合,由于温度较低时蠕变较小,为了便于拟合,未考虑400 ℃下的数据,根据文献[13]中试验数据对Norton蠕变模型进行了非线性拟合,得到了一组拟合参数,C1=9.39×10−14,C2=4.676,C3=24310。由于试验数据较大,拟合难度大,该组参数能吻合试验的部分数据,涵盖了大部分试验温度值。
一般来说,垂直于焊缝方向的残余应力对结构的疲劳裂纹扩展作用影响较大[14],因此本文重点研究垂直于焊缝上的焊接残余应力。经过计算,得到了热处理前后平板沿路径1的横向残余应力(沿X轴方向)和纵向残余应力(沿Y轴方向),并与文献[4]中的相关试验结果进行了比对研究。
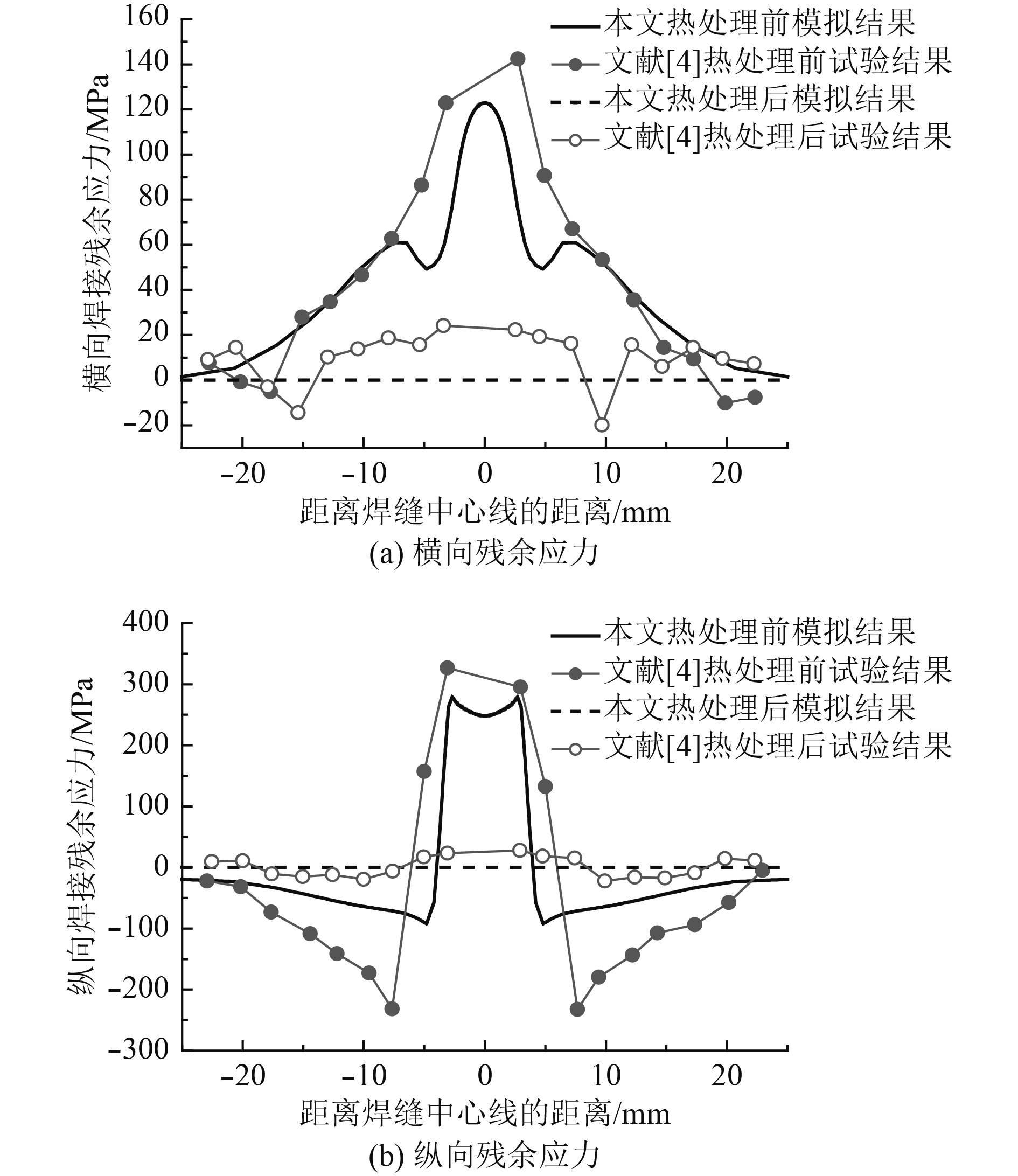
从图3可以看出,C4对接焊路径1上:
|
图 3 热处理前后路径1残余应力 Fig. 3 Residual stress of path 1 before and after heat treatment |
1)热处理前横向残余应力和纵向残余应力在焊缝附近均为拉应力,且纵向残余拉应力较大;
2)热处理后横向残余应力和纵向残余应力均有较大程度的降低;
3)横向残余应力和纵向残余应力数值模拟结果上与试验结果基本吻合,而纵向残余应力吻合得更好一些。
因此,本文热处理前后焊接残余应力的数值模拟方法合适。
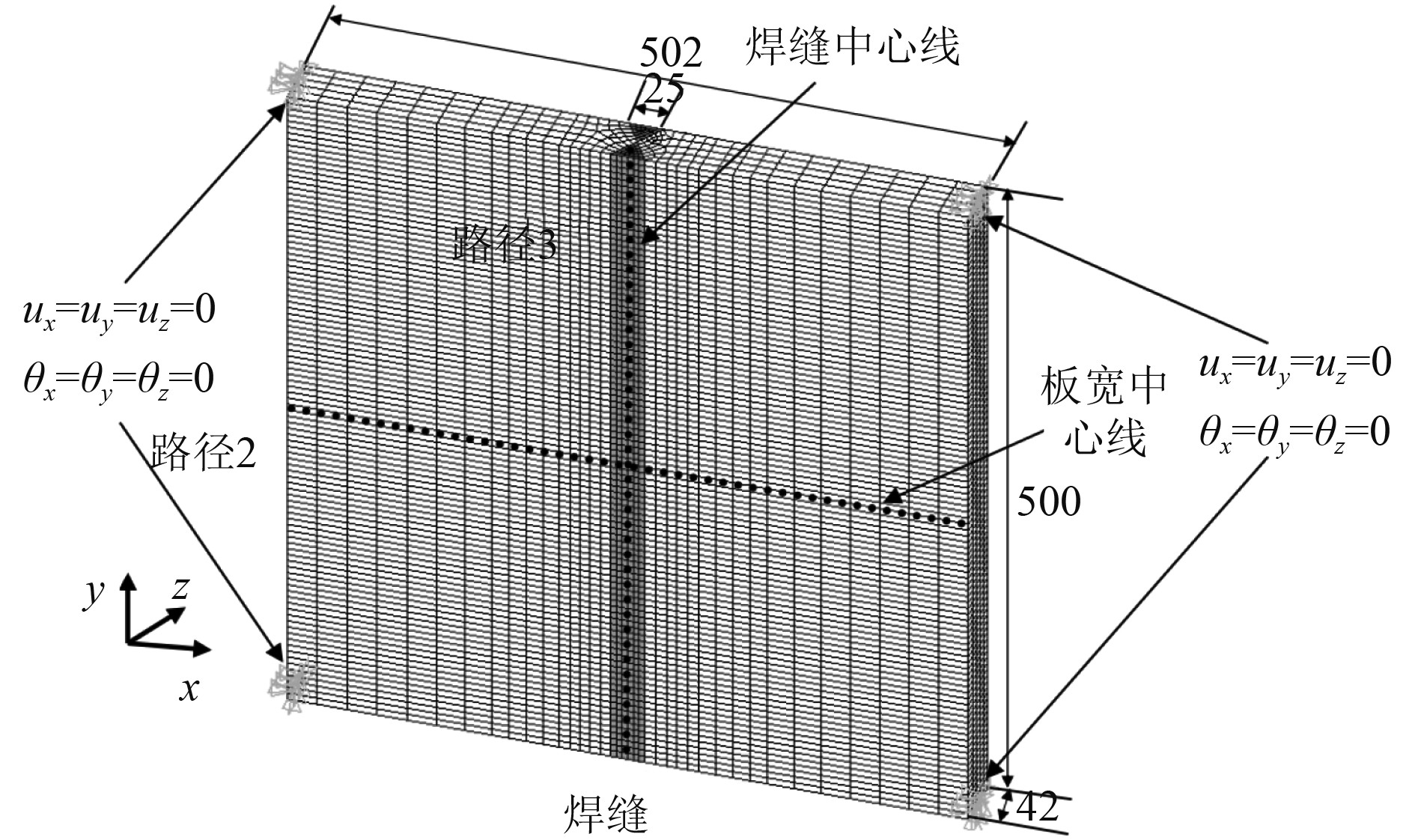
3 Ti80对接焊平板热处理的数值模拟研究Ti80对接焊平板由2块500 mm×250 mm×42 mm的Ti80板对接焊而成,焊接剖口为双V型剖口,表面焊缝宽度为25 mm,钝边为2 mm。将模型的4个角边刚性固定以防止其在计算过程中产生刚体位移,如图4所示。采用双面多道交替焊,在同一层焊道上遵循从左到右的焊接顺序。
|
图 4 Ti80对接焊平板有限元模型(单位: mm) Fig. 4 Finite element model of Ti80 butt welding plate (Unit: mm) |
设X轴垂直于焊缝中心线,Y轴沿焊缝长度方向,Z轴沿板厚方向;路径2为沿平板表面板宽中心线方向,路径3为沿平板表面焊缝中心线方向(见图4)。
3.1 Ti80对接焊平板材料属性对接焊平板选用的材料为Ti80钛合金,其屈服强度σs为800 MPa,弹性模量E为1.16×105 MPa,泊松比为0.3。
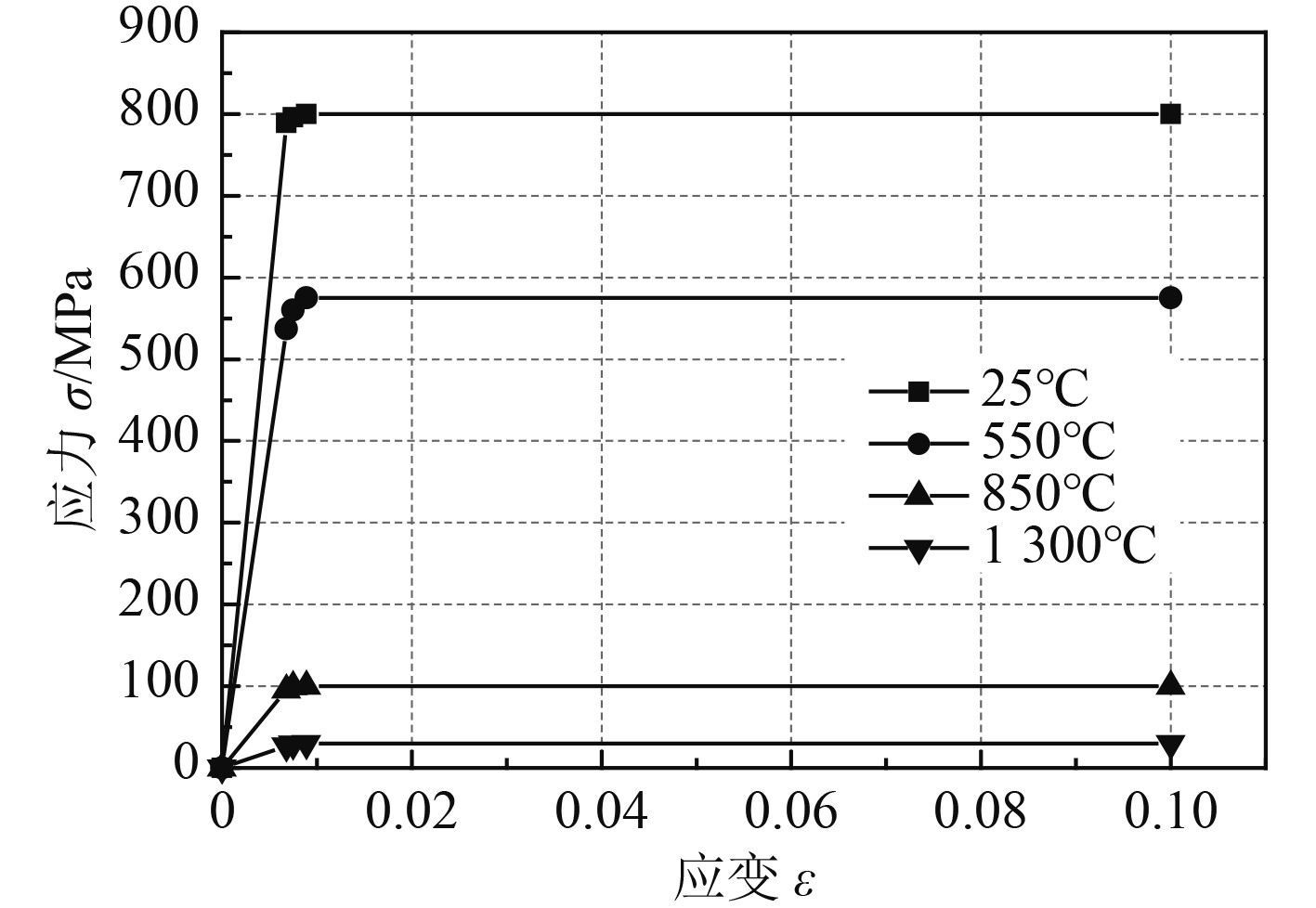
对于Ti80材料不同温度下的力学性能,本文根据文献[15]中Ti75材料的力学性能,采用线性插值法来近似求得。Ti80钛合金在不同温度场下的材料性能如表1所示,其力学性能如图5所示。
|
|
表 1 Ti80材料热物理性能参数 Tab.1 Thermal and physical properties parameters of Ti80 materials |
|
图 5 不同温度下Ti80的应力-应变关系 Fig. 5 The relation of stress-strain of Ti80 at different temperatures |
采用第2节中相同的数值模拟方法进行Ti80对接焊平板热处理前后焊接残余应力研究。即首先基于热弹塑性理论,利用Ansys的APDL语言编制Ti80对接焊平板模型残余应力数值模拟程序来模拟板的焊接过程;然后采用Norton模型进行焊后热处理的数值模拟。设焊接速度为3.5 mm/s左右,焊接最高温度为1300 ℃。因为未找到Ti80相关的高温蠕变参数,所以参考本文2.1节中TC4的蠕变参数,同时考虑到这2种钛合金在屈服强度上的差异,对其进行修正,修正方法如下[16]:
| $ \varepsilon _{{cr}}'={\rm{C}}_1{\left( {\frac{{{\sigma _{{s}1}}}}{{{\sigma _{{s}2}}}}\sigma } \right)^{{C_2}}}{e^{\left( { - \frac{{{C_3}}}{T}} \right)}}={\rm{C}}_1'{\sigma ^{{C_2}}}{{e}^{\left( { - \frac{{{C_{\rm{3}}}}}{T}} \right)}}\text{。} $ | (4) |
式中:
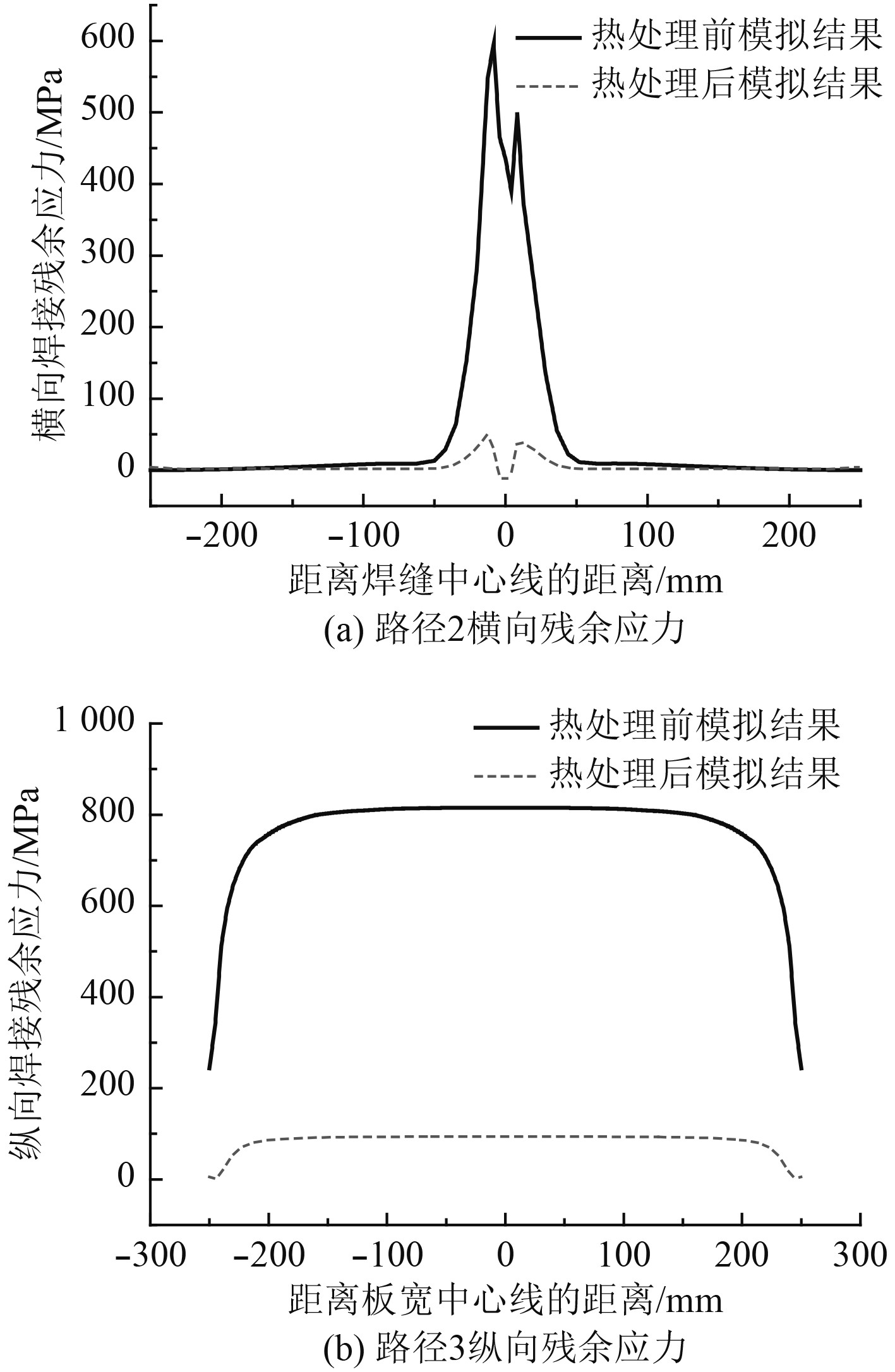
结合相关钛合金热处理文献[17],选择热处理工艺方案为:以20 ℃/min的速率升温至640 ℃,在640 ℃保温2 h,然后随炉冷却4 h至室温。因为升温过程中,温度较低,时间较短,所以在低于400 ℃时可以不考虑蠕变,只考虑温度超过400 ℃的加热阶段及保温阶段蠕变对应力的消除作用。经过计算,得到了热处理前后Ti80对接焊平板沿路径2(见图4)上的横向残余应力和沿路径3(见图4)上纵向残余应力,如图6所示。
|
图 6 热处理前后路径2和路径3上的残余应力 Fig. 6 Residual stress on path 2 and 3 before and after heat treatment |
由图6可知,Ti80对接焊平板:
1)焊后热处理前,路径2上焊缝附近的横向残余应力和路径3上的纵向残余应力均有较大的拉应力,纵向残余应力大于横向残余应力。由于焊接工艺的影响,路径2上横向残余应力呈不对称双峰分布。
2)通过焊后热处理,路径2上焊缝附近的横向残余拉应力和路径3上的纵向残余拉应力均有较大程度地降低,残余应力进行了重新分布;路径2上的横向残余拉应力峰值降幅约为92%,路径3上纵向残余拉应力降幅约为88%。
4 结 语1)通过对TC4对接焊平板热处理前后残余应力的数值模拟和试验结果比对研究,认为采用Norton蠕变模型进行焊后热处理的数值分析方法比较合理可靠。
2)Ti80对接焊平板有较大的横向残余拉应力和纵向残余拉应力,通过焊后热处理工艺,残余拉应力均在很大程度上得到了降低,平均降幅在90%左右。因此,通过焊后热处理工艺可以降低残余拉应力对结构力学性能可能产生的不利影响。
| [1] |
蒋文春, 王炳英, 巩建鸣. 焊接残余应力在热处理过程中的演变[J]. 焊接学报, 2011, 32(4): 45-48, 115. |
| [2] |
姜云禄, 余陈, 陈静, 等. 钛合金窄间隙TIG焊试板热处理前后表面残余应力研究[J]. 航空制造技术, 2018, 61(8): 62-66. |
| [3] |
余陈, 张宇鹏, 房卫萍, 等. 焊后热处理对100 mm TC4钛合金电子束焊接头残余应力的影响[J]. 材料热处理学报, 2018, 39(7): 151-155. |
| [4] |
YAN G, CRIVOI A, SUN Y, et al. An Arrhenius equation-based model to predict the residual stress relief of post weld heat treatment of Ti-6Al-4V plate[J]. Journal of Manufacturing Processes, 2018, 32: 763-772. DOI:10.1016/j.jmapro.2018.04.004 |
| [5] |
闻雅. TC4钛合金球壳体电子束焊接接头性能及应力分析[D]. 哈尔滨: 哈尔滨工业大学, 2014.
|
| [6] |
李有华, 刘智宇, 王新, 等. 热处理对TA15钛合金厚板残余应力的影响研究[J]. 中国钛业, 2015(3): 15-17. |
| [7] |
金俊龙, 万晓慧, 郭德伦. TC17钛合金焊接及局部热处理残余应力的数值模拟[J]. 航空制造技术, 2019, 62(12): 30-35. |
| [8] |
ANDRADE E N C. On the viscous flow in metals, and allied phenomena[J]. Proceedings of the Royal Society of London.Series A, Containing Papers of a Mathematical and Physical Character, 1910, 84(567): 1-12. DOI:10.1098/rspa.1910.0050 |
| [9] |
DORN J E. Some fundamental experiments on high temperature creep[J]. Journal of the Mechanics and Physics of Solids, 1955, 3(2): 85. DOI:10.1016/0022-5096(55)90054-5 |
| [10] |
FIELDS B A, FIELDS R J.Elevated temperature deformation of structural steel[R]. Gaithersburg: National Institute of Standards and Technology, 1989.
|
| [11] |
NORTON F H.The creep of steel at high temperatures[M]. New York: McGraw-Hil Inc., 1929.
|
| [12] |
LIU Chuan, LUO Ying, YANG MIN, et al. Three-dimensional finite element simulation of welding residual stress in RPV with two J-groove welds[J]. Welding in the World, 2017, 61(1): 151-160. DOI:10.1007/s40194-016-0392-y |
| [13] |
王伟, 李华冠, 杨吟飞, 等. Ti6Al4V钛合金薄板退火畸变数值模拟及试验验证[J]. 金属热处理, 2016, 41(1): 204-210. |
| [14] |
Al-MUKHTAR, A.M.. Consideration of the residual stress distributions in fatigue crack growth calculations for assessing welded steel joints[J]. Fatigue & Fracture of Engineering Materials & Structures, 2013, 36(12): 1352-1361. |
| [15] |
黄伯云, 李成功, 石力开, 等. 中国材料工程大典第四卷, 有色金属材料材料工程(上册)[M]. 北京: 化学工业出版社. 2005.
|
| [16] |
张建勋, 刘川著. 焊接应力变形有限元计算及其工程应用. 北京: 科学出版社, 2015. 04.
|
| [17] |
GJB 3763A-2004, 钛及钛合金的热处理[S].
|
 2021, Vol. 43
2021, Vol. 43
