加筋板是船体结构的基本要素,合理确定其尺寸是舰船结构轻量化设计的有效途径。在加强筋尺寸的设计与局部强度校核中,需要综合考虑总纵弯曲应力与局部载荷共同作用下的构件结构响应,并采用许用应力折减系数(Cs)作为许用安全系数。目前大部分规范中的Cs没有反映出构件实际受总纵弯曲应力影响程度与构建位置的关系,也没有考虑局部载荷作用方向、加强筋剖面对称性的影响,给出的系数Cs为一个偏保守的常量。这样虽然保证了设计的安全性,但在经济型和结构优化方面有所欠缺。
了解船体板架承载机理是设计板架的前提,近年来,关于船体加筋板承载能力分析和优化设计的研究成果丰硕。陈彦廷等[1]指出船舶在航行过程中受多种载荷作用,具体到板和加筋板受力体现为面内的轴向压缩或拉伸力、板内弯矩和周边剪切,以及面外侧向受力(如货物、设备等重物作用和水压力)。刘春正等[2]利用有限元计算分析研究了整体初始挠度的幅值与半波数对极限载荷的影响和典型位置的应力特性,并整理了初始挠度对加筋板极限载荷的影响因子计算方法。王伟等[3]忽略了材料非线性影响,基于理论分析推导了四边简支加筋板的整体屈曲临界应力求解公式,并用有限元结果对比验证。朱旭光等[4]基于HCSR规范要求,结合加筋板的受力特征和典型节点设计经验,研究并开发了加筋板屈曲优化程序。
民规(如DNV、共同规范)和劳氏军规对许用应力折减系数的取值有所差异,且均没有给出推导过程。本文通过对比DNV民规和劳氏军规,以及非线性有限元计算分析,研究加强筋的许用弯曲应力折减系数的取值,考虑局部载荷作用位置、型材剖面对称性等因素的影响,丰富了舰船局部强度校核方法的技术背景,为加筋板局部强度评估提供支撑。
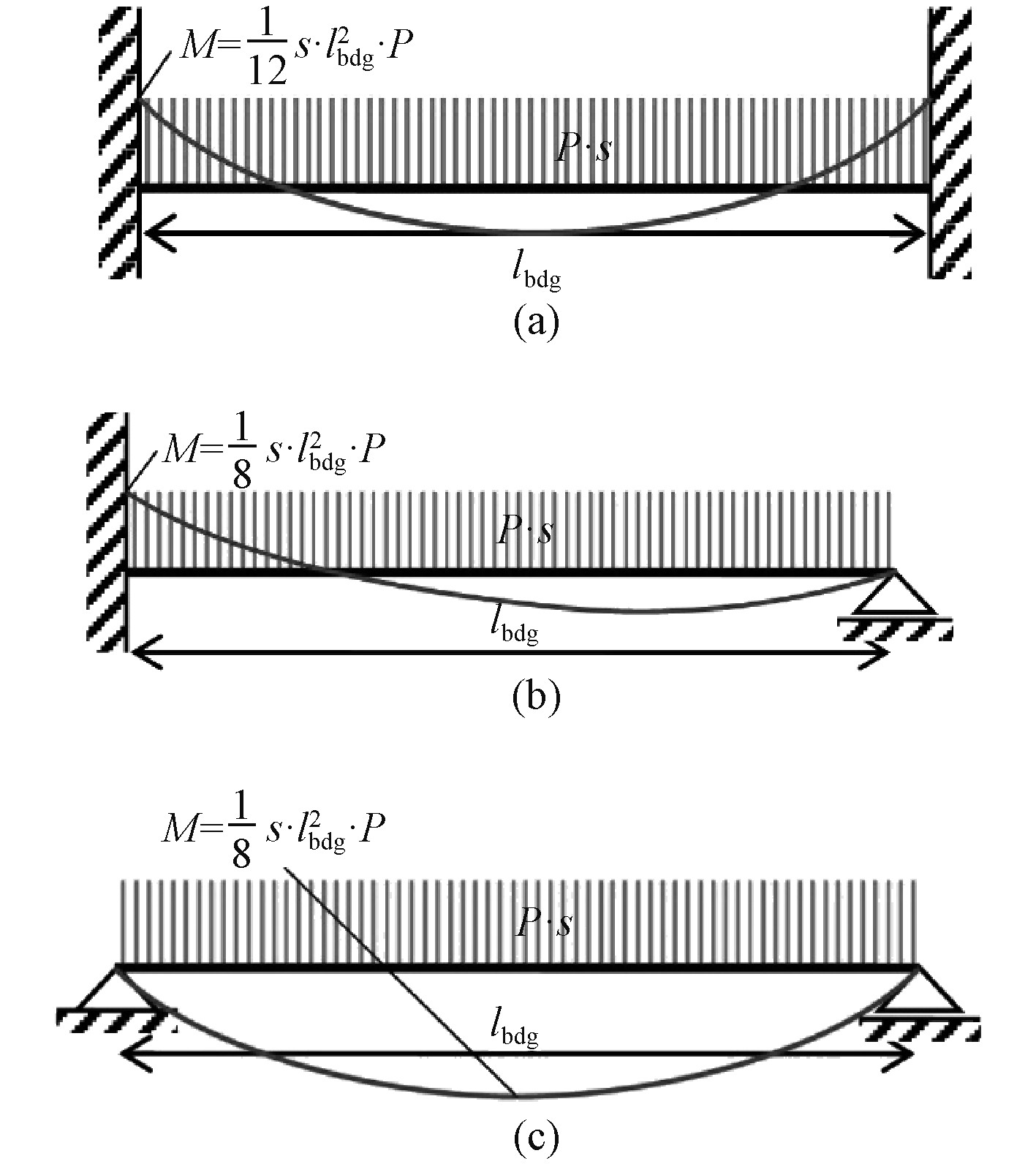
1 侧向载荷作用下的加筋板简化力学模型校核加强筋局部强度时,可以简化为如图1所示的弹性梁模型来分析。梁两端的边界条件有:两端简支、两端刚性固定、一端简支一端刚性固定,受到的局部载荷为均布载荷P。图1(a)可以看出连续梁穿过强横梁的简化模型,如舷侧纵骨穿过强肋骨(或舱壁)同时受舷外水压力。图1(b)及图1(c)为非连续梁受均布压头的简化模型。最大弯矩值和位置如图中所示。
|
图 1 不同边界条件的加强筋简化模型 Fig. 1 Stiffener simplified model with different BC |
加强筋受局部载荷和总纵弯曲应力,它们共同作用、相互影响,最终作用效果取决于它们的符号。以下主要研究连续梁,即图1(a)的情况,简化为两端刚固受侧向载荷,侧向载荷可能作用在板的一侧,也可能作用在加强筋的一侧。若侧向均布载荷作用位置的不同,其产生的局部弯曲应力在加强筋端部的符号相反,再与总纵应力合成,由于加强筋上翼板的应力不同,对应的许用应力也不同。
局部载荷引起的最大应力在最大弯矩处筋的上翼板。假定跨中弯矩与端部弯矩的之间的关系为:
| $ {\sigma }_{lb-midspan}=-\frac{1}{{f}_{m}}{\sigma }_{lb-ends}\text{,} $ |
其中,
综合考虑总纵弯曲应力和局部弯曲应力,梁端部应力极限状态为:
| $ {\sigma }_{hg}+{\sigma }_{lb-ends}\leqslant {R}_{eH}\text{,} $ |
筋的局部许用弯曲应力为:
| $ {\sigma }_{perm}={R}_{eH}-{\sigma }_{hg}\text{,} $ | (1) |
梁跨中的极限状态为:
| $ {\sigma }_{hg}+{\sigma }_{lb-midspan}={\sigma }_{hg}-\frac{1}{{f}_{m}}{\sigma }_{lb-ends}\leqslant {R}_{eH}\text{,} $ |
筋的局部许用弯曲应力为:
| $ {\sigma }_{perm}={f}_{m}({R}_{eH}-{\sigma }_{hg}) \text{。}$ | (2) |
由式(1)和式(2)限定条件,且筋的应力不可超过材料的屈服极限,许用应力应满足:
| $ {\sigma _{perm}} = min\{ {R_{eH}},{R_{eH}} - {\sigma _{hg}},{f_m}({R_{eH}} - {\sigma _{hg}})\} \text{。} $ | (3) |
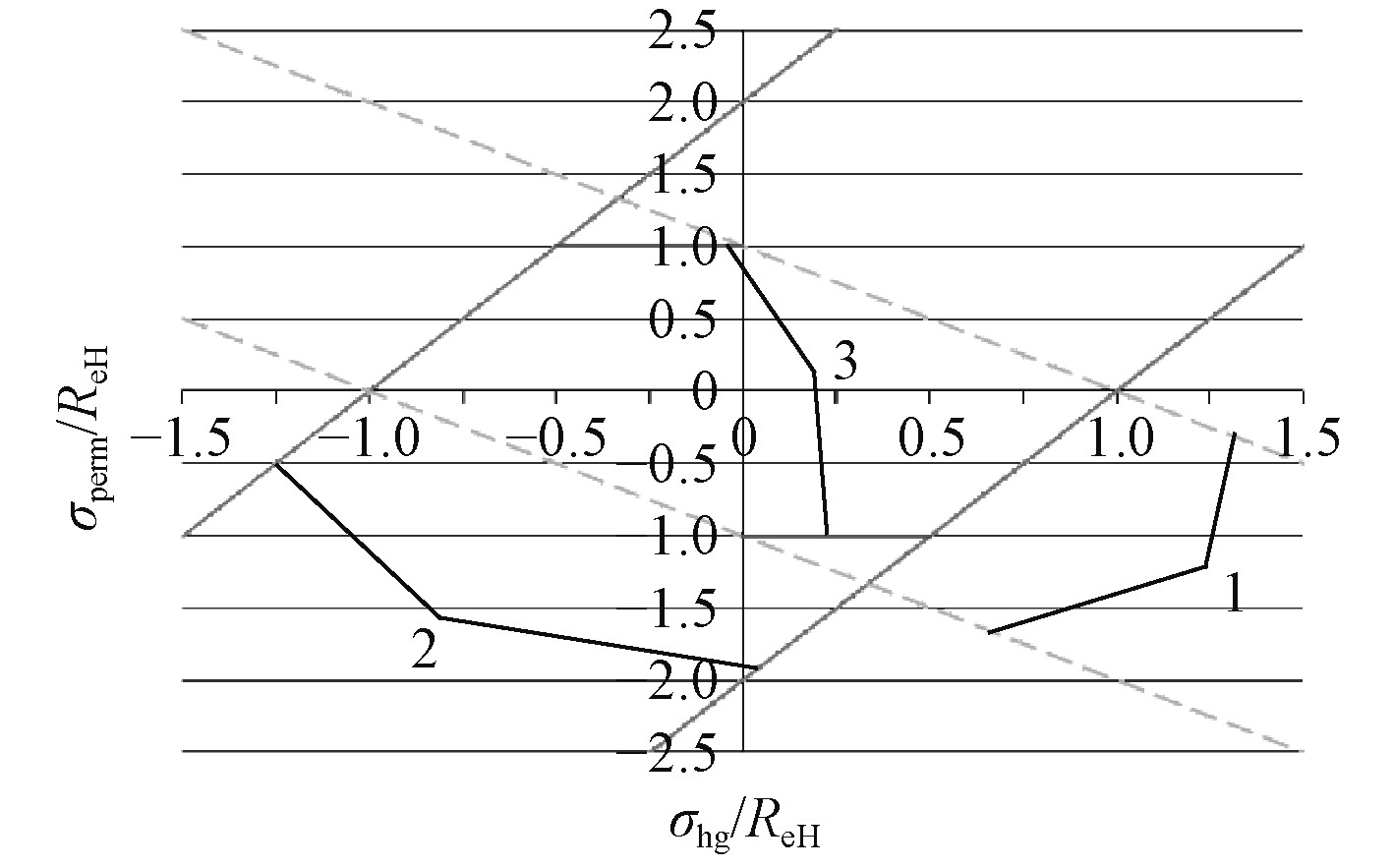
若为连续梁两端刚固的情况,
|
图 2 许用应力范围示意 Fig. 2 Permissible stress area |
在一、三象限,总纵弯曲应力与局部应力的符号相同,二、四象限表示总纵弯曲应力与局部应力的符号相反。计应力符号正为受拉、负号为受拉,可以看出一象限总纵弯曲应力为拉力,局部载荷作用在筋的一侧;三象限总纵弯曲应力为压力,局部载荷作用在板的一侧;二象限总纵弯曲应力为拉力,局部载荷作用在板的一侧;四象限总纵弯曲应力为压力,局部载荷作用在筋的一侧。
2 常用规范对比LR军规中规定许用应力折减系数由下式表达:
| $ {C}_{s}=0.9\left(1.83-\frac{{\sigma }_{hg}}{{\sigma }_{a}}\right) \text{。}$ |
其中:
DNVGL规范中,对于连续构件规定许用应力折减系数如表1所示。
|
|
表 1 连续构件
|
表中,
|
|
表 2 |
总体上看,劳氏军规中采用的许用应力折减系数整体比DNV保守,对于NS1,NS2类型的入级舰船Cs最大取值为0.95,相当于DNV中的AC-II,而对于NS3类型舰船Cs最大取值为0.75,比DNV中的AC-I还要保守。
DNV的局部强度衡准定义了3个等级,其中AC-I不允许加强筋超过其材料屈服极限,即弹性设计,承受静态局部载荷;AC-II允许加强筋最大塑性变形量为新建造标准[7]的1/4,承受静态+动态局部载荷;AC-III允许加强筋最大塑性变形量为新建造标准的1/2,用于一些液舱淹没、测试等极端工况。相比较劳氏军规,DNV规范更为细致,考虑了载荷作用方向、型材剖面对称性的影响。
3 加强筋的许用应力折减系数分析基于上述理论分析,综合考虑总纵弯曲应力和局部载荷的相互影响,考虑几何非线性、材料非线性,用有限元软件Abaqus计算一系列加筋板模型,通过对比、分析计算结果,验证许用应力折减系数Cs取值的影响因素,并拟合了基于有限元结果的Cs曲线。本文研究是针对连续梁两端刚固的模型,非连续梁的情况研究方法类似。
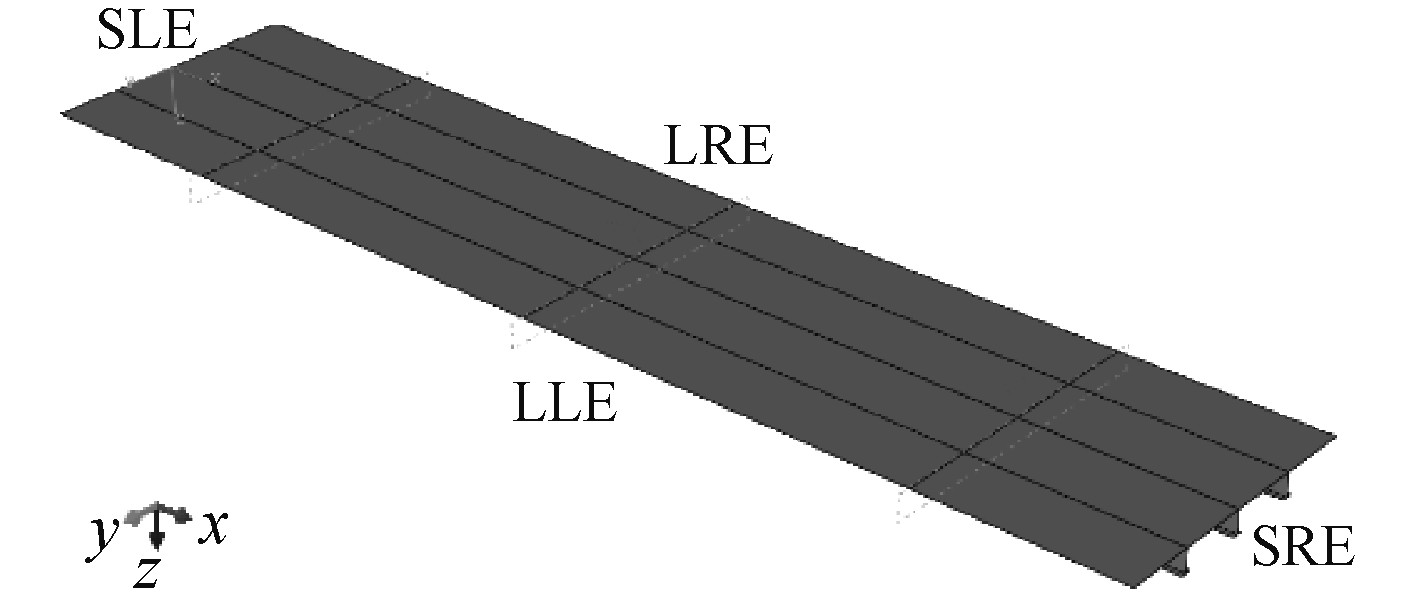
3.1 有限元模型简述采用非线性有限元软件Abaqus建模计算,有限元模型为1/2l+l+l+1/2l的加筋板,包括3根加强筋,左右各半段纵骨跨距的延伸段,如图3所示。其中,强横梁未建出,用边界条件模拟其与加强筋的限制关系。
|
图 3 有限元模型 Fig. 3 FEM model |
其中,l为相邻强横梁之间的距离。模型边界条件为:
SLE θy=θz=0,且x方向无相对位移,
SRE Ux=θy=θz=0,
LLE Uy=Uz=θx=θy=θz=0,
LRE Uz=θx=θy=θz=0,
横梁所在位置 Uz=0,y方向无相对位移。
Ux,Uy,Uz表示x,y,z方向的线位移,θx,θy,θz表示x,y,z方向的角位移。
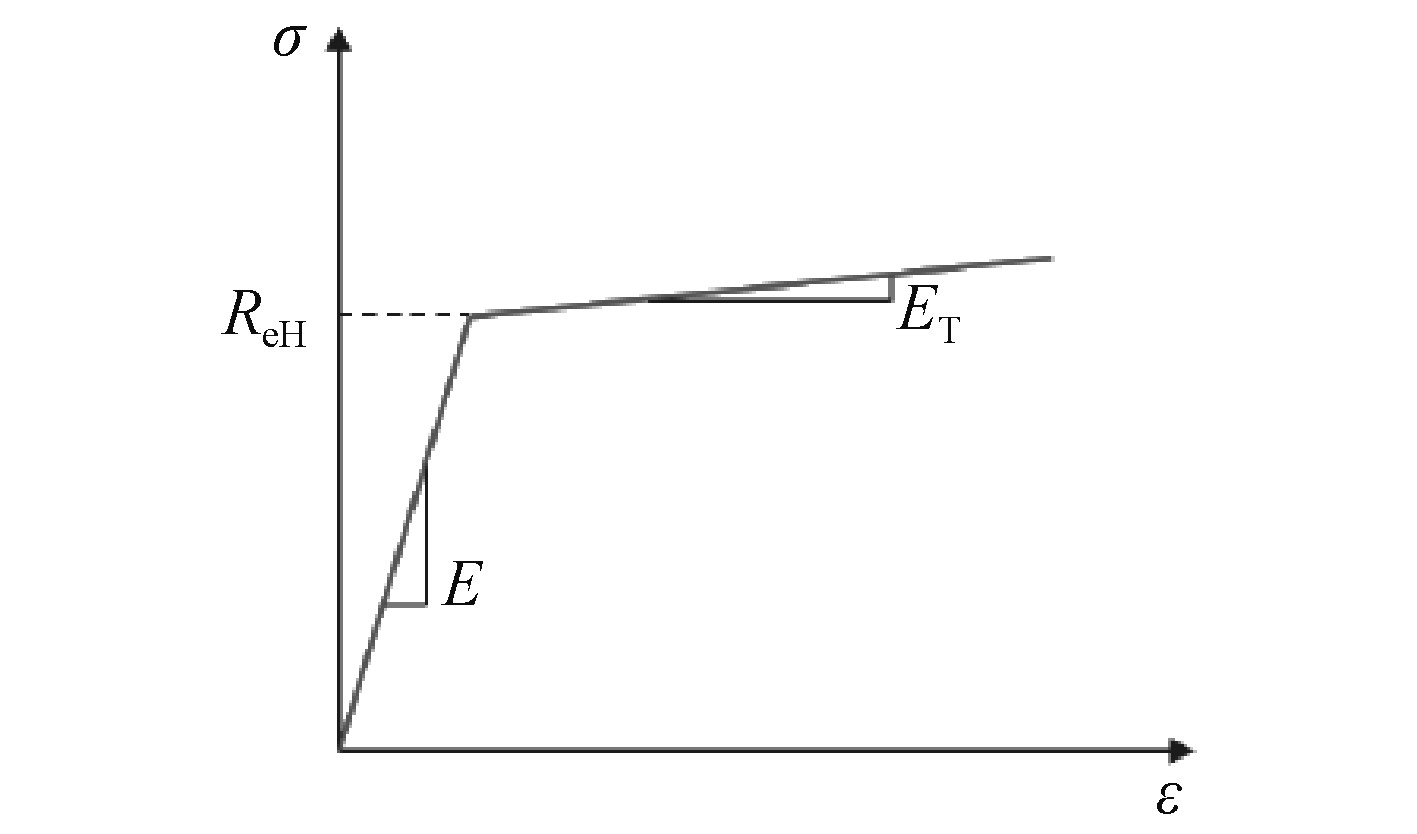
模型全部用S4R板单元建成,沿厚度方向5个积分点。沿纵骨跨距120个单元,纵骨间距20个单元,加强筋腹板10个单元。材料的弹性模量E=206000 N/mm2,泊松比0.3,采用双折线硬化模型,正切模量Et=1000 N/mm2,如图4所示。
|
图 4 材料硬化模型 Fig. 4 Material hardening model |
根据第1节的力学模型,两端刚固的边界条件下,使加强筋上翼板达到材料屈服限的理论侧向载荷为:
| $ {P}_{theory}=\frac{12{R}_{eH}Z}{s{l}^{2}}\text{,} $ | (4) |
参照DNV规范中的三级许用衡准:AC-I,AC-II,AC-III分别以其对应的塑性变形量作为有限元计算中的侧向载荷许用衡准。例如,对于AC-II塑性变形为1/4建造标准[7],按照最严格的的规定即为0.5‰l。
用有限元分析得到的许用应力折减系数定义为:
| $ {C}_{s}=\frac{{P}_{FEM}}{{P}_{theory}}\text{。} $ | (5) |
具体的加载方法为:假定一个总纵弯曲应力加在加筋板短边,如
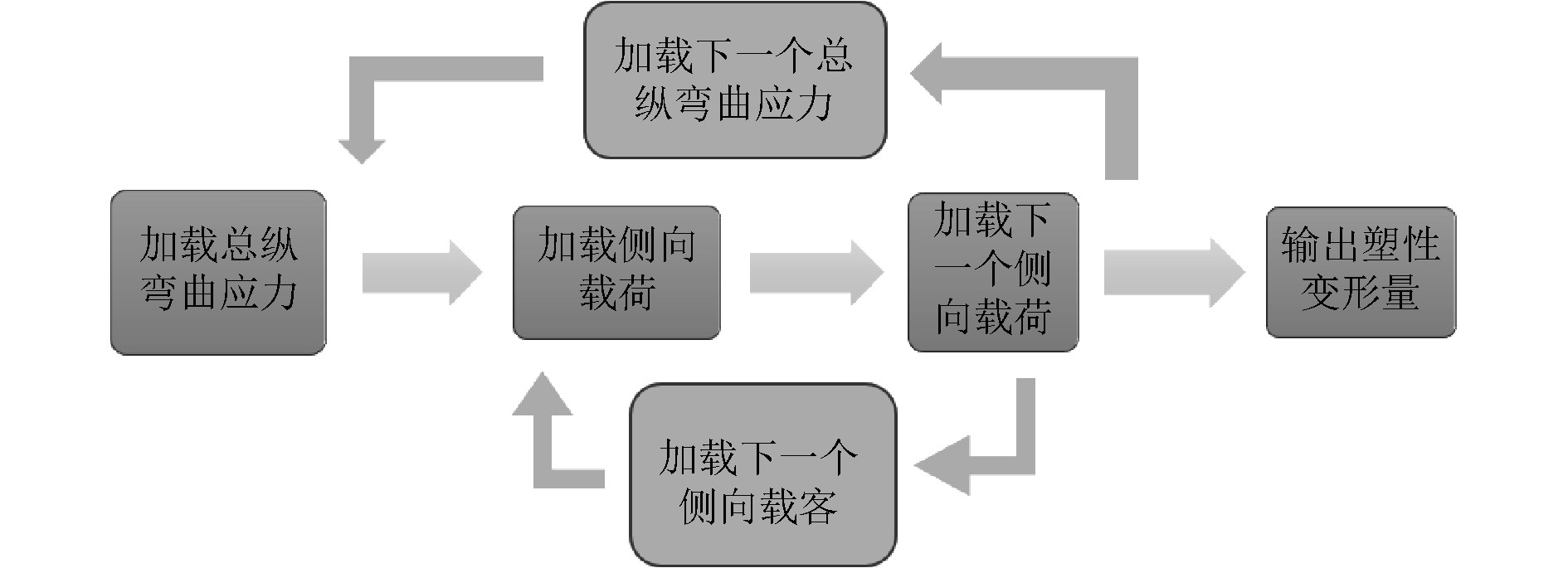
|
图 5 加载流程 Fig. 5 Process of loading |
以1组计算模型为例,模型跨长4800 mm,板厚13 mm,加强筋剖面尺寸为T 125x9/250x7.5,侧向载荷作用在板一侧,受总纵弯曲压应力,材料屈服极限为355 N/mm2,有限元计算的变形、应力结果如图6所示。

|
图 6 有限元计算结果 Fig. 6 FEM calculation result |
模型计算完毕后,读出每一分析步的塑性变形,得到不同
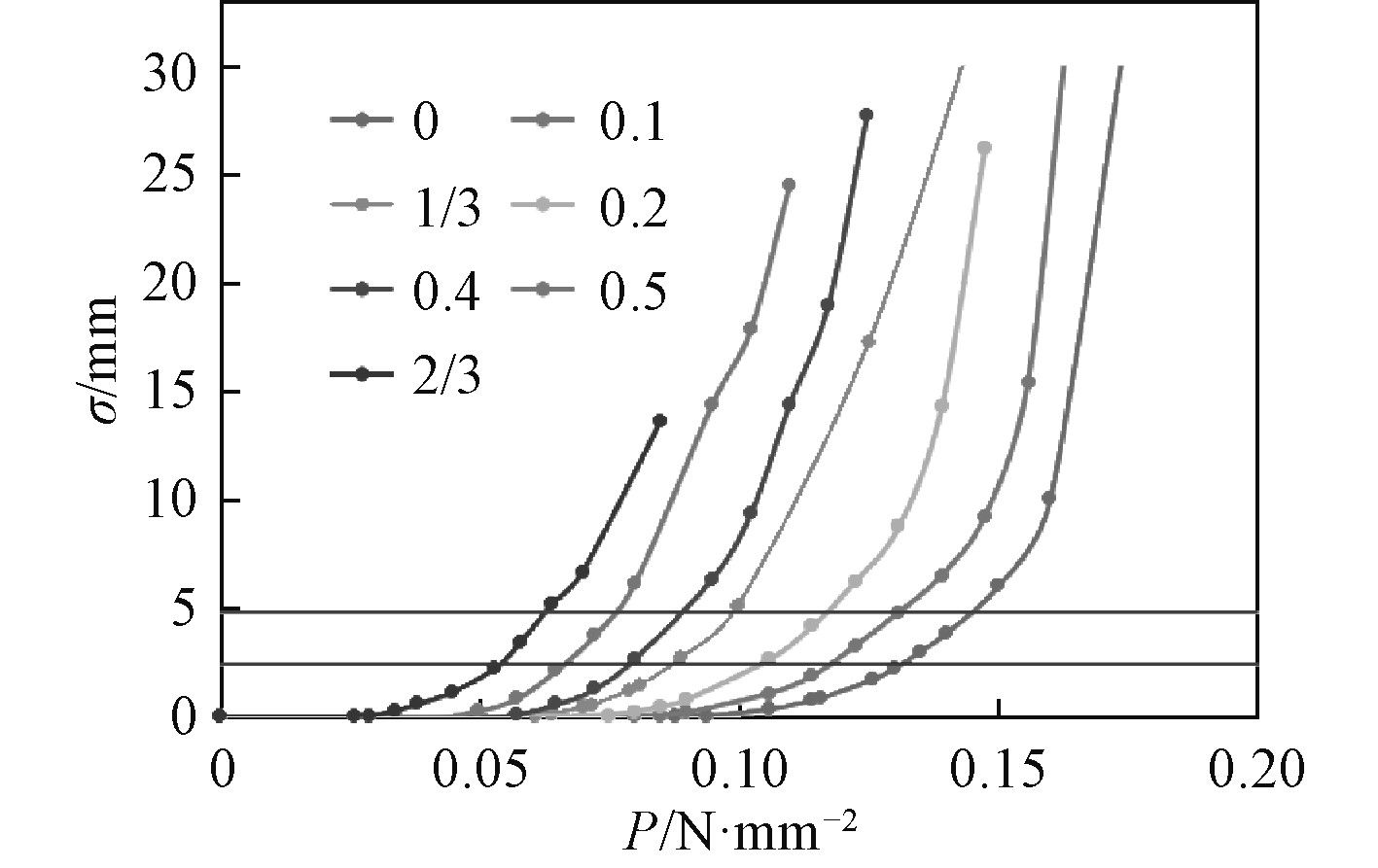
|
图 7 侧向载荷-塑性变形曲线 Fig. 7 Lateral load-plastic deformation curve |
有限元计算中,施加的侧向压力逐步增大,直到到达某一压力水平(塑性变形量达到预期),或加筋板崩溃,则计算停止,有限元计算无法加载完所有假设的侧向载荷。图8中
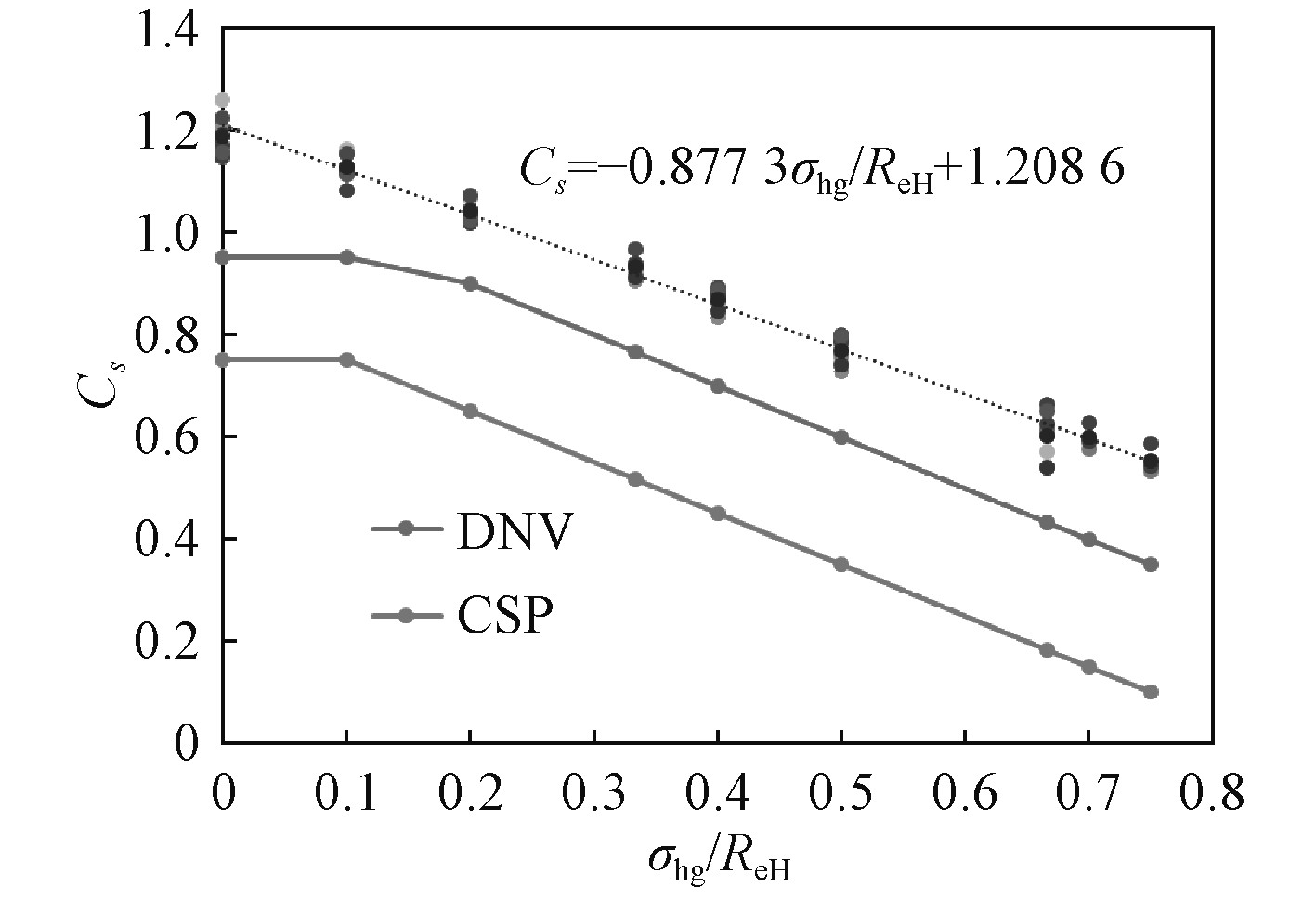
|
图 8 Cs曲线拟合结果(AC-II) Fig. 8 Regression result of Cs(AC-II) |
按照上述方法,计算一系列的模型,读取结果,拟合出Cs曲线。计算的模型参数如表3所示。这些模型均受压缩的总纵弯曲应力,侧向压力作用在板的一侧,且加强筋剖面均为对称截面,筋的跨距、间距、剖面尺寸有所不同,材料屈服极限均为355 N/mm2。
|
|
表 3 模型几何参数 Tab.3 Geometry parameters of models |
由图8AC-II计算结果可知,对于不同的加筋板模型,得到各模型的Cs曲线集中在一定范围之内,取平均值并拟合出Cs方程。计算结果说明,应力折减系数Cs曲线与加筋板几何尺寸无直接关系,只与构件的总纵弯曲应力的水平有关。而有限元的计算结果与DNV(AC-II)、CSR(S)的斜率大致相同。
3.3 型材剖面对称性的影响为了验证型材对称性对局部许用应力的影响,以之前计算过的模型T-a,T-b,T-g为对比,建立与之剖面模数几乎相同的加强筋剖面为角钢的模型,模型的几何信息对比如表4所示。这些模型均受压缩的总纵弯曲应力,侧向压力作用在板的一侧,所有材料屈服限均为355 N/mm2。
|
|
表 4 模型几何参数 Tab.4 Geometry parameters of models |
计算结果对比如图9所示,当剖面模数接近、载荷情况相同时,不对称剖面的加强筋的Cs小于对称剖面的Cs。取6个模型(3组)的T型材与角钢的Cs比值,平均后约为1.12,与文献[6]中Cs所述的趋势一致。这里只给出了AC-II衡准下的Cs值,AC-III结果类似。
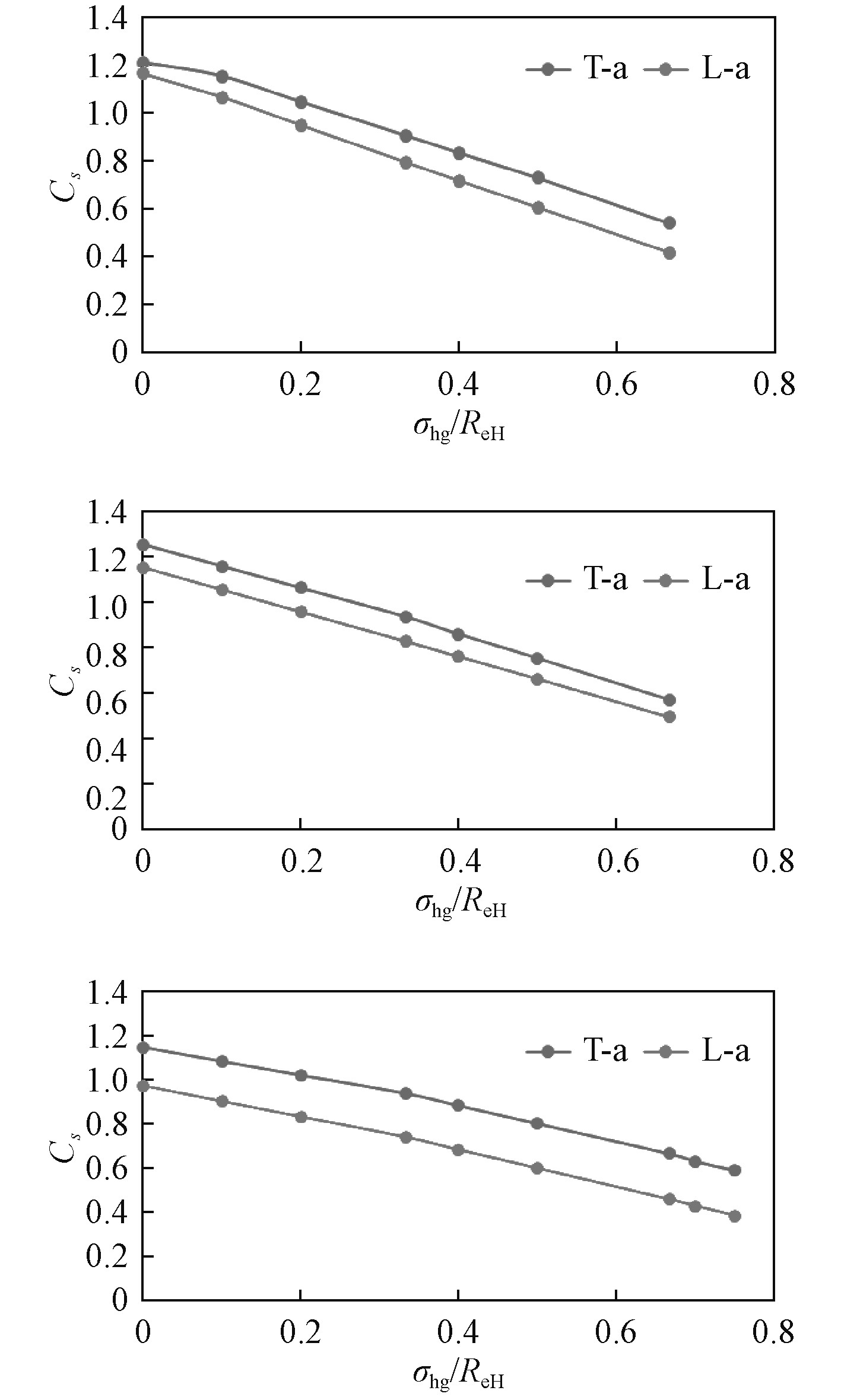
|
图 9 3组对称剖面与不对称剖面模型Cs曲线 Fig. 9 Cs Curve of 3 pairs of models with symmetric and asymmetric stiffener section |
由前面的理论分析,局部侧向载荷作用在板的一侧和筋的一侧会导致加筋板承载能力的不同。将前面的L-a,L-b,T-a计算模型稍作修改,将局部侧向载荷加载到筋的一侧,得到对比模型L-a-S,L-b-S,T-a-S。这几组模型的总纵弯曲应力均为压应力,结果对比如图10所示。
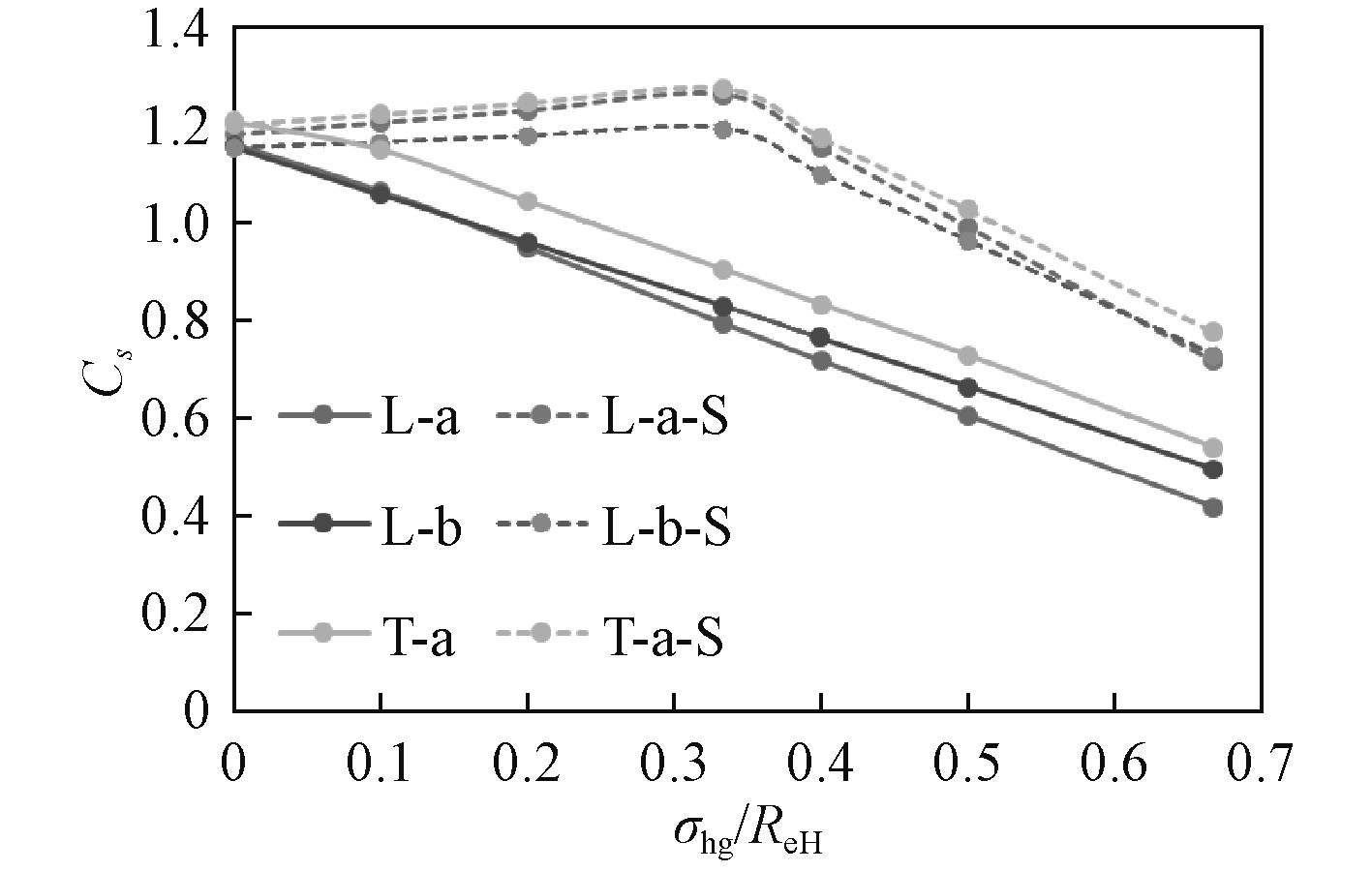
|
图 10 载荷作用方向不同对比模型Cs曲线 Fig. 10 Comparison of Cs Curve of models with different loading directions |
可以看出,在其他载荷情况相同的情况下,若两端受压应力,局部载荷作用在筋的一侧时的Cs会略大于局部载荷作用在板一侧时的Cs,与文献[6]中Cs所述的趋势一致。
4 结 语本文通过理论分析、非线性有限元计算,对比各组模型计算结果,得出以下几点结论:
1)有限元方法拟合的许用应力折减系数(Cs)曲线高于劳氏军规和DNVGL规范给出的曲线,但斜率大致相当。可以看出即使按照IACS建造标准[7]中最严格的变形要求,规范中的Cs取值也有一定裕度。考虑到加强筋弹性设计,故各规范对常规工况时的Cs值几乎都限定在1以下。
2)DNVGL规范细致地考虑了局部载荷作用位置、型材剖面对称性对Cs的影响,即局部侧向载荷作用在加筋板的不同侧时,Cs取值不一样(例如,两端受压时,作用在筋的一侧更利于与加筋板承载);加强筋型材的对称性也会影响Cs取值,对称型剖面材更有利于承载。而其他规范未考虑这些因素,或只是偏保守地降低Cs的取值。
3)本文的研究对探索舰船三维设计工作也具备一定的借鉴性。编制针对舰船的结构设计、局部强度校核的程序时,可充分考虑总纵弯曲应力对局部强度的影响,获取不同位置准确的
| [1] |
陈彦廷, 于昌利, 桂洪斌. 船体板和加筋板的屈曲及极限强度研究综述[J]. 中国舰船研究, 2017, 12(1): 54-62. DOI:10.3969/j.issn.1673-3185.2017.01.009 |
| [2] |
刘春正, 吴梵, 牟金磊. 含初试挠度加筋板的极限承载能力分析[J]. 舰船科学技术, 2017, 39(5): 10-15. DOI:10.3404/j.issn.1672-7619.2017.05.003 |
| [3] |
王伟, 吴梵. 单根加筋板整体屈曲临界应力计算与分析[J]. 船舰科学技术, 2010, 32(10): 3-7. |
| [4] |
朱旭光, 吕毅宁. 基于协调共同规范的船体加筋板结构的优化设计[J]. 船海工程, 2015, 44(4): 1-4. DOI:10.3963/j.issn.1671-7953.2015.04.001 |
| [5] |
LR. Rules and regulations for classification of naval ships[S]. 2011.
|
| [6] |
DNV-GL. Rules for classification of ships[S]. 2019
|
| [7] |
IACS-NO. 47 Shipbuilding and repair quality standard, Rev. 7[S]. 2010.
|
| [8] |
IACS. Common structural rules for bulk carriers and oil tankers[S]. 2019.
|
 2021, Vol. 43
2021, Vol. 43
