0 引　言

复合材料具有比强度、比刚度高、抗腐蚀等优点，有利于实现船体结构的轻量化设计，因此受到设计者越来越多的关注。在复合材料船体结构中，帽型加筋板是常见的结构形式，然而由于复合材料的各向异性，复合材料加筋板受压破坏时表现出复杂的破坏过程及形式^[1]，这增加了复合材料加筋板的应用难度，因此研究复合材料加筋板在面内压缩作用的下的极限承载能力具有重要的工程意义。

由于复合材料加筋板破坏行为的复杂性，各国学者对其压缩载荷下的破坏行为进行了大量的试验研究^[2-7]。相较于试验法，数值模拟具有成本低、周期短等优点，因此得到更广泛应用。孔斌等^[8-9]以轴压作用下的加筋板为研究对象，采用Abaqus软件对其屈曲过程、内力分布与传载特性进行模拟分析；常园园等^[10]采用非线性有限元方法基于连续损伤状态变量对复合材料加筋板进行渐进失效分析，讨论了加强筋和壁板的刚度比的影响；高晶晶等^[11]基于非线性有限元方法，将材料的Hashin准则与胶层界面的二次应力准则引入到有限元模型中，研究复合材料加筋板的后屈曲损伤与破坏行为；赵维涛等^[12]利用渐进失效理论采用Hashin与Quads准则对复合材料加筋板的极限压缩强度进行预测；徐丽等^[13]利用Ansys软件对骨材间距、芯材等因素对复合材料帽型加筋结构强度和刚度的影响进行讨论；潘康华等^[14]对组合载荷下复合材料夹层板架的承载能力进行数值模拟。然而，现阶段对复合材料加筋板的研究主要针对航空的层合板结构，其对船体复合材料结构的指导比较有限。在船体方面，复合材料加筋板的研究主要集中在极限强度及其影响因素方面，缺乏对结构破坏机理、内部损伤规律等方面的讨论，这不利于复合材料船体结构设计的发展。

本文以船体夹芯复合材料帽型加筋板（下文简称“加筋板”）为研究对象，基于复合材料的二维hashin准则与胶层界面的最大应力准则，采用非线性有限元方法对其在面外均布载荷与面内压缩联合作用下的破坏行为进行渐进失效分析，并采用子模型技术对破坏区域进行局部建模分析，基于Shokrieh-Hashin准则研究破坏区域蒙皮的铺层损伤规律。

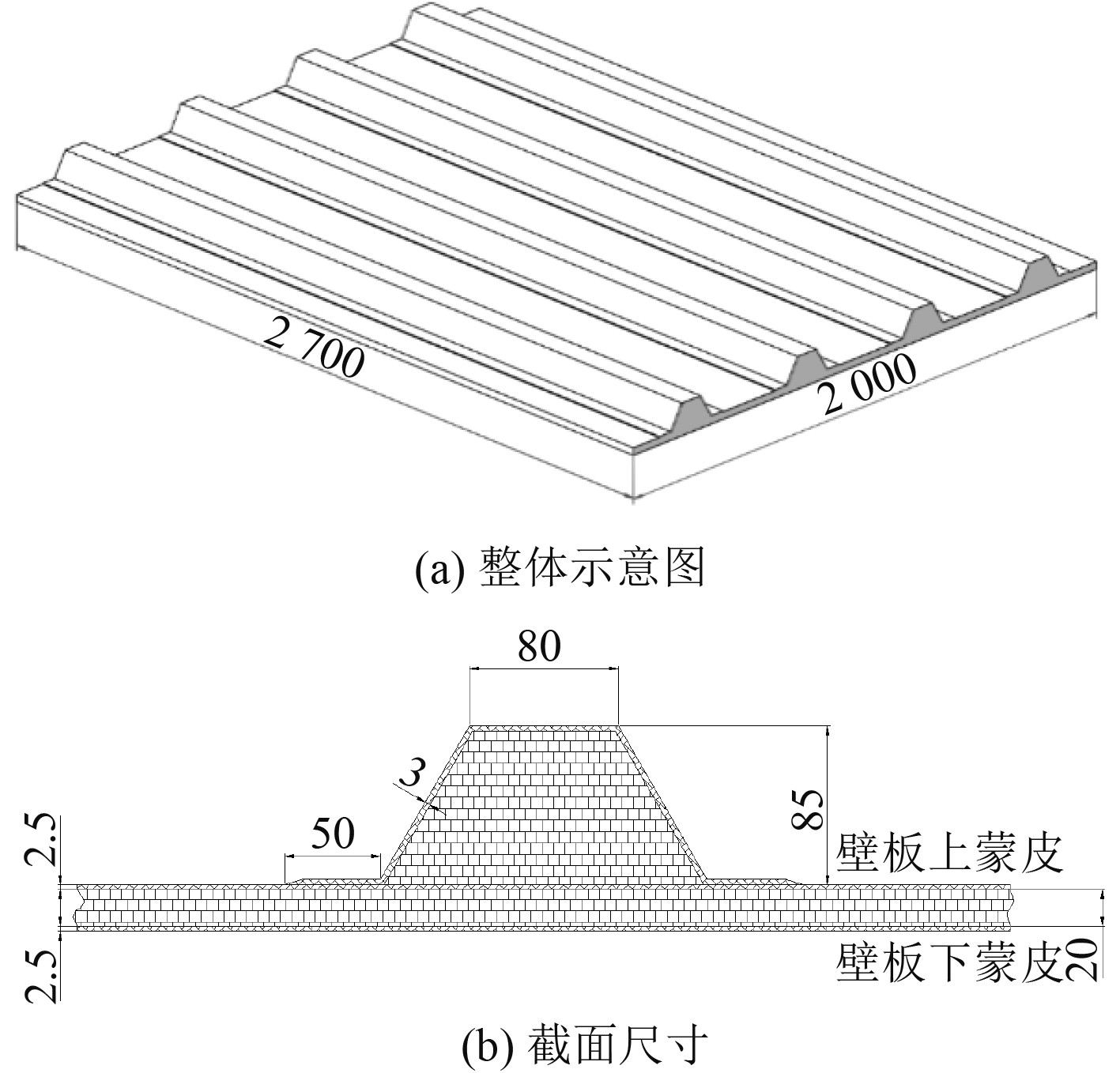
1 复合材料帽型加筋板基本参数

本文讨论的加筋板结构形式及尺寸如图1所示，采用共固化工艺成型，包括面板、腹板、凸缘、壁板蒙皮与芯材。蒙皮为玻璃纤维增强复合材料，其中加强筋蒙皮铺层为12层，壁板蒙皮为10层；芯材为聚氯乙烯泡沫，相关材料与强度参数见表1～表3。

2 有限元分析模型

本文采用Abaqus有限元软件对加筋板进行非线性数值模拟，蒙皮、芯材分别采用SC8R单元与C3D8R单元模拟，芯材与蒙皮、加强筋与壁板之间的胶层界面则采用COH3D8单元模拟，该单元基于Dudgale-Barenblatt的Cohesive Zone理论，综合强度理论和断裂力学方法，适用于模拟复合材料分层与胶层破坏。

对于载荷条件，加筋板应用于客舱甲板，受到人员、货物等引起的面外作用，根据规范取为0.0045 MPa的面外均布载荷^[15]，同时通过参考点在面内施加位移压缩载荷；对于边界条件，在加筋板两端施加简支约束，有限元模型如图2所示。在分析过程中，先对模型进行特征值屈曲分析，将结果乘以缺陷比例系数后作为初始几何挠度作用于模型，以考虑初始几何挠度对加筋板的影响。

3 渐进失效模型 3.1 蒙皮的失效准则与退化模型

本文基于二维Hashin准则^[16]开展复合材料的失效分析，包括4种典型的失效模式。

纤维拉伸失效（ $\widehat {{\sigma _{11}}} \geqslant 0$ )：

$ \left(\frac{\widehat{{\sigma }_{11}}}{{X}_{T}}\right)^{2}+\left(\frac{\widehat{{\tau }_{12}}}{{S}_{L}}\right)^{2}\geqslant 1 \text{,} $

(1)

纤维压缩失效（ $\widehat {{\sigma _{11}}} < 0$ ）：

$ \left(\widehat{\frac{{\sigma }_{11}}{{X}_{C}}}\right)^{2}\geqslant 1 \text{,} $

(2)

基体拉伸失效（ $\widehat {{\sigma _{22}}} \geqslant 0$ ）：

$ \left(\frac{\widehat{{\sigma }_{22}}}{{Y}_{T}}\right)^{2}+\left(\frac{\widehat{{\tau }_{12}}}{{S}_{L}}\right)^{2}\geqslant 1 \text{,} $

(3)

基体压缩失效（ $\widehat {{\sigma _{22}}} < 0$ ）：

$ \left(\frac{\widehat{{\sigma }_{22}}}{2{S}_{T}}\right)^{2}+\left[\left(\frac{{Y}_{C}}{2{S}_{T}}\right)-1\right]\frac{\widehat{{\sigma }_{22}}}{{Y}_{C}}+\left(\frac{\widehat{{\tau }_{12}}}{{S}_{L}}\right)^{2}\geqslant 1 \text{。} $

(4)

式中： $\widehat {{\sigma _{11}}}$ ， $\widehat {{\sigma _{22}}}$ ， $\widehat {{\tau _{12}}}$ 分别为有效应力σ的分量；X_T，X_C代表轴向的拉伸、压缩强度；Y_T，Y_C代表横向的拉伸、压缩强度；S_L，S_T代表复合材料轴向，横向的剪切强度。

对于刚度退化模型，本文采用基于连续介质损伤力学的损伤状态变量对复合材料属性进行退化。平面应力状态下，复合材料失效前表现为线弹性，本构关系为：

$\sigma = {C_o}\varepsilon \text{,} $

(5)

复合材料损伤开始之后，材料的本构关系为：

$\sigma = {C_d}\varepsilon \text{。} $

(6)

其中：

$\begin{split} &{C}_{d}=\frac{1}{D}\\ &\left[\!\!\!\!\!\begin{array}{ccc}(1-{d}_{f}){E}_{1}\!\!\!&\!\!\! (1\!-\!{d}_{f})(1\!-\!{d}_{m}){\nu }_{12}{E}_{1}\!\!\!&\!\!0\\ (1\!-\!{d}_{f})(1\!-\!{d}_{m}){\nu }_{12}{E}_{2}\!\!\!&\!\!\! (1-{d}_{m}){E}_{2}\!\!\!&\!\! 0\\ 0\!\!\!&\!\!\! 0\!\!\!&\!\! D(1\!-\!{d}_{s}){G}_{12}\end{array}\!\!\!\!\!\right]\text{。}\end{split}$

(7)

式中： $D = 1 - (1 - {d_f})(1 - {d_m}){\nu _{12}}{\nu _{21}}$ ，d_f ，d_m，d_s分别代表纤维、基体、纤基剪切的损伤状态变量，可由损伤变量 ${d_f}^t$ ， ${d_f}^c$ ， ${d_m}^t$ ， ${d_m}^c$ 推导。

3.2 芯材本构模型

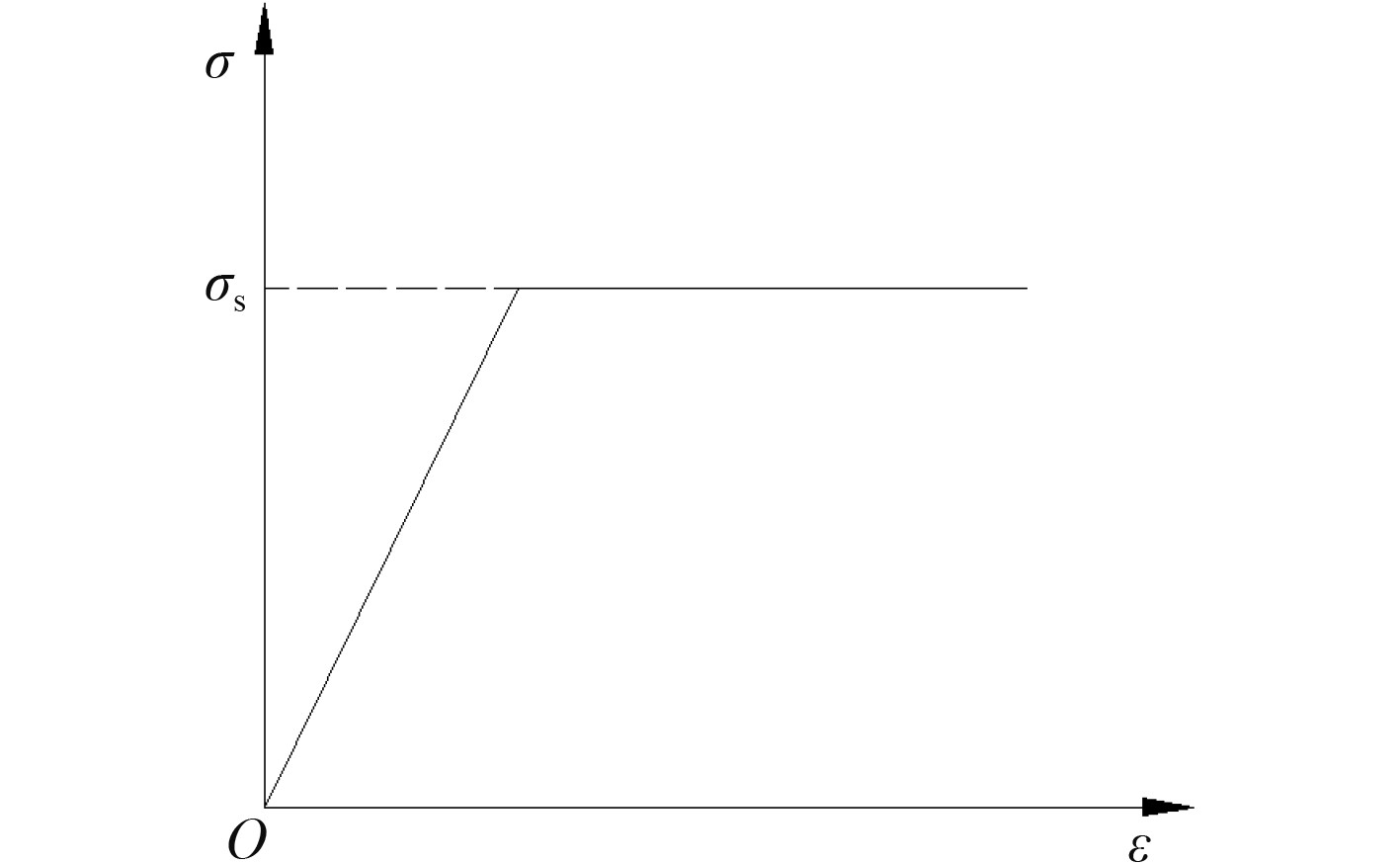
相比于复合材料，芯材的力学性能表现为各向同性，在受载时伴随有明显的塑性变形，因此可采用理想弹塑性模型模拟芯材的本构关系，如图3所示。

3.3 胶层的失效准则与退化模型

本文采用最大应力准则判断胶层界面的失效：

$ max\left\{\frac{\langle {t}_{n}\rangle }{{t}_{n}^{0}},\frac{{t}_{s}}{{t}_{s}^{0}},\frac{{t}_{t}}{{t}_{t}^{0}}\right\}=1 \text{。}$

(8)

式中：t_n，t_s，t_t分别表示界面的法向名义应力与2个切向上的名义应力； $t_n^0$ ， $t_s^0$ ， $t_t^0$ 分别表示界面的Ⅰ型、Ⅱ型、Ⅲ型的破坏强度。

刚度退化采用基于能量控制的线性软化，定义损伤变量为：

$D = \frac{{\delta _m^f(\delta _m^{\max } - \delta _m^0)}}{{\delta _m^{\max }(\delta _m^f - \delta _m^0)}}\text{。}$

(9)

式中： ${\delta _m}^{\max }$ 为单元节点的最大张开量， ${\delta _m}^o$ 为损伤产生时单元的节点张开量； ${\delta _m}^f$ 为完全失效（D=1）时的单元节点张开量，其反映材料在复杂应力状态下的断裂能释放率，本文采用B-K（Benzeggagh-Kenane）准则确定：

${G_C} = {G_{IC}} + ({G_{IIC}} - {G_{IC}}){\left(\frac{{{G_I} + {G_{II}}}}{{{G_I} + {G_{II}} + {G_{III}}}}\right)^\eta }\text{。}$

(10)

其中：G_Ⅰ，G_Ⅱ，G_Ⅲ为界面的法向和两个切向的应变能释放率，G_ⅠC，G_ⅡC为法向和切向的临界应变能释放率，η为材料常数。

损伤变量D直接使界面的应力分量折减：

$ {t}_{n}=\left\{ \begin{array}{l}(1-D){\overline{t}}_{n},{{}_{}}_{}{\overline{t}}_{n}\geqslant 0;\\ {\overline{t}}_{n},{{}_{}}_{}{{}_{}^{}}_{}{\text{otherwise}}\text{。}\end{array} \right. $

(11)

${t_s} = (1 - D){\overline t _s}\text{,}$

(12)

${t_t} = (1 - D){\overline t _t}\text{。}$

(13)

其中： $\overline {{t_n}} $ ， $\overline {{t_s}} $ ， $\overline {{t_t}} $ 为根据界面的线弹性预测的牵引应力分量。

4 数值模拟的验证

为了验证本文数值方法的准确性，以文献[5]中试件2的轴压试验为算例进行对比。

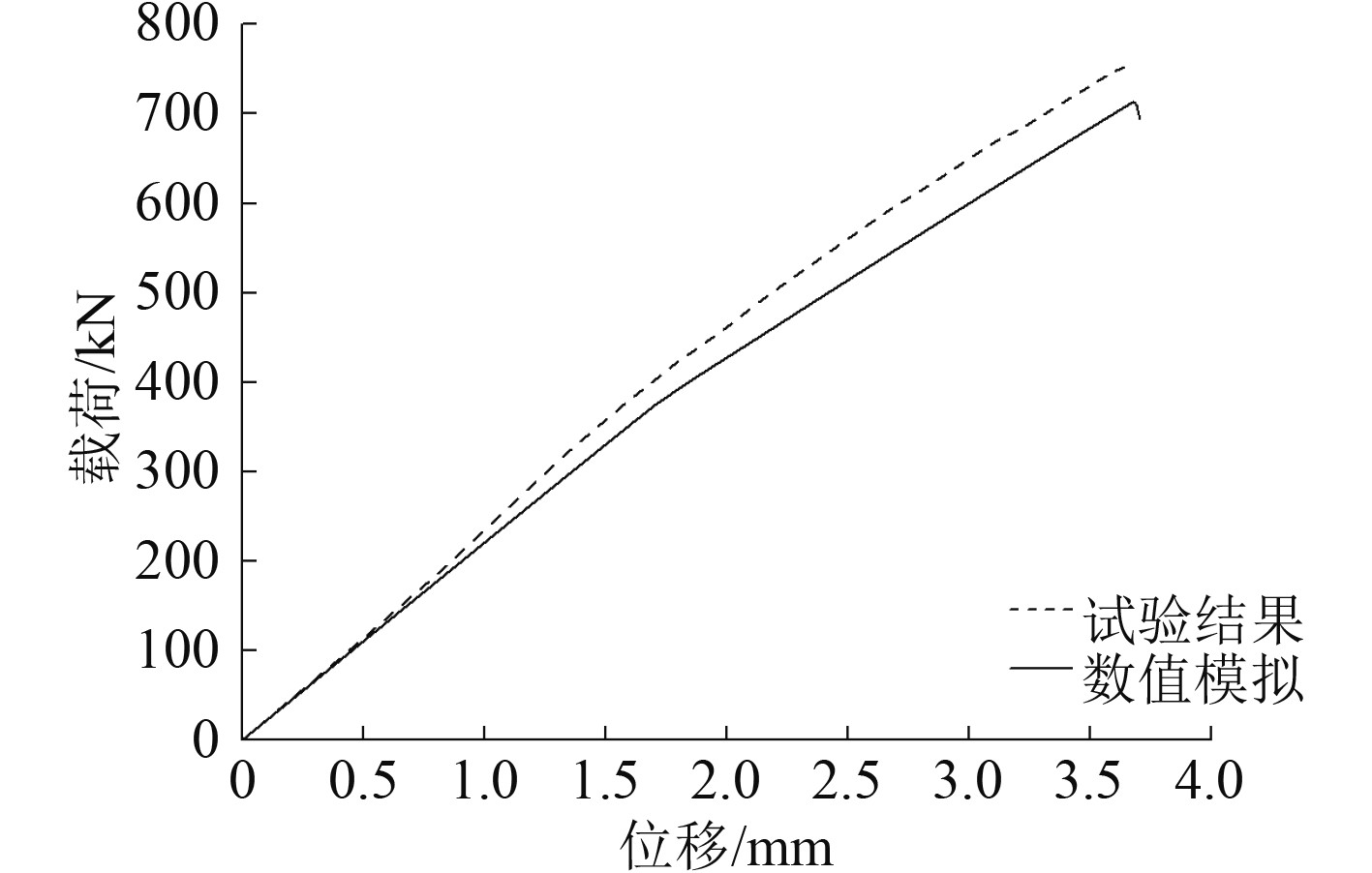
基于本文的分析方法对试件2进行建模计算，结果显示在受压过程中模型产生多阶屈曲，最终因壁板与加强筋的脱粘失效而被压溃破坏。图4为数值模拟与试验的载荷-位移曲线，由图可知两者在轴压作用下的结构响应基本相同，都包括线弹性阶段与后屈曲阶段。

相应的屈曲载荷与极限载荷结果如表4所示。模拟结果与试验结果相对误差较小，满足工程精度要求，由此可知本文的数值模拟方法是可靠准确的。

5 复合材料帽型加筋板的整体破坏分析

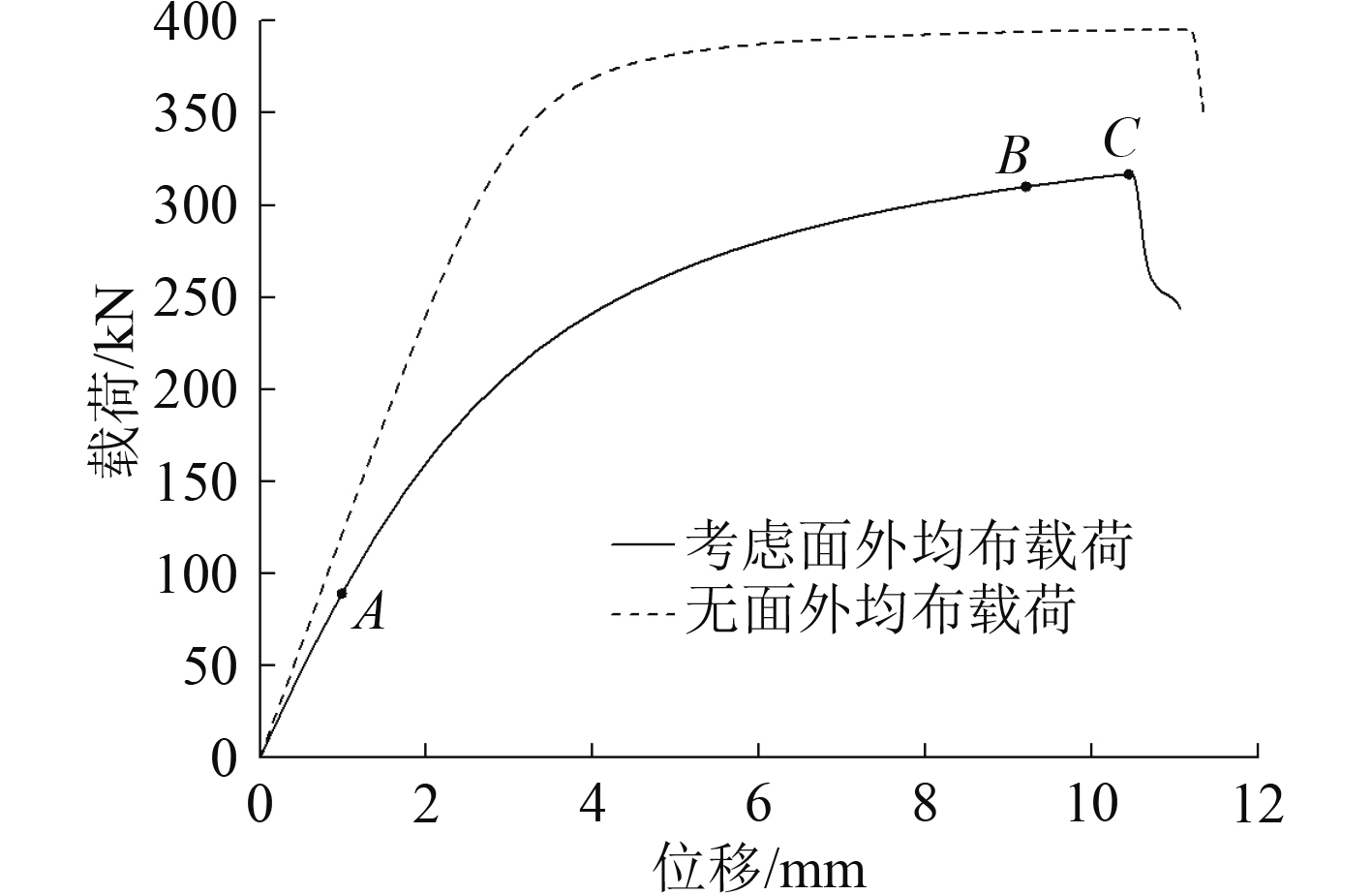
通过有限元分析可得，加筋板的极限载荷为316.8kN，相应加载点的载荷-位移曲线如图5所示。由图可知面外均布载荷对加筋板的极限承载能力造成严重的削弱作用，其中极限载荷降低了19.9%，刚度减小了24.3%，初始屈曲载荷降低量最大，达到67.5%，对应结果见表5。

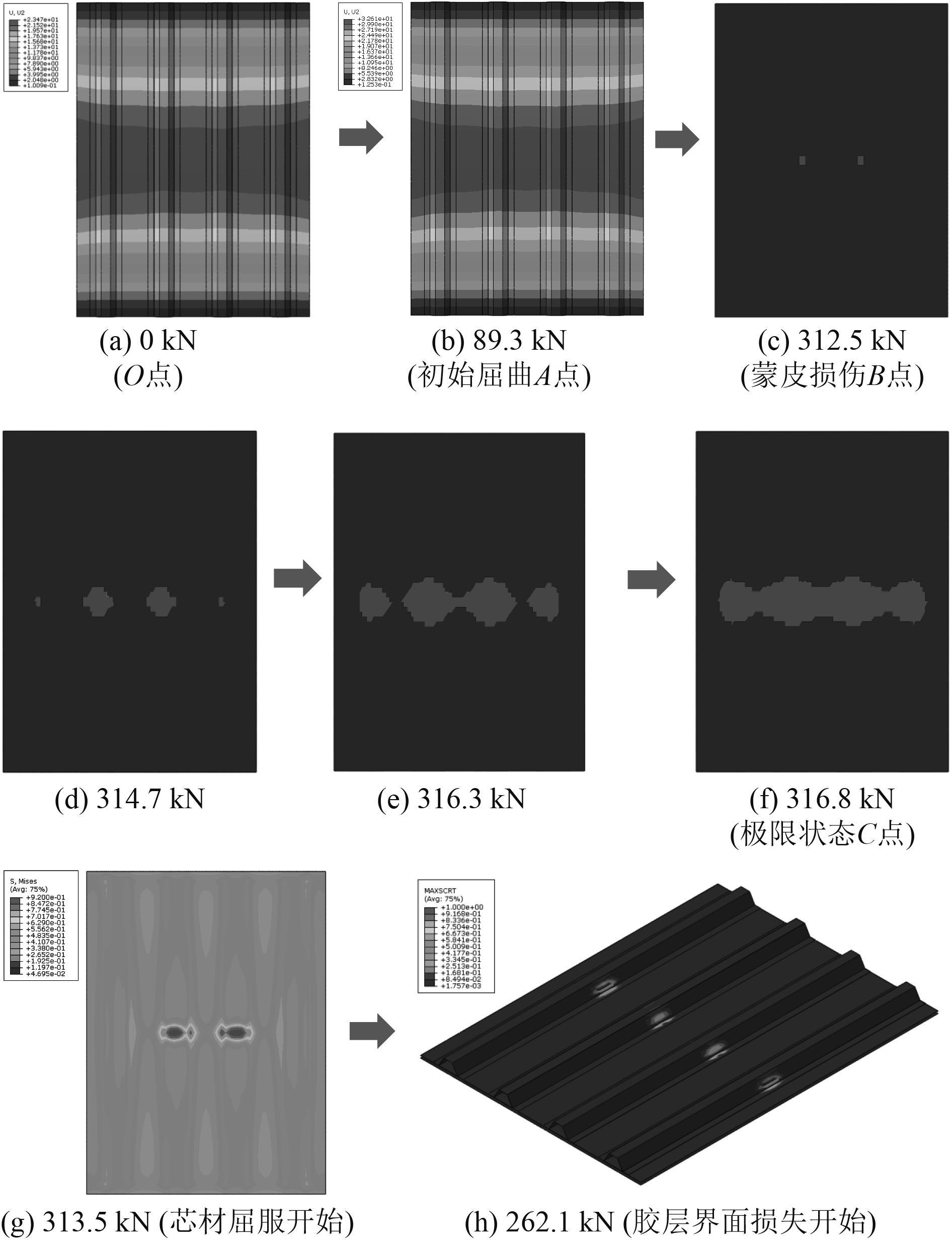
图6为加筋板的渐进破坏过程，结合载荷-位移曲线可知，加筋板的整体响应包括3部分：线弹性阶段OA、后屈曲阶段AC以及失效破坏阶段。在起始点，由于加筋板受到面外均布载荷，因此已产生一定的面外变形；随着压缩载荷的施加，曲线达到初始屈曲载荷A点，加筋板呈现出整体一阶屈曲变形，之后加筋板开始进入后屈曲阶段，刚度不断减弱；当载荷增加到312.5 kN时，中间2条加强筋下方的无筋一侧的壁板蒙皮首先开始出现纤维压缩失效，对应于曲线中的B点；接着，随着载荷的增加蒙皮的失效区域迅速扩展，壁板蒙皮的原有失效区域进一步扩大，同时边缘2条加强筋下的壁板蒙皮也开始出现失效，最终失效区域相连形成大面积的连贯失效，此时加筋板达到极限状态C点，载荷增加至316.8 kN。随后，载荷-位移曲线突降，加筋板丧失承载能力，芯材屈服破坏，胶层界面损伤产生，蒙皮的压缩失效不断扩展，最终壁板在中间被压溃折断，如图7所示。

总结加筋板的失效机理为：压缩载荷使加筋板产生较大的面外屈曲变形，壁板蒙皮受到较大的压应力，使得加强筋下方的壁板蒙皮首先产生纤维压缩失效，蒙皮的承载能力减弱；随着载荷的继续增加，失效区域迅速沿横向扩展，当蒙皮失效区域覆盖所有4条加强筋后，壁板蒙皮失去承载能力，进而导致加筋板整体破坏，达到极限状态；壁板芯材也迅速发生屈服破坏，加筋板被压溃折断。由此分析可知，壁板蒙皮的纤维压缩失效及扩展是导致加筋板整体破坏的直接原因，而应力分量S₁₁是加筋板破坏的主要因素。

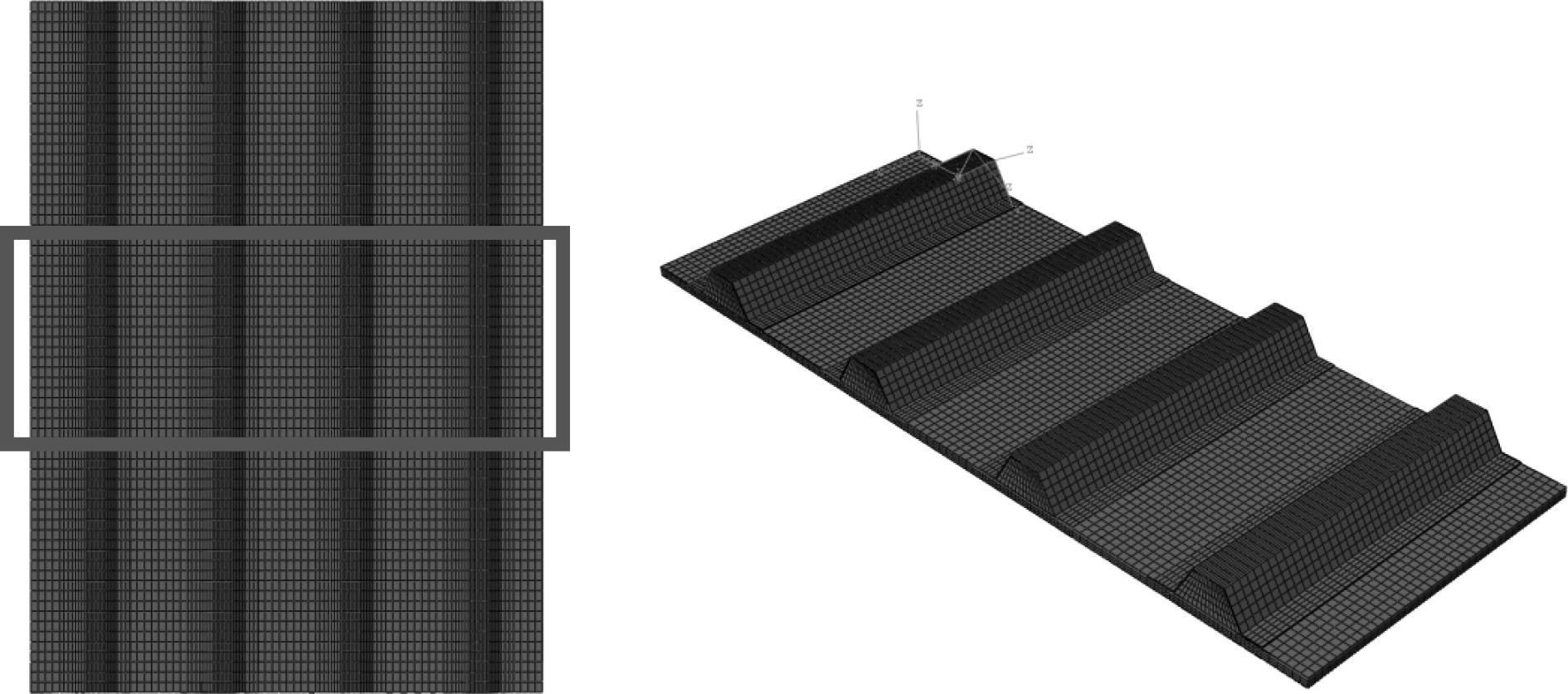
6 复合材料帽型加筋板的局部破坏分析

在加筋板的整体破坏分析中，无法准确分析蒙皮内各铺层的损伤状况，因此以加筋板的整体模型为基础，通过验证分析后选取中间800 mm范围的区域建立子模型进行局部破坏分析，如图8所示。子模型中蒙皮采用C3D8R单元模拟，每一铺层对应一层单元，芯材与胶层的单元则保持不变。

6.1 失效准则与刚度退化模型

本文选取Shokrieh-Hashin准则^[17]作为子模型复合材料的失效判据，除了考虑纤维拉伸、纤维压缩、基体拉伸、基体压缩4种失效模，还综合考虑了纤维基体的剪切失效、拉伸分层以及压缩分层。

纤维拉伸失效（ $ {\sigma }_{11}>0$ ）：

$ {\left( {\frac{{{\sigma _{11}}}}{{{X_T}}}} \right)^2} + {\left( {\frac{{{\tau _{12}}}}{{{S_{12}}}}} \right)^2} + {\left( {\frac{{{\tau _{13}}}}{{{S_{13}}}}} \right)^2} \geqslant 1 \text{,} $

(14)

纤维压缩失效（ $ {\sigma }_{11}<0$ ）：

$ {\left( {\frac{{{\sigma _{11}}}}{{{X_c}}}} \right)^2} \geqslant 1 \text{,} $

(15)

基体拉伸失效（ $ {\sigma }_{22}>0$ ）：

$ {\left( {\frac{{{\sigma _{22}}}}{{{Y_T}}}} \right)^2} + {\left( {\frac{{{\tau _{12}}}}{{{S_{12}}}}} \right)^2} + {\left( {\frac{{{\tau _{23}}}}{{{S_{23}}}}} \right)^2} \geqslant 1 \text{,} $

(16)

基体压缩失效（ $ {\sigma }_{22}<0$ ）：

$ {\left( {\frac{{{\sigma _{22}}}}{{{Y_{\rm{c}}}}}} \right)^2} + {\left( {\frac{{{\tau _{12}}}}{{{S_{12}}}}} \right)^2} + {\left( {\frac{{{\tau _{23}}}}{{{S_{23}}}}} \right)^2} \geqslant 1 \text{,} $

(17)

纤维基体剪切失效（ $ {\sigma }_{11}<0$ ）：

$ {\left( {\frac{{{\sigma _{11}}}}{{{X_{\rm{c}}}}}} \right)^2} + {\left( {\frac{{{\tau _{12}}}}{{{S_{12}}}}} \right)^2} + {\left( {\frac{{{\tau _{13}}}}{{{S_{13}}}}} \right)^2} \geqslant 1 \text{,} $

(18)

拉伸分层（ $ {\sigma }_{33}>0$ ）：

$ {\left( {\frac{{{\sigma _{33}}}}{{{Z_T}}}} \right)^2} + {\left( {\frac{{{\tau _{13}}}}{{{S_{13}}}}} \right)^2} + {\left( {\frac{{{\tau _{23}}}}{{{S_{23}}}}} \right)^2} \geqslant 1 \text{,} $

(19)

压缩分层（ $ {\sigma }_{33}<0$ ）：

$ {\left( {\frac{{{\sigma _{33}}}}{{{Z_{\rm{c}}}}}} \right)^2} + {\left( {\frac{{{\tau _{13}}}}{{{S_{13}}}}} \right)^2} + {\left( {\frac{{{\tau _{23}}}}{{{S_{23}}}}} \right)^2} \geqslant 1 \text{。} $

(20)

通过编写用户子程序USDFLD，定义4个场变量FV1～FV4，基于刚度折减系数建立相应的刚度退化模型，退化方案如表6所示。

6.2 蒙皮铺层的失效分析

子模型无筋一侧的壁板蒙皮产生纤维失效（FV1）与纤维基体剪切失效（FV3）2种破坏形式，2种破坏形式的发生时间与位置基本相同，因此蒙皮的破坏可概括为1方向的纤维压缩失效，具体包括纤维基体的剪切分离与纤维的压溃。

由于2种破坏形式的扩展规律基本相同，因此以纤维失效（FV1）为例分析各铺层的失效过程，表7为每一铺层的损伤扩展过程，其中第1层为壁板蒙皮的最外层，第10层为与芯材相连的最内层。由图分析可知，每一层复合材料的损伤扩展规律相同，均为中间2条加强筋下方区域首先破坏，接着边缘2条加强筋下方的蒙皮也发生破坏，同时中间的破坏区域扩大并逐渐相连，最后在极限状态下加强筋下方的蒙皮发生连贯失效。对于不同铺层，失效面积从外向内逐渐减小，且第1到第5层的面积减小速率较快，第6到第10层的减小速率较慢，因此可得出蒙皮的纤维失效由外向内扩展，且外层的扩展速率更快。

7 结　语

本文在通过与公开试验结果对比验证数值模拟方法准确性的前提下，基于非线性有限元方法对夹芯复合材料帽型加筋板在面内压缩与面外均布载荷作用下的极限承载力进行渐进失效分析，最终得出以下结论：

1）面外均布载荷对面内受压加筋板的极限承载力具有明显的削弱作用，因此研究相关问题时不应忽略面外均布载荷的影响。

2）在面内压缩与面外均布载荷的共同作用下，加筋板的破坏模式为整体一阶屈曲破坏，极限载荷为316.8 kN，其载荷-位移曲线包括线弹性、后屈曲与失效破坏3个阶段。无筋一侧壁板蒙皮的压缩失效是导致加筋板整体破坏的直接原因，当4条加强筋下的蒙皮形成连贯失效区域时，加筋板达到极限状态，接着芯材发生屈服破坏，胶层界面产生损伤，最终加筋板在中间被压溃折断。

3）基于Shokrieh-Hashin准则对加筋板破坏区域的子模型进行分析，破坏位置蒙皮的纤维失效从最外层向最内层扩展，外层的失效面积大于内层，外5层的纤维失效扩展速率更快。每一铺层的失效区域及扩展规律一致，与加筋板整体模型的蒙皮渐进失效过程相同。