2. 武汉理工大学 高性能舰船技术教育部重点实验室,湖北 武汉 430063
2. Key Laboratory of High Performance Ship Technology, Ministry of Education, Wuhan University of Technology, Wuhan 430063, China
在世界各国经济不断发展的同时,对能源的需求也日益增多[1],航运业是联系各国贸易的重要纽带,但同时也是耗能大户,如何提高船舶能效,减少污染成为了目前亟待解决的问题。有研究表明,减少船舶的整体重量,不仅能够有效提高船舶能效,还能减少建造船舶钢材的使用[2]。而在轻量化的过程中必定会存在舶结构强度不够、安全系数降低、某些部位振动剧烈甚至振裂等安全问题,因此在保证安全参数不下降的情况下,减轻船舶的重量就成为了研究焦点。
加筋板作为船舶中的基本结构单元,对其开展轻量化设计研究并推广,将有助于全船整体重量的减少,达到全船轻量化的目的。加筋板的强度是其重要安全指标之一,大量的实验研究[3]和模拟研究[4]讨论不同变量参数对极限强度的影响,也有的通过研究解析解的方式探究其强度变化规律[5]。所以以强度为核心参数的结构优化是研究重点,Singh等[6]开展了加强筋位置优化,利用曲线加强筋代替原均布直线的布置,Badran等[7-8]研究并设计了一种新型的Y型加强筋剖面,能够提供更多的抗扭转强度。除了力学特性,振动特性同样也是加筋板的重要特性之一,张文春等[9]就运用模态叠加法对纵向混合构型加筋板在线激励作用下振动特性开展了相关研究工作,同样也有学者以振动控制为目标的结构优化研究[10]。
在结构优化研究中,一般只考虑力学特性或振动特性其中之一,鲜有同时考虑振动与重量的结构优化研究,而船舶的加筋板要保证一定强度同时,对振动控制也有一定的要求。而在结构优化中,重量、强度、刚度三者间相互关联,互相影响,为了能够实现轻量化和振动的协同设计,在力学分析的基础上加入单位激励的谐响应分析,并约束分析频段内的最大位移值,在优化后的校核计算中也将自由模态频率的分布情况作为校核的重要指标,以达到协同设计的目的。
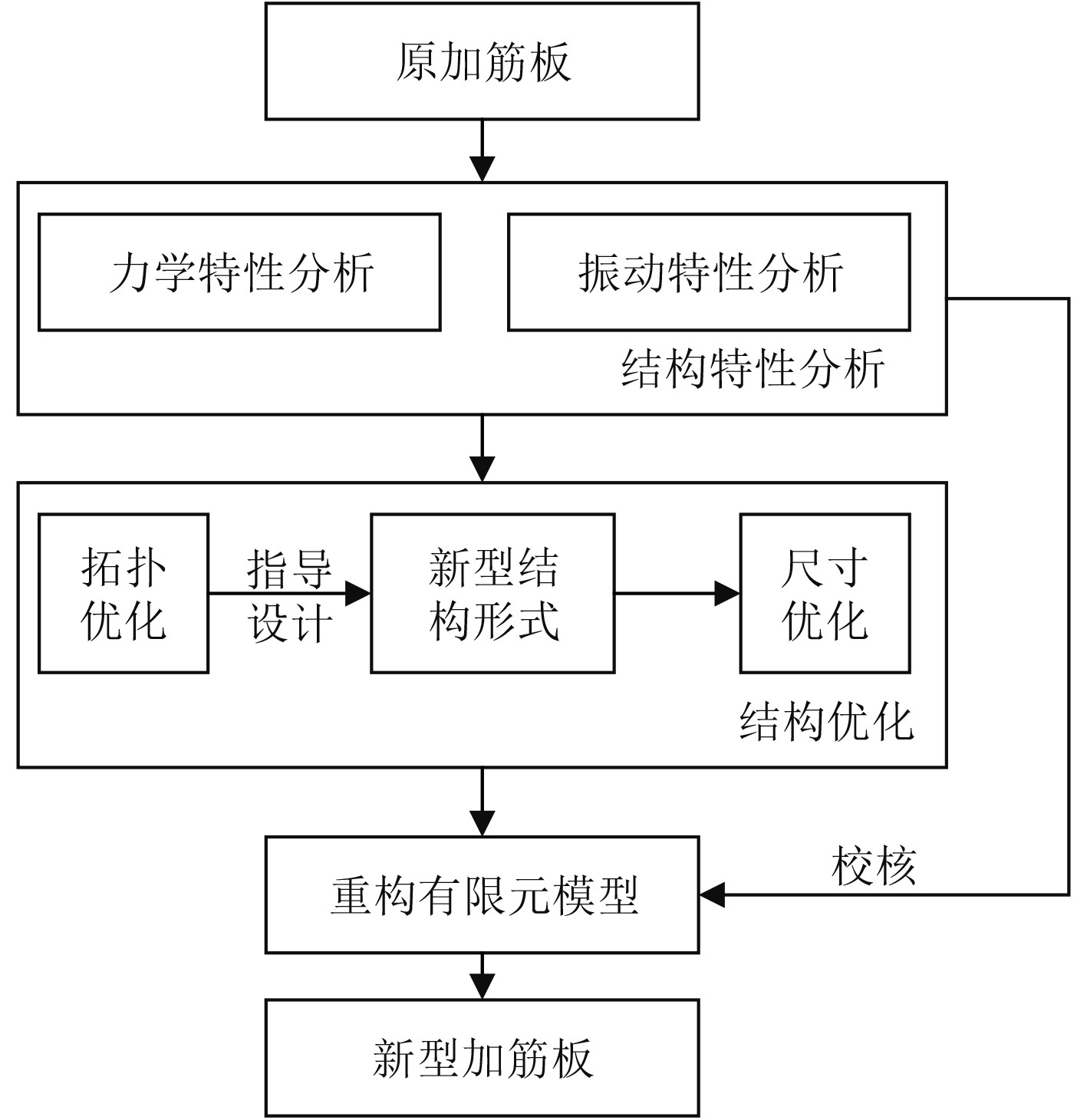
如图1所示,本文基于OptiStruct结构优化软件,采用拓扑优化和尺寸优化相结合的方法,全面考虑加筋板的力学和振动特性,以最小重量为目标,对加筋板结构开展轻量化与振动的协同设计。根据优化结果和实际生产需求重构模型,并与原加筋板进行对比,验证优化结果的有效性。最后将详细分析腹板与底板的夹角大小对新型加筋板特性的影响。
|
图 1 结构优化流程示意图 Fig. 1 Structure optimization process |
基于OptiStruct软件开展加筋板轻量化设计研究,其优化过程分为拓扑优化和尺寸优化两步,与概论设计和详细设计2个阶段相对应,通过拓扑优化改变拓扑结构,设计新型加筋板结构形式,再进行尺寸优化,寻找约束条件下尺寸参数的最优解。
1.1 拓扑优化拓扑优化采用变密度法进行求解,材料的固有属性与材料密度定义为非线性关系。在拓扑优化过程中,定义优化区域内的材料密度分布在0~1之间,通过查看优化后材料的分布情况,指导优化设计工作。材料的密度和弹性模量的非线性关系可以表示为如下关系[11]:
| $\left\{ \begin{array}{l} E = {\eta ^\alpha }{E_0} \text{,}\\ \nu = {\nu _0} \text{。}\\ \end{array} \right.$ | (1) |
式中:
拓扑优化以最小质量为优化目标,考虑平衡方程和约束条件,寻找最优材料密度分布。计算过程中通过改变优化区域内单元密度,迭代计算。经过拓扑优化后,设置合适阈值,删除材料密度小于阈值的单元,从而形成新的拓扑结构。其优化模型为下式:
| $\left\{ \begin{array}{l} {\rm{Find}}\begin{array}{*{20}{l}} {}& \end{array}{\bf{\eta }} = {{\rm{(}}{\eta _1},{\eta _2}, \cdots ,{\eta _n})^{\rm{T}}} \text{,}\\ {\rm{Min}}\begin{array}{*{20}{l}} {}&{\begin{array}{*{20}{l}} \end{array}} \end{array}Mass = {\bf{\eta }}*{V_0} \text{,}\\ {\rm{s.t.}}\begin{array}{*{20}{c}} {}& \end{array}\;\;\;{Y_{\min }} < {Y_i} < {Y_{\max }} \text{,}\\ \begin{array}{*{20}{l}} {}&{}&{}&{} \end{array}\varepsilon \leqslant {\eta _i} \leqslant 1\text{,}\begin{array}{*{20}{l}} {}&{} \end{array}(i = 1,2, \cdots ,n) \text{,}\\ \begin{array}{*{20}{l}} {}&{}&{}&{} \end{array}{\eta _i} = 1\text{,}\begin{array}{*{20}{l}} {}&{} \end{array}(i = {J_1},{J_2}, \cdots ,{J_k}) \text{,}\\ \begin{array}{*{20}{l}} {}&{}&{}&{} \end{array} {{K}} {\bf{\delta }} = {{F}} \text{。}\\ \end{array} \right.$ | (2) |
式中:
轻量化与振动的协同设计就是在优化过程中,将振动分析的响应值合理引入到约束变量
尺寸优化对应产品详细设计阶段,其设计变量与刚度矩阵一般为简单的线形关系,优化变量一般为构件的尺寸参数。式(3)为尺寸优化的数学模型。
| $ \left\{ \begin{array}{l} {\rm Find}\begin{array}{*{20}{c}} {}&{}&{} \end{array}{{X}} = {[{X_1},{X_2}, \cdots ,{X_n}]^{\rm{T}}}\begin{array}{*{20}{c}} \in &{\left[ {{X_{\min }},{X_{\max }}} \right]}\text{,} \end{array}\\ {\rm Min}\begin{array}{*{20}{c}} {}&{}&{} \end{array} Mass\text{,}\\ {\rm{s.t}}\begin{array}{*{20}{c}} {}&{}&{\begin{array}{*{20}{c}} \end{array}} \end{array}\;\;\;{Y_{\min }} < {Y_i} < {Y_{\max }}\text{,}\\ \begin{array}{*{20}{c}} {}&{}&{}&{\begin{array}{*{20}{c}} \end{array}} \end{array}\;\;\; {{K}} {{\delta }} = {{F}} \text{。} \end{array} \right. $ | (3) |
式中:
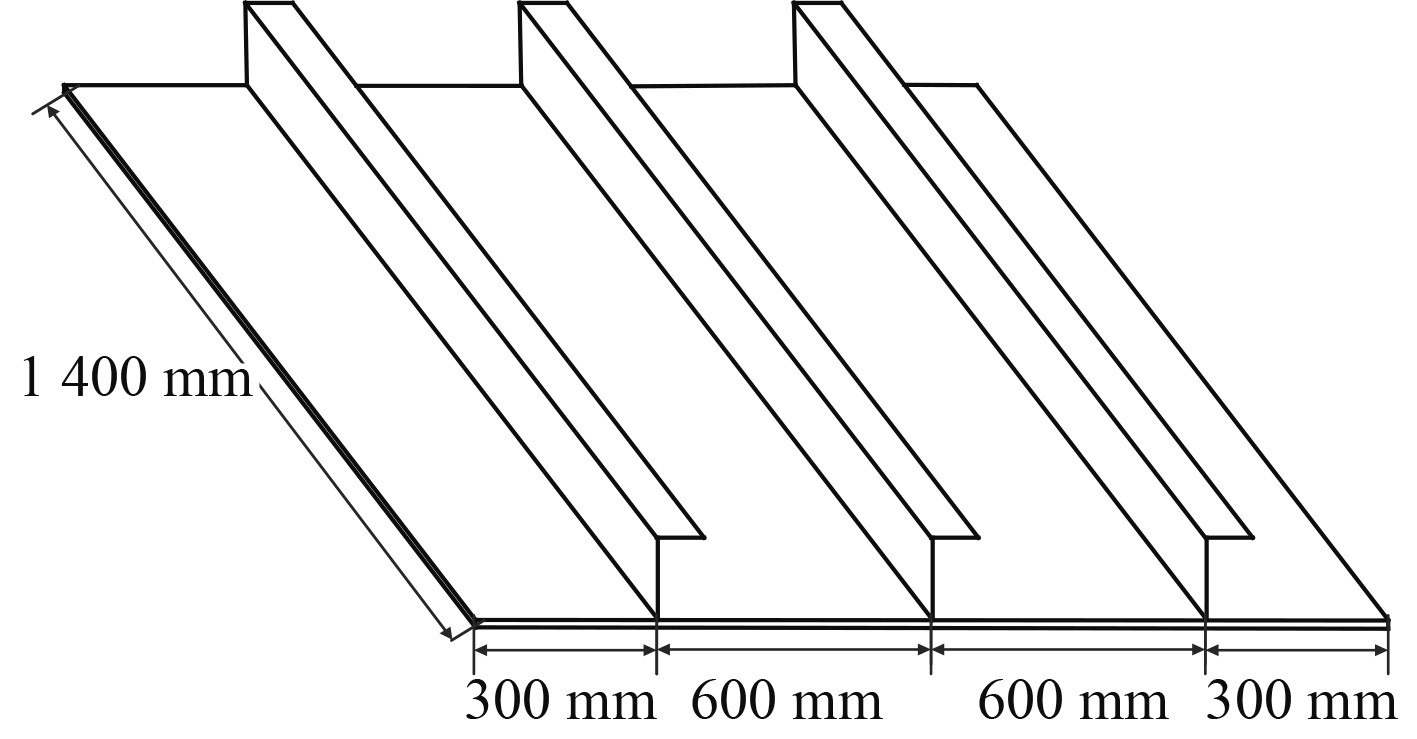
加筋板是船舶的基本结构单元,开展结构优化设计工作前,首先需要对加筋板的特性进行分析,并以此作为后续优化的参考和约束。以某船舶上层建筑为研究对象,截取了一段包括3条L型加强筋的板,具体尺寸如图2所示。
|
图 2 加筋板示意图 Fig. 2 Stiffened plate |
底板厚6 mm,L型材的尺寸为75×50×5。有限元模型全部采用PSHELL壳单元,其中网格尺寸最大20 mm,为提高局部计算进度及到后期的优化工作,将加强筋处的网格细化到5 mm。板材和加强筋的材料为钢材,弹性模量210000 MPa,泊松比0.3,密度7.85*10−9 mm3/t,临界阻尼比0.03。为了模拟截断加筋板的边界,分别在四条边上创建了4个中点,将网格的边界点与此点通过刚性单元绑定,如图3所示。

|
图 3 加筋板有限元模型 Fig. 3 Finite element model of stiffened plate |
如表1所示,一共分析了10个工况,其中前6个工况分析板材抗外力的能力,是板材强度的体现;工况7和工况8是屈曲强度分析,体现了板材整体的稳定性;最后两工况分别计算了自由模态和谐响应,代表了板材振动特性。经过有限元计算后,将计算结果汇总到表1中的计算结果。
|
|
表 1 详细工况及计算结果汇总表 Tab.1 Summary of detailed operating conditions and calculation results |
如表1所示,在强度分析中,均布载荷使得加筋板产生了较大形变和应力,将作为后续拓扑优化应力约束的参考。由于加强筋是单向的,所以2个方向的抗扭转能力和屈曲强度呈现较大差距,后续优化过程中将对2个方向分别约束,避免过约束或欠约束。振动分析中,谐响应的最大振幅对应频率与第2阶模态频率相近,两者存在一定的关联,但单一的模态频率或谐响应来表征振动特性不够全面,因此2种振动分析都是必不可少的,也是后续协同振动控制结构优化的重要约束条件。
3 优化设计及结果讨论通过结构特性分析得到的应力应变、屈曲强度和频率特性分别表征了板材的强度和振动特性,各个工况下的计算值将作为后续优化过程中的约束条件,进一步开展结构优化研究。结构优化在满足原板性能不降低的约束下,以最小质量为优化目标,通过拓扑优化得到材料分布情况,从而指导重新设计新型结构形式,在根据尺寸优化结果确定最终板材厚度。
3.1 结构优化由于船舶中加强筋的布置距离与船舶肋距相关,所以选定3条加强筋所在的立方体空间为拓扑优化空间,同时设置了对称约束和拔模约束,如图4所示。为提高优化精度,对优化区域的网格进行了加密处理,网格尺寸为5 mm。

|
图 4 加筋板有限元优化模型 Fig. 4 Finite element optimization model |
由于拓扑优化属于概论设计阶段,优化结果仅作为后续设计的指导,因此可以适当放宽约束条件,从而使得计算更容易收敛,优化效率提高。在拓扑优化中,对应变施加强制约束,将应力转换为参考约束,即优化过程中允许有少量网格的应力大于约束值。表2为各工况下具体约束的大小,应变最大放宽不超过0.2 mm,屈曲强度放宽不超过10%,而为了能够更好控制振动,对谐响应工况下的最大位移约束提高了约10%。
|
|
表 2 拓扑优化约束 Tab.2 Topology optimization constraints |
图5为拓扑优化结果局部图。其顶部和两侧区域材料较为重要,中心部分的材料被掏空,所以将其设计为空心的加强筋,两侧相对于顶板来说存在一些挖空部分,能够通过挖孔的方式进一步降低重量。考虑到实际的加工需要,先不对侧边进行镂空处理。

|
图 5 加筋板拓扑优化结果 Fig. 5 Topology optimization results |
根据拓扑优化结果,重新设计了图6所示的加强筋形式。新结构保持高度和顶板宽度不变,腹板与底板之间的角度为45°,并且除去了底板。经过计算发现,去除底板导致垂直于加强筋方向的屈曲强度大大降低,而增加少量支撑能够大幅提高屈曲强度。因此构建了如图7所示有限元模型,去除底板后增加了3块均布的支撑板。腹板与底板之间的角度将在后续做详细的讨论。

|
图 6 梯形加强筋局部 Fig. 6 Part of trapezoidal stiffened plate |

|
图 7 轻量化加筋板有限元模型 Fig. 7 Lightweight stiffened plate finite element model |
根据拓扑优化结果建立模型后,利用尺寸优化进行加筋板的详细设计,以确定最终尺寸参数。尺寸优化设定更严格的约束条件,以保证最终优化的有效性,具体约束如表3所示。由于底板表面积降低,均布压力值调整为0.014 MPa,使得总体载荷值略大于之前的载荷,以保证优化有效性。在一般工程应用中,达到第1阶屈曲值后,就已经对结构产生了破坏,所以只约束第1阶屈曲强度。
|
|
表 3 尺寸优化约束 Tab.3 Size optimization constraints |
如表4所示,优化前尺寸参照原加筋板尺寸设定(面板5 mm,L型材75×50×5),上下限是在原尺寸的基础上上下浮动。经过尺寸优化后,得到表中优化后尺寸,考虑到实际制造过程中使用冲压工艺造价更低,最终确定为厚度5 mm的均质板。
|
|
表 4 尺寸优化变量参数及优化结果 Tab.4 Variable constraints and optimization results |
根据表4中尺寸优化结果,重构有限元模型,在保证载荷不降低的前提下,适当调整载大小和施加位置,重新对比分析各工况下的优化后加筋板的特性参数,将最终的计算结果汇总到表5。
|
|
表 5 优化前后特性对比 Tab.5 Performance comparison before and after optimization |
如表5所示,所有工况下最大应变值都小于原加筋板的计算值,除工况4的最大应力增大了13 MPa以外,其他工况的最大应力都有所减少,2个方向的屈曲强度也有显著提升,固有频率增大,在谐响应工况下,最大位移降低了0.3 mm,板的质量由原139.3 kg降低到112.5 kg,在原基础上减少了19.2%的重量。工况4中应力出现了大于原加筋板的情况,这是因为板整体厚度比原加筋板减少1 mm,导致点载荷施加在薄板处后,应力出现了增大的情况,但是应变比原加筋板有所减小,所以认为在此工况下为优化后强度没有降低。
在振动特性分析中,优化后模态频率排列与原加筋板同阶振型对应,相同振型对应频率的增加间接说明了加筋板整体刚度的增加质量降低,固有频率向高频方向的移动使得建造后上层建筑的振动很容易控制。在谐响应分析中,最大振动位移降低0.3 mm,即振动位移级峰值降低6 dB,显示了振动控制的有效性。
总体上,优化后的加筋板不仅具有较轻的重量,而且具有较高的强度和良好的振动特性,能够广泛适用于船舶的上层建筑。但由于面板不完整和对点载荷较敏感的特点,也具有一定的局限性,不适用于船舶外壳和机舱等位置。
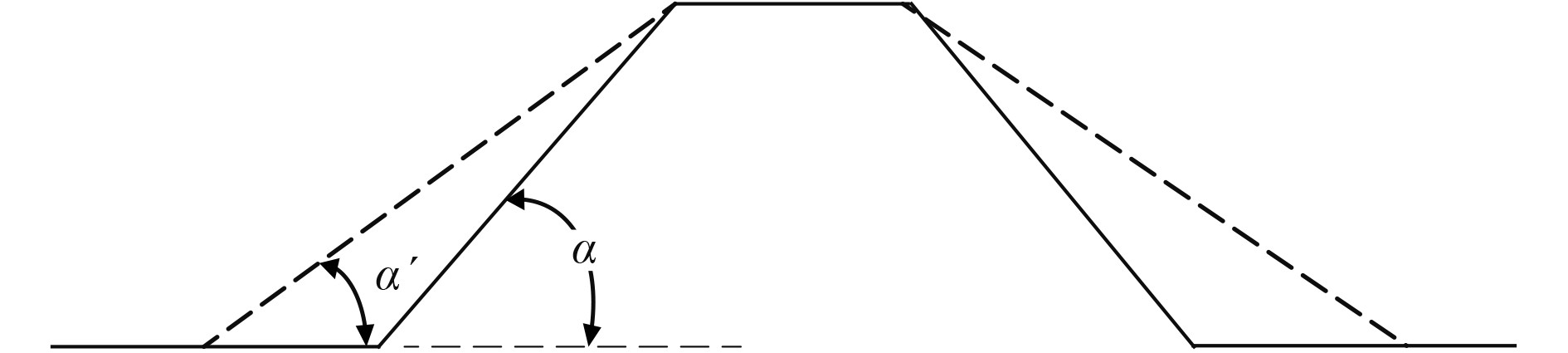
4 腹板与底板的夹角对板材特性的影响在新型加筋板设计中,腹板与底板的夹角是所有参数中影响最为复杂的参数,也是影响新型板性能的重要参数,故将对其进行详细对比分析研究。有限元分析中,所有板材均为5 mm,保持顶板宽度及梯形高度不变,以腹板与底板之间的角度α作为变量,如图8所示,虚线为改变α后腹板的位置。
|
图 8 梯形加强筋局部示意图 Fig. 8 Part of trapezoidal stiffener |
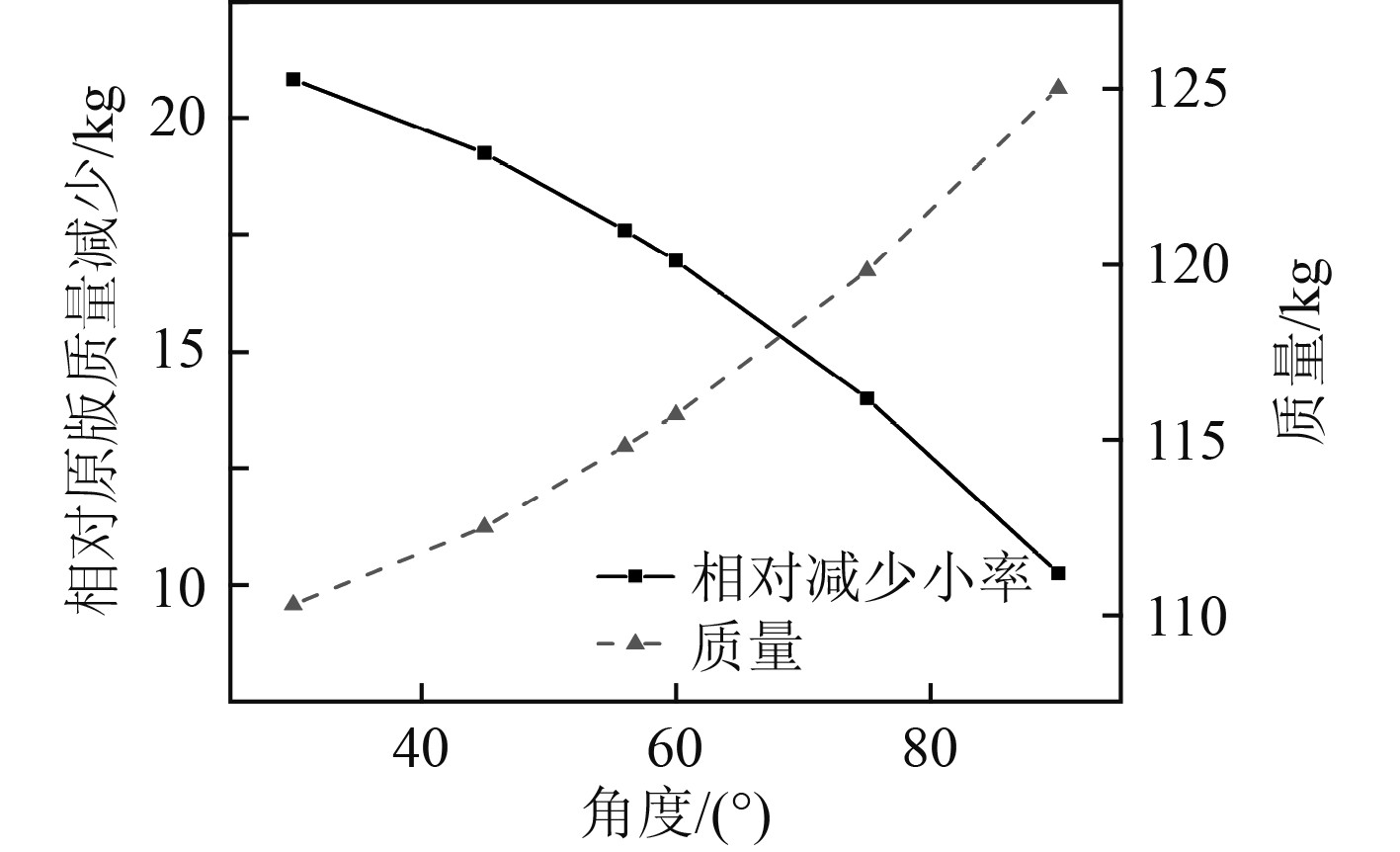
如图9所示,随着角度的减小,整体重量而减少,变化率略微降低。由于整体厚度的下降,夹角即使在90°的情况下,也相比于原板降低10.2%。
|
图 9 质量变化曲线 Fig. 9 Curve of weight change |
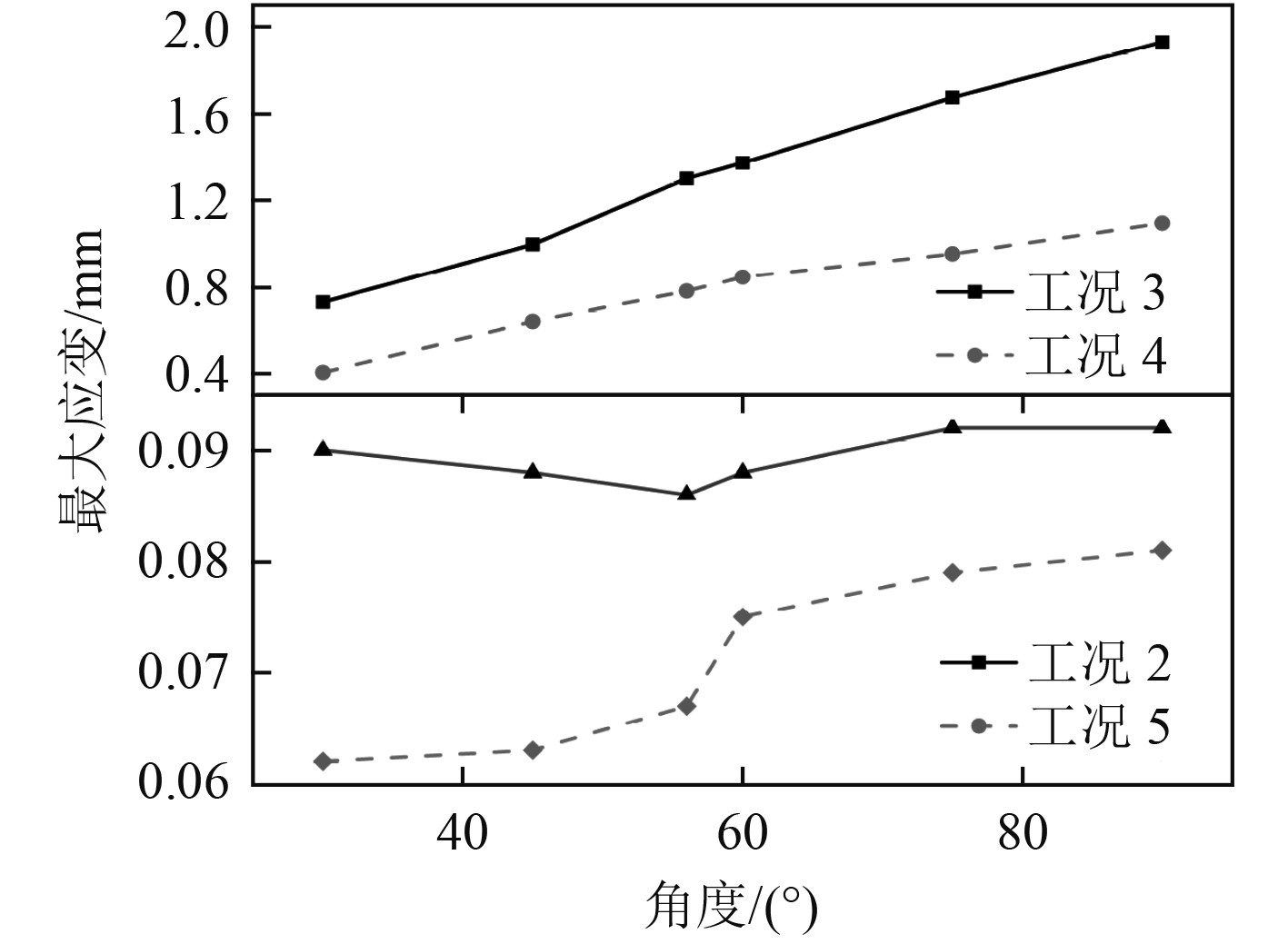
图10为最大应变随角度变化曲线图,工况1和工况2趋势相同,工况5和工况6趋势相同,故只展示变化明显的4个工况。随着角度增加,工况3、工况4和工况5的最大应变呈总体呈上升趋势,而在工况2的最大应变先略微下降后增加。
|
图 10 最大应变曲线 Fig. 10 Maximum strain curve |
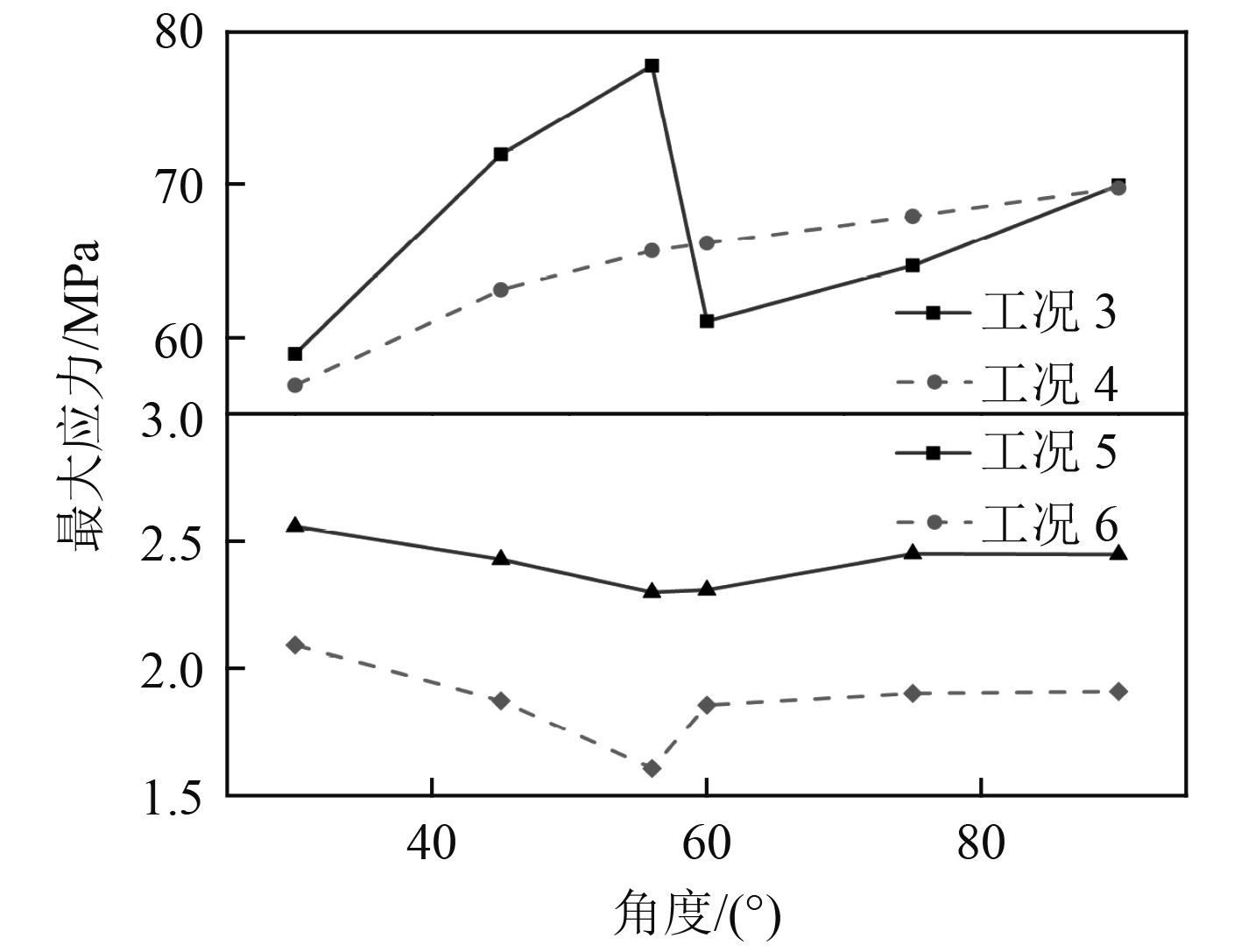
图11为最大应力随角度变化曲线图,由于工况1、工况2与工况5趋势相同,所以不予展示。在均布载荷的作用下,夹角为60°使最大应力突然减小,这是由于随着夹角的增加,底板面积逐渐增大,为保持总载荷不变,单位面积载荷减小,而角度的增加,也使得腹板对垂直于底板方向的支撑增强,因此出现了突变,这也导致了除工况4以外其他工况在60°附近存在一个最大应力极小值;而随着角度继续增加,面积增加所带来的强度降低更加显著,故呈小幅上升趋势。总体上,角度对板材各工况下的强度影响辅助,小角度将有助于提高板材的整体强度。
|
图 11 最大应力曲线 Fig. 11 Maximum stress curve |
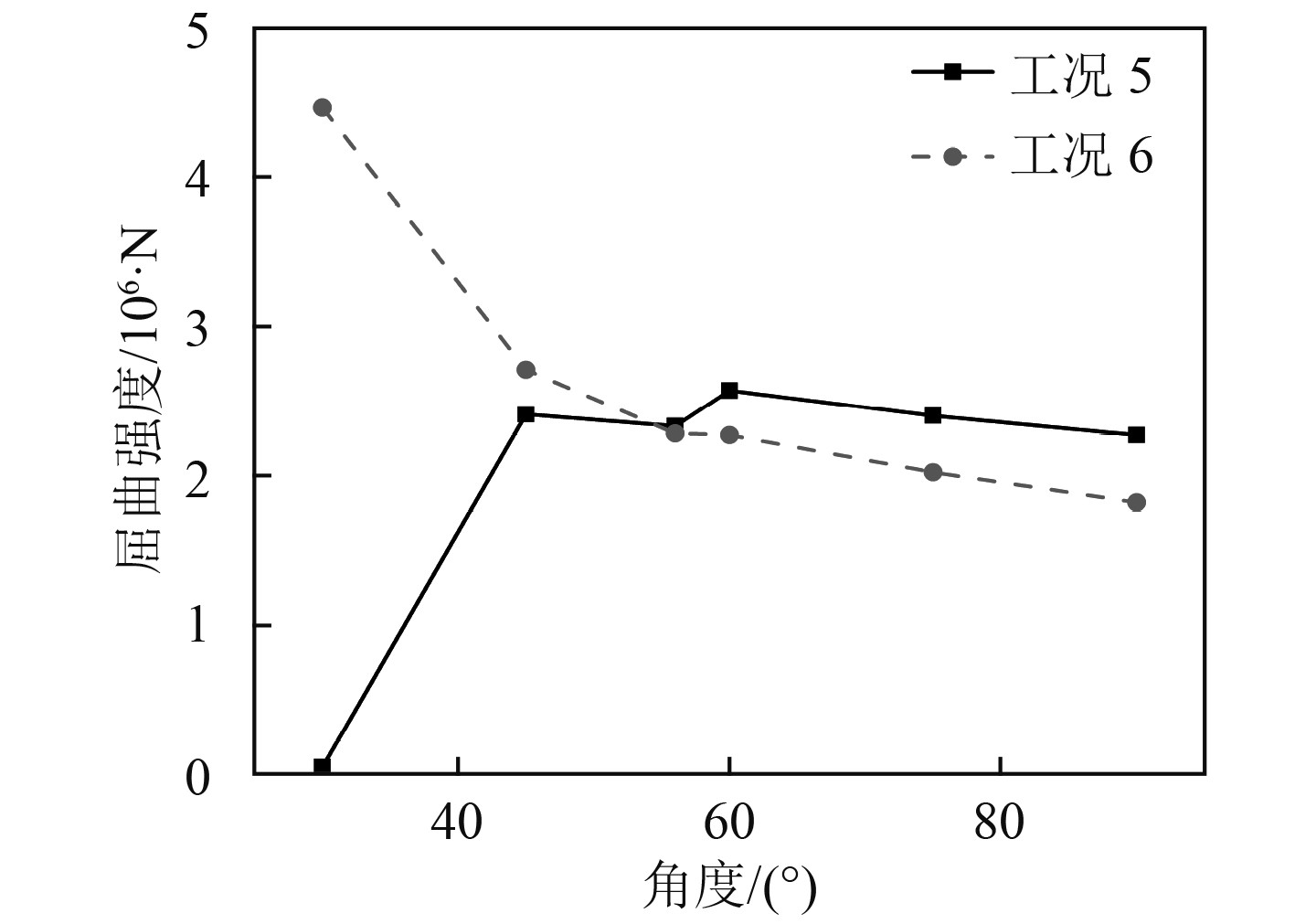
如图12所示,在屈曲分析中,角度从30°增加到45°垂直加强筋方向的屈曲强度大幅度增加,另一个方向的屈曲强度则大大降低,而随着夹角的继续增加,两者均略微有所下降,因此较小角度会导致一个方向屈曲强度大大降低,稳定性大大降低。
|
图 12 屈曲强度曲线 Fig. 12 Curve of buckling strength |
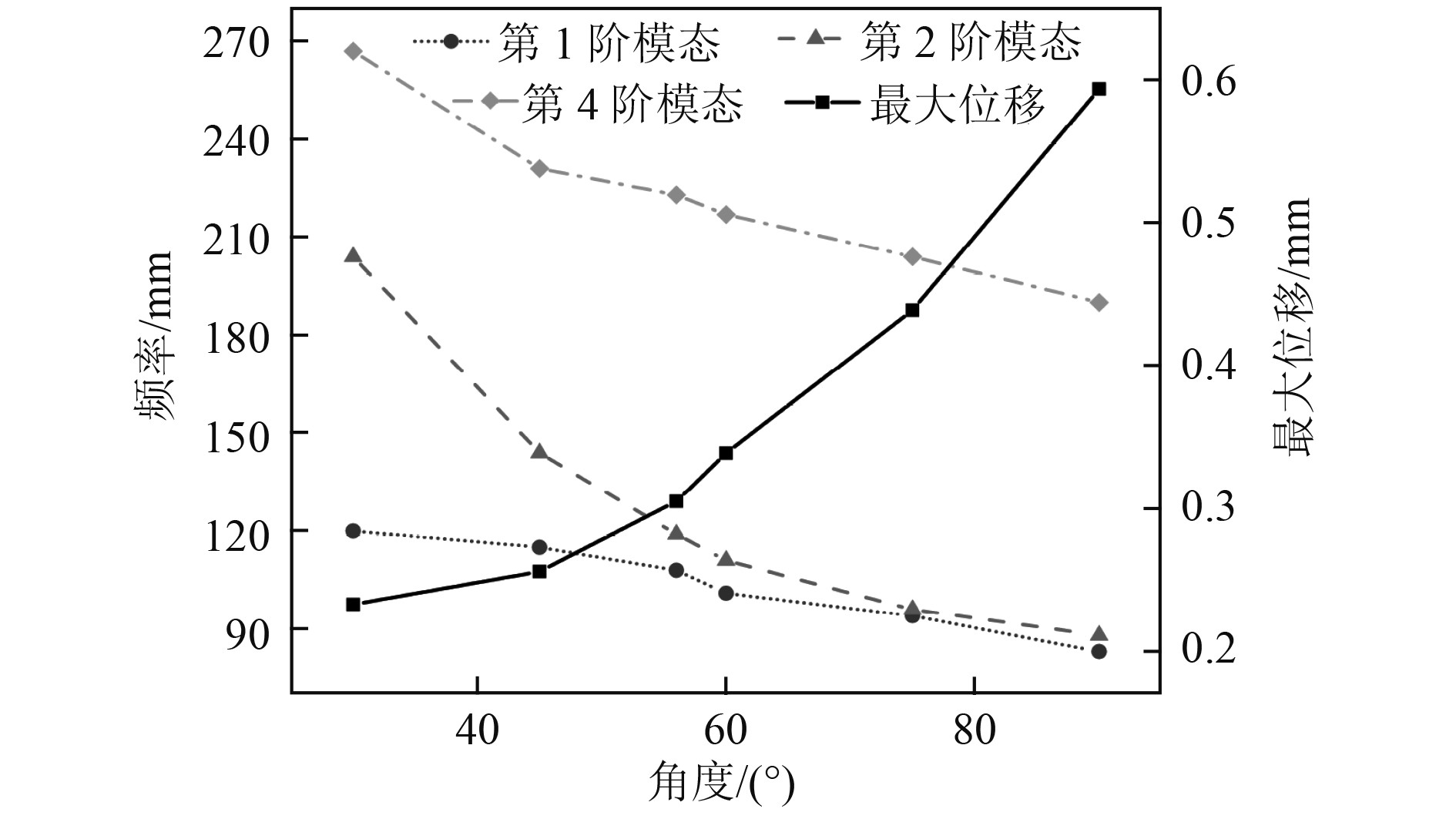
图13为相同振型的频率变化和谐响应分析峰值频率和位移曲线。其中最大振动位移随角度增加而增加,增长率也有所提高,3个相同振型的模态频率随着角度的增加而降低。曲线变化情况反映了板材刚度随角度的增加而减小,这与底板面积的增加而带来的相对刚度的降低和质量的增加时密不可分的。
|
图 13 模态频率变化和谐响应最大位移曲线 Fig. 13 Maximum displacement curve of harmonious response of modal frequency change |
综上分析,夹角为45°时,重量、振动都得到了很好的控制,2个方向的屈曲强度也处于较高水平,强度总体满足需求。
5 结 语以船舶上层建筑的加筋板为研究对象,开展了轻量化设计研究工作取得了以下成果:
1)在整体强度不降低前提下,实现减重19.2%,底板中心激励的振动最大位移级峰值降低6 dB,实现了加筋板的振动控制和轻量化协同设计。
2)采用拓扑优化和尺寸优化相结合,在优化约过程中引入谐响应分析,并约束分析频段内的最大位移值能够有效控制振动,可避免轻量化所带来的振动加剧的问题。
3)采用上述方法,对局部特定工作条件下的结构开展结构优化将获得更好的效果。
| [1] |
邓节军. 基于动力分配的船舶能耗最优化算法研究[J]. 舰船科学技术, 2018, 40(22): 19-21. |
| [2] |
李碧英. 航运业节能减排现状及其低碳发展的途径[J]. 工程研究-跨学科视野中的工程, 2012(3): 260-269. |
| [3] |
YUAN H X, CHEN X W, THEOFANOUS M, et al. Shear behaviour and design of diagonally stiffened stainless steel plate girders[J]. Journal of Constructional Steel Research, 2019, 153: 588-602. DOI:10.1016/j.jcsr.2018.11.015 |
| [4] |
刘一夫, 任慧龙, 张鑫. 几种截面形式铝合金加筋板极限强度数值研究[J]. 船舶工程, 2018, v. 40(S1): 249-253. |
| [5] |
ZHOU W, LI Y, SHI Z, et al. An analytical solution for elastic buckling analysis of stiffened panel subjected to pure bending[J]. International Journal of Mechanical Sciences, 2019, 161: 105024. |
| [6] |
SINGH K, ZHAO W, JRAD M, et al. Hybrid optimization of curvilinearly stiffened shells using parallel processing[J]. Journal of Aircraft, 2019, 56(3): 1068-1079. DOI:10.2514/1.C035069 |
| [7] |
LEHETA H W, BADRAN S F, ELHANAFI A S. Ship structural integrity using new stiffened plates[J]. Thin-Walled Structures, 2015, 94: 545-561. DOI:10.1016/j.tws.2015.05.018 |
| [8] |
BADRAN S F, NASSEF A O, METWALLI S M. A comparison of buckling strength of Y and T stiffeners in ship plating[J]. Marine technology, 2008, 45(3): 125-131. |
| [9] |
张文春, 段树林, 赵连行. 线激励下船舶混合构型加筋板的振动特性[J]. 船舶力学, 2016, 20(7): 858-865. DOI:10.3969/j.issn.1007-7294.2016.07.009 |
| [10] |
高处, 刘文夫, 邱伟强, 等. I型夹芯金属夹层板振动特性数值仿真分析[J]. 噪声与振动控制, 2018, 38(4): 76-80. DOI:10.3969/j.issn.1006-1355.2018.04.015 |
| [11] |
洪清泉, 赵康, 张攀, 等. OptiStruct & HyperStudy理论基础与工程应用[M]. 北京: 机械工业出版社, 2017: 4–6.
|
 2021, Vol. 43
2021, Vol. 43
