潜艇具有侦察、攻击、掩护等多种功能,是大国海军不可或缺的战略性武器。潜艇耐压结构是潜艇的主体结构,是保证潜艇强度、稳定性、速度等全艇性能的重要保障,故潜艇耐压结构的优化设计十分重要。
以往潜艇、潜器的优化设计像潘涛[1]、王燕[2]大多都是追求重量最轻的单一目标,而结构重量越轻,稳定性却也会越差。对于大型潜艇来说,设法提高稳定性十分重要。将重量与稳定性综合考虑,既能减少造价、更易控制重量分配,同时也能提高艇体安全性,便于适合高强度材料的使用。对于多目标优化问题,经典的求解方法有加权法、约束法、目标规划法和极大极小法等,优化权重系数不论是由决策者确定,还是由优化方法自动调整,都存在着局限性[3-4]。采用多目标遗传算法获取Pareto最优解组,再利用最小距离法[5]选取最优解,可以克服上述不足。
由于探潜技术水平的不断提升,潜艇采用大潜深、超大潜深技术是提高其隐蔽性的重要途径之一,这样甚至能有效地规避反潜武器的攻击[6]。钛合金是一种广泛用于潜艇上的优质新型材料,它具有重量轻、强度大、耐腐蚀、生物兼容性好等诸多优点[7]。潜艇本身属于大型结构,其每次的稳定性分析都涉及大量计算,若直接采用有限元软件进行分析优化,需要反复循环求解新的迭代方程,其时间成本过大,不具有可操作性[8]。运用BP神经网络的非线性映射关系代替有限元方法计算的迭代方程式进行分析,其效率高,精度好,且遗传算法具有并行性、随机性、全局化等优点,与BP神经网络优势互补。因此,本文采用BP神经网络与遗传算法联合优化(以下简称BP-GA算法)方法,研究最大下潜深度达600 m的超大潜深潜艇,且采用新型材料钛合金的耐压艇体的优化问题,更加具有实用性。
1 壳体结构的主要参数确定以某级潜艇数据为母型,其最大排水量16000 t,采用双壳体设计,最大航速可达32 kn,其潜深可以达到600 m[9]。本文潜艇数据取排水量16000 t,储备浮力系数为0.3,最大下潜深度为600 m。
1.1 主尺度估算根据陈明高等[10]常规潜艇排水量和主尺度的确定新方法中排水量表达式:
| $ {K}_{1}D+{K}_{2}{D}^{\frac{2}{3}}+{K}_{3}{D}^{\frac{1}{2}}+{K}_{4}=D\text{,} $ | (1) |
计算潜艇的主尺度:
| $ L=\psi {\nabla }^{1/3},B=\frac{L}{\lambda }={W}_{B}R \text{,} $ | (2) |
导出计算表达式:
| $\begin{split} \psi =& \frac{L}{{{\nabla ^{\frac{1}{3}}}}} = \sqrt[3]{{{\rho _w}g}}\times \Biggr\{ 5 + \left[ {\lambda - \left( {7.4 + 4\left( {\frac{w}{D} - 0.35} \right)} \right)} \right]\times \\ &{t_g}\left[ {22.16 + 9.6\left( {\frac{w}{D} - 0.15} \right)} \right] + 0.064\times \\ &\left. {sin \left[ {\frac{{\lambda - \left( {7.4 + 4\left( {\frac{W}{D} - 0.35} \right)} \right)}}{{13 - \left( {7.4 + 4\left( {\frac{W}{D} - 0.35} \right)} \right)}}\text{π} } \right]} \right\}\text{。} \end{split}$ | (3) |
其中:
根据上述计算表达式,给出如表1所示的主尺度估算结果。
|
|
表 1 主尺度估算结果 Tab.1 Main scale estimation result |
取长宽比为11的数据,艇首艇尾是标准的水滴型,艇体中段都采用简单平直的圆型断面构造,长度大约是该艇长度的80%,锥体倾角为15°,可以得出如表2所示的主尺度。
|
|
表 2 潜艇主尺度 Tab.2 Main scale of submarines |
根据《潜艇》[11]计算可得:
极限深度
工作深度
设计计算深度
根据《规范》[12]中5.2.1核潜艇壳板中面周向应力的要求初步计算耐压壳的厚度及肋骨厚度,如下式:
| $ {\sigma }_{2}^{0}={K}_{2}^{0}{P}_{c}R/t,{\sigma }_{2}^{0}\leqslant 0.9{\sigma }_{s} \text{。}$ | (4) |
其中:
耐压壳材料选取比重小、强度高、耐高温、抗腐蚀性强的TC4钛合金,其性质如表3所示,经计算其厚度初步选取76 mm。
|
|
表 3 退火钛合金性质 Tab.3 Annealed titanium alloy properties |
虽然钛合金有着上述诸多优点,然而钛开发量较少,价格高昂,用作耐压壳的需求量大,成本高,且钛合金弹性模量低,变形大。对于和耐压壳尺寸相比的微小结构—肋骨来说,其结构小,稳定性高,且应力偏小,破坏可能性低,选取价格较为低廉的高强钢就可以满足要求。故肋骨选取HY-100 steel,其性质如表4所示,尺寸根据《规范》[12]初步取为
|
|
表 4 HY-100 steel的性质 Tab.4 HY-100 steel properties |
遗传算法是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的一种随机算法模型,是一种基于“适者生存”的高度并行、随机和自适应的优化算法。它将问题的求解表示成染色体的适者生存过程,通过染色体群的一代代不断进化,包括复制、交叉和变异等操作,最终收敛到“最适应环境”的个体,从而求得问题的最优解或满意解[13]。遗传算法的主要步骤为:编码,初始群体的生成,适应性值评估检测,选择,交叉,变异。其运算流程如图1所示。
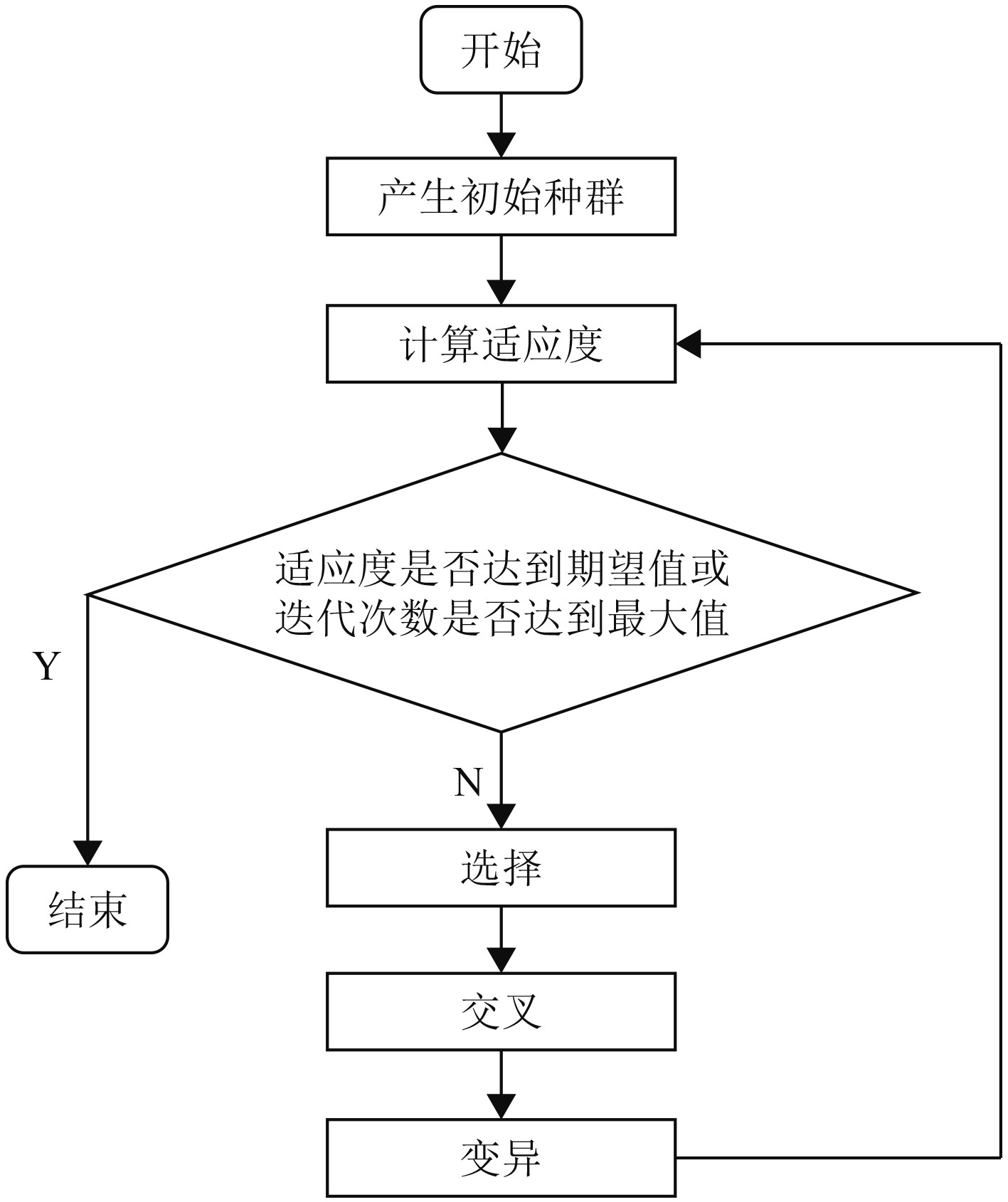
|
图 1 遗传算法流程图 Fig. 1 Genetic algorithm flow chart |
BP神经网络是一种按误差逆向传播算法训练的多层前馈网络,其基本思想是梯度下降法,利用误差反传,反复学习训练,使网络的实际输出值和期望输出值的误差均方差均为最小。神经网络既是并行处理和大规模平行计算的基础,又是高度非线性动力学系统和自适应组织系统,可用来描述认知、决策及控制智能行为[14-15]。具有非线性映射能力,擅于从输入和输出信号中寻找规律,不需要精确的数学模型,并行计算能力强,易于进行软硬件的编程计算[16]。BP神经网络结构由输入、输出、隐含层组成,如图2所示。
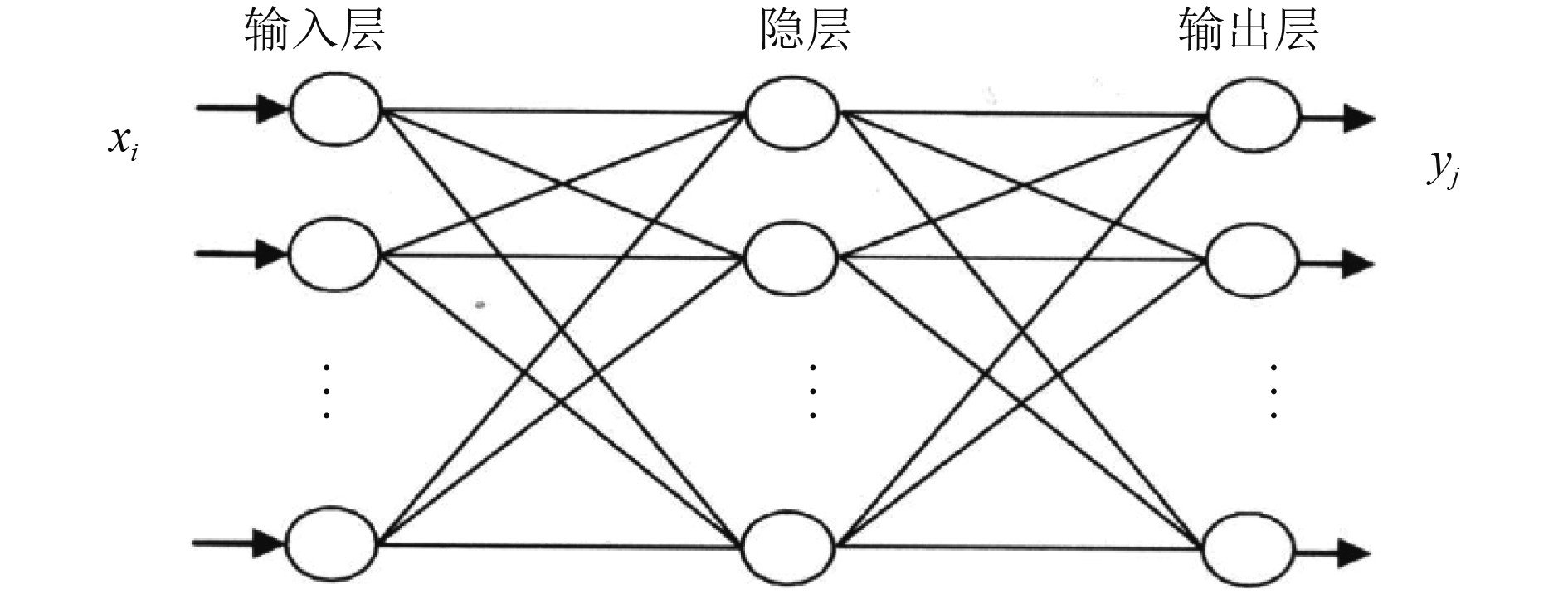
|
图 2 BP神经网络结构 Fig. 2 Neural network structure |
BP算法的实质是利用最陡下降法,具有简单、计算量小、并行性强等优点,但它的学习过程收敛速度慢,容易陷入局部极小点,算法不完备,鲁棒性不好,网络性能差[14]。遗传算法具有很强的鲁棒性,能处理复杂的目标函数,避免收敛于局部最优,具有全局搜索能力,但同时遗传算法通常的效率比其他传统的优化方法低,遗传算法容易过早收敛。由上面的分析可知BP和GA的优缺点间存在很大的互补性,所以本文提出BP-GA算法[17]。
3 基于BP-GA算法的环肋锥柱壳优化设计 3.1 优化策略以及流程首先在Matlab平台上使用拉丁超立方体抽样的方法生成600个样本点用于训练神经网络,其中50个样本点用于验证神经网络的精确度。然后利用有限元软件Ansys对环肋锥柱壳的强度和稳定性进行分析计算,得出相应的结构重量及总体失稳临界压力。采用BP神经网络分别建立起样本点和结构重量之间、样本点与失稳临界压力之间的映射关系,并对神经网络进行训练[18]。再调用一种基于NSGA-Ⅱ算法的多目标优化函数gamultiobj进行全局寻优,得到Pareto前沿。其中,fitnessfcn为适应度函数,是通过目标函数与设计变量之间的函数关系式转换的,而其函数关系式则是由前面的BP神经网络训练得到。在本次优化中,利用BP神经网络建立起的设计变量与结构重量、总体失稳临界压力2个目标函数之间的关系式分别为
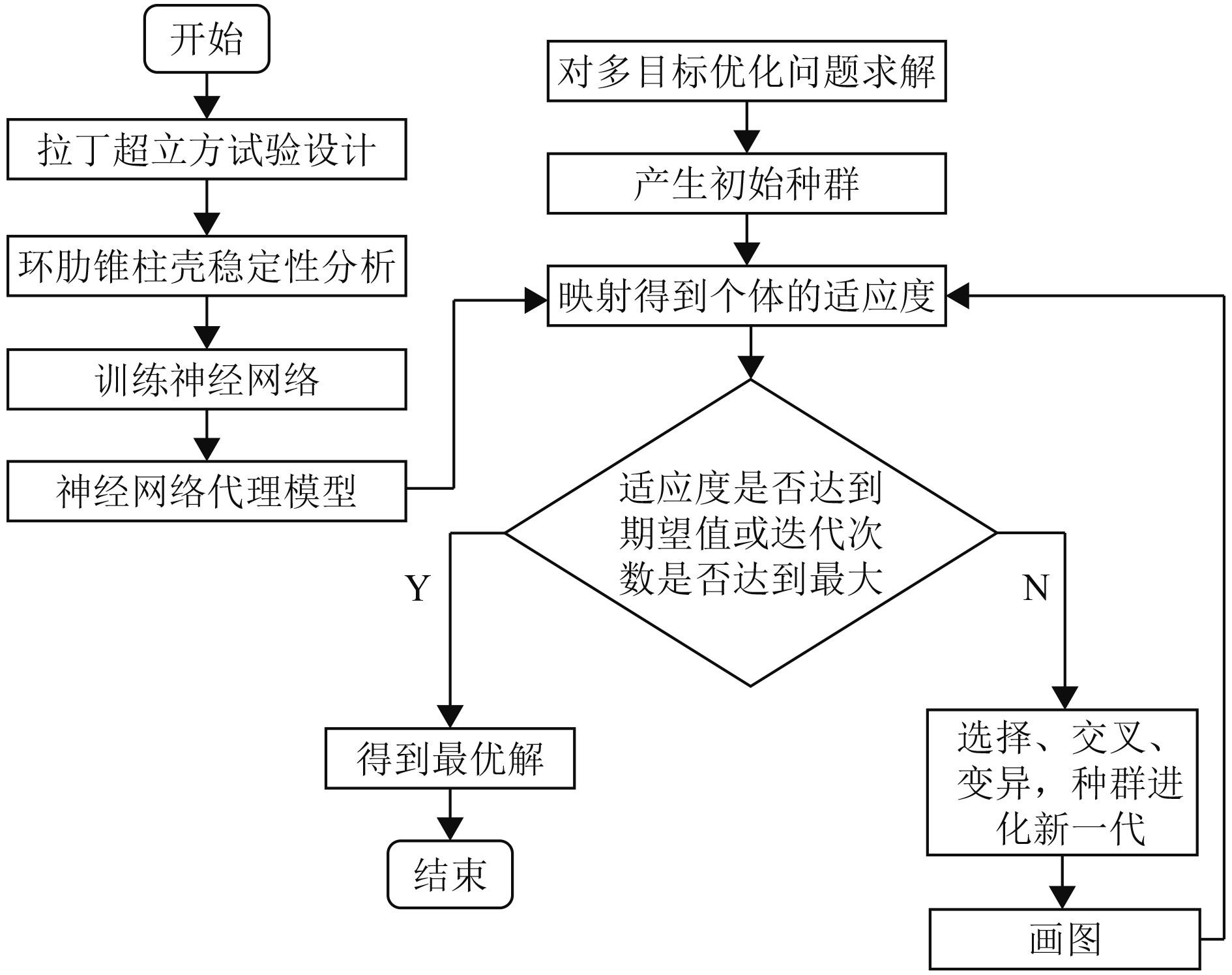
|
图 3 BP-GA算法优化流程 Fig. 3 Flow chart of BP-GA |
优化时采用的是1/2耐压壳简化得到的环肋锥柱壳几何模型,如图4所示。材料参数及其数据如下:耐压壳厚度t=76 mm,锥柱结合处的耐压壳会有应力集中问题,需要增厚处理,本文取1.5倍的耐压壳厚度,t0=114 mm;肋骨尺寸如上文h=416 mm,b=145 mm,t1=78 mm,肋骨间距lm=582 mm。用有限元软件Ansys进行建模,部分模型如图5所示,应力图及1阶屈曲模态如图6所示。
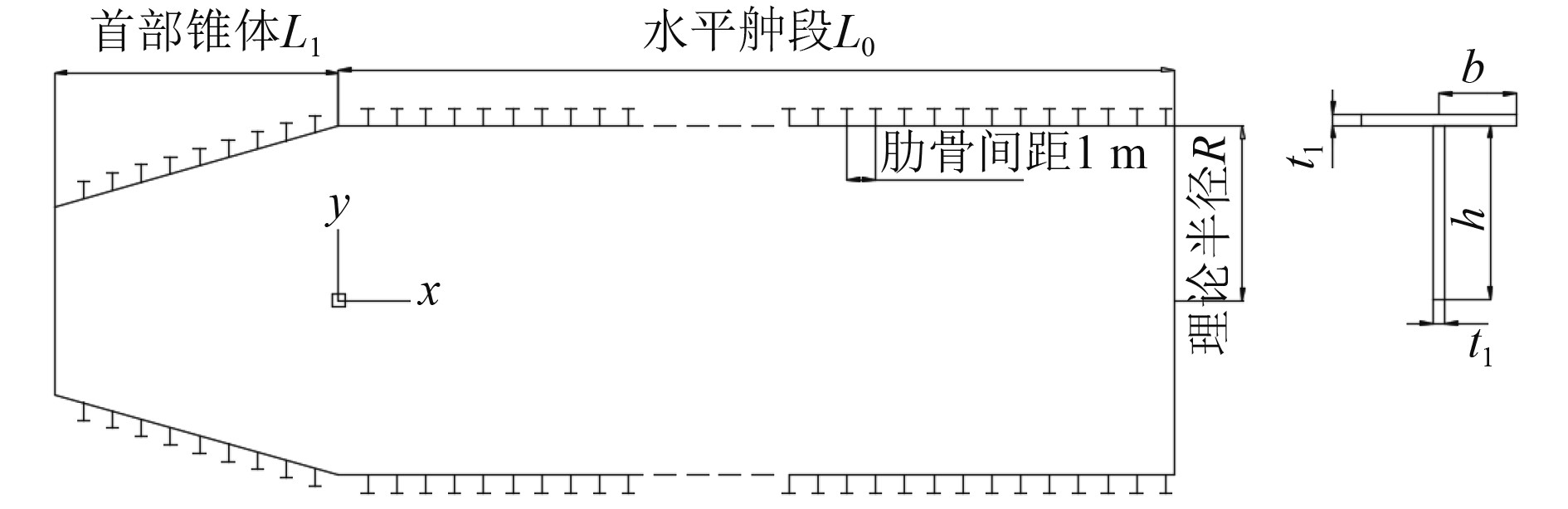
|
图 4 环肋锥柱壳几何模型 Fig. 4 Geometric model of ring-stiffened cone-cylinder shell |
|
图 5 有限元模型(部分) Fig. 5 Finite element model(partial) |

|
图 6 环肋锥柱壳应力图及1阶屈曲模态 Fig. 6 Stress diagram and first-order buckling mode of ring-stiffened cone-cylinder shell |
根据舱段总体稳定性要求,
环肋锥柱壳的目标函数为:
| $ {\rm minf}\left(x\right)=\left\{{f}_{1}\left(x\right),\frac{1}{{f}_{2}\left(x\right)}\right\}\text{。} $ | (5) |
其中:
设计变量以及取值范围如表5所示,所有变量均为离散变量。其中,t为环肋锥柱壳壳体厚度。
|
|
表 5 设计变量及取值范围 Tab.5 Design variables and range of values |
为了衡量神经网络代理模型的预测值和样本值的差别采用平均相对变动值(Average Relative Variance,ARV)[19],其定义为:
| $ ARV=\frac{\displaystyle\sum _{i=1}^{N}{\left[x\left(i\right)-\widehat{x}\left(i\right)\right]}^{2}}{\displaystyle\sum _{i=1}^{N}{\left[x\left(i\right)-\stackrel{-}{x}\left(i\right)\right]}^{2}}\text{。} $ | (6) |
其中:N为验证模型的样本数量;
为选取合适数目的样本点进行神经网络训练,本文分别计算200个、400个、600个这3组样本点的代理模型,从中选取50个样本点进行验证,并计算平均相对变动值ARV。如表6所示,当样本点数目为200时,结构重量的平均相对变动值为
|
|
表 6 平均相对变动值ARV Tab.6 Average relative variance |
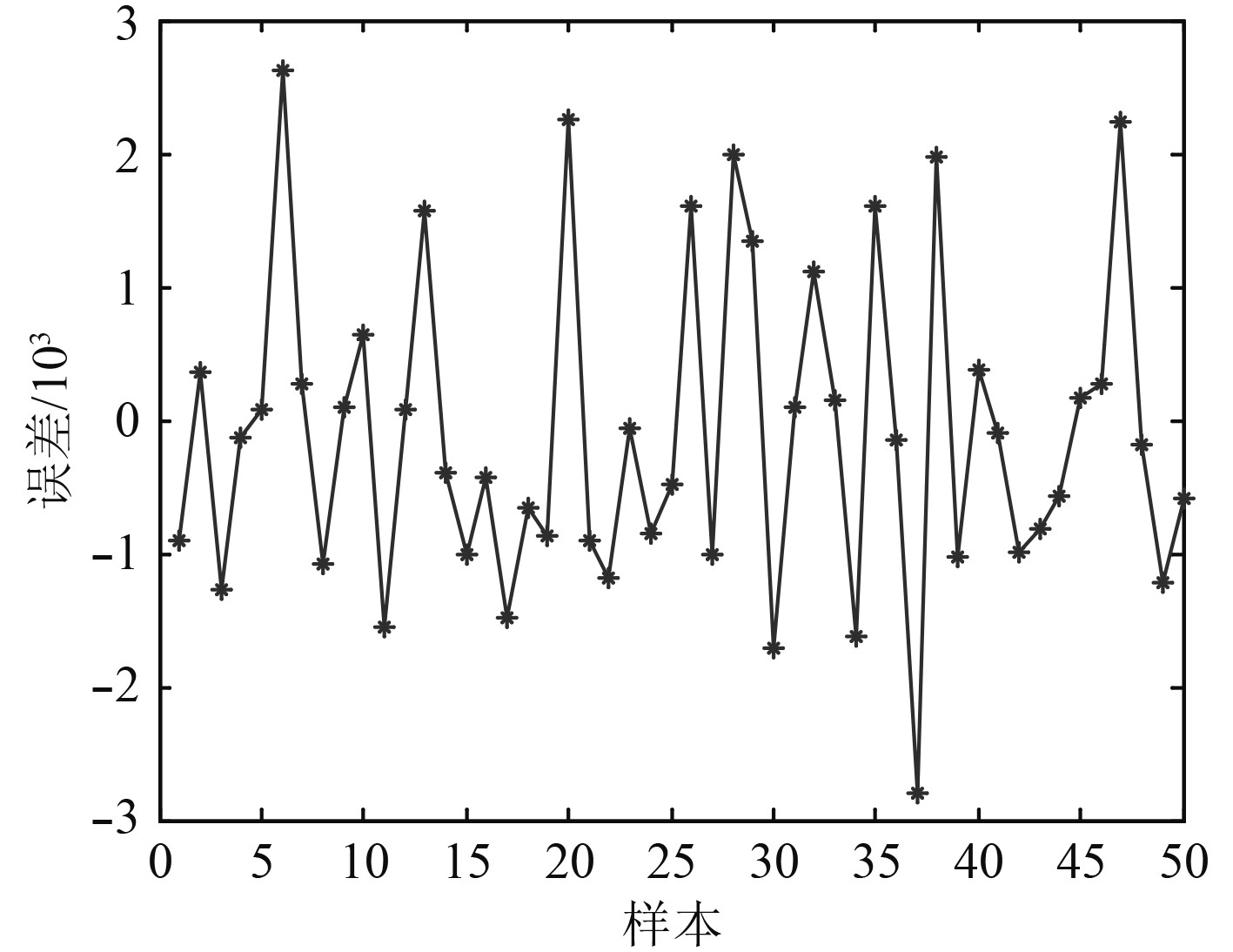
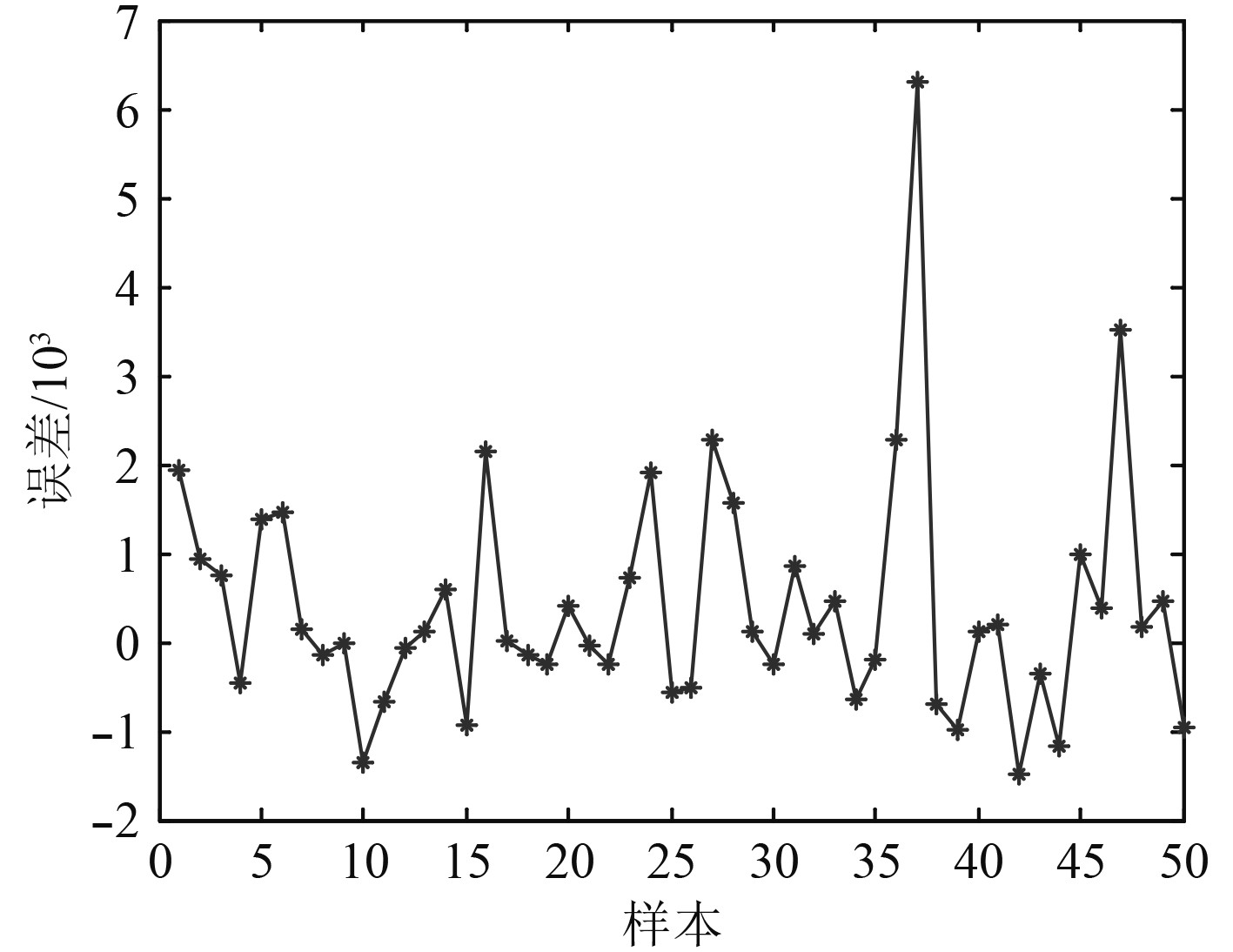
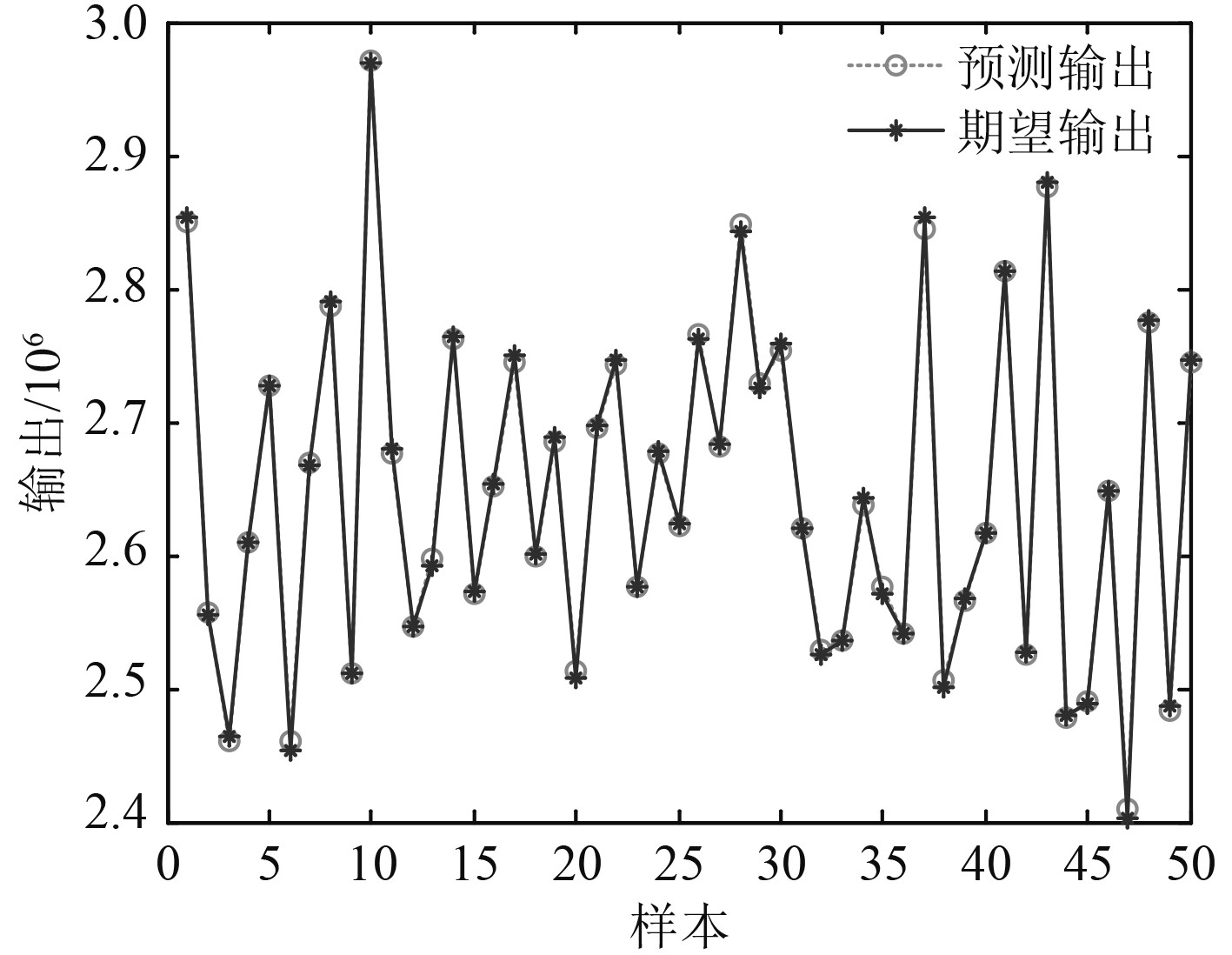
600个样本点的BP神经网络训练结果如图7和图8所示。可知,其结构重量预测的最大误差绝对值不到3×10−3,总体临界压力误差绝对值不足7×10−3,误差均很小,说明神经网络的映射精度较高。由此,可得到预测的结构重量与失稳临界压力,如图9和图10所示。
|
图 7 BP网络的结构重量预测误差 Fig. 7 BP network structural weight prediction error |
|
图 8 BP网络失稳临界压力预测误差 Fig. 8 BP network instability critical pressure prediction error |
|
图 9 BP网络的结构重量预测输出 Fig. 9 BP network structure weight prediction output |
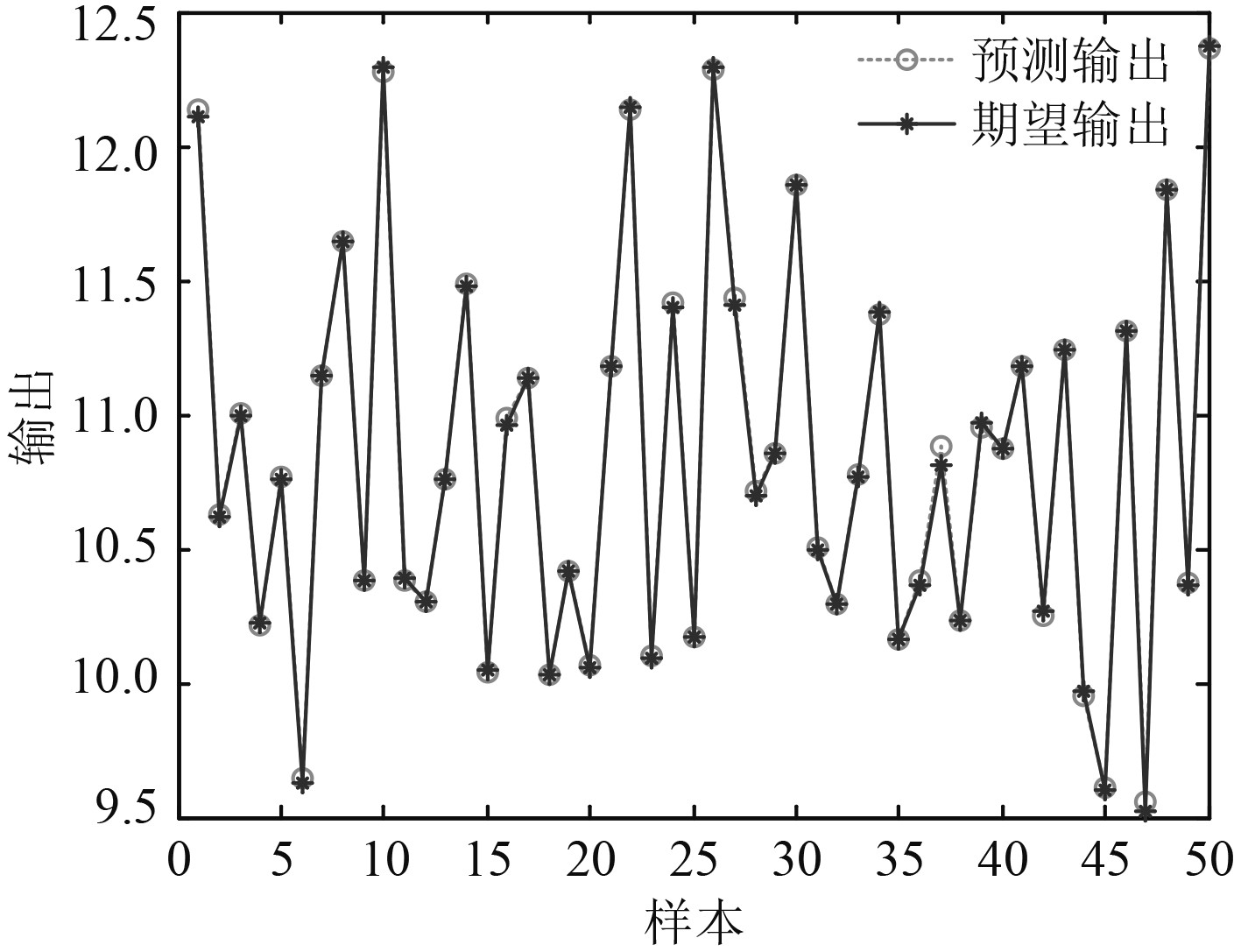
|
图 10 BP网络失稳临界压力预测输出 Fig. 10 BP network instability critical pressure prediction output |
通过多目标遗传算法得到的Pareto前沿如图11所示。Pareto最优解即为可行域边界最优前沿上的解,也是多目标问题的有效解。可以看到当改善结构重量时,带来的必然是失稳压力的损失,反之亦然。
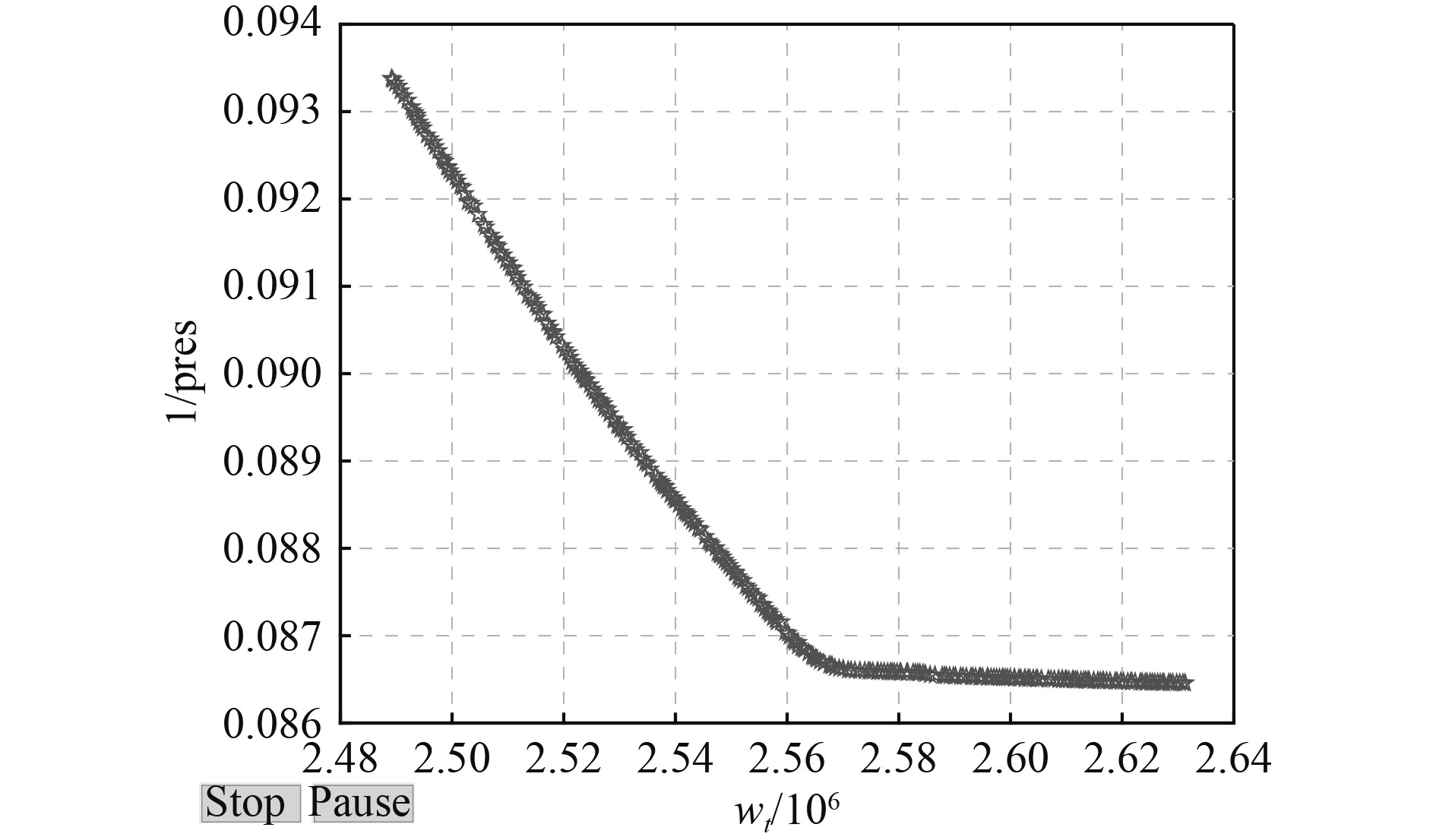
|
图 11 帕累托前沿 Fig. 11 Pareto frontier |
Pareto前沿中共有300组Pareto最优解,表7展示部分结果。
|
|
表 7 部分帕累托最优解 Tab.7 Partial Pareto optimal solution |
实际应用中,还需要从多个最优解中选取一个作为多目标优化的最终解,本文引用孙光勇[5]的最小距离选择方法(TMDSM),从帕累托前沿中选取最优解。其原理为:D是从拐点到“乌托邦点”的距离,也就是TMDSM中的最小距离,而拐点就是最优点,由此得到的优化结果如表8所示。
|
|
表 8 优化结果 Tab.8 Optimization Results |
从表8可以看出,经过BP-GA优化后,环肋锥柱壳的结构重量比初始时下降了2.81%,总体失稳临界压力也提高了5.19%,由于变量的初始选值与最终优化值相近,所以优化效果不突出,但仍得到了改善,说明优化合理。
由于上述优化结果是在BP神经网络建立起的映射关系的基础上,利用遗传算法进行优化搜索计算,最后需要将数据再代入有限元计算中,对BP神经网络映射的精度进行检验。如表9所示,与最优解中的结果相比,环肋锥柱壳的结构重量误差为
|
|
表 9 有限元验证 Tab.9 Finite element verification |
根据上文的计算结果wt=2588.17 t,考虑首部球端,可以估算出耐压壳的重量d1=2×1.02×wt=5279.87 t,本文潜艇的最大排水量为D=16000 t。根据《现代潜艇设计理论与技术》[20]中所述,现代柴电潜艇中结构重量占43%,攻击型核潜艇中结构重量占45%。双壳潜艇的外壳十分薄,本文取1/4耐压壳重量,再加上舱壁等结构,非耐压壳结构重量约为1500 t,故结构重量占最大排水量的42.4%<45%,所以潜艇自重满足要求,上文的优化设计合理。
5 结 语本文基于多目标优化理论,依据重量排水量估算核潜艇主尺度,经过有限元计算校核结构重量、应力、失稳临界压力。以环肋锥柱壳的结构重量、总体失稳临界压力为目标,利用BP神经网络得到变量与优化目标之间的非线性映射关系,代替有限元方法计算的迭代方程式进行分析,然后利用遗传算法进行优化设计,得到理想的优化结果,由此可知:
将神经网络与遗传算法相结合的方式解决复杂问题、大型计算的多目标优化计算,能达到互补优势,不仅能克服神经网络易陷入局部最优的劣势,还能提高遗传算法的计算效率,避免过早收敛的现象发生,并在环肋锥柱壳的优化问题中得到较好的效果。故该方法在潜艇耐压壳上具有一定的价值,未来可以尝试推广至其他大型结构的优化设计上。
| [1] |
潘涛. 深潜器耐压结构强度分析与优化设计[D]. 哈尔滨: 哈尔滨工程大学, 2010. PAN Tao. Strength analysis and optimum design of compressive structure of deep submersible[D]. Harbin: Harbin Engineering University, 2010. |
| [2] |
王燕. 潜艇结构的优化设计方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2010. WANG Yan. Research on the optimization design method of submarine structure[D]. Harbin: Harbin Engineering University, 2010. |
| [3] |
刘栋. 改进微粒群算法在多目标优化问题中的应用[D]. 济南: 山东师范大学, 2008. LIU Dong. Application of improved particle swarm optimization in multi-objective optimization problems. Application of improved particle swarm optimization in multi-objective optimization problems[D]. Jinan: Shandong Normal University, 2008. |
| [4] |
李学斌, 朱学康. 潜艇耐压圆柱壳的多目标优化设计[J]. 中国造船, 2009, 50(1): 10-17. LI Xue-bin, ZHU Xue-kang. Multi-objective optimization design of submersible pressure-resistant cylindrical shell[J]. China Shipbuilding, 2009, 50(1): 10-17. DOI:10.3969/j.issn.1000-4882.2009.01.002 |
| [5] |
Guangyong SUN, Guangyao LI, Zhihui GONG, etc. Multiobjective robust optimization method for drawbead design in sheet metal forming[J]. Materials & Design, 2010, 31(4): 1917-1929. |
| [6] |
张彩坤, 陈国琳, 王磊. 国外核潜艇大潜深技术发展趋势[J]. 舰船科学技术, 2011, 33(12): 134-137. ZHANG Cai-kun, CHEN Guo-lin, WANG Lei. Development trend of large submersible technology for foreign nuclear submarines[J]. Ship Science and Technology, 2011, 33(12): 134-137. DOI:10.3404/j.issn.1672-7649.2011.12.032 |
| [7] |
孟宪斌, 易彩虹, 吴小玲, 等. 钛及钛合金复合材料发展及工业应用[J]. 中国化工装备, 2013, 6: 3-7. MENG Xian-bin, YI Cai-hong, WU Xiao-ling, et al. Development and industrial application of titanium and titanium alloy composite materials[J]. China Chemical Equipment, 2013, 6: 3-7. DOI:10.3969/j.issn.1671-0525.2013.03.001 |
| [8] |
程远胜, 孙莹, 闫国强, 等. 基于神经网络与遗传算法的潜艇舱壁结构优化[J]. 中国造船, 2008, 49(4): 81-86. CHENG Yuan-sheng, SUN Ying, YAN Guo-qiang, et al. Optimization of submarine bulkhead structure based on neural network and genetic algorithm[J]. China Shipbuilding, 2008, 49(4): 81-86. DOI:10.3969/j.issn.1000-4882.2008.04.011 |
| [9] |
变色脸. 中国潜艇赶超世界先进, 完美静音性能让美国直呼不可能[EB/OL]. https://bbs.tiexue.net/post2_12673364_11.html, 2017-8-3. Color changing face. Chinese submarine catches up with the world's advanced, perfect mute performance makes it impossible for the United States to call directly [EB / OL]. https://bbs.tiexue.net/post2_12673364_11.html, 2017-8-3. |
| [10] |
陈明高, 石仲堃. 常规潜艇排水量和主尺度的确定新方法[J]. 中国舰船研究, 2006, 1(2): 38-41. CHEN Ming-gao, SHI Zhong-kui. A new method for determining the displacement and principal dimensions of conventional submarines[J]. China Ship Research, 2006, 1(2): 38-41. DOI:10.3969/j.issn.1673-3185.2006.02.009 |
| [11] |
GJB 64.2A-1997, 舰船船体规范 潜艇[S]. 北京: 国防科学技术工业委员会, 1997. GJB 64.2A-1997, Ship hull specifications submarine[S]. Beijing: National Commission for Science, Technology and Industry for National Defense, 1997. |
| [12] |
GJB-Z 21A-2001, 潜艇结构设计计算方法[S]. 北京: 国防科学技术工业委员会, 1991. GJB-Z 21A-2001, Calculation method of submarine structure design[S]. Beijing: National Commission for Science, Technology and Industry for National Defense, 1991. |
| [13] |
陈皓. 遗传算法求解一类带工艺约束的并行机调度问题[D]. 武汉: 华中科技大学, 2005. CHEN Hao. Genetic algorithm for a class of parallel machine scheduling problems with process constraints[D]. Wuhan: Huazhong University of Science and Technology, 2005. |
| [14] |
朱小梅, 郭志钢, 杨先凤. 基于遗传算法BP神经网络优化证券组合投资[J]. 江汉大学学报(自然科学版), 2005, 33(3): 47-50. ZHU Xiao-mei, GUO Zhi-gang, YANG Xian-feng. Optimizing portfolio investment based on genetic algorithm BP neural network[J]. Journal of Jianghan University (Natural Science), 2005, 33(3): 47-50. |
| [15] |
刘猛. 云计算平台下神经网络方法研究[D]. 成都: 电子科技大学, 2011. LIU Meng. Research on neural network method under cloud computing platform[D]. Chengdu: University of Electronic Science and Technology of China, 2011. |
| [16] |
刘天舒. BP神经网络的改进研究及应用[D]. 哈尔滨: 东北农业大学, 2011. LIU Tianshu. Improved research and application of BP neural network[D]. Harbin: Northeast Agricultural University, 2011. |
| [17] |
卢纯, 石秉学. 采用BP-GA算法的一种LSI神经网络的电路设计[J]. 清华大学学报(自然科学版), 2001, 41(1): 103-106. LU Chun, SHI Bingxue. Circuit design of an LSI neural network using BP-GA algorithm[J]. Journal of Tsinghua University (Science and Technology), 2001, 41(1): 103-106. DOI:10.3321/j.issn:1000-0054.2001.01.027 |
| [18] |
张宇, 黄小平, 闫小顺. 基于神经网络和粒子群算法的环肋圆柱壳优化设计[J]. 舰船科学技术, 2016, 38. ZHANG Yu, HUANG Xiao-ping, YAN Xiao-shun. Optimization design of ring-ribbed cylindrical shell based on neural network and particle swarm algorithm[J]. Ship Science and Technology, 2016, 38. DOI:10.3404/j.issn.1672-7619.2016.04.008 |
| [19] |
陈果. 神经网络模型的预测精度影响因素分析及其优化[J]. 模式识别与人工智能, 2005, 18(5): 528–534. (3): 5–9. CHEN Guo. Analysis and optimization of influencing factors on prediction accuracy of neural network models[J]. Pattern Recognition and Artificial Intelligence, 2005, 18 (5): 528–534. (3): 5–9. |
| [20] |
马运义, 许建. 现代潜艇设计理论与技术[M]. 哈尔滨: 哈尔滨工程大学出版社, 2012: 70.
|
 2021, Vol. 43
2021, Vol. 43
