船舶作为水上交通工具,长期处于恶劣的海洋环境中,船体结构会受到风、浪和海流等自然载荷的作用,同时还可能受到碰撞、搁浅或其他意外载荷作用,使得结构容易产生各种形式的损伤,导致承载能力下降,影响安全[1]。裂纹是舰船结构典型损伤形式之一,对船体结构影响巨大,国内外专家针对裂纹损伤识别开展了众多研究。由于固有频率仅与结构的固有特性有关,抗干扰能力强,且容易获得,因此有很多损伤识别方法研究都是基于固有频率变化而进行的[2-5]。这些研究验证了通过频率变化识别损伤的有效性,在很多领域进行了成功应用。但是为简化问题,多数研究以梁结构作为研究对象。而船体结构多为板和骨架组合成的板架结构,结构更为复杂,研究较少。
本文以加筋板这一典型船体结构形式作为研究对象,通过数值仿真和模型试验相结合的方法,研究不同裂纹对加筋板频率特性的影响规律,为典型船体结构裂纹损伤识别提供技术参考。
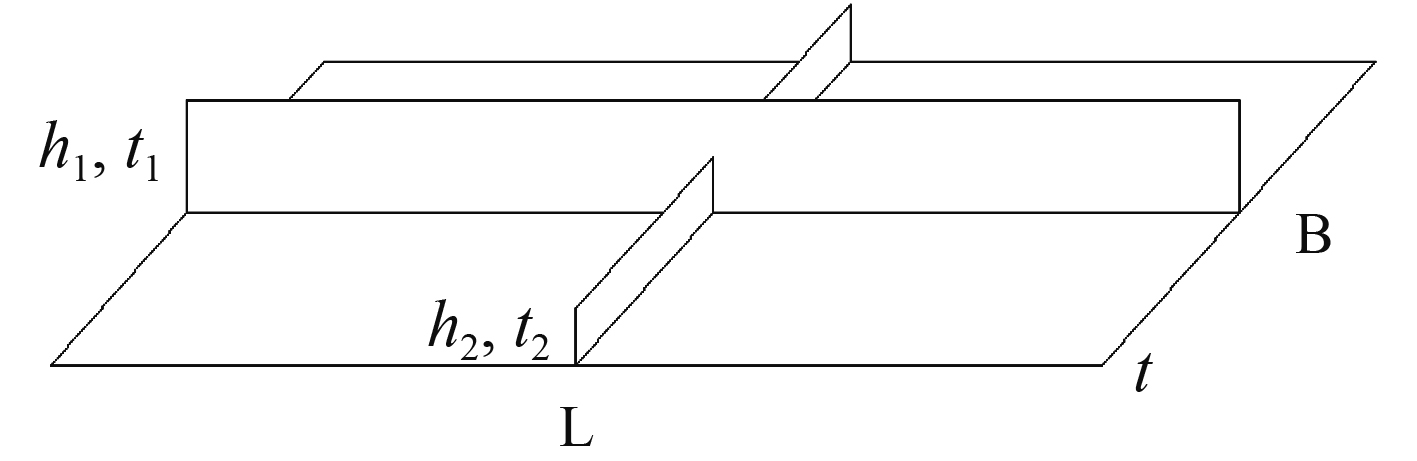
1 带有裂纹的典型船体结构模型选取 1.1 典型船体结构形式的选取船体结构一般由船体板和骨架组成,所以选择加筋板为研究对象。加筋板由矩形外板和2根相互垂直的加强筋组成,如图1所示。L为外板板长,B为宽,t为板厚;h1,h2分别为十字加强筋高,t1,t2分别为厚度。
|
图 1 加筋板模型示意图 Fig. 1 Schematic diagram of stiffened plate model |
随着技术的不断发展,现代舰船大多采用厚度较小的高强度钢,船体结构易产生裂纹的热点一般位于焊趾、部分焊透的焊根或角焊缝、板材的自由边等位置。依据《船体结构疲劳强度指南》,疲劳裂纹的失效模式主要有4种,通过对4种典型疲劳裂纹失效模式的分析,按照裂纹出现的位置可以归纳为两类:1)产生于自由边界的裂纹;2)产生于焊缝处的裂纹。根据实际情况,船体板与板之间的焊接一般会错开骨架所在位置,若板与板之间焊缝处产生裂纹,则可以认为裂纹出现在板格中间。因此,裂纹的位置可以选在自由边、板面内,或者加强筋上。
裂纹的分类根据发生的位置、几何形状上可以分为表面裂纹、深埋裂纹、穿透裂纹。在舰船实际服役过程中,船体结构在交变载荷作用下,易产生穿透裂纹。因此,本文以穿透型裂纹为对象进行研究。
2 带有裂纹的典型船体结构固有频率研究 2.1 数值仿真及模型试验结构固有频率的获取方法有多种:解析法、试验法和仿真法。解析法通常适用于简单结构,处理复杂结构较为困难;试验法比较精确,但是成本较高,往往受到试验数量限制;仿真法可以对大量的模型进行规律性研究,但是仿真结果的准确程度需要试验验证。本文采用仿真和试验相结合的方法,首先利用仿真和试验对一定数量相同的典型工况进行分析,利用试验结果对仿真方法进行验证后,再利用相同的方法和参数设置开展大量仿真研究。
数值仿真和验证性试验设计了5类结构模型:完整结构模型、边裂纹模型、中间裂纹模型、纵筋裂纹模型和横筋裂纹模型,数值模型和实物模型一致。试验中每类加筋板模型制作3块,均采用Q235钢制作,图2为试件与工装,二者之间采用螺栓连接。选取板格中心作为测点,使用加速度传感器进行数据采集,获得加速度的频响曲线,另外设计试验平台固定试件,模拟固支边界条件。试验采用单点激励多点拾振的模态识别方法,用力锤进行敲击,加速度传感器通过动态数据采集仪进行数据采集,每个试件锤击3次,记录1组加速度频响曲线,每个试件进行3组测量。

|
图 2 试件与工装 Fig. 2 Specimen and tooling |
通过仿真及试验分别获得了各个模型的1~7阶固有频率,如表1所示。
|
|
表 1 仿真和试验中模型的各阶固有频率(Hz) Tab.1 Natural frequencies of models in simulation and experiments(Hz) |
由表中数据可知,各类模型固有频率大部分试验结果和仿真结果都较为接近,35组对比数据相差均在20%以内,大多数对比数据相差在10%以内,证明了仿真方法的有效性。由于裂纹的出现,模型的各阶固有频率会有所降低,模型2和模型3的各阶固有频率降低明显,模型4和模型5固有频率变化不大,表明板上的裂纹对固有频率影响较大,加强筋上的裂纹对频率影响较小。
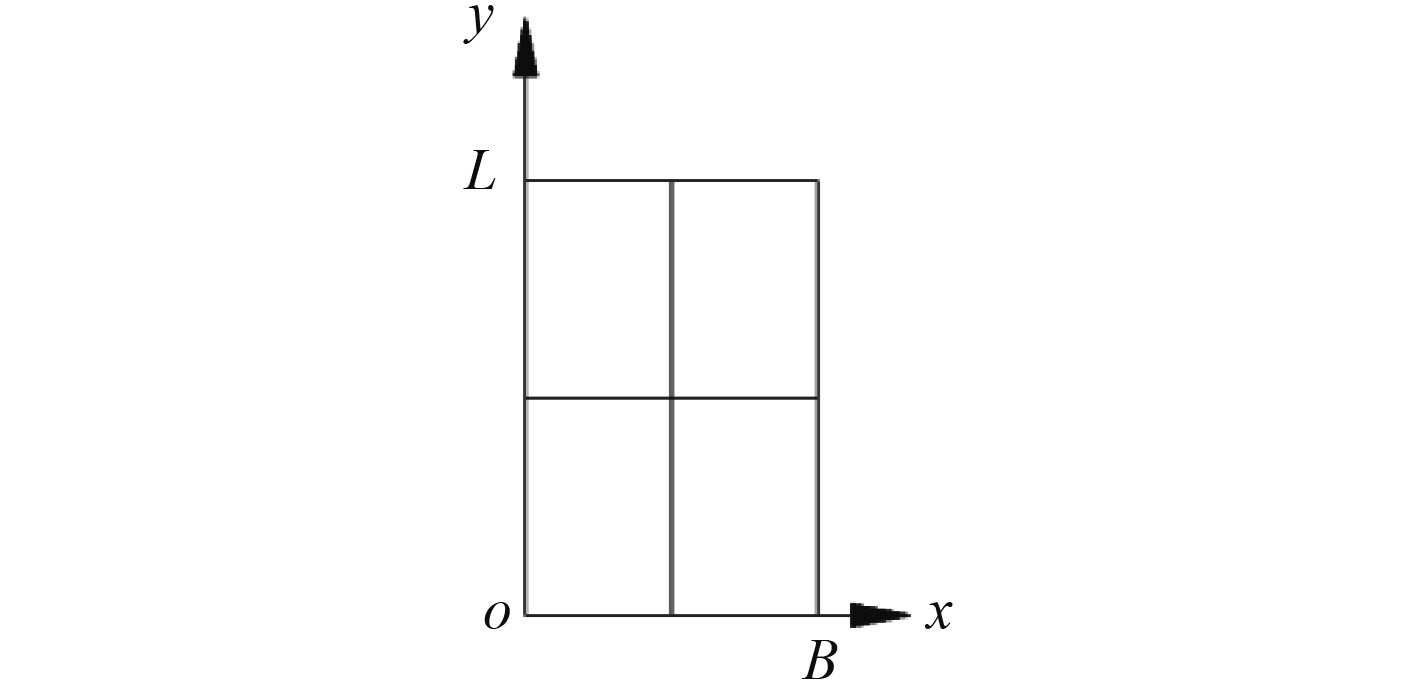
3 裂纹损伤对模型固有频率的影响规律分析 3.1 研究工况根据初步仿真和试验结果,加强筋上裂纹对频率影响较小,后续规律性研究主要针对板上出现裂纹的情况。建立坐标系如图3所示,设板的一角为坐标原点,沿板宽方向为X轴,板长方向为Y轴。针对穿透型裂纹损伤,边裂纹以裂纹边界尖端的坐标定位裂纹位置,中间裂纹则以裂纹的中心坐标对裂纹进行定位。为分析含裂纹损伤结构的频率变化规律,通过改变裂纹位置、裂纹长度建立了40种含有裂纹的加筋板模型。其中,根据裂纹位置不同可以分为:边裂纹4种,中间裂纹4种;根据裂纹长度不同分为0.05B,0.1B,0.15B,0.2B,0.25B五种情况,同时为了对比建立了一个无裂纹模型。具体模型参数如表2所示。
|
图 3 坐标系示意图 Fig. 3 Coordinate system diagram |
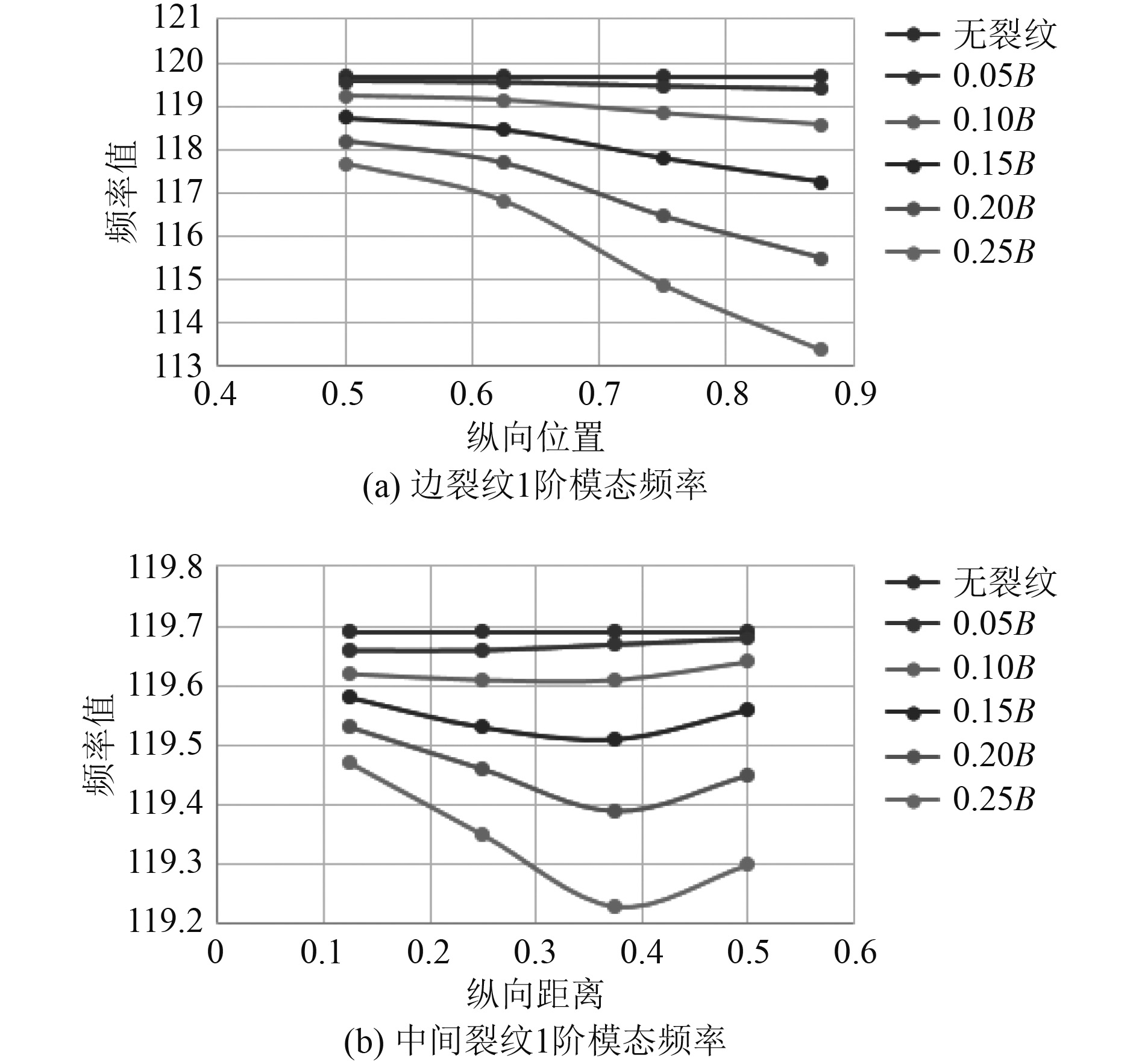
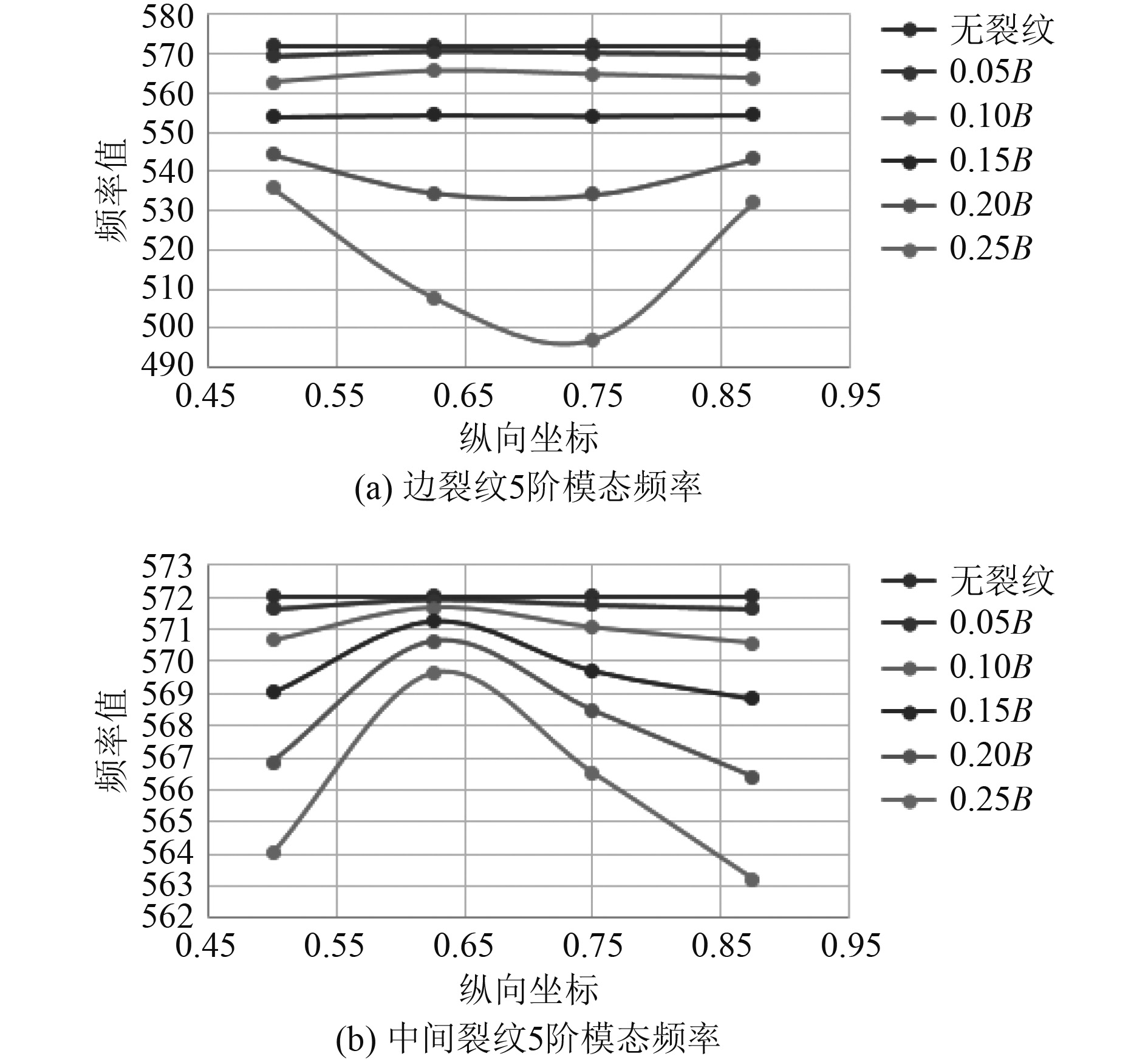
通过有限元仿真计算,得到表1所列的41个模型的频率特性,从仿真结果看裂纹出现后模型的各阶固有频率都有不同程度的下降。下面重点从裂纹位置和裂纹长度2个方面对模型的前5阶频率特性进行分析,以1阶和5阶模态为例进行重点分析。各工况下,模型1阶和5阶固有频率值及其变化量详见表3和表4,其中裂纹长度为0代表模型结构不存在裂纹损伤。不同长度裂纹模型1阶和5阶固有频率值随位置的变化曲线如图4和图5所示。
|
|
表 2 模型参数 Tab.2 Model parameters |
|
|
表 3 一阶模态频率值(Hz) Tab.3 Frequency of first-order modal(Hz) |
|
图 4 一阶模态频率 Fig. 4 Frequency of first order modal |
|
|
表 4 五阶模态频率值(Hz) Tab.4 Frequency of fifth-order modal(Hz) |
|
图 5 五阶模态频率 Fig. 5 Frequency of fifth-order modal |
通过分析表2和表3的数据及图5和图6曲线的相对关系,可以得出以下初步规律:
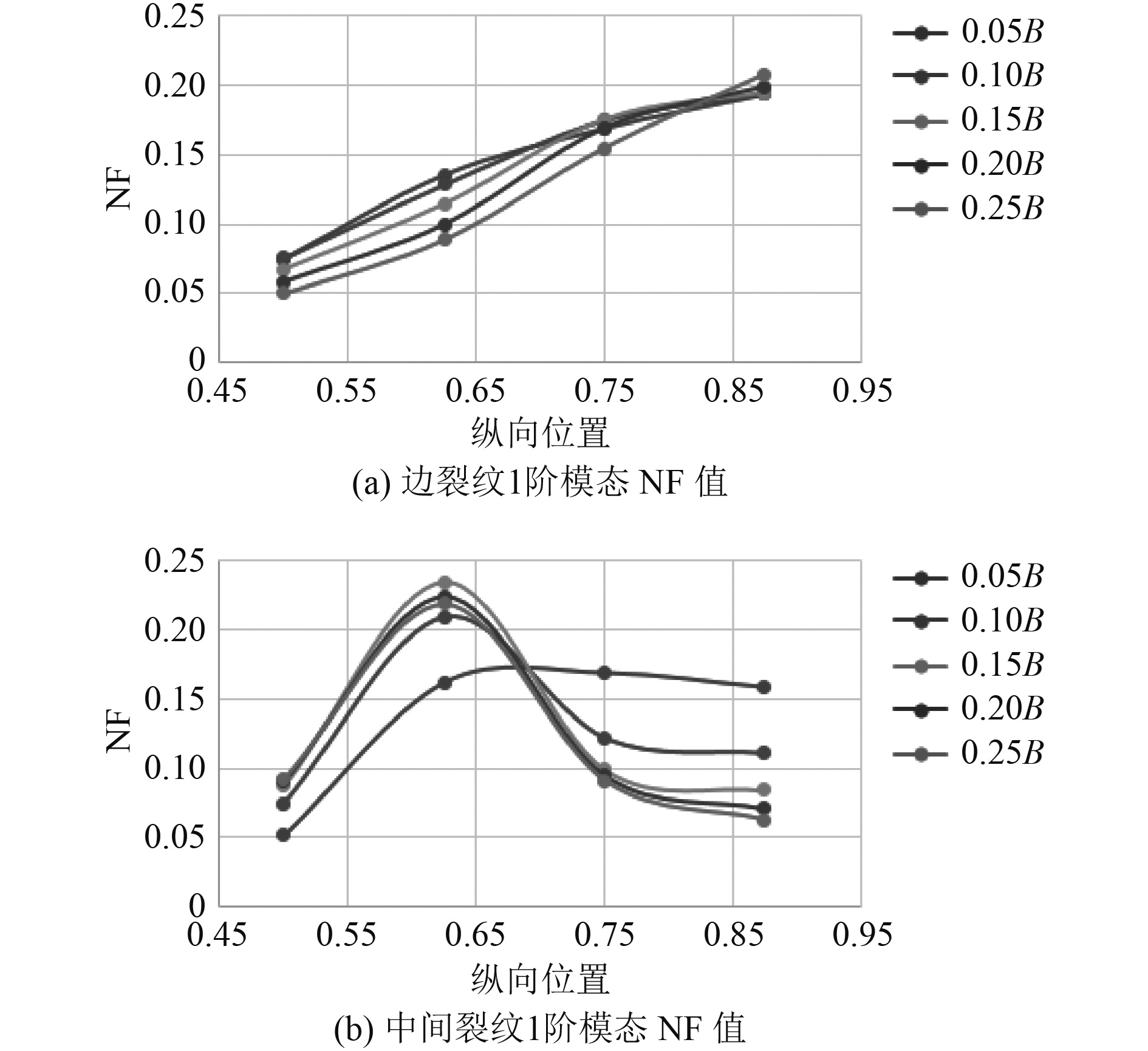
|
图 6 一阶模态NF值 Fig. 6 NF of first-order modal |
1)当损伤位置不变时,结构的各阶固有频率随着裂纹长度的变化规律相同,随着裂纹长度的增加,结构各阶的固有频率都单调减小。
2)结构的固有频率对边裂纹更为敏感,边裂纹结构固有频率影响的数值明显大于中间裂纹对固有频率的影响。
3)当裂纹长度不变时,结构不同阶数的固有频率随位置的变化规律有很大差异:为方面起见,主要分析裂纹纵向位置从中间加强筋向自由端变化固有频率的变化情况,对于边裂纹结构,1阶固有频率单调减小,5阶固有频率在裂纹较短时变化不明显,在裂纹较长时随着纵坐标的增大,先减小后增大;对于中间裂纹,1阶固有频率先减小后增大,5阶固有频率先增大后减小。
3.3 正规化频率变化率分析损伤识别需要从不同角度选择特征参数,除了固有频率绝对值外,还常常使用正规化频率变化率。设典型结构无裂纹损伤时的i阶频率为
| $ {F_i} = \left( {{f_{0i}} - {f_{1i}}} \right)/{f_{0i}}\text{,} $ | (1) |
正规化频率变化率定义为:
| $N{F_i} = {F_i}/\sum\limits_{j = 1}^n {{F_j}}\text{。} $ | (2) |
同样以1阶和5阶正规化频率变化率为例进行分析。表5和表6分别为结构的1阶和5阶正规化频率变化率。图6和图7分别为1阶和5阶正规化频率变化率的变化曲线。
|
|
表 5 一阶正规化频率变化率NF1 Tab.5 The value 1 of NFCR |
|
|
表 6 五阶正规化频率变化率NF5 Tab.6 The value 5 of NFCR |

|
图 7 五阶模态NF值 Fig. 7 NF of fifth-order modal |
根据表5和表6中的数据及图6和图7中的曲线,正规化频率变化率NF的变化规律与固有频率变化规律差别较大:对于结构1阶模态,边裂纹损伤位置由中间到加筋板两端,NF值不断增加;中间裂纹NF值先增加后减小;对于结构5阶模态,边裂纹较发散,裂纹长度较大时,NF值先增加后减小;中心裂纹损伤位置由中间加筋板到两端,NF值先减小后增加。
由于正规化频率变化率NF的变化规律与固有频率变化规律是相互独立的,与裂纹位置、长度等因素有关,也可以作为裂纹识别的特征参数。
4 结 语为研究裂纹损伤对典型船体结构振动特性的影响,选择加筋板作为典型船体结构,选择穿透性裂纹作为典型损伤形式,通过有限元仿真计算与结构的固有模态试验方法,针对裂纹位置、长度对结构频率和频率变化率的影响规律开展了研究,得到初步结论如下:
1)加筋板结构频率的变化对板上的裂纹较为敏感,受加强筋上的裂纹影响较小。
2)通过对比分析可知,损伤位置不变时,随着裂纹长度的增加,频率值会不断减小,而在同等条件下,边裂纹引起的频率变化要明显大于中间裂纹的频率变化;频率的变化还与模态阶数有关,不同阶数对频率变化的敏感程度不同,与频率的对应模式也不同,是反映频率规律的重要一环。
3)不同阶数的正规化频率变化率也随着裂纹位置、裂纹长度的变化而变化,且呈现出与频率变化不同的规律,也可以作为识别裂纹的重要特征参数。
| [1] |
赵耕贤, 詹志鹄. 船体结构损坏事故案例分析[J]. 上海造船, 2010(3): 63-66, 77. ZHAO Geng-xian, ZHAN Zhi-hao. Case analysis of ship structure damage accident[J]. Shanghai Shipbuilding, 2010(3): 63-66, 77. |
| [2] |
SALAWU O S. Detection of structural damage through changes in frequency: a review[J]. Engineering Structures, 1997, 19(9): 718-723. DOI:10.1016/S0141-0296(96)00149-6 |
| [3] |
CERRI M N, VESTRONI F. Detection of damage in beams subjected to diffused cracking[J]. Journal of Sound and Vibration, 2000, 234(2): 259-276. DOI:10.1006/jsvi.1999.2887 |
| [4] |
吴国荣, 张晓君. 含裂纹梁自由振动分析[J]. 船舶力学, 2007, 11(5): 798-803. WU Guo-rong, ZHANG Xiao-jun. Analysis on free vibration of the cracked beams[J]. Journal of Ship Mechanics, 2007, 11(5): 798-803. DOI:10.3969/j.issn.1007-7294.2007.05.019 |
| [5] |
刘文光, 郭隆清, 贺红林, 等. 基于固有频率的呼吸式裂纹梁损伤识别方法[J]. 中国机械工程, 2017, 28(6): 702-707. LIU Wen-guang, GUO Long-qing, HE hong-lin, et al. A damage identification method of a breathing cracked beam[J]. China Mechanical Engineering, 2017, 28(6): 702-707. DOI:10.3969/j.issn.1004-132X.2017.06.011 |
| [6] |
李火坤, 段峰虎. 基于多阶频率的弧形闸门主框架损伤识别研究[J]. 水电能源科学, 2012, 30(3): 107-109. LI Huo-kun, DUAN Feng-hu. Damage detection of main frame of radial gate based on multi-order frequencies[J]. Water Resources and Power, 2012, 30(3): 107-109. DOI:10.3969/j.issn.1000-7709.2012.03.033 |
| [7] |
贾超. 基于动力特性的结构损伤识别方法研究[D]. 吉林: 吉林建筑大学, 2017. JIA Chao. Based on the dynamic characteristics of the structure damage identification research[D]. JiLin: Jilin Jianzhu University, 2017. |
 2021, Vol. 43
2021, Vol. 43

