0 引　言

数据采集装置内部装有电路单元、元器件等电子部件，以及导热零件、风扇等机械部件。考虑到舰船摇晃、温度高等复杂环境对装置的干扰，为了保障装置安全、稳定运行，提高装置的使用效率、寿命，需要对其进行全面的总体设计。传统的数据采集装置设计中，往往只针对单场环境下，如温度场环境，从整机工作环境、内部元器件发热量、散热路径等方面分析，设计得到符合总体尺寸要求及散热需求的设计方案，满足元器件最高工作温度要求等；又或者只针对结构力学环境下，结合数据采集装置的振动分析试验、冲击试验等结果数据，设计得到符合结构力学强度要求的设计方案^[1]，如李玲娜^[2]使用有限元热仿真分析软件进行流体动力学分析和热仿真分析，对机箱部件进行热仿真计算，验证机箱热设计的可靠性；高志巧^[3]使用结构分析软件，对某星载机箱进行冲击响应谱和随机振动的力学分析，实现了结构的优化设计。

然而，数据采集装置在实际工作中，由于环境温度变化和器件自身发产生热应力，热会影响结构使其发生一定程度的变形，随之内部元器件的位置也会发生变化，元器件功能性能也会受到影响。从温度场的角度看，结构变形同样改变温度场的边界和热源的位置进而影响温度分布。所以实际工作中的数据采集装置的结构位移场、应力场和温度场是耦合在一起的。传统数据采集装置的设计，单方面考虑结构场和温度场，针对热学场或力学场作用下的优化是不够的，只有对热-结构多场耦合优化设计，才能获得数据采集装置最优设计方案，因此，数据采集装置的设计是一个典型的多场耦合多目标优化设计问题。

多目标优化方法目前有两大类，经典优化方法和智能优化方法；经典优化方法通常先将多目标优化问题转化为单目标优化问题，再应用单目标优化算法求解，如加权求和法、目标规划法等；该类方法需要在优化前获取偏好信息（如权重），而对于实际工程问题的各目标偏好信息在优化前通常很难准确获取，往往依靠经验人工设定，与实际情况可能存在偏差；单目标优化算法一次只能获取一个最优解，当问题具有多个峰值解时，该方法需要多次计算，从而求解效率低下^[4]。特别地，如果问题的决策空间和目标空间关系复杂，经典方法往往容易陷入局部最优，而很难获取全局最优解。

智能优化算法包括进化算法、群智能算法、神经网络算法等。其中进化算法工程应用广泛，该算法将问题求解过程与动物染色体适者生存进化过程类比，通过染色体的逐代进化收敛到最适应环境的个体，即问题最优解。与经典优化方法不同，进化算法对初始预设值的质量要求较低。从初始种群开始进化，通过基因复制、选择、交叉、变异等算子逐步寻优，且只需对目标函数值进行计算，不需要目标函数对设计参数的导数信息。对于多目标优化问题，Deb提出非支配解排序的进化算法（Non-dominated Sorting Genetic Algorithm，NSGA）应用比较广泛，主要有2种算法，即NSGA-I^[5]和NSGA-II。与NSGA-I相比，NSGA-II引入了快速排序算法、拥挤度方法和精英策略，其中精英策略将父类和子类中的最好个体保留至下一代，保证了所有进化的最优个体不会被选择、变异等算子操作丢失，但是该算子也降低了基因的多样性，导致过早收敛。受自然界跳变基因（Jumping Genes，JG）^[6]的启发，近来发展了多个带有JG算子的NAGA-II算法，根据编码方式，JG算子引入方式有多种，如二进制编码的NSGA-II-JG，NSGA-II-mJG，NSGA-II-aJG^[7]等，实数编码的RJGGA^[8]，RNSGA-II-SBJG等。引入JG算子可以提升基因多样性，保障全局寻优。

面对多目标进化算法获取的方案解集，设计人员需要开展综合评价或决策，选取满意解。该过程可借助邓聚龙的灰色关联度分析（Grey relational analysis）方法，该方法应用灰色关联度来定量表示属性之间关系的强弱、大小和次序，根据研究对象和参考序列之间的距离以及参数曲线形状相似度来判断它们的接近性，通常理想最优解为参考序列，理想最优解是各个指标都达到最优的解。如果某个方案和理想最优解的关联度最大，可认为该方案是最终满意解。

本文针对数据采集装置结构优化设计问题，建立数据采集装置结构参数化模型，针对数据采集装置参数化模型进行热-结构多场耦合有限元分析，基于响应面构建方法，将复杂的多场耦合仿真分析简化为简单的近似模型，并利用近似模型采用NSGA-II多目标优化算法对数据采集装置进行多目标优化，编制灰色关联度分析程序，用于优化解集的综合评价。综合考虑了元器件排布方式、数据采集装置设计尺寸等因素对结构变形、温度分布及总体质量的影响，并给出优化后的数据采集装置设计参数。

1 理　论 1.1 热结构耦合分析

热-结构耦合分析是指计算温度场产生的热应力对结构中应力、应变和位移等影响的分析^[9]。部件工作于温度变化的情况，由于温度变化而产生的胀缩受到结构或部件的外部或内部约束的限制而不能自由进行，那么这些结构或部件内将产生热应力。因此，要研究物体的热应力就必须首先知道物体中的温度场。耦合场分析相互作用非线性程度不高的情况下，顺序耦合法更有效，计算量更小，操作更容易。

热-结构耦合分析采用有限元方法求解以下方程^[10]：

物理方程

$ {\sigma _{ij}} = 2G{\varepsilon _{ij}} + ({A_e} - {\beta _T}){\delta _{ij}}\text{，} $

(1)

平衡方程

$ {\nabla ^2}{u_i} + \frac{1}{{1 - 2\mu }}\frac{{\partial {\varepsilon _{kk}}}}{{\partial i}} - \frac{{2(1 + \mu )}}{{1 - 2\mu }}\frac{{\partial T}}{{\partial i}} + \frac{{{f_i}}}{G} = 0\text{，} $

(2)

协调方程

$\begin{split} {\nabla ^2}{\delta _i} + \frac{1}{{1 + \mu }}\frac{{{\partial ^2}{\delta _{kk}}}}{{\partial {i^2}}}=& - {\alpha _E}\left( {\frac{1}{{1 - \mu }}{\nabla ^2}T + \frac{1}{{1 + \mu }}\frac{{{\partial ^2}T}}{{\partial {i^2}}}} \right) - \\ &\left( {\frac{\mu }{{1 - \mu }}\frac{{\partial {f_i}}}{{\partial i}} + 2\frac{{\partial {f_i}}}{{\partial j}}} \right)\text{。}\end{split} $

(3)

式中： $\ \beta =\dfrac{{{\alpha _E}}}{{1 - 2\mu }} = \gamma {\alpha _E} + 2G$ ， $G=\dfrac{E}{{2(1 + \mu )}}$ ， ${\rm{A }}= \dfrac{{\mu E}}{{(1 + \mu )(1 - 2\mu )}}$ ， ${\delta _{kk}} = {\delta _{xx}} + {\delta _{yy}}$ ， ${\varepsilon _{kk}} = e = {\varepsilon _{xx}} + {\varepsilon _{yy}} + {\varepsilon _{zz}}$ ， $E$ 为弹性模量， $\alpha $ 为线膨胀系数， $\mu $ 为泊松比， ${f_i}(i = x,y,z)$ 为单位体积力在坐标轴上的分量。

1.2 响应面构建技术

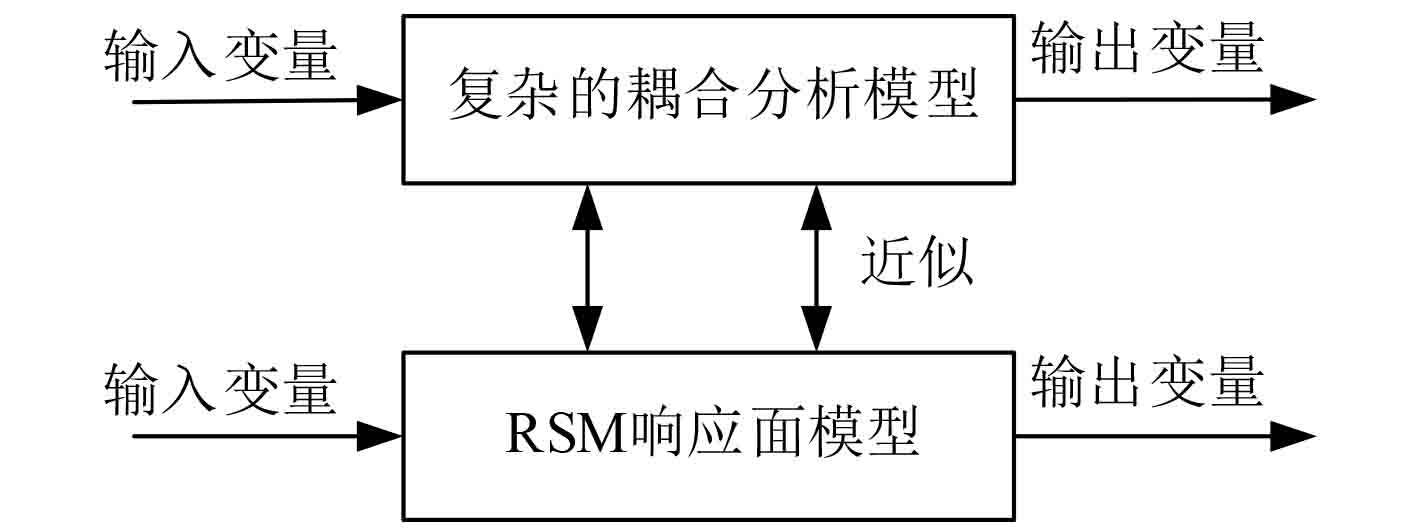
在优化计算分析时，模型按照多学科设计优化算法进行调度运行，它们之间存在大量的数据交换，由于这些分析模型非常复杂，因此运行过程往往十分费时。为了提高仿真计算效率，可使用拉丁超立方取样策略进行试验设计方法，构造样本点，基于响应面方法构建近似代理模型，用简单的数学模型来替代复杂的热-结构耦合分析模型进行分析计算，二者间关系如图1所示。

常用响应面模型主要有4种：多项式函数模型，Kriging函数模型、径向基函数（简称RBF）函数模型以及神经网络模型。RBF函数模型以径向函数为基函数，通过线性叠加构造出来的大的模型即为径向函数响应面模型，在同时考虑模型的精度和鲁棒性时，径向基函数模型具有较好的可靠性^[1]。其基本形式为：

$ f(x) = \sum\limits_{i = 1}^n {{w_i} \cdot } \phi ({r^i}) = {W^{\rm T}}\varPhi \text{，} $

(4)

其中， $W(x) = {({w_1} \cdot \cdot \cdot {w_n})^{\rm T}}$ ， $\varPhi = {(\phi ({r^1}), \cdot \cdot \cdot ,\phi ({r^n}))^{\rm T}}$ ， ${w_i}$ 是权系数， $\phi (r)$ 是径向函数， ${r^i} = \left\| {x - {x^i}} \right\|$ 是待测点 $x$ 于样本点 ${x^i}$ 之间的欧式距离。

在径向基函数模型中，常用的径向函数有：高斯函数（G）、调和样条函数（PS）、多二次函数（MQ）、逆多二次函数（IMQ）、C2阶紧支撑函数（C2）等。径向基函数模型的特性随着所采用的径向函数的不同而不同。当径向基函数模型在采用G函数或IMQ函数为基函数时，模型会因为径向函数的影响而具有局部估计的特点，而采用MQ函数作为核函数时，模型又会具有全局估计的特点。径向基函数模型的是一种灵活性好，结构简单，计算量也相对较少而且效率比较高的代理模型。

为了确定近似模型预测精度，还需要比较近似模型预估值与误差样本点之间差异，近似模型精度检验常用指标有确定系数（ ${R^2}$ 也称决定系数）^[10]。

确定系数（ $ {R}^{2} $ ）值域为[0, 1]，值越大表面近似模型逼近实际模型程度越高，通常可接受范围是大于0.8。确定系数（ $ {R}^{2} $ ）可以表示为：

${R^2}{\rm{ = }}\frac{{{S_R}}}{{{S_T}}}\text{，} $

(5)

式中， ${S}_{R}={\displaystyle\sum\limits_{i=1}^{{n}_{S}}({y}_{\text{近似}}-{y}_{\text{平均}}}{)}^{2}{)}^{2}$ ， ${S}_{T}=\displaystyle\sum\limits_{i=1}^{{n}_{S}} ({y}_{\text{实际}}-{y}_{\text{平均}})^{2}$ ， ${n_S}$ 为误差样本点个数， $ {y}_{\text{近似}}$ 为近似模型样本误差点预估值， $ {y}_{\text{平均}}$ 为实际模型误差样本点真实响应平均值， $ {y}_{\text{实际}}$ 为实际模型误差样本点真实响应值。

1.3 多目标优化模型及其求解方法

多目标优化问题一般表述为：

$ \min F(x) = \min \left[ {{f_1}(x),{f_2}(x), \cdot \cdot \cdot ,{f_n}(x)} \right]\text{，} $

(6)

$ {\rm{s.t.}}\;{x^L} \leqslant x \leqslant {x^U}\text{，} $

(7)

$ {h_i}(x) = 0,\;i = 1,2, \cdot \cdot \cdot I\text{，} $

(8)

$ {g_j}(x) = 0,\;j = 1,2, \cdot \cdot \cdot J\text{。} $

(9)

其中， $x = \left\{ {{x_1},{x_2}, \cdot \cdot \cdot {x_m}} \right\}$ ， $m$ 为设计变量得数量， $n$ 为优化目标的数量， ${x^U}$ 和 ${x^L}$ 分别为设计变量的上限和下限，I和J分别为等式约束和不等式约束的数量。多目标优化问题，往往存在一系列解，每个解至少存在一个目标值优于其他解的目标值，即非支配解或Pareto解，所有这些解构成的集合称为Pareto最优解集。

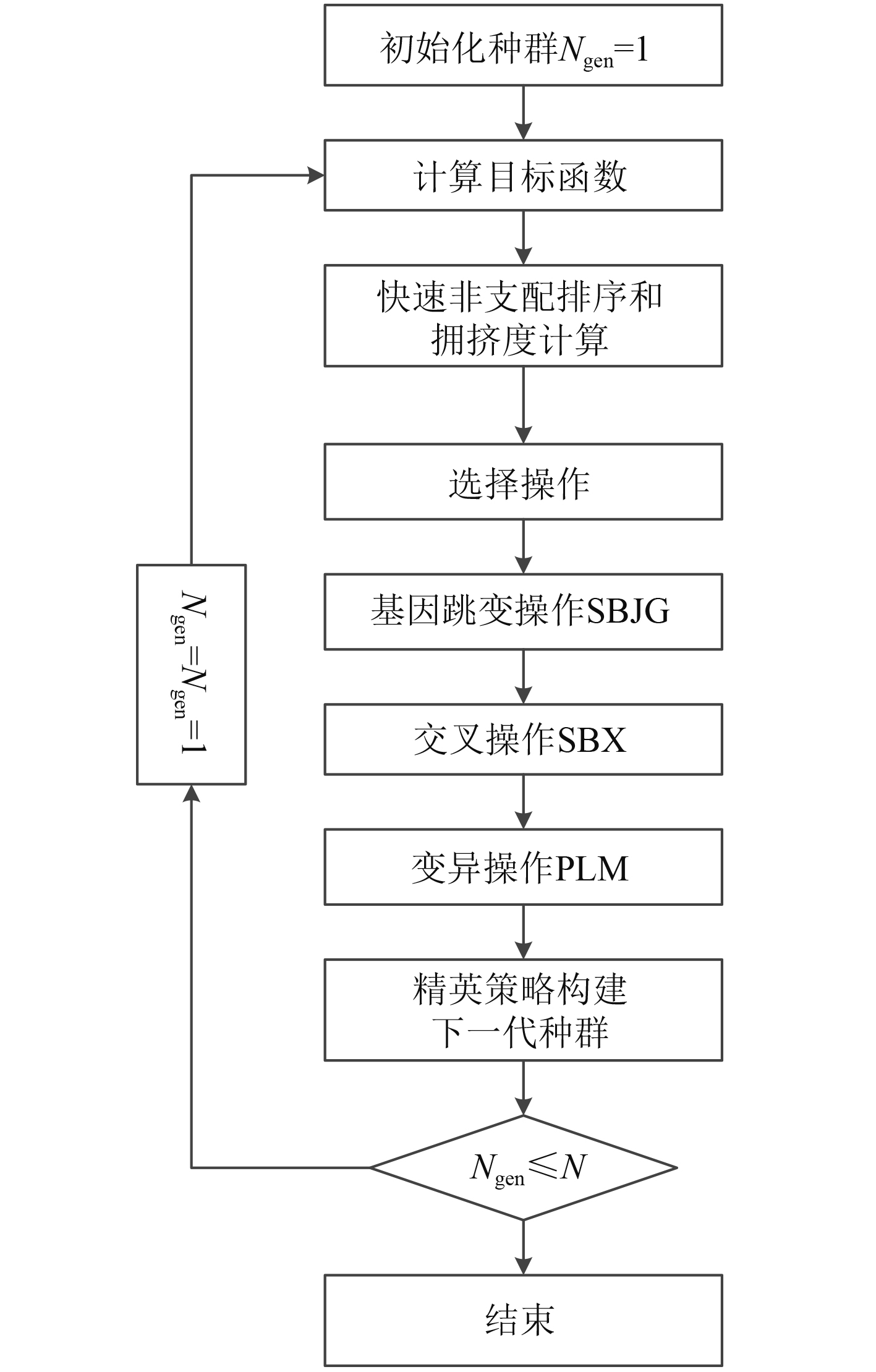
Ramteke等提出的RNSGAII-SBJG算法是进化算法的一种，该方法在实数编码的RNSGA-II的框架下，通过模拟二进制编码JG算子，构建SBJG算子。RNSGA-II-SBJG算法计算流程如图2所示。包括种群初始化，适应度计算，以及选择、交叉和变异等环节，其中SBX和PLM分别为交叉算子和变异算子，与RNSGA-II算法相同。

SBJG是模拟二进制跳变基因的实数编码跳变基因算子。当某个染色体的跳变概率 ${P_{JG}}$ 小于预先设定值时，对该染色体进行基因跳变操作如下式：

$ {x'_{ij}} = {x_{ij}} + (x_i^U - x_i^L){\alpha _{ij}}\text{。} $

(10)

其中： ${x_{ij}}$ ， ${x'_{ij}}$ 分别为第i个设计变量在第j代跳变前和跳变后的数值； $x_i^U$ 和 $x_i^L$ 分别为第i个设计变量 ${x_i}$ 的上限和下限； $ {\alpha }_{ij} $ 是一个随机数，符合下式的分布函数：

${\alpha _{ij}} = \left\{ {\begin{array}{*{20}{l}} {{{\left[ {2rand} \right]}^{\frac{1}{{{\eta _{JG}} + 1}} - 1}}},&{rand < 0.5}\text{，}\\ {1 - {{\left[ {2(1 - rand)} \right]}^{\frac{1}{{{\eta _{JG}} + 1}} - 1}}},&{rand \geqslant 0.5}\text{，} \end{array}} \right.$

(11)

其中，rand是一个随机数， $ {\eta }_{JG}\in [jgs1,jgs2] $ ， $jgs1$ 和 $jgs2$ 为随机正整数。

1.4 决　策

Pareto解集的每一个解均为非支配解，从而需要从中选择满意解作为最终设计方案，即进行综合评价或决策。本文采用熵权和灰色关联度分析对Pareto解集进行综合评价，计算关联度系数，对设计方案进行排序，关联度系数最大的选为最终设计方案。

通常，将多目标优化的目标函数作为决策属性，灰色关联度分析需要考虑各属性的权值，这里采用熵权法计算目标函数的权重。熵的概念来自热力学，表示一个信息源发出的信号状态的不确定程度，熵权表示某指标在决策或评估问题中提供的有用信息量的多少，即指标的相对重要程度。如果某个指标的熵越小，就表明其指标值的变异程度越大，提供的信息量越多，在评价中所起的作用也越大。

对评价对象Y，其熵权的计算过程如下：

1）对 ${y_{ij}}$ （最后一代种群中第j个目标函数的第 $ i $ 个结果）进行归一化处理

为方便起见，仍记为 ${y_{ij}}$ ；

2）计算指标比重 ${p_{ij}}$

$ {p_{ij}} = \frac{{{y_{ij}}}}{{\displaystyle\sum\limits_{i = 1}^n {{y_{ij}}} }}\;i = 1, \cdot \cdot \cdot ,s\;j = 1, \cdot \cdot \cdot ,t\text{；} $

(12)

3）计算指标熵值 ${e_j}$

$ {e_j} = - \frac{1}{{\ln s}}\sum\limits_{i = 1}^s {{p_{ij}}\ln } {p_{ij}}\text{；} $

(13)

4）计算指标权值 ${w_j}$

$ {w_j} = \frac{{1 - {e_j}}}{{t - \displaystyle\sum\limits_{j = 1}^t {{e_j}} }}\text{。} $

(14)

灰色关联度分析的主要步骤如下：

1）选择参考和比较序列，对指标进行规范化处理；

2）选择用于分析序列间关系的计算模型，计算关联系数；

3）计算关联度，根据关联度数值进行排序。

第j个评价指标 ${y_j}$ （通常就是目标函数）和最优向量Z的关联系数 ${\xi _i}({Y_j},Z)$ 按下式计算：

$ {\xi _i}({Y_j},Z) = \frac{{{\Delta _{\min }} + \rho {\Delta _{\max }}}}{{{\Delta _{ij}} + \rho {\Delta _{\max }}}}\text{。} $

(15)

其中： ${\Delta _{\min }} = \mathop {\min }\limits_i \mathop {\min }\limits_j \left| {{y_{ij}} - {z_i}} \right|$ ； ${\Delta _{ij}} = \left| {{y_{ij}} - {z_i}} \right|$ ； ${\Delta _{\max }} = \mathop {\max }\limits_i \mathop {\max }\limits_j \left| {{y_{ij}} - {z_i}} \right|$ ； $\ \rho $ 是分辨系数，通常取ρ = 0.5。

将各指标的关联系数 ${\xi _i}({Y_j},Z)$ 与权值 ${w_j}$ 相结合，可得到最优解：

$ {R_{Opt}} = \mathop {\max }\limits_i \sum\limits_{j = 1}^t {{\xi _i}({Y_j},Z){w_j}}\text{。} $

(16)

2 某数据采集装置的总体优化设计 2.1 物理模型和设计变量

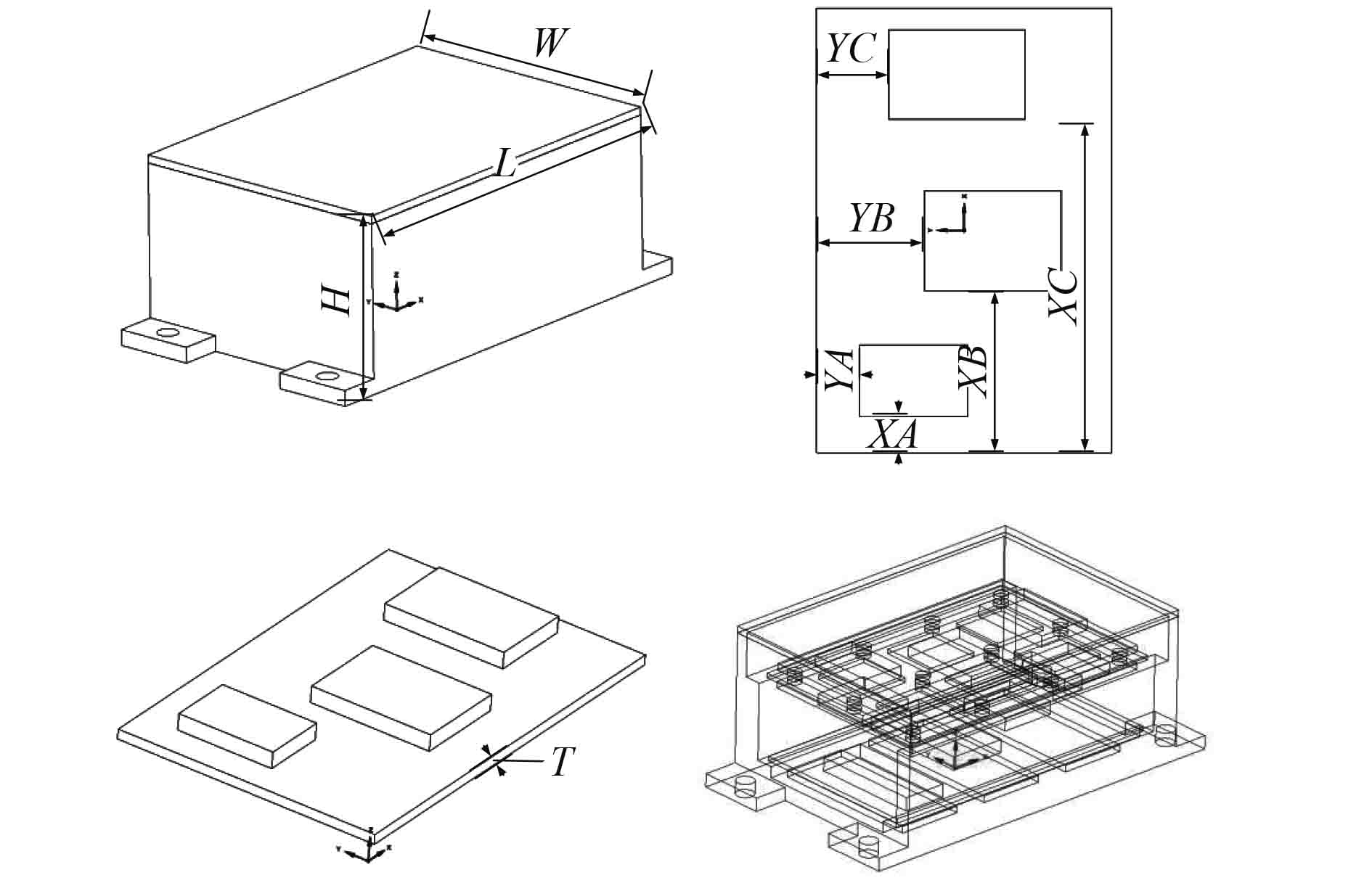
对某数据采集装置进行多目标优化设计，对内部元器件排布位置进行设计，保证数据采集装置总体变形尽可能小、温度分布尽可能均匀。其次，在满足数据采集装置强度的前提下，尽可能减少总体质量。按数据采集装置水平放置、元器件正常运行工况，对数据采集装置进行设计，即设计输入变量为： $L,W,H, T,{X_A},{Y_A},{X_B},{Y_B},{X_C},{Y_C}$ ，输出变量为基板变形D、内外最大温差△T和总质量m，设计变量如图3所示。

2.2 基于热-结构耦合分析的近似建模

数据采集装置的热-结构耦合分析可以采用顺序耦合法计算，首先求解装置温度场，然后将温度场作为热边界条件加载到结构上，计算出装置基板变形及结构热应力。近似建模通常采用实验设计（Design of Experiments，DOE）方法开展，本文采用拉丁超立方（Latin Hypercube）技术对10个结构优化变量（因子）在整个优化空间中进行采样，初始化样本点总数（水平）均为120。在采样时每个因子在其可行域中均匀采样，最后随机组合，这样每个因子的每个水平均只研究一次。同时，应用DOE数据进行响应面拟合，采用RBF方法的多种基函数进行拟合，并进行对比验证，找出合适的基函数。最终，针对不同参数，使用不同的基函数进行响应面拟合，分别得到 $RS{M_D}$ （最大变形）、 $RS{M_{\Delta T}}$ （内外最大温差）、 $RS{M_m}$ （总质量）及 $RS{M_s}$ （最大等效应力）4个响应面确定系数，如表1所示。可以看出，采用径向基函数方式拟合创建的响应面，确定系数均大于0.9，能够较好地对数据采集装置热-结构耦合分析模型进行近似。

2.3 多目标优化条件

综合考虑数据采集装置基板变形D，内外最大温差△T、总质量m及结构等效应力S，进行多目标优化设计。选定数据采集装置长度L、宽度W、高度H、第1层基板厚度T、元器件A横向位置X_A、纵向位置Y_A、元器件B横向位置X_B、纵向位置Y_B、元器件C横向位置X_C及纵向位置Y_C为设计变量，目标是基板变形D最小，内外最大温差△T最小及总质量m最小，约束条件则是结构等效应力S不超过90 MPa。

设计变量：

$ x = \left\{ {L,W,H,T,{X_A},{Y_A},{X_B},{Y_B},{X_C},{Y_C}} \right\}\text{，} $

各变量的取值范围如下： $L \in \left[ {72.0,\;81.4} \right]$ ， $W \in \left[ {53.35,\;57.75} \right]$ ， $H \in \left[ {61.0,\;71.5} \right]$ ， $T \in \left[ {2.7,\;3.3} \right]$ ， ${X_A} \in \left[ {9,\;11} \right]$ ， ${Y_A} \in \left[ {10.8,\;13.2} \right]$ ， ${X_B} \in \left[ {40.5,\;49.5} \right]$ ， ${Y_B} \in \left[ {27,\;33} \right]$ ， ${X_C} \in \left[ {80.5,\;93.15} \right]$ ， ${Y_C} \in \left[ {18,\;22} \right]$ 。

目标函数：

$ \min F(x) = \min \left\{ {D,\Delta T,m} \right\}\text{，} $

约束条件：

$ S \leqslant 90\ {\rm{MPa}}\text{。} $

2.4 多目标优化分析

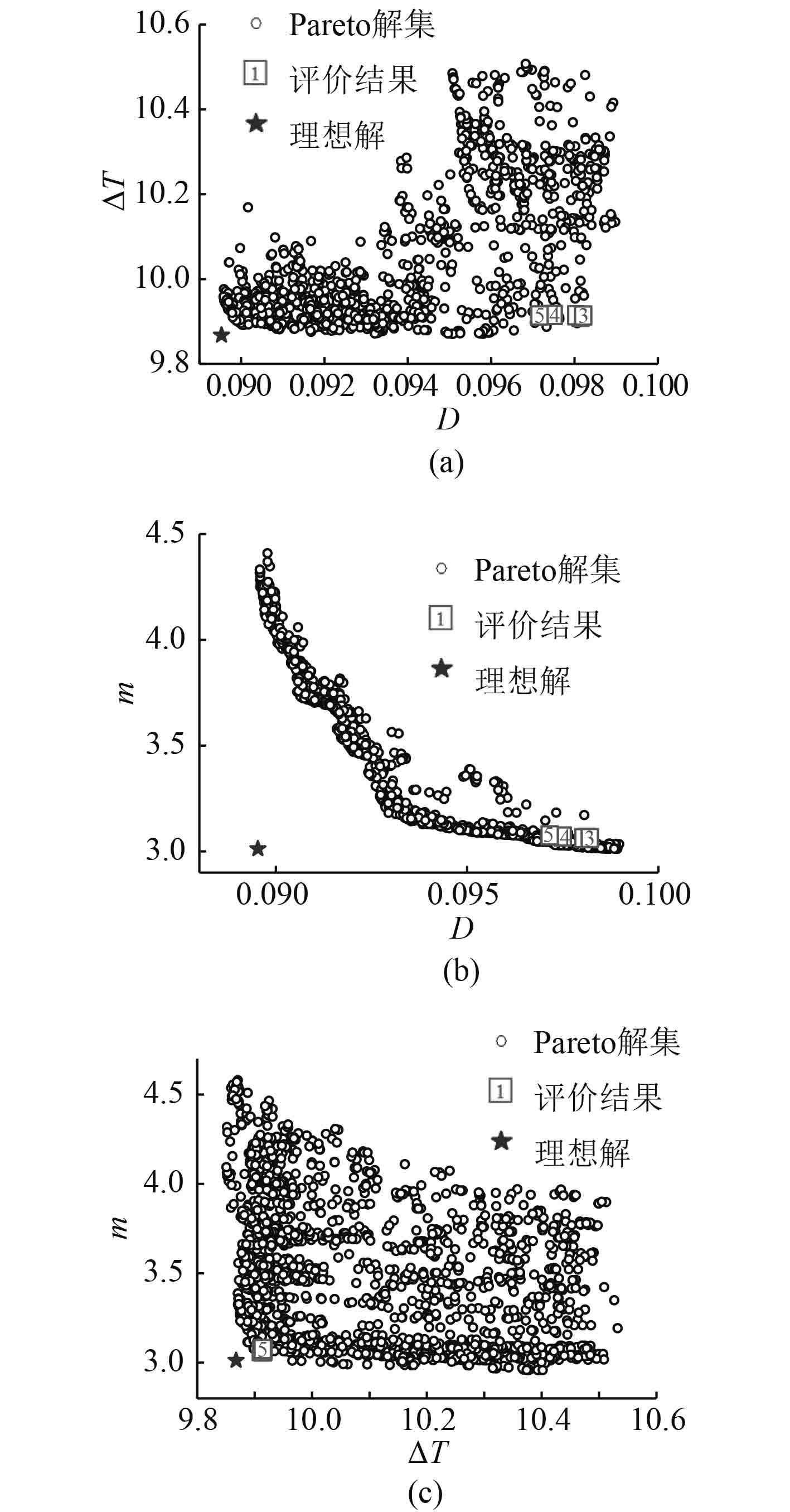
设定初始化400个种群，进化1000代，随机生成6个种子数计算6次，去掉重复解后，共筛选出Pareto解约1200个，目标函数Pareto解散点图如图4所示。可以看出，Pareto解集的目标散点分布比较均匀、分布范围清晰可见。

由图4（a）可以看出，数据采集装置内外温差 $\Delta T$ 与箱体最大变形量D基本成正线性关系，变形越大温差越大；由图4（b）可以看出，最大变形D与总质量m也基本成负线性关系，结构质量越大，抗变形能力越强；由图4（c）可以看出，数据采集装置总质量m与箱体内外温差 $\Delta T$ 关系不明显。

2.5 决　策

不改变设计变量范围和约束条件，分别对数据采集装置基板变形D，内外最大温差△T、总质量m为目标进行单目标优化设计，可以获得3个单目标解，最优解和对应的设计变量如表2所示。由3个单目标组成的理想解为（0.0895，9.8677，3.0122）。

通过信息熵方法获取3个目标函数的权重为 ${w_D} = 0.229\;0$ ， ${w_{\Delta T}} = 0.233\;8$ ， ${w_m} = 0.537\;2$ 。然后计算Pareto解集与理想解间的灰色关联度并排序，排在前五的方案见表3，它们在Pareto解集中的结果分布图如图4。

在这5个方案中，方案5的变形虽然最小，但质量却是最大的；方案4与方案5相似，质量较方案5更小。方案2和方案3，质量都比较小，都是偏上游的，不过温差较方案1大，可作为方案1的备选方案。方案1的温差最小，同时质量也处于上游处，所以方案1优于其余方案。

将方案1设计参数生成几何模型和分析模型，再进行热-结构耦合分析，并与响应面计算结果进行对比验证。如表4所示，可以看出，通过响应面代理模型计算出的结果与有限元分析得到的结果基本一致，但计算时间相差很多，在普通计算机上，响应面代理模型计算用时为毫秒级，而有限元分析从几何建模、前处理、计算、后处理用时至少4 h，可见响应面模型的应用大大缩短了计算用时。

3 结　语

本文采用带有跳变基因和精英策略的非支配排序的多目标遗传算法（RNSGA-II-SBJG）进行数据采集装置优化设计，并基于灰色关联度分析方法对Pareto解集进行综合评价与排序，确定满意的优化解。考虑了数据采集装置尺寸参数、元器件位置参数、基板厚度对数据采集装置性能、热性能的影响，并结合热-结构耦合物理场分析，建立了热-结构耦合多目标优化设计模型，并对某数据采集装置进行了优化计算与设计方案决策，结果表明：

1）采用热-结构多场耦合的分析模型，能够准确模拟数据采集装置在工作环境中，热应力分布情况，将热、结构等性能指标作为多目标优化指标，才能从整体上对数据采集装置进行优化设计；

2）基于径向基函数的响应面方法可以较好的拟合采集装置尺寸参数、元器件位置参数、基板厚度和变形、应力、质量间的复杂函数关系；

3）RNSGA-II-SBJG算法能够快速求解数据采集装置多目标优化设计问题，且给出的Pareto解集分布比较均匀；

4）基于熵权和灰色关联度分析的综合评价方法简便有效，对优化结果的排序合理，便于设计者根据使用目标选择优化方案。

应用本文的建模、优化与决策方法，结合精细化输入(如数据采集装置夹层等部件尺寸和位置参数)和多场耦合（如考虑热分布对数据采集装置元器件电磁性能的影响）方法，可进一步开展数据采集装置热-结构-电磁多目标优化设计工作。