0 引　言

对水下目标进行识别和跟踪对于潜艇、鱼雷、水下无人潜航器等来说至关重要，是保证它们安全作业的重要环节。为了保证自身安全，不主动向外辐射能量的前提下，被动地对目标运动状态进行估计是很有必要的。而单站纯方位目标跟踪所需观测者少、隐蔽性强，应用场景广泛^[1-2]。距离目标较近时由于方位抖动影响更大，使得滤波容易出现不稳定、甚至发散的情况。同时，这种情形下的一个难点是目标状态的潜在不完全可观测性，因此状态估计难度更大^[3-4]。

单站纯方位目标跟踪是非线性问题，非线性滤波是解决这一问题常用的有效方法之一。扩展卡尔曼滤波（Extanded Kalman Filter，EKF）^[5]是较早应用于目标跟踪的非线性滤波方法，但其仅为1阶近似，线性化误差较大，滤波的精度和稳定性较差^[6]。采样型方法是实现非线性滤波的另一类方法，包括确定性采样和随机采样。以粒子滤波^[7]（Particle Filter，PF）为代表的随机性采样计算量过大，且可能会出现粒子退化或贫乏的问题，在工程应用中具有局限性^[8]。

确定性采样方法包括无迹卡尔曼滤波（Unscented Kalman Filter，UKF）^[9]、容积卡尔曼滤波^[10]（Cubature Kalman Filter，CKF）、中心差分卡尔曼滤波（Central Difference Kalman Filter，CDKF）^[11-12]等。其中UKF是应用最广泛的一种方法^[13-14]，可达至少2阶近似，但需要根据运动或观测模型的非线性来选择α，β，λ三个参数，难以找到参数的最优值。在UKF基础上的平方根无迹卡尔曼滤波（Square Root Unscented Kalman Filter，SR-UKF）也是一种用途广泛的滤波方法，具有较好的稳定性，是一种经典的平方根类的方法，在水下目标跟踪中有较好的效果^[15-16]。因此本文也将SR-UKF作为一种对比方法加入到仿真中。

CDKF也是确定性采样方法中的一种，它选取采样点的方式与UKF不同。CDKF基于Sterling 多项式插值公式，对非线性函数按中心差分形式逼近，可达至少2阶近似。CDKF精度与UKF相当，且只需调整1个参数h。因此CDKF在目标跟踪^[17-18]、导航系统^[19]等方面都有较好应用。但单站纯方位目标跟踪系统的可观测性差、观测噪声影响大，致使滤波器不稳定^[3-4]，尤其在目标距离近的情况下这种现象更常见。

本文目的是解决在近距离的纯方位观测情况中，单站纯方位目标跟踪中CDKF容易出现的滤波不稳定问题。因此提出了一种CDKF的改进方法，在采样点的协方差和量测协方差中采用QR分解计算协方差平方根，而在协方差平方根更新时使用更为稳定的奇异值分解（Singular Value Decomposition，SVD）进行计算，提高算法的稳定性和估计精度。

1 问题描述和滤波方法 1.1 单站纯方位目标跟踪

对于水下目标，在许多情况下，目标的运动是非机动的。因此，近似等速（Nearly Constant Velocity，NCV）模型^{[5, 20]}适用于水下被动目标跟踪场景。本文考虑二维平面运动模型，非机动目标和机动的观测站。

目标的运动状态可以表示为向量：

${{{X}}_k} = \left[ {{x_k}}\quad {{{\dot x}_k}}\quad {{y_k}}\quad {{{\dot y}_k}} \right]^{\rm{T}} $

其中： ${x_k}$ ， ${y_k}$ 表示目标位置对应的坐标， ${\dot x_k}$ ， ${\dot y_k}$ 表示目标的速度分量。对于NCV模型，目标匀速直线运动，系统的状态方程可表示为：

${{X}}\left( {k + 1} \right) = {{\varPhi}} {{X}}\left( k \right) +{{w}}\left( k \right)\text{。}$

(1)

其中： ${{\varPhi}} $ 为状态转移矩阵； ${{w}}\left( k \right)$ 为均值为0方差为 ${{Q}}$ 的系统噪声：

${{\varPhi}} = \left[ {\begin{array}{*{20}{c}} 1&{\Delta t}&0&0 \\ 0&1&0&0 \\ 0&0&1&{\Delta t} \\ 0&0&0&1 \end{array}} \right]\text{，}$

(2)

${{Q}} = \delta _q^2\left[ {\begin{array}{*{20}{c}} {\dfrac{{\Delta {t^3}}}{3}}&{\dfrac{{\Delta {t^2}}}{2}}&0&0 \\ {\dfrac{{\Delta {t^2}}}{2}}&{\Delta t}&0&0 \\ 0&0&{\dfrac{{\Delta {t^3}}}{3}}&{\dfrac{{\Delta {t^2}}}{2}} \\ 0&0&{\dfrac{{\Delta {t^2}}}{2}}&{\Delta t} \end{array}} \right]\text{。}$

(3)

其中： $\delta _q^2$ 为系统过程噪声强度； $\Delta t$ 为采样间隔。

系统的观测方程可表示如下：

${{{Z}}_k} = f({{{X}}_k}) + {{{v}}_k}\text{。}$

(4)

其中： ${{v}}\left( k \right)$ 为均值为0方差为 ${{R}}$ 的观测噪声。对于单站纯方位目标跟踪系统，观测函数为：

$ f({{{X}}_k}){\rm{ = arctan[(}}{y_k} - y_k^{(o)})/ ({x_k} - x_k^{(o)})] $

纯方位目标跟踪是典型的非线性滤波问题，式（1）和式（4）组成了系统状态空间模型。对于单站纯方位量测来说，观测站机动是系统完全可观测的必要条件而非充分条件，观测站的机动情况对滤波效果起着关键作用，但在近距离追击目标的情况下，观测站较大机动容易丢失目标，因此只能小机动或者不机动，因此系统可观测性受限。

1.2 中心差分卡尔曼滤波

假设系统状态变量是服从高斯分布的，且均值和协方差已知。CDKF的核心思想是利用斯特林多项式插值公式，将非线性方程按中心差分形式展开，无需计算函数的雅可比矩阵。非线性函数 $f(x)$ 在 $x = \bar x$ 处展开的2阶斯特林多项式插值公式为：

$f(x) \approx f(\bar x){\rm{ + }}f{'_D}(\bar x)(x - \bar x) + f'{'_D}(\bar x){(x - \bar x)^2}/2!\text{，}$

(5)

其中， $f{'_D}(\bar x)$ 为一阶差分算子， $f'{'_D}(\bar x)$ 为二阶差分算子：

$f{'_D}(\bar x){\rm{ = [}}f(\bar x + h\delta ) + f(\bar x + h\delta )]/2h\text{，}$

(6)

$f'{'_D}(\bar x){\rm{ = [}}f(\bar x + h\delta ) + f(\bar x + h\delta ) - 2f(\bar x)]/{h^2}\text{。}$

(7)

其中：h为中心差分半步长，其取值可决定采样点的分布区间，适合于高斯分布的h最佳取值为 $\sqrt 3 $ ； $\delta $ 为均值为0，与x具有相同协方差的随机变量。式（6）可以看作是用中心差分运算代替泰勒级数展开中的求导运算，用1阶和2阶中心差分算子来代替1阶和2阶导数。

文献[11]中的中心差分滤波器和文献[12]中的差分滤波器都是基于斯特林多项式插值公式，本质上是相同的，也就是CDKF。CDKF通过确定性加权的采样点（Sigma点）来近似状态变量的分布函数，并通过采样点的非线性变换，估计非线性变换后状态变量的均值和协方差。L维的状态向量 ${{X}}\left( k \right)$ 需要构造 $2L + 1$ 个Sigma采样点，Sigma点与真实的状态向量有着相同的均值、方差和高阶中心距。常规CDKF用于目标跟踪的具体步骤如下：

步骤1　 k=0时，初始化状态向量和协方差

${{\hat{{ X}}}_0} = E({{{X}}_0})\text{，}$

(8)

${{{P}}_0} = E[({{\hat{{ X}}}_0} - {{{X}}_0}){({{\hat{{ X}}}_0} - {{{X}}_0})^{\rm{T}}}]\text{。}$

(9)

k>0时，进行步骤2到步骤8。

步骤2　采样点和对应权值

$\left\{ \begin{array}{l} {{{\chi}} }_{0,k-1}={\widehat{{X}}}_{k-1},i=0\text{，}\\ {{{\chi}} }_{i,k-1}={\widehat{{X}}}_{k-1}+h{\left(\sqrt{{{P}}_{k-1}}\right)}_{(i)},i=1\cdots L \text{，}\\ {{{\chi}} }_{i,k-1}={\widehat{{X}}}_{k-1}-h{\left(\sqrt{{{P}}_{k-1}}\right)}_{(i-L)},i=L\cdots 2L\text{，} \end{array} \right.$

(10)

$\left\{ {\begin{array}{*{20}{l}} {w_{_i}^{^{(m)}} = ({h^2} - L)/{h^2}} \text{，}\\ {w_{_i}^{^{(m)}} = 1/2{h^2},i = 1 \cdots 2L}\text{，} \end{array}} \right.$

(11)

${w^{(c1)}} = 1/4{h^2}\text{，}$

(12)

${w^{(c2)}} = ({h^2} - 1)/4{h^2}\text{，}$

(13)

其中， ${\left( {\sqrt {{{{P}}_{k - 1}}} } \right)_{(i)}}$ 表示矩阵 $\sqrt {{{{P}}_{k - 1}}} $ 的第i列。

步骤3　时间更新

$ {{{\chi }}_{i,k|k - 1}} = {{\varPhi }}{{{\chi }}_{i,k|k - 1}},i = 0,1 \cdots 2L\text{，} $

(14)

$ {{\hat{{ X}}}^ - }_k = \sum\limits_{i = 0}^{2L} {w_{_i}^{^{(m)}}{{{\chi }}_{i,k|k - 1}}}\text{。} $

(15)

步骤4　采样点协方差矩阵

$\begin{split} {{P}}_k^ - =& \sum\limits_{i = 1}^L \left[ {w_{c1}}{{\left( {{{{\chi }}_{i,k|k - 1}} - {{{\chi }}_{L + i,k|k - 1}}} \right)}^2} +\right.\\ &\left.{w_{c2}}{{\left( {{{{\chi }}_{i,k|k - 1}} + {{{\chi }}_{L + i,k|k - 1}} - 2{{{\chi }}_{0,k|k - 1}}} \right)}^2} \right] + {{Q}}\text{。}\end{split}$

(16)

步骤5　采样点点集更新

$\left\{ \begin{array}{l} {{{\chi}} }_{0,k-1}={\widehat{{X}}}{}_{k-1}^{-},i=0\text{，}\\ {{{\chi}} }_{i,k-1}={\widehat{{X}}}{}_{k-1}^{-}+h{\left(\sqrt{{{P}}_{k-1}^{-}}\right)}_{(i)},i=1\cdots L\text{，}\\ {{{\chi}} }_{i,k-1}={\widehat{{X}}}^{-}{}_{k-1}-h{\left(\sqrt{{{P}}_{k-1}^{-}}\right)}_{(i-L)},i=L\cdots 2L \text{。} \end{array} \right.$

(17)

步骤6　量测及其协方差更新

${{{\varXi }}_{i,k|k - 1}} = f({{{\chi }}_{i,k|k - 1}}),i = 1,2 \cdots 2L\text{，}$

(18)

${{\hat{{ Z}}} }_k^ - = \sum\limits_{i = 0}^{2L} {w_i^{(m)}{{{\varXi }}_{i,k|k - 1}}}\text{，}$

(19)

$\begin{split}{{P}}_k^{(z)} =& \sum\limits_{i = 1}^L \left[ {w_{c1}}{{\left( {{{{\varXi }}_{i,k|k - 1}} - {{{\varXi }}_{L + i,k|k - 1}}} \right)}^2} +\right.\\ &\left.{w_{c2}}{{\left( {{{{\varXi }}_{i,k|k - 1}} + {{{\varXi }}_{L + i,k|k - 1}} - 2{{{\varXi }}_{0,k|k - 1}}} \right)}^2} \right] + {{R}}\text{，}\end{split}$

(20)

$ {{P}}_{k}^{(xz)}=\sqrt{{w}^{(c1)}{{P}}_{k}^{-}}（{\Xi }_{1:L,k|k-1}-{{{\varXi}} }_{L+1:2L,k|k-1}{)}^{\rm{T}}\text{。}$

(21)

步骤7　卡尔曼增益和目标状态更新

${{{\kappa }}_k} = {{P}}_k^{(xz)}/{{P}}_k^{(z)}\text{，}$

(22)

$ {\widehat{{X}}}_{k}={\widehat{{X}}}{}_{k}^{-}+{{{\kappa}} }_{k}({{ Z}}_{k}-{\widehat{{Z}}}{}_{k}^{-})\text{。}$

(23)

步骤8　状态协方差更新

${{{P}}_k} = {{P}}_k^ - - {{{\kappa }}_k}{{P}}_k^{(z)}{{{\kappa }}_k}^{\rm{T}}\text{。}$

(24)

在 $k = 1,2 \cdots K$ 时，循环步骤2到步骤8，即可完成CDKF滤波。

2 本文所提方法

CDKF方法是一种应用广泛的确定性采样的非线性滤波方法，但在单站纯方位目标跟踪中，容易出现滤波不稳定甚至发散的情形。为了解决这一问题，本文提出一种奇异值分解平方根中心差分卡尔曼滤波（Singular Value Decomposition Square Root Central Difference Kalman Filter，SVDSR-CDKF）。不同于常规的平方根方法，它在计算采样点的协方差和量测协方差中采用QR分解，而在计算状态协方差更新阶段使用奇异值分解。

2.1 协方差的QR分解

与常规的平方根方法相同，本方法同样对采样点协方差和量测协方差进行QR分解。QR分解可表示为 ${{A}} = {{QR}}$ ，它将矩阵A分解为一个正规正交矩阵Q和一个上三角矩阵R的乘积，则容易推导出：

$ {{{A}}^{\rm{T}}}{{A}} = {({{QR}})^{\rm{T}}}{{QR}} = {{{R}}^{\rm{T}}}{{R}}\text{。} $

用采样点协方差矩阵QR分解得到的 ${{S}}_k^ - $ 代替 $\sqrt {{{P}}_k^ - } $ ，则

$\begin{split}&{{S}}_k^ - =\\ &{\rm{ QR}}\left\{ {\left[\!\!\!\!\!\! {\begin{array}{*{20}{c}} {\sqrt {{w_{c1}}} {{\left( {{{{\chi }}_{1:L,k|k - 1}} - {{{\chi }}_{L + 1:2L,k|k - 1}}} \right)}^{\rm{T}}}} \\ {\sqrt {{w_{c2}}} {{\left( {{{{\chi }}_{1:L,k|k - 1}} + {{{\chi }}_{L + 1:2L,k|k - 1}} \!-\! 2{{{\chi }}_{0,k|k - 1}}} \right)}^{\rm{T}}}} \\ {{{\sqrt {{Q}} }^{\rm{T}}}} \end{array}} \!\!\!\!\!\right]} \right\}\text{。}\end{split}$

(25)

其中，QR{}表示QR分解，返回结果为分解后得到的上三角矩阵。用量测协方差矩阵的QR分解 ${{S}}_k^{(z)}$ 代替 $\sqrt {{{P}}_k^{(z)}} $ ，则

$\begin{split}&{{S}}_k^{(z)}=\\ &{\rm{QR}}\left\{ {\left[ \!\!\!\!\!\!\!{\begin{array}{*{20}{c}} {\sqrt {{w_{c1}}} {{\left( {{{{\varXi }}_{1:L,k|k - 1}} - {{{\varXi }}_{L + 1:2L,k|k - 1}}} \right)}^{\rm{T}}}} \\ {\sqrt {{w_{c2}}} {{\left( {{{{\varXi }}_{1:L,k|k - 1}} \!+\! {{{\varXi }}_{L + 1:2L,k|k - 1}} \!-\! 2{{{\varXi }}_{0,k|k - 1}}} \right)}^{\rm{T}}}} \\ {{{\sqrt {{R}} }^{\rm{T}}}} \end{array}} \!\!\!\!\!\right]} \right\}\text{。}\end{split}$

(26)

2.2 奇异值分解协方差平方根更新

常规的平方根方法采用Cholesky分解计算状态协方差的平方根。Cholesky分解要求被分解的矩阵是正定的,而对于纯方位单站目标跟踪，尤其是近距离时，方位噪声扰动大和观测站机动的影响，常规的平方根CDKF在状态协方差平方根更新有时可能出现非正定的情形，导致滤波不能正常进行。奇异值分解不受被分解矩阵正定性的限制，相比于Cholesky分解更加稳定和易于实现。因此本文提出在CDKF的状态协方差更新阶段，用奇异值分解的方法构造状态协方差的平方根。

若 ${{A}} \in {{{R}}^{m \times n}}(m \geqslant n)$ ，则矩阵 ${{A}}$ 的奇异值分解为：

${{A}} = {{U\Lambda }}{{{T}}^{\rm{T}}} = {{U}}\left[ {\begin{array}{*{20}{c}} {{S}}&0 \\ 0&0 \end{array}} \right]{{{T}}^{\rm{T}}}\text{，}$

(27)

其中， ${{U}} \in {{{R}}^{m \times m}}$ ， ${{T}} \in {{{R}}^{n \times n}}$ ， ${{\varLambda }} \in {{{R}}^{m \times n}}$ ， ${{S}}{\rm{ = diag}}({{\rm{s}}_1}, {{\rm{s}}_2}, \cdots \cdots {{\rm{s}}_{\rm{r}}})$ ， ${{\rm{s}}_1} \geqslant {{\rm{s}}_2} \geqslant \cdots \cdots \geqslant {{\rm{s}}_{\rm{r}}} \geqslant 0$ 是 ${{A}}$ 的奇异值。

单站纯方位目标跟踪系统，状态方程的协方差矩阵为：

${{P}} = E[({\hat{{ X}}} - {{X}}){({\hat{{ X}}} - {{X}})^{\rm{T}}}]\text{。}$

(28)

${{P}}$ 是一个对称矩阵，对其进行奇异值分解后可得 ${{U}} = {{V}}$ ，故可得：

$\sqrt {{P}} = {{U}}\sqrt {{S}}\text{。} $

(29)

因此可以用 ${{U}}\sqrt {{S}} $ 代替 $\sqrt {{P}} $ 。所以对于CDKF中的步骤8，用下面的方式来代替：

首先，计算状态协方差更新，其中用QR分解得到的 ${{S}}_k^ - $ 代替 $\sqrt {{{P}}_k^ - } $ ， ${{S}}_k^{(z)}$ 来代替 $\sqrt {{{P}}_k^{(z)}} $ ：

${{{P}}_k} = {{S}}{_{ k} ^{-{\rm{T}}}}{{S}}_k^ - - {{{\kappa }}_k}{{S}}_k^{(z)}{({{{\kappa }}_k}{{S}}_k^{(z)})^{\rm{T}}}\text{，}$

(30)

然后，对更新后的状态协方差进行奇异值分解：

$({{U}},{{{S}}^{(d)}},{{V}}) = svd({{{P}}_k})\text{，}$

(31)

其中， ${{U}},{{{S}}^{(d)}},{{V}}$ 分别对应式(27)中的 ${{U}},\;{{\varLambda }},\;{{T}}$ 。最后令协方差矩阵平方根为：

${{{S}}_k} = {{U}}\sqrt {{{{S}}^{(d)}}} \text{。}$

(32)

用式（30）～式（32）代替CDKF中的步骤8，可以得到一种基于奇异值分解的状态协方差平方根更新方式。由于奇异值非负，因此 $\sqrt {{{{S}}^{(d)}}} $ 总是有意义的。即使式（30）的协方差是非正定的，也可以完成奇异值分解，并计算得到 ${{{S}}_k}$ 。

2.3 奇异值分解平方根CDKF流程

本文所提出的奇异值分解平方根的中心差分卡尔曼滤波方法建立在1.2节所述的CDKF方法的框架之上，具体步骤如下：

步骤1　 k=0时，初始化状态向量和协方差分解阵

${{\hat{{ X}}}_0} = E({{{X}}_0})\text{，}$

(33)

${{{S}}_0} = {\rm{chol\{ }}E[({{\hat{{ X}}}_0} - {{{X}}_0}){({{\hat{{ X}}}_0} - {{{X}}_0})^{\rm{T}}}]{\rm{\} }}\text{，}$

(34)

其中，chol代表Cholesky分解。

步骤2　采样点及其权值

$\left\{ \begin{array}{l} {{{\chi}} }_{0,k-1}={\widehat{{X}}}{}_{k-1}^{-},i=0\text{，}\\ {{{\chi}} }_{i,k-1}={\widehat{{X}}}{}_{k-1}^{-}+h{{S}}_{k-1}{}_{(i)},i=1\cdots L\text{，}\\ {{{\chi}} }_{i,k-1}={\widehat{{X}}}{}_{k-1}^{-}-h{{S}}_{k-1}{}_{(i-L)},i=L\cdots 2L\text{，} \end{array} \right.$

(35)

$\left\{ {\begin{array}{*{20}{l}} {w_{_i}^{^{(m)}} = ({h^2} - L)/{h^2}}\text{，} \\ \begin{array}{l} w_{_i}^{^{(m)}} = 1/2{h^2},i = 1 \cdots 2L\text{，} \\ {w^{(c1)}} = 1/4{h^2}\text{，} \\ {w^{(c2)}} = ({h^2} - 1)/4{h^2} \text{。}\end{array} \end{array}} \right.$

(36)

步骤3　时间更新

$ {{{\chi }}_{i,k|k - 1}} = {{\varPhi }}{{{\chi }}_{i,k|k - 1}},i = 0,1 \cdots 2L\text{，} $

(37)

${{\hat{{ X}}} }_k^ - = \sum\limits_{i = 0}^{2L} {w_{_i}^{^{(m)}}{{{\chi }}_{i,k|k - 1}}}\text{。} $

(38)

步骤4　采样点协方差的QR分解

${{S}}_k^ - {\rm{ = QR}}\left\{ {\left[ {\begin{array}{*{20}{c}} {\sqrt {{w_{c1}}} {{\left( {{{{\chi }}_{1:L,k|k - 1}} - {{{\chi }}_{L + 1:2L,k|k - 1}}} \right)}^{\rm{T}}}} \\ {\sqrt {{w_{c2}}} {{\left( {{{{\chi }}_{1:L,k|k - 1}} + {{{\chi }}_{L + 1:2L,k|k - 1}} - 2{{{\chi }}_{0,k|k - 1}}} \right)}^{\rm{T}}}} \\ {{{\sqrt {{Q}} }^{\rm{T}}}} \end{array}} \right]} \right\}\text{。}$

(39)

步骤5　采样点集更新

$\left\{ \begin{array}{l} {{{\chi}} }_{0,k-1}={\widehat{{X}}}{}_{k-1}^{-},i=0 \text{，}\\ {{{\chi}} }_{i,k-1}={\widehat{{X}}}{}_{k-1}^{-}+h{{S}}_{k}^{-}{}_{(i)},i=1\cdots L\text{，}\\ {{{\chi}} }_{i,k-1}={\widehat{{X}}}{}_{k-1}^{-}-h{{S}}_{k}^{-}{}_{(i-L)},i=L\cdots 2L\text{，} \end{array} \right.$

(40)

步骤6　量测更新

${{{\varXi }}_{i,k|k - 1}} = f({{{\chi }}_{i,k|k - 1}}),i = 1,2 \cdots 2L\text{，}$

(41)

${{\hat{{ Z}}}^ - }_k = \sum\limits_{i = 0}^{2L} {w_i^{(m)}{{{\varXi }}_{i,k|k - 1}}}\text{。} $

(42)

步骤7　量测协方差阵QR分解

$\begin{split}&{{S}}_k^{(z)}=\\ &{{ QR}}\left\{ {\left[\!\!\!\!\!\!\! {\begin{array}{*{20}{c}} {\sqrt {{w_{c1}}} {{\left( {{{{\varXi }}_{1:L,k|k - 1}} - {{{\varXi }}_{L + 1:2L,k|k - 1}}} \right)}^{\rm{T}}}} \\ {\sqrt {{w_{c2}}} {{\left( {{{{\varXi }}_{1:L,k|k - 1}} \!+\! {{{\varXi }}_{L + 1:2L,k|k - 1}} \!-\! 2{{{\varXi }}_{0,k|k - 1}}} \right)}^{\rm{T}}}} \\ {{{\sqrt {{R}} }^{\rm{T}}}} \end{array}} \!\!\!\!\!\right]} \right\}\text{。}\end{split}$

(43)

步骤8　卡尔曼增益和目标状态更新

$ {{P}}_{k}^{(xz)}=\sqrt{{w}^{(c1)}}{{S}}_{k}^{-}({{{\varXi}} }_{1:L,k|k-1}-{{{\varXi}} }_{L+1:2L,k|k-1}{)}^{\rm{T}}\text{，}$

(44)

${{{\kappa }}_k} = ({{P}}_k^{(xz)}/{{S}}{_k^{(z){\rm{T}}}}){{S}}_k^{(z)}\text{，}$

(45)

$ {\widehat{{X}}}_{k}={\widehat{{X}}}{}_{k}^{-}+{{{\kappa}} }_{k}({{Z}}_{k}-{\widehat{{Z}}}{}_{k}^{-})\text{。}$

(46)

步骤9　状态协方差平方根更新

${{{P}}_k} = {{S}}{_k^{-{\rm{T}}}}{{S}}_k^ - - {{{\kappa }}_k}{{S}}_k^{(z)}{({{{\kappa }}_k}{{S}}_k^{(z)})^{\rm{T}}}\text{，}$

(47)

$({{U}},{{{S}}^{(d)}},{{V}}) = svd({{{P}}_k})\text{，}$

(48)

${{{S}}_k} = {{U}}\sqrt {{{{S}}^{(d)}}}\text{。}$

(49)

3 仿真实验

为了验证本文所提方法在单站纯方位目标跟踪中的有效性和优势，在3种常见的近距离跟踪轨迹情形下进行仿真。初始状态观测站获取的距离误差5%，速度误差5%，初航向误差的均方差为3°。方位估计周期为100 ms，系统的观测噪声协方差 ${{R}} = 3$ ，过程噪声强度 $\delta _q^2{\rm{ = 0}}{\rm{.1}}$ 。分别用CDKF、常见的平方根类方法SR-UKF以及本文所提的奇异值分解平方根CDKF方法进行100次蒙特卡罗实验。

用均方根误差（RMSE）来衡量估计偏差。定义均方根误差如下：

$\begin{split} &{\rm{RMSE}} = \\ &\sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {\left[ {{{\left( {{x_{true}}(i) - {{\hat x}_k}(i)} \right)}^2} + {{\left( {{y_{true}}(i) - {{\hat y}_k}(i)} \right)}^2}} \right]} }\text{。} \end{split}$

(50)

情形1：直线拦截目标轨迹。

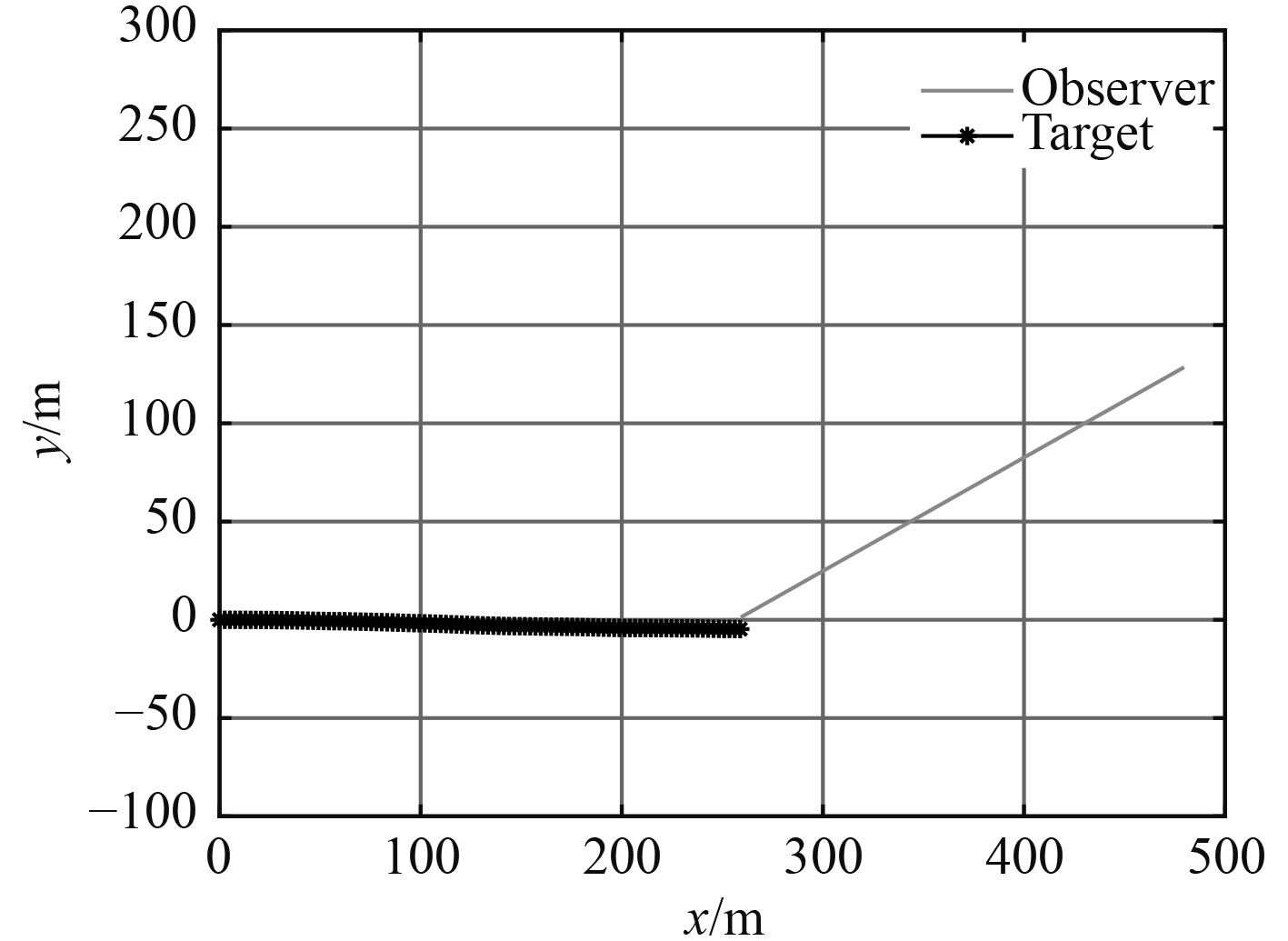
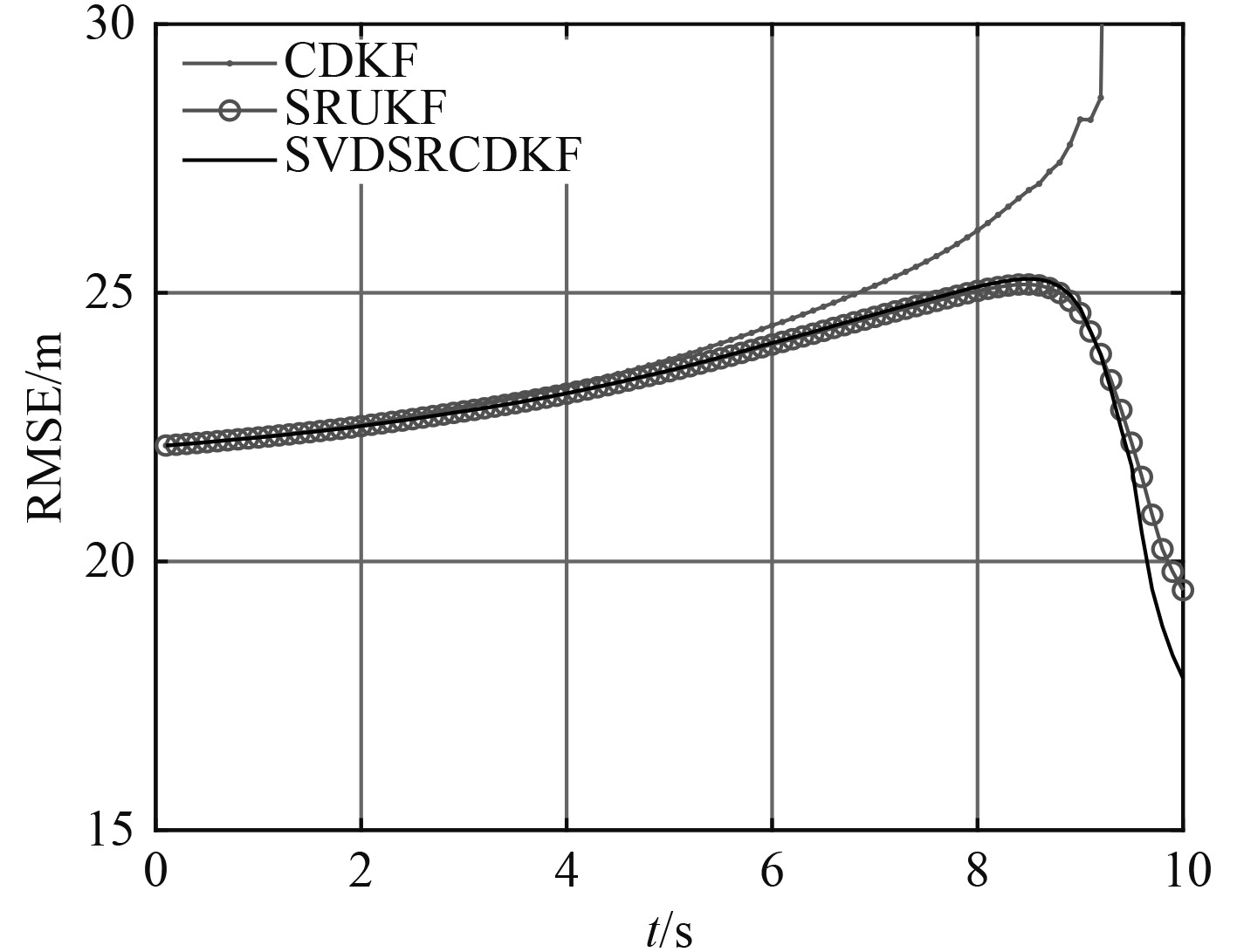
目标以50 kn速度向东做匀速直线运动。观测站初始位置坐标为（480，128），以50 kn的速度向南偏西60°方向运动，观测时间10 s。这种情形下的运动态势如图1所示。图2为100次蒙特卡罗实验统计的3种方法的均方根误差比较。

为了验证不同观测噪声协方差下所提方法的有效性，在观测噪声协方差为1°～5°的条件下分别进行100次蒙特卡洛实验，统计3种方法的平均RMSE，结果如表1所示。

情形2：观察者近距离提前角追踪目标。

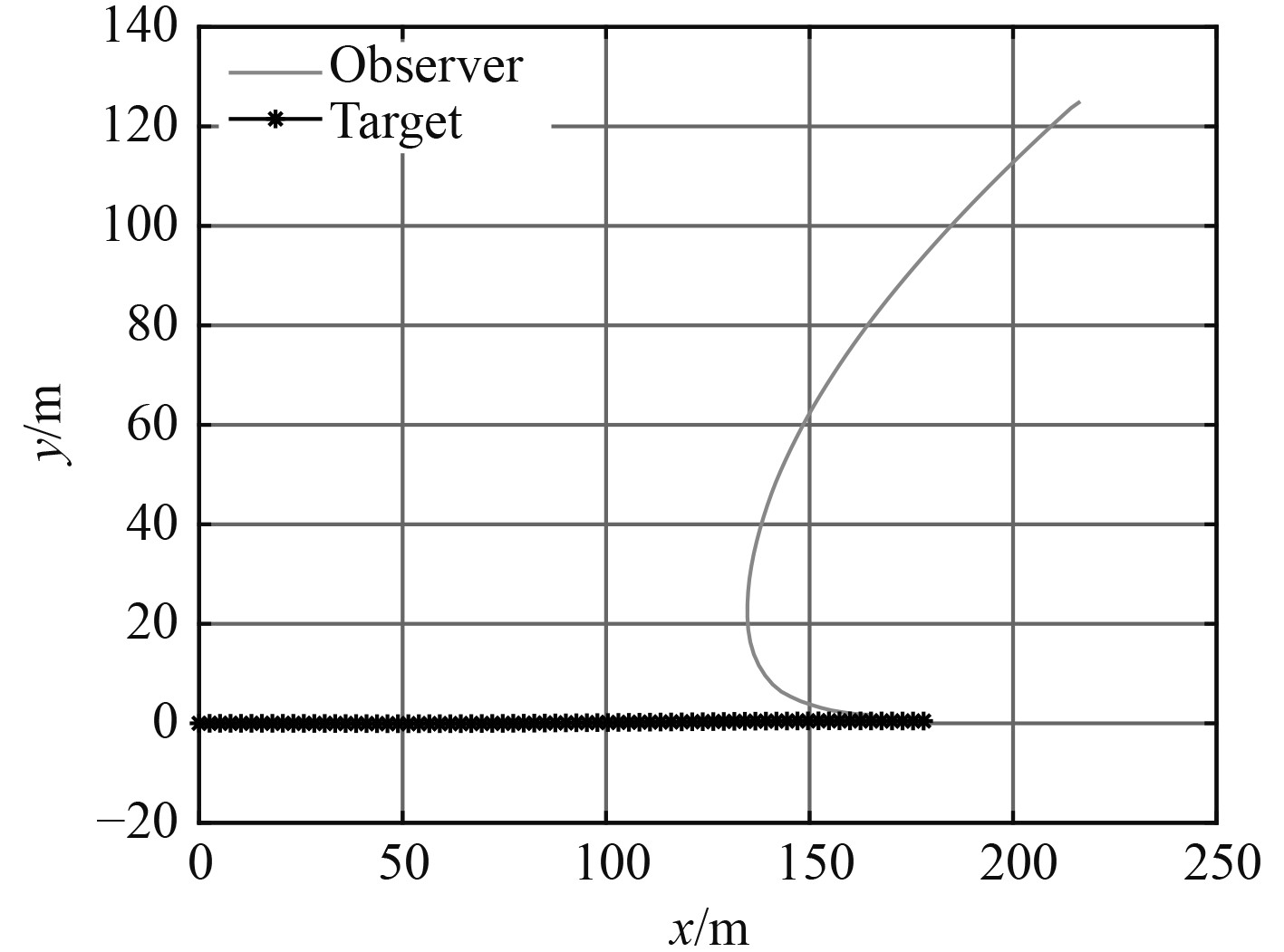
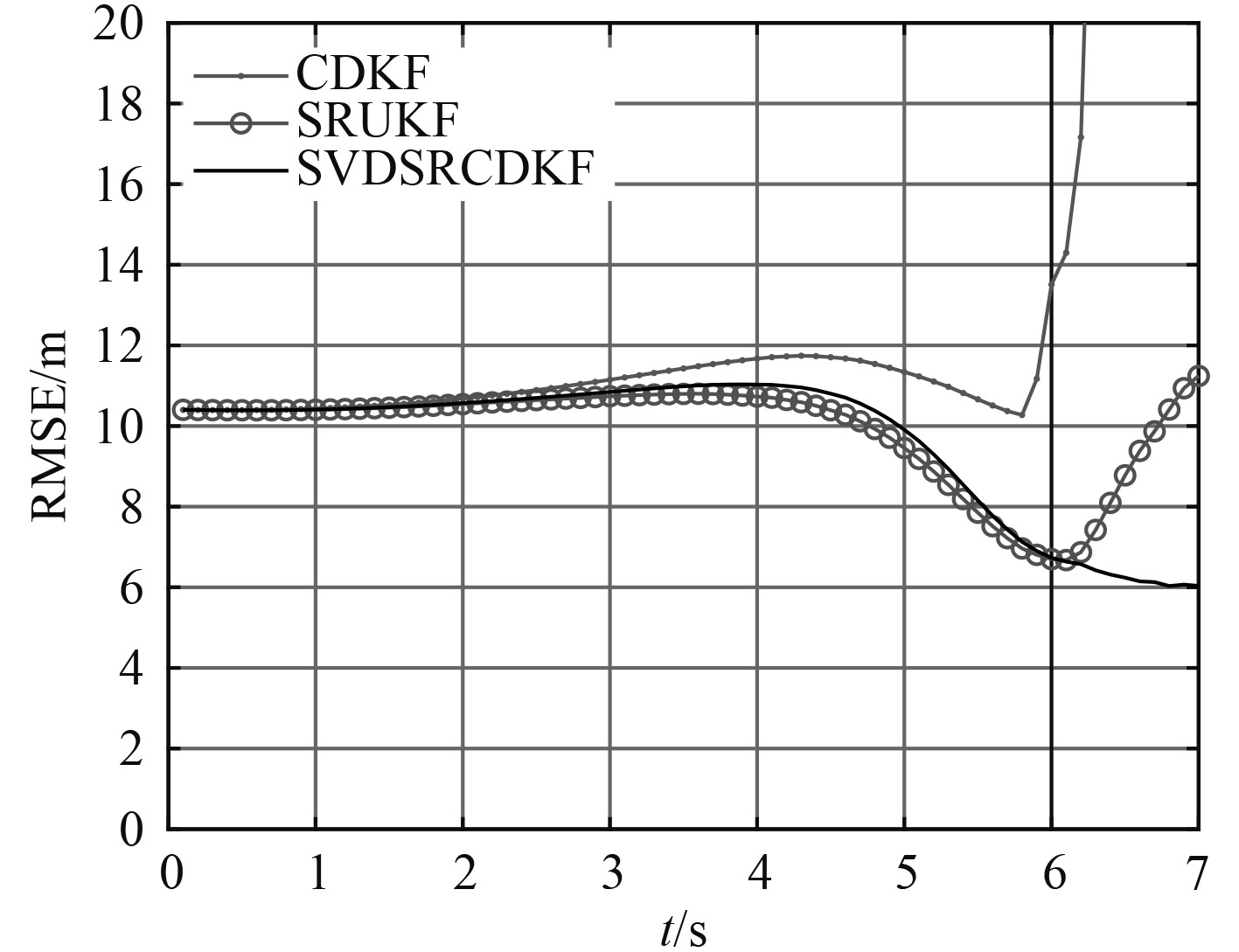
目标以50 kn速度向东匀速直线运动，观测站在目标北偏东60°方向距目标250 m处，以50 kn的速度、7°的提前角追踪目标，观测时长为7 s。图3展示了这一情形下的目标和观测站的运动态势。统计100次蒙特卡罗实验结果，3种方法的均方根误差比较如图4所示。

在观测噪声协方差为1°～5°的条件下，统计100次实验中3种方法的平均RMSE，如表2所示。

情形3：观测站迎面拦截态势。

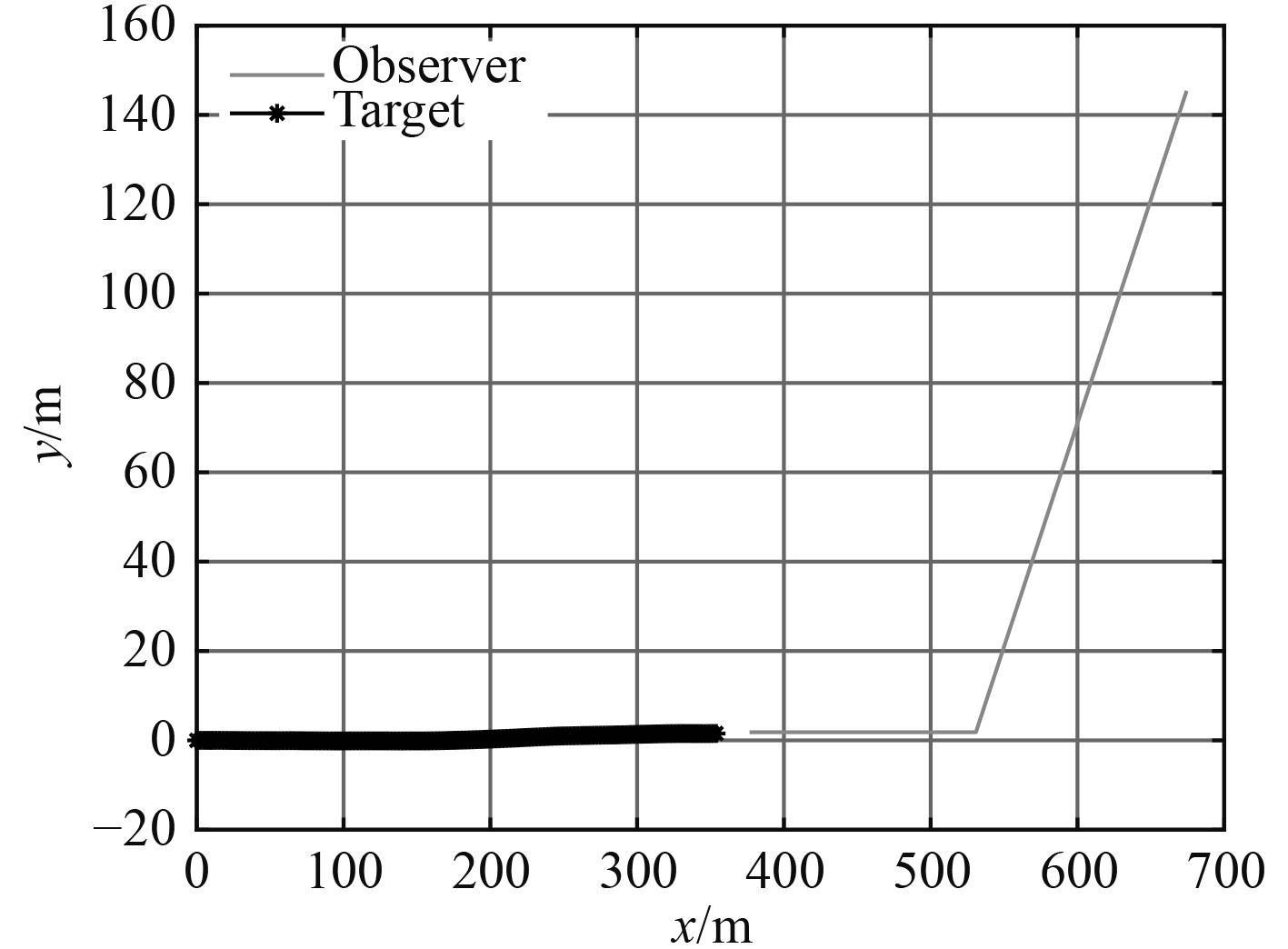
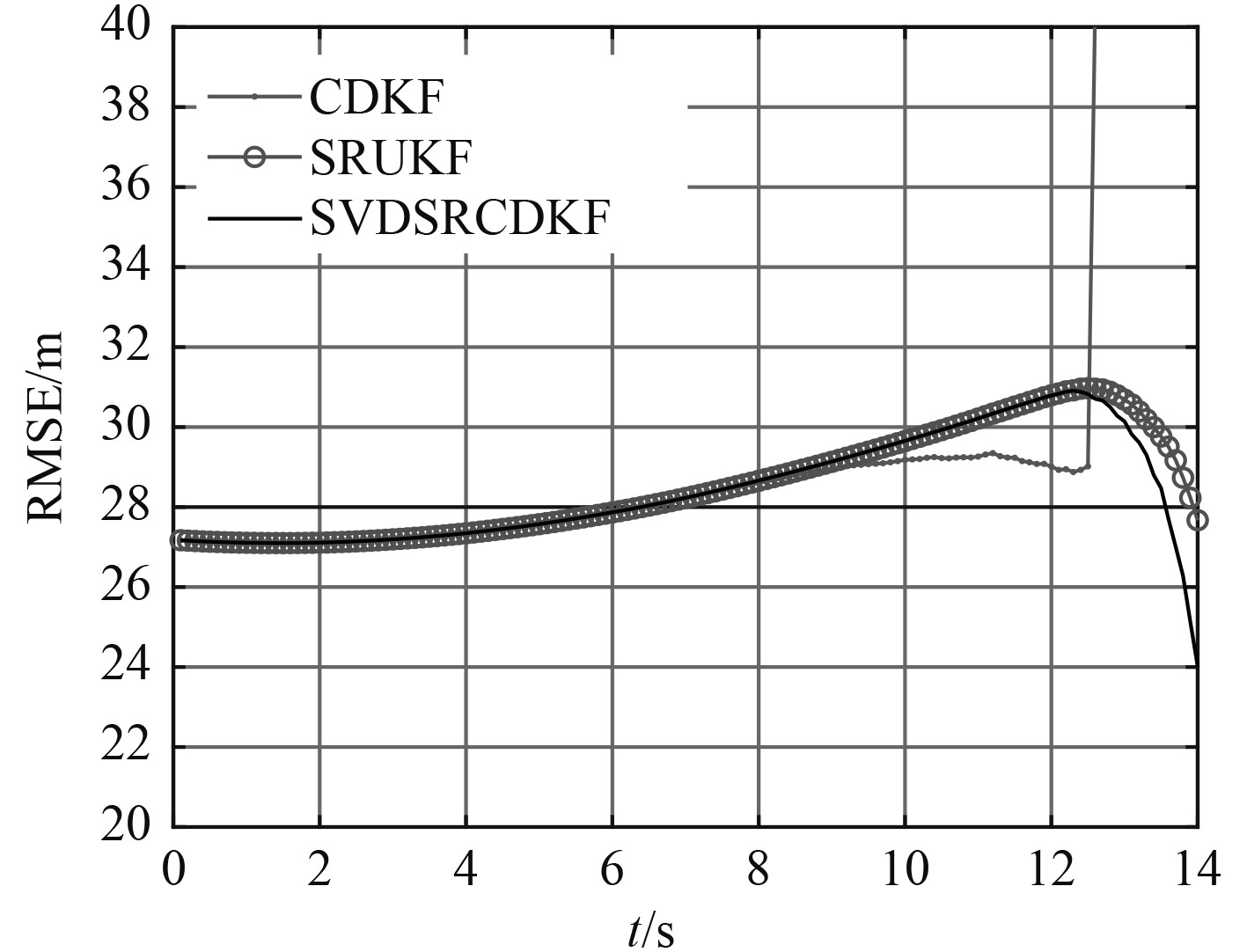
目标以50 kn速度向东做匀速直线运动。观测站初始位置坐标为（454，145），以50 kn的速度向南偏西45°方向匀速直线运动。8 s后观测站转向正西方向以50 kn速度向目标匀速直线运动，观测时长共计14 s。情形3的运动态势如图5所示。3种方法100次蒙特卡罗实验后的均方根误差如图6所示。3种方法观测噪声协方差为1°～5°时，100次实验的平均RMSE如表3所示。

综合3种情形下各滤波器的仿真结果，对于同一目标不同的跟踪轨迹得到的跟踪误差是不同的，这说明对于单站纯方位目标跟踪而言，观测站的机动直接影响估计效果。但实际中肩负其他作业任务的观测站不一定可以执行最优观测轨迹，这对滤波方法的性能提出了更高要求。而3种不同的观测轨迹中，对比3种滤波方法的误差可以得到相似的结论：常规的CDKF方法由于容易出现发散，导致平均误差较大，各种情形下其均方根误差都是最大的。SR-UKF方法作为一种经典的平方根类的方法，用于水下纯方位目标跟踪具有较好效果，各种情形下误差均低于CDKF方法。本文所提的SVDSR-CDKF方法解决了CDKF在几种情形中容易发散的问题，且滤波误差最低。在3种仿真情形下和各种不同的观测噪声协方差下，本文提出的SVDSR-CDKF方法均具有最低的均方根误差。

4 结　语

针对单站纯方位目标分析中有时容易出现的滤波器不稳定、易发散的情况，本文提出一种SVDSR-CDKF方法。该方法以CDKF方法为基础，在计算采样点协方差和量测协方差时采用QR分解计算协方差平方根，而在状态协方差更新阶段使用奇异值分解。通过2种不同的方式计算协方差的平方根代替协方差矩阵参与运算，增强算法的稳定性。为验证所提方法效果，进行了3组不同情形的仿真实验，比较常规CDKF方法、经典的平方根类方法SR-UKF方法和本文所提的SVDSR-CDKF方法，并在每种情形下调整不同的观测噪声进行各方法的均方根误差比较。结果表明，本文所提方法避免了常规CDKF容易发散的情形，且具有比常规CDKF和SR-UKF更低的滤波误差。综合各项仿真结果表明，本文提出的SRSVD-CDKF方法是一种精度高、稳定性好的纯方位目标跟踪方法。对于本文的未尽之处，未来考虑在以下方向进行研究：一是探索该方法对于跟踪机动目标的效果；二是考虑该方法对于三维模型中目标的跟踪。