0 引　言

在水下探测和通信中，声波有着不可替代的优势^[1]，而声呐通过对声信号进行转换和处理实现对水下目标的侦察和定位，声呐能否有效发挥其作用不仅与声呐自身性能有着密不可分的关系^[2]，与声呐所处的海洋环境同样息息相关。声呐所在区域的海洋环境作为声信号的载体对声波在其中传播有较大的影响。Jensen^[3]关于海洋环境对声信号的影响多集中在水平方向上声能量的衰减，对深度方向上声能量分布有较少研究。由于海洋声信道上下分别受到海面和海底的制约，其边界条件的不相同，导致声能量在深度方向上的分布并不均匀，当传播距离一定时，不同接收点深度的声传播损失差异可达20 dB，因此研究不同条件下深度方向上的声传播损失最小值的位置即最佳深度对声呐探测和水声通信有一定帮助。

国内外学者对最佳深度做了一定研究：Weston^[4-5]对声场的平均声强进行了研究，通过计算等声速梯度条件下深度方向上的距离平均声强，得出声强在声源深度和声源对称深度存在峰值，且峰值比平均声强大50%；Gershfeld^[6]通过对声传播损失和信噪比的计算得出浅海声传播的最佳深度与声源点深度相同的结论，并研究了声源位置、海底类型、声速梯度和声源频率对最佳深度的影响；Ferla^[7]基于前人结论对声源深度未知时的最佳深度位置进行了研究；王晓宇等^[8]分别对理想Pekeris波导和实际浅海分层波导情况下的水平线列阵最佳布放深度进行研究，得出最佳布放深度应与声源深度相同。

现有的研究^[9-10]只针对最佳深度的现象进行了归纳和总结，并没有探索影响最佳深度的根本原因，且得出的结论存在一定的局限性。本文对影响最佳深度的因素进行了研究，通过对理想液体波导中简正波阶数对最佳深度影响的研究，得出简正波模态叠加是产生最佳深度的根本原因，并较为全面地总结了不同环境下最佳深度的规律。

1 理论公式

浅海声传播问题可以近似采用单位强度的谐和点声源在水平均匀的分层波导中的响应来模拟，任意一点的声压 $p$ 满足如下波动方程^[11]：

$\nabla \left(\frac{1}{\rho }\nabla p\right) - \frac{1}{{\rho {c^2}(z)}} = - \frac{{\delta (z - {z_s})\delta (r)}}{{2\text{π} r}}\text{。}$

(1)

式中： $p(r,z,t)$ 为与水平距离r、深度z和时间t相关的声压； $c(z),\rho (z)$ 分别为与深度相关的声速和密度， $s(t)$ 代表点声源强度。

在柱坐标系下上述方程转化为：

$\frac{1}{r}\frac{\partial }{{\partial r}}\left(r\frac{{\partial p}}{{\partial r}}\right) + \rho (z)\frac{\partial }{{\partial z}}\left(\frac{1}{{\rho (z)}}\frac{{\partial p}}{{\partial z}}\right) + \frac{{{w^2}}}{{{c^2}(z)}}p = - \frac{{\delta (r)\delta (z - {z_s})}}{{2\text{π} r}}\text{。}$

(2)

计算区域的边界条件、海水深度和c(z)均和r没有关系，因此可以进行如下设置： $p(r,z) = \varPhi (R)\varPsi (Z)$ ，并将此表达式代入上述方程整理后得：

$\frac{1}{\varPhi }\left[ {\frac{1}{r}\frac{{\rm{d}}}{{{\rm{d}}r}}\left(r\frac{{{\rm{d}}\varPhi }}{{{\rm{d}}r}}\right)} \right] + \frac{1}{\Psi }\left[ {\rho (z)\frac{{\rm{d}}}{{{\rm{d}}z}}\left(\frac{1}{{\rho (z)}}\frac{{{\rm{d}}\varPsi }}{{{\rm{d}}z}}\right) + \frac{{{w^2}}}{{{c^2}(z)}}\varPsi } \right] = 0\text{，}$

(3)

上述方程加号左右两侧分别是只关于 $r$ 和 $z$ 的函数，因此使等式满足的唯一办法就是方括号内的值同时为常数，选取这一常数值为 $k_{rm}^2$ 进行分离：

$\rho (z)\frac{{\rm{d}}}{{{\rm{d}}z}}\left[ {\frac{1}{{\rho (z)}}\frac{{{\rm{d}}{\varPsi _m}(z)}}{{{\rm{d}}z}}} \right] + \left[ {\frac{{{w^2}}}{{{c^2}(z)}} - k_{rm}^2} \right]{\varPsi _m}(z) = 0\text{，}$

(4)

由于海面即 $z = 0$ 被设置为压力释放边界，海底 $z = D$ 在足够深处被设置为绝对硬边界，则函数 $\varPsi $ 同时满足：

$\varPsi (0) = 0,{\left. {\frac{{{\rm{d}}\varPsi }}{{{\rm{d}}z}}} \right|_{z = D}} = 0\text{，}$

(5)

${\varPsi _m}(z)$ 表示当常数值为 ${k_{rm}}$ 时的函数。

利用 ${\varPsi _m}(z)$ 的正交性，在对 ${\varPsi _m}(z)$ 进行归一化后声压的任意解可以表示为解空间里模式函数之和，即声压可以用以下形式表示：

$p(r,z) = \sum\limits_{m = 1}^\infty {{\varPhi _m}(r)} {\varPsi _m}(z)\text{。}$

(6)

将上述表达式代入声压波动方程中并进行简化得到：

$\begin{split}&\sum\limits_{m = 1}^\infty {\left\{ {\frac{1}{r}\frac{{\rm{d}}}{{{\rm{d}}r}}\left(r\frac{{{\rm{d}}{\varPhi _m}(r)}}{{{\rm{d}}r}}\right){\varPsi _m}(z) + k_{rm}^2{\varPhi _m}(r){\varPsi _m}(z)} \right\}} = \\ &\qquad - \frac{{\delta (r)\delta (z - {z_s})}}{{2\text{π} r}}\text{，}\end{split}$

(7)

运用模式函数的正交性质得到：

$\frac{1}{r}\frac{{\rm{d}}}{{{\rm{d}}r}}\left[ {r\frac{{{\rm{d}}{\varPhi _n}(r)}}{{{\rm{d}}r}}} \right] + k_{rn}^2{\varPhi _n}(r) = - \frac{{\delta (r){\varPsi _n}({z_s})}}{{2\text{π} r\rho ({z_s})}}\text{。}$

(8)

上述方程为标准贝塞尔方程，其解采用汉克尔函数形式：

${\varPhi _n}(r) = \frac{i}{{4\rho ({z_s})}}{\varPsi _n}({z_s})H_0^{(1,2)}({k_{rn}}r)\text{。}$

(9)

由于声压解满足无穷远辐射条件，所以解选用第一类汉克尔函数 $H_0^{(1)}$ ，省去时间项 $\exp ( - iwt)$ ，并用汉克尔函数展开式代入得到：

$p(r,z) = \frac{i}{{p({z_s})\sqrt {8\text{π} } }}{e^{ - i\text{π} /4}}\sum\limits_{m = 1}^\infty {{\varPsi _m}({z_s}){\varPsi _m}(z)} \infty \frac{{i{k_{rm}}r}}{{\sqrt {{k_{rm}}} }}\text{，}$

(10)

在海洋声场计算中，声压并不总是有意义的，当声压为复数时，其表示压力幅值和相位，为更清楚地描述声场，采用声传播损失描述：

$TL(r,z) = - 20\log \left| {\frac{{p(r,z)}}{{{p_0}(r = 1)}}} \right|\text{，}$

(11)

其中： ${p_0}$ 为在无穷大的自由空间中单位强度的点声源产生的声压， ${p_0}(r) = \dfrac{{{\varepsilon ^{i{k_0}r}}}}{{4\text{π} r}}$ 。

将其代入声传播损失表达式中：

$TL(r,z) = - 20\log \left| {\frac{1}{{\rho ({z_s})}}\sqrt {\frac{{2\text{π} }}{r}} \sum\limits_{m = 1}^\infty {{\varPsi _m}({z_s}){\varPsi _m}(z)} \infty \frac{{i{k_{rm}}r}}{{\sqrt {{k_{rm}}} }}} \right|\text{。}$

(12)

上式的传播损失是基于不同模态简正波之间相位叠加的结果，如果忽略简正波之间的相位差异，只考虑简正波携带的能量多少，通过这种方式叠加则产生非相干损失。Jensen通过对比不同模态的非相干叠加与1/3倍频层平均后的声传播损失测量结果，发现非相干叠加的声传播损失计算结果和1/3倍频层平均的测量结果一致。验证说明了非相干叠加的计算结果在描述传播规律时可以代替相干叠加。下面给出非相干叠加的计算公式：

$ T{L}_{\rm{Inc}}(r,z)=-20\mathrm{log}\frac{1}{\rho ({z}_{s})}\sqrt{\frac{2\text{π} }{r}}\sqrt{{\displaystyle \sum _{m=1}^{\infty }{\left|{\Psi }_{m}({z}_{s}){\Psi }_{m}(z）\frac{i{k}_{rm}r}{\sqrt{{k}_{rm}}}\right|}^{\rm{2}}}}\text{。}$

(13)

2 最佳深度的影响因素研究 2.1 模型参数

选取如图1所示的海洋环境进行计算，单位强度的谐和点源位于海水层 ${z_0}$ 处，海水和海底层密度和声速均保持不变，海底为半无限液体海底，声信号在传播过程中分别受到海面和海底边界条件的影响，海底参数的选取会对声传播有一定影响，本文采用Hamilton^[12-13]总结的大陆架附近的海底参数进行计算，部分参数选取如表1所示。

声信号在实际海水中传播时会产生能量损失，这种能量损失不仅包括扩展损失，还包括海底衰减损失和海水衰减损失。试验证明，声能量在海底衰减的多少与频率相关，且频率越高，能量衰减越大，不同类型海底与频率相关的衰减系数见表1。海水中的衰减系数与频率同样存在一定关系，本文采用Thorp^[14]总结的海水衰减系数与频率的关系进行计算。

$a(f) = \frac{{0.11{f^2}}}{{1 + {f^2}}} + \frac{{44{f^2}}}{{4\;100 + {f^2}}} + 0.000\;3 \times {f^2} + 0.003\;3\text{。}$

(14)

2.2 模型计算

浅海声场比深海声场有着更为复杂的传播状况，声波在其中传播受到多种因素的影响，本文主要考虑声源频率、声源深度、海水深度和海底参数对最佳深度的影响。

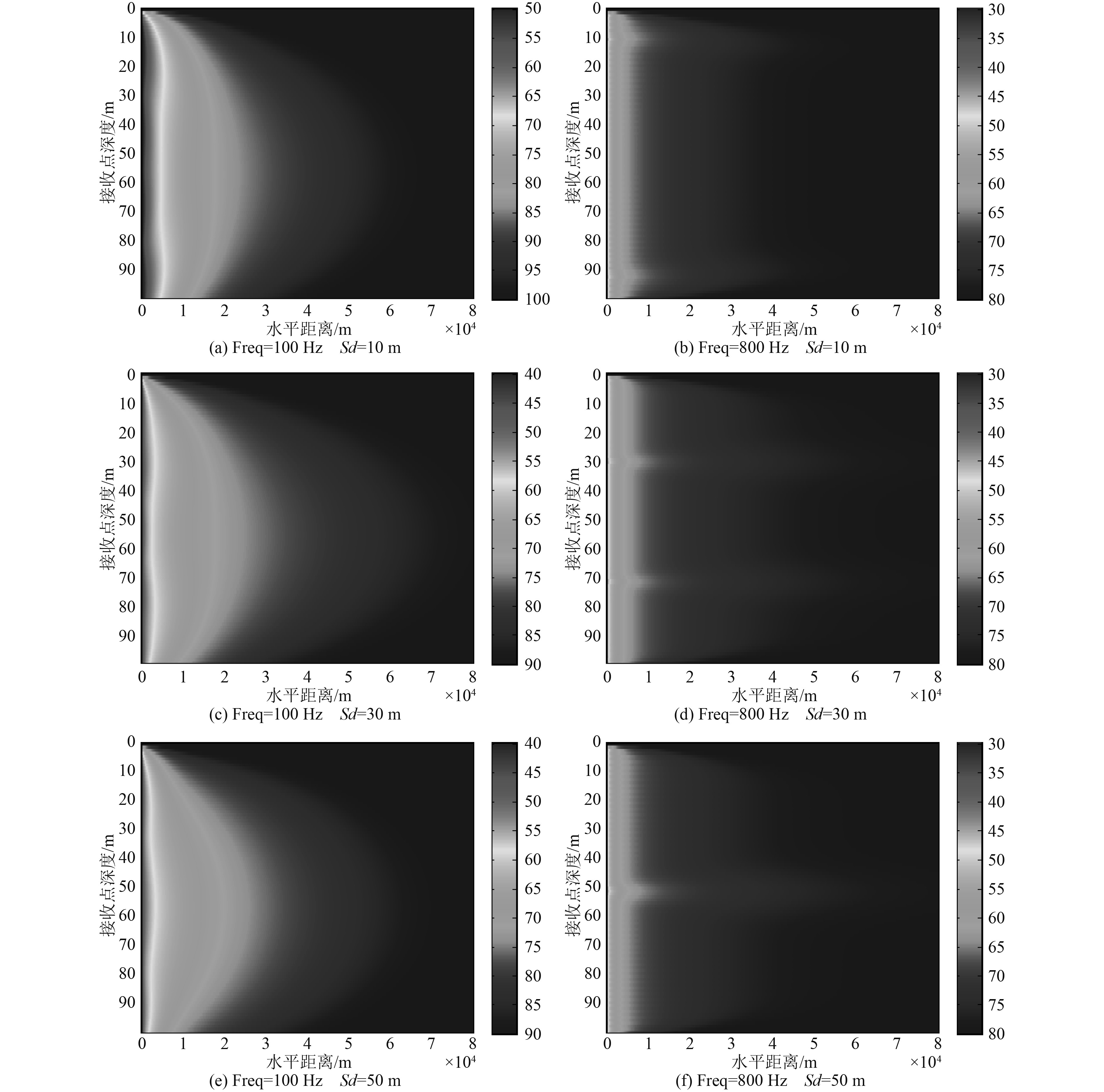
2.1.1 声源参数对最佳深度的影响

不同频率的点声源在海水中激发的声场不同，同一频率的声源在不同位置也会激发不同的声场。为研究声源参数对最佳深度的影响，本文选取点声源频率Freq分别为100 Hz和800 Hz，海水深度为100 m，海底参数为泥，分别计算放置于10，30和50 m处的点声源激发声场的非相干声传播损失场，结果如图2所示。

从上述现象可以得出：声源频率和声源深度对最佳深度有很大影响，在低频时，无论声源深度为多少，在近场和远场时最佳深度始终在海水层中部，在高频时，最佳深度位于声源深度和声源的对称深度，且频率越大，距离声源点水平距离越近，该最佳深度现象就越明显。

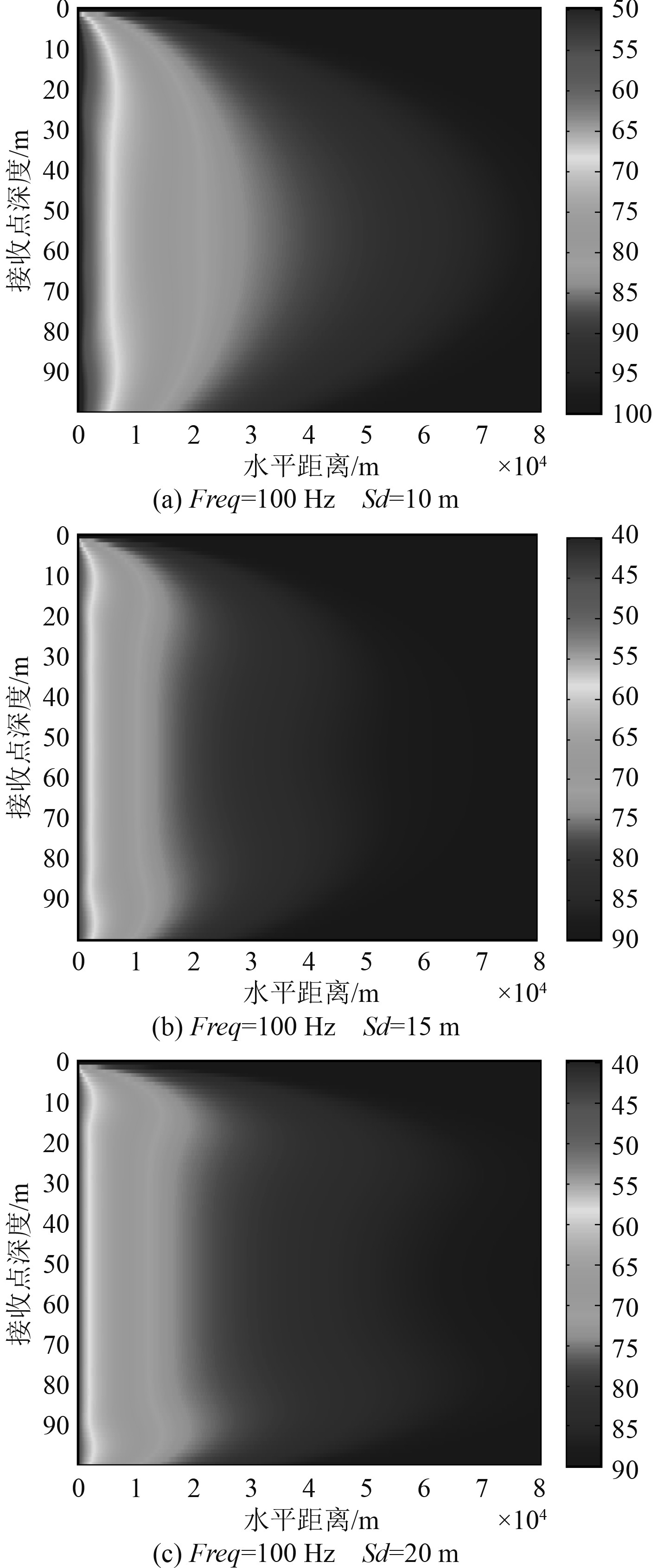
2.2.2 海水参数对最佳深度的影响

海水参数中声速剖面的存在对声场有很大影响，张旭芝^[15]已经对此做了一定研究，本文主要研究等声速情况下的最佳深度。为研究海水深度对最佳深度的影响，选取海水深度为100，150和200 m，声源频率为100 Hz，声源点深度分别设置为10，15和20 m，其余参数保持不变，得到声传播损失随距离和深度变化如图3所示。

从图3可以看出：海水深度不同导致靠近海面处放置的点声源激发的声场也不同，水深100 m，声源深度10 m条件下，声传播损失随距离和深度变化的伪彩图在近场和远场均呈现为弧形，该现象说明海水层中间处为最佳深度；水深为150 m，声源深度15 m条件下，近场的声传播损失出现弓形现象，说明在近场处最佳深度位于声源深度和声源的对称深度时，随着传播距离的增大，最佳深度向中间移动，传播至远场变为弧形，最佳深度位于海水中间处；水深200 m，声源深度20 m时，在近场和远场均出现弓形现象，随着传播距离的增大，弓形曲线的峰值向海水中部移动。

从上述现象可以得出海水深度对最佳深度有很大影响，海水深度越大，近场处的最佳深度位于声源深度和声源的对称深度的现象就越明显，当声传播较远距离后，最佳深度由声源深度和其对称深度向海水中部移动。

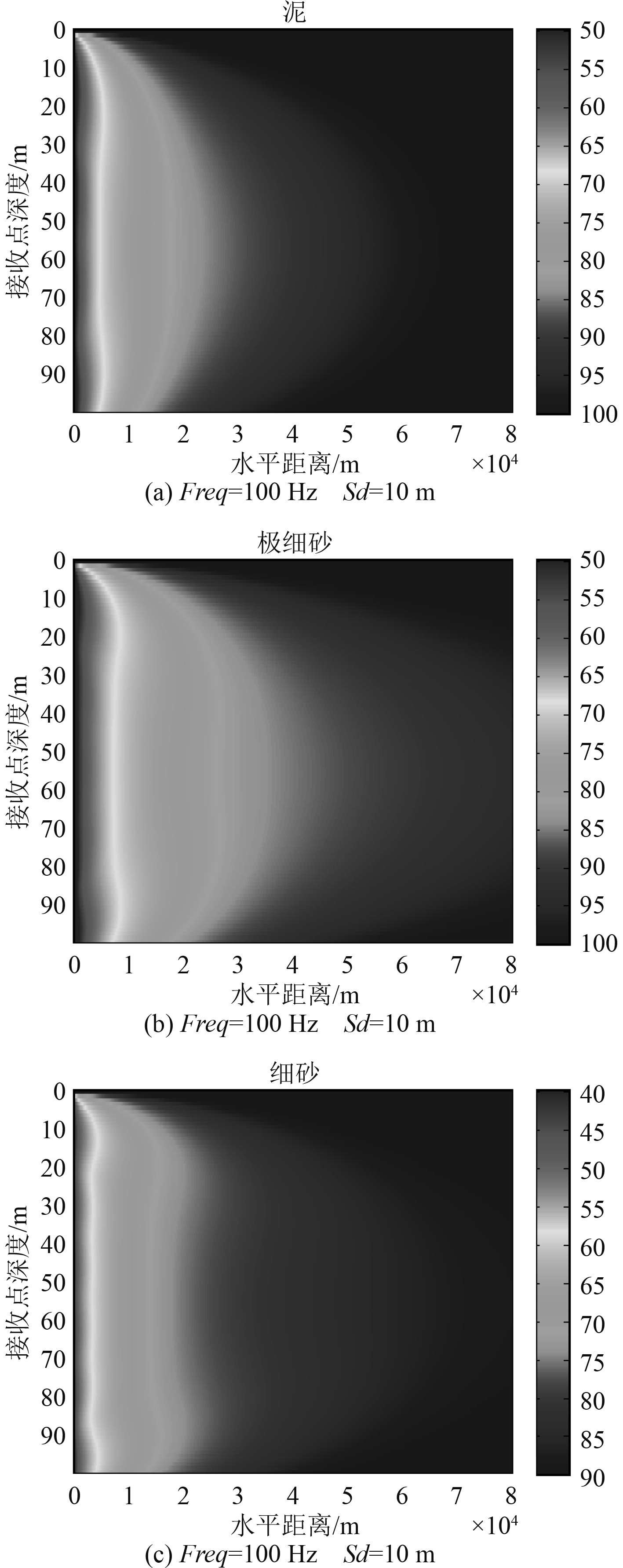
2.2.3 海底参数对最佳深度的影响

浅海边界条件对声传播的影响较深海更为显著，不同海底参数下的声传播也不同，本文选取表1中泥、极细砂和细砂三类海底进行计算，研究海底参数对最佳深度的影响。声源频率为100 Hz，声源深度为10 m，其余参数均与图1一致。得到声传播损失伪彩图如图4所示。

由图4可知：随着海底参数的变化，最佳深度的现象变化相对较小，海底类型为细砂时才出现相对明显的最佳深度位于声源深度和声源的对称深度的现象。可以得出海底参数对最佳深度影响相对较小。

本节研究声源参数、海水参数和海底参数对最佳深度的影响，从上述结论初步得出声源频率、声源深度和海水深度对最佳深度的影响最大，与Gershfeld和Ferla得出结论不同的是，最佳深度并不总是出现在声源深度和声源的对称深度，在频率较低、海水深度较小情况下，最佳深度出现在海水层中间处。

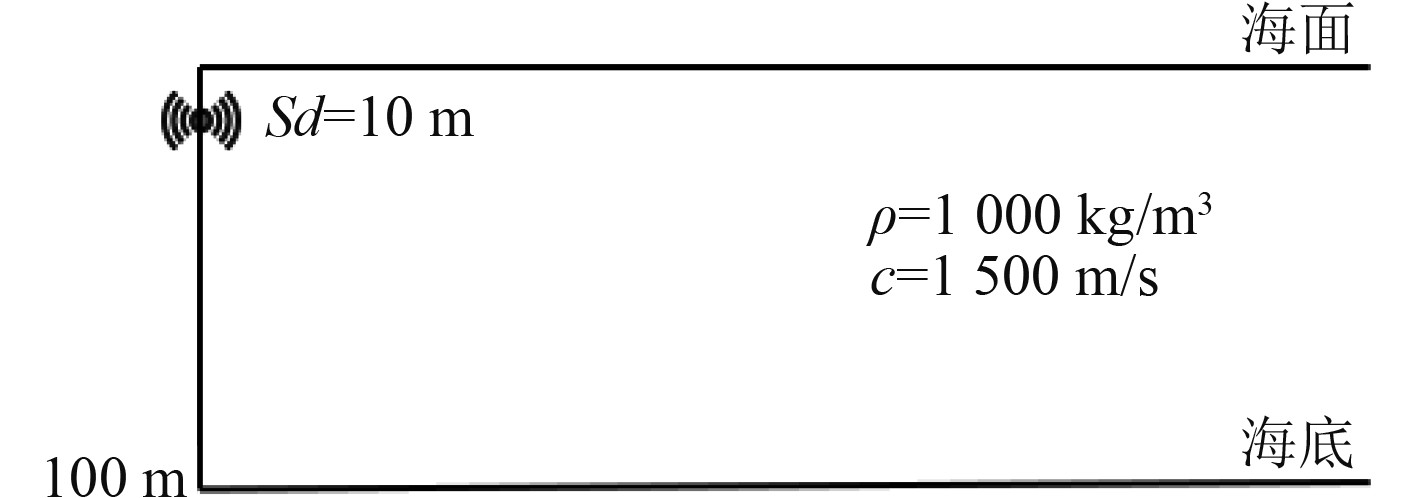
3 简正波模态主导的最佳深度研究

由波动理论可知，海水深度和声源频率是影响海水中简正波阶数的直接因素，因此为探究影响最佳深度的根本原因，本文研究了由海水深度和声源频率主导的简正波模态阶数对最佳深度的影响，通过对理想液体波导（见图5）中简正波阶数对最佳深度影响的研究来验证简正波叠加是产生最佳深度的根本原因，并总结最佳深度的相关规律。

3.1 理想液体波导中的最佳深度研究

理想液体波导是简化了的实际海洋环境，在波导中海面和海底均设置为全反射边界，声波在界面处只有反射没有透射，只存在水平扩展损失。这种边界条件的设置对远距离传播的情况是合理的，这是因为对远场起主要贡献的是掠射角较小的声波，而小掠射角在实际海底处的反射类似全反射边界处的反射。

3.1.1 理想液体波导中的简正波

理想液体波导中的声场是由各阶简正波叠加得到的，每一阶简正波的幅值与海水深度密切相关，为得到各阶简正波与深度相关的位移幅值，下面对理想液体波导中的位移势函数的表达式进行推导，其计算模型和参数如图6所示。

由波动理论可知：声场的位移势函数 $\psi $ 同样满足波动方程，在图6所示的柱坐标系下的理想液体波导中，其满足以下的波动方程：

$\frac{1}{r}\frac{\partial }{{\partial r}}(r\frac{{\partial \psi }}{{\partial r}}) + \rho (z)\frac{\partial }{{\partial z}}(\frac{1}{{\rho (z)}}\frac{{\partial \psi }}{{\partial z}}) + \frac{{{w^2}}}{{{c^2}(z)}}\psi = - \frac{{{S_w}\delta (r)\delta (z - {z_s})}}{{2\text{π} r}}\text{，}$

(15)

其中 ${S_w}$ 为点声源强度，运用积分变化法得出总声场的积分表达式为：

$\psi (r,z) = \int_0^\infty {\psi ({k_r},z)} {J_0}({k_r}r){k_r}{\rm{d}}{k_r}\text{，}$

(16)

其中 ${J_0}({k_r}r) = \dfrac{1}{2}[H_0^{(1)}({k_r}r) + H_0^{(2)}({k_r}r)]$ ， ${k_r}$ 为水平波数， ${k_r}$ 与公式中 ${k_{rm}}$ 的区别在于 ${k_{rm}}$ 代表某阶简正波的水平波数， ${k_r}$ 满足 ${k_r} = \sqrt {{k^2} - k_z^2} $ ， ${k_z}$ 为垂直波数，满足：

${k_z} = \frac{{m\text{π} }}{D}\text{，}$

(17)

则 ${k_r}$ 可以表示为 ${k_r} = \sqrt {{k^2} - {{\left( {\dfrac{{m\text{π} }}{D}} \right)}^2}}$ 。

理想波导的位移势函数的无限积分形式可以转换为无限个留数之和：

$\psi (r,z) = - \frac{{i{S_w}}}{{2D}}\sum\limits_{m = 1}^\infty {\sin ({k_{zm}}z)} \sin ({k_{zm}}{z_0})H_0^{(1)}({k_{rm}}r)\text{，}$

(18)

${k_{zm}}$ 代表某阶简正波的垂直波数。只有当 ${k_{rm}}$ 为实数时，简正波才会对声场真正做出贡献，因此简正波阶数m必须满足 $\dfrac{{m\text{π} }}{D} < k$ 即 $m < \dfrac{{kD}}{\text{π} } = \dfrac{{2fD}}{c}$ 因此式（18）又可以表示为：

$\psi (r,z) = - \frac{{i{S_w}}}{{2D}}\sum\limits_{m = 1}^M {\sin ({k_{zm}}z)} \sin ({k_{zm}}{z_0})H_0^{(1)}({k_{rm}}r)\text{。}$

(19)

M满足 $M = \left[ {\dfrac{{2fD}}{c}} \right]$ 。从式（19）中可以看出当点声源位置确定时，式中 $\sin ({k_{zm}}{z_0})$ 为定值，在深度方向上，位移势函数只与z有关，且与z成正弦函数关系，由于 ${k_{zm}}$ 同样满足式（17），下图给出水深100 m，声源深度10 m，频率100 Hz情况下的前5阶简正波模态与深度相关的位移幅值：

3.1.2 理想液体波导中简正波阶数对最佳深度的影响

为研究理想液体波导中简正波阶数对最佳深度的影响，本文计算了在图6条件下频率为100 Hz，海水中的简正波阶数分别为1，2，5，10时的声传播损失伪彩图和不同阶简正波模态图，结果如图7所示。

可以看出：当波导中只有1阶简正波时，声场的最佳深度和简正波最大幅值均出现在50 m处；当波导中存在2阶简正波时，声场的最佳深度和前2阶简正波叠加后幅值最大处吻合；随着简正波阶数的增多，最佳深度从50 m处分别向海面和海底移动，波导中对称地出现最佳深度，当海水中简正波阶数足够多时，最佳深度稳定在声源深度和其对称深度处。

下面解释了在理想波导中为什么在声源的对称深度同样会出现最佳深度的现象：

任意接收点深度和其对称深度满足深度之和为海水深度D，设接收点深度为 ${z_r}$ ，其对称深度为 $D - {z_r}$ ，接收点深度为 ${z_r}$ 时的位移势函数：

$\psi (r,{z_r}) = - \frac{{i{S_w}}}{{2D}}\sum\limits_{m = 1}^M {\sin ({k_{zm}}{z_r})} \sin ({k_{zm}}{z_0})H_0^{(1)}({k_{rm}}r)\text{，}$

(20)

其对称接收点深度的位移势函数为：

$\psi (r,D - {z_r}) = - \frac{{i{S_w}}}{{2D}}\sum\limits_{m = 1}^M {\sin ({k_{zm}}(D - {z_r}))} \sin ({k_{zm}}{z_0})H_0^{(1)}({k_{rm}}r)\text{，}$

(21)

由于 ${k_{zm}}$ 满足 ${k_{zm}} = \dfrac{{m\text{π} }}{D}$ ，代入上述公式中得到：

$\begin{split}\psi (r,D - {z_r}) =& - \frac{{i{S_w}}}{{2D}}\sum\limits_{m = 1}^M {\sin \left(\frac{{m\text{π} }}{D}(D - {z_r})\right)}\times\\ & \sin ({k_{zm}}{z_0})H_0^{(1)}({k_{rm}}r) = \psi (r,{z_r})\text{，}\end{split}$

(22)

由上述推导可知在理想液体波导条件下声传播损失的大小在深度方向上关于 $z = \dfrac{D}{2}$ 对称，因此最佳深度也总是对称存在的。

Buckingham^[16]经理论推导解释了在海水中简正波足够多时，最佳深度位于声源深度和其对称深度的原因，本文从简正波叠加的角度来解释上述现象：在声源产生的所有简正波中，各阶简正波的量级并不相同，其量级大小与该阶简正波在声源深度处的幅度成正比，如图7中的第5阶简正波在与声源深度和声源的对称深度相同时具有最大幅值，所以第5阶简正波的量级最大，叠加后的声场在声源深度和声源的对称深度能量最高，所以其为最佳深度。

总结本节结果得出以下结论：在声源位置一定情况下，简正波阶数时影响最佳深度的唯一因素，当海水中只有1阶简正波时，最佳深度和简正波幅值最大处吻合，都位于海水层中间处，随着简正波个数的不断增多，最佳深度也不断地向海面和海底移动，当简正波个数足够多时，最佳深度均位于声源深度和声源的对称深度。

4 结　语

本文运用简正波方法对浅海声传播的最佳深度进行研究，通过研究最佳频率的影响因素和不同环境下简正波阶数对最佳深度的影响，得出以下结论：

1）声源深度、声源频率和海水深度对最佳深度的影响最大，声源频率和海水深度通过影响海水中简正波阶数来影响最佳深度，声源深度通过影响简正波的量级来影响最佳深度。

2）在声源位置一定时，最佳深度只与简正波阶数有关，当海水只有1阶简正波时，最佳深度与第1阶简正波幅值最大处位于相同位置，随着简正波阶数增大，最佳深度从中间处分别向海面和海底移动，当简正波个数足够多时，最佳深度稳定在声源深度和声源的对称深度。