2. 武汉第二船舶研究所,湖北 武汉 430064
2. Wuhan Second Ship Design and Research Institute, Wuhan 430064, China
电机具有较高的加工精度和装配精度要求。在高转速、长寿命的运转条件下,在保持足够的拉脱强度和保证转动灵活的功能前提下,为了进一步提高转子的可靠性,改善振动噪声指标,需要进一步提高电机的一致性和装配精度。
电机的定、转子不是一个整体的材料,而是由许多层的磁性材料片叠压而成,磁性材料片间的装配预紧力、整体刚度与阻尼抑振性能之间存在矛盾。通过开展电机定转子铁芯低振动叠压制造技术研究,获取电机定转子铁芯磁力片结构刚度最优控制参数,实现电机低振动制造。
设备的接触面提供了30%~50%的静刚度和90%的阻尼值[1]。特定频段内,系统动力学特性由刚度控制,因此有必要研究电机定转子铁芯的结构刚度对电机振动噪声的影响特性。
电机定转子磁力片的加工表面在显微镜下观察可以发现,表面有随机分布的微凸体。当与其他构件连接时,构件之间的接触是由这些微凸体接触、挤压、变形完成。微凸体存在的直接影响就是真实接触面积小于名义接触面积,此现象会对系统的刚度造成一定程度的影响。
本文将磁钢片视作理想弹性垫片,因而,理想弹性垫片、粗糙接触面就构成了一个接触对,二者以串联的形式连接,接触对的法向总刚度为:
| $\frac{1}{K}=\frac{1}{{{K_1}}} + \frac{1}{{{K_2}}}\text{。}$ | (1) |
式中:
从式(1)可以看出,磁钢片的刚度越大,对系统整体刚度的影响越小,相比较磁钢片之间的接触刚度而言,磁钢片本身的刚度属于大量。因此定转子的总体刚度由磁钢片之间接触片的法向刚度决定。
本文将采用分形接触理论分析法向接触刚度与磁钢接触压力之间的关系,这对于设备厂制定相应的加工工艺,并实现设备低噪声建造工艺具有指导意义。
1 磁钢片法向刚度接触模型单个微凸体形貌高度为[2]:
| $z\left( x \right)={G^{D - 1}}{l^{2 - D}}\cos \frac{{\text{π} x}}{l},$ | (2) |
式中:
在
| $\delta =z\left( 0 \right)={G^{D - 1}}{l^{2 - D}}={G^{D - 1}}{\left( {a'} \right)^{2 - D}},$ | (3) |
在微观尺度条件下,可得到微凸体的曲率半径表达式为:
| $R={\left( {{{\left| {\frac{{{d^2}z\left( x \right)}}{{d{x^2}}}} \right|}_{x=0}}} \right)^{ - 1}}=\frac{{{l^D}}}{{{\text{π} ^2}{G^{D - 1}}}}=\frac{{{{\left( {a'} \right)}^{2 - D}}}}{{{\text{π} ^2}{G^{D - 1}}}},$ | (4) |
依据Hertz接触理论,微凸体的临界变形量
| ${\delta _C}={\left( {\frac{{\text{π} K{\sigma _y}}}{{2E}}} \right)^2}R={\left( {\frac{H}{{2E}}} \right)^2}\frac{{{{\left( {a'} \right)}^{2 - D}}}}{{{G^{D - 1}}}}\text{。}$ | (5) |
式中:
当
| ${a'_c}={G^2}{\left( {\frac{{2E}}{H}} \right)^{\frac{2}{{D - 1}}}},$ | (6) |
根据Hertz弹性接触理论,弹性载荷可以表示为:
| ${P_e}\left( \delta \right)=\frac{4}{3}E{R^{\frac{1}{2}}}{\delta ^{\frac{3}{2}}},$ | (7) |
由图1可以得到接触点截面面积的表达式为:
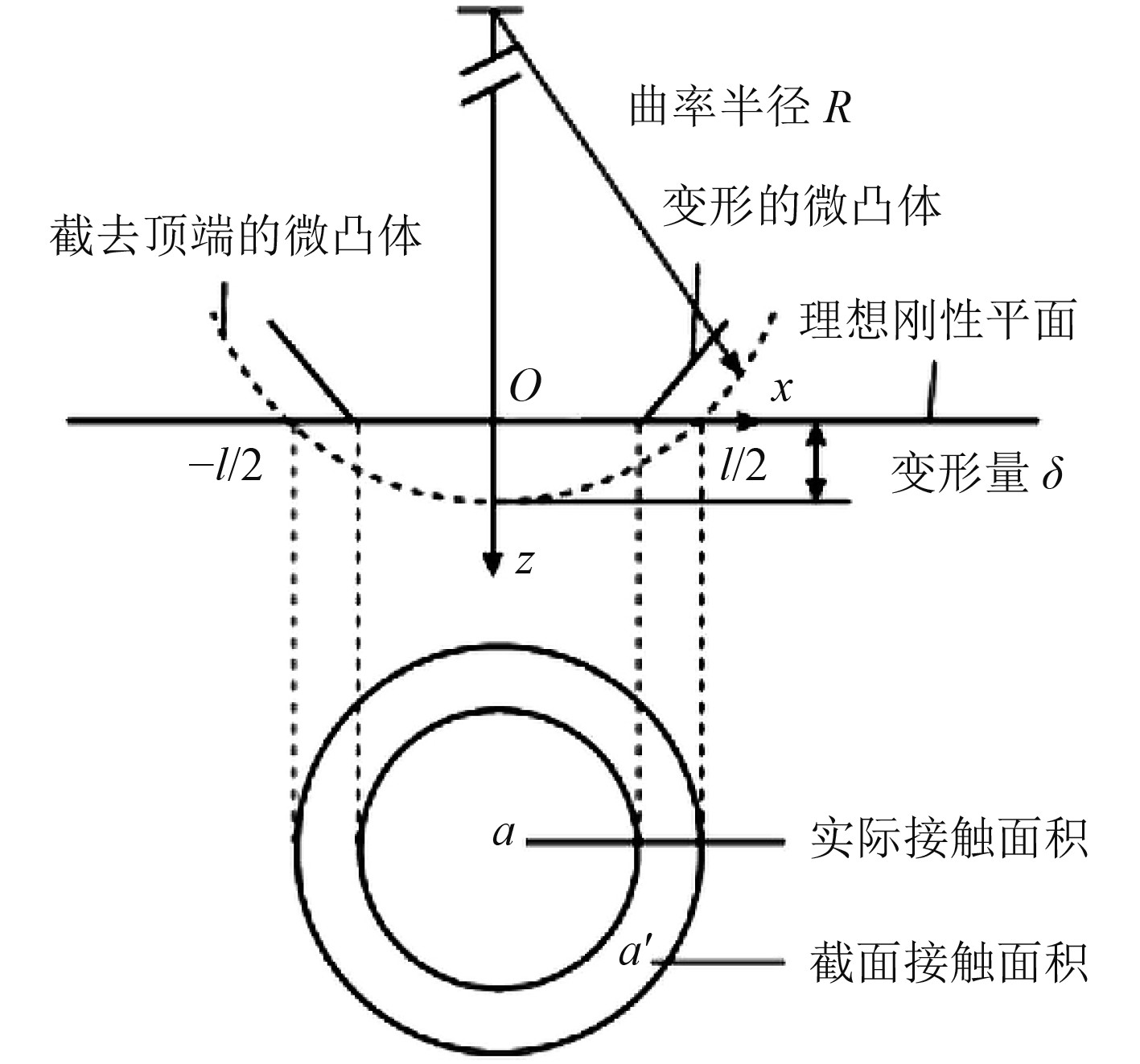
|
图 1 微凸体接触模型 Fig. 1 Contact model of asperity |
| $a=\text{π} {r^2}=\pi \left( {{R^2} - {{(R - \delta )}^2}} \right)=2\text{π} r\delta - \text{π} {\delta ^2} \approx 2\text{π} r\delta ,$ | (8) |
微凸体截面接触面积
| $a'=2a,$ | (9) |
单个微凸体的法向接触刚度可以由式(7)微分得到:
| ${k_n}=\frac{{{\rm{d}}{P_e}\left( \delta \right)}}{{{\rm{d}}\delta }}=2E{R^{\frac{1}{2}}}{\delta ^{\frac{1}{2}}}=E{a'^{\frac{1}{2}}}=\frac{{2E}}{{\sqrt {\text{π}} }}\sqrt a \text{。}$ | (10) |
接触点面积的分布规律等用幂函数表示如下:
| $n\left( a \right)=\frac{D}{2}\frac{{a_m^{\frac{D}{2}}}}{{{a^{\frac{D}{2} + 1}}}},$ | (11) |
式中,
实际接触面积总和
| ${a_m}=\frac{{2 - D}}{D}{A_r},$ | (12) |
结合式(10)和式(11),可以得到整体法向接触刚度为:
| ${K_n}\!=\!\int_{\frac{{{{a'}_c}}}{2}}^{{a_m}} {{k_n}n\left( a \right){\rm{d}}a} {\rm{=}}\frac{{EDa_m^{\frac{D}{2}}}}{{\sqrt {2\text{π} } \left( {1 - D} \right)}}\left( {a_m^{\frac{{1 - D}}{2}} - {{\left( {\frac{{{{a'}_c}}}{2}} \right)}^{\frac{{1 - D}}{2}}}} \right)\text{。}$ | (13) |
根据式(13),已知复合弹性模量
由上面的推导可知,若已知材料的硬度
葛世荣[3]在研究粗糙表面的分形特征时,利用回归分析法得到了分形维数
对于磁钢片来说,为车削表面,因此有:
| $D=1.22{R_a}^{ - 0.083}\text{,}$ |
同时,根据王鹏[4]的假设:
| ${R_a}={G^{D - 1}}\text{,}$ |
定义粘合率:
| $\eta ={{{A_r}} / A}\text{。}$ |
|
|
表 1 铁芯压力与磁钢片粘合率关系表 Tab.1 Relationship between iron core pressure and lamination rate of magnetic steel sheet |
联合式(6)、式(9)、式(12)~式(15)、式(19)和式(20),可将粗糙结合面的法向接触刚度Kn与表面粗糙度Ra、粘合率η联系起来。若已知表面粗糙度和粘合率,便可估算结合面的法向接触刚度。
3 法向刚度实例计算与分析电机磁钢片选用铝镍钴合金硅磁钢片,尺寸等效为D300 mm×10 mm×3 mm,选用50WW600热轧硅钢,接触对材料的属性参数值汇总如表2所示。理论总接触面积为A=π×300×10 mm2。
|
|
表 2 材料的性能参数表 Tab.2 Character parameters of materials |
电机磁钢由轧制而成,工作面的表面粗糙度Ra一般能达到6.4~1.6 μm。一般工艺水平下,粘合率η最大能达到10%~20%。因此,通过对磁钢片施加不同的压力,计算铁芯在不同的压力下法向刚度,预估振动影像效果。不同压力下对应的粘合率见表1所示,同时选取Ra=6.3μm,通过这几种组合情况分析法向接触刚度的变化,并作对比分析。
利用表2的材料参数,并结合上面的算式,得到不同粘合率情况下的接触刚度如表3所示。
|
|
表 3 不同压力情况下的铁芯刚度 Tab.3 Stiffness of iron core under different pressures |
通过对比表3的数据可以得出,电机定转子磁力片不同叠压力时,铁芯的结构刚度不同,随着叠压力的增大,磁钢片粘合率增大,铁芯刚度随之增大,在2.7~2.8 t的情况下铁芯刚度增大最为明显。
因此,通过对电机定转子磁力片施加不同叠压力,可以改变电机定转子铁芯刚度,从而影响电机的动力学特性。
4 电机振动噪声源特性分析为了验证叠压力对定转子铁芯刚度和振动噪声性能的影响,以某泵用电机为研究对象,通过开展机组的振动噪声特性测试,分析影响电机振动噪声的关键因素,从而提出相应的改进措施。测试分析结果和相应的改进措施如表4和表5所示。
|
|
表 4 机组振动噪声测试结果 Tab.4 Test results of vibration and noise of Pump |
|
|
表 5 工艺改进措施 Tab.5 Process improvement measures |
针对表4分析可看出,设备电机特性主要集中在900~1000 Hz及4100~4500 Hz频段之间。根据振动细化谱分析及声源定位,初步判定该频段振动特性来自于电机转子,原因是由于铁芯叠压预紧力无要求,导致的电叠压不均匀,形成了轴频谐波振动。因此,这部分振动幅值的降低与电机的加工工艺、装配工艺的改进优化关系很大,初步给出了改进措施和方法(见表5)。
5 定子工艺改进 5.1 改进目标定转子铁芯和之间的间隙一起组成电机的磁路,其质量的好坏直接关系到产生损耗的多少和引起振动的高低,通过对定转子铁芯叠压预紧力的计算优化,保证合适的预紧力,降低三相异步电动机的振动和电磁噪声。
5.2 改进内容由振源分析可知电机在~900 Hz,~4500 Hz产生了较大的振动,通过合理的加工工艺,控制冲片尺寸和叠压预紧力,保证粘合率系数,提高定转子铁芯质量,避免和减少电机振动超差。
5.3 改进措施严格控制转子铸铝质量,熔铝液温度不超过700 ℃;浇口浇铝不足或低陷不得超过规定的尺寸;端环缩孔不允许超过3处,其深度小于5 mm,直径小于7 mm;铸铝转子铁芯长度公差控制在+3.0 mm;铸铝转子铁芯斜槽公差±IT18;端环IT16,铸铝后的浇口和铝渣清除干净;
在工装模具上新开冲分模、压装、扩孔模,且冲片槽型冲制定位分为两步,在工艺上新开了定位基准,以减少误差。转工步时用工艺轴紧固,同时夹好标签,防止正反片错乱。叠装时采用专用的叠压机,叠压专用压机300 t(可调),借助压装模,采用以内径为径向定位孔,以嵌线槽为轴向定位基准,以槽样棒为辅助定位,以“三合一”的新工艺确保定冲片叠压符合工艺要求,并用扣片扣紧,完成定子铁心的制作。叠压过程中多次试压,初次试压压力2.4 t,如发现效果不理想,加压0.5 t,直至叠压完成后,铁芯内外圆整齐,符合图纸规定尺寸公差要求。
6 振动噪声测试 6.1 测试工装测试工装如图2所示。电机定转子装配后,采用额定转速空载运转,同时测量电机机脚处的振动。

|
图 2 电子铁芯不同刚度振动测试工装 Fig. 2 Different stiffness vibration test tooling for electronic iron core |
5种不同叠压刚度下的电机定转子铁芯振动噪声测试结果如表6所示。从表中数据分析可以发现,随着电机定转子铁芯叠压预紧力的增大,机脚振动总级随之下降,同时~900 Hz及~4100 Hz的轴频谐波振动也有降低。
|
|
表 6 各叠压力下的电机振动数据(dB) Tab.6 Motor vibration level under each stack pressure |
因此,通过采用调整定转子磁钢片的叠压预紧力,改变电机定转子整体刚度,从而改善电机振动性能的工艺是可行的。预紧力的选择应通过数值预估和试验测试相结合,不能太小,也不能过分增大。
7 结 语本文以某泵用电机为研究对象,开展机组的振动噪声特性测试,分析并得出某频段振动特性来自于电机转子的结论。主要原因是由于电机定转子叠压预紧力无要求,导致的叠压不均匀,形成轴频谐波振动。
针对电机定转子叠压预紧力,利用法向刚度接触模型预估叠压预紧力对铁芯刚度的影响,得到适合电机定转子叠压的预紧力估计值。根据预估到的叠压预紧力估计值,开展几种规格的电机定转子叠压,并利用专用工装测试不同叠压预紧力下的电机振动情况,从而得到了有利于电机振动控制的最佳叠压预紧力。
| [1] |
赵宏林, 丁庆新, 曾鸣, 等. 机床结合部特性的理论解析及应用[J]. 机械工程学报, 2008, 44(12): 208-214. |
| [2] |
尤晋闽, 陈天宁. 基于分形接触理论的结合面法向接触参数预估[J]. 上海交通大学学报, 2011, 45(9): 1275-1280. |
| [3] |
葛世荣. 粗糙表面的分形特征与分形表达研究[J]. 摩擦学学报, 1997, 17(1): 73-80. |
| [4] |
王鹏, 李天匀, 朱翔, 等. 隔振系统中垫片表面工艺质量与法向接触刚度的关系[J]. 中国舰船研究, 2013, 8(4): 59-63. |
 2021, Vol. 43
2021, Vol. 43
