随着船舶载重量的提高以及经济性的要求,柴-柴联合动力装置以其独特的优势得到越来越多的应用。双机并车装置的应用既节省了舱容,又有效地提高了船舶的装载量。每台柴油机可单独运行,安全性较高,且在军舰上可实现由巡航航速到战斗航速较快的转换,提高了机动性和灵活性[1]。提供了较广的功率范围,对油耗率和燃油品质无特殊要求,相对于柴-燃联合等动力装置具有更好的经济性[2]。
传统的推进轴系扭振频域计算方法,难以处理柴油机双机并车推进装置的并车与解列过程中突变载荷等非稳态工况的影响,因此有必要从时域上对轴系扭振分析方法进行研究。传统的推进轴系扭转振动响应计算聚焦于稳态计算,传递矩阵法、系统矩阵法等可以取得满意的稳态计算结果,但频域扭振计算方法在处理瞬态扭振问题时具有较大的局限性。推进轴系在扭矩突变的瞬态扭振计算研究方面,吴帅[3]、杨红军[4]和Ronald D. Barro[5]等建立了有限元连续模型以及集总参数的离散模型,采用NewMark-β法、Wilsion-θ法从时域求解轴系扭转振动微分方程组,基于该算法对船舶推进轴系的瞬态响应进行了计算,计算结果与实船测试结果基本一致,具有工程实用性。因此,在特定载荷下,可用NewMark逐步积分法求解传动系统的扭转振动微分方程,获得系统的动态特性。本文对柴油机双机并车轴系建立了模型,利用Matlab编程进行仿真计算,得到该轴系的时域动态响应。与频域计算结果对比验证其正确性,以时域方法求解两柴油机并车过程中相位差以及柴油机转速对柴油机曲轴应力的影响,研究并车冲击载荷作用下在各轴段产生的应力值,以及冲击载荷对整个轴系的影响。
1 计算模型的建立本文以GHD622V20柴油机双机并车装置为例,主机为10缸4冲程V列式柴油机,额定功率和额定转速分别为2900 kW,1750 r/min。左右两侧主机、弹性联轴器相同,具有高度对称性。当量模型的主支从右侧主机减振器开始到螺旋桨,分支系统从离合器外部开始到左侧主机减振器,由于主齿轮输出法兰之后质量点较少,这样简化可以使得分支点处的质量号和与之相连的质量号之差最小,减小动力矩阵带宽,从而减少计算量。
船舶推进轴系扭转振动的瞬态扭振计算的集总参数模型主要为经典频域模型和缩减模型,对于缩减模型来说最经典的是将柴油机和螺旋桨各作为一个质量点,虽然对于双机并车等复杂轴系可大幅度减少求解时间,但是该模型存在着无法考虑减振器阻尼以及曲轴的响应等问题,因此本文采用经典频域模型[6]。由于双机并车轴系的复杂性,在计算过程中可忽略相对于主支转动惯量很小的分支,减少分段,对于计算结果并无实质性影响[7]。但是对于双排高弹性联轴器简化为单排时,可能会发生漏掉某一阶固有频率的现象,应尽量根据高弹性联轴器的实际情况来简化。
V型机为了得到较好的柴油机扭转振动情况、轴承负荷状态以及柴油机的平衡,可能选取交替式发火,具有跳隔和互相补偿的情况,其同一排上两缸可能并不是依次发火。
因此,为充分考虑各缸激励,需要将两列气缸分别简化为不同的质量点,分别计算各缸产生的激励。V型机ν谐次气体压力瞬时激励力矩为:
| $T_{\rm{\nu }}{\rm{ = }}{T_0}{\rm{ + }}\sum {{t_{\rm{\nu }}}} (\cos {{\rm{\theta }}_{\rm{k}}} + i\sin {{\rm{\theta }}_{\rm{k}}})\text{。}$ |
式中:T0为单缸平均扭矩的数值;
简化后的当量参数模型如图1所示。

|
图 1 双机并车推进轴系当量模型 Fig. 1 The equivalent system of twin-engine parallel operation shafts |
对于含有分支系统的惯量矩阵与直链式相同;刚度矩阵在其第i行上,主对角线元素为与第i质量相邻的质量号,非对角元素具有非零值的列号为与第i质量相邻的质量号,其值为该两质量间弹性元件刚度的负值;阻尼矩阵可分解为外阻尼矩阵与内阻尼矩阵的和,外阻尼矩阵形式与惯量矩阵相同,内阻尼矩阵形式与刚度矩阵相同。
2 激励力矩分析 2.1 柴油机激励力矩船舶柴油机轴系扭转振动的激振力主要来自于柴油机气缸气体压力、运动部件惯性力与重力以及螺旋桨在不均匀伴流场中产生的交变切向力等,其中以柴油机气缸内气体压力产生的激振力为主[8],扭转振动的激振力矩如下式:
| ${T_g} = \frac{\text{π} }{4}{D^2}R{{\rm{P}}_T}\text{。}$ | (1) |
可见,柴油机气缸内部气体压力所产生的扭转振动激振力矩是由作用在曲柄销上的切向力PT引起的。
对PT进行傅里叶展开可得:
| $\begin{split} {P_T} =& {a_0} + \sum\limits_{h = 1}^\infty {({a_h}} \cos (f\omega t) + {b_h}\sin (f\omega t)) = \\ &{c_0} + \sum\limits_{h = 1}^\infty {({c_h}} \sin (f\omega t + {{\rm{\phi }}_h})\text{。} \end{split} $ |
式中:f为傅里叶简谐系数;ω为PT的圆频率;
若以柴油机回转角速度Ω代替PT的圆频率ω,则该方程可由基于简谐分析的频域计算过渡到时域计算。
对于单台柴油机推进系统,柴油机各缸按照一定的顺序发火,推进轴系上受到的是变化规律相同且彼此相差一定相位的激励力矩作用。而双机并车轴系2台柴油机的相位差是变化的,激励力矩也具有一定的随机性。
2.2 并车产生的冲击当船舶需要加速、减速或保持航速进行并车时,1台柴油机带负荷正常运行,另1台柴油机不带负荷逐渐加速到与第1台柴油机相同的转速,两柴油机并车。并车后不带负荷的柴油机逐渐加速,其调速特性曲线向上平移,在此过程中通过调整两柴油机调速特性曲线,进行功率分配,直到各承担50%负荷,达到所需转速[9]。
在柴油机并入的过程中,一般来说冲击作用由离合器的接合所引起,离合器的主、从动端未达到同步时离合器处于滑摩阶段,此时离合器传递摩擦转矩,随着作用力的逐渐增大,摩擦转矩逐渐增大,主、从端同步后扭矩迅速下降到与驱动系统加速的惯性扭矩相等,在此过程中产生冲击并在轴系中传递[10]。
由于并入柴油机带来转矩变化可能导致轴系发生倒拖导致熄火等现象,在并入瞬间对轴系产生冲击,轴系在冲击作用下产生的位移和应力响应直接关系到船舶动力系统的生存能力[11]。并入瞬时会有转速和扭矩的突变,导致柴油机突加负荷时会有黑烟超负荷等情况,对后传动装置等整个系统产生冲击,例如作用在轴段上的冲击扭矩,发生齿轮敲击以及离合器发热打滑等现象。且柴油机并入系统后,整个系统的动力学参数发生变化,其固有频率也会发生改变,并车转速选择不当时将会导致发生共振[12],而战斗舰艇更需要良好的快速并车性能,因此,对于双柴油机并车联合动力装置有必要求解在并车转速下的冲击响应。
对冲击响应问题的计算分析,既可以在频域内进行也可以在时域内进行。在频域内求解冲击响应的方法主要包括:平方根法(SRSS)、O’Hara法以及动态设计法(DDAM)等。在时域内求解冲击响应方法主要包括:模态叠加法和直接积分法。一般来说,冲击载荷是时间的函数,因此,本文利用直接积分法的NewMark-β法求解冲击响应。
3 时域瞬态响应计算时域瞬态扭振计算不同于频域稳态扭振计算,频域稳态扭振计算中的激励为周期性激励,可采用解析法求得推进轴系各部件的振动响应随转速变化的关系;而时域瞬态扭振计算将时间历程进行离散化处理,把扭转振动微分方程分解为各离散时间点的方程,其激励为瞬态激励,可采用数值仿真方法在某一转速下求得推进轴系各部件的动态响应随时间变化的关系。因而,可直观观测轴系在特定转速下随时间变化的扭转振动特性。时域计算方法主要有振型叠加法、逐步积分法(直接积分法),振型叠加法适用于线性系统和简单阻尼的情况,逐步积分法可以计算任意激励下的线性和非线性响应。
NewMark-β法属于逐步积分法的隐式单步法,引入了参数γ和β,分别对线性加速度法中的位移增量和速度增量进行了修正。当γ≥1/2,β≥γ/2时,NewMark-β法无条件稳定,本文选取γ=1/2,β=1/4,即平均加速度法来进行计算[13]。
NewMark-β算法的计算精度取决于时间步长与最短固有周期的比值,对于本系统来说,最短固有周期已确定,计算精度取决于时间步长的选取。步长太大导致结果会有一定的偏差,步长越小计算精度越高,但计算占用内存较大,计算成本高。本文选取的步长为计算转速下柴油机曲轴转过1°所需的时间。
对该轴系按照现有原则简化为集总参数模型后,该轴系振动微分方程可写为:
| $ {J} {\ddot \varphi } + {C} {\dot \varphi } + {K} \varphi = {T({\rm{t}})} \text{。}$ | (2) |
式中:J,C,K分别为系统的惯量矩阵、阻尼矩阵和刚度矩阵;
NewMark-β法假设在时间范围内加速度呈线性变化,基本假定为:
| ${\left\{ {\dot \varphi } \right\}_{{\rm{t}} + \Delta t}} = {\left\{ {\dot \varphi } \right\}_{\rm{t}}} + [(1 - {\rm{\gamma }}){\left\{ {\ddot \varphi } \right\}_{\rm{t}}} + {\rm{\gamma }}{\left\{ {\ddot \varphi } \right\}_{{\rm{t}} + \Delta {\rm{t}}}}]\Delta t\text{,}$ | (3) |
| ${\left\{ \varphi \right\}_{{\rm{t}} + \Delta {\rm{t}}}} = {\left\{ \varphi \right\}_{\rm{t}}} + {\left\{ {\dot \varphi } \right\}_{\rm{t}}}\Delta {\rm{t}} + [(1/2 - {\rm{\beta }}){\left\{ {\ddot \varphi } \right\}_{\rm{t}}} + {\rm{\beta }}{\left\{ {\ddot \varphi } \right\}_{{\rm{t}} + \Delta {\rm{t}}}}]\Delta {t^2}\text{。}$ | (4) |
由式(4)可知,Newmark-β每步积分均要满足t+Δt时刻的动力方程:
| $ {J} { {\ddot \varphi } _{t + \Delta t}} + {C} { {\dot \varphi }_{t + \Delta t}} + {K} { \varphi_{t + \Delta t}} = { {T}_{t + \Delta t}}\text{,}$ | (5) |
联立式(6)与式(7),可得:
| ${\left\{ {\ddot \varphi } \right\}_{t + \Delta t}} = \frac{1}{{{\rm{\beta }}\Delta {t^2}}}({\left\{ \varphi \right\}_{t + \Delta t}} - {\left\{ \varphi \right\}_t}) - \frac{1}{{{\rm{\beta }}\Delta t}}{\left\{ {\dot \varphi } \right\}_t} - \left(\frac{1}{{2{\rm{\beta }}}} - 1\right)\Delta t{\left\{ {\ddot \varphi } \right\}_t}\text{,}$ | (6) |
| ${\left\{ {\dot \varphi } \right\}_{t + \Delta t}} = \frac{{\rm{\gamma }}}{{{\rm{\beta }}\Delta t}}({\left\{ \varphi \right\}_{t + \Delta t}} - {\left\{ \varphi \right\}_t}) + \left(1 - \frac{{\rm{\gamma }}}{{\rm{\beta }}}\right){\left\{ {\dot \varphi } \right\}_t} + \left(1 - \frac{{\rm{\gamma }}}{{2{\rm{\beta }}}}\right)\Delta t{\left\{ {\ddot \varphi } \right\}_t}\text{,}$ | (7) |
将式(8)和式(9)代入式(7),可得:
| $ {K} { \varphi_{t + \Delta t}} = { {T}_{t + \Delta t}}\text{,}$ | (8) |
其中,有效刚度矩阵与有效载荷分别为:
| $\left\{ \begin{array}{l} {k} = {K} + \dfrac{{\rm{\gamma }}}{{{\rm{\beta }}\Delta t}} {C} + \dfrac{1}{{{\rm{\beta }}\Delta {t^2}}} {J} \text{,}\\ { {t}_{t + \Delta t}} = { {T}_{t + \Delta t}} + {M} [\dfrac{1}{{{\rm{\beta }}\Delta {t^2}}}{\left\{ \varphi \right\}_t} + \dfrac{1}{{{\rm{\beta }}\Delta t}}{\left\{ {\dot \varphi } \right\}_t} + \\ \qquad\quad\;\; \left(\dfrac{1}{{2{\rm{\beta }}}} - 1\right){{\ddot \varphi } _t}] + {C} [\dfrac{{\rm{\gamma }}}{{{\rm{\beta }}\Delta t}}{ \varphi _t} +\\ \qquad\quad\;\; \left(\dfrac{{\rm{\gamma }}}{{\rm{\beta }}} - 1\right){{\dot \varphi } _t} + \left(\dfrac{{\rm{\gamma }}}{{2{\rm{\beta }}}} - 1\right)\Delta t{ {\ddot \varphi }_t}]\text{。} \end{array} \right.$ |
求解方程(10)可得到每一时刻下的扭转角位移,及某一转速下的第i质量点与i+1质量点间轴段的转角差及轴段应力。
由频域计算得,该双机并车轴系在950 r/min时曲轴扭转应力值最大。根据上文所述,使用Matlab编程利用NewMark-β法进行时域计算,在该转速下该轴段的动态应力响应如图2所示。由图2可知,曲轴动态应力稳定值为(30.72-(−30.75))/2=30.735 MPa,与频域计算结果相同。

|
图 2 共振转速下曲轴动态应力响应时程曲线 Fig. 2 The curve of crankshaft stress changes with time at resonance speed |
图3为并车转速下的曲轴动态应力时程曲线。通过图2与图3可知,在不同转速下曲轴运行达到稳定时间基本相同。
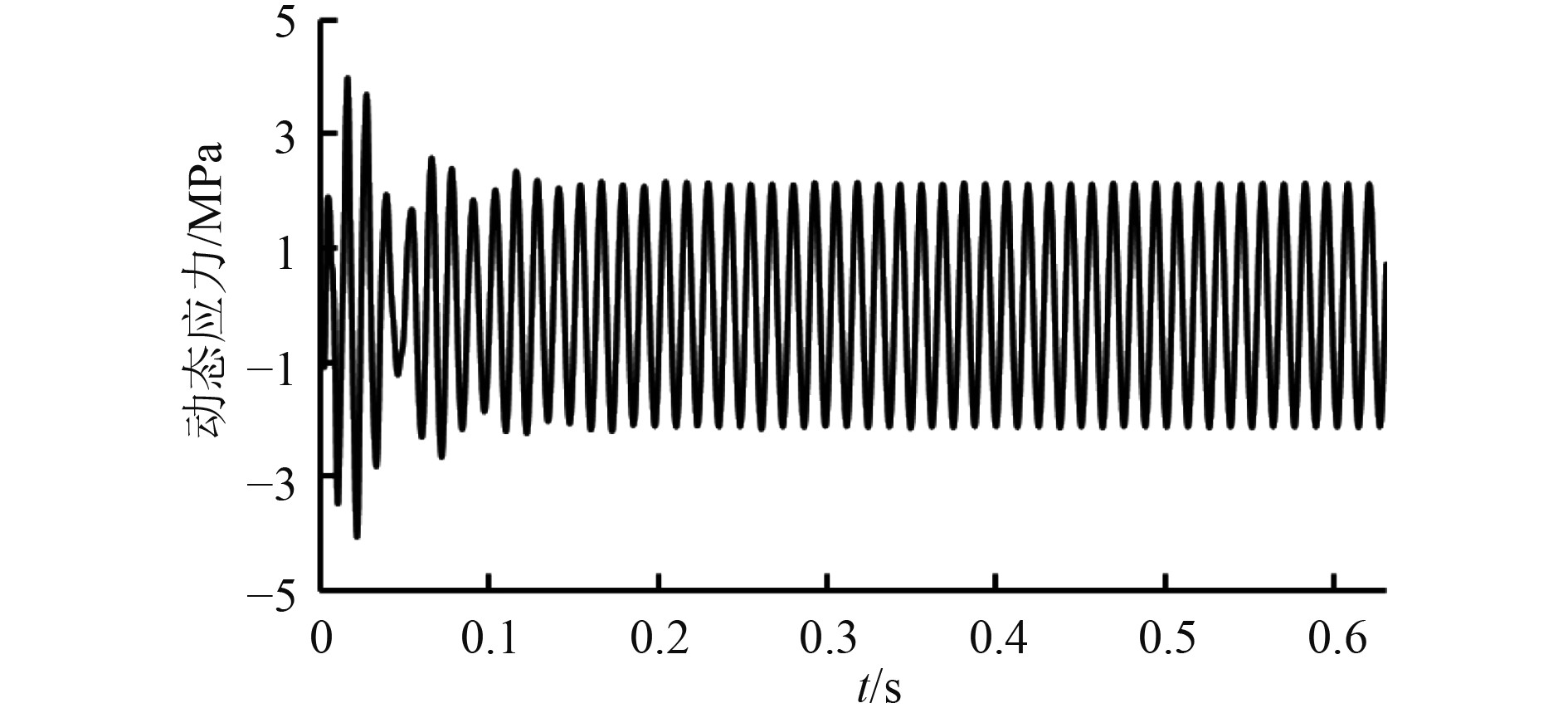
|
图 3 并车转速下曲轴动态应力响应时程曲线 Fig. 3 The curve of crankshaft dynamic stress change with time at twin-engine parallel operation speed |
由图4可知,轴系以950 r/min启动瞬间,曲轴动态扭矩达49.51 kNm,在轴系运转约1.025 s后曲轴动态动态扭矩趋于稳定,稳定运行时为(13.24-(-13.23))/2=13.235 kNm。
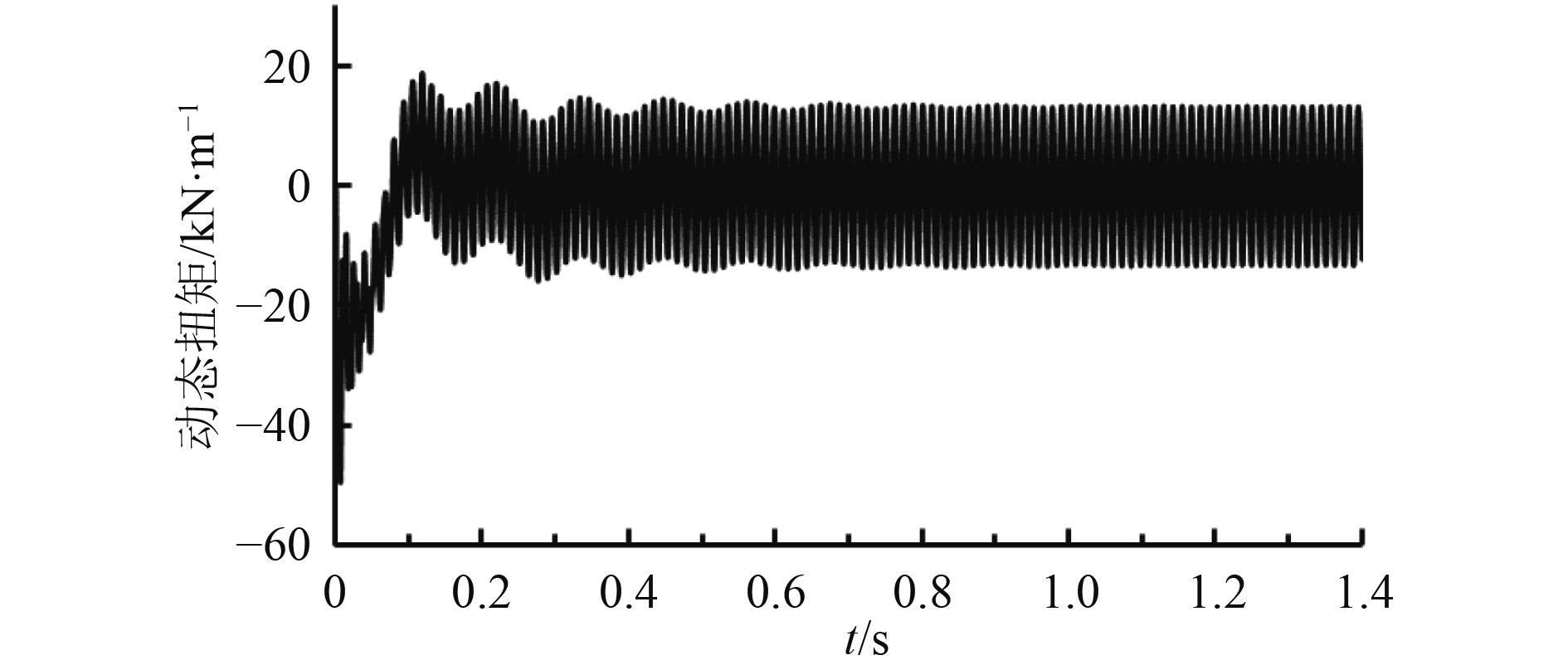
|
图 4 曲轴动态扭矩响应时程曲线 Fig. 4 The curve of crankshaft torque changes with time |
利用NewMark-β法计算该轴系全转速范围内曲轴应力值与频域对比,如图5所示。可知,该方法可以较好地反映轴系真实运行情况。

|
图 5 NewMark-β法与频域计算结果对比 Fig. 5 The comparison of NewMark-β and frequency calculation results |
对于柴油机产生的扭转振动来说,干扰力矩输入轴系的能量与柴油机的相对振幅矢量和的数值成正比[14]。单台柴油机各缸之间发火间隔角固定,相对振幅矢量和的值固定,但在实际运行过程中随着工况的变化,并车齿轮箱中的离合器时而脱开时而合上,在1台柴油机工作的情况下,另1台柴油机并入轴系的过程中,只需满足功率为0,转速与第1台相同,2台柴油机并车后产生的相位差是随机的,因此2台柴油机之间不同的相位差所产生扭转振动的响应是不同的。
两柴油机相位差以30°为间隔,计算0~720°每一相位差角下的轴段应力值随柴油机转速变化曲线,得到图6,即两柴油机在不同的相位差、不同转速下柴油机曲轴应力三维曲线。柴油机转速为950 r/min时,将转速间隔加密后得到图7,共振转速下柴油机曲轴应力随相位差角变化曲线,即图6在共振转速下的切片图,两柴油机相位差角为225°和585°时轴段应力最大。
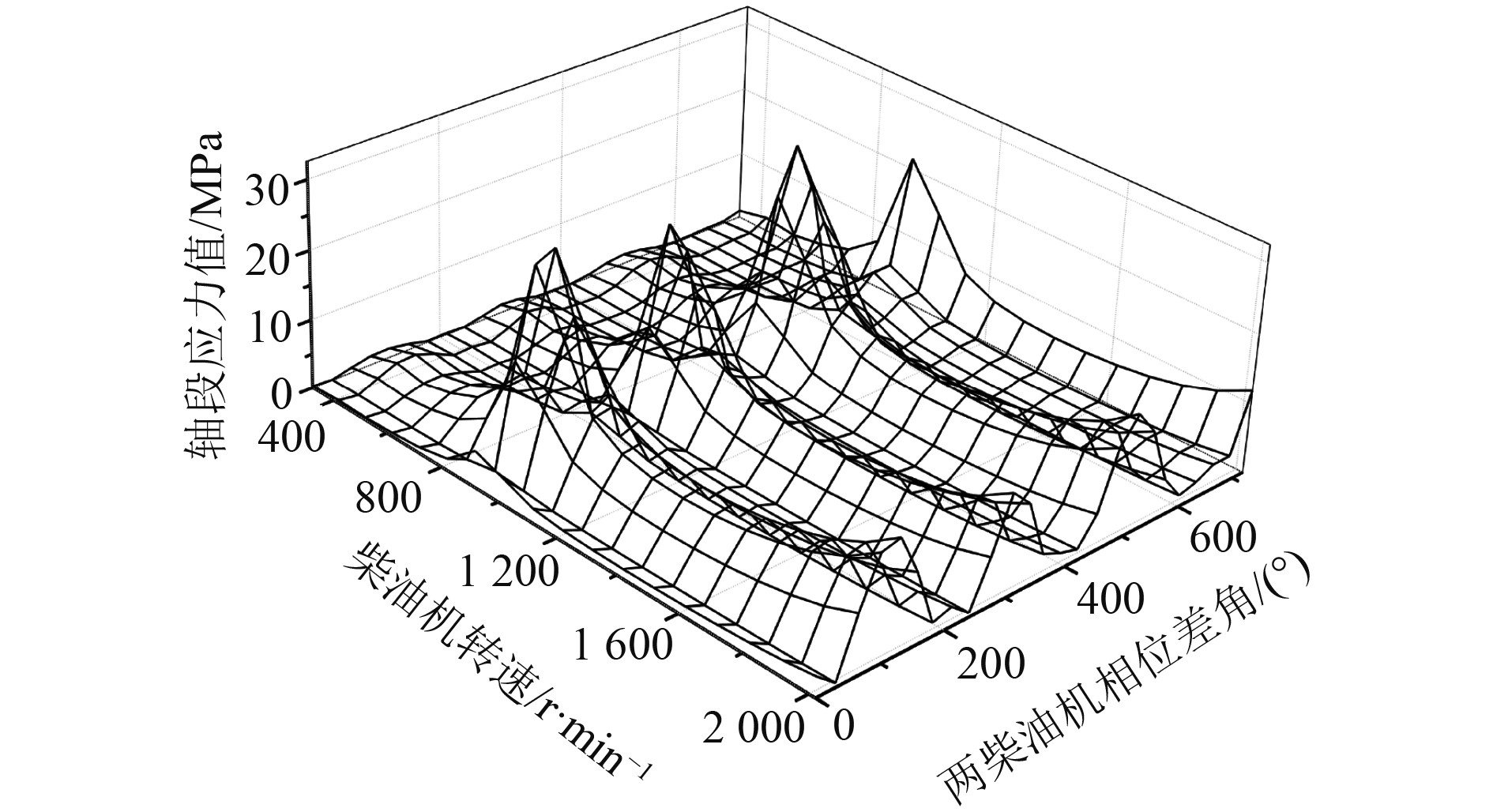
|
图 6 不同相位差在全转速下轴段应力值 Fig. 6 Shaft stress value at different speeds with different phase differences |
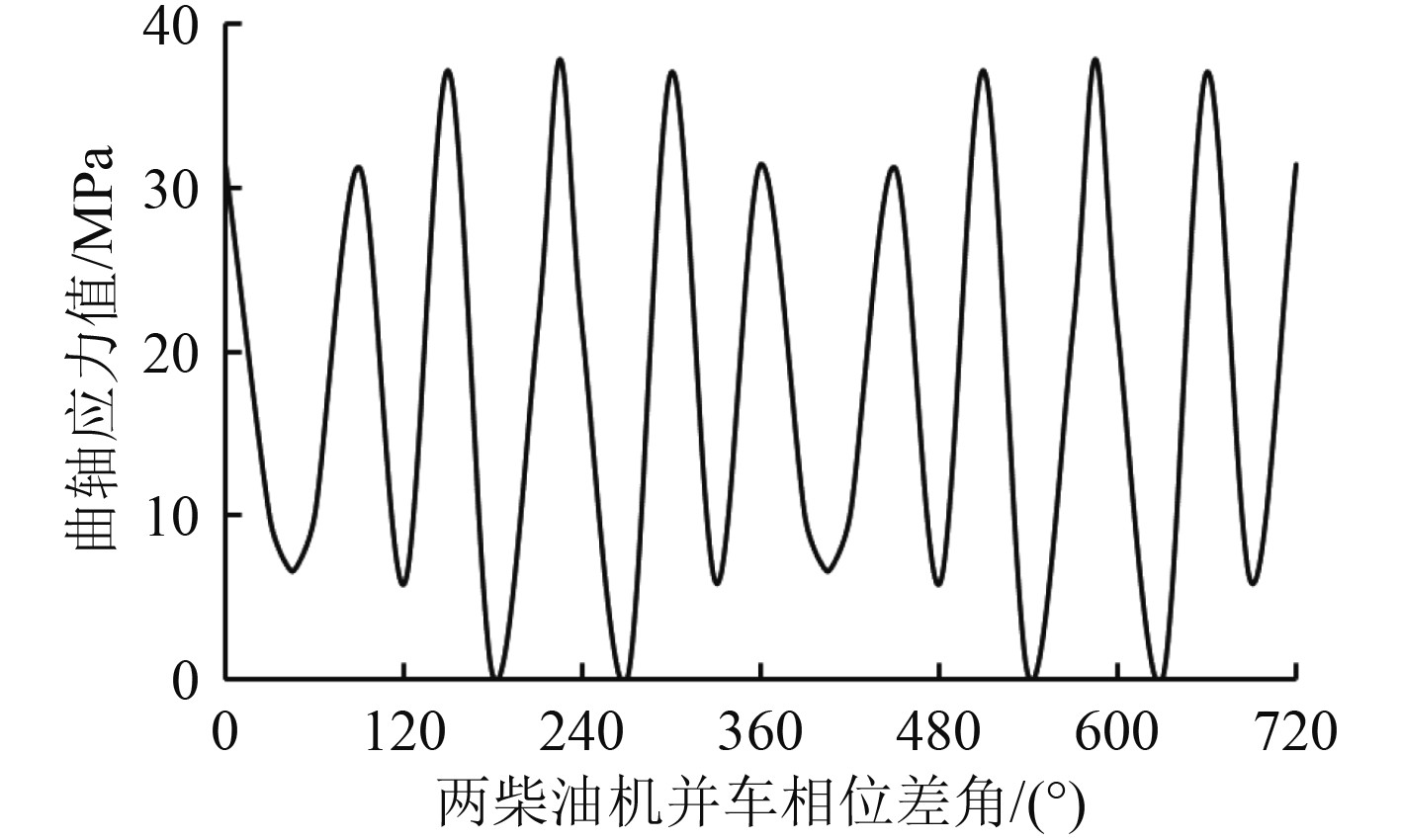
|
图 7 共振转速时不同相位差下的轴段应力值 Fig. 7 Shaft pressure values at different phase differences at resonance speed |
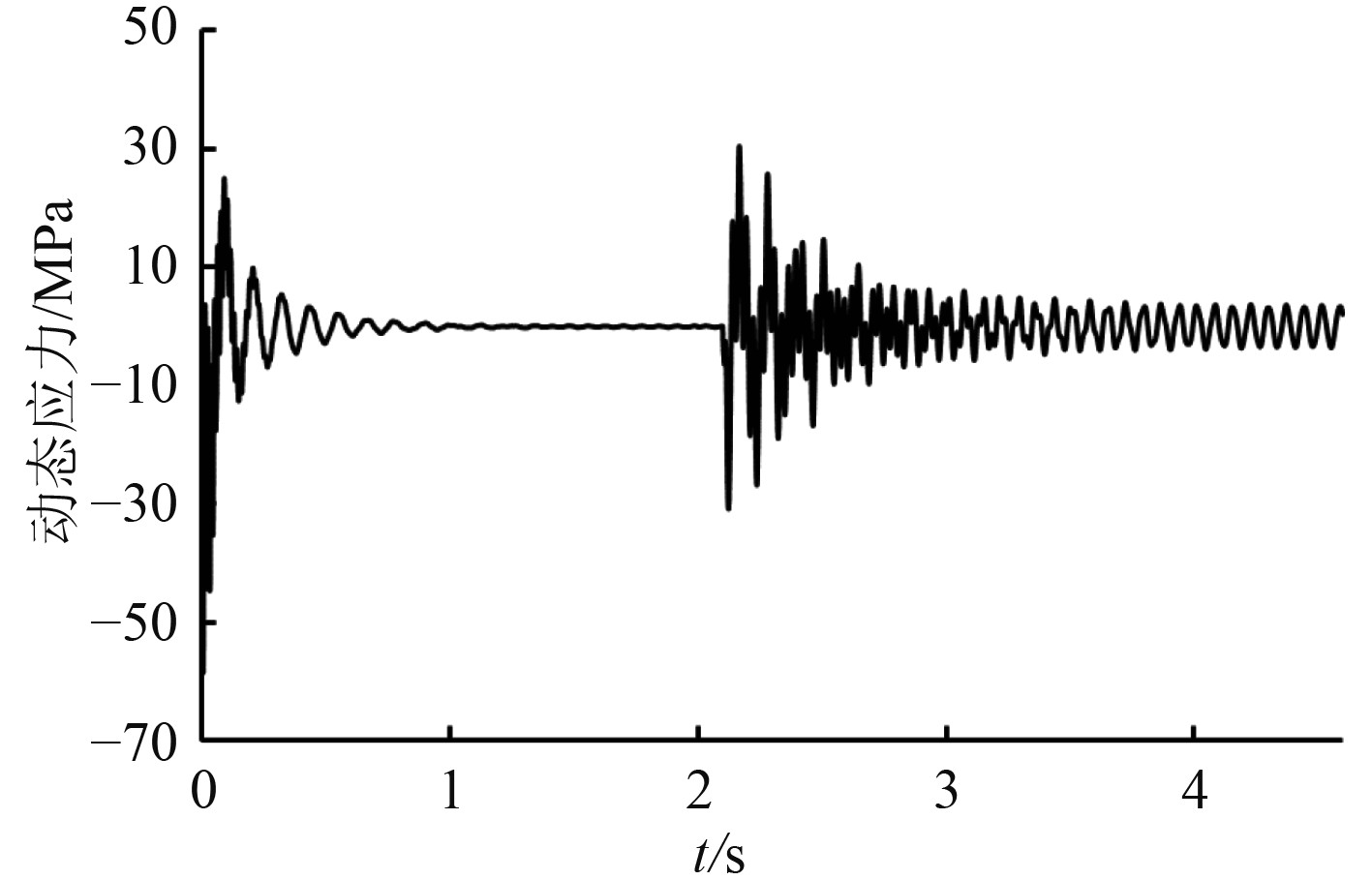
本文采用德国海军规范BV043/85所提供的冲击函数,为便于观察,放大冲击函数的幅值。进行瞬态响应计算时,根据两柴油机各缸发火顺序,以时间为自变量在各气缸集中质量点施加激励力矩,从第2 s开始并入柴油机的曲轴扭转应力如图8所示[15]。
|
图 8 并车冲击响应 Fig. 8 The shock response of parallel operation |
在0 s时,单台柴油机以并车转速750 r/min启动,另1台空载柴油机逐渐加速到与第1台柴油机相同转速,在第2 s时第1台柴油机运行稳定后并入,并入柴油机的调速特性曲线下移,第1台柴油机调速特性曲线上移,直到各分配50%负荷,完成并车,在此过程中转速保持不变。
在柴油机并入同时,冲击载荷作用在离合器接合处。冲击载荷持续时间为22.5 ms,冲击过后约1.1 s轴系恢复稳定。
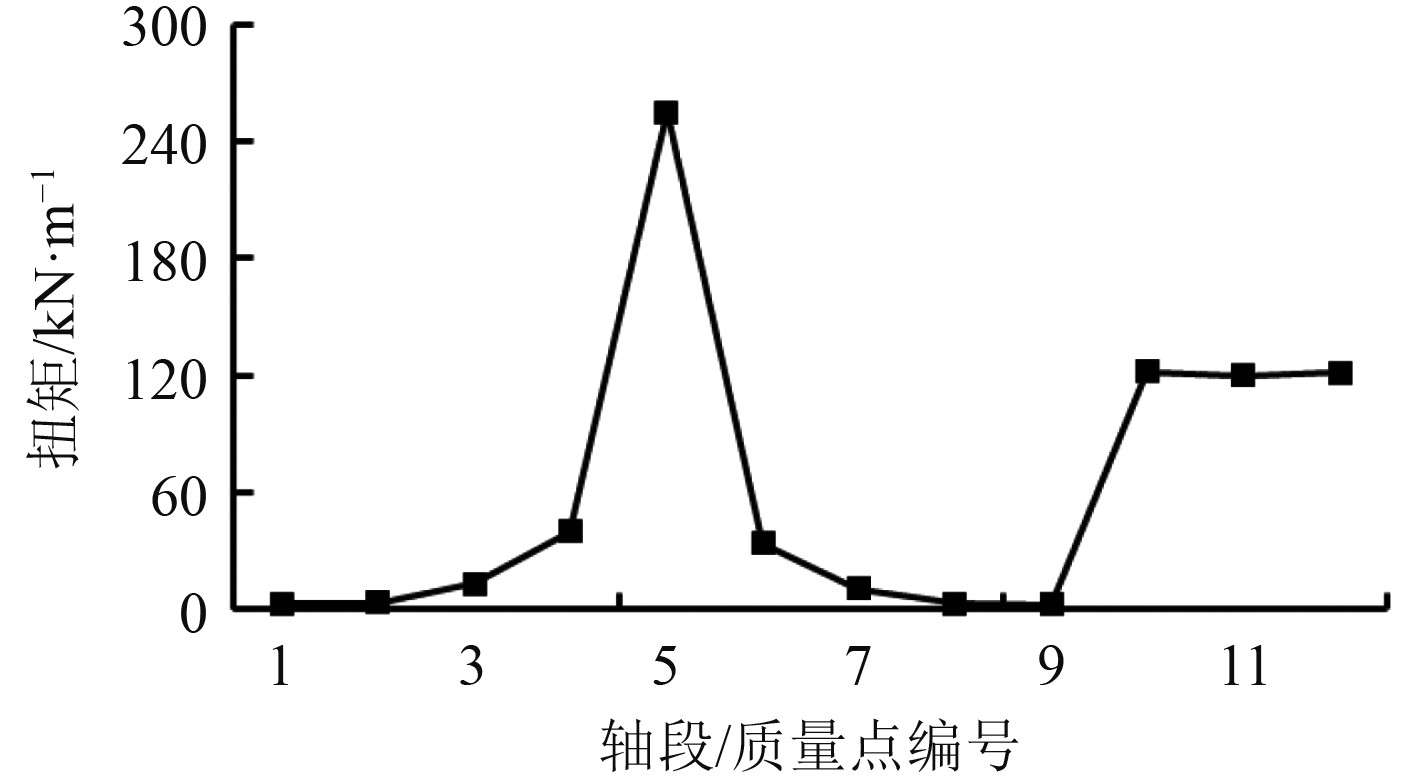
图9为各质量点、轴段在冲击作用下的扭矩幅值,编号对应轴段、质量点如表1所示。在轴系运行第2 s,冲击扭矩作用于离合器结合处,即5号质量点处。离合器结合处扭矩最大,各中间轴、螺旋桨轴次之,经过两侧轴系中高弹性联轴器的吸收,2台柴油机各曲轴、减振器处扭矩最小。
|
|
表 1 编号对应轴段/质量点 Tab.1 The number corresponding to the shaft or mass point |
|
图 9 并车冲击扭矩的的传递 Fig. 9 The transmission of the impact torque generated by parallel operation |
1)建立柴油机双机并车推进轴系的当量模型,为充分考虑各缸的激励,提出将柴油机每一缸作为一个质量点。利用NewMark-β法进行时域扭振计算,求得共振转速下每一时刻的柴油机曲轴轴段应力、扭矩,以及全转速下的曲轴扭振应力,计算结果与基于频域计算的解析法基本一致,验证了时域计算方法的正确性。
2)计算分析两柴油机间相位差的随机性对曲轴应力的影响,由于并车产生的两柴油机相位差变化,各转速下的曲轴应力值会发生变化,但其共振转速几乎不变;两柴油机并车相位差在0~720°范围内变化时,曲轴应力以360°为周期变化,在每个周期内存在一个应力达到最大的并车相位差角。
3)考虑了柴油机并车时对轴系产生的冲击响应,得到并车冲击下的曲轴动态应力,在冲击载荷的作用下,曲轴应力急剧增加,但其幅值小于柴油机运行所产生的应力值,且持续时间较短,因此并车过程一般不会造成轴段应力过大而发生事故;计算了由于并车产生的冲击扭矩作用在各轴段、质量点的扭矩幅值,发现冲击扭矩的传递具有一定的对称性,由离合器接合处向两台柴油机的自由端方向逐渐减小,但对并入柴油机各曲轴轴段、减振器的影响略大于原先运行的柴油机,对中间轴和螺旋桨轴所产生的影响大于两柴油机。该方法可用来选择合适的并车转速,使得并车过程对轴系运行影响最小,并且对联合动力装置并车过程中产生的突加载荷分析有一定意义。
| [1] |
王德山, 竺华君, 苏善旺. 船用柴油机的双机并车[J]. 船舶, 2010, 21(5): 28-32. |
| [2] |
吴杰长, 陈国钧, 安玉昌, 等. 柴油机并车控制器试验平台及监测分析系统研究[J]. 内燃机学报, 2002, 20(3). |
| [3] |
吴帅, 吴文伟, 熊晨熙. 冰载荷下柴油机推进轴系扭振的数值方法研究[J]. 舰船科学技术, 2018, 40(15): 89-95. |
| [4] |
杨红军, 车驰东, 张维竞, 等. 基于威尔逊θ法的船舶推进轴系扭转振动计算[J]. 船舶工程, 2014(4): 46-49. |
| [5] |
BARRO R D, EOM K T, LEE D C. Transient torsional vibration response due to ice impact torque excitation on marine diesel engine propulsion shafting[J]. Transactions of the Korean Society for Noise and Vibration Engineering, 2015, 25(5): 321-328. |
| [6] |
廖鹏飞, 周瑞平, 李江. 冰区船舶电力推进轴系瞬态扭振计算研究[J]. 推进技术, 2018, 39(8): 215-222. |
| [7] |
赵进刚, 刘刚, 王伟吉. 船舶复杂轴系扭转振动计算研究[J]. 中国舰船研究, 2010(6): 65-69. |
| [8] |
陈之炎. 船舶推进轴系振动[M]. 北京: 人民交通出版社, 1987.
|
| [9] |
陈虞涛, 曾凡明, 陈国钧, 等. 船舶并车推进装置负荷均衡控制策略研究[J]. 舰船科学技术, 2008, 30(5): 24-27. |
| [10] |
CHEN T, CHEN H. Universal approximation to nonlinear operators by neural networks with arbitrary activation functions and its application to dynamical systems[J]. IEEE Transactions on Neural Networks, 1995, 6(4): 911-917. DOI:10.1109/72.392253 |
| [11] |
汪玉, 计晨, 杜俭业, 等. 舰船动力轴系冲击响应性能分析[J]. 振动与冲击, 2011(5): 164-168. |
| [12] |
黄文超. 柴油机双机并车装置控制系统研究[D]. 上海: 上海交通大学, 2010.
|
| [13] |
KRAUSE R, WALLOTH M. Presentation and comparison of selected algorithms for dynamic contact based on the Newmark scheme ☆[J]. Applied Numerical Mathematics, 2012, 62(10): 1393-1410. DOI:10.1016/j.apnum.2012.06.014 |
| [14] |
陈大荣. 船舶内燃机设计[M]. 北京: 国防工业出版社, 1995.
|
| [15] |
朱俊飞, 周瑞平, 胡义, 等. 带齿轮副船舶推进轴系动态响应仿真研究[J]. 振动与冲击, 2013, 32(9): 100-104. |
 2021, Vol. 43
2021, Vol. 43

