钛合金材料广泛地应用于耐压壳结构中,壳体结构在服役期间会承受海水周期性的往复载荷,由此造成的疲劳损伤可能会产生裂纹,成为影响结构安全的重要因素。因此对金属疲劳断裂的分析一直是工程的研究热点。大多情况下,结构疲劳分析采用确定性的方法进行,然而不论是材料特性、载荷本身等都具有不确定性的特征,而这些特征正是影响疲劳寿命的不确定性因素。针对这些疲劳裂纹扩展过程中存在的不确定性,有必要采用可靠性理论[1]对裂纹扩展进行分析。
传统疲劳可靠性方法的缺陷主要是没有考虑到已经存在的裂纹对结构产生的影响,而断裂力学恰好弥补了这一缺点。一些学者提出了可靠性理论与裂纹扩展理论相结合的办法并开展了疲劳裂纹扩展理论工程上的可靠性研究[2-5],但以往的Paris疲劳裂纹扩展模型具有很多局限性,它不能包括裂纹扩展的小裂纹阶段。对此,为了解决传统的裂纹扩展模型可靠性分析中存在的局限性,李向阳等[6-8]对新近提出的裂纹扩展模型进行对比,发现McEvily模型能够解释比较多的异常疲劳现象,并提出了针对不同材料的变斜率改进形式,改进后的McEvily模型对疲劳短裂纹和长裂纹均具有良好的疲劳预测能力。随后,王一飞等[9]也将裂纹扩展率分子项的幂指数由固定值改为变量,验证了该模型具备对不同材料的裂纹扩展进行预报的能力。S.Ishihara[10]在钛合金疲劳寿命周期内,进行了一系列高低周循环试验得到了裂纹长度与加载循环次数的函数关系,确定了McEvily模型的本构关系且试验结果与预测结果高度吻合。R.Kumble等基于裂纹张开位移考虑的裂纹扩展模型在应力比R=0载荷情况下,提出了一种修正裂纹扩展表达式以反映裂纹闭合影响下的McEvily关系。李旭东[11]通过对不同温度下6151-T6合金的研究,获得了一种基于可靠性理论的裂纹扩展速率表达式。罗广恩等[12]基于改进McEvily模型预测深海结构表面裂纹的疲劳寿命,得到了结构的疲劳寿命和表面裂纹扩展的形貌变化。许斐然[13]采用改进McEvily裂纹扩展模型,预测压缩循环载荷下深海结构物的疲劳寿命,并将预测结果与试验结果进行对比,结果表明此模型可为相关循环的压缩载荷下的结构疲劳寿命评估提供参考。康健[14]通过对McEvily公式的深入研究,综合考虑弹塑性行为的影响、裂纹闭合效应,得出McEvily改进公式对疲劳裂纹扩展寿命具有更强的评估能力。这些针对McEvily模型的疲劳裂纹扩展研究也为本文中模型的选取提供了思路。
本文在疲劳分析中引入可靠性理论,将裂纹扩展模型中的不确定参数作为统计变量,结合改进McEvily裂纹扩展模型和疲劳寿命可靠性模型,建立疲劳裂纹扩展可靠性的极限状态方程,利用一次二阶矩法对可靠度指标及参数敏感性进行计算分析,并与传统的Paris裂纹扩展模型可靠度进行对比。
1 基于疲劳裂纹扩展模型的可靠性 1.1 改进McEvily裂纹扩展模型的疲劳可靠性 1.1.1 极限状态方程的建立疲劳累积损伤模型由于描述的参量不同,因此结构的功能函数有很多种,这就导致在极限状态建立的过程中有了较多的选择。但根据本文的实际情况考虑,应当选择以应力循环数为变量的疲劳寿命模型为结构功能函数,即可表示为:
| $g(X) = {N} - {N_d} \text{。} $ | (2) |
其中:
根据李向阳的改进McEvily模型基础上可以定义裂纹尺寸从
| $ \int {{\rm{d}}N = \int {\frac{{{\rm{d}}a}}{{A{{({\rm{M}})}^m}}}} }\text{,} $ | (3) |
即可知:
| $ \int_{{a_0}}^{{a_c}} {\frac{{{\rm{d}}a}}{{A{{({\rm{M}})}^m}}}} = {N_c} - {N_0} = \int_0^{{N_c}} {{\rm{d}}N}\text{,} $ | (4) |
因此可得:
| $ \varphi ({a}_{1}, \;{a}_{2})={\displaystyle {\int }_{{a}_{1}}^{{a}_{2}}\frac{{\rm{d}}a}{A{({\rm{M}})}^{m}}}\text{。} $ | (5) |
其中,A和m为裂纹扩展过程中的不确定性参数。
| $ \varphi ({a}_{0},{a}_{c})-\varphi ({a}_{0},{a}_{{}_{d}})=0\text{,} $ | (6) |
即由此可得结构功能函数:
| $ g(x) = \varphi ({a_0},{a_c}) - \varphi ({a_0},{a_d}){\rm{ = }}\int_{{a_0}}^{{a_c}} {\frac{{{\rm{d}}a}}{{A{{({\rm{M}})}^m}}}} - ({N_{_d}} - {N_0})\text{,} $ | (7) |
当疲劳破坏发生时
| $ Z{\rm{ = }}\int_{{a_0}}^{{a_c}} {\frac{{{\rm{d}}a}}{{A{{({\rm{M}})}^m}}}} - ({N_d} - {N_0}){\rm{ = }}0\text{。} $ | (8) |
式中:
| $ \begin{split} M =& \Delta {K_{eff}} - \Delta {K_{effth}} = {K_{\max }} - {K_{op}} - \Delta {K_{effth}}=\\ &\sqrt {\text{π} {r_e}\left(sec\frac{\text{π} }{2}\frac{{{\sigma _{\max }}}}{{{\sigma _Y}}} + 1\right)} \left(1 + Y\sqrt {\frac{a}{{2{r_e}}}} \right){\sigma _{\max }}(1 - R) - \\ &(1 - {e^{ - ka}})({K_{op\max }} - R{K_{\max }}) - \Delta {K_{effth}}\text{。}\\[-10pt] \end{split} $ | (9) |
其中:
由上述内容中提出的基于改进McEvily裂纹扩展模型得到的极限状态方程式(8),当疲劳循环数达到
| $g(x) = \varphi ({a_0},{a_c}) - \varphi ({a_0},{a_N}){\rm{ = }}\int_{{a_0}}^{{a_c}} {\frac{{{\rm{d}}a}}{{A{{({\rm{M}})}^m}}}}- {N_d}=0\text{,}$ |
此时的疲劳可靠度可表示为:
| $ \begin{split} {P_r} =& P(N \gg {N_d})=\\ &P\left[ {\int_{{a_0}}^{{a_c}} {\frac{{da}}{{A{{({\rm{M}})}^m}}}} - {N_d} \geqslant 0} \right]\text{,} \end{split} $ | (10) |
| $\begin{split}{\rm{M }}=& \sqrt {\text{π} {r_e}\left({\rm{sec}}\frac{\text{π} }{2}\frac{{{\sigma _{\max }}}}{{{\sigma _Y}}} + 1\right)} \left(1 + {\rm{Y}}\sqrt {\frac{a}{{2{r_e}}}} \right){\sigma _{\max }}(1 - {\rm{R}}) -\\ &(1 - {{{e}}^{ - ka}})({K_{op\max }} - {\rm{R}}{K_{\max }}) - \Delta {K_{effth}}\text{。}\end{split}$ |
根据上面的模型分析可知,所涉及到的主要参量为:不确定材料参数A,m;初始裂纹尺寸
|
|
表 1 模型参数统计特征 Tab.1 Statistical characteristics of random variables |
在极限状态模型计算中,默认不确定参数为正态分布。根据一次二阶矩中的中心点法,通过Matlab进行编程计算,可得到裂纹扩展过程中的可靠度指标以及失效概率。本文中基于改进McEvily裂纹扩展模型得到了载人潜水器钛合金材料的可靠度指标
基于Paris疲劳裂纹扩展模型的极限状态方程及其参数不确定变量的表达式,则当材料循环寿命次数达到
| $ \begin{split} {P_r} = &P(N \geqslant {N_d}) =\\ &P\left( {\int_{{a_0}}^{{a_c}} {\frac{{da}}{{C{{(\Delta {\rm{K}})}^n}}}} - {N_d} \geqslant 0} \right)\text{。} \end{split} $ | (1) |
根据上面的极限状态方程所涉及的不确定参数变量主要包括:不确定材料参数C,n;初始裂纹尺寸
|
|
表 2 Paris模型参数统计特征 Tab.2 Statistical characteristics of Paris model parameters |
基于Paris极限状态计算模型下,不确定参数变量默认为正态分布。采用一次二阶矩的验算点法来进行计算,得到其可靠度为4.08及失效概率为
将模型中各随机变量变异系数取不同数值时对应的可靠度指标和失效概率分别列于图1~图9中。
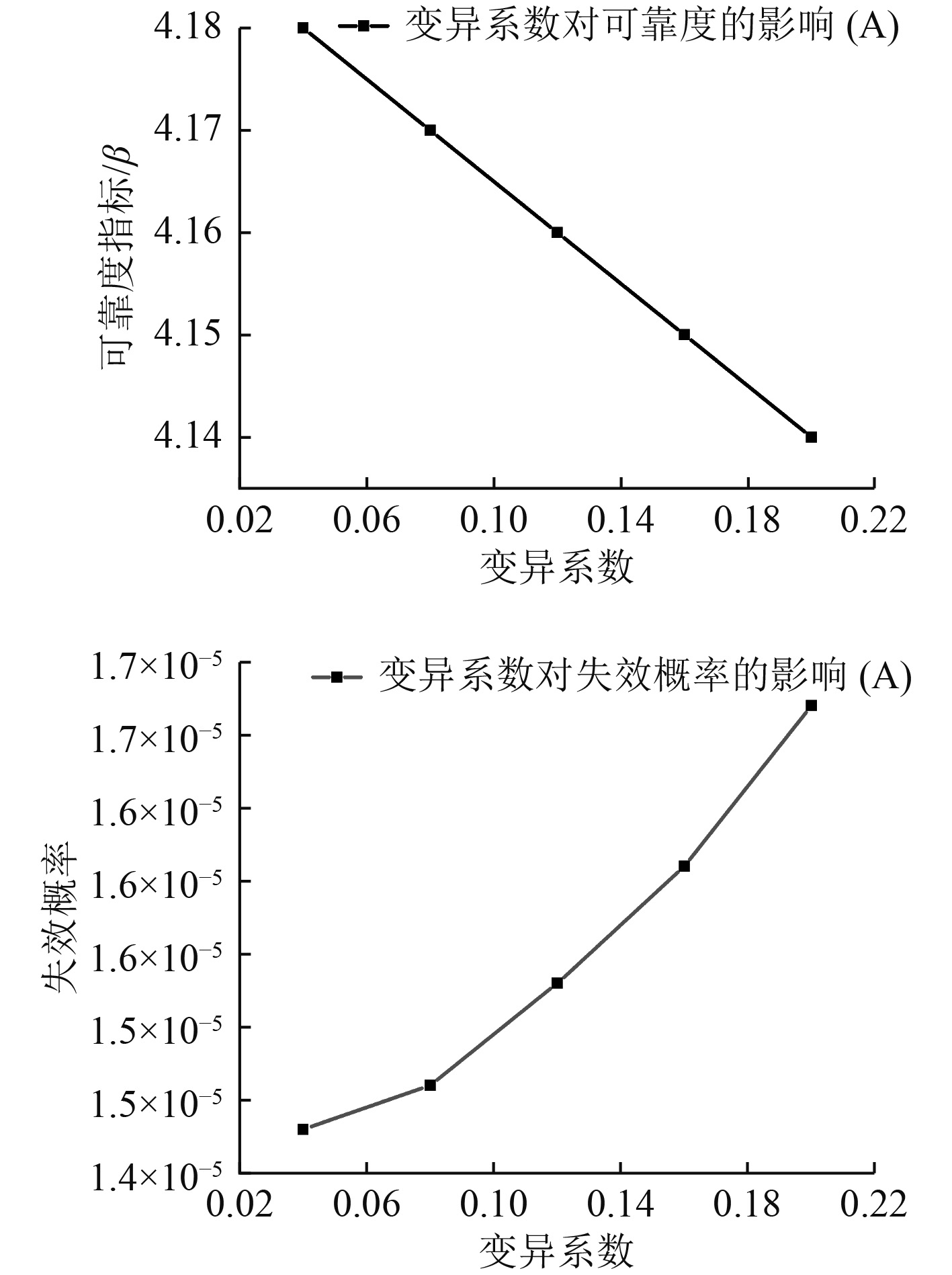
|
图 1 随机变量A的变异系数对可靠性的影响曲线 Fig. 1 The influence curve of variation coefficient of random variable A on reliability |
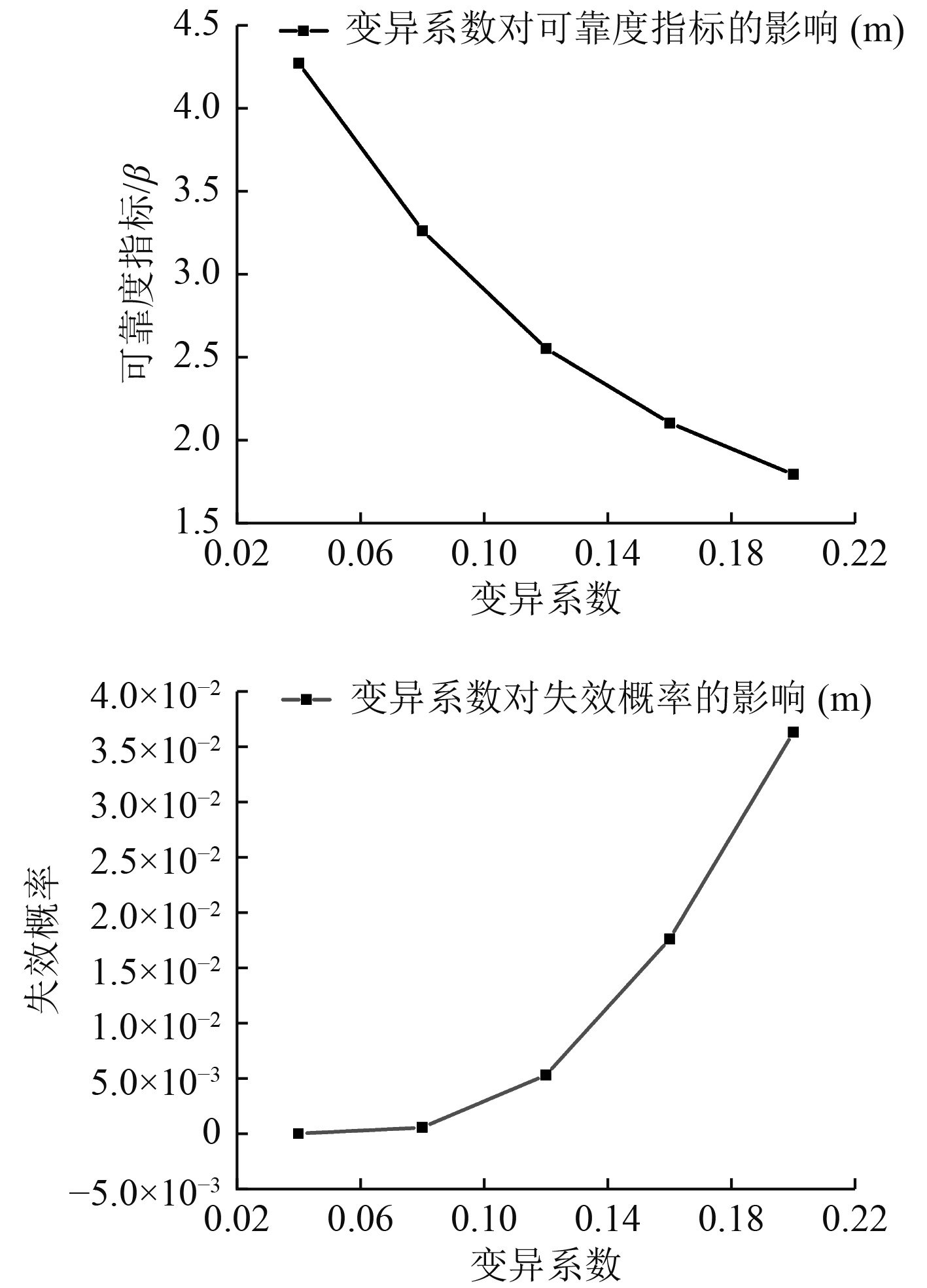
|
图 2 随机变量m的变异系数对可靠性的影响曲线 Fig. 2 The influence curve of variation coefficient of random variable m on reliability |

|
图 3 随机变量k的变异系数对可靠性的影响曲线 Fig. 3 The influence curve of variation coefficient of random variable k on reliability |
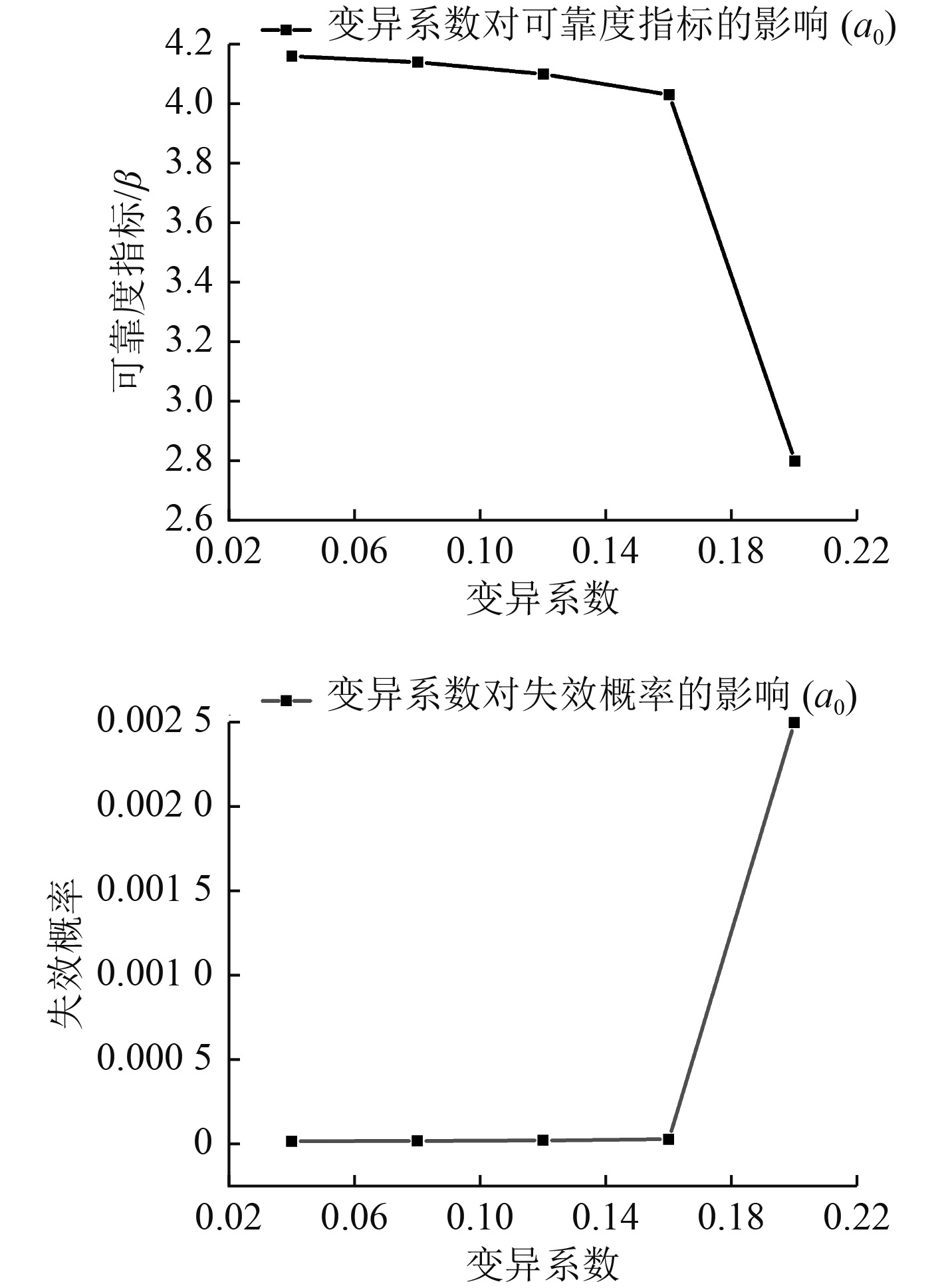
|
图 4 随机变量a0的变异系数对可靠性的影响曲线 Fig. 4 The influence curve of variation coefficient of random variable a0 on reliability |
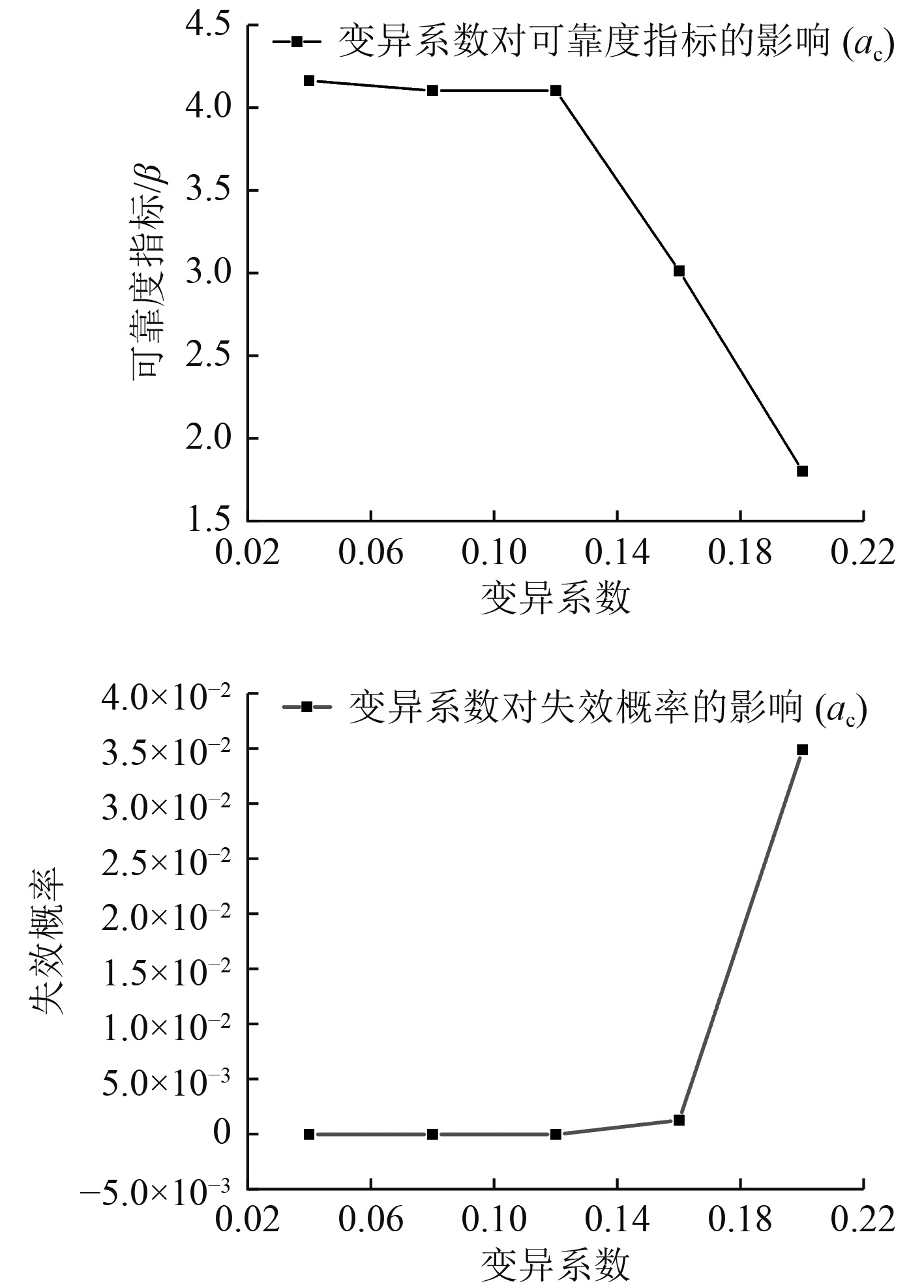
|
图 5
随机变量
|
|
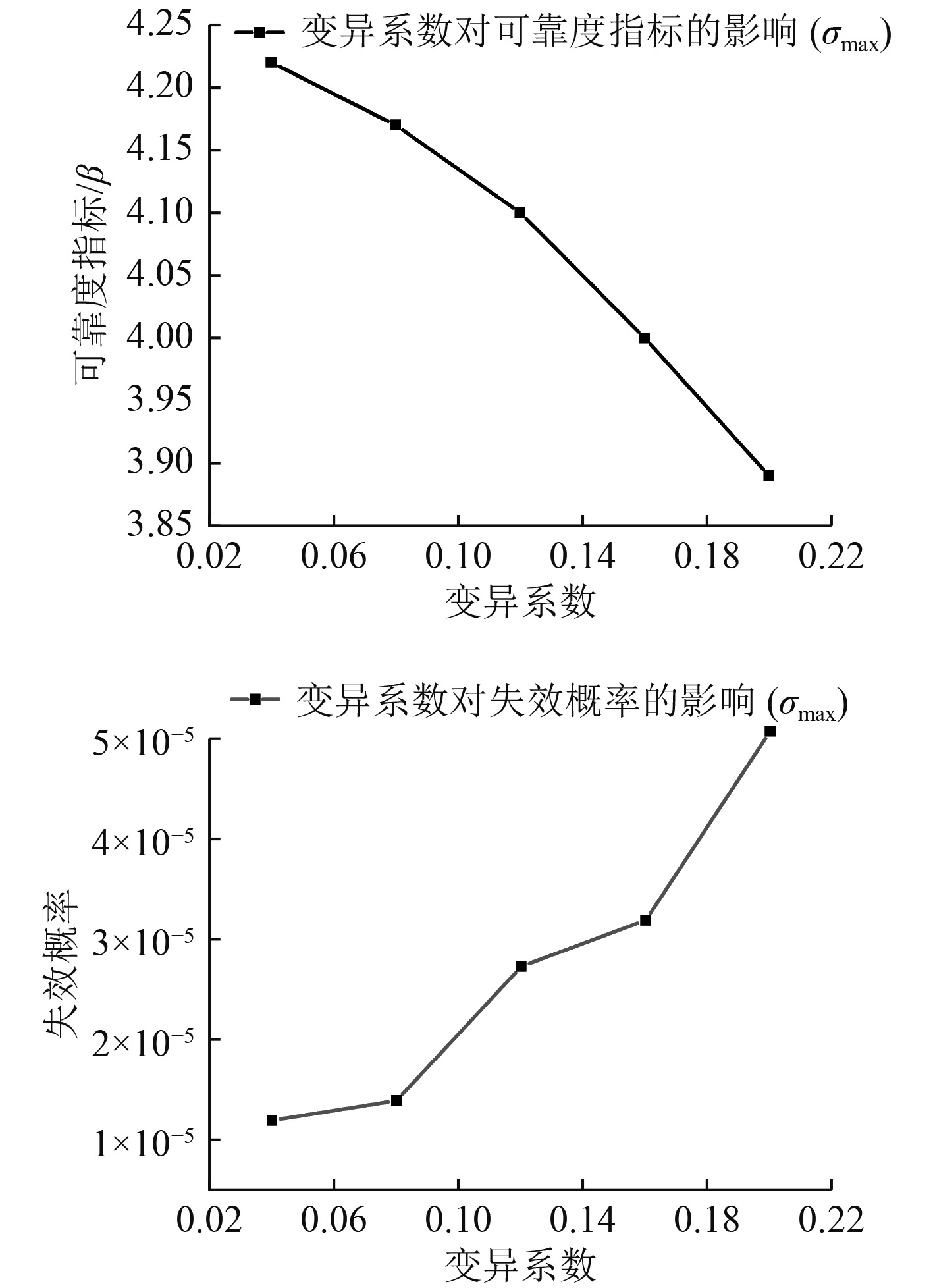
图 6
随机变量
|
|
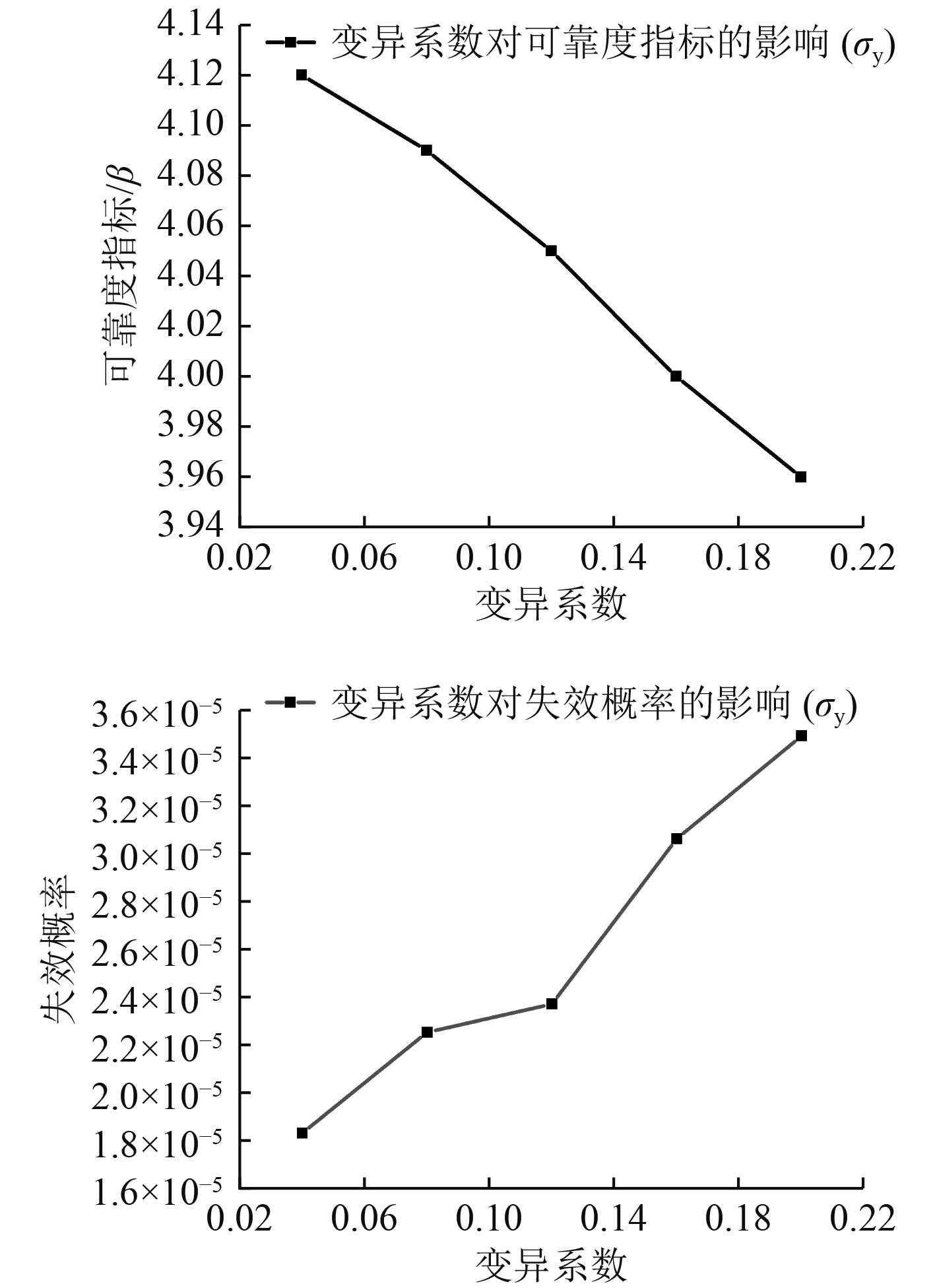
图 7
随机变量
|
|
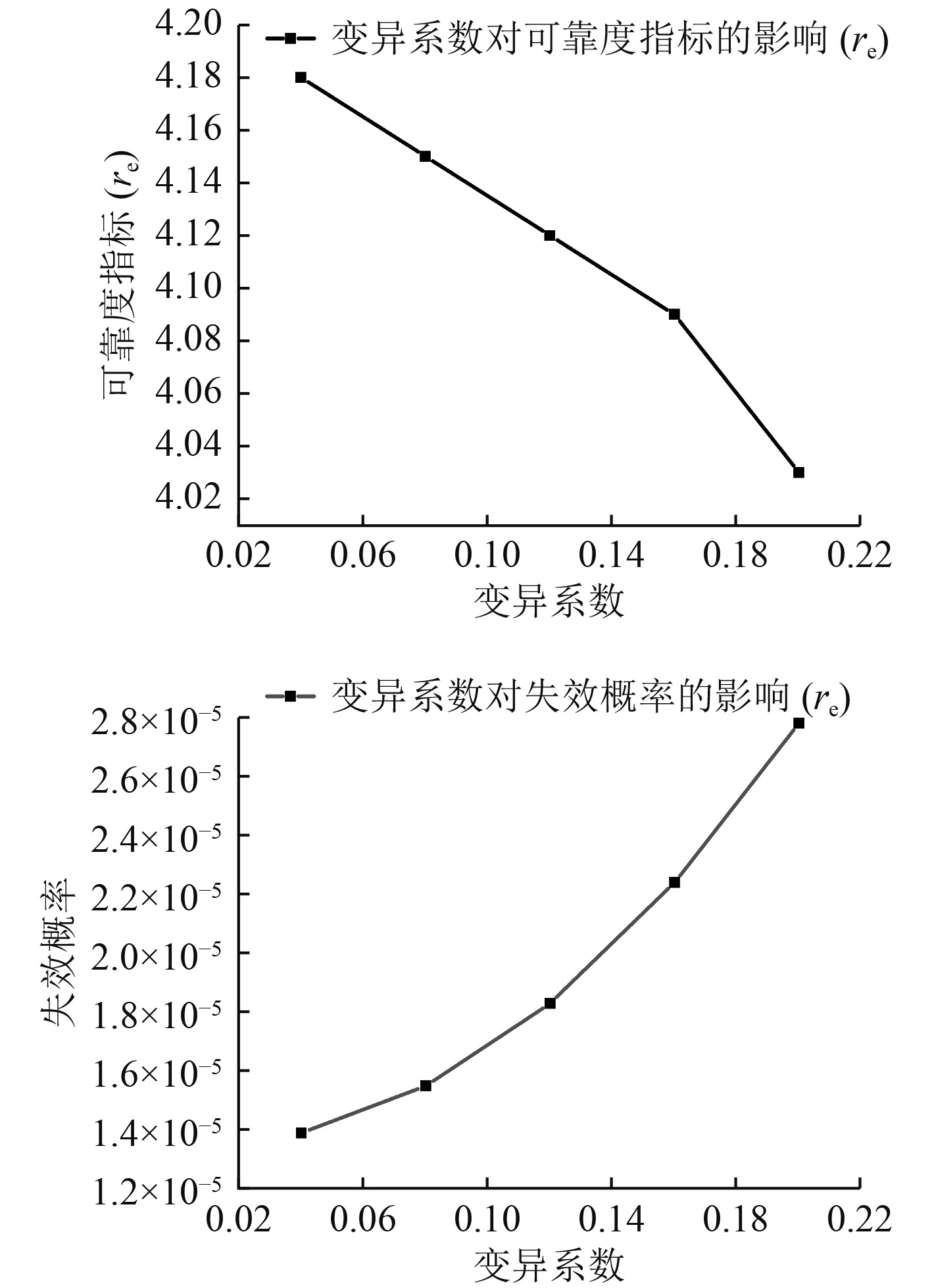
图 8
随机变量
|
|
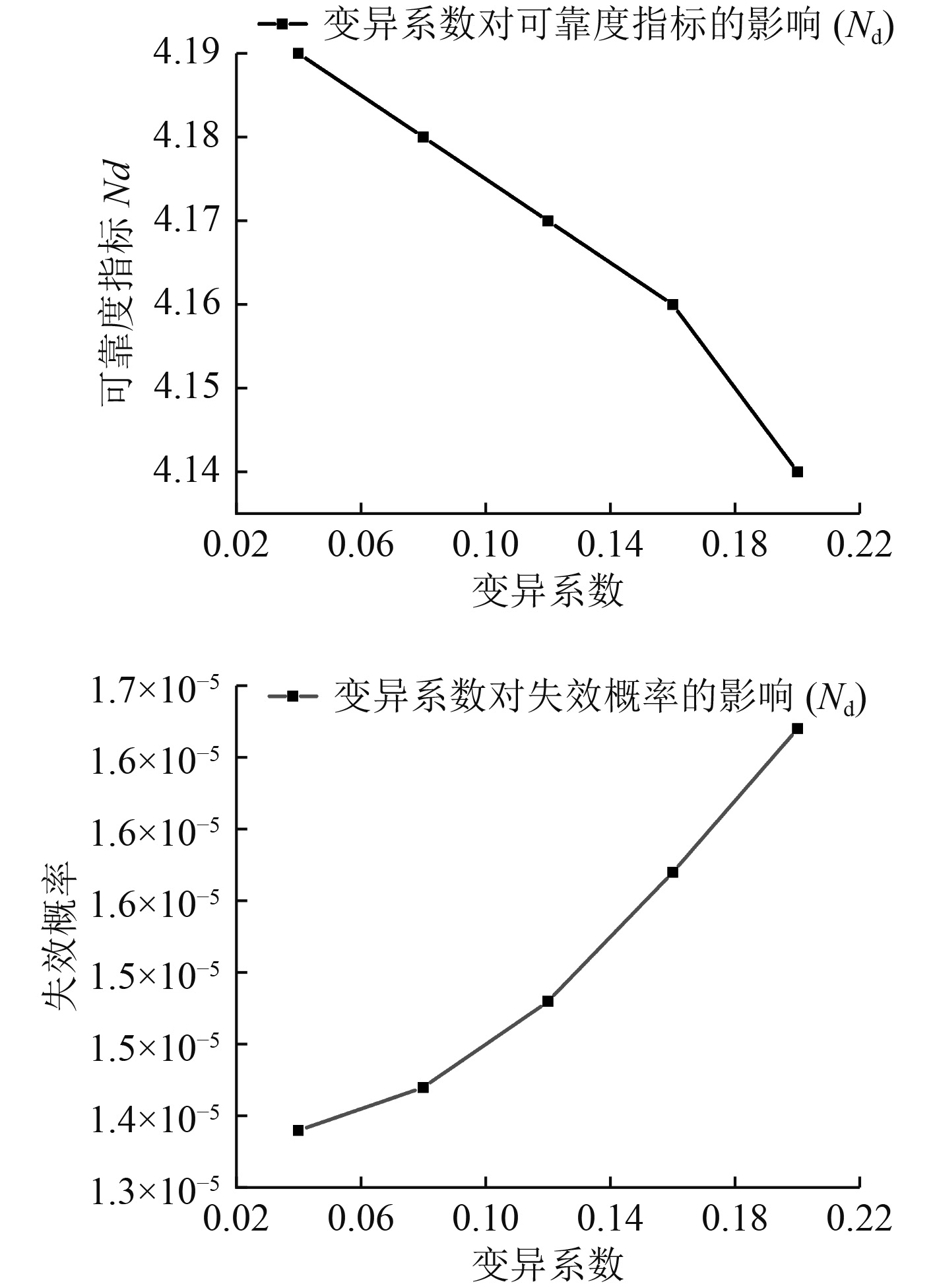
图 9
随机变量
|
由以上结果可知,材料参数A、最大应力
小裂纹扩展过程中的主要影响参数即裂纹闭合水平k,其变异系数从0.16过渡到0.2时,失效速率有进一步增长趋势。其原因可能是,变异系数的改变导致了裂纹扩展速率的增加,进而影响了可靠度的变化。又考虑到,在低周疲劳中的结构70%以上寿命用于小裂纹扩展阶段,因此提出一个包含小裂纹扩展的疲劳可靠性分析模型十分必要。
3 结 语本文基于断裂力学疲劳裂纹扩展理论以及可靠性理论,分别建立了改进McEvily疲劳裂纹扩展公式和Paris疲劳裂纹扩展公式的可靠性计算模型。对提出的计算模型采用了一次二阶矩的验算点法作为可靠性的计算方法。对载人潜水器钛合金材料疲劳裂纹扩展的可靠度指标及参数敏感性进行了计算及分析,得到以下结论:
1)基于改进McEvily裂纹扩展可靠性计算模型,经计算得到可靠度指标
2)基于改进McEvily裂纹扩展模型下的极限状态方程,对模型中随机变量的参数进行了灵敏度分析。不确定材料参数m、初始裂纹尺寸
| [1] |
WIRSCHING P H. Application of reliability methods to fatigue analysis and design [M]. 2006.
|
| [2] |
X.P.HUANG W C C. A general constitutive relation for fatigue crack growth analysis of metal structures [J]. 金属学报(英文版), 16(5): 342−54.
|
| [3] |
CUI, W-C. A feasible study of fatigue life prediction for marine structures based on crack propagation analysis [J]. Proceedings of the Institution of Mechanical Engineers Part M Journal of Engineering for the Maritime Environment, 217(1): 11−23.
|
| [4] |
NEWMAN J A, PIASCIK R S. Interactions of plasticity and oxide crack closure mechanisms near the fatigue crack growth threshold [J]. International Journal of Fatigue, 26(9): 923−7.
|
| [5] |
ISHIHARA S, MCEVILY A J. Analysis of short fatigue crack growth in cast aluminum alloys [J]. International Journal of Fatigue, 24(11): 1169−74.
|
| [6] |
李向阳, 崔维成, 张文明. 钛合金载人球壳的疲劳寿命可靠性分析[J]. 船舶力学, 2006, 10(2): 82-6. DOI:10.3969/j.issn.1007-7294.2006.02.011 |
| [7] |
李向阳, 崔维成, 张文明, 等. 一种改进的疲劳裂纹扩展表达式[J]. 船舶力学, 2006, 10(1): 54-61. DOI:10.3969/j.issn.1007-7294.2006.01.008 |
| [8] |
XIANG-YANG L I, CUI W C, ZHANG W M, et al. A modified constitutive relation for fatigue crack growth[J]. Journal of Ship Mechanics, 2006, 10(1): 54-61. |
| [9] |
王一飞, 王燕舞, 吴晓源, 等. 有效应力强度因子范围门槛值与载荷比关系的研究[J]. 船舶力学, 2008, 12(3): 440-53. DOI:10.3969/j.issn.1007-7294.2008.03.012 |
| [10] |
ISHIHARA S, MCEVILY A J. On the early initiation of fatigue cracks in the high cycle regime [C]. Proceedings of the 12th International Conference on Fracture, ICF12, F, 2009.
|
| [11] |
李旭东, 张连峰, 朱武峰, 等. 铝合金高温低周疲劳裂纹扩展可靠性评估[J]. 装备环境工程, 2013(5): 134-8. |
| [12] |
罗广恩, 崔维成. 基于改进McEvily模型的深海结构表面裂纹疲劳扩展模拟 [J]. 船舶力学, 2013(6): 645−55.
|
| [13] |
许斐然罗, 沈言. 基于改进McEvily模型的结构压-压疲劳寿命预测方法[J]. 舰船科学技术, 2018, 40(23): 61-67. |
| [14] |
康健左, 师小红. 康健, 等. McEvily公式的改进及其在疲劳扩展寿命评估中的应用[J]. 军械工程学院学报, 2007(1): 35-38. |
 2021, Vol. 43
2021, Vol. 43
