2. 河南省水下智能装备重点实验室 河南 郑州 450015;
3. 中国海洋大学 机械电子工程学院,山东 青岛 266003
2. Henan Key Laboratory of Underwater Intelligence Equipment, Zhengzhou 450015, China;
3. Department of Mechanical and Electrical Engineering, Ocean University of China, Qingdao 266003, China
橡胶减震器是发射装置重要组成部分,布置在发射筒的周向环形空间,起到气密、导向、适配、减震等作用。发射装置减震器一般采用橡胶等材质,工作过程需要承受长时间预压,间歇式瞬态大能量冲击载荷作用。橡胶除了具有明显的超弹性外,还具有蠕变等时间、温度相关的粘弹性力学特性。橡胶长时间压缩下力学性能的变化,影响减震器长期贮存使用寿命问题,以及发射过程的安全性。
蠕变研究的是材料“长期使用性能”,即形变、应力随时间和温度变化的现象与过程,是材料静态粘弹性的基本表现。由于问题的复杂性和特殊性,工程一般多采用试验方式分析橡胶减震器的蠕变性能[1-3],但试验往往有一定的离散性,且长时间蠕变试验周期过长、成本大,很难得出规律性结论。在仿真应用方面,目前常采用Kelvin模型、Burgers模型和标准线性固体模型等线性机械模型描述材料的蠕变行为,但这些本构模型往往都有一定的局限性。近些年随着非线性粘弹性材料的研究急剧增加,非线性粘弹性理论不断得到完善,对非线性粘弹性本构模型的研究取得了大量的进展。Hanyga[4]、高庆等[5]研究了材料的多重积分型本构模型,但多重积分型本构方程由于应力、应变关系式过于复杂,本构模型参数不能从试验中直接确定,难以在工程上推广应用;幂律关系型本构关系函数数形式简单、数值实现方便,在蠕变变形范围小的工况中应用广泛[6];Bemstein,Kearsley和Zapas[7-8]依据Green-Rivlin,Coleman和Noll理论,详尽地研究了有限变形的应力松弛问题,推导了不可压缩固体和流体的非线性粘弹性本构关系,建立了BKZ理论;Christensen将非线性橡胶弹性理论扩展到了非线性粘弹性的情况,提出了一种适用于不可压缩橡胶类材料的非线性粘弹性理论。Luo[9-12]根据工程学原理,引入损伤函数,在超弹性本构的基础上,通过蠕变/松弛强度系数和蠕变/松弛软化系数描述橡胶材料的蠕变特性。工程中实测获得的工程对象随时间的响应(如载荷、变形位移等)隐式地蕴含着材料的本构信息,即工程对象的应力-应变本构关系和模型参数,学者们应用不同系统识别模拟工具,针对本构模型选择(模型辨识)及其参数确定等问题进行研究[13]。
本文开展减震器材料静态力学以及48 h变载压缩蠕变试验,构建基于损伤函数的时变蠕变本构模型,利用abaqus/UHYPER用户子程序接口对本构模型进行二次开发,完成本构模型参数识别。为更好地描述橡胶减震器蠕变损伤的力学特性,采用Von Mises屈服准则来评估橡胶材料的蠕变残余变形,建立一种考虑永久变形的修正蠕变本构模型。
1 试验研究 1.1 静态力学试验静态力学试验的目的是获取橡胶材料在单轴拉伸、等双轴拉伸及平面拉伸变形下的应力-应变关系,并拟合得到相应的本构模型参数。
试验设备包括电子万能试验机(型号WDW-10)、激光引伸仪(型号LE-05)裁刀、试样基板、游标卡尺等。试验温度保持在常温恒温(23 ℃ ± 2°环境温度)。试验件与试验过程、应力应变曲线,如图1所示。
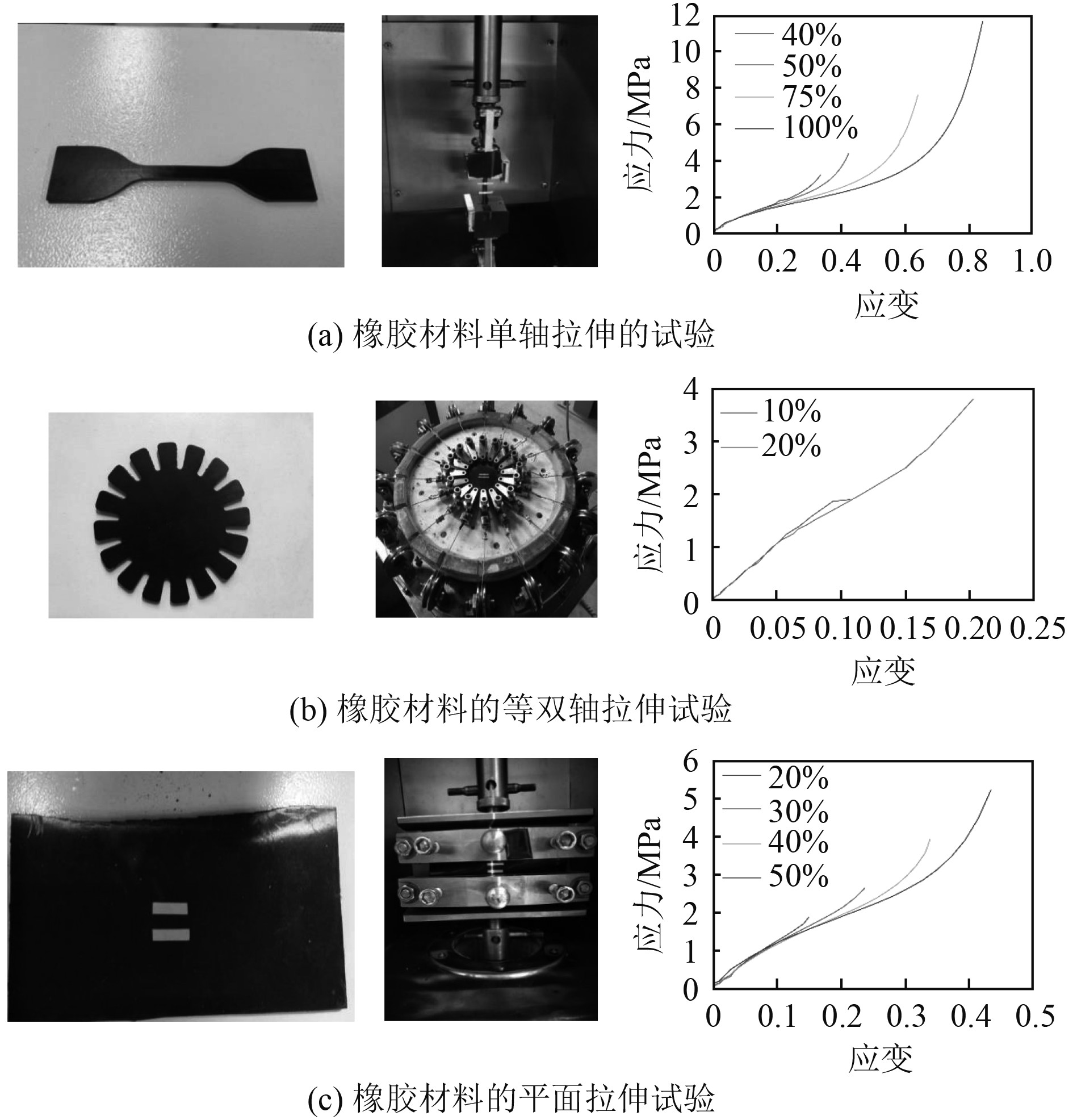
|
图 1 橡胶材料的静态力学性能试验 Fig. 1 Static mechanical properties test of rubber materials |
时变蠕变力学试验参考国家标准《GB19242-2003硫化橡胶在压缩或剪切状态下蠕变的测定》进行,试验设备与橡胶材料静态力学性能试验设备相同。具体试验流程为:将橡胶材料试样放置于实验机夹具正中心,调整试验机,使夹具刚好与橡胶材料试样接触并且处于不受力状态,调节压缩试样变形至中等变形,再返回原位,重复几次,完成机械调节。机械调节的全过程在标准室内温度下进行,机械调节在试验之间间隔最长不超过48 h。机械调节结束后,开始正式试验,在不超过15 s的时间内施加全力于试样上,并且不明显过量;达到满负荷力之后,在不同的时间测定试样的变形,这个力在整个试验过程中保持恒定,力保载即48 h。橡胶材料的压缩蠕变试验外载荷分别取为1000 N,1500 N。对于橡胶材料,仅进行常温压缩蠕变试验。在试验过程中,记录橡胶材料在不同加载条件下的蠕变试验数据(时间、变形及载荷)。
橡胶试样在不同加载水平下的蠕变试验结果,如图2所示。
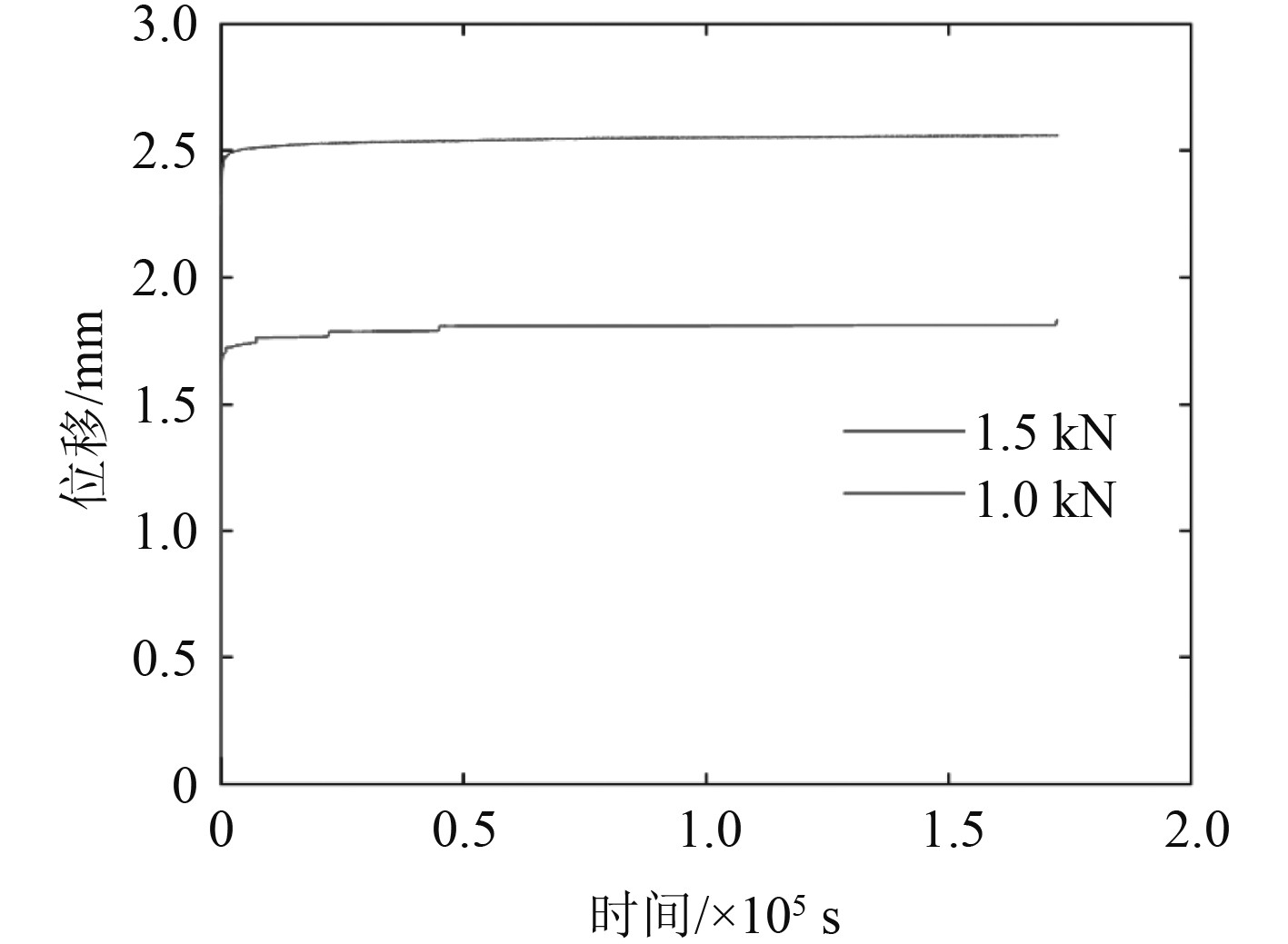
|
图 2 橡胶试件不同加载水平下蠕变试验结果 Fig. 2 Creep test results of rubber specimens under different loading levels |
由图2可知,随着时间的增加,橡胶材料的蠕变曲线斜率逐渐减小,表明橡胶的蠕变变形速率随着时间的增加而逐渐变慢。
2 材料本构模型及参数辨识 2.1 超弹性本构模型橡胶材料的静态力学特征可采用基于应变能函数的超弹本构模型来描述。基于应变不变量表示的连续介质唯象模型可写成:
| $ {W_{hyper}} = W\left( {\overline I } \right) + W\left( J \right) \text{。} $ | (1) |
式中:
| ${\bar I_1} = \bar \lambda _1^2 + \bar \lambda _2^2 + \bar \lambda _3^2 \text{,}$ | (2) |
| ${\bar I_2} = \bar \lambda _1^{ - 2} + \bar \lambda _2^{ - 2} + \bar \lambda _3^{ - 2} \text{。}$ | (3) |
式中:
| $J = \sqrt {\det (B)} = \det (F) \text{。}$ | (4) |
式中,F为变形梯度张量,计算如下式:
| $F{\rm{ = }}\left\{ {\begin{array}{*{20}{c}} {{\rm{1 + }}\dfrac{{\partial {u_1}}}{{\partial {x_1}}}}&{\dfrac{{\partial {u_1}}}{{\partial {x_2}}}}&{\dfrac{{\partial {u_1}}}{{\partial {x_3}}}} \\ {\dfrac{{\partial {u_2}}}{{\partial {x_1}}}}&{{\rm{1 + }}\dfrac{{\partial {u_2}}}{{\partial {x_2}}}}&{\dfrac{{\partial {u_2}}}{{\partial {x_3}}}} \\ {\dfrac{{\partial {u_3}}}{{\partial {x_1}}}}&{\dfrac{{\partial {u_3}}}{{\partial {x_2}}}}&{1 + \dfrac{{\partial {u_3}}}{{\partial {x_3}}}} \end{array}} \right\} \text{。}$ | (5) |
根据式(1)可推导出不同的超弹本构模型,其中多项式模型被广泛应用于预测橡胶材料在外荷载激励下的力学响应。多项式模型可写为:
| $ \begin{split} {W_{hyper}} =& \sum\limits_{i + j = 1}^N {{C_{ij}}{{\left( {{{\overline I }_1} - 3} \right)}^i}} {\left( {{{\overline I }_2} - 3} \right)^j} +\\ &\sum\limits_{i = 1}^N {\frac{1}{{{D_{ij}}}}{{\left( {{J_{el}} - 1} \right)}^{2i}}} \text{,} \end{split} $ | (6) |
式中:Cij,Dij为橡胶材料的超弹系数,可通过橡胶的超弹力学试验来确定。
对于式(6)取前两项,则可得目前有限元计算中应用最广泛的Mooney-Rivlin模型,其表达式为:
| $ \begin{split} {W_{hyper - MN}} = &{C_{10}}\left( {{{\overline I }_1} - 3} \right) + {C_{01}}\left( {{{\overline I }_2} - 3} \right) + \\ &\frac{1}{{{D_1}}}{\left( {{J_{el}} - 1} \right)^2} \text{。} \end{split} $ | (7) |
超弹本构模型可用于分析橡胶材料的静力学特性,但其与时间效应无关,无法描述橡胶的粘弹性特性。为了评估橡胶材料在常量载荷作用下的蠕变效应,需对传统超弹本构模型进行修正。引入带有损伤意义的蠕变函数Wc-r,将橡胶材料的蠕变变形与时间相连,并假设蠕变变形与应变不变量
| ${W_{hyper}} = W\left( {\overline I } \right) + W\left( J \right) + {W_{c - r}} \text{。}$ | (9) |
为描述时变损伤效应,构建幂函数形式的蠕变损伤函数,其具体表达式为[10-13]:
| ${W_{c{\rm{ - r}}}} = {k_1}\left( T \right){t^{{r_1}\left( T \right)}}({\overline I _1} + {\overline I _2}) \text{。}$ | (10) |
从数学角度考虑,式(8)为连续函数;从工程学方面考虑,式(9)提出的蠕变函数其参数均具有物理含义。其中T为荷载加载结束时刻的时间,k表征蠕变的损伤幅值,代表蠕变强度,r为衰减系数,描述了损伤随时间衰减的程度。
2.3 本构模型参数识别从本质上来说,式(8)提出的唯象蠕变本构模型是修正的超弹性本构模型,因此超弹性本构模型参数识别的准确度极为重要。根据最小二乘原理,利用橡胶材料的单轴拉伸、等双轴拉伸、平面拉伸试验数据,拟合得到本构模型参数。文献[14]提出采用拟合优度
| ${{{R}}^2} = 1{\rm{ - }}{\sum\limits_{i = 1}^n {\left( {{P_{\rm{i}}} - \mathop P\limits^ - } \right)} ^2}\Biggr/\sum\limits_{i = 1}^n {\left( {\mathop {{P_i}}\limits^ - - {P_i}} \right)} \text{。} $ | (11) |
式中:
|
|
表 1 橡胶材料超弹性本构模型参数 Tab.1 Parameters of hyperelastic constitutive model for rubber materials |
为进一步验证模型参数的准确性,通过Abaqus有限元软件,对橡胶材料的静态力学特性进行数值模拟。根据试样尺寸,建立橡胶试件的轴对称几何模型(Φ29 mm×12.5 mm),模型的上端与解析刚体相连,并在橡胶与刚体之间进行自由度耦合设置。采用CAX4HT单元对模型进行网格划分,有限元模型如图3所示。

|
图 3 橡胶试件有限元模型 Fig. 3 Finite element model of rubber specimen |
将数值模拟的静态压缩特性与试验结果进行对比,如图4所示。
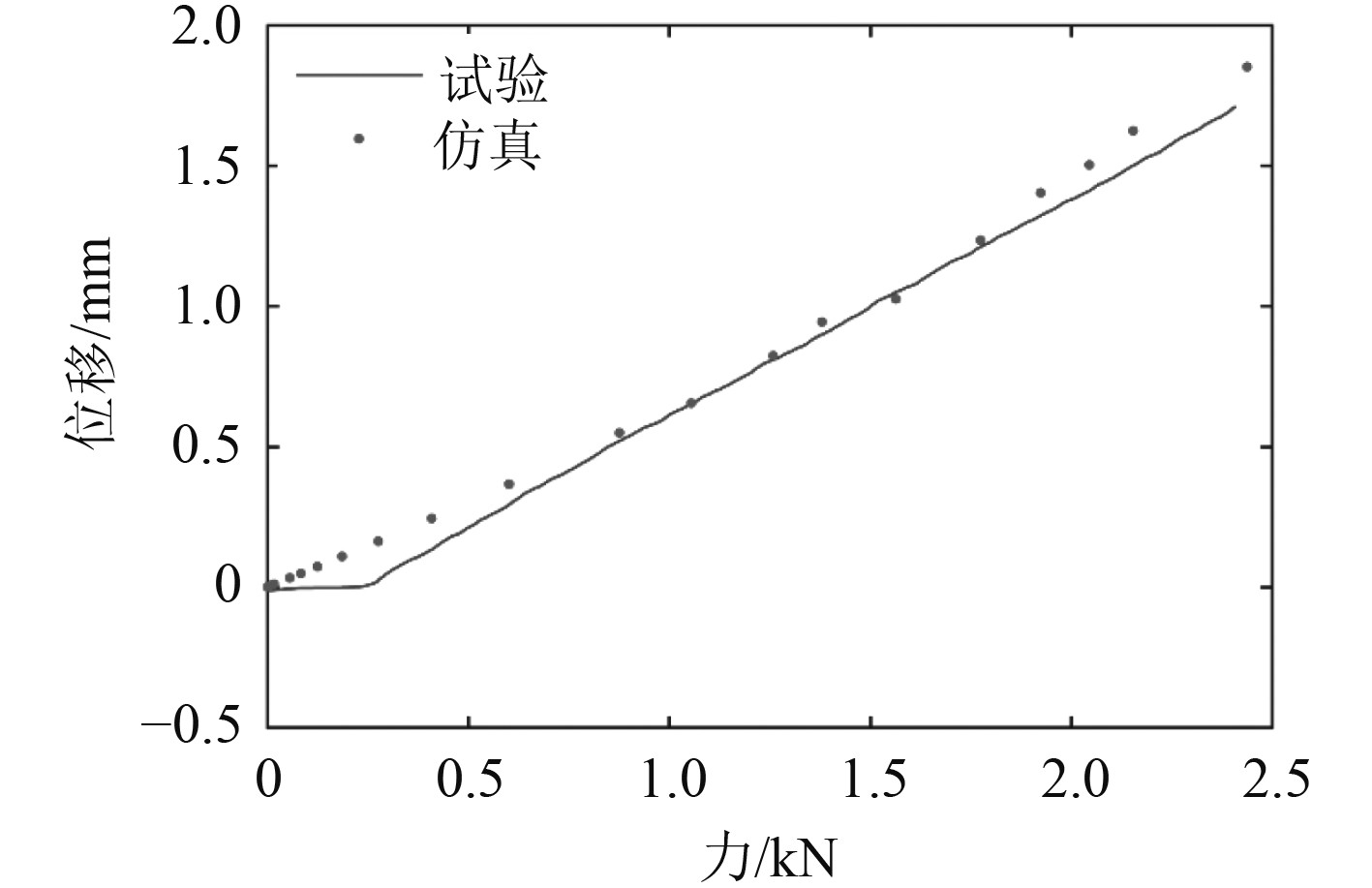
|
图 4 橡胶材料静态压缩试验与仿真结果对比 Fig. 4 Comparison of static compression test and simulation results of rubber materials |
由图4可知,试验与仿真结果吻合度较好,这说明超弹本构模型及参数选取合理,能够表征橡胶在加载阶段的非线性弹性特性,数值模拟精度良好。
基于式(10),利用Abaqus用户自定义子程序UHYPER,将提出的蠕变本构模型通过Fortran语言进行编译,并将编译的子程序与有限元软件进行关联,开展橡胶材料的蠕变数值模拟。参照压缩蠕变的试验过程,仿真分析2种加载水平(1.0 kN和1.5 kN)下48 h的时变蠕变行为。
为明确蠕变本构参数对蠕变特性的影响程度,开展参数敏感性分析,敏感性范围定为±20%。具体分析过程为:1)选择一组蠕变参数作为参考参数,这里选取常温1.5 kN作用下的橡胶蠕变参数(k0,r0)作为参考值;2)改变一个蠕变参数的数值并保持另一个蠕变参数数值不变,分析时变蠕变变形的变动范围,如图5所示。

|
图 5 幂指数蠕变本构模型参数敏感性分析 Fig. 5 Parameter sensitivity analysis of power exponent creep constitutive model |
不断调整蠕变参数k和r,使仿真结果与试验得出时间-蠕变变形误差变小;分别对不同加载水平(1000 N和1500 N)的时间-蠕变变形试验数据进行拟合,最终得出蠕变参数拟合结果(见表2)。
|
|
表 2 橡胶蠕变参数拟合结果(23 ℃) Tab.2 Fitting results of rubber creep parameters(23 ℃) |
为考察时变蠕变本构模型及参数的模拟精度,与橡胶试件不同载荷下的时间-蠕变变形进行对比。结果表明,试验与仿真预测结果吻合度较好(见图6)。
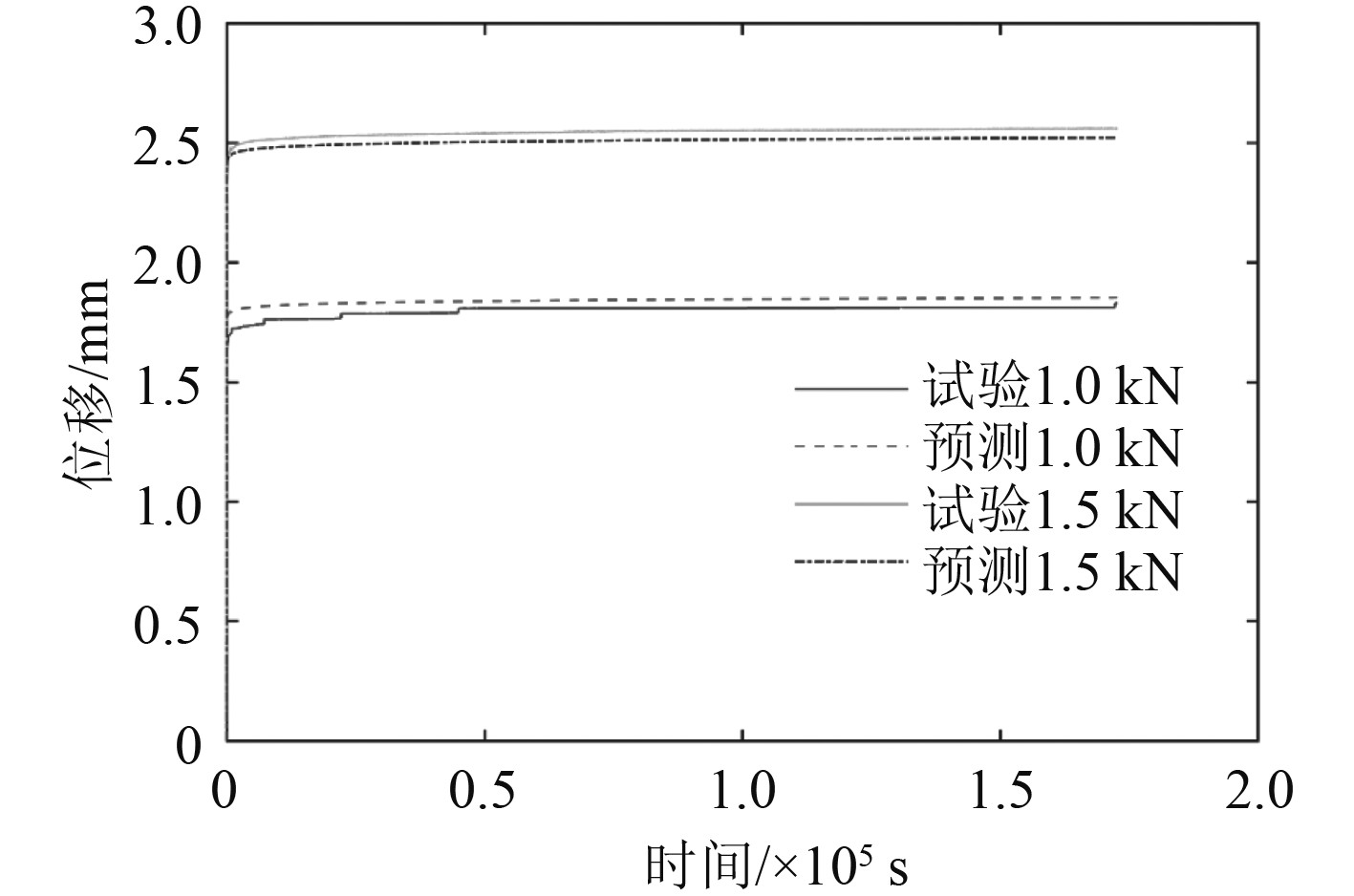
|
图 6 橡胶试件时间-变形仿真与试验结果对比 Fig. 6 Comparison of time deformation simulation and experimental results of rubber specimen |
为了详细地说明时变蠕变变形规律,图7对比了仿真得出的不同时刻橡胶材料的轴向蠕变变形。在蠕变过程中,橡胶材料的变形随时间增加呈现非线性的变化特性。

|
图 7 橡胶试件轴向蠕变变形分布 Fig. 7 Distribution of axial creep deformation of rubber specimens |
由图7可见,橡胶的轴向变形云图呈现分层的现象:在材料底部,由于受到边界条件的限制,变形量近似为0;在材料顶部,由于载荷条件的影响,变形量最大;而在其他区域,变形是逐渐变化的。这种蠕变变形的分层现象并未因蠕变时间的改变而发生变化。此外,材料的最大蠕变变形随着时间的增加而增大,材料自由表面的膨胀效应也随着时间的推移而愈发明显。
在超弹性本构模型的基础上引入蠕变损伤函数,构建的时变蠕变本构模型,很好描述了橡胶材料的压缩蠕变性能。
3 减震器蠕变性能分析建立橡胶减震器的有限元模型,如图8所示。模型上端与解析刚体相接触,下端与刚性体连接,采用具有6个自由度的C3D8HT单元对模型进行网格划分。载荷沿橡胶减震器垂直方向施加于上端解析刚体上,并通过刚体与橡胶器件之间的自由度耦合传递至器件。为了防止解析刚体与橡胶材料相互渗透,对接触区域进行面与面接触设置。

|
图 8 橡胶减震器有限元模型 Fig. 8 Finite element model of rubber shock absorber |
在橡胶减震器上表面加载2.1 t的载荷,橡胶减震器在在室温条件下48 h蠕变过程中的应力分布云图(见图9)。

|
图 9 橡胶减震器在不同时刻的应力分布云图 Fig. 9 Stress distribution nephogram of rubber shock absorber at different times |
橡胶减震器在蠕变过程中的位移分布云图,如图10所示。

|
图 10 橡胶减震器在不同时刻的位移分布云图 Fig. 10 Displacement distribution nephogram of rubber shock absorber at different times |
由图9和图10可知,在蠕变过程中橡胶减震器的应力最大值始终出现在器件的外侧位置;橡胶器件与材料的分布云图相似,均出现了分层现象,但器件的分层变形不如材料的明显,这是由于器件结构效应引起的。随着蠕变时间的增加,减震器的蠕变变形也在不断增加,橡胶减震器蠕变行为的时间-蠕变变形曲线如图11所示。
|
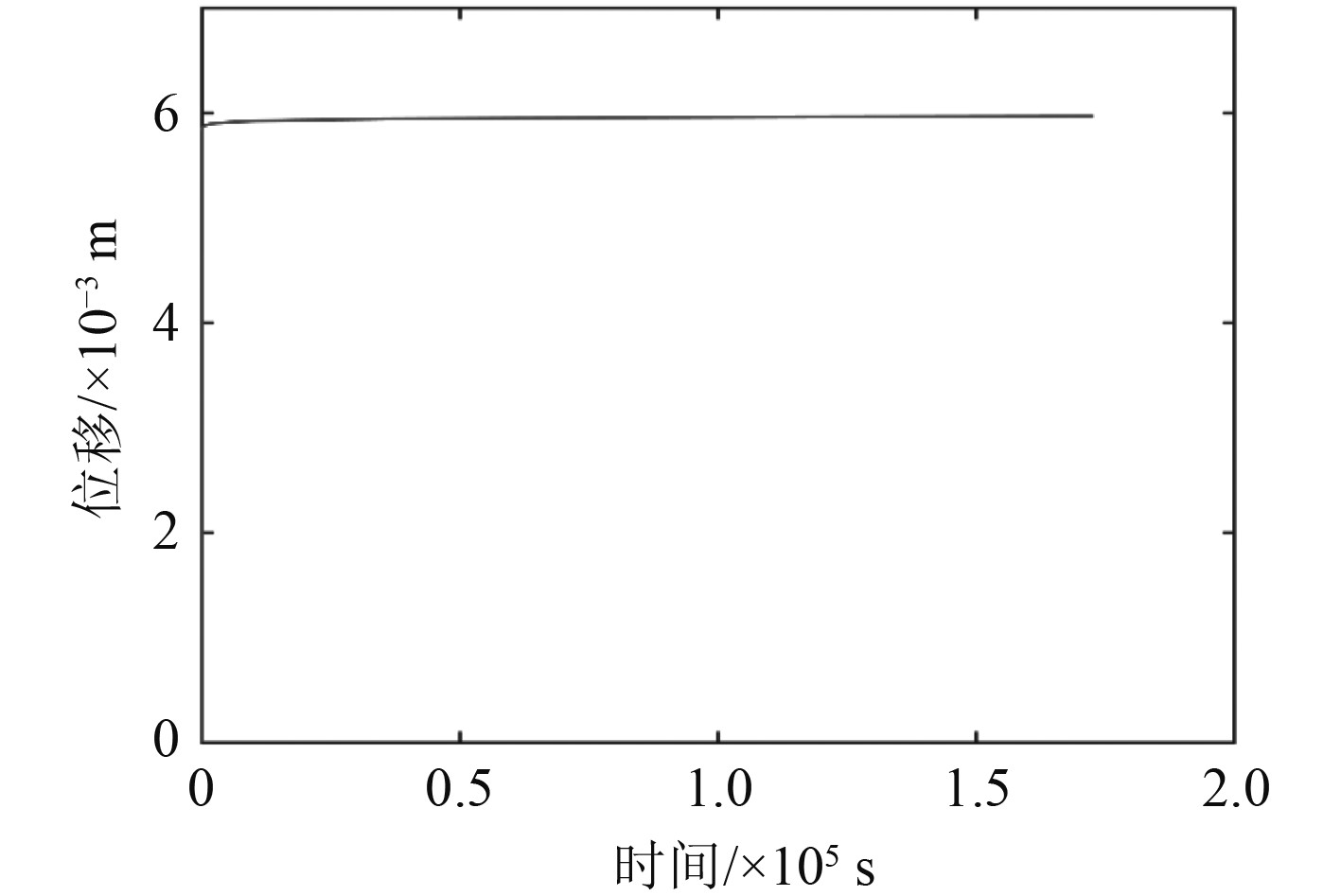
图 11 橡胶减震器时间-蠕变变形曲线 Fig. 11 Time creep deformation curve of rubber shock absorber |
由图11可知,橡胶减震器在15 s时的蠕变变形为5.43 mm,48 h后蠕变变形达到5.97 mm,在整个时变过程中,蠕变变形较为平缓。
为了描述橡胶减震器在蠕变条件下的损伤永久变形,我们对时变蠕变本构模型进行进一步扩展,采用Von Mises屈服准则来评估橡胶材料的蠕变残余变形,提出一种考虑永久变形的修正蠕变本构模型,其表达式为:
| ${W_{hyper}} = W(I){\rm{ + }}W(J) + {W_{creep}} + {W_{VonMises}} \text{,}$ | (12) |
式中,基于屈服准则的分段本构方程为:
| $\left\{ {\begin{array}{*{20}{l}} {{\sigma _p} = {K_p}\varepsilon } \text{,}&{{\sigma _p} \leqslant {\sigma _{y0}}} \text{,}\\ {{\sigma _p} = {\sigma _{y0}} + H_0^{'}\left( {\varepsilon - {\varepsilon _{y0}}} \right)} \text{,}&{{\sigma _{y0}} \leqslant {\sigma _p} \leqslant {\sigma _{y1}}} \text{,}\\ {{\sigma _p} = {\sigma _{y1}} + H_1^{'}\left( {\varepsilon - {\varepsilon _{y1}}} \right)} \text{,}&{{\sigma _{y1}} \leqslant {\sigma _p} \leqslant {\sigma _{y1}}} \text{,}\\ {{\sigma _p} = {\sigma _{y2}} + H_2^{'}\left( {\varepsilon - {\varepsilon _{y2}}} \right)} \text{,}&{{\sigma _{y2}} \leqslant {\sigma _p}} \text{。} \end{array}} \right.$ | (13) |
式中:
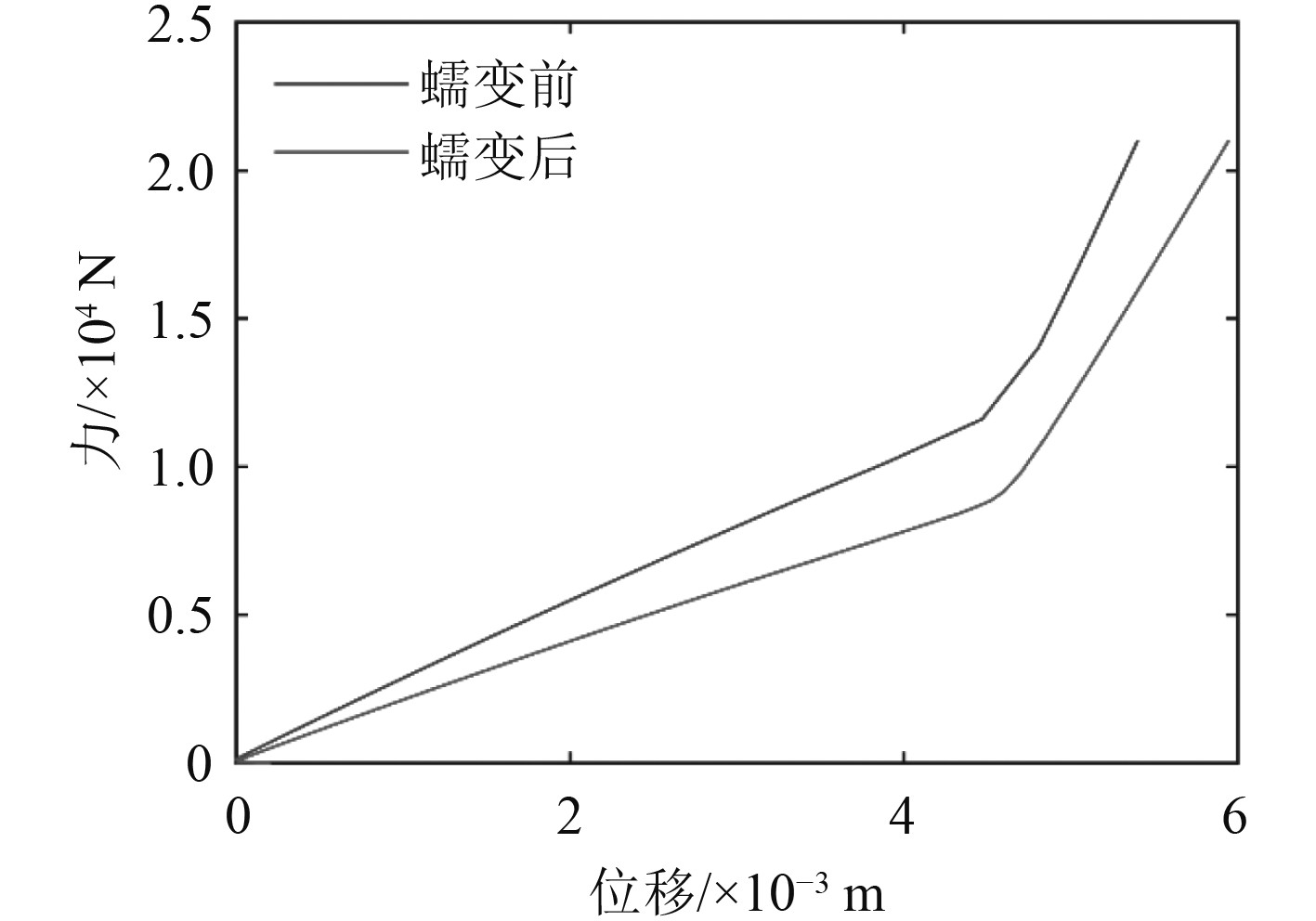
橡胶器件蠕变前后的刚度变化,如图12所示。
|
图 12 橡胶器件蠕变前后刚度对比 Fig. 12 Comparison of stiffness of rubber components before and after creep |
由图12可知,当位移为5 mm时,减震器未蠕变前的承载为17 045.4 N,引入蠕变损伤后的器件承载力为13 430.2 N,降低了21.2%。定义等效刚度为:
| $E{\rm{ = }}\frac{{\Delta F}}{{\Delta x}}\text{。}$ | (14) |
其中,
橡胶减震器蠕变前与损伤蠕变后静态变形不同位移处的应力分布云图,如图13所示。

|
图 13 蠕变前后不同位移处应力分布云图 Fig. 13 Nephogram of stress distribution at different displacements before and after creep |
由图13可知,减震器在考虑蠕变损伤效应后,其静态变形的最大应力呈现退化趋势。当静态位移为1 mm时,蠕变前与蠕变后的应力最大值分别为0.41 MPa和0.17 MPa;当位移为3 mm时,蠕变前/后的应力最大值分别为1.10 MPa和0.67 MPa;当位移为5 mm时,蠕变前/后的应力最大值分别为1.80 MPa和1.33 MPa。
4 结 语本文开展了减震器橡胶材料在1000 N和1500 N两种载荷水平下48 h蠕变试验研究,通过对蠕变试验数据分析,可以得出以下结论:
1)在超弹性本构模型的基础上,引入损伤意义的蠕变函数,将荷载引起的橡胶材料的蠕变与时间相连,构建了时变蠕变本构模型;采用Von Mises屈服准则来评估橡胶材料的蠕变残余变形,提出一种考虑永久变形的修正蠕变本构模型。
2)通过Abaqus/UPYPER用户子程序,将橡胶材料的时变蠕变本构模型用Fortran语言编译,构建了橡胶材料及减震器蠕变性能仿真分析模型。
3)对不同载荷水平下的橡胶材料的蠕变试验曲线对比,仿真与实验结果吻合度较好,说明时变蠕变本构模型很好的描述了橡胶材料的蠕变性能,且预测精度满足工程应用。
4)通过橡胶减震器48 h压缩蠕变试验与仿真结果对比,验证了方法的可行性。
| [1] |
束立红, 何琳. 聚氨酯隔振器蠕变特性力学模型试验研究[J]. 噪声与振动控制, 2012, 32(2): 147-150. SHU L H, HE L. Mechanical model for creep performance testing and analysis of polyurethane isolator[J]. Noise and Vibration Control, 2012, 32(2): 147-150. |
| [2] |
刘迪辉, 范迪, 欧阳雁峰, 等. 温度对橡胶隔振器力学性能的影响[J]. 噪声与振动控制, 2014, 34(3): 203-206. LIU D H, FAN D, OUYANG Y F, et al. Temperature effect on mechanical properties of rubber isolators[J]. Noise and Vibration Control, 2014, 34(3): 203-206. |
| [3] |
杭超, 范勇军, 苏尔敦, 等. 不同环境温度下橡胶隔振器振动性能研究[J]. 科学技术与工程, 2017, 17(2): 135-139. HANG C, FAN Y J, SU E D, et al. Research on dynamic character of rubber vibration isolator within different temperature range[J]. Science Technology and Engineering, 2017, 17(2): 135-139. |
| [4] |
A. HANYGA, M. SEREDYFISKAB.. Multiple-integral viscoelastic constitutive equations[J]. International Journal of Non-Linear Mechanics, 2007, 42(5): 722-732. |
| [5] |
高庆, 林松, 杨显杰. 丁基橡胶粘弹性材料的非线性蠕变本构描述[J]. 应用力学学报, 2007, 24(3): 386-390. GAO Q, LIN S, YANG X J. Constitutive description for nonlinear creep behavior of viscoelastic material buty1[J]. Chinese Journal of Applied Mechanics, 2007, 24(3): 386-390. |
| [6] |
康永刚, 张秀娥. 修正的高分子材料蠕变模型[J]. 材料科学与工程学报, 2013, 31(6): 924-928. KANG Y G, ZHANG X E. Modified creep models for polymer materials[J]. Journal of Materials Science & Engineering, 2013, 31(6): 924-928. |
| [7] |
W. N. FINDLEY, J. S. LAI, K. ONARAN. Creep and relaxation of nonlinear viscoelastic materials[M]. North Holland Publishing Company, 1976.
|
| [8] |
CHRISTENSEN. R. M.. A comprehensive theory of yielding and failure for isotropic materials[J]. Journal of Engineering Materials and Technology, 2007, 129(2): 173-181. |
| [9] |
LUO Robert Keqi, ZHOU Xiaolin, Jinfeng. Numerical prediction and experiment on rubber creep and stress relaxation using time-dependent hyperelastic approach[J]. Polymer Testing, 2016, 52: 246-253. |
| [10] |
LUO R. K. simulation and experiment for rubber springs[J]. Proc IMechE Part L: J Materials: Design and Applications, 2016, 230: 681-688. |
| [11] |
LUO Robert Keqi. Creep modelling and unloading evaluation of the rubber suspensions of rail vehicles[J]. Proc IMechE Part F: J Rail and Rapid Transit, 2016, 230(4): 1071-1087. |
| [12] |
LUO Robert Keqi, WU Xiaoping, PENG Limin. Creep loading response and complete loading-unloading investigation of industrial anti-vibration systems[J]. Polymer Testing, 2015, 46: 134-143. |
| [13] |
李厚民, 束立红, 戴杰, 等. 利用参数反演预测聚氨酯隔振器的蠕变曲线[J]. 湖北工业大学学报, 2014, 29(1): 72-75. LI H M, SHU L H, DAI J, ZHANG Y. Predicting creep curve of polyurethane vibration isolator by inversion analysis method[J]. Journal of Hubei University of technology, 2014, 29(1): 72-75. |
| [14] |
胡晓玲, 刘秀, 李明. 等. 炭黑填充橡胶超弹性本构模型的选取策略[J]. 工程力学, 2014, 31(5): 34-42. HU Xiao-ling, LIU Xiu, LI Ming, et al. Selection strategies of hyperplastic constitutive models for carbon black filled rubber[J]. Engineering Mechanics, 2014, 31(5): 34-42. |
 2021, Vol. 43
2021, Vol. 43
