船舶运动数学模型是船舶运动仿真与控制问题的核心[1]。运动数学模型可以提供船舶操纵性限制条件,辅助人或系统进行路径规划,可以嵌入控制系统中以提高控制的精度,更是船舶运动模拟器的基础。
传统的建立船舶运动数学模型的方法是根据MMG模型结构[2]或者Abkowitz模型结构[3],求解其中的水动力导数。求解水动力导数的方法中,经验公式估算十分快速,但是准确性依赖于所积累的数据和船型;约束模试验数据准确,但是成本太高,也存在尺度效应问题。系统辨识可以从包含噪声的数据中建立数学模型,并且可以不依赖于经典船舶运动数学模型结构,因此成为目前主流的建模方法。传统的辨识方法如最小二乘法、极大似然法等由于精度过度依赖模型和初值,逐渐被以神经网络为代表的新型辨识方法取代。近年来,扩展卡尔曼滤波器(EKF)[4]、撑向量回归(SVR)[5]、萤火虫算法[6]、人工蜂群算法[7]、多目标群智能算法[8]等都被应用在了船舶系统辨识领域。以神经网络为代表的不依赖经典船舶数学模型结构的辨识方法要想得到准确的辨识结果,需要输入输出数据中包含船舶完整的操纵性信息。以EKF为代表的对经典船舶数学模型中的水动力导数进行辨识的方法由于已经引入了数学模型结构这一先验信息,往往需要更少的数据进行辨识,但辨识的精度十分依赖经典数学模型结构,并且存在参数漂移和动力相消[9]的问题。
扩展卡尔曼滤波器利用一阶泰勒级数将非线性项线性化,因此适用于非线性系统,也可以进行参数辨识,但是因为忽略了高阶项,在非线性较强时误差大。无迹卡尔曼滤波器[10](Unscented Kalman Filter,UKF)是无迹变换[11](Unscented Transformation,UT)与标准卡尔曼滤波器的结合,目的是为了提高非线性系统滤波的精度和效率。UKF利用UT来进行均值和协方差的非线性传递,其思想是近似非线性函数的概率分布而不是近似非线性函数。UKF相比EKF有着更高的精度,并且不用计算雅可比矩阵,因此被广泛应用于导航、目标跟踪等领域。
本文采用精度更高的UKF,结合成本相对较低的自航试验对目标三体船进行辨识。针对三体船自身特点对MMG模型结构进行化简,去掉了作用不大的水动力导数,并设计了不同的控制方式进行分步辨识,以减轻动力相消的问题。通过参数的试验测量值与辨识值的对比,验证了本文辨识出参数的准确性;通过模型预报数据与试验观测数据的对比,验证了本文建立的三体船数学模型的准确性,具有较高的工程意义和参考价值。
1 无迹卡尔曼滤波器介绍 1.1 无迹变换随机向量
| $ {\chi _i} = \left\{ {\begin{array}{l} {\bar X,i = 0}\text{,}\\ {\bar X + \left( {\sqrt {(n + \lambda ){P_{xx}}} } \right)_i^{\rm{T}},i = 1, \cdots ,n}\text{,}\\ {\bar X - \left( {\sqrt {\left( {n + \lambda } \right){P_{xx}}} } \right)_i^{\rm{T}},i = n + 1, \cdots ,2n}\text{。} \end{array}} \right. $ | (1) |
式中:
对
| $ \left\{ {\begin{array}{l} {{Y_i} = f\left( {{\chi _i}} \right),i = 0, \cdots ,2n}\text{,}\\ {\bar Y = \displaystyle\sum\nolimits_{i = 0}^{2n} {W_i^{\left( m \right)}} {Y_i}}\text{,}\\ {{P_{yy}} = \displaystyle\sum\nolimits_{i = 0}^{2n} {W_i^{\left( c \right)}} ({Y_i} - \bar Y){{({Y_i} - \bar Y)}^{\rm{T}}}}\text{,}\\ {W_0^{\left( m \right)} = \lambda /(n + \lambda )}\text{,}\\ {W_0^{\left( c \right)} = \lambda /(n + \lambda ) + 1 - {\alpha ^2} + \beta }\text{,}\\ {W_i^{\left( m \right)} = W_i^{\left( c \right)} = \lambda /\left[ {2\left( {n + \lambda } \right)} \right],i = 1, \cdots ,2n}\text{。} \end{array}} \right. $ | (2) |
式中:
为叙述方便,将上述无迹变换过程用函数
| $ \left\{ {\begin{array}{l} {\bar Y,{P_{yy}} = UT(\bar X,{P_{xx}},f)}\text{,}\\ {\bar Z,{P_{zz}} = UT(\bar X,{P_{xx}},h)}\text{,}\\ {{P_{zy}} = U{T_c}\left( {\bar X,{P_{xx}},f,h} \right) = \displaystyle\sum\nolimits_{i = 0}^{2n} {W_i^{\left( c \right)}} ({Z_i} - \bar Z){{({Y_i} - \bar Y)}^{\rm{T}}}}\text{。} \end{array}} \right. $ | (3) |
对n维离散的非线性系统,状态空间模型如下式:
| $ \left\{ {\begin{array}{*{20}{c}} {{X_k} = f\left( {{X_{k - 1}},{U_k}} \right) + {w_k}}\text{,}\\ {{Z_k} = h\left( {{X_k}} \right) + {v_k}}\text{。} \end{array}} \right. $ | (4) |
式中:
UKF的基本过程与标准卡尔曼滤波器一致,在误差协方差矩阵预报和更新时都用无迹变换来计算,递推公式如式(5)~式(8)所示。
状态估计预报、误差协方差矩阵预报:
| $ \left\{ {\begin{array}{*{20}{c}}{X}_{k|k-1},{P}_{k|k-1}^{{'}}=UT({X}_{k-1},{P}_{k-1},f)\text{,}\\ {P}_{k|k-1}={P}_{k|k-1}^{{'}}+{Q}_{k}\text{,}\end{array}} \right. $ | (5) |
滤波增益:
| $ \left\{ {\begin{array}{*{20}{c}}{Z}_{k|k-1},{P}_{zz}^{{'}}=UT\left({X}_{k|k-1},{P}_{k|k-1},h\right)\text{,}\\ {P}_{zz}={P}_{zz}^{{'}}+{R}_{k}\text{,}\\ {P}_{xz}={UT}_{c}\left({X}_{k|k-1},{P}_{k|k-1},f,h\right)\text{,}\\ {G}_{k}={P}_{xz}{{P}_{zz}}^{-1}\text{,}\end{array}} \right. $ | (6) |
状态估计更新:
| $ {X}_{k}={X}_{k|k-1}+{G}_{k}({Z}_{k}-{Z}_{k|k-1})\text{,} $ | (7) |
误差协方差矩阵更新:
| $ {P}_{k}={P}_{k|k-1}-{G}_{k}{P}_{zz}{{G}_{k}}^{T}\text{。} $ | (8) |
安装完成的目标三体船如图1所示,3个船体都采用了S标准型,其主要参数如表1所示。三体船的推进装置为船体两侧的1对螺旋桨,采用差分推力来控制前进和转向。

|
图 1 安装完成的目标三体船 Fig. 1 Installed trimaran |
|
|
表 1 船体主尺度信息 Tab.1 Main parameters of trimaran |
基于MMG模型建立目标三体船的运动数学模型结构,三自由度操纵性方程如下式:
| $ \left\{ {\begin{array}{*{20}{c}} {\left( {m + {m_x}} \right)\dot u - \left( {m + {m_y}} \right)rv = {X_H} + {X_P}}\text{,}\\ {\left( {m + {m_y}} \right)\dot v - \left( {m + {m_x}} \right)ru = {Y_H} + {Y_P}}\text{,}\\ {\left( {{I_{zz}} + {J_{zz}}} \right)\dot r = {N_H} + {N_P}}\text{。} \end{array}} \right. $ | (9) |
式中:
| $ \left\{ {\begin{array}{*{20}{c}} {{X_H} = {X_{uu}}\left| u \right|u + {X_{rr}}{r^2}}\text{,}\\ {{Y_H} = {Y_v}v + {Y_r}r}\text{,}\\ {{N_H} = {N_v}v + {N_r}r + {N_{rr}}\left| r \right|r}\text{。} \end{array}} \right. $ | (10) |
式中:
假设推力系数为进速系数的一次函数关系,如下式:
| $ \left\{ {\begin{array}{*{20}{c}} {{K_T} = {a_0} + {a_1}{J_p}}\text{,}\\ {{J_p} = \dfrac{{(1 - {w_p})u}}{{nD}}}\text{。} \end{array}} \right. $ | (11) |
式中:
单个螺旋桨的推力
| $ \left\{ {\begin{array}{*{20}{c}} {T\left( {n,u} \right) = \left( {1 - t} \right)\rho {n^2}{D^4}{K_T} = {T_{nn}}{n^2} + {T_{un}}un}\text{,}\\ {{T_{nn}} = {a_0}\rho {D^4}(1 - t)}\text{,}\\ {{T_{un}} = {a_1}\rho {D^3}(1 - t)(1 - {w_p})}\text{。} \end{array}} \right. $ | (12) |
式中:
对三体船,2个螺旋桨X方向位置与船重心X位置一致,距离船中的距离为
| $ \left\{ {\begin{array}{*{20}{c}} {{X_P} = T\left( {{n_l},u + rl} \right) + T({n_r},u - rl)}\text{,}\\ {{Y_P} = 0}\text{,}\\ {{N_P} = [T\left( {{n_l},u + rl} \right) - T({n_r},u - rl)]l}\text{。} \end{array}} \right. $ | (13) |
式中:
上述模型结构中,需要确定的参数为
构建系统状态向量
| $ { \left\{ {\begin{array}{l} {X\! \!=\!\! {{\left[ {u,\!v,\!r,\!x,\!y,\psi ,\!{X_{uu}},\!{X_{rr}},\!{Y_v},\!{Y_r},\!{N_v},\!{N_r},\!{N_{rr}},\!{T_{nn}},\!{T_{un}}} \right]}^{\rm{T}}}}\!\text{,}\\ {U = {{[{n_l},{n_r}]}^{\rm{T}}}}\text{,}\\ {Z = {{\left[ {u,v,r,x,y,\psi } \right]}^{\rm{T}}}}\text{。} \end{array}} \right.} $ | (14) |
状态转移函数和系统观测函数如下式:
| $ { \left\{ {\begin{array}{*{20}{c}} {f\left( {X,U} \right) = \left[ {\begin{array}{*{20}{c}} {u + \dot u \cdot dt}\\ {v + \dot v \cdot dt}\\ {r + \dot r \cdot dt}\\ {x + (u \cdot {\rm{cos}}\psi - v \cdot {\rm{sin}}\psi ){\rm{d}}t}\\ {y + (u \cdot {\rm{sin}}\psi + v \cdot {\rm{cos}}\psi ){\rm{d}}t}\\ {\psi + r \cdot {\rm{d}}t}\\ {{X_{uu}}}\\ \cdots \\ {{T_{un}}} \end{array}} \right]}\\ {h\left( X \right) = \left[ {{I_{6 \times 6}},{{\bf{0}}_{6 \times 9}}} \right]X} \end{array}} \right.\text{。}} $ | (15) |
其中
系统辨识过程中,可能会出现参数漂移或动力相消[9]的情况,例如在式(9)中如果
|
|
表 2 附加质量、转动惯量值 Tab.2 Added mass and moment of inertia |
为获取目标船参数辨识所需的观测数据序列,进行目标船静水中的自航试验。目标船上搭载了AHRS,GPS传感器,可以实时地获取位置、速度、姿态信息。目标船由岸上的遥控器进行操控,控制信号通过WIFI发送给船上的电机驱动器,以控制2个螺旋桨的转速。首先进行多组目标船直航试验,再进行多组目标船S型回转试验,将传感器观测数据记录下进行离线辨识。
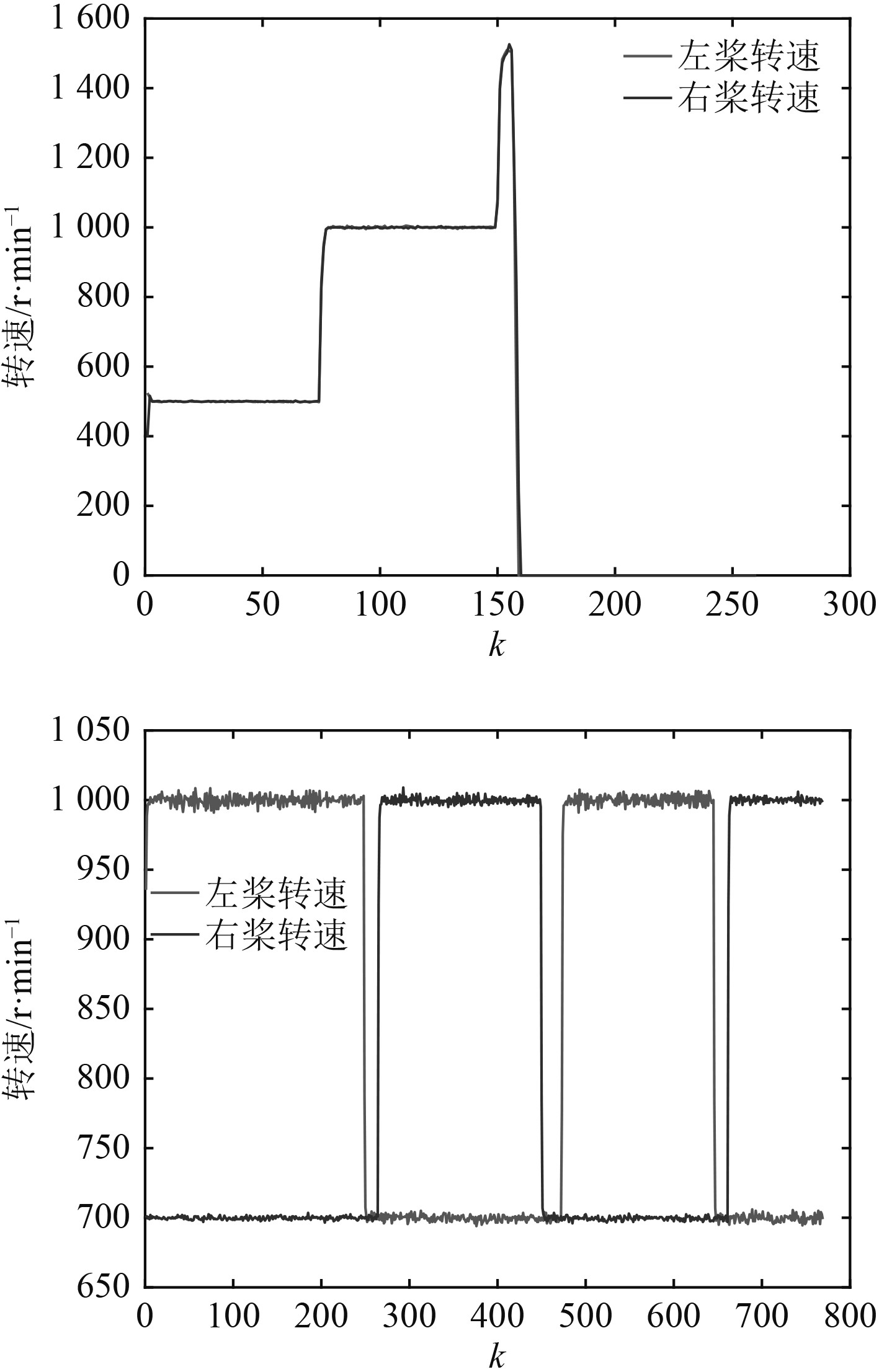
3 目标船运动数学模型辨识结果直航试验和S型回转试验螺旋桨转速信号如图2所示。将多组直航试验观测数据辨识的得到的参数
|
图 2 直航试验和S型回转试验螺旋桨转速信号 Fig. 2 Propeller speed on straight sailing test and S rotation test |
|
|
表 3 参数辨识结果 Tab.3 Results of parameter identification |
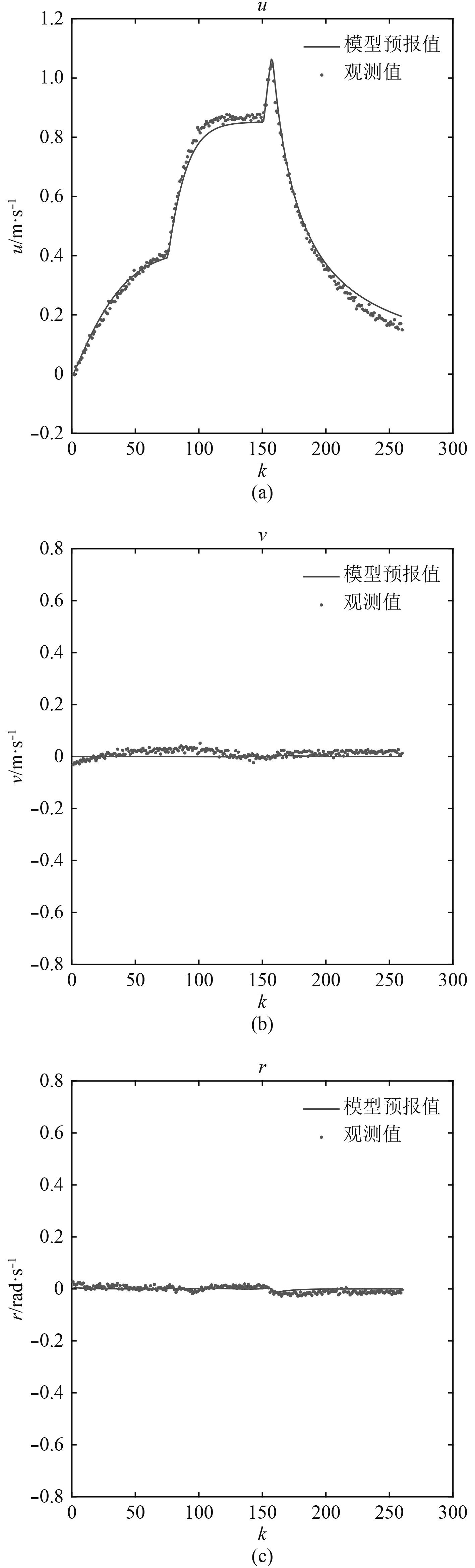
将辨识出的参数代入运动数学模型,并将模型预报的结果与实际观测数据进行比较,直航试验对比结果如图3所示,S型回转试验对比结果如图4所示。由对比结果可以得出,直航试验观测的
|
图 3 直航试验模型预报的结果与实际观测数据对比 Fig. 3 Comparison between model prediction result and observed data on straight sailing test |
|
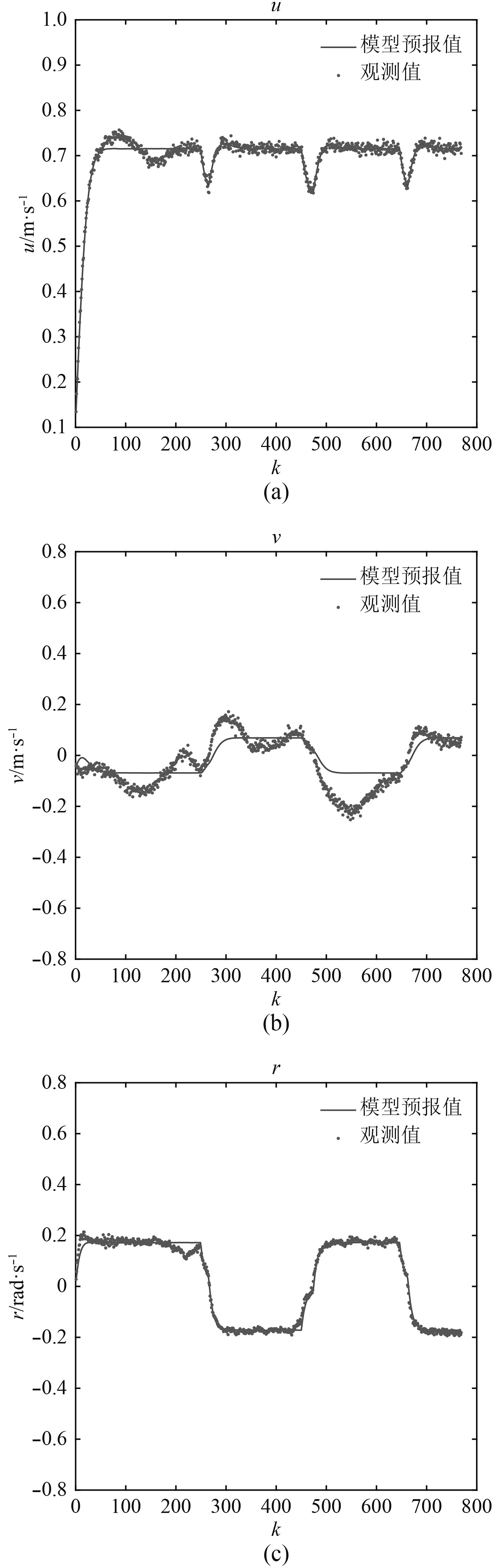
图 4 S型回转试验模型预报的结果与实际观测数据对比 Fig. 4 Comparison between model prediction result and observed data on S rotation test |
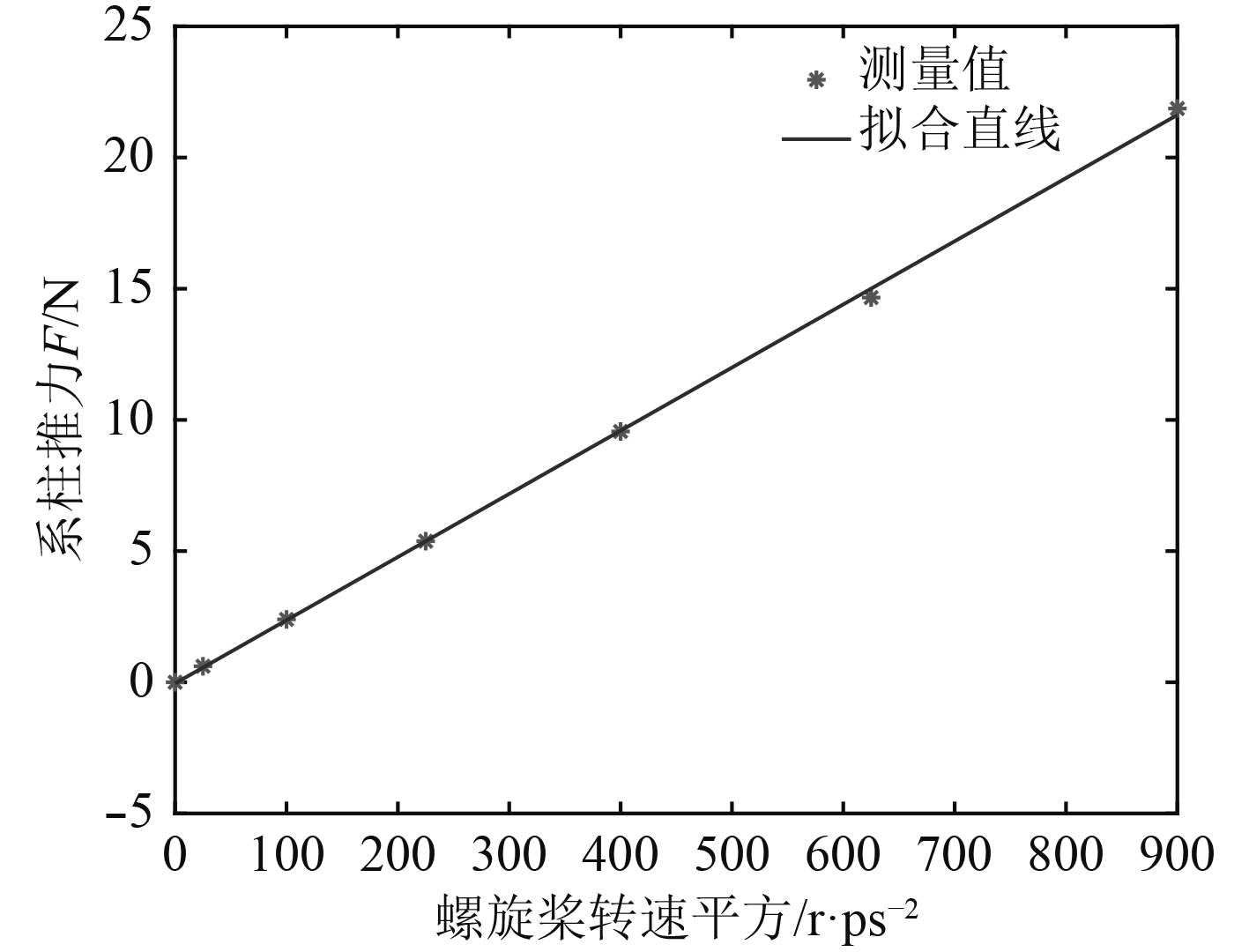
辨识的参数中,
|
|
表 4 试验结果与系统辨识结果比较 Tab.4 Comparison between test result and identification result |
|
图 5 系柱推力测量结果线性拟合 Fig. 5 Linear regression of propeller bollard thrust |
本文针对目标三体船,基于MMG模型建立了其运动数学模型结构,利用无迹卡尔曼滤波器结合自航试验数据对模型中的参数进行辨识。为减轻动力相消带来的影响,结合三体船特点对模型结构进行了化简,并设计了不同的航行方式和分步辨识方法。模型预报的速度、转首角速度与实际观测值十分吻合,对其中可以由试验测量的系柱推力系数,试验测量值与辨识值误差很小,验证了本文辨识方法的有效性和优越性。
| [1] |
杨盐生, 贾欣乐. 船舶运动数学模型: 机理建模与辩识建模[M]. 大连: 大连海事大学出版社, 1999: 57−58.
|
| [2] |
小川阳弘. MMG报告-I操纵运动の数学モデルにつぃて[J]. 日本造船学会志, 1977(575): 175-184. OGAWA Youko. MMG report- I A mathematical model of the ship maneuverability[J]. Journal of Japan shipbuilding Society, 1977(575): 175-184. |
| [3] |
ABKOWITZ M A. Lectures on ship hydrodynamics: steering and maneuvrability[M]. Hydro-og Aerodynamisk Laboratorium, Hydrodynamics Department, 1964.
|
| [4] |
Abkowitz M A. Measurement of hydrodynamic characteristics from ship maneuvering trials by system identification[R]. 1980.
|
| [5] |
侯先瑞. 基于支持向量回归机的波浪中船舶运动辨识建模研究[D]. 上海: 上海交通大学, 2017. HOU Xian-rui. Identification modeling of ship motions in waves based on support vector regression[D]. Shanghai JiaoTong University, 2017. |
| [6] |
张丽娜. 萤火虫算法研究及其在船舶运动参数辨识中的应用[D]. 哈尔滨: 哈尔滨工程大学, 2017. ZHANG Li-na. Research on firefly algorithm and its application in parameter identification of ship motions[D]. Harbin Engineering University, 2017. |
| [7] |
田延飞, 胡山川, 黄立文, 等. 基于人工蜂群算法的船舶运动模型参数离线辨识[J]. 信息技术, 2017(11): 49-52. TIAN Yan-fei, HU Shan-chuan, HUANG Li-wen, et al. Off-line parameter identification of mathematical ship motion model based on artificial bee colony algorithm[J]. Information Technology, 2017(11): 49-52. |
| [8] |
万冬冬. 基于多目标群智能算法的船舶横向运动参数辨识方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2018. WAN Dong-dong. Ship lateral motion parameter identification method based on multi-objective swarm intelligence[D]. Harbin Engineering University, 2018. |
| [9] |
HWANG W Y. Cancellation effect and parameter identifiability of ship steering dynamics[J]. International Shipbuilding Progress, 1982, 29(332): 90-102. DOI:10.3233/ISP-1982-2933201 |
| [10] |
WAN E A, VAN Der Merwe R. The unscented Kalman filter for nonlinear estimation[C]//Proceedings of the IEEE 2000 Adaptive Systems for Signal Processing, Communications, and Control Symposium (Cat. No. 00EX373). Ieee, 2000: 153−158.
|
| [11] |
JULIER S J. The scaled unscented transformation[C]//Proceedings of the 2002 American Control Conference (IEEE Cat. No. CH37301). IEEE, 2002, 6: 4555−4559.
|
| [12] |
周昭明, 盛子寅, 冯悟时. 多用途货船的操纵性预报计算[J]. 船舶工程, 1983(6): 21-29+36+4. ZHOU Zhao-ming, SHENG Zi-yin, FENG Wu-shi. Prediction and calculation of maneuverability of multi-purpose cargo ship[J]. Ship Engineering, 1983(6): 21-29+36+4. |
 2021, Vol. 43
2021, Vol. 43
