2. 中国人民解放军 92578部队,北京 100161
2. No.92578 Unit of PLA, Beijing 100161, China
作为现代海军作战力量的重要组成部分,潜艇在空间立体作战及战略威慑中均发挥着无可替代的作用[1]。当前按照动力来源,潜艇可分为核动力及常规动力两大类,前者多在深海中隐蔽航行,其续航力及水下潜航时间均远优于常规动力潜艇,然而对于近海岸侦察、打击及巡逻等军事任务,各国则更多地应用排水量相对较小的常规动力潜艇。受于作战环境及战术限制,近岸航行的常规动力潜艇往往需要完成近水面换气发电、救援、发射导弹及潜望镜深度瞭望等战术动作,较于深水潜航状态,近水面航行的潜艇受到文丘里效应的影响,潜艇水动力随潜深、航速均呈现较为明显的变化。
在早期潜艇操纵过程中,国内外学者已认识到潜艇近水面航行时水动力性能的变化[2],并认为当潜深
近年来,随着粘流CFD技术的快速发展,基于Fluent,Star-CCM+及CFX等商用软件平台可快速获取不同航态下潜艇的水动力性能,极大地提高了工程效率和研发周期,张楠等[8-9]较早地应用粘流计算软件开展了近水面航行潜艇数值计算,其重点分析了潜艇周围流场特性及近水面对螺旋桨伴流的影响,并未对潜深及航速等因素展开分析;ZHANG[10]通过试验及数值方法分析了AUV近水面航行时下潜困难的现象,分析了影响AUV下潜的主要因素;Wilson H S[11]则应用CFX软件以Suboff标模裸艇体为研究对象,开展了不同潜深及航速下潜艇水动力性能分析,但其选用模型长仅为1.556 m,其结论对于带有附体及更大模型尺度潜艇是否适用还有待进一步研究。
1 数值方法 1.1 控制方程及湍流模型文中以RANS方程作为求解潜艇近水面航行的基本方程,其具体形式如下:
| $ \begin{split} \frac{\partial }{{\partial t}}\left( {\rho {u_i}} \right) + &\frac{\partial }{{\partial {x_j}}}\left( {\rho {u_i}{u_j}} \right) = - \frac{{\partial p}}{{\partial {x_i}}} + \rho {f_i} + \\ &{\frac{\partial }{{\partial {x_j}}}\left[ {{\mu _0}\left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right) - \frac{2}{3}{\mu _0}\frac{{\partial {u_l}}}{{\partial {x_l}}}{\delta _{ij}}} \right] + \frac{\partial }{{\partial {x_j}}}\left( { - \rho \overline {{u_i^\prime}u_j^\prime } } \right)}\text{,} \end{split} $ | (1) |
式中:
湍流模式选取SST
| $ {\frac{\partial }{{\partial t}}(\rho k) + \frac{\partial }{{\partial {x_i}}}\left( {\rho k{u_i}} \right) = \frac{\partial }{{\partial {x_j}}}\left( {{\Gamma _k}\frac{{\partial k}}{{\partial {x_j}}}} \right) + {G_k} - {Y_k} + {S_k}}\text{,} $ | (2) |
| $ {\frac{\partial }{{\partial t}}(\rho \omega ) + \frac{\partial }{{\partial {x_i}}}\left( {\rho \omega {u_i}} \right) = \frac{\partial }{{\partial {x_j}}}\left( {{\Gamma _\omega }\frac{{\partial \omega }}{{\partial {x_j}}}} \right) + \!{G_\omega } - \!{Y_\omega } +\! {S_\omega }}\text{。} $ | (3) |
式中:
Star CCM+商用软件中提供了多种网格划分方式,由于潜艇近水面航行计算的关键在于自由液面兴波的准确捕捉,因此本文中选用六面体切割体网格划分策略对计算域进行网格离散。
切割体网格技术的优势在于能够确保流体域内绝大部分网格为排列规则的六面体网格,同时通过对近艇体壁面区域进行网格加密设置可对潜艇周围的湍流区域进行准确模拟,且对于过于复杂的几何结构,边界层内网格自适应地采用其他形状的网格结构形式,以满足物面形状及网格质量的要求。其生成原理及步骤如下:
步骤1 首先根据艇周围加密区设置及域边界确定网格的生成边界,如图1(a)所示,边界层外边界与域边界圈定的区域为中心网格区,艇体壁面与边界层外边界间的区域为边界层区;
步骤2 在整个计算域及周围生成初始体网格(见图1(a)),用第1步确定的边界进行裁剪,裁剪后的网格如图1(b)所示;
步骤3 根据网格密度设置对中心网格区内网格疏密程度进行控制,并进一步提高网格质量;
步骤4 在边界层区域内,根据物面形状自适应地生成网格。

|
图 1 网格生成示意图 Fig. 1 Configuration of meshing strategy |
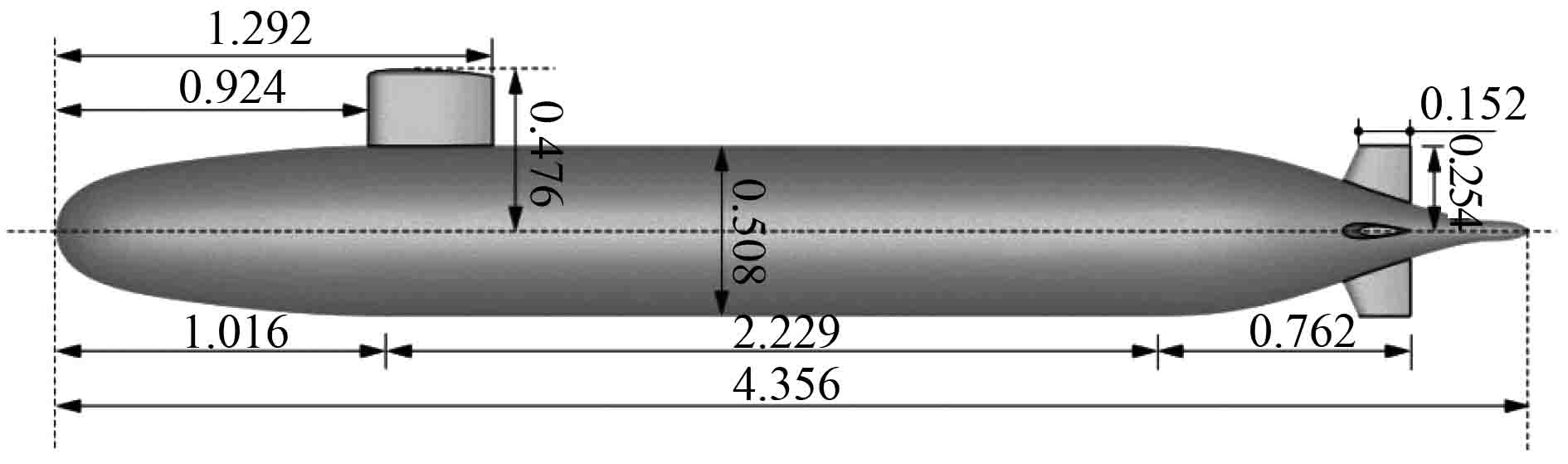
以美国国防高级研究计划局(DARPA)公布的Suboff全附体模型为研究对象,该模型由主艇体、指挥台围壳及十字型尾舵组成,模型主参数如图2所示。将潜艇中心线距自由液面的距离与艇体直径的比值定义为无因次潜深(见图3),即
|
图 2 Suboff潜艇模型主尺度参数 Fig. 2 Main particulars of Suboff |

|
图 3 潜深无因次化定义 Fig. 3 Definition of submarine’s non-dimensional depth |
本文开展傅氏数
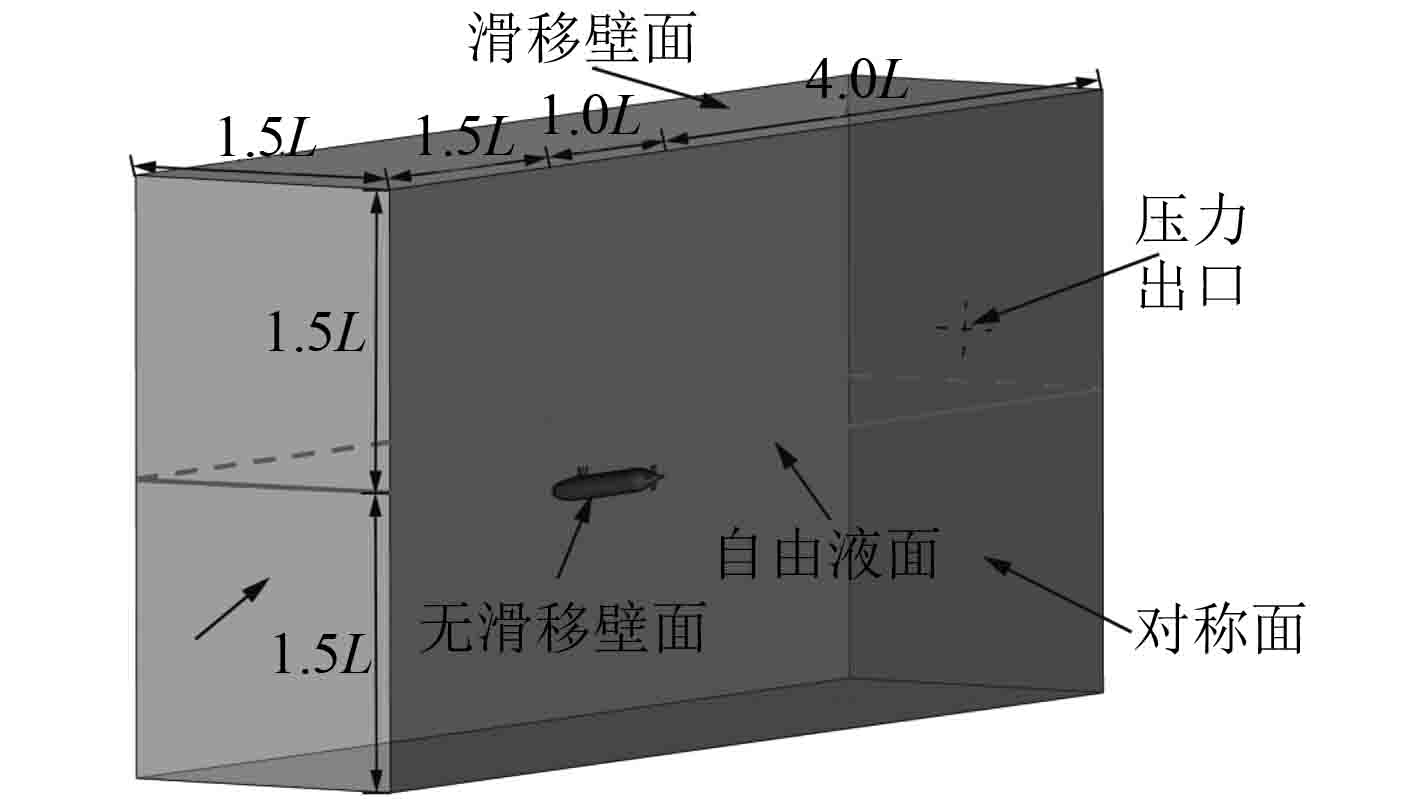
由于Suboff潜艇模型及流场均关于艇体中纵剖面对称,为减小计算量取一半潜艇开展计算,如图4所示。计算域大取为长宽高为5.5L×1.5L×3.0L的方形域,边界条件设置如下:
1)距离艇首1.5倍艇长,边界条件设置为速度入口;
2)距离艇尾4倍船长,边界条件设置为压力出口,压力为未扰动时边界压力;
3)流域的上、下及右边界设置无滑移、不可穿透壁面;
4)流域左边界设置为对称面;
5)艇体表面定义为无滑移、不可穿透边界条件,边界条件设置为无滑移壁面。
|
图 4 计算域大小及边界条件设置 Fig. 4 Computational domain and boundary conditions |
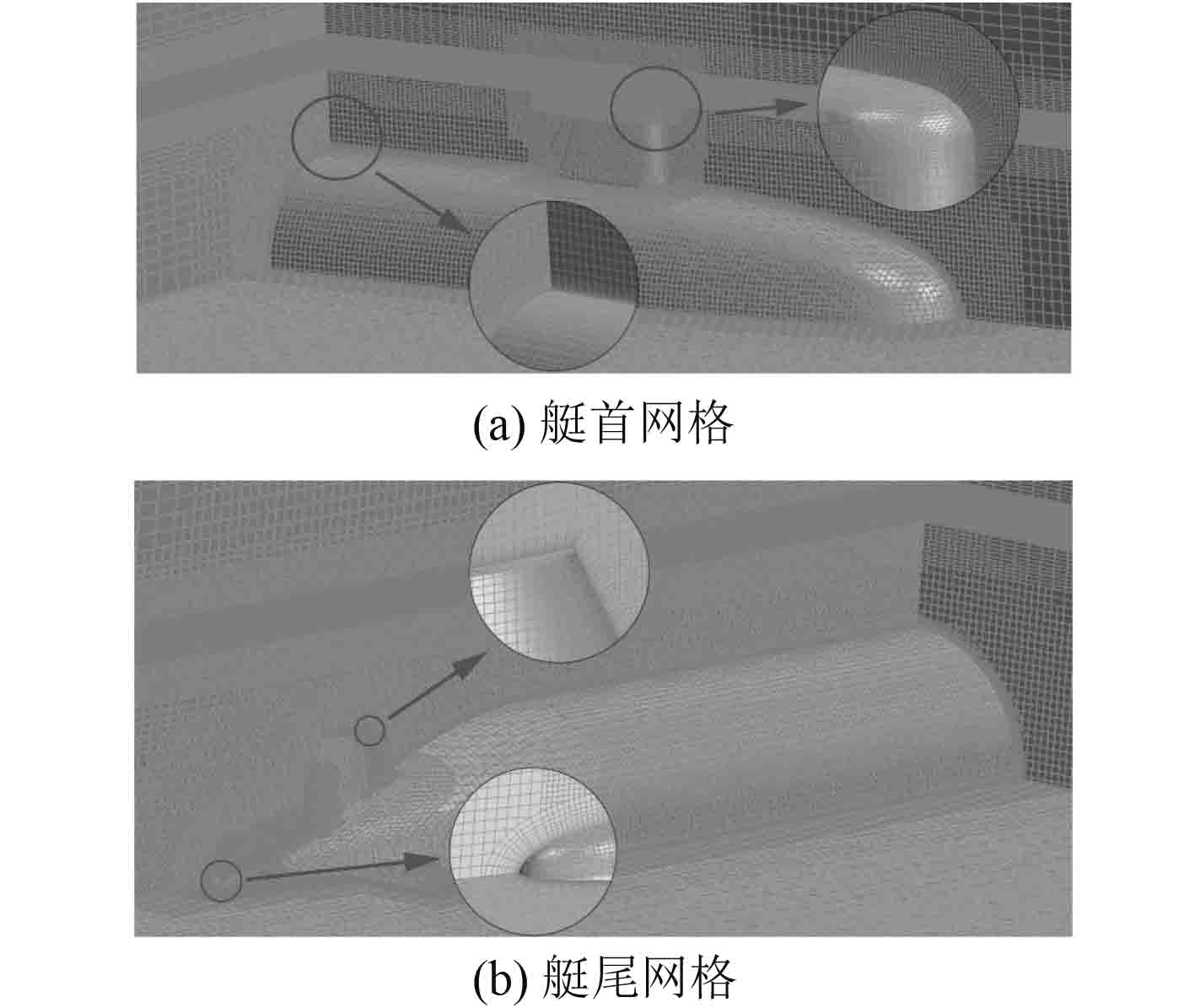
在网格离散过程中,为准确地捕捉两相流的水气分界面,对自由液面附近区域进行网格加密。此外,在艇体近壁面设定了局部加密区,确保壁面y+~1,并对指挥台及尾舵处的网格进行了细化处理,船体表面及域剖面网格如图5所示,总网格数为215万。
|
图 5 艇体表面及域剖面网格 Fig. 5 Mesh for submarine's surface and domain profile |
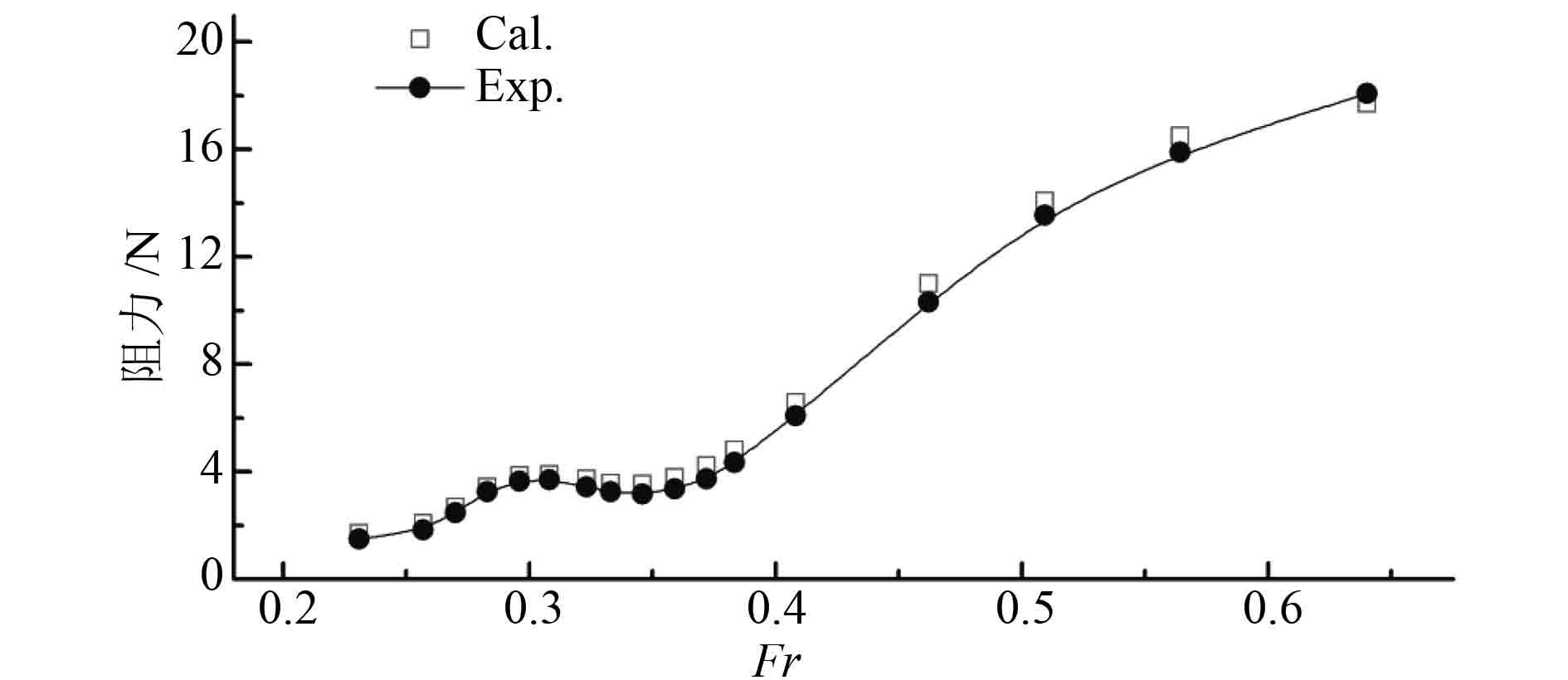
为验证上述计算方法的可行性,以Suboff模型裸艇体为计算对象,模型长1.556 m,试验数据参见文献[11]。计算域设置及模型无因次潜深的定义与前述模型相同。图6为该模型无因次潜深
|
图 6 阻力计算值与试验结果对比(H* = 1.1) Fig. 6 Comparison of calculation and experimental results for submarine’s resistance at H* = 1.1 |
由图6中近水面裸艇体阻力随傅氏数的变化可知,随着航速的增大,潜艇近水面航行时艇体阻力呈现先增大后减小再增大的变化趋势,这与深水航行存在较大差异。
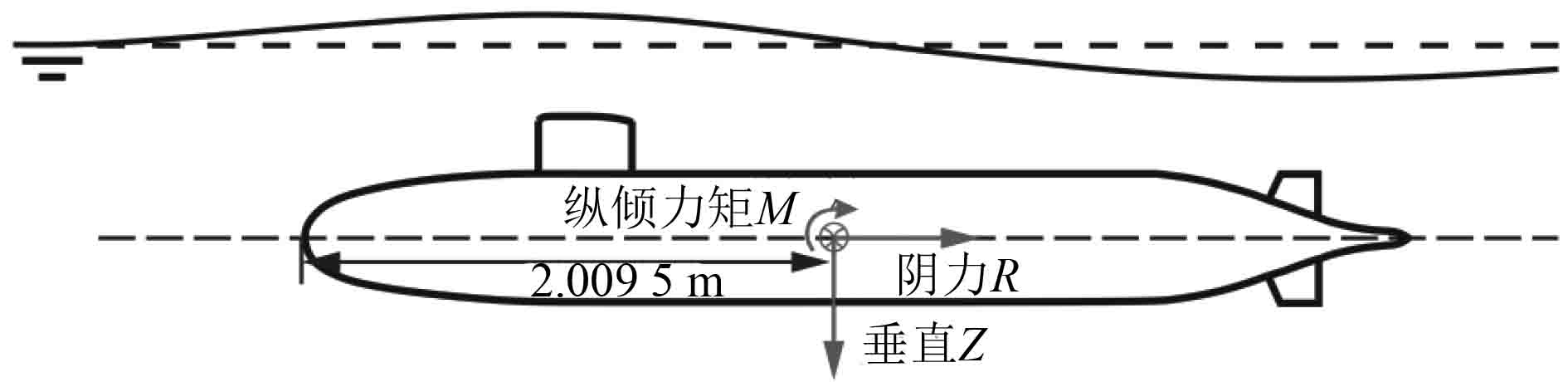
5 计算工况与结果分析 5.1 力、力矩定义为便于计算与分析,设定潜艇重心与浮心纵向位置相同,即距艇首2.0095 m,并定义潜艇近水面航行时所受阻力、垂向力及对重心的纵倾力矩的正方向如图7所示。其中,潜艇垂向力中不包含艇体所受浮力。力及力矩系数定义如下:
|
图 7 潜艇受力及力矩定义 Fig. 7 Definition of force and torque for submarine |
| $R' = R/(0.5 \times \rho \times {L^2} \times {U^2})\text{,}$ |
| $Z' = Z/(0.5 \times \rho \times {L^2} \times {U^2})\text{,}$ |
| $ M' = M/(0.5 \times \rho \times {L^3} \times {U^2})\text{。}$ |
式中:
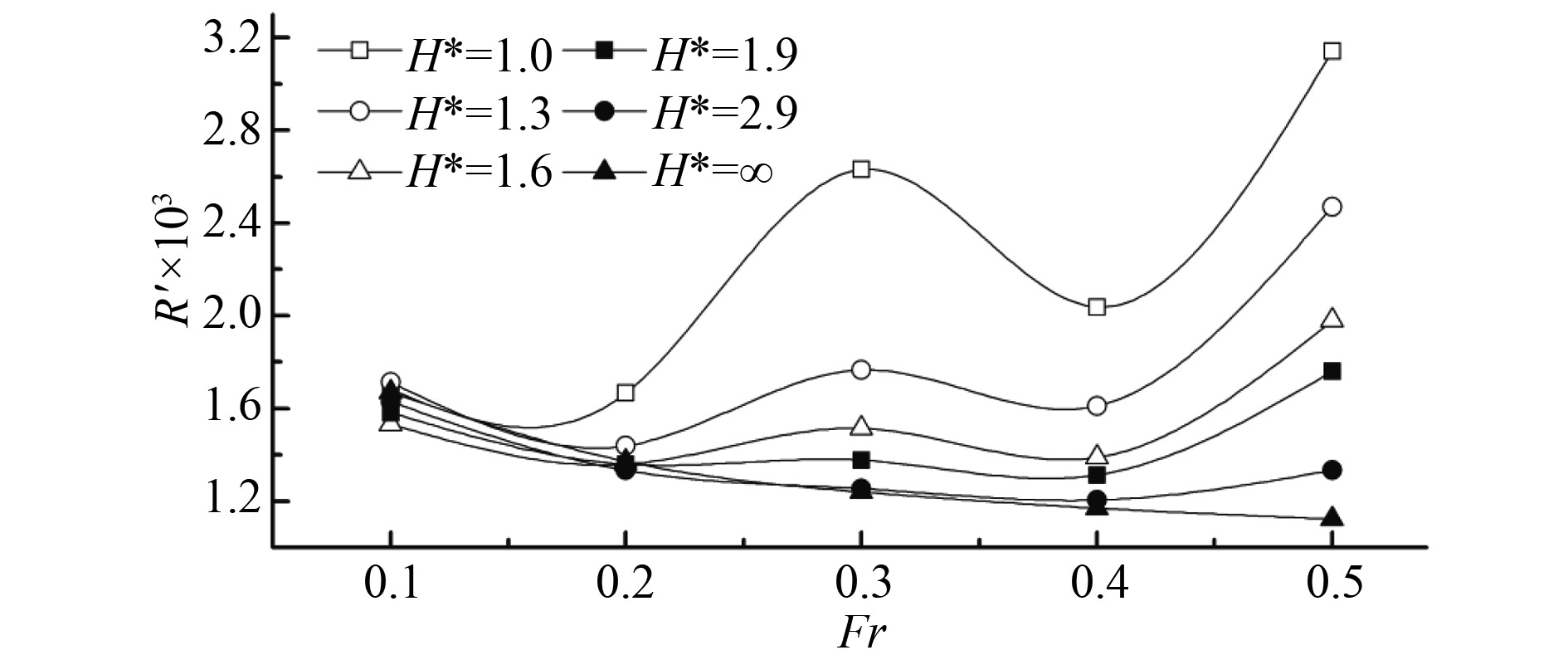
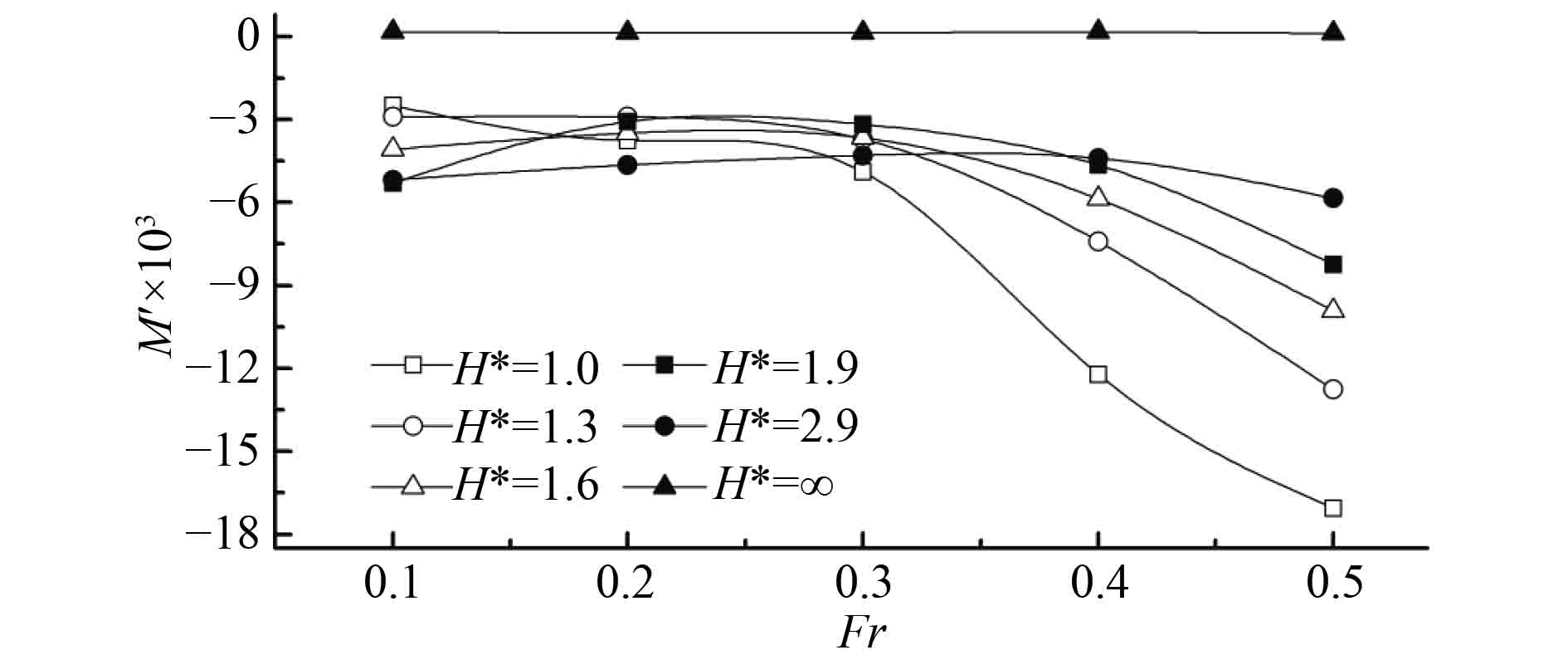
图8~图10分别给出了不同潜深下潜艇阻力系数、垂向力系数及纵倾力矩系数随傅氏数Fr的变化规律,分析可得:
|
图 8 阻力系数随傅氏数Fr的变化 Fig. 8 Resistance coefficient of submarine at different Fr |
|
图 10 纵倾力矩系数随傅氏数Fr的变化 Fig. 10 Trimming moment coefficient of submarine at different Fr |
1)潜艇无因次潜深
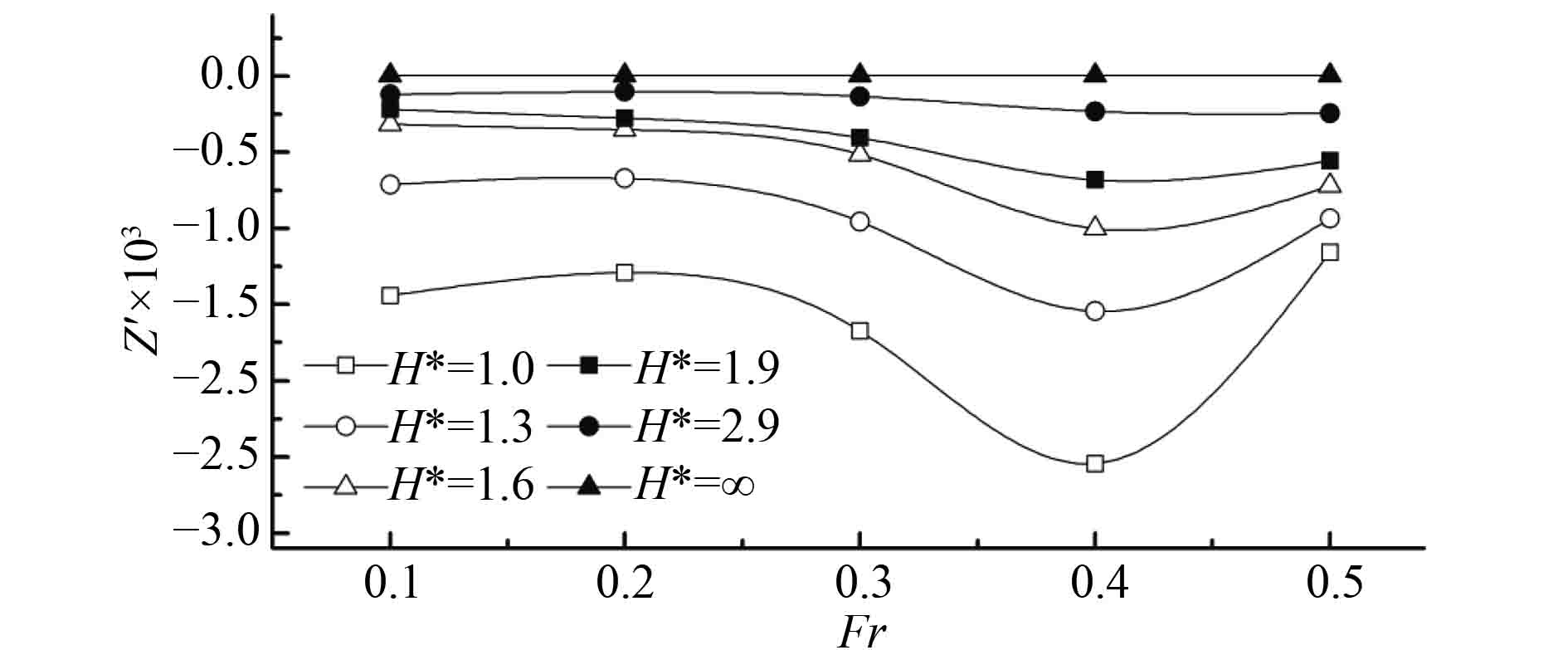
2)不同潜深下,潜艇垂向力系数随傅氏数
3)在无限水深下,潜艇纵倾力矩系数均远小于近水面航行工况,其值趋近于0;而在近水面工况下(
|
图 9 垂向力系数随傅氏数Fr的变化 Fig. 9 Vertical force coefficient of submarine at different Fr |
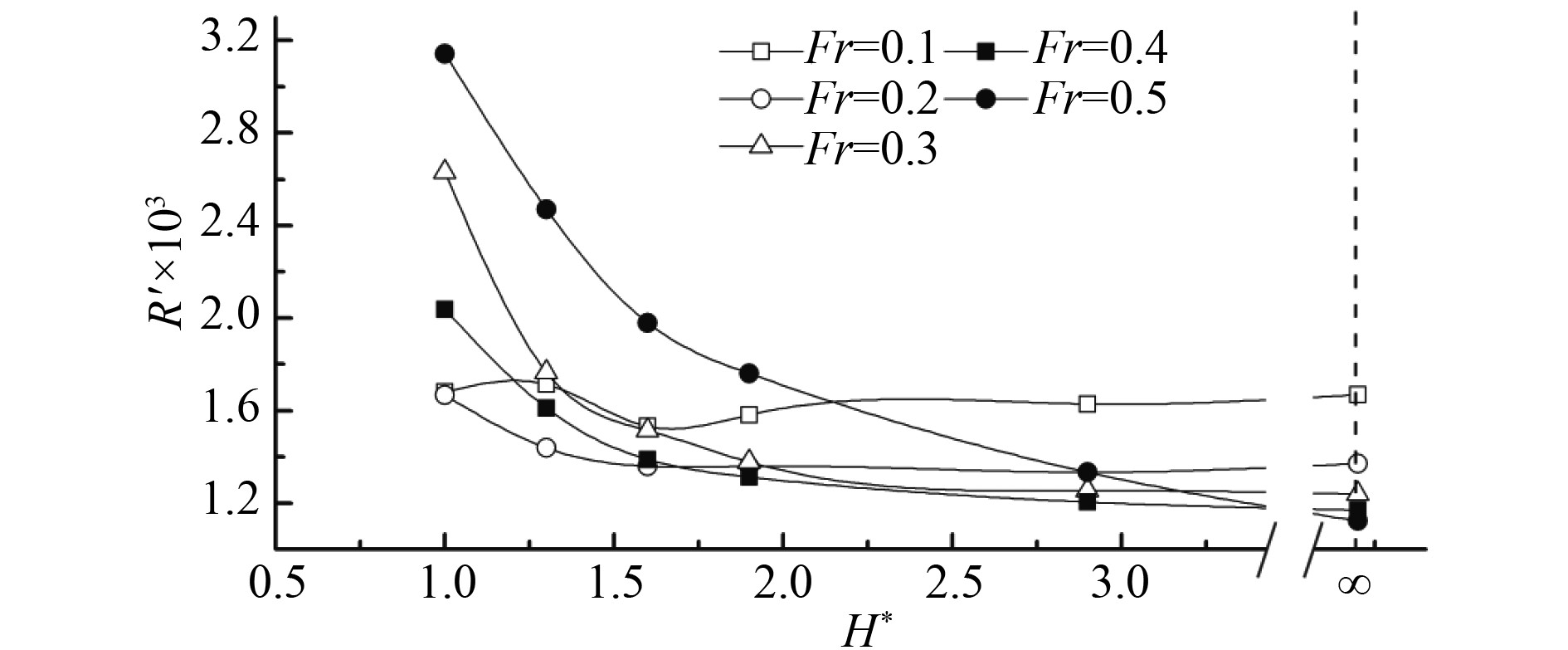
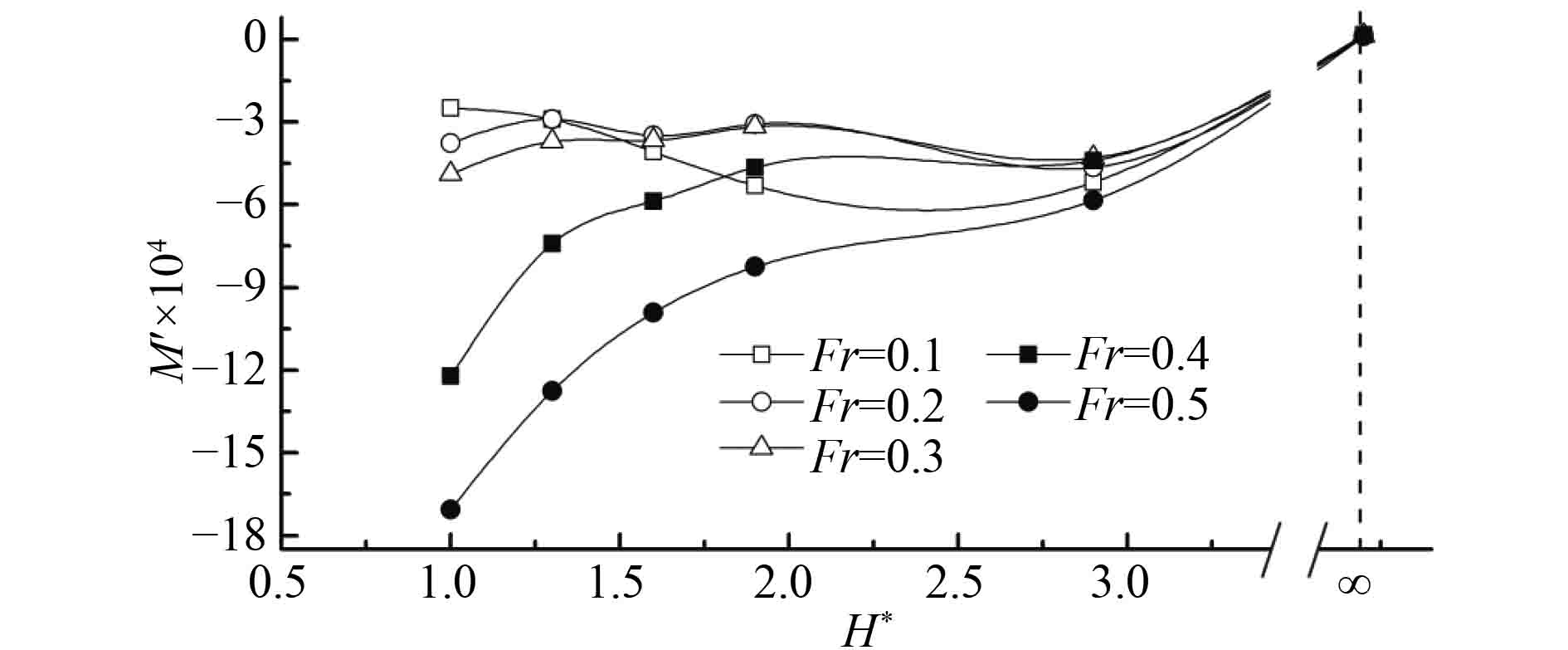
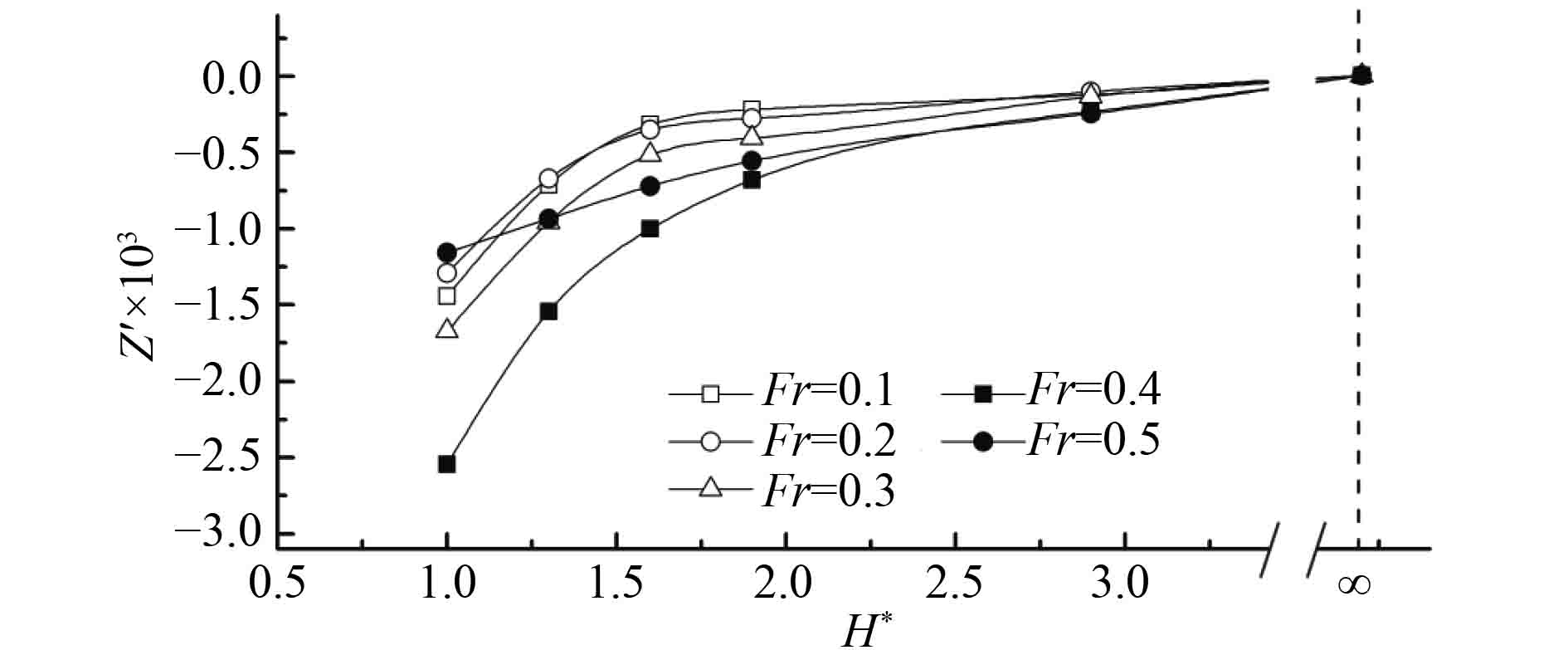
通过对比分析不同潜深下潜艇水动力的差异可直观分析潜艇水动力随潜深的变化趋势,潜艇阻力系数、垂向力系数及纵倾力矩系数随无因次潜深的变化曲线如图11~图13所示。
|
图 11 阻力系数随潜深的变化 Fig. 11 Resistance coefficient of submarine at different depths |
|
图 13 纵倾力矩系数随傅氏数Fr的变化 Fig. 13 Trimming moment coefficient of submarine at different depths |
由图可知:
1)在低航速下(
2)相较于阻力性能,潜艇近水面航行时受到向上的垂向吸力,且一定航速下,随着潜深的不断增大,自由液面的吸力作用逐渐减弱,并在
3)由图13可知,在研究航速及潜深范围内,潜艇均受到埋首的纵倾力矩,而当
|
图 12 垂向力系数随潜深的变化 Fig. 12 Vertical force coefficient of submarine at different depths |
由潜艇所受力及力矩分析可知,不同潜深下潜艇近水面航行时的水动力随航速的变化规律基本趋于一致,潜深越小,潜艇水动力受自由液面的影响也越大,因此,取定潜深
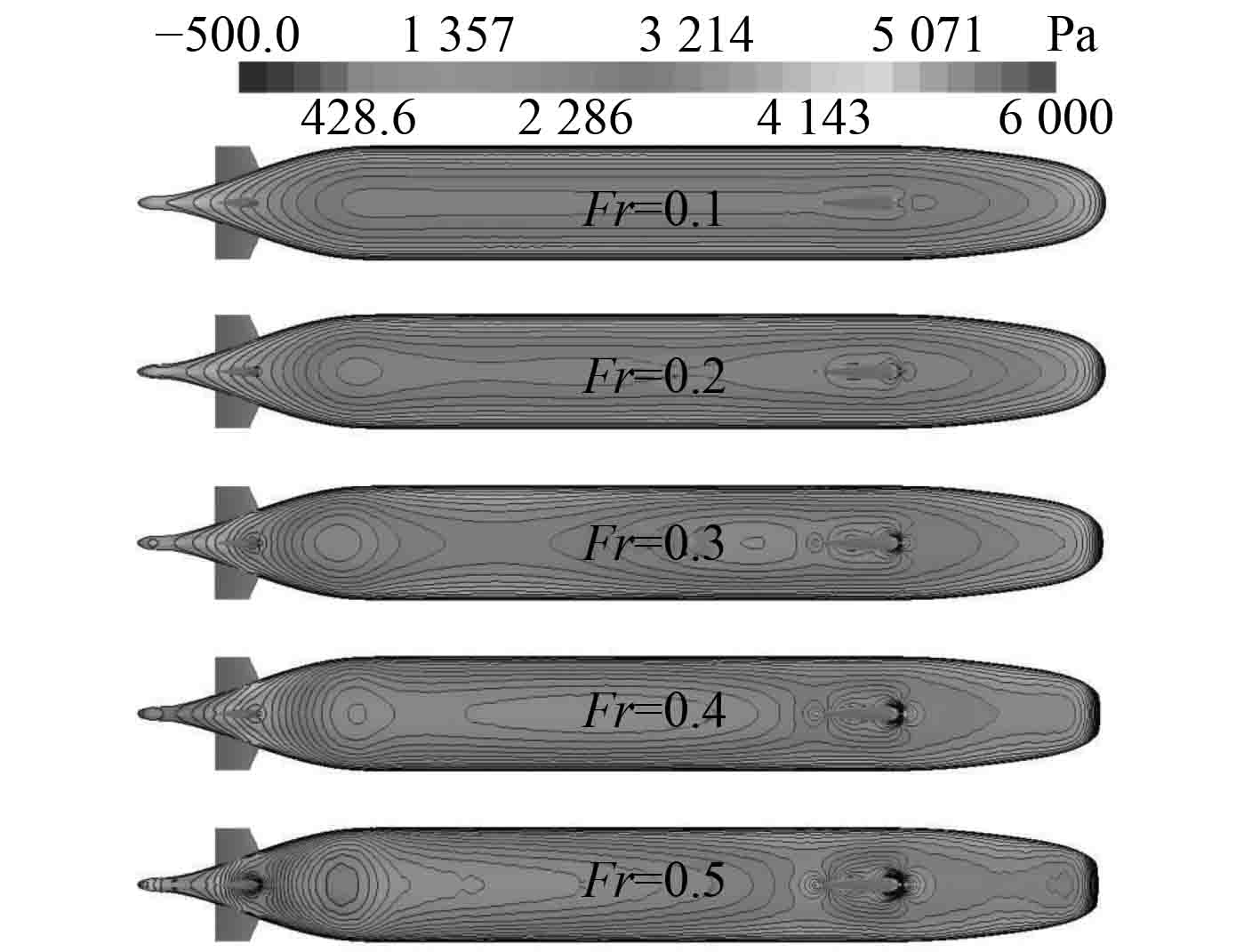
|
图 14 不同航速下主艇体表面压力分布(H* = 1.0) Fig. 14 Pressure distribution on submarine's hull at different advancing velocity(H* = 1.0) |
同等航速下,潜深是影响潜艇水动力的重要因素,图15给出了航速

|
图 15 不同潜深下自由液面波高图(Fr = 0.5) Fig. 15 Wave patterns for submarine advancing near free surface in different depths at Fr = 0.5 |
通过开展潜艇近水面水动力性能数值分析,得出如下结论:
1)基于切割体网格技术及RANS方法能够较为准确地模拟潜艇近自由液面水动力性能;
2)潜深直接影响潜艇水动力,当无因次潜深
3)近自由液面条件下(
| [1] |
约翰•帕克著. 马小皎译. 世界潜艇百科全书[M]. 北京: 机械工业出版社, 2015.
|
| [2] |
施生达. 潜艇操纵性[M]. 北京: 国防工业出版社, 1995.
|
| [3] |
冯学知, 蒋强强, 缪泉明, 等. 潜体波浪中近水面不同潜深和航向时运动和波浪力计算[J]. 船舶力学, 2002, 6(2): 1-14. FENG Xue-zhi, JIANG Qiang-qiang, MIU Quanming, et al. Compution of motion and wave forces for a submarine running near free surface in different depth of immersion and direction[J]. Journal of Ship and Mechanics, 2002, 6(2): 1-14. |
| [4] |
孙伯起, 缪泉明, 冯学知, 等. 潜艇近水面波浪力的数值计算方法[J]. 船舶力学, 1997, 1(1): 21-26. SUN Bo-qi, MIAO Quan-ming, FENG Xue-zhi, et al. A numerical method for the calculation of the wave forces acting on a submarine travelling near the free surface[J]. Journal of Ship and Mechanics, 1997, 1(1): 21-26. |
| [5] |
GOURLAY T, DAWSON E. A havelock source panel method for near-surface submarines[J]. Journal of Marine Science and Application, 2015, 14: 215-224. |
| [6] |
戴余良, 刘祖源, 俞科云, 等. 近水面潜艇波浪力计算研究评述[J]. 舰船科学技术, 2007, 29(2): 41-46. DAI Yu-liang, LIU Zu-yuan, YU Ke-yun, et al. A comment on the calculation methods of wave forces for a submarine under waves[J]. Ship Science and Technology, 2007, 29(2): 41-46. |
| [7] |
DAWSON E. An investigation into the effects of submergence depth, speed and hull length-to-diameter ratio on the near-surface operation of conventional submarines[D]. Hobart Australia: University of Tasmania, 2014.
|
| [8] |
张楠, 沈泓萃, 姚惠之. 潜艇近海底与近水面绕流数值模拟研究[J]. 船舶力学, 2007, 11(4): 498-507. ZHANG Nan, SHEN Hong-cui, YAO Hui-zhi. Numerical simulation of flow around submarine operating close to the bottom or near surface[J]. Journal of Ship and Mechanics, 2007, 11(4): 498-507. |
| [9] |
ZHANG Nan, ZHANG Sheng-li. Numerical simulation of hull/propeller interaction of submarine in submergence and near surface conditions[J]. Journal of Hydrodynamics, 2014, 26(1): 50-56. |
| [10] |
ZHANG Hong-wei, LI Jin-cui, WANG Yan-hui, et al. Numerical and experimental investigation of the problem of diving difficulty of autonomous underwater vehicles[J]. Journal of Ship Mechanics, 2016, 20(3): 277-287. |
| [11] |
WILSON H S. An investigation into the wavemaking resistance of a submarine travelling below the free surface[D]. Launceston Australia: National Centre of Maritime Engineering and Hydrodynamics, 2009.
|
| [12] |
LARSSON L, RAVEN H. Ship resistance and flow[M]. New York: Society of Naval Architects and Marine Engineering, 2010.
|
 2021, Vol. 43
2021, Vol. 43
