2. 哈尔滨 大电机研究所,黑龙江 哈尔滨 150001;
3. 哈尔滨工程大学 海洋可再生能源研究所,黑龙江 哈尔滨 150001;
4. 工业和信息化部电子第五研究所,广东 广州 510000
2. Harbin Institute of Large Electrical Machinery, Harbin 150001, China;
3. Institute of Ocean Renewable Energy System, Harbin Engineering University, Harbin 150001, China;
4. The Fifth Electronics Research Institute of Ministury of Industry and Information Technology, Guangzhou 510000, China
随着能源问题日益严峻,作为一种清洁海洋可再生能源,潮流能具有储量丰富、分布集中且可预测性强等优点。如何高效开发和利用潮流能已受到国内外学者的关注[1]。水平轴叶轮是一种常见的潮流能发电装置,具有效率较高,功率波动较小,自启动性能良好等特点[2]。目前,已经在海上部署了一些商用前的水平轴潮流能叶轮原型,典型代表有:英国MCT公司的SeaFlow系列,英国TGL公司的Alstom,挪威Hammerfest公司的HS系列,新加坡Altantis公司的AR,AK系列[3]。哈尔滨工程大学设计的水平轴叶轮10 kW的“海明I号”,2×100 kW的“海能II号”[4]。
叶片是水平轴潮流能装置一级能量转换的核心部件,叶片型线设计对能量转换效率和运行稳定性至关重要,直接影响发电效率。叶片的性能主要取决选取的翼型形状以及沿展长方向的形状变化。前者根据翼型气动力性能选择,后者主要由沿展长方向各叶素截面的弦长和桨距角确定[5-6]。水平轴叶轮的叶片设计方法主要有:基于圆盘理论的简化风车模型,基于涡流理论的Schmitz模型、Glauert模型和Wilson模型。其中Glauert模型考虑了轴向、切向诱导因子,设计结果具有较高的精度[7]。
本文基于哈尔滨工程大学承担的国家公益性项目要求,完成水平轴潮流能叶轮的设计,研究并发展一套水平轴潮流能叶轮水动力性能有效的预报方法,为今后水平轴潮流能叶轮的性能设计建立可靠的理论分析方法,积累准确的实验数据。针对项目要求的技术参数与环境参数,应用Glauert涡流设计理论,对水平轴定桨距叶轮的结构形式进行设计,并采用BEM叶素动量理论和CFD数值模拟方法对设计的水轮机进行载荷与性能的预报。总结出系统的设计方法与预报方法,归纳出水平轴叶轮的载荷特点。
1 叶片设计的Glauert涡流设计理论对于有限展长的叶片,其叶轮尾流中存在叶尖涡和叶根涡。美国Amherst大学改进的Glauert涡流理论,考虑了叶轮引起的涡流影响,是目前应用较为广泛的理论之一[8]。
|
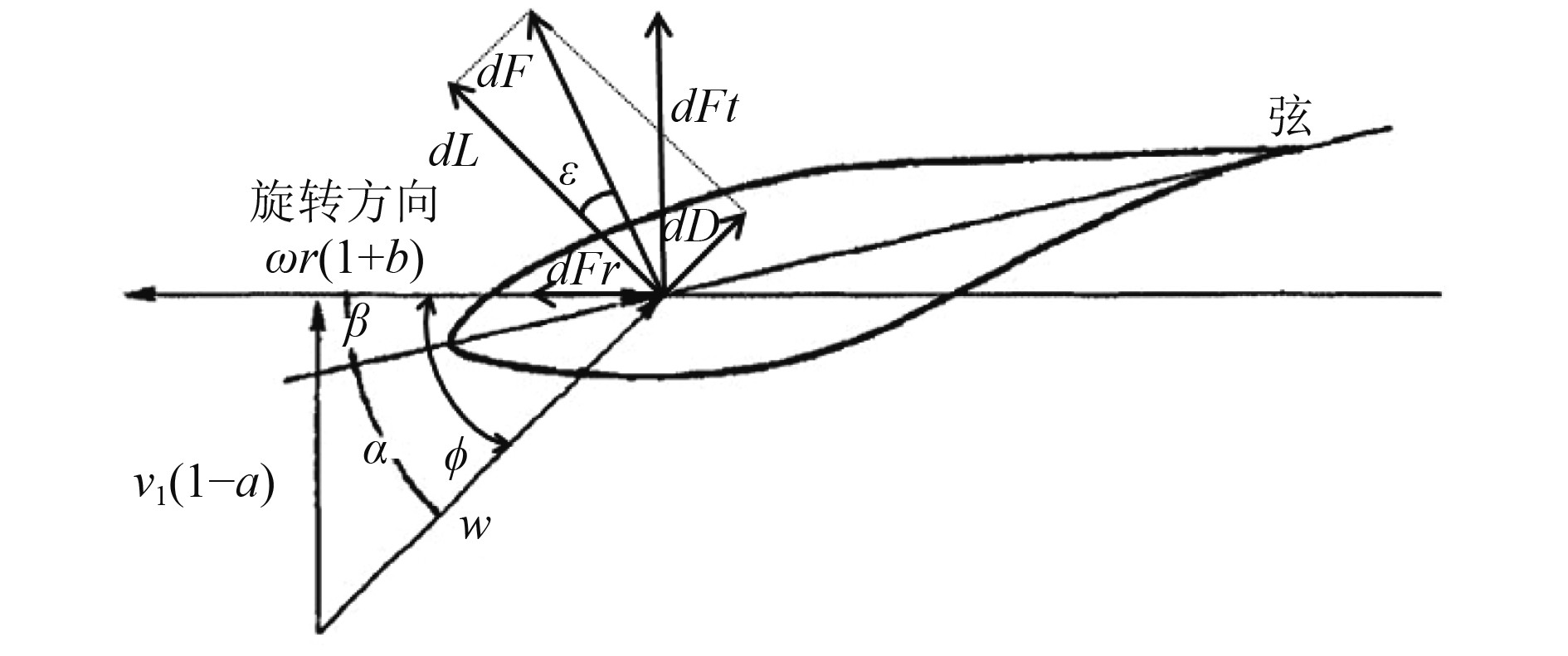
图 1 叶素受力示意图 Fig. 1 The force diagram of blade element |
对于每个叶素来说,考虑涡流的影响,假设轴向和切向诱导速度子分别为a和b,则叶素的相对来流速度为:
| $\vec w = {\vec v_1}(1 - a) + \vec \omega r(1 + b)\text{,}$ | (1) |
叶素的入流角和桨距角可表示为:
| $\phi = \arctan \left(\frac{{{v_1}(1 - a)}}{{\omega r(1 + b)}}\right)\text{,}$ | (2) |
| $\beta = \phi - \alpha\text{,} $ | (3) |
根据动量定理,作用在
| ${\rm{d}}T = 4{\text{π}} \rho v_1^2a(1 - a)r{\rm{d}}r\text{,}$ | (4) |
| ${\rm{d}}M = 4{\text{π}} \rho \omega {v_1}b(1 - a){r^3}{\rm{d}}r\text{,}$ | (5) |
根据叶素理论,可得:
| $ \begin{split} & {\rm{d}}T = \frac{1}{2}N\rho l{w^2}{C_T}{\rm{d}}r\text{,} \\ & {\rm{d}}M = \frac{1}{2}N\rho l{w^2}{C_M}r{\rm{d}}r \text{。} \end{split} $ | (6) |
其中:
| $ \begin{split} & {C_T} = {C_l}\cos (\phi ) + {C_d}\sin (\phi )\text{,} \\ & {C_M} = {C_l}\sin (\phi ) - {C_d}\cos (\phi )\text{。} \end{split} $ | (7) |
联立上式,并根据三角关系转化可得:
| $ \begin{split} & {C_l}lN = \frac{a}{{1 - a}}\frac{{8{\text{π}} r\cos \varepsilon {{\sin }^2}\phi }}{{\cos (\phi - \varepsilon )}}\text{,} \\ & {C_l}lN = \frac{b}{{1 + b}}\frac{{4{\text{π}} r\cos \varepsilon \sin (2\phi )}}{{\sin (\phi - \varepsilon )}} \text{,} \end{split} $ | (8) |
| $ \begin{split} & A = \frac{a}{{1 - a}} = \frac{{\cos (\phi - \varepsilon )}}{{8{\text{π}} r\cos \varepsilon {{\sin }^2}\phi }}\text{,} \\ & B = \frac{b}{{1 + b}} = \frac{{\sin (\phi - \varepsilon )}}{{4{\text{π}} r\cos \varepsilon \sin (2\phi )}}\text{,} \end{split} $ | (9) |
| $\frac{A}{B} = \frac{{a(1 + b)}}{{(1 - a)b}} = \cot (\phi - \varepsilon )\cot \phi \text{。}$ | (10) |
假设每一个叶素均在理想状态下运行,定义
| $\frac{A}{B} = \frac{{a(1 + b)}}{{(1 - a)b}} = {\cot ^2}\phi \text{,}$ | (11) |
其中:
| $\cot \phi = \lambda \frac{{1 + b}}{{1 - a}}\text{,}$ | (12) |
| ${\lambda ^2} = \frac{{a(1 - a)}}{{b(1 + b)}}\text{,}$ | (13) |
| $b = \sqrt {\frac{1}{4} + \frac{{a - {a^2}}}{{{\lambda ^2}}}} - \frac{1}{2}\text{。}$ | (14) |
叶素圆环的功率和能量利用率表达为:
| ${\rm{d}}P = \omega {\rm{d}}M = 4{\text{π}} \rho {v_1}{\omega ^2}b(1 - a){r^3}{\rm{d}}r\text{,}$ | (15) |
| $ Cp = \frac{{{\rm{d}}P}}{{\dfrac{1}{2}{\rm{d}}mv_1^2}} = \frac{{4{\text{π}} \rho {v_1}{\omega ^2}b(1 - a){r^3}{\rm{d}}r}}{{\dfrac{1}{2}2{\text{π}} r\rho {v_1}{\rm{d}}rv_1^2}} = 4{\lambda ^2}b(1 - a)\text{,} $ | (16) |
将式(14)代入上式,则有:
| $ Cp = 4{\lambda ^2}\left(\sqrt {\frac{1}{4} + \frac{{a(1 - a)}}{{{\lambda ^2}}}} - \frac{1}{2}\right)(1 - a)\text{。} $ | (17) |
对
| $a = f(\lambda )\text{。}$ | (18) |
若叶轮半径、叶轮转速和来流速度给定,则
| $\phi = f(\lambda )\text{,}$ | (19) |
将式(8)进行无量纲处理,由于变量
| ${l_c} = \frac{{{C_l}Nl}}{r} = \frac{a}{{1 - a}}\frac{{8{\text{π}} {{\sin }^2}\phi }}{{\cos (\phi )}} = f(a(\lambda ),\phi (\lambda ))\text{。}$ | (20) |
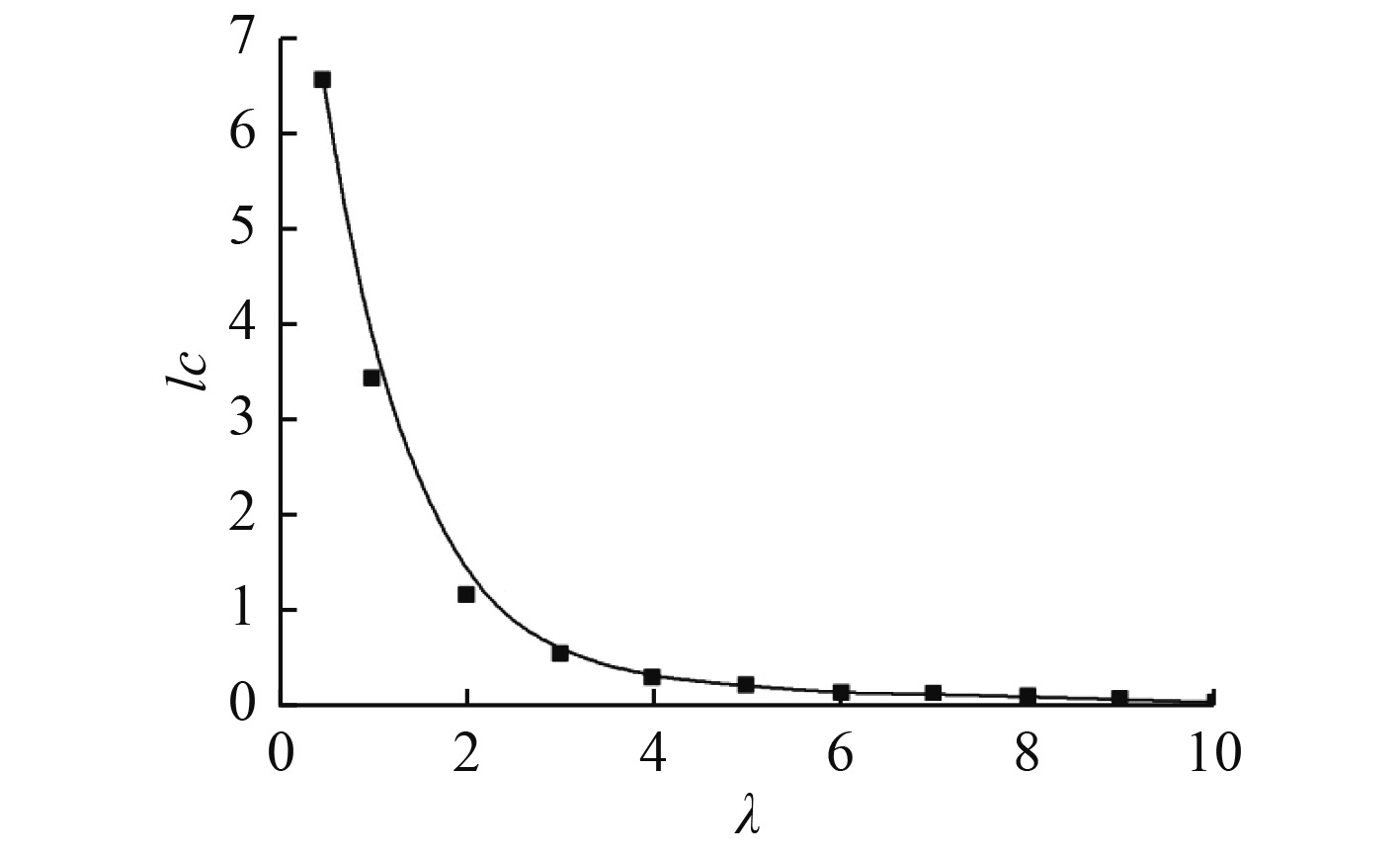
上述推导表明形状参数
|
图 2
叶片形状参数与速比
|
|
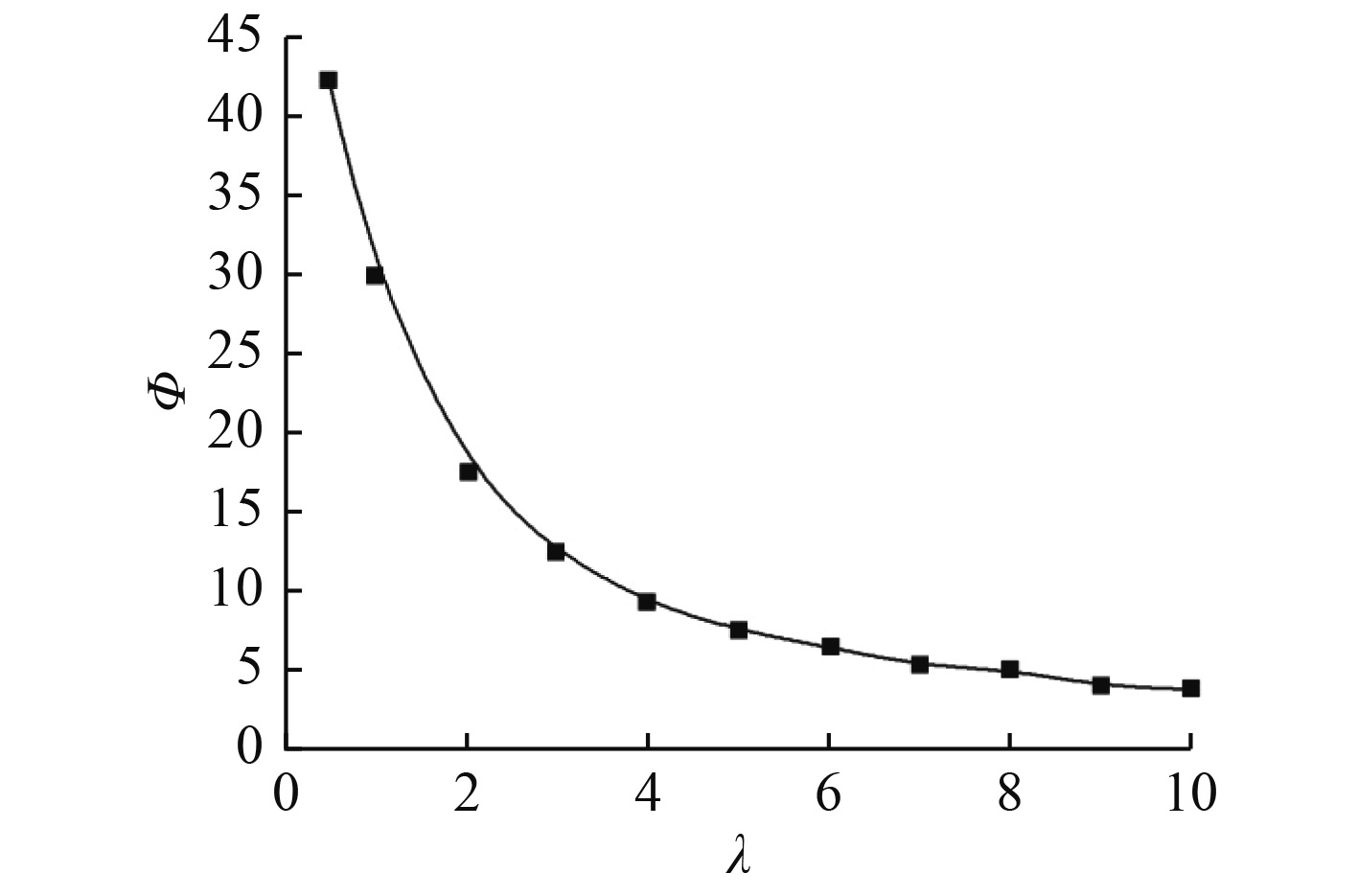
图 3
叶片入流角与速比
|
叶片弦长l、叶片截面翼型的攻角
| $l = \frac{{r{l_c}}}{{{C_l}N}}\text{,}$ | (21) |
| $\alpha = {\alpha _0} + \frac{{{C_l}}}{{{K_l}}}\left(1 + \frac{3}{{{R_z}}}\right)\text{,}$ | (22) |
| ${R_z} = \frac{R}{{{L_m}}}\text{,}$ | (23) |
| ${K_l} = \frac{{{C_{L\max }}}}{{{\alpha _{L\max }} - {\alpha _0}}}\text{。}$ | (24) |
式中:r为叶片不同位置的半径,形状参数
叶片沿展长的型线通过叶素的弦长和桨距角确定,叶片设计的流程如下:
1)根据额定输出功率确定叶轮的扫掠面积S;
2)确定叶轮直径D;
3)根据水轮机工作速比为
4)计算不同叶素的尖速比
5)计算不同叶素的入流角
6)确定不同叶素的叶片形状参数
7)根据形状参数
8)计算叶片的平均弦长
9)确定叶片各叶素的桨距角;
10)验证设计叶片是否满足设计要求。
采用NREL风机标准翼型S809,该翼型最优攻角为6.08°,根据上述流程计算叶素截面的弦长与桨距角,图4为设计完成的三维叶片图。

|
图 4 叶片三维示意图 Fig. 4 Three dimensional diagram of turbine blade |
采用BEM叶素动量理论与CFD数值模拟的2种方法,对本文设计的模型进行载荷与性能的预报。
3.1 BEM叶素动量理论方法通过Matlab将BEM叶素动量理论编程,即可用于叶轮载荷与性能的计算。BEM方法的求解流程如下[9]:
1)首先给出诱导速度因子
2)根据公式计算每个叶素翼型的来流角度;
3)计算每个叶素翼型的攻角
4)根据上一步得到的攻角
5)计算当前叶素的推力系数
6)根据公式重新计算
7)返回步骤2,重新迭代,直至满足容差要求。
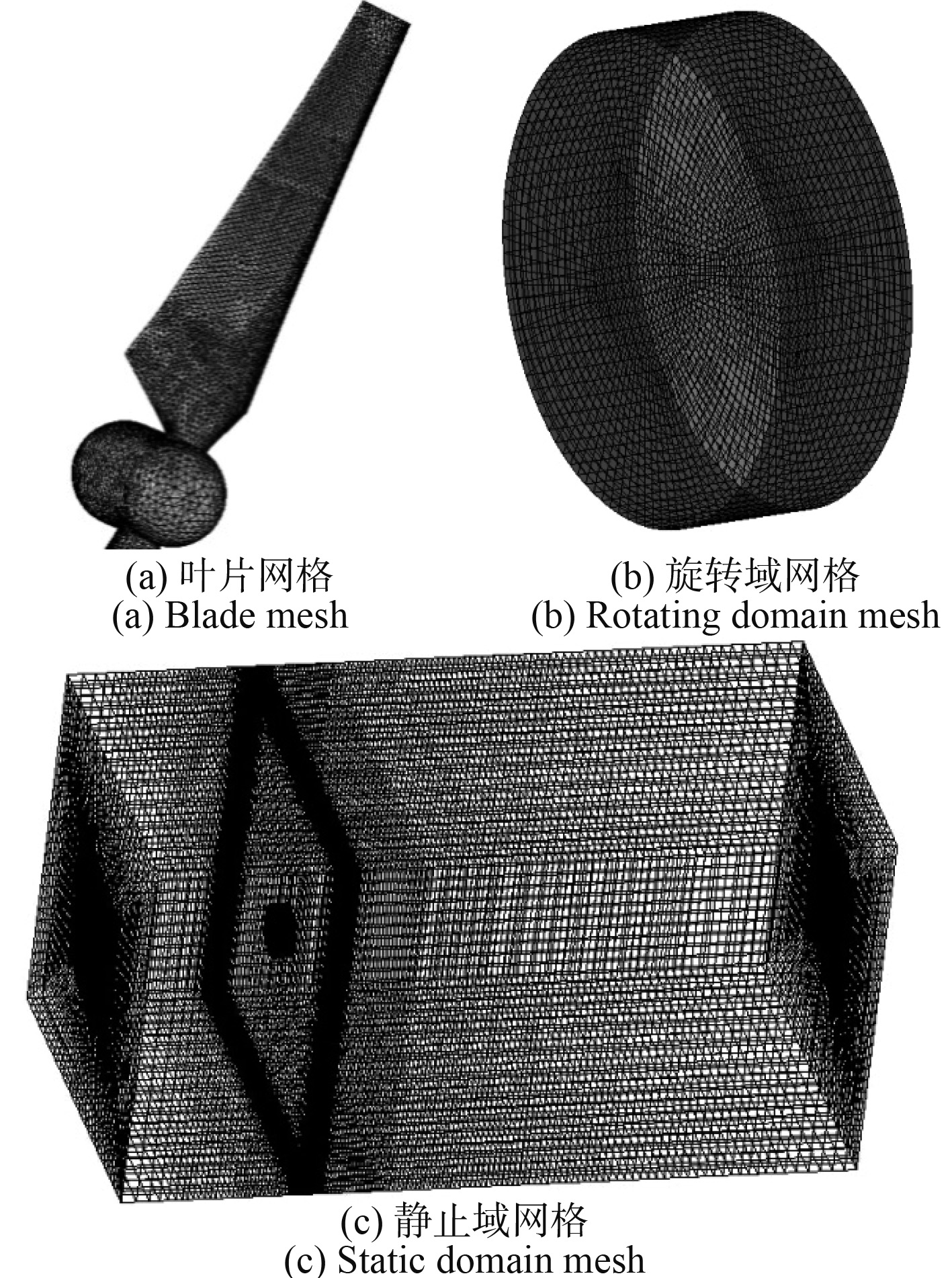
3.2 CFD数值模拟方法水平轴叶轮CFD数值模拟主要使用滑移网格方法,设置叶轮距离入口和两侧壁面均为3~4D(D为叶轮直径),距离出口8~10D。旋转域采用圆柱体,静止域采用长方体或圆柱体均可。静止域采用结构化网格,旋转域采用非结构网格,网格效果如图5所示。为充分模拟边界层效应,使得湍流模拟较为准确,需保证叶片表面
|
图 5 计算域网格示意图 Fig. 5 Schematic diagram of computational domain mesh |
边界条件的设置为:大气压为参考压力,给定重力加速度的方向。入口边界为速度入口,给定均匀来流速度、湍流参数。流体计算域的左右两侧和底面为自由滑动壁面。流体计算域的出口和顶部为开放的压力边界,相对压力设为0。叶片和轮毂表面设置为不可滑移壁面。给定旋转域旋转角速度,静止域和旋转域之间通过滑移交界面连接。计算中湍流模型采用SST模型,求解器为瞬态求解器,时间步长为叶轮旋转3°所用的时间。
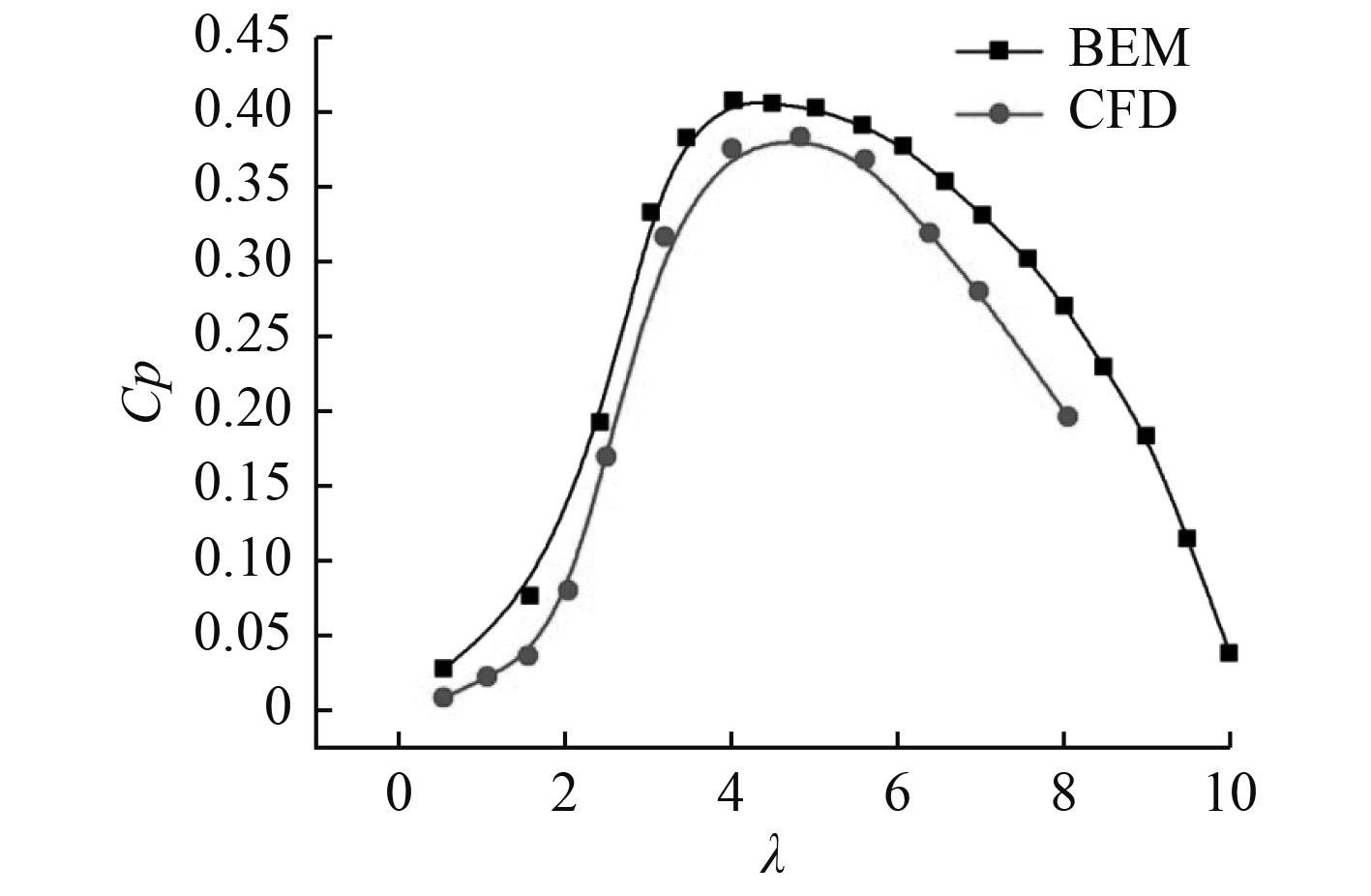
4 计算结果与分析基于上述2种方法的计算,图6对比了叶轮能量利用率
|
图 6
水平轴潮流能水轮机
|
可以看出,2种方法得到的能量利用率曲线随速比的变化趋势相同,均先增大后减小。
通过对比图中的结果可以发现,BEM方法因忽略流体沿展向的流动,以及粘性摩擦等,计算结果偏高。BEM方法和CFD方法的误差在可接受的范围内,对于叶轮水动力性能的预报均有较高的精度。因此考虑到时间成本,基于BEM方法继续对此叶轮的载荷特性进行研究,得到的叶轮的转矩系数、轴向载荷系数随速比的变化规律。
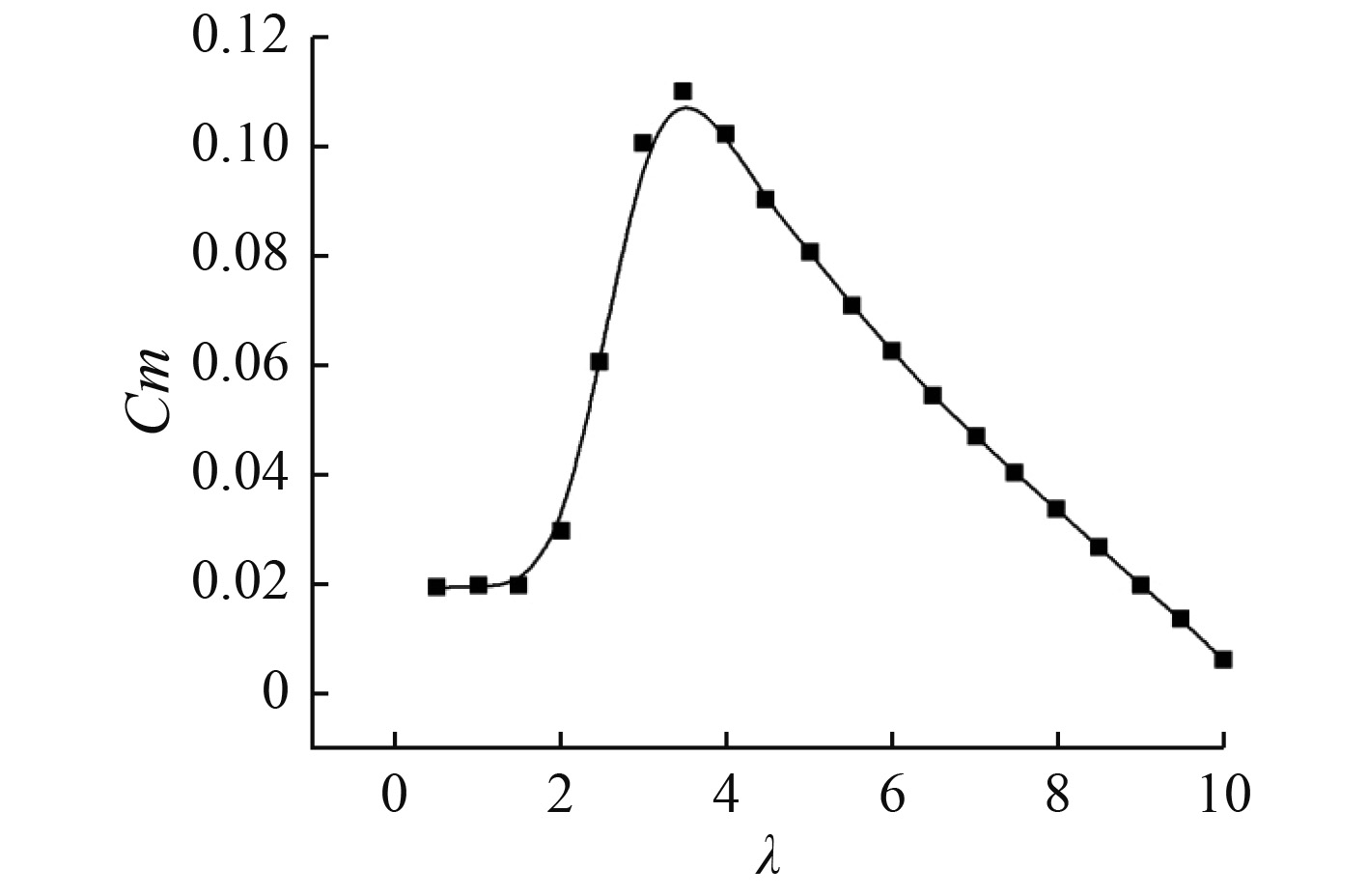
从图7可以看出,在低速比时,叶轮转速系数较低,即叶轮启动时的主动力矩较小。因此在设计轴系,水仓密封等时,需考虑轴系间的摩擦不易过大,否则会出现较难启动的问题。随着转速的增大,叶轮的主动转矩迅速增大,当
|
图 7 叶轮转矩系数随速比变化曲线 Fig. 7 Variation curve of turbine torque coefficient with speed ratio |
|
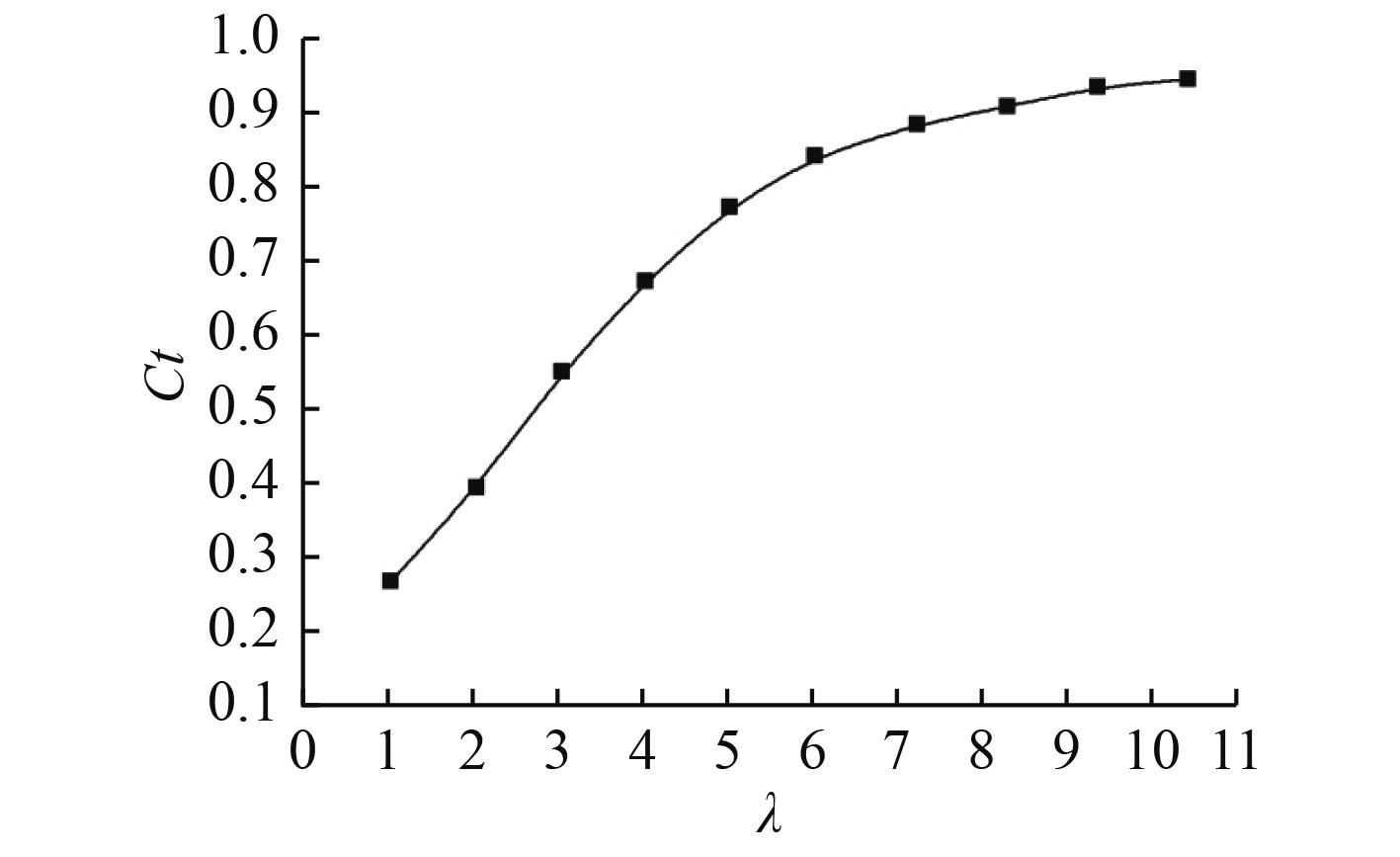
图 8 叶轮轴向载荷系数随速比变化曲线 Fig. 8 Variation curve of turbine axial load coefficient with speed ratio |
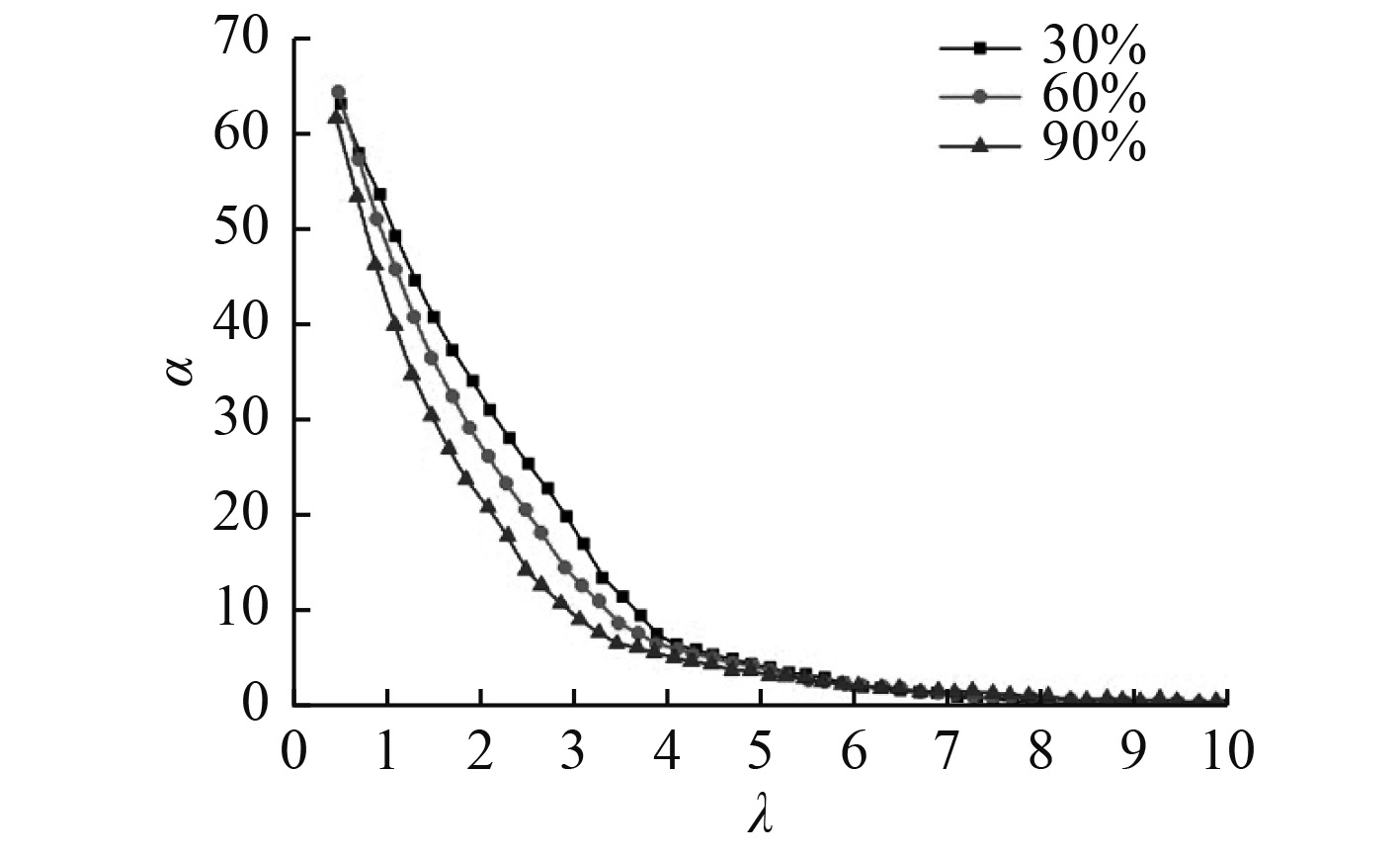
为进一步分析叶片表面的载荷分布情况,选取叶片沿展长方向3个位置进行对比分析(30%,60%和90%叶展位置的叶素)。
从图9可以看出,当低速比时,叶轮根部叶片的攻角较大,处于失速状态,效率较低。随着速比的增大,叶片的转速增大,叶片的攻角减小。为了使叶轮在工作速比时效率达到最优,叶轮设计时应尽量保证不同位置处的叶素,在工作速比时的攻角均达到最优。在最优速比
|
图 9
不同展长位置处攻角
|
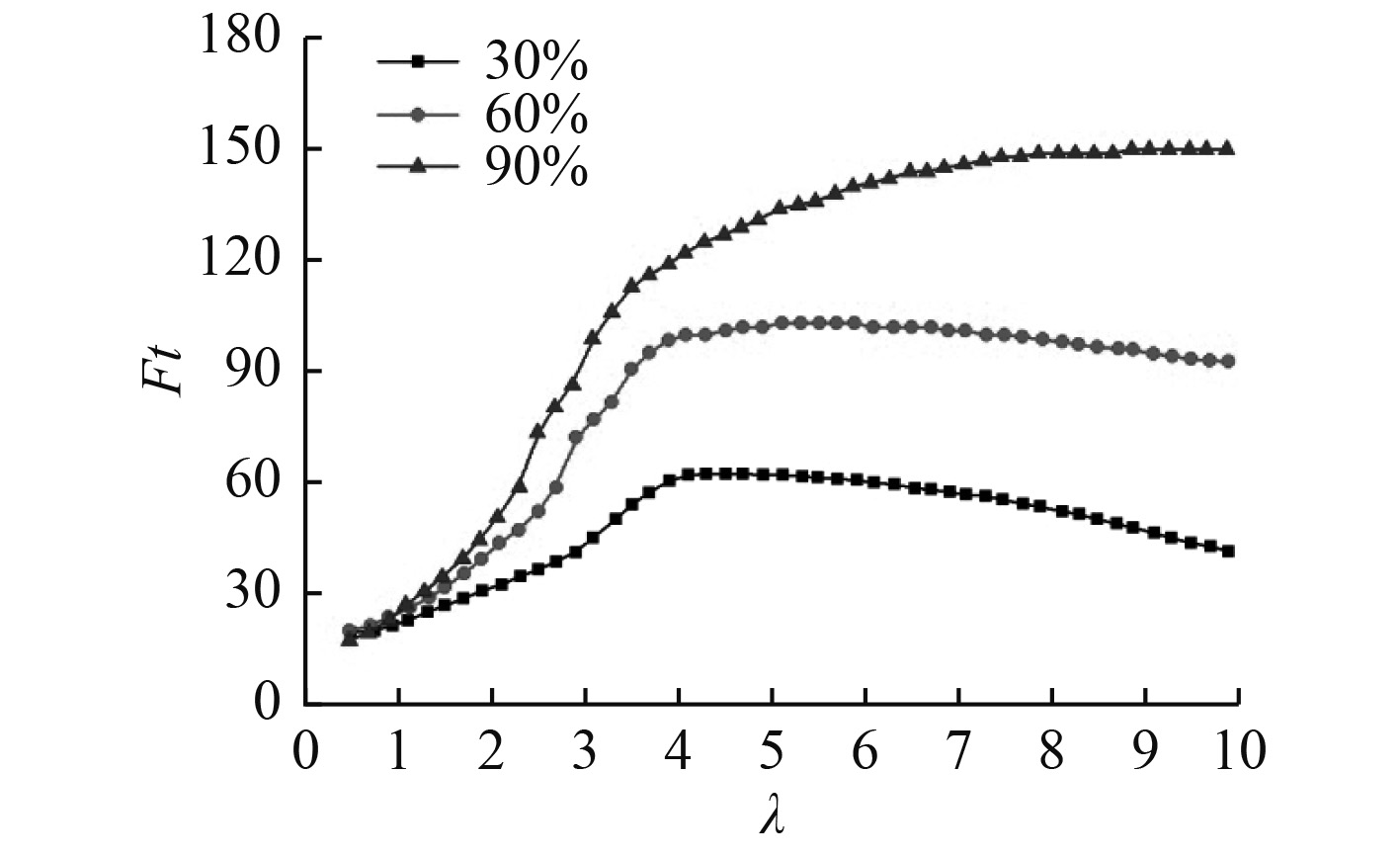
从图10和图11中的载荷曲线可以看出,不同叶素位置对于推力与转速的贡献是不同的,在靠近叶根的位置,由于转速较低,且轮毂涡流系统所产生的涡旋尾流的影响,使得靠近轮毂处的叶片所受的轴向推力载荷较小,同时其动力转矩也较小。随着叶素的半径加大,轴向推力载荷与转矩均有所变大,转矩在速比
|
图 10
不同展长位置处轴向推力Ft随速比
|
|
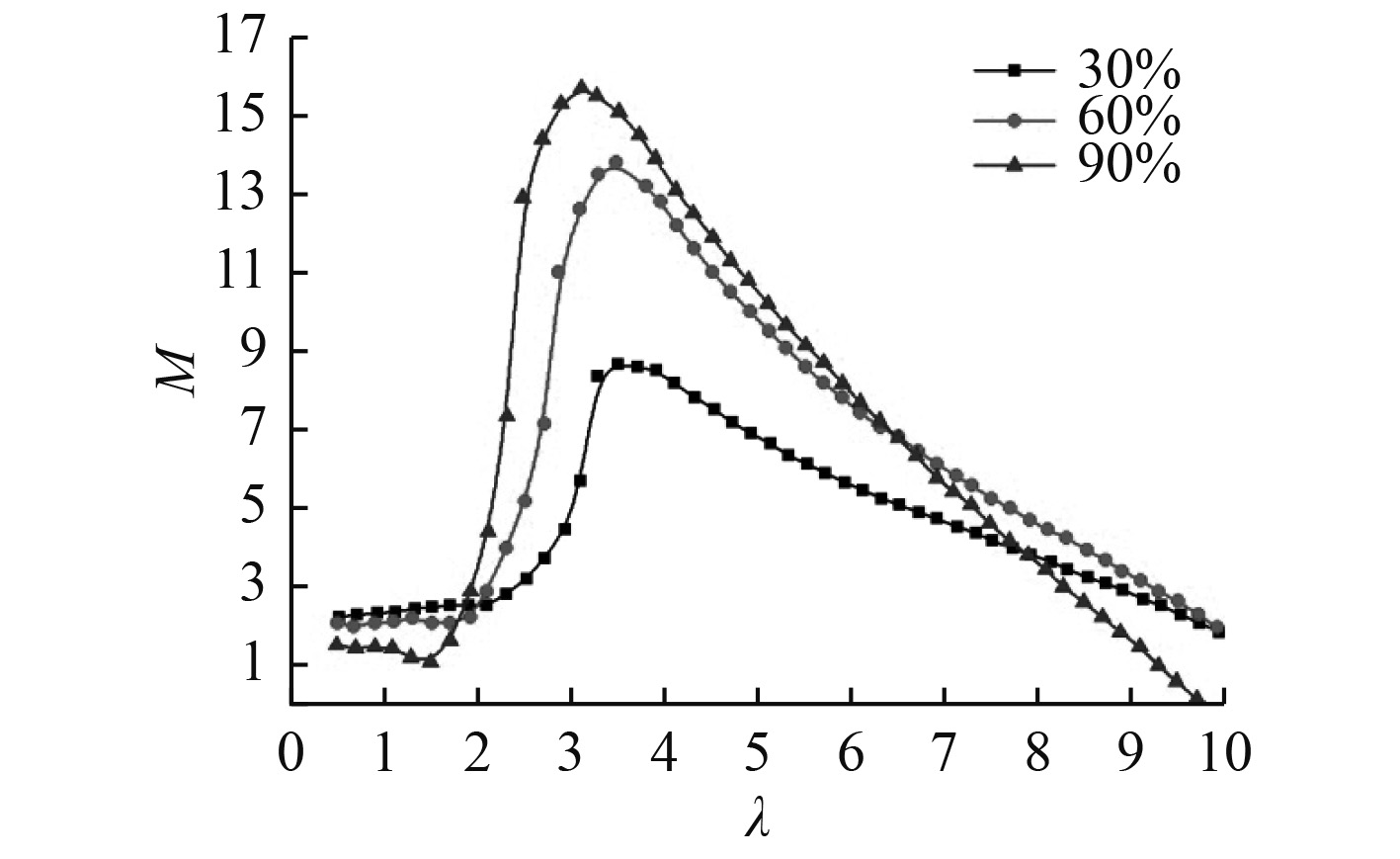
图 11
不同展长位置处转矩M随速比
|
本文基于Glauert涡流设计理论进行水平轴潮流能叶轮的设计,并采用BEM叶素动量理论与CFD数值模拟2种方法,对所设计的叶轮模型进行载荷与性能的预报,证明此水轮机模型的工作性能达到了设计要求。由研究结果可知:
1)叶片的形状参数和入流角只与工作速比有关,与翼型气动性能无关;
2)对于水平轴叶轮水动力性能的预报,BEM方法和CFD方法均有较高的精度;
3)叶轮在最优速比时转矩并不是最大的,叶轮转矩的最大值提前了0.5个速比;
4)工作速比下,提供叶片旋转转矩的部位主要分布在叶片展向上60%~90%处;
5)在低速比时,30%~60%小半径处叶素的转矩贡献更大,即小半径处的叶素对叶轮的自启动性能起着至关重要的作用。
| [1] |
HANCOCK K J, SOVACOOL B K. International political economy and renewable energy: hydroelectric power and the resource curse[J]. Social Science Electronic Publishing, 2018. |
| [2] |
WANG S Q, KE S, GANG X, et al. Hydrodynamic analysis of horizontal-axis tidal current turbine with rolling and surging coupled motions[J]. Renewable Energy, 2017, 102: 87-97. DOI:10.1016/j.renene.2016.10.036 |
| [3] |
张亮, 李新仲, 耿敬, 等. 潮流能研究现状2013[J]. 新能源进展, 2013, 1(1): 53-68. DOI:10.3969/j.issn.2095-560X.2013.01.006 |
| [4] |
张亮, 尚景宏, 张之阳, 等. 潮流能研究现状2015——水动力学[J]. 水力发电学报, 2016, 35(2): 1-15. DOI:10.11660/slfdxb.20160201 |
| [5] |
刘安. 水平轴潮流能水轮机叶片的空化特性数值模拟及优化设计[D]. 镇江: 江苏大学, 2018.
|
| [6] |
张德胜, 刘安, 陈健, 等. 采用粒子群算法的水平轴潮流能水轮机翼型多目标优化[J]. 浙江大学学报(工学版), 2018, 52(12): 2349-2355. DOI:10.3785/j.issn.1008-973X.2018.12.013 |
| [7] |
陈存福. 潮流能水平轴水轮机叶片优化及水动力性能研究[D]. 青岛: 中国海洋大学, 2012.
|
| [8] |
王晓航. 水平轴潮流能水轮机叶片设计与水动力特性研究[D]. 哈尔滨: 哈尔滨工程大学, 2015.
|
| [9] |
万德成, 程萍, 黄扬, 等. 海上浮式风机气动力-水动力耦合分析研究进展[J]. 力学季刊, 2017(3): 5-27. |
| [10] |
王树齐, 肖钢, 张亮, 等. 潮流能水平轴水轮机支撑立柱干扰研究[J]. 华中科技大学学报(自然科学版), 2014, 42(4): 81-85. |
 2021, Vol. 43
2021, Vol. 43
