2. 广东海洋大学 海运学院,广东 湛江 524088;
3. 大连海事大学 航运经济与管理学院,辽宁 大连 116026
2. Maritime College, Guangdong Ocean University, Zhanjiang 524088, China;
3. School of Maritime Economics and Management, Dalian Maritime University, Dalian 116026, China
随着科研水平的提高及经济发展的需要,新型集装箱船都趋于大型化和高速化。目前,中高速集装箱船面临着如何既能提高船速又能保证节能高效的问题。船舶的主推进装置−螺旋桨来说,则成为船舶高速化和节能高效性发展的重点研发对象。因此,如何更有效提高螺旋桨的敞水性能和节能高效性能已经成为国内外众多船舶水动力学专家的研究热点,而作为特种船舶高速推进装置的大侧斜螺旋桨来说,当它的叶片的每个半径切面不同时通过高伴流区,并凭借其侧斜角较大的特殊结构导致由螺旋桨引起的轴承力和表面力特性减小。可以认为,螺旋桨的侧斜结构是可以提高螺旋桨敞水性能及节能高效性的。因此,鉴于大侧斜螺旋桨所具备的侧斜分布特性,探究在螺旋桨的侧斜分布对于其敞水性能以及节能高效性的影响对于发展高速节能型民用船舶有着重大意义。
近年来,国内外有很多专家学者对螺旋桨的水动力学模拟仿真实验进行了研究:Tran Ngoc[1]以RANSE法为工具并对螺旋桨的敞水性能进行了数值模拟仿真实验,计算结果与试验值较为吻合;Sahoo P K[2]进行了CFD预测与推进器模拟,结果表明CFD方法对于螺旋桨的性能预报较为精确;Bennaya M[3]进行了非均匀入流下船舶螺旋桨诱导水动力周期力的CFD估算等研究,模拟仿真了非定常流场下的螺旋桨水动力实验,表明CFD仿真实验结果值与试验值基本吻合;周斌等[4]对反旋向侧斜导管螺旋桨进行了水动力学仿真模拟实验,计算表明反旋向侧斜螺旋桨在改善螺旋桨性能方面具备潜力;饶志强等[5]以七叶侧斜螺旋桨为研究对象并对该桨的各项参数进行了优化处理,处理结果表明该桨进行了侧斜分布优化后,螺旋桨效率比原桨高;任万龙等[6]基于粒子群算法,以侧斜分布作为优化变量,推力系数作为约束条件展开了螺旋桨优化设计的研究,研究结果表明螺旋桨的侧斜分布将会一定程度上改善螺旋桨的敞水性能;张瑞等[7]研究了侧斜分布对螺旋桨水动力特性的影响,以艇后螺旋桨为研究对象并对其水动力特性进行了水动力学数值模拟仿真实验,结果表明当螺旋桨侧斜角增加时,将导致螺旋桨轴系推力的振荡波动得到明显改善;蔡昊鹏等[8]以性能预报工具与智能寻优算法相结合的方法,采用算法优化的方式设计螺旋桨的侧斜分布,表明经过该算法优化后的螺旋桨侧斜分布将在螺旋桨的推进性能以及高效节能性能方面表现优异;曹峰等[9]以非定常流场下五叶侧斜螺旋桨为研究对象并研究了其流固耦合特性,进而对该螺旋桨的敞水特性进行了水动力学模拟仿真实验,结果表明仿真实验结果与试验结果基本一致,同时证明了CFD仿真方法的精确性和有效性。
以上研究内容表明近年来国内外水动力学方面的专家学者对于CFD仿真方法是否能够用于准确预报螺旋桨的敞水性能这一问题进行了讨论和研究,同时对于螺旋桨侧斜分布问题的研究也表明螺旋桨的侧斜分布对螺旋桨推进性能的改良具有一定影响。因此,本文首先对仿真实验的精确性进行了验证,将仿真结果与水池试验结果进行对比分析后发现相差不大,因此可以认为本仿真实验是具备可靠性的。然后通过3种不同的侧斜分布(40°,50°,60°)螺旋桨的对比验证探究螺旋桨的侧斜分布对其敞水性能方面的影响,结果表明侧斜角的增大有助于提高螺旋桨的推力以及效率。
1 理论基础 1.1 控制方程在解决任何流体问题之前,首先要做的是对控制方程的建立。假定水流与螺旋桨的流动分析中没有热交换发生,则可直接将连续方程与动量方程作为控制方程使用。其连续性方程为:
| $\frac{{\partial \rho }}{{\partial t}} + \frac{{\partial \left( {\rho u} \right)}}{{\partial x}} + \frac{{\partial \left( {\rho v} \right)}}{{\partial y}} + \frac{{\partial \left( {\rho w} \right)}}{{\partial z}} = 0{\text{,}}$ | (1) |
其动量守恒方程为:
| $\begin{split} &\frac{{\partial \left( {\rho u} \right)}}{{\partial t}} + {\rm{div}}\left( {\rho u{u}} \right) = - \frac{{\partial \rho }}{{\partial x}} + \frac{{\partial {\tau _{xx}}}}{{\partial x}} + \frac{{\partial {\tau _{yx}}}}{{\partial y}} + \frac{{\partial {\tau _{zx}}}}{{\partial z}} + {F_x}{\text{,}}\\ &\frac{{\partial \left( {\rho v} \right)}}{{\partial t}} + {\rm{div}}\left( {\rho v{u}} \right) = - \frac{{\partial \rho }}{{\partial y}} + \frac{{\partial {\tau _{xy}}}}{{\partial x}} + \frac{{\partial {\tau _{yy}}}}{{\partial y}} + \frac{{\partial {\tau _{zy}}}}{{\partial z}} + {F_y}{\text{,}}\\ &\frac{{\partial \left( {\rho w} \right)}}{{\partial t}} + {\rm{div}}\left( {\rho w{u}} \right) = - \frac{{\partial \rho }}{{\partial z}} + \frac{{\partial {\tau _{xz}}}}{{\partial x}} + \frac{{\partial {\tau _{yz}}}}{{\partial y}} + \frac{{\partial {\tau _{zz}}}}{{\partial z}} + {F_z}{\text{。}} \end{split}$ | (2) |
式中:
本文的水动力学仿真实验选择计算精度较高且收敛速度较快的Realizable
| ${\rho \frac{{{\rm{D}}k}}{{{\rm{D}}t}} = \frac{\partial }{{\partial {x_i}}}\left[ {\left( {{\mu _l} + \frac{{{\mu _t}}}{{{\sigma _\varepsilon }}}} \right)\frac{{\partial k}}{{\partial {x_i}}}} \right] + {G_k} + {G_b} - \rho \varepsilon }{\text{,}}$ | (3) |
| $\begin{split}\frac{{{\rm{D}}(\rho \varepsilon )}}{{{\rm{D}}t}} + \frac{{{\rm{D}}\left( {\rho \varepsilon {\mu _l}} \right)}}{{{\rm{D}}{x_i}}} =& \frac{\partial }{{\partial {x_j}}}\left[ {\left( {{\mu _l} + \frac{{{\mu _t}}}{{\sigma \varepsilon }}} \right)\frac{{\partial \varepsilon }}{{\partial {x_i}}}} \right] + \\ &\rho {C_1}E\varepsilon - \rho {C_2}\frac{{{\varepsilon ^2}}}{{k + \sqrt {v\varepsilon } }}{\text{。}}\end{split} $ | (4) |
其中:
| $\begin{split} &{\sigma _\varepsilon } = 1.2,\quad {\sigma _k} = 1.0,\quad {C_2} = 1.9{\text{,}}\\ &{C_1} = \max \left( {0.43,\frac{\eta }{{\eta + 5}}} \right){\text{,}} \end{split}$ | (5) |
| ${\eta = {{\left( {2{E_{ij}} \cdot {E_{ij}}} \right)}^{\frac{1}{2}}}\frac{k}{\varepsilon }}{\text{,}}$ | (6) |
| ${{E_{ij}} = \frac{1}{2}\left( {\frac{{\partial {\mu _i}}}{{\partial {x_j}}} + \frac{{\partial {\mu _j}}}{{\partial {x_i}}}} \right)}{\text{。}}$ | (7) |
以Hassan Ghasseni研究的五叶大侧斜螺旋桨为例,开展中高速集装箱船高效推进器的设计研究。首先完成大侧斜螺旋桨模型的建立,掌握了HSP-5的主要几何参数,(如表1所示)。之后,通过几何前处理软件处理分析表1数据,并生成如图1所示的五叶大侧斜螺旋桨。
|
|
表 1 五叶大侧斜螺旋桨的主要参数 Tab.1 Main dimensions of the propeller HSP-5 |

|
图 1 五叶大侧斜螺旋桨三维模型 Fig. 1 Three-dimensional model of five-blade high skew propeller |
由图1可知,该桨运用型值表法,并通过SolidWorks建模软件完成对五叶大侧斜螺旋桨的三维模型。
2.2 建立计算域针对螺旋桨的数值模拟方法有多种,鉴于仿真环境设定需求的区别可分为稳态方法的MRF、瞬态方法的RBM及OM。对于水动力仿真,存在2种流场的设定:定常流域和非定常流域。由于本文主要考察侧斜桨和常规桨在仿真实验中所能产生的推力值和扭矩值以及效率,因此采用MRF方法对所研究螺旋桨进行水动力学模拟仿真实验即可。为了模拟螺旋桨在敞水中的运行,推进器应放置在较大的计算流域中,以减少边界对螺旋桨流体动力学仿真结果的影响。但是,如果计算流域过大将会导致计算负担加重,计算时间也将会延长。仿真实验情况为螺旋桨处在静止的流域,假设该流域中的水是有设定初速地从入口面进入并从出口面流出。根据相对运动原理,可用于模拟螺旋桨在流域中旋转且前进的状态。因此计算域分为2个部分,一部分是不包含螺旋桨的静止计算域,另一部分是包含螺旋桨的旋转计算域,其中静止计算域模拟了均匀来流的行进情况,而旋转计算域则模拟了螺旋桨的旋转情况,Fluent中提供的MRF模型即多重参考系模型正是用来模拟相对旋转及行进的仿真实验,这样设置的流域与实际情况是相符的。
计算坐标系设置在螺旋桨轴上的直角坐标系,坐标系原点为螺旋桨轴心,X轴正方向指向计算域的出口方向且与桨轴重合。内计算域进口距原点0.5R,且出口距原点0.5R;外计算域进口距内计算域进口为3R,且外计算域出口距内计算域出口为10R。整体计算域设置如图2所示。
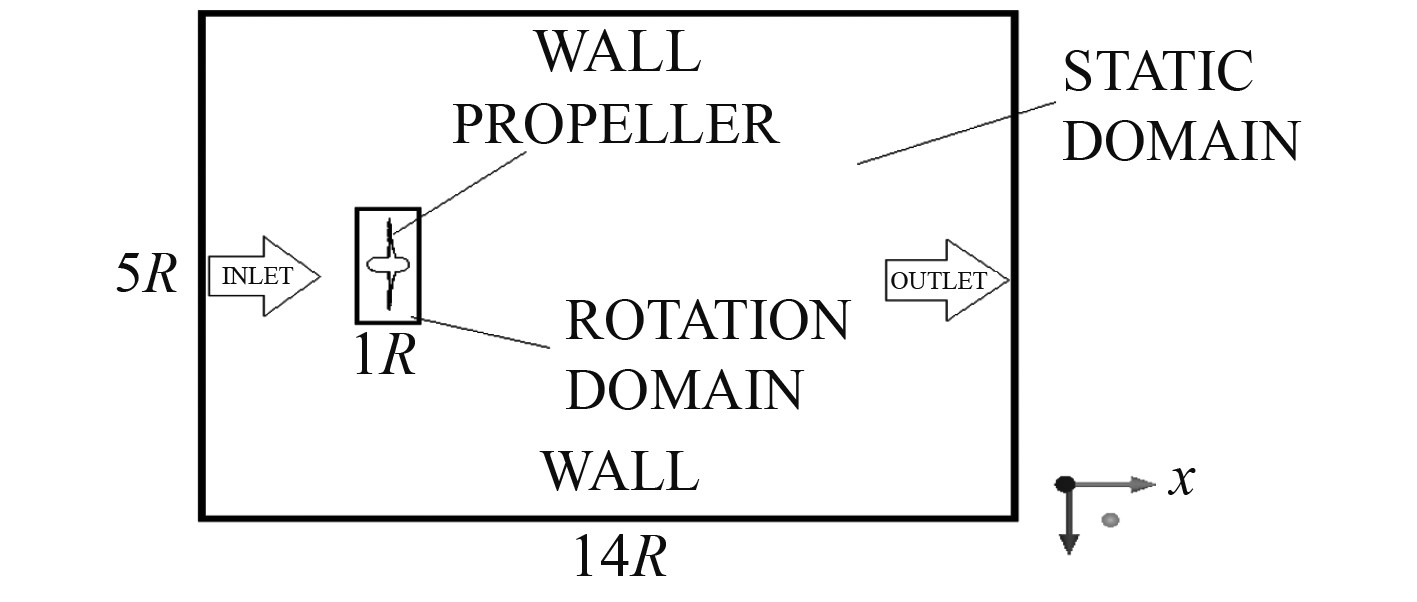
|
图 2 计算域设置 Fig. 2 Calculation domain settings |
对于水动力仿真模拟来说,结果的质量如何在很大程度上取决于网格捕捉围绕螺旋桨水流的特征有多成功。本文的模拟中,将为旋转区域及其周围使用切割体网格生成器网格模型,并使用拉伸网格网格生成器网格化轴周围的静态区域,这样可以最大程度降低计算成本。
旋转区域和四周静态区域之间的交界面形状为圆柱形。因此,本文采取让交界面每一侧的网格单元都互相垂直,即在交界面的任一侧生成一个单棱柱层网格单元。如图3所示,网格模型采用了切割体网格生成器、拉伸网格生成器、棱柱层网格生成器和表面重构,并将Base Size设为0.03 m,棱柱层厚度设为20%,棱柱层数设为5。此外,为了对螺旋桨周围水流更加精确的捕捉,在旋转域周围设定了体积控制,Relative Size设为50%,0.015 m。如图4所示,网格处理对螺旋桨的桨叶随边及导边进行了特征线的控制,其中,Relative Minimum Size为2%且Relative Target Size设为5%。之后,分别对桨叶以及桨毂进行了网格尺寸的加密,有效提升了网格质量,最终生成如图3所示的整体网格Cells值为 6611235,Faces值为19732320,Vertices值为7064064。
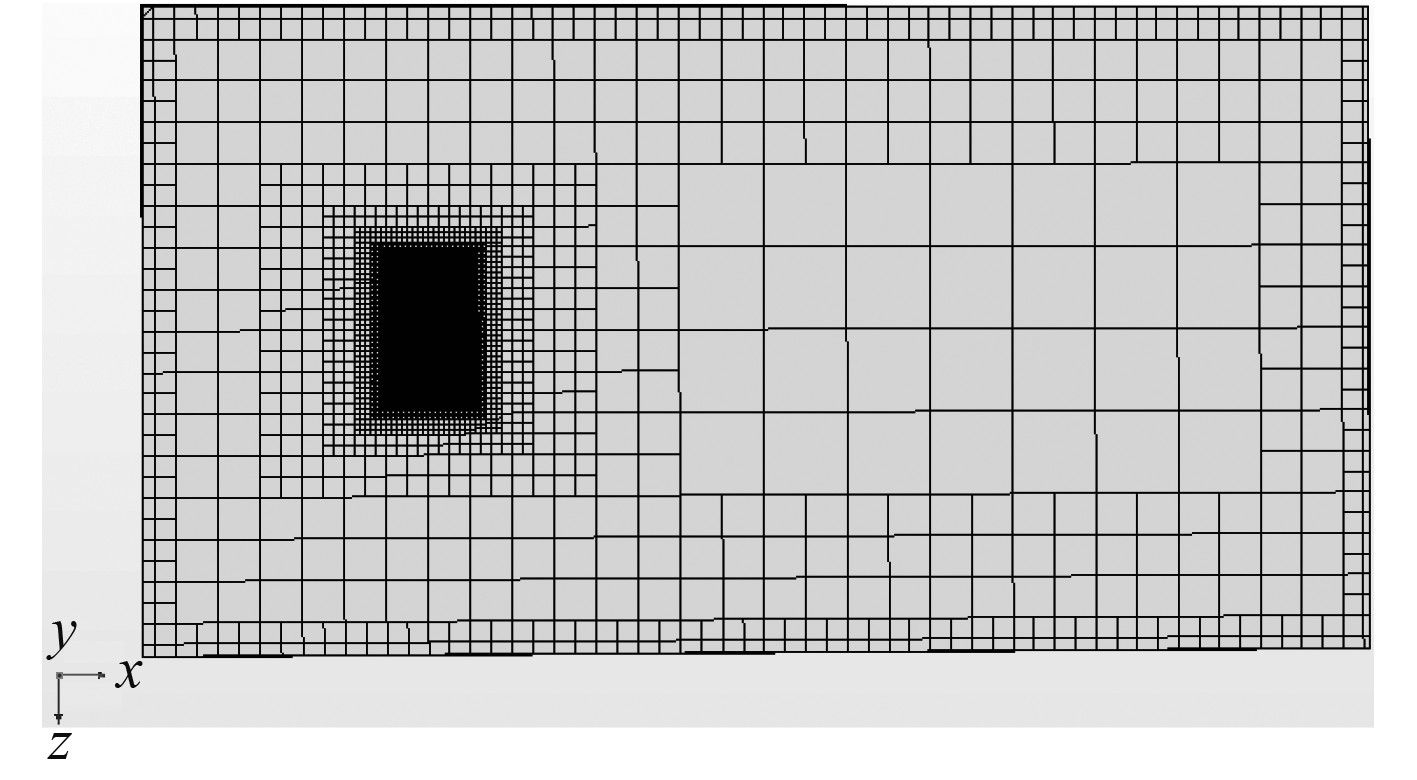
|
图 3 整体网格XZ平面截图 Fig. 3 Screenshot of XZ plane of overall grid |

|
图 4 螺旋桨面网格 Fig. 4 Propeller surface grid |
STAR-CCM+是一个完整的多物理场解决方案,它可以用于实际条件下工作的产品和设计,并通过STAR-CCM+仿真软件实现了对五叶大侧斜螺旋桨的数值模拟仿真。在Region中分别对旋转域和静止域中的Parts进行边界条件的定义:首先,在旋转域与静止域之间建立交界面,确保初始条件的正常设置;然后,对静止域中的进口Inlet设为速度进口,且速度幅值设为6.09 m/s,对静止域的出口Outlet设为压力出口,以及对静止域的壁面Wall设为壁面,其余条件默认即可。最后,对旋转域的螺旋桨设为壁面,并改变物理值中的运动规范为旋转,旋转速度为360 r/min,旋转方向为(−1.0,0.0,0.0)。在连续体中的Physics设置为
根据进速系数来设置均匀来流的速度,由公式
| $J = \frac{{{V_A}}}{{nD}}{\text{,}}$ | (8) |
得,当J=0.7时,计算域进速度为6.09 m/s。
3.2 水动力学仿真实验的可靠性与精确性验证以360 r/min的转速,分别进行J=0.3~0.9的仿真实验,并将仿真结果与试验结果进行对比分析,以此保证仿真的可靠性与精确性。仿真结果与水池试验结果的对比如表2所示。
|
|
表 2 五叶大侧斜螺旋桨的敞水特性对比 Tab.2 Comparison of open water characteristics of the HSP-5 |
图5为HSP-5五叶大侧斜螺旋桨敞水性能曲线,且包含了仿真实验结果与水池试验结果的对比。可以看出:该桨的仿真试验结果与水池试验结果相差无几,但对于推力系数曲线来说,在进速系数为0.3~0.5范围内时,仿真结果比试验结果略低;而进速系数为0.5~0.8范围内时,仿真结果比试验结果略高;在进速系数为0.8~0.9时,仿真结果又再次略低于试验结果。对于扭矩系数曲线来说,在进速系数为0.3~0.55范围内,仿真结果比试验结果略低;在进速系数为0.55~0.9范围内,仿真结果比试验结果较高。效率曲线几乎一致。
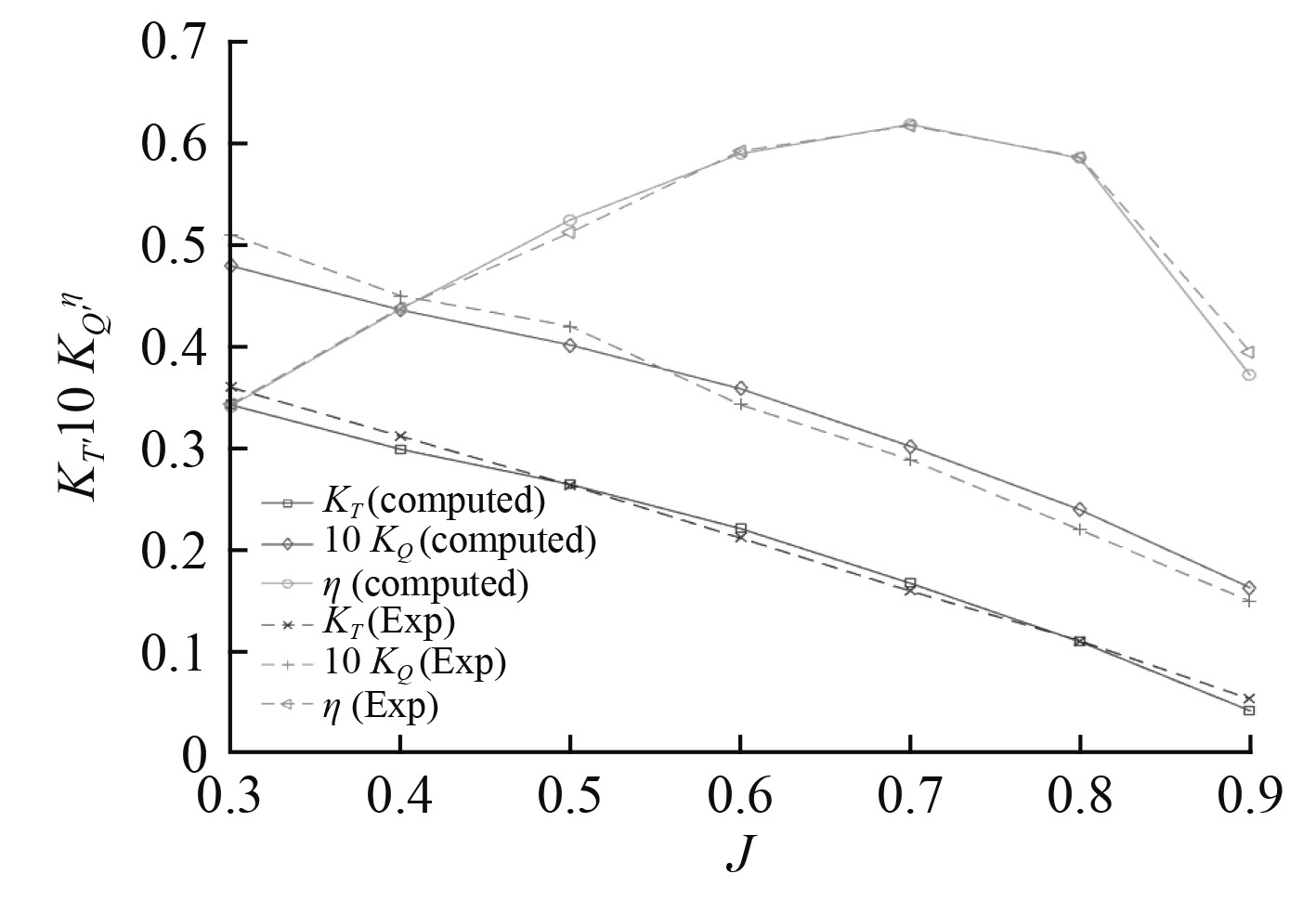
|
图 5 五叶大侧斜螺旋桨敞水性能曲线 Fig. 5 Open water performance curve of five-blade high skew propeller |
以上对比实验说明,模型尺度模拟与水池试验数据基本吻合,误差在4%左右。因此,认为仿真实验具备可靠性和精确性。
4 后处理后处理的目的是有效地观察和分析流动计算结果。随着计算机图形功能的提高,通过后处理功能的动态模拟流动效果,直观地分析仿真结果。对于五叶大侧斜螺旋桨的仿真结果后处理分别是压力标量图、速度矢量图以及等值线图。当J=0.7时,大侧斜螺旋桨的推力面和吸力面的压力分布云图如图6和图7所示,其速度矢量图如图8和图9所示。
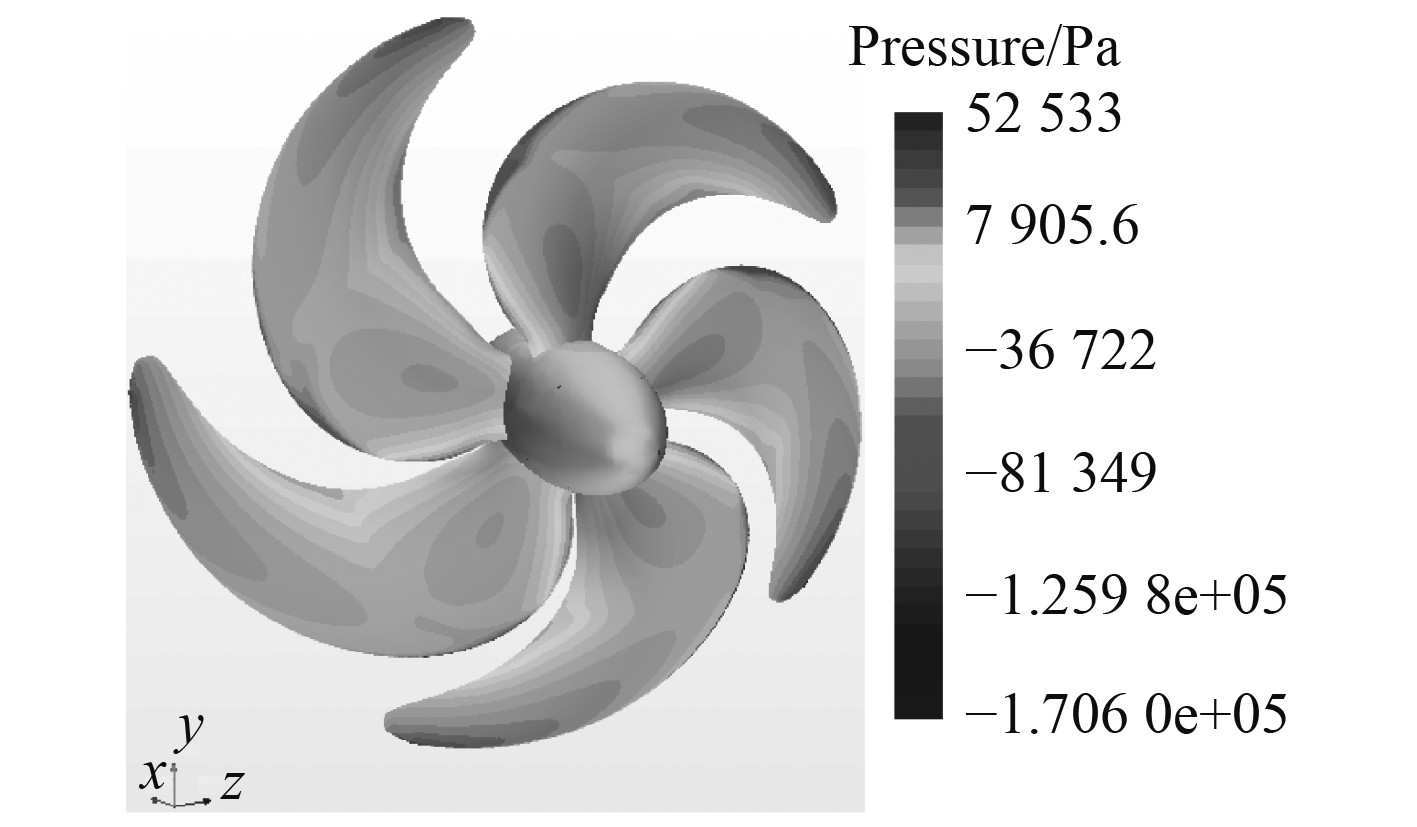
|
图 6 推力面压力标量图 Fig. 6 Scalar plot of thrust surface pressure |
|
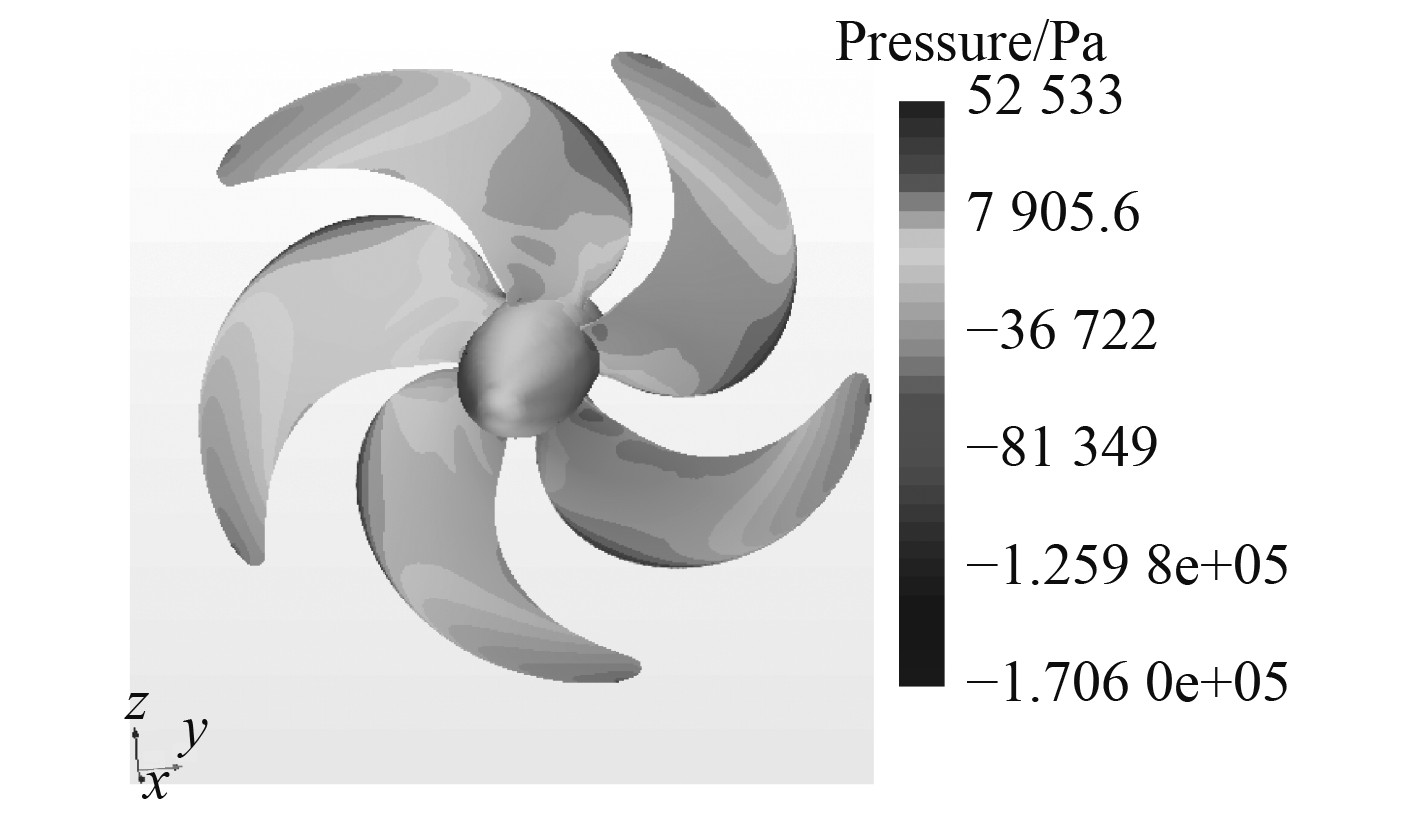
图 7 吸力面压力标量图 Fig. 7 Scalar plot of suction surface pressure |
|
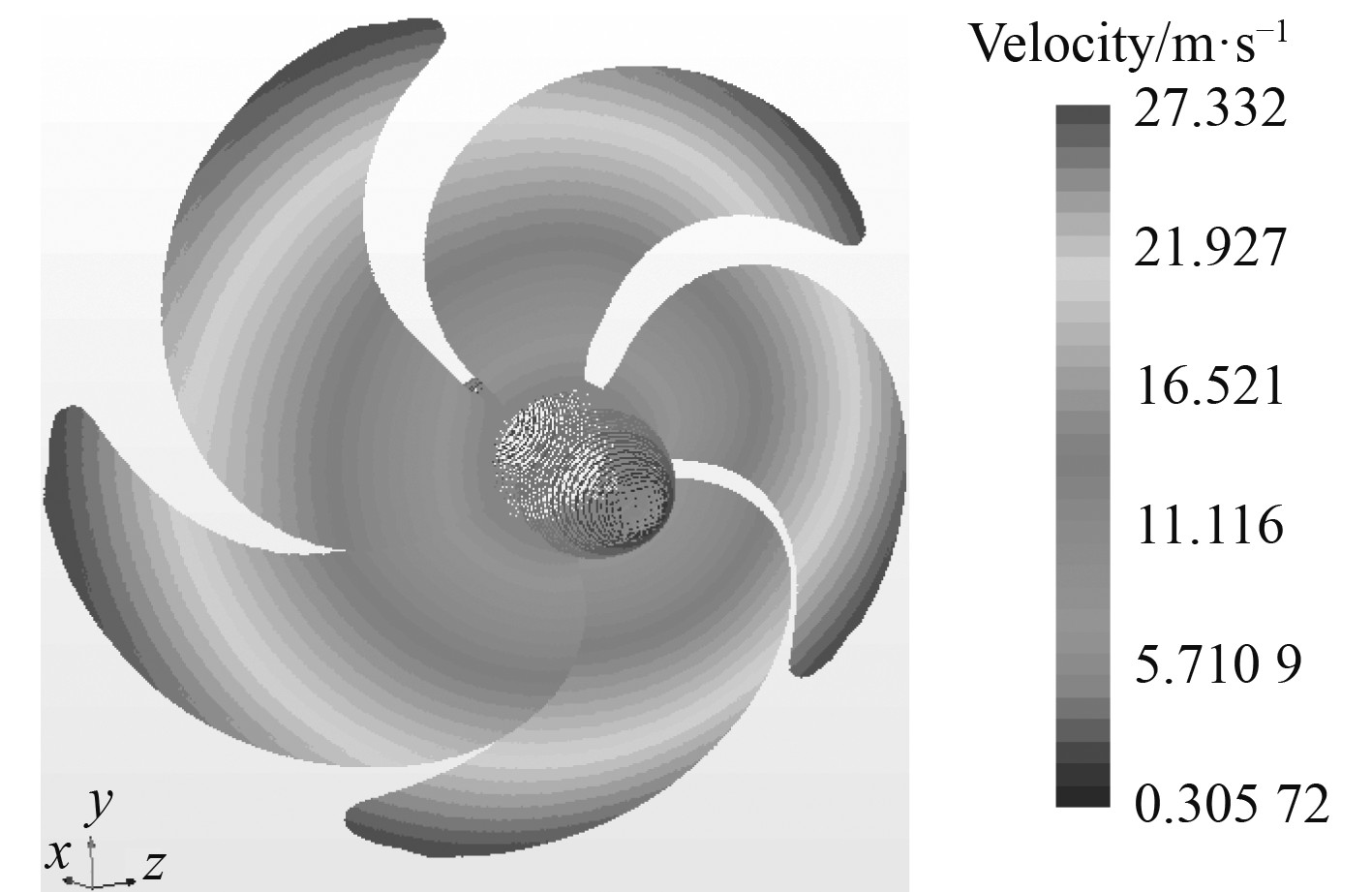
图 8 推力面速度矢量图 Fig. 8 Velocity vector diagram of thrust surface |
|
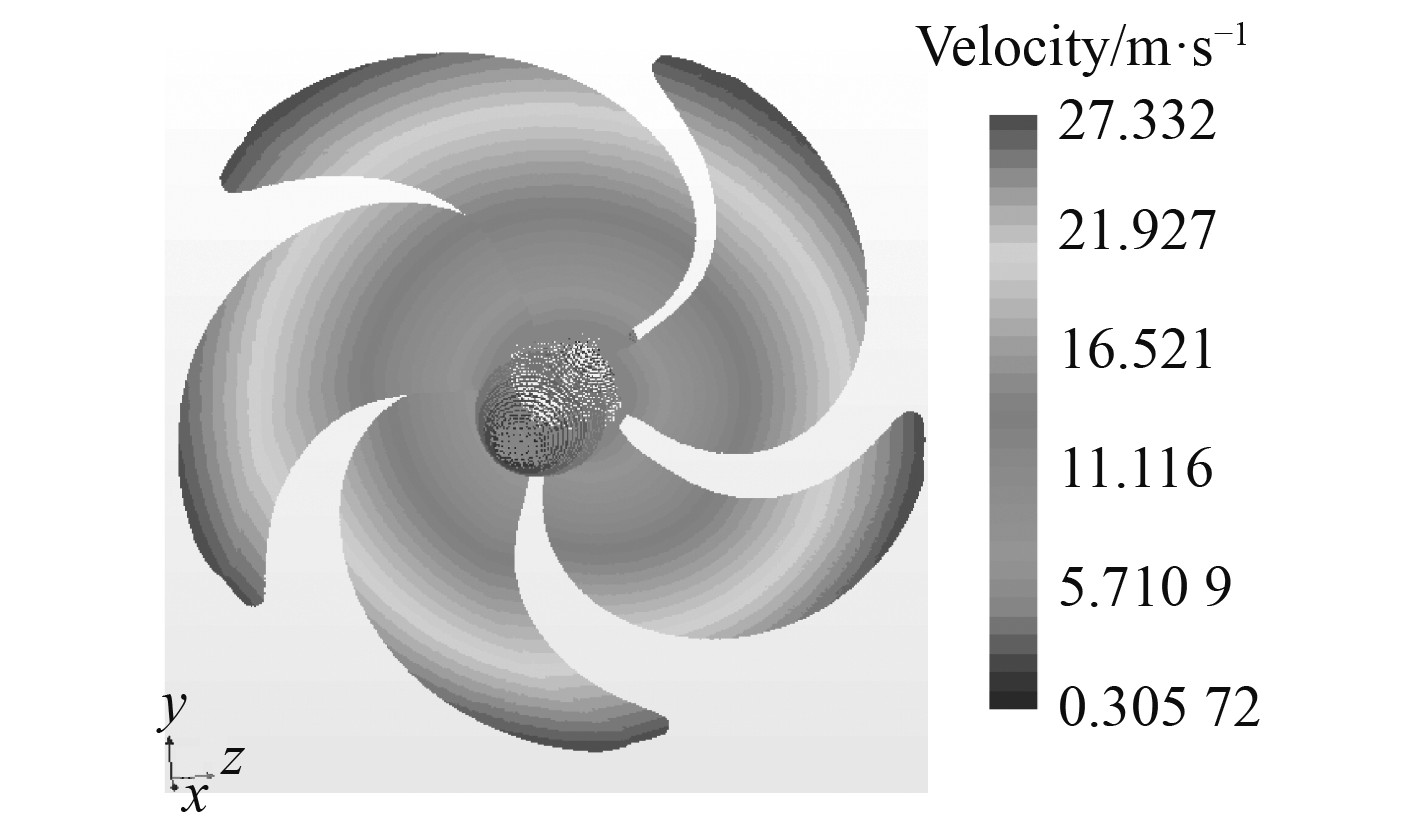
图 9 吸力面速度矢量图 Fig. 9 Velocity vector diagram of suction surface |
由图6和图7可知,推力面的压力分布整体范围上均比吸力面的压力分布的值要大,且最大压力为52533 Pa以及最大负压为(−1.7060e+05)Pa。由图8和图9可知,螺旋桨表面的速度从螺旋桨轴的中心到叶片的尖端逐渐增大,最大值在叶梢处生成,速度为27.332 m/s。
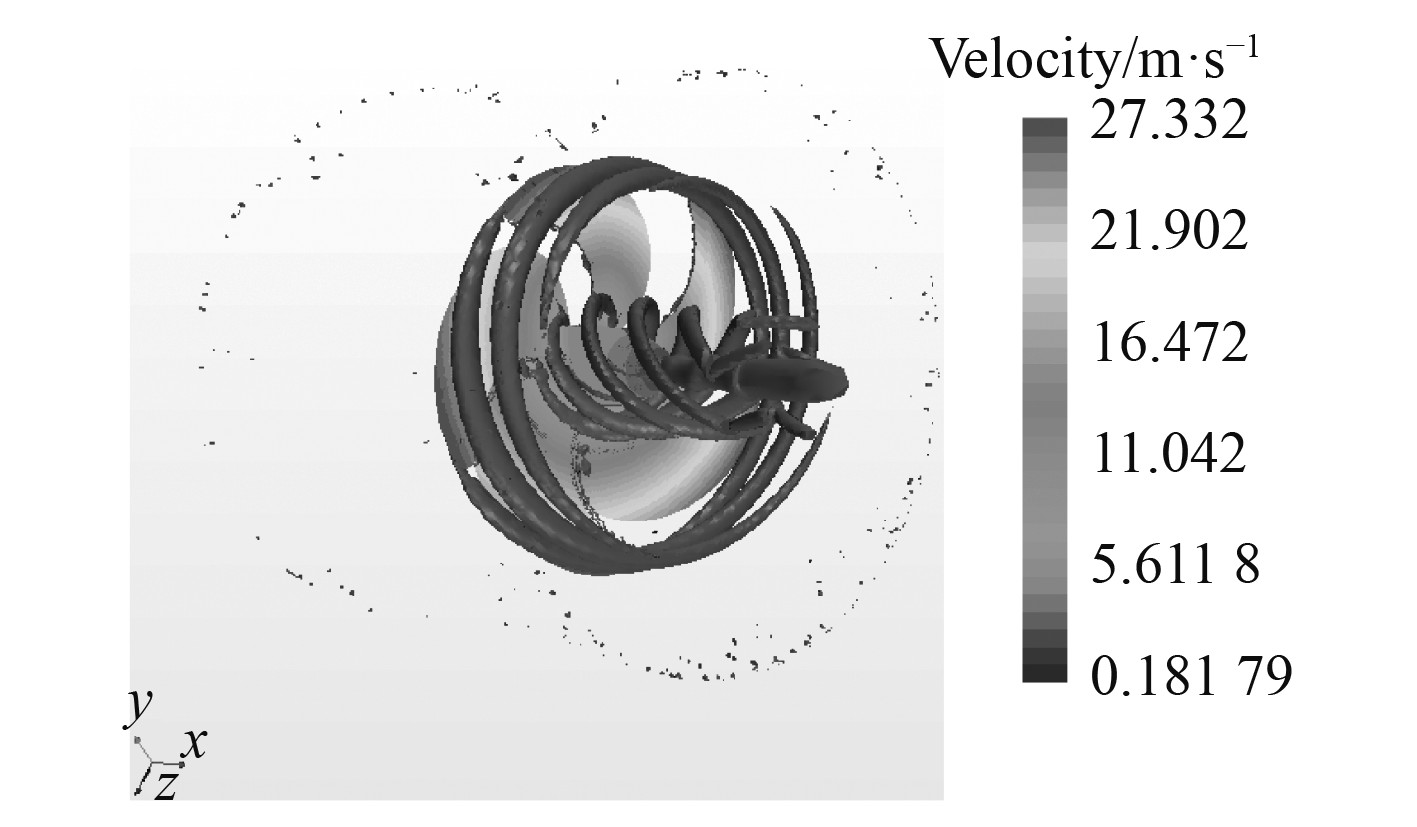
对于衍生零部件中等值面的标量场选择为Q-Criterion,值为400.0/s2。编辑速度矢量图后,大侧斜螺旋桨的尾流迹线如图10和图11所示。尾流中存在内涡和外涡,并都趋于收敛状态。

|
图 10 螺旋桨尾流迹线图 Fig. 10 Propeller wake trace diagram |
|
图 11 尾流迹线斜视图 Fig. 11 Oblique view of wake trace |
原型五叶大侧斜螺旋桨侧斜为55°,改变其侧斜分布,选取侧斜角分别为另40°,50°和60°,其他几何参数与原型桨保持一致,得到如图12所示的三个大侧斜螺旋桨。仿真实验设置均与原型桨仿真实验相同,仿真结果如表3~表5所示。
|
|
表 3 40°侧斜角五叶大侧斜螺旋桨的水动力性能 Tab.3 Hydrodynamic performance of the HSP-5 propeller(40°) |
|
|
表 5 60°侧斜角五叶大侧斜螺旋桨的水动力性能 Tab.5 Hydrodynamic performance of the HSP-5 propeller(60°) |
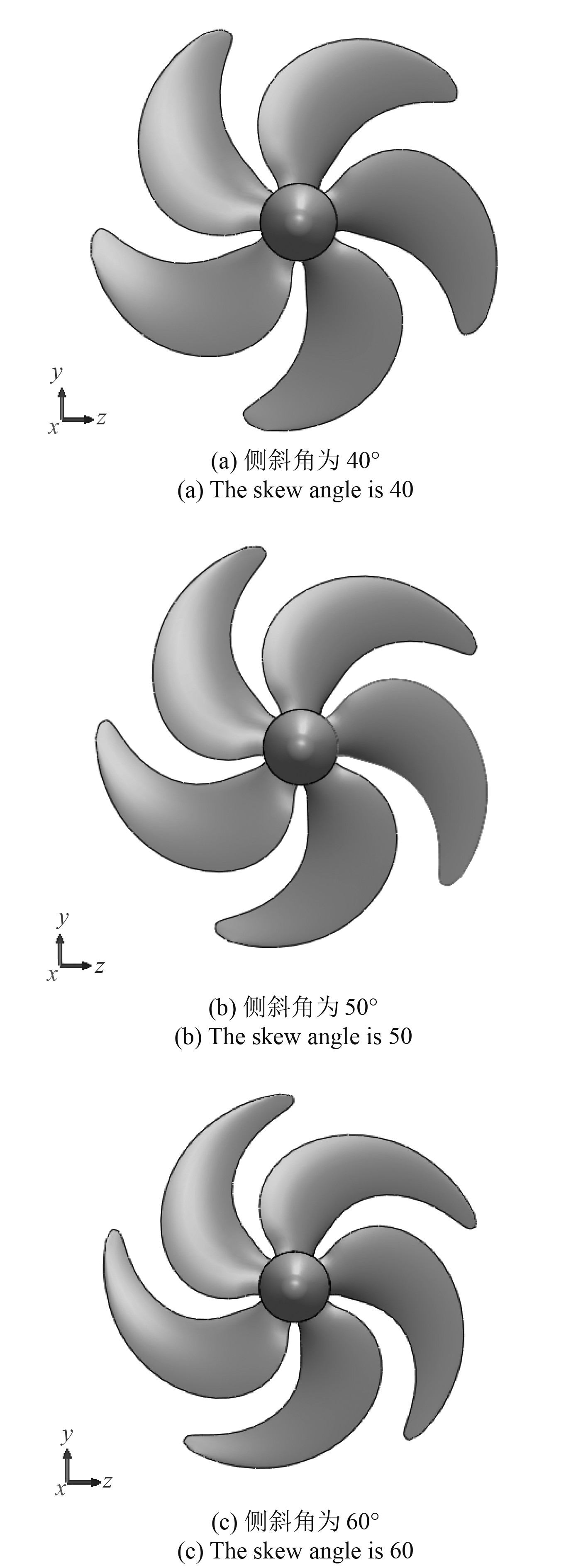
|
图 12 不同侧斜分布的大侧斜螺旋桨三维图 Fig. 12 Three-dimensional view of high skew propeller with different skew distribution |
可知,随着侧斜角度的增大,螺旋桨所能达到的推力系数以及扭矩系数也随之增大,且效率也会随之提高。侧斜角度的增大可以被认为,在一定转速下可为船舶航行提供更加强劲的推进性能,并且使船舶推进器更具备高效性。
|
|
表 4 50°侧斜角五叶大侧斜螺旋桨的水动力性能 Tab.4 Hydrodynamic performance of the HSP-5 propeller(50°) |
本文探究大侧斜螺旋桨的侧斜分布对于其敞水性能的影响。在验证仿真精确性后,进行3个侧斜角分别为40°,50°和60°的大侧斜螺旋桨的三维建模以及网格划分并进行数值仿真模拟的研究。仿真结果显示,随着侧斜角度的增大,对于螺旋桨的推进性能以及高效性能是有利的。因此,在民用船舶的高速性和高效节能性发展的船舶推进装置螺旋桨的提升方面,螺旋桨的设计优化阶段可以考虑增大螺旋桨的侧斜角来提高其敞水性能和节能高效性能。然而,随着侧斜分布结构的应用,螺旋桨的桨叶部分以及桨叶叶根与桨榖交接处的加工难度和其铸造成本也将相应增加。因此,对于螺旋桨的设计应结合螺旋桨几何参数优化和加工成本及难度方面的影响因素,达到既能省时节约又能与船舶设计理念匹配,并满足其高效的推进性能需求的目的。
| [1] |
TRAN N, NGUYEN M. Comparison of different approaches for calculation of propeller open water characteristic using RANSE method [J]. Naval Engineers Journal, 2018, 3.
|
| [2] |
LU L, PAN G, SAHOO P K. CFD prediction and simulation of a pumpjet propulsor[J]. International Journal of Naval Architecture & Ocean Engineering, 2016, 8(1): 110-116. |
| [3] |
BENNAYA M, ZHANG W P, HEGAZE M M. Estimation of the induced hydrodynamic periodic forces of marine propeller under non-uniform inflow via CFD[J]. Applied Mechanics & Materials, 2013, 467(3): 293-299. |
| [4] |
周斌. 反旋向侧斜导管螺旋桨水动力性能研究[A]. 中国造船工程学会(Chinese Society of Naval Architecture and Marine Engineering), 2017: 8.
|
| [5] |
饶志强, 杨晨俊. 七叶侧斜螺旋桨水动力性能优化[J]. 中国造船, 2016(4).
|
| [6] |
任万龙, 郝宗睿, 周忠海, 等. 基于侧斜的螺旋桨优化设计[J]. 船舶工程, 2016(s2): 148−151.
|
| [7] |
蔡昊鹏, 马骋, 陈科, 等. 确定螺旋桨侧斜分布的一种数值优化方法[J]. 船舶力学, 2014(7): 771−777.
|
| [8] |
张瑞, 王先洲, 张志国, 等. 侧斜变化对螺旋桨水动力及变形振动特性的影响[J]. 中国舰船研究, 2015, 10(06): 87−94.
|
| [9] |
曹峰, 李巍, 尤云祥. 五叶侧斜螺旋桨流固耦合特性的非定常数值模拟[J]. 水动力学研究与进展A辑, 2013, 28(05): 575−584.
|
| [10] |
黄斌, 熊鹰, 王波. 基于粒子群算法的螺旋桨侧斜分布优化[J]. 中国舰船研究, 2016(6).
|
| [11] |
黄璐. 基于粘流/势流耦合的螺旋桨性能预报方法研究[D]. 北京: 中国舰船研究院, 2015.
|
 2021, Vol. 43
2021, Vol. 43
