大型船舶空气尾流场是航行时受上层建筑、船体运动以及海洋大气边界层等的影响,在船体周围和尾部附近产生的复杂气流扰动,会危及飞机海上降落安全。据美国安全中心统计,受空气尾流场的影响,飞行员海上降落过程中遇到生命危险的概率远高于民航飞行员、陆基飞行员及宇航员等其他类型的飞行员[1]。所以,大型船舶空气尾流场的相关研究一直是备受关注的热点问题之一[2]。目前大型船舶空气尾流场的主要研究方法普遍采用以计算流体力学(CFD)数值模拟为主,以实验测量进行验证,几种方法互相补充配合。在CFD研究中,常用的方法包括雷诺平均Navier-Stokes方程(RANS)、大涡模拟(LES)、直接数值模拟(DNS)、脱体涡模拟(DES)等[3-11]。
目前对大型船舶空气尾流场的研究已经越来越精细化,不断趋近于空气尾流场的实际规律特性。但是还存在一些问题,包括:对大型船舶空气尾流场中直接影响飞机海上降落的下滑道气流场关注不够;CFD数值模拟、实验结果与实际的工程化模型的对比研究还较少;从防治角度开展的空气尾流特性研究较少。鉴于此,本文从现实需求出发,增加下滑道气流场的分析,开展大型船舶空气尾流场的CFD数值模拟、实验等方法的综合分析,从防治角度研究空气尾流场的特性。首先采用基于雷诺平均方法(RANS)的Spalart-Allmaras模型(简称SA模型)对整个大型船舶空气尾流场进行全面数值模拟分析,然后针对理想工况条件对下滑道气流场从CFD数值模拟、实验结果以及美军标MIL-F8785C等角度进行综合分析。在传统研究方法的基础上加入现有工程化模型进行综合分析,更贴近工程应用层面。为大型船舶空气尾流场的防治提供参考依据。
1 方法与模型 1.1 基本控制方程N-S方程由连续性方程、动量守恒方程和能量守恒方程组成,用来描述粘性流体的运动。不同过程则主要由边界条件和初始条件来区别,其矢量形式如下式[12]:
| $\begin{split}\left\{ \begin{array}{l} \dfrac{{\partial \rho }}{{\partial t}} + \nabla \cdot \left( {\rho V} \right) = 0 \text{,} \\ \dfrac{{\partial \left( {\rho V} \right)}}{{\partial t}} + \nabla \cdot \left( {\rho VV} \right) = \rho f + \nabla \cdot P\text{,} \\ \dfrac{{\partial \left( {\rho E} \right)}}{{\partial t}} + \nabla \cdot \left( {\rho VE} \right) = \rho f \cdot V + \nabla \cdot \left( {P \cdot V} \right) + \nabla \cdot \left( {k\nabla T} \right) + S \text{。} \end{array} \right.\\[-43pt]\end{split}$ | (1) |
根据Stokes假设,由于本文讨论的是航母周围的空气流动为均质不可压缩运动,即▽ρ=0、▽V=0,加上不考虑热交换问题,可忽略能量守恒方程,所以控制方程可转化为:
| $\left\{ \begin{array}{l} \nabla \cdot V = 0 \text{,} \\ \dfrac{{\partial \left( {\rho V} \right)}}{{\partial t}} + \nabla \cdot \left( {\rho VV} \right) = \rho f - \nabla p + \nabla \cdot \left( {2\mu S} \right) \text{。}\\ \end{array} \right.$ | (2) |
式中:ρ为密度,kg/m3;t为时间,s;V为速度矢量,m/s;f为体积力矢量,m/s2;P为作用于流体面上的应力;E为单位质量流体所具有的总能量;k为流体导热系数,W/(m·K);T为温度,K;S为能量源项,W/m3。
1.2 基于雷诺平均方法的SA模型SA模型的提出是为了改善代数混合长度模型模拟的结果,发展适用于复杂流动模拟的、提供比两方程湍流模型更简单的模型[13]。SA模型的应变量
SA湍流模型表达式[14]为:
| $\begin{split} \frac{{\partial \hat v}}{{\partial t}} + {u_j}\frac{{\partial \hat v}}{{\partial {x_j}}} =& {c_{b1}}\left( {1 - {f_{t2}}} \right)\hat S\hat v - \left[ {{c_{w1}}{f_w} - \frac{{{c_{b1}}}}{{{\kappa ^2}}}{f_{t2}}} \right]{\left( {\frac{{\hat v}}{d}} \right)^2} +\\ &\frac{1}{\sigma } \left[ {\frac{\partial }{{\partial {x_j}}}\left( {\left( {v + \hat v} \right)\frac{{\partial \hat v}}{{\partial {x_j}}}} \right) + {c_{b2}}\frac{{\partial \hat v}}{{\partial {x_i}}} \cdot \frac{{\partial \hat v}}{{\partial {x_i}}}} \right] \text{。} \end{split} $ | (3) |
式中:
采用某型大型船舶实际尺度模型[15]经过平滑处理后作为几何模型。同时为了模拟大型船舶在海上漂浮的状态,去掉了原模型水线以下部分(如图1所示),由于不考虑海浪的影响,将处理后的船底水平面作为下边界。整个计算域尺寸1400 m×450 m×220 m,内计算域尺寸为340 m×70 m×100 m。网格采用三维六面体结构多面体网格,船体附近采用加密网格,近壁面采用标准壁面函数。边界条件设置如图1所示。

|
图 1 大型船舶几何模型 Fig. 1 Large-scale ship geometry model |
1)入口边界面,位于大型船舶模型船头正对一个船长L位置的平面,选用速度入口边界类型,u = U,v = w = 0,其中U为来流速度;
2)出口边界面,位于大型船舶模型船尾正对3个船长L位置的平面,选用压力出口边界类型;
3)壁面边界,船体表面为无滑移壁面,上下左右边界设置为滑移壁面。
1.3.2 工况设置大型船舶空气尾流场模拟的工况主要是甲板风(WOD)风向角和风速的设置。设航向即船头正对方向为0°,顺时针为正。研究表明甲板风平行于飞机降落的斜角甲板时为最安全的海上降落环境,而斜角甲板中线与船体中线成7°夹角,所以此时甲板风风向角为−7°。此外再考虑大型船舶完全顶风,即0°角,以及右舷15°受风的情况,在此范围之外,侧向风过于显著,不适合飞机海上降落,故不予考虑(见图2)。甲板风风速采用9 m/s,12 m/s以及15 m/s,一共9种工况。控制面选取包括水平面、纵向垂直剖面与横向垂直剖面3种,各选取有代表性的控制面。运行计算的迭代步数超过1000步,使计算完全收敛。

|
图 2 甲板风风向角 Fig. 2 Direction of WOD |
计算结果包括速度场和流线分布,通过对不同工况条件下空气尾流场进行对比分析,选出其中流场品质最佳的情况,并与实验测量结果以及美军标MIL-F-8785C进行对比分析。
2.1 速度场及流线分析速度场包括速度标量场和速度矢量场2种情况。由图3可知,速度标量场中甲板以下船尾附近存在着一个明显的低速区,对应矢量场(见图4)中水平方向为一对近似对称的涡旋,而垂直剖面方向为一个垂直方向的大涡旋区,流线分析有相似的特征(见图5)。这是空气尾流场中最明显、面积最大的涡旋区,是大型船舶尾部下沉气流的主要来源,会对飞机海上降落产生影响。所以也是防治研究的重点区域。几种工况下这一特征是相似的,同时也存在一些差异,主要表现在:1)船尾涡旋区在风向角不同的情况下其位置与流场结构有一定差异,−7°与0°的流场结构较接近,而15°在接近船尾附近区域的下沉气流分量更加明显;2)在相同风向角下,风速越大涡旋越明显,12 m/s和15 m/s在船尾附近的下沉气流更明显(见图4(a))。

|
图 3 船尾的速度标量场(甲板风风向角−7°,风速15 m/s) Fig. 3 Velocity scalar field near stern (WOD: −7°, 15 m/s) |

|
图 4 风向角为−7°甲板风风速为15 m/s船尾的速度矢量场 Fig. 4 Velocity vector field near stern (WOD: −7°, 15 m/s) |
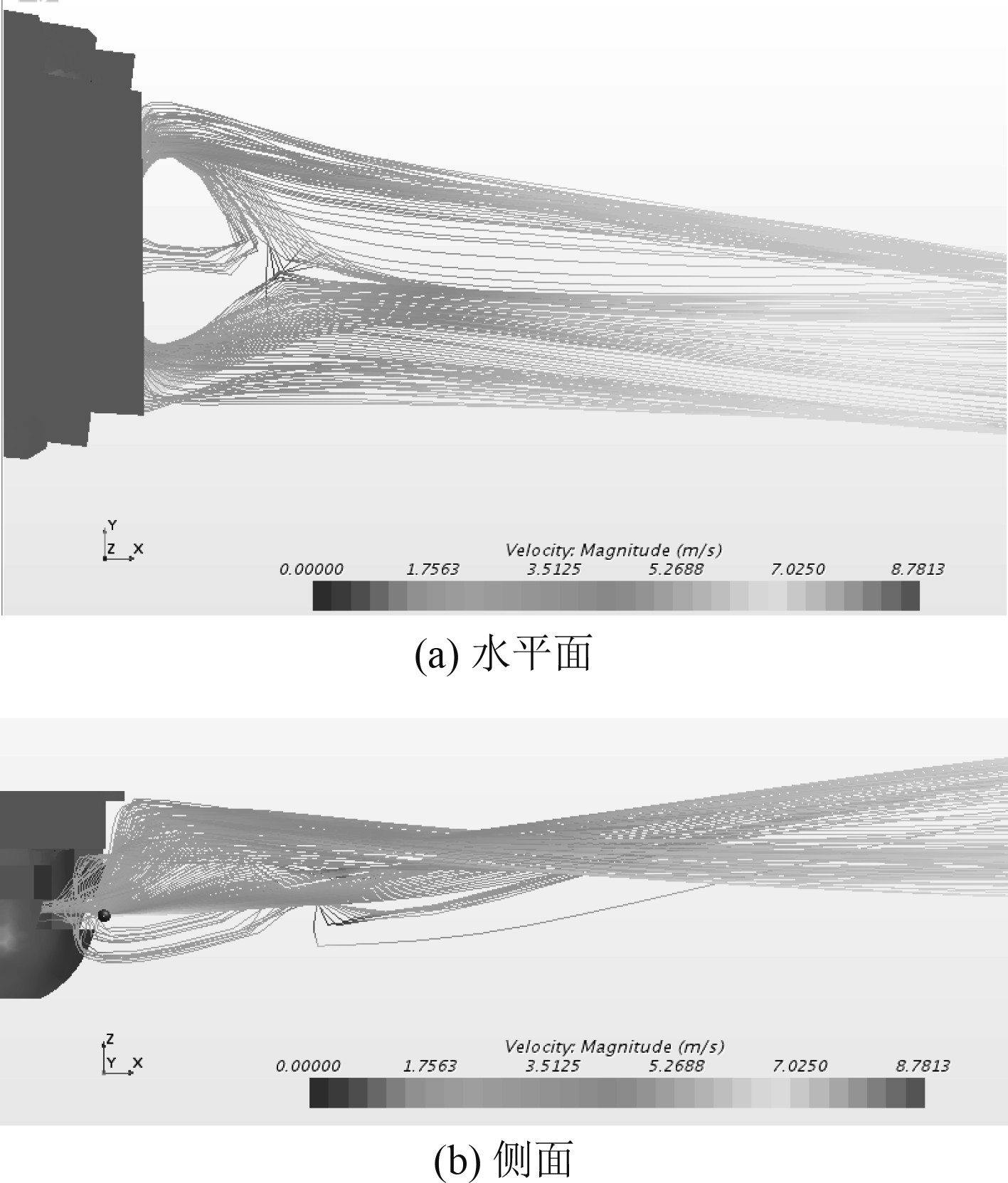
|
图 5 流线分析 Fig. 5 Streamline analysis |
在甲板以上,船尾部涡旋区消失,而上层建筑后部的气流扰动出现(见图6,以甲板风为12 m/s时距甲板3m处水平面为代表,其他几种情况略)。对比3种风向角可以分析得到,在15°风向角时岛后部气流扰动最明显,并对甲板后半部及船尾区域产生明显的影响,速度梯度较大,而−7°与0°两种风向角下上层建筑后部气流扰动的影响偏弱,其中−7°时速度场分布最均匀,速度矢量场及流线的特征与之相似(图略)。在以往的研究中大多只关注船尾气流特征,而对上层建筑后部气流扰动的关注不够。从飞机海上降落安全角度出发,船尾部的涡旋区以及上层建筑后部的气流扰动区都是大型船舶空气尾流场防治研究中需要重点关注的区域。文献[16]中将其界定为一个次级空气尾流场,即“上层建筑空气尾流场”,也是防治研究的对象之一。

|
图 6 甲板风速12 m/s甲板上方10 m处的速度标量场 Fig. 6 Velocity scalar field on the surface of 10 m above deck |
综上分析,甲板风风向角为−7°时空气流场是最理想的工况条件,适于作为飞机降落的最佳条件。而对飞机影响最直接的部分是下滑道气流场,是重点关注的区域。需提取空气尾流场中下滑道区域数值计算结果,并对比前期的实验测量[16]结果与工程化模型−美军标MIL-F-8785C“雄鸡尾流”模型做综合分析。
2.2 下滑道空气尾流场特性研究下滑道是飞机海上降落所经过的航迹线,在水平方向与斜角甲板中线重合,垂直方向与水平面呈3.5°夹角。大型船舶空气尾流场对飞机海上降落安全的影响集中体现在下滑道气流场的特征上。但是国内的研究大多对这一重点区域重视不足。尤其是在数值模拟、实验结果与现有国外工程化标准对比的综合研究较少,缺乏实用性的研究结论,所以难以形成我国的标准化模型。国外工程化模型的代表是美军标MIL-F-8785C,其中稳态分量即“雄鸡尾流”模型是目前研究的参考依据。在CFD计算结果中提取下滑道区域,结合文献[16]的实验结果,三者做对比分析,实验数据与CFD数值模拟数据均为-7°甲板风风向角条件。分析中取为海上降落点到船尾一个船长的下滑道区域。根据美军标MIL-F-8785C,分成水平分量和垂直分量。水平分量的方向是与下滑道向一致的方向,垂直分量是竖直方向。
2.2.1 水平分量的对比分析水平分量的对比分析如图7所示(以15 m/s为例),三者分析的大体趋势一致,12 m/s和15 m/s情况下在船尾到200 m左右范围内CFD值总体上小于实验测量值与美军标MIL-F-8785C的水平分量,在200~300 m三者值比较接近。其中低速条件下,即9 m/s情况三者整体上较为接近,而在甲板风速度较大条件下,CFD计算的风速在下滑道不同区域的空间分布差异逐渐显现出来,说明CFD计算结果能反映出下滑道气流场水平分量的细节特征,而在美军标MIL-F-8785C中由于工程应用的需要,滤掉了一些细节特征,实验测量由于取的是平均值,同样会滤掉风的变化。总体上三者趋势相近,都反映出水平风在飞机海上降落过程中,沿下滑道飞行时相对于海面一直处于顺风状态,在距船尾250 m及更远处下滑道气流场水平分量在逐渐减小,250 m附近达到最小,而后逐渐增大。在总体相同趋势中有局部的差异,美军标MIL-F-8785C中显示的是线性增大,实验结果在增大过程中有一定的变化,但总体趋势增大,而CFD计算结果变化复杂,在增大的总体趋势中有局部的复杂变化。这是从另外一个角度反映大型船舶空气尾流场特性。

|
图 7 大型船舶下滑道空气尾流场3种结果的对比 Fig. 7 Compare of three results of large-scale ship airwake |
下滑道气流场中的垂直分量的影响比水平分量更大。由三者垂直分量的对比分析可知,总体趋势实验测量结果与CFD计算结果更接近,而与美军标MIL-F-8785C的垂直分量差别较大,具体表现在以下两点:1)实验与CFD的下气流最显著区位置相比美军标MIL-F-8785C距离船尾部更近,在船尾到30 m的范围内,而后者的计算结果在距船尾60~70 m之间;2)船尾后气流由下沉向上升转变的速度变化,实验和CFD结果比美军标MIL-F-8785C更平缓。此外,三者有一个明显的相似之处:在位于船尾后部150 m附近都存在一个从下沉气流到上升气流的转换区,由于垂直分量的方向变化,正是下滑道气流场中气流变化最明显的区域,从CFD计算、实验测量和美军标MIL-F-8785C三个角度都证明了这个区域的存在。说明飞机海上降落中,在距船尾150 m以外,一直受垂直上升气流的影响,在经过150 m的位置后转为垂直下沉气流,在船尾附近达到最大,美军标MIL-F-8785C显示为距船尾70 m附近,实验为距船尾30 m处,最接近船尾,为10 m处。综合分析,在工程应用中可将船尾后10~70 m都作为下沉气流显著区域,是飞机海上降落需关注的重点区域之一,也是防治的重点对象及防治效果的衡量标准之一。这样就将研究的结果转化为实际的工程指标。
3 结 语本文采用国际上常用的以CFD方法为主、以实验验证为辅,并结合工程化标准的新型研究方法综合分析了适用于工程化应用和防治的大型船舶空气尾流场特性,可为工程应用以及防治研究提供参考。研究中得到了大型船舶空气尾流场的总体特征,也分析了下滑道气流场的特征以及对飞机海上降落影响最大的气流转换区和下沉气流显著区的位置。在此基础上分析大型船舶空气尾流场防治所应关注的重点区域。主要结论包括:
1)大型船舶空气尾流场最明显的特征是船尾甲板下方存在明显的涡旋区,水平方向为一对近似轴对称的涡旋,垂直纵向剖面上是一个明显的涡旋,不同风向角和风速下略有不同。这是空气尾流场最明显的气流扰动区域,是防治的重点区域。
2)经CFD计算结果分析上层建筑后部气流扰动对船尾部气流的影响明显,其中在-7°风向角下影响最小,在15°风向角下影响最大。这是传统研究所忽略的部分,同时也是空气尾流场防治所需关注的重要部分。
3)大型船舶下滑道气流场的计算结果与实验、美军标MIL-F-8785C对比分析表明:下滑道气流场中在距船尾150 m处存在气流转换区,船尾10~70 m存在下沉气流显著区,飞机海上降落过程中最应重视这2个区域。在大型船舶空气尾流场防治研究中,这2个区域是防治效果重要的参考评估指标。
大型船舶空气尾流场研究的最高目标是实现改变其结构、消除其影响的防治技术,本文研究的大型船舶空气尾流场规律特性可为其防治技术提供参考和研究支撑,并可在此基础上加入海浪、气候变化等其他海洋大气环境因素的空气尾流场特征。
| [1] |
贺少华, 刘东岳, 谭大力, 等. 载机舰船气流场相关研究综述[J]. 舰船科学技术, 2014, 36(2): 1-7. DOI:10.3404/j.issn.1672-7649.2014.02.001 |
| [2] |
王金玲. 舰船空气尾流场特性数值研究[D]. 哈尔滨: 哈尔滨工程大学, 2016.
|
| [3] |
Susan A. Polsky, Christopher W. S. Bruner. A computational study of unsteady ship airwake[C]// The RTO AVT Symposium, Loen, NATO Research and Technology Organisation, 2003, (SYA)25.
|
| [4] |
Susan A. Polsky, CFD prediction of airwake flowfields for ships experiencing beam winds.[J]21st Applied Aerodynamics Conference 23-26 June 2003, Orlando, Florida: 1-13.
|
| [5] |
CAMELLI F E, SOTO, LOHNER R etc. Topside LPD17 row and temperature study with an implicit monolithic scheme[C]// 41st AIAA Aerospane Sniennes Meeting&Exhibit, Reno, Nevada, 6- January 2003, AIAA paper 2003−0969.
|
| [6] |
CAMELLIF, LOHNER R, SANDBERG W etc. VLES study of ship stack gas dynamics[C]// 42nd AIAA Aerospane Sniennes Meeting and Exhibit, Reno, NV, 5-8 January 2004, AIAA paper 2004: 72.
|
| [7] |
G. F. Syms. Simulation of simplified-frigate airwakes using a lattice-Boltzmann method[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2008, 96: 1197-1206. |
| [8] |
Murray R. Snyder, Hyung Suk Kang etc. USNA ship air wake program overview[J]. 29th AIAA Applied Aerodynam- ics Conference 27-30 June 2011, Honolulu, Hawaii.
|
| [9] |
Daniel Linton, Ben Thornber. A study of LES methods for simulation of ship airwakes[J]. AIAA Aviation13-17 June 2016, Washington, D. C. 46th AIAA Fluid Dynamics Conference.
|
| [10] |
Franklin D. Roberson, Hyung S. Kang, Murray R. Snyder. Ship air wake CFD comparisons to wind tunnel and YP ship results[J]. 29th AIAA Applied Aerodynamics Conference 27-30 June 2011, Honolulu, Hawaii.
|
| [11] |
FORREST, JAMES S, OWEN etc. An investigation of ship airwakes using detached- eddy simulation[J]. Computers and Fluids, 2010, 39(4): 656-673. |
| [12] |
彭思, 王汉封, 李石清. 顶部定常吸气对高层建筑模型气动力的影响[J]. 哈尔滨工业大学学报, 2017, .49(12): 159-164. DOI:10.11918/j.issn.0367-6234.201703123 |
| [13] |
Zhang Qiang, Yang Yong. A new simpler rotation/curvature correction method for Spalart-Allmaras turbulence model[J]. Chinese Journal of Aeronautics, 2013, 26(2): 326-333. |
| [14] |
陈江涛, 张培红, 周乃春, 等. 基于SA湍流模型的DES方法应用[J]. 北京航空航天大学学报, 2012, 38(7): 905-909. |
| [15] | |
| [16] |
苏轼鹏, 金良安, 刘文鹏. 舰岛对航母下滑道空气尾流场特征影响的实验研究[J]. 中国测试, 2018, 245(12): 12-18. DOI:10.11857/j.issn.1674-5124.2018.12.003 |
 2021, Vol. 43
2021, Vol. 43
