0 引　言

当船舶遭遇恶劣海况时，船体和波浪会有很强的相互作用，因此导致船首与水面产生瞬时剧烈的砰击。这种结构物入水砰击过程是一个涉及到气液固三相的强流固耦合问题，入水瞬间产生的砰击力很大，极易危害船舶安全，对船舶结构甚至是船上人员造成极大的危险。在救生船下水、导弹入水等过程中同样涉及到类似的砰击过程，因此研究此过程中结构物和自由液面的相互作用意义重大。

入水砰击问题的研究开始于von Karman^[1]和Wagner^[2]的研究，von Karman^[1]基于二维刚性楔形体模型和附加质量理论，首次给出了入水问题的理论解法，Wagner^[2]基于线性势流理论并考虑自由面抬升对入水问题解法提出了有效的改进；之后，Dobrovol’ skaya^[3]基于Wagner^[2]的理论首次给出了二维楔形体入水的相似解；Greenhow和Lin^[4]通过一系列实验拍摄了不同速度和形状的圆球和楔形体入水过程中水面的变化情况，但是他们的结果并不清晰；Zhao和Faltinsen^[5]运用完全非线性的势流理论求解了楔形体入水过程中速度与压力的变化并通过实验验证了此方法在压力分布计算上有一定的准确性。随着计算流体力学（CFD）理论和计算机能力的发展，基于Navier-Stokes 方程的数值方法也逐渐被运用于楔形体入水过程的计算中。Kleefsman等^[6]采用有限体积法（FVM）并使用流体体积比函数（VOF）方法进行自由面捕捉，并将垂向速度和砰击力与实验结果进行对比，证明此方法有很好的准确性；王加夏等^[7]将VOF法和有限元法耦合，研究三维楔形体结构入水砰击时结构动态响应特性及板厚对结构变形效应的影响规律；Zhang等^[8]使用结合隐式界面追踪法（level set）的浸没边界法（Immersed Boundary Method）来研究楔形体入水问题，但所得到的楔形体上的压力分布结果并不理想。无网格方法由于其便于处理自由表面和大变形的特点，在楔形体入水问题中也得到了很好的应用。Koshizuka等^[9]使用移动粒子半隐式方法（MPS）模拟了破碎波与浮体的相互作用，并由此验证了无网格方法在处理大变形问题上的能力；陈翔等^[10]将此方法应用在楔形体入水问题中；Oger等^[11]使用经典的弱可压缩SPH方法模拟了楔形体入水问题并与Zhao和Faltinsen^[5]的实验进行了对比，结果吻合良好，验证了SPH方法在解决入水砰击问题上的适用性；龚凯等^[12]使用改进的固壁处理方法得到了更准确的计算结果。

SPH方法是一种纯拉格朗日的无网格方法，它首先被应用于天体物理的模拟中^[13-14]，后来被用于多种流体力学的研究中，如造波^[15]、多相流^[16]和流固耦合^[17]等。该方法将整个流场离散为一系列相互作用的粒子，并通过插值将流场中的物理量在离散的粒子上进行表达。SPH方法的主要优势在于无需定义空间网格，从而避免了自由表面大变形问题中网格的扭曲变形导致的计算精度下降和计算时间增加。随着高性能计算的发展，SPH方法计算效率低的缺点也逐渐被克服，它在处理各种问题，特别是传统网格方法无法很好解决的大变形问题上有很大的潜力。

本文主要工作为使用SPH方法研究二维楔形体入水砰击问题，分析楔形体斜升角和入水速度对入水作用力的影响。首先介绍SPH方法的基本理论，随后从2个方面验证此方法的准确性：一是验证本方法计算入水过程中楔形体运动、受力和压力分布的准确性；二是进行楔形体入水实验，验证本方法计算自由表面变形的准确性。最后利用SPH数值模拟得到不同斜升角和入水速度的楔形体受力情况，分析这2种因素的影响。

1 SPH方法介绍 1.1 基本理论

SPH方法的理论基础是积分插值理论^[18]。考虑粘性作用，可以得到如下质量守恒方程和动量守恒方程：

$ \frac{{\rm{d}}\rho }{{\rm{d}}t}=-\rho \nabla ·\stackrel{\rightharpoonup }{v}\text{，}$

(1)

$ \frac{{\rm{D}}\stackrel{\rightharpoonup }{v}}{{\rm{D}}t}=-\frac{1}{\rho }\stackrel{\rightharpoonup }{\nabla }P+\stackrel{\rightharpoonup }{g}+\stackrel{\rightharpoonup }{\Theta }\text{。}$

(2)

其中 $ \stackrel{\rightharpoonup }{\Theta }$ 代表粘性项。从上述N-S方程中可以推导中多种形式的SPH表达式。本文采用的方程如下：

$ \frac{{\rm{d}}{\rho }_{i}}{{\rm{d}}t}={\sum\limits_{j}{m}_{j}}{\stackrel{\rightharpoonup }{v}}_{ij}{\stackrel{\rightharpoonup }{\nabla }}_{i}{W}_{ij}\text{，}$

(3)

$ \frac{{\rm{d}}\stackrel{\rightharpoonup }{{v}_{i}}}{{\rm{d}}t}=-{\sum\limits_{j}{m}_{j}}\left(\frac{{P}_{j}}{{\rho }_{j}^{2}}+\frac{{P}_{i}}{{\rho }_{i}^{2}}+{\Pi }_{ij}\right){\stackrel{\rightharpoonup }{\nabla }}_{i}{W}_{ij}+\stackrel{\rightharpoonup }{g}\text{，}$

(4)

其中 ${\Pi _{ij}}$ 是用于减少不稳定性的人工粘性项，其形式如下：

$ {\Pi }_{ij}=\left\{\begin{array}{l}\dfrac{-\alpha \overline{{c}_{ij}}{\mu }_{ij}}{\overline{{\rho }_{ij}}}\text{，}\;\;{\stackrel{\rightharpoonup }{v}}_{ij}{\stackrel{\rightharpoonup }{r}}_{ij}<0\text{，}\\ 0\text{，}\;\;\;\;\;{\stackrel{\rightharpoonup }{v}}_{ij}{\stackrel{\rightharpoonup }{r}}_{ij}>0\text{。}\end{array}\right.$

(5)

式中： $\overline {{c_{ij}}} = ({c_i} + {c_j})/2$ ， $\overline {{\rho _{ij}}} = ({\rho _i} + {\rho _j})/2$ ， $ {\stackrel{\rightharpoonup }{v}}_{ij}={\stackrel{\rightharpoonup }{v}}_{i}-{\stackrel{\rightharpoonup }{v}}_{j}$ ， $ {\stackrel{\rightharpoonup }{r}}_{ij}={\stackrel{\rightharpoonup }{r}}_{i}-{\stackrel{\rightharpoonup }{r}}_{j}$ ， $ {\mu }_{ij}=h{\stackrel{\rightharpoonup }{v}}_{ij}{\stackrel{\rightharpoonup }{r}}_{ij}/({r}_{ij}^{2}+0.01{h}^{2})$ ， $\alpha $ 为耗散系数， $\alpha = 0.01$ 。

经典的SPH方法认为流体是弱可压缩的。因此可以使用状态方程来计算流体压力而不需要引入泊松方程，这使得计算更有效率并且适合于并行计算。Monaghan^[19]提出了如下的状态方程：

$P = B\left[ {{{\left( {\frac{\rho }{{{\rho _0}}}} \right)}^\gamma } - 1} \right]\text{，}$

(6)

流体为水时， $\gamma \!=\! 7$ ， $B \!=\! c_0^2{\rho _0}/\gamma$ ， ${c_0} = c({\rho _0}) = {\left. {\sqrt {(\partial P/\partial \rho )} } \right|_{{\rho _0}}}$ ， ${\rho _0}$ 是流体的参考密度， ${c_0}$ 是规定的流体声速。值得注意的是流体的压缩率被限制在1% 以内，从而避免计算的时间步长过小。

1.2 关键设置 1.2.1 光滑函数

无网格方法的核心问题之一是如何基于以任意方式分散的一组节点有效地执行函数逼近而不使用提供节点连接性的预定义网格。SPH方法使用光滑函数来解决这个问题。光滑函数的选择至关重要，因为它决定了插值模式并且定义了粒子的影响区域。选择合适的光滑函数，可以提高精度和稳定性。

光滑函数是无量纲的粒子间距 $q$ 的函数， $q = r/h$ ，其中 $r$ 是任意2个粒子的间距， $h$ 是光滑长度。本文使用的五次光滑函数^[20]如下：

$W(r,h) = {\alpha _D}{\left( {1 - \frac{q}{2}} \right)^4}\left( {2q + 1} \right)\text{，}\;\;\;\;0 \text{≤} q \text{≤} 2\text{。}$

(7)

其中 ${\alpha _D}$ 在二维问题中为 $7/4\text{π} {h^2}$ ，在三维问题中为 $21/16\text{π} {h^3}$ 。

1.2.2 边界设置

SPH方法中边界的设置并不像网格方法中那样简单，边界的设置影响着计算的稳定性和准确性。原因在于边界附近粒子的支持域是截断的，缺少了一部分支持域的粒子参数计算会出现很大误差，边界条件的设置需要尽可能减少这种误差。本文使用的是动态边界条件（DBC）^[21]，边界固体粒子满足与流体粒子相同的方程，但是它们不会在流体的作用力下运动，而是保持固定或者根据预先设置的运动方程运动。当流体粒子靠近壁面时，壁面粒子的密度会增大，压力也随之增大，对流体粒子形成的排斥力可以阻止流体穿过边界。

1.2.3 时间积分格式

多种时间积分方法都可用于SPH方程的积分求解。本文使用的Verlet方法^[22]计算耗时少且结果的准确性较好。其计算方法如下：

$\left\{ \begin{array}{l} v_i^{n + 1} = v_i^{n - 1} + 2\Delta t\dfrac{{{\rm{d}}v_i^n}}{{{\rm{d}}t}} \text{，} \\ r_i^{n + 1} = r_i^n + \Delta tv_i^n + 0.5\Delta {t^2}\dfrac{{{\rm{d}}v_i^n}}{{{\rm{d}}t}} \text{，} \\ \rho _i^{n + 1} = \rho _i^{n - 1} + 2\Delta t\dfrac{{{\rm{d}}\rho _i^n}}{{{\rm{d}}t}} \text{。} \end{array} \right.$

(8)

2 楔形体入水过程中的运动和受力分析

楔形体入水问题中最受关注的是楔形体的运动状态和受力情况。本节对二维楔形体自由入水过程进行模拟，分析此过程中楔形体运动速度的变化，砰击力的变化以及不同瞬间的压力分布，验证SPH方法计算楔形体入水砰击时运动状态和受力情况的准确性。

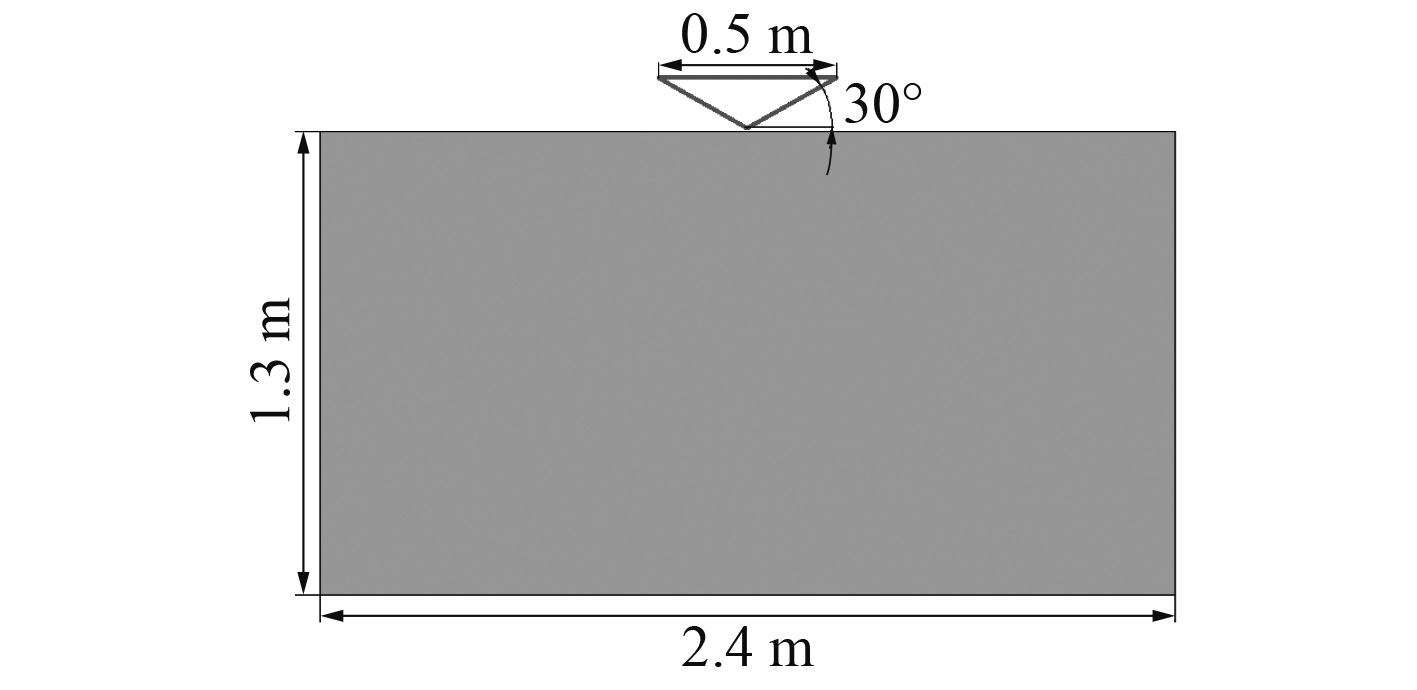
2.1 数值模型

针对二维楔形体入水问题建立数值模型，其中水池长2.4 m，高1.3 m，以此保证入水砰击的过程中壁面反射不会对楔形体受力产生干扰。楔形体形状为等腰三角形，顶边长度为0.5 m，斜升角（即斜边与水平方向的夹角）为30°。在楔形体入水前的瞬间，它的垂向速度为6.15 m/s，随后自由入水，如图1所示。

计算时流体中的声速 ${c_0}$ 为67.7 m/s，是入水速度的10倍以上，以此确保流体压缩率小于1%。计算中使用的二维楔形体为实心刚体，重量为241 kg，在二维平面内自由运动。粒子初始间距设置为0.0012 m，粒子总数近300万，计算的总下落时间为0.024 s。

2.2 结果分析

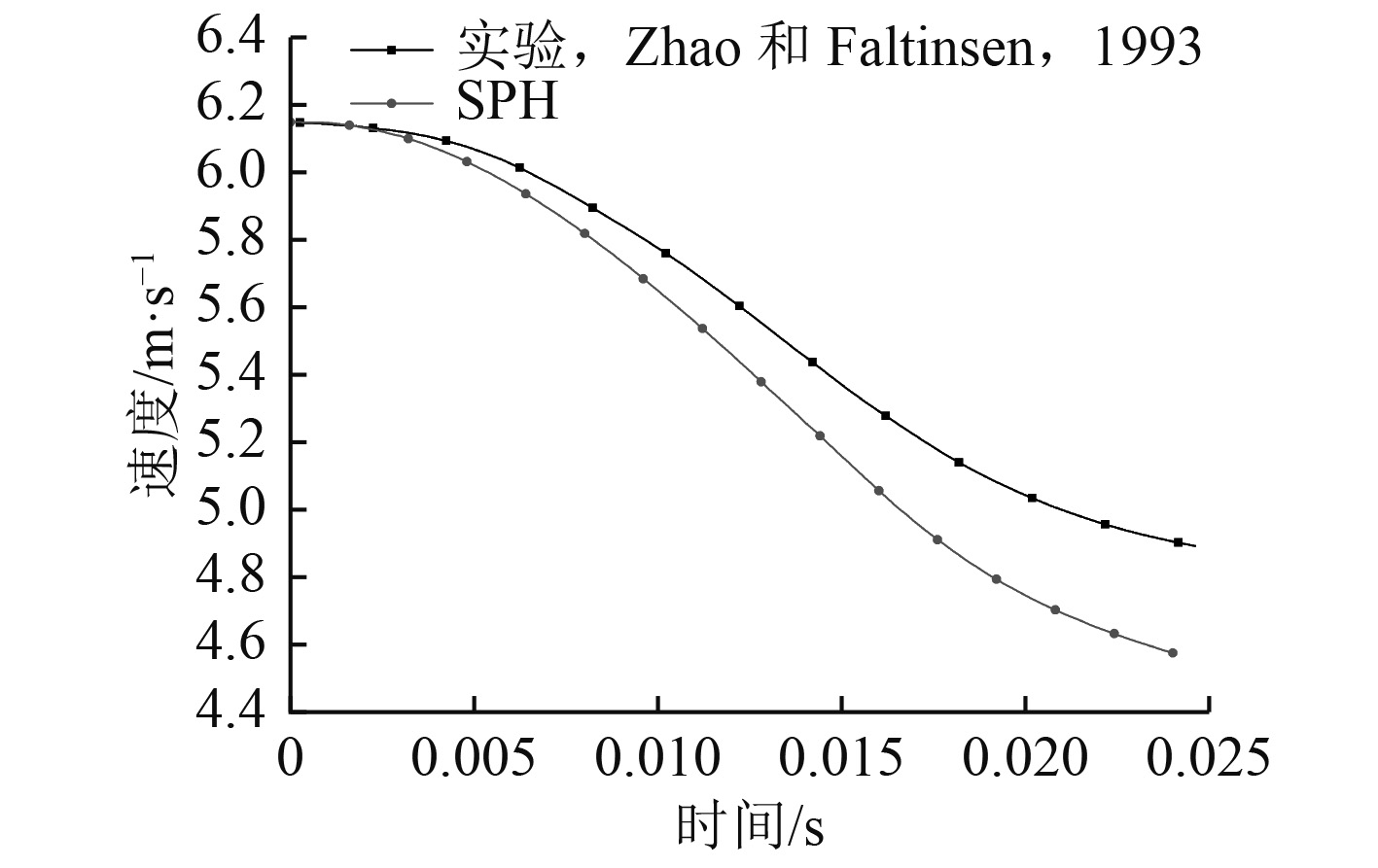
首先分析自由入水后的垂向速度变化，本次计算结果与Zhao和Faltinsen^[5]的实验结果进行对比（见图2）。首先可以看出两者在变化趋势上有高度的一致性，下落加速度在计算时间内呈现出相同的先增大后减小的特征。由于模型实验存在三维效应，数值和实验结果会有一定程度的差异。在入水后的0.003 s内，本文结果与实验非常吻合，其后SPH方法速度衰减开始快于实验，在0.015 s时SPH方法速度比实验结果小4.1%，最终速度的差异为6.7%。

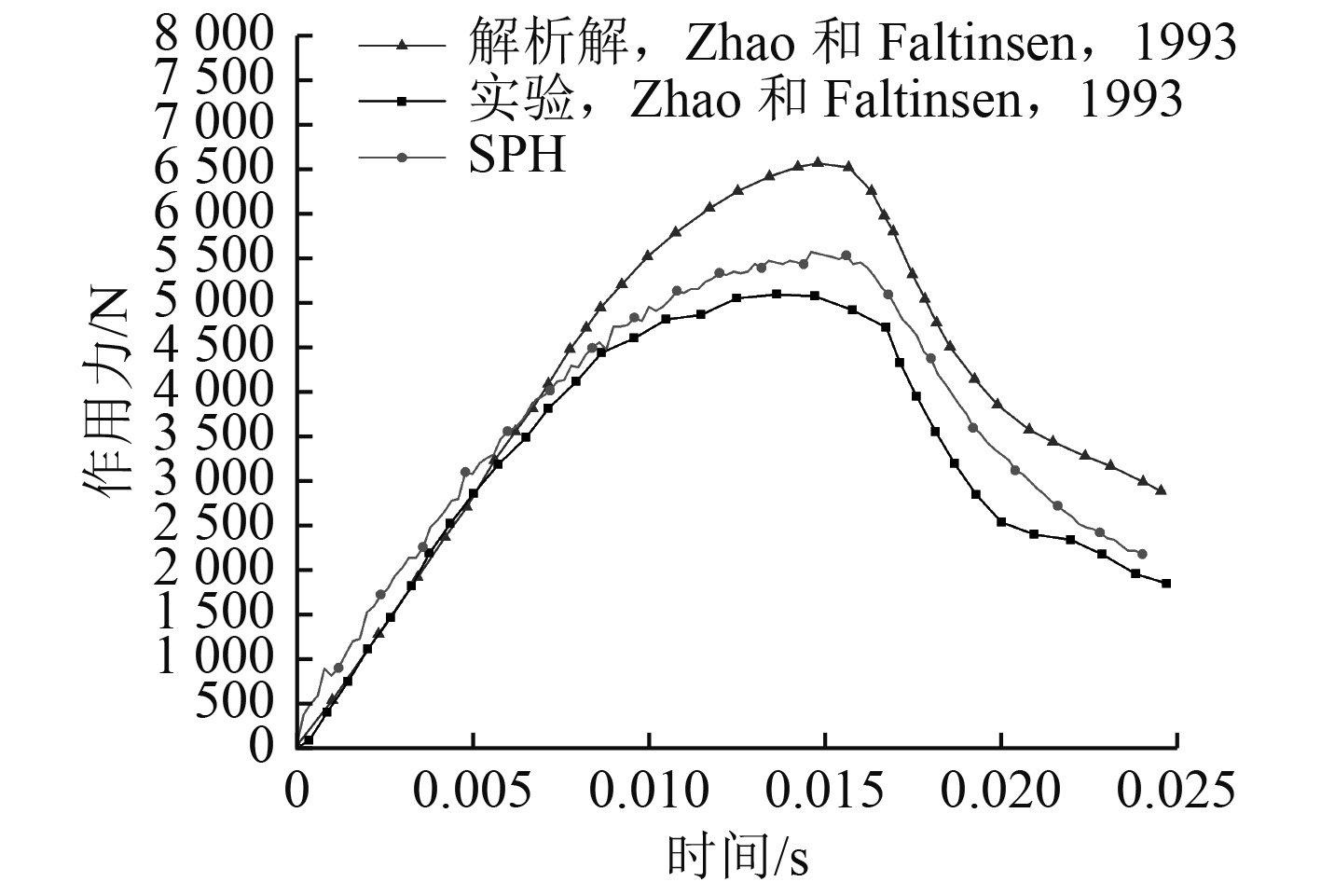
在砰击入水的过程中，流体对楔形体的垂向瞬时砰击力变化是研究中关注的重点问题之一。本文将SPH方法的砰击力计算结果与Zhao和Faltinsen^[5]的实验结果和解析解对比，结果如图3所示。可以看出，三者的变化趋势一致且结果十分接近。入水后的0.06 s内，解析法与实验结果吻合度良好，SPH方法结果略微偏大；0.06 s之后解析法和SPH结果都大于实验值，但SPH方法结果更接近实验：在砰击力峰值处，SPH方法的结果相比实验大10%，而解析解相比实验大30%；入水后0.02 s，SPH方法和实验相差达到最大值30%，此时解析解和实验相差为50%。说明SPH方法能更准确地计算楔形体入水砰击过程中的垂向砰击力变化。同时可以看出，砰击力的计算结果和入水速度的变化趋势相符，SPH计算的砰击力大于实验值，因此入水减速更快。

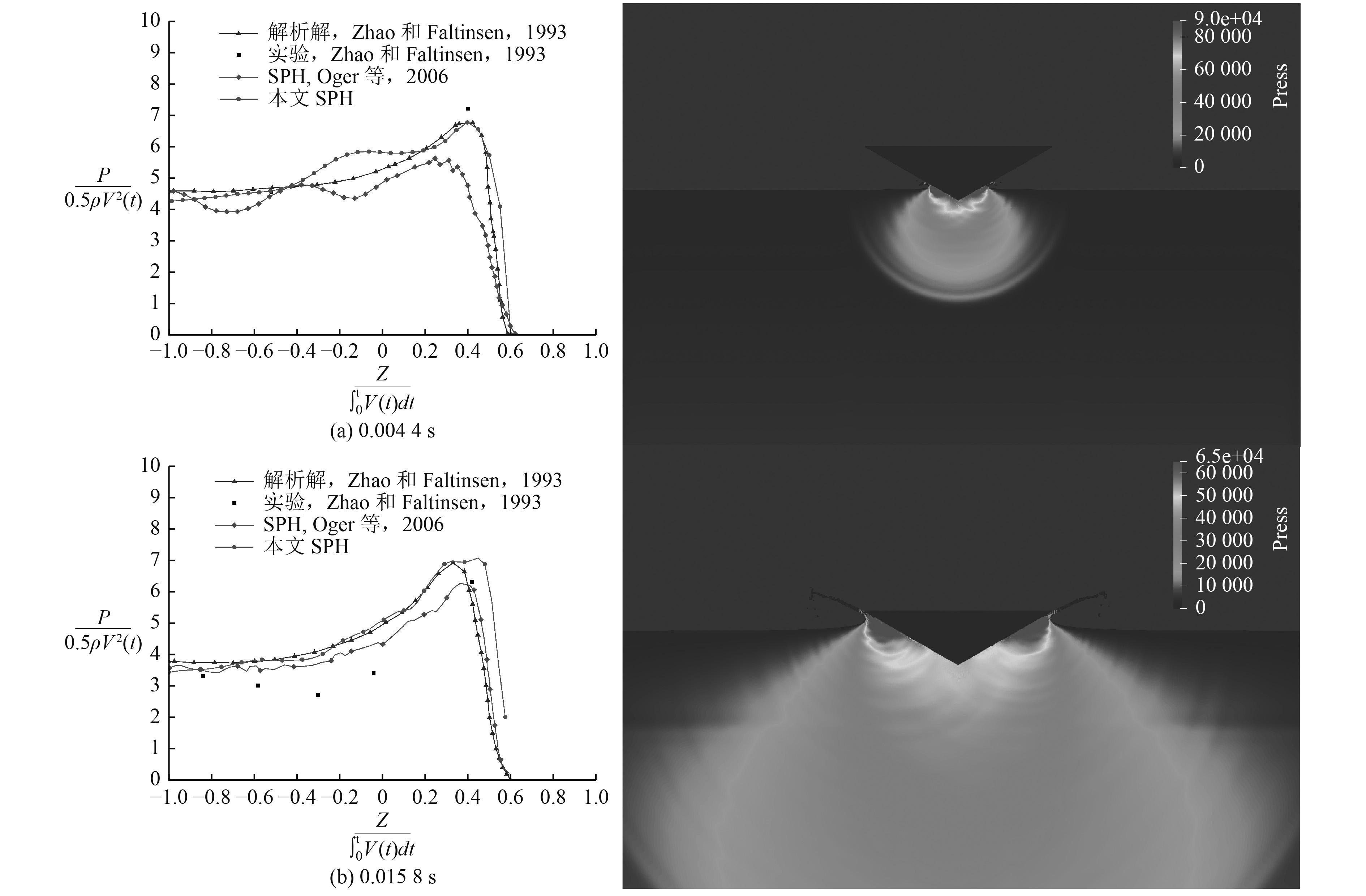
通过以上分析可知，SPH方法在砰击力的计算上有很好的准确性。接下来通过研究不同瞬间楔形体表面压力分布的计算结果，更深入地验证SPH方法在分析楔形体所受作用力上的准确性。本文选取了2个特定的时间点（t=0.0044 s和t=0.0158 s）来分析沿着楔形体表面的压力分布，将其与Zhao和Faltinsen^[5]的实验结果和解析解以及Oger等^[11]的SPH结果进行对比，结果如图4所示。由于SPH方法存在压力不稳定的问题，特别是在边界上问题更严重，本文在SPH方法中使用了delta-SPH^[23]来减少这种不稳定的影响。delta-SPH即在连续性方程中加入扩散项，使其变为：

$ \frac{{\rm{d}}{\rho }_{i}}{{\rm{d}}t}={\sum\limits_{j}{m}_{j}}{\stackrel{\rightharpoonup }{v}}_{ij}{\stackrel{\rightharpoonup }{\nabla }}_{i}{W}_{ij}+2{\delta }_{\Phi }h{c}_{0}{\sum\limits_{j}({\rho }_{j}-{\rho }_{i})}\frac{{\stackrel{\rightharpoonup }{r}}_{ij}{\stackrel{\rightharpoonup }{\nabla }}_{i}{W}_{ij}}{{\stackrel{\rightharpoonup }{r}}_{ij}^{2}}\frac{{m}_{j}}{{p}_{j}}\text{。}$

(9)

其中 ${\delta _\Phi }$ 的值取为0.1。由于SPH方法在边界上的压力计算不准确，本文参考Oger等^[11]的做法，使用流体粒子压力的平均值代替边界上的压力值，具体做法为以楔形体表面边界点为圆心，取半径为6 h的范围内所有流体压力的平均值作为此边界点压力值。图中横坐标为楔形体与自由表面接触点的无量纲纵坐标，纵坐标为无量纲压力。其中P为压力，V为楔形体运动速度，竖直向下为正方向，Z为楔形体与自由表面接触点的纵坐标，原点在静水面，竖直向上为正方向。

图4左图为2个时刻压力分布对比结果，右图为对应时刻SPH方法计算的压力分布图。从右图可以看出，delta-SPH的使用有效保证了SPH结果中压力分布的稳定性，2个时刻的液体内部压力分布都有比较合理的梯度变化。从左图可以看出，对于2个时刻的压力分布，3种非实验方法得到的结果比实验大，其中同样有实验三维效应的原因。图4（a）中本文的SPH方法很好地捕捉到了压力峰值的位置，并且与解析解的结果整体一致；图4（b）中本文所用SPH方法的压力分布结果在压力峰值点前都与解析解十分吻合，并且压力峰值点也能准确捕捉。图4（b）的结果在楔形体上缘迅速下降但是并不为0，除了SPH方法压力计算存在的问题外，一部分原因是提取压力时采用的平均算法导致边缘压力变大。对比Oger等^[11]的SPH结果，本次研究的结果在t=0.0044 s时整体更接近解析解，较好地捕获到了压力分布的峰值；在t=0.0158 s时大部分区域都更接近解析解，只有靠近边缘的区域由于平均算法的问题误差相对较大。

以上分析证明SPH方法在处理楔形体入水砰击问题时，能够准确地计算速度变化、砰击力变化和不同时刻压力分布，说明SPH方法在这一问题上有很好的适用性。

3 自由表面变形验证实验

楔形体砰击入水是楔形体和液体表面互相作用的过程，其中既有楔形体的受力和运动，也有自由表面由于楔形体砰击和挤压产生的变形和射流，同时自由表面的变化也将在入水的后续过程中影响楔形体的受力和运动，如气穴的产生和封闭等将对楔形体产生二次作用力。过去的大多数研究都只关注了楔形体受力而没有考虑自由表面变形，为从这一角度验证SPH方法在楔形体入水问题上的适用性，进行相应的实验研究。

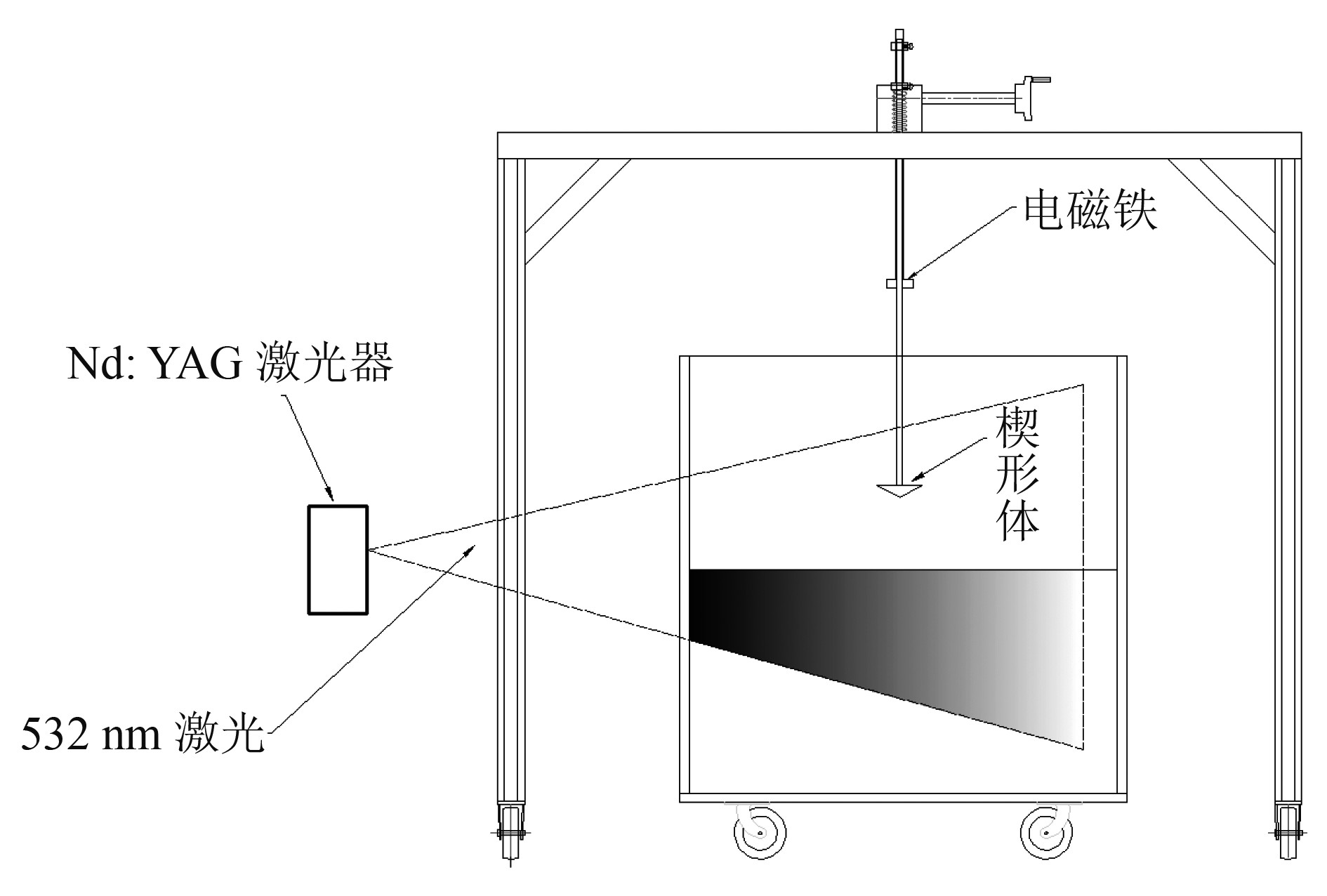
3.1 实验设置

本次实验使用自行设计和搭建的实验装置完成，主要包括以下设备：上表面长0.3 m，宽0.1 m，斜升角30°，总重量为4 kg的楔形体；长1 m，宽0.35 m，高1 m的有机玻璃缸；型号为Vision Miro eX4，帧数1000 fps，像素800×600的高速相机；波长为532 nm的Nd:YAG激光器。实验设置如图5所示。

本次实验采用的是自由落体的入水方式。为保证实验的二维性，将水缸和楔形体的宽度设置地尽量接近，同时可以减少正面溅射的水花，使拍摄结果更加清晰。使用电磁铁作为释放装置，用2根光滑导轨限制楔形体释放之后的自由度，使其在下落过程中不会翻转和偏移。为防止外界光源和其他物体的干扰，保证实验拍摄效果，本次实验在黑暗环境中进行，使用激光器发出的片光作为光源。

实验设置2种不同的入水高度，分别为0.05 m和0.1 m。实验开始时，首先将楔形体固定在指定高度，开启高速相机和激光器，将相机和激光器分别调整至光轴正对楔形体宽度方向和长度方向的中轴线，相机成像清晰。随后启动相机录制，将电磁铁断电，释放楔形体，利用高速相机捕捉楔形体入水过程中的自由表面变形和射流飞溅现象。

3.2 结果对比

利用SPH方法建立与本次实验相同的容器和楔形体的二维数值模型，计算相同高度下楔形体入水砰击过程，可以得到数值模拟的自由表面变形结果。下面将SPH方法的结果和实验结果对比以验证此方法的准确性。

图6为入水高度0.05 m时的对比，其中左侧为实验结果，右侧为SPH方法的结果，可以看出实验结果中水和空气以及水和楔形体的交界面都被很好地捕捉到了，射流的轮廓也清晰可见。图6（a）入水时间为0.05 s，自由表面由于楔形体的作用向两侧产生变形，并产生高速射流。可以看出SPH方法对此时的自由表面变形有比较准确的计算，与实验结果的形状十分吻合，在射流的模拟上相对较弱，其中部分原因是数值方法的粒子尺度较大，同时未考虑表面张力的作用。图6（b）入水时间为0.136 s，自由表面变形增大，射流也更加明显，可以看出此时SPH方法不仅对变形有很好的准确性，同时也能够有效模拟出射流飞溅的效果，射流分离位置和角度吻合良好。此时随着楔形体的下落，上方的自由表面开始重新向中间靠拢，即将产生闭合，这一时刻楔形体上方的自由表面接近竖直，本方法对此也有准确的计算。

图7为入水高度0.1 m时的对比，相对于0.05 m的入水高度，高度增加之后入水速度增大，因此将拍摄范围增大以捕捉到相同时长的入水过程。图7（a）入水时间为0.05 s，可以看出SPH方法对此时的自由表面变形同样有比较准确的计算，由于入水速度增加，砰击力也增大，因此自由表面变形更大，挤压变形的趋势在大砰击力的作用下明显更向竖直方向倾斜。图7（b）入水时间为0.136 s，SPH方法同样很好地模拟出了自由表面变形和射流飞溅的现象，也可看出楔形体上方自由表面即将向中间靠拢的倾向。在入水高度为0.05 m时，这一时刻被楔形体挤压而抬升的自由表面已经有明显的回落趋势，而入水高度增大时，由于砰击力变大，自由表面上液体上升速度增大，因此速度降为0并开始回落的时间更晚。SPH计算结果中同样可以看到不同高度的这一区别：相对于入水高度0.05 m的情况，入水高度0.1 m时，楔形体附近自由表面靠拢趋势更不明显，静水面以上的自由表面尚未有明显往下塌陷的趋势。

从以上分析可以看出，2种入水高度下，SPH计算结果和实验结果都有很好的吻合度。楔形体入水时本方法对自由表面形状变化的模拟十分接近实验结果，射流的情况也有一定程度的相似性，说明SPH方法可以很好地模拟入水砰击时的自由表面变化情况，也从另一个侧面表明SPH对楔形体入水砰击过程的计算是十分准确的。

4 楔形体斜升角和入水速度的影响 4.1 楔形体斜升角的影响

楔形体的斜升角会对入水砰击力产生影响，其中需要重点关注的是砰击作用时间和最大砰击力。本文选取20°，30°，40°，50°和60°五种斜升角的楔形体，计算其入水砰击力随时间的变化，计算过程中保持每个楔形体顶边长度为0.1 m，质量为20 kg，入水速度为3 m/s，限制楔形体只能在竖直方向做直线运动。

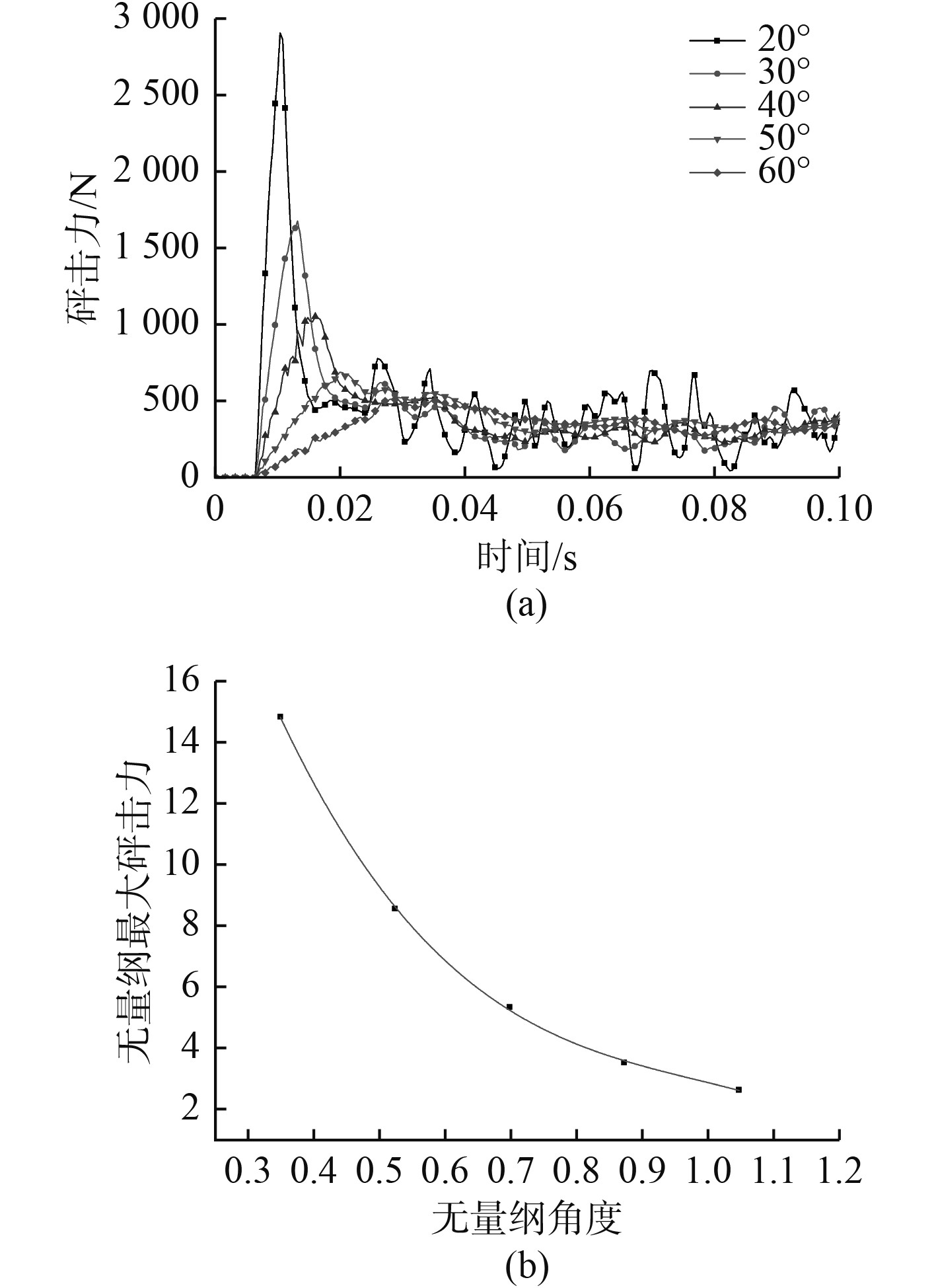
每个楔形体的计算结果如图8（a）所示。从图中可以看出，斜升角越小，入水砰击力在越短的时间内达到最大值，且下降速度更快。可以看出，随着斜升角的增大，最大入水砰击力的减小非常明显，其中斜升角为20°时最大砰击力为2909.4 N，60°时最大砰击力为516.0 N，前者是后者的5.64倍，说明改变斜升角对砰击力的影响很大。图8（b）给出了不同斜升角下的无量纲的最大入水砰击力及其3次拟合曲线，曲线方程为：

$\overline F = - 33.33{\overline r ^3} + 98.35{\overline r ^2} - 102.00\overline r + 39.85\text{。}$

(10)

其中无量纲入水砰击力 $\overline F = F/(mg)$ ， $F$ 为入水砰击力， $m$ 为楔形体质量；无量纲斜升角 $ \overline{r}=r·\text{π} /180^\circ $ ， $r$ 为斜升角。可以看出入水砰击力和楔形体斜升角的三次方成正比。

4.2 入水速度的影响

除了斜升角以外，楔形体入水的速度也是需要考虑的重点因素之一，本文选择从1 m/s到6 m/s共6种入水速度，分析入水速度变化对砰击力的影响。计算中采用的楔形体顶边长度为0.1 m，斜升角为30°，质量为20 kg，限制其只能在竖直方向作直线运动。

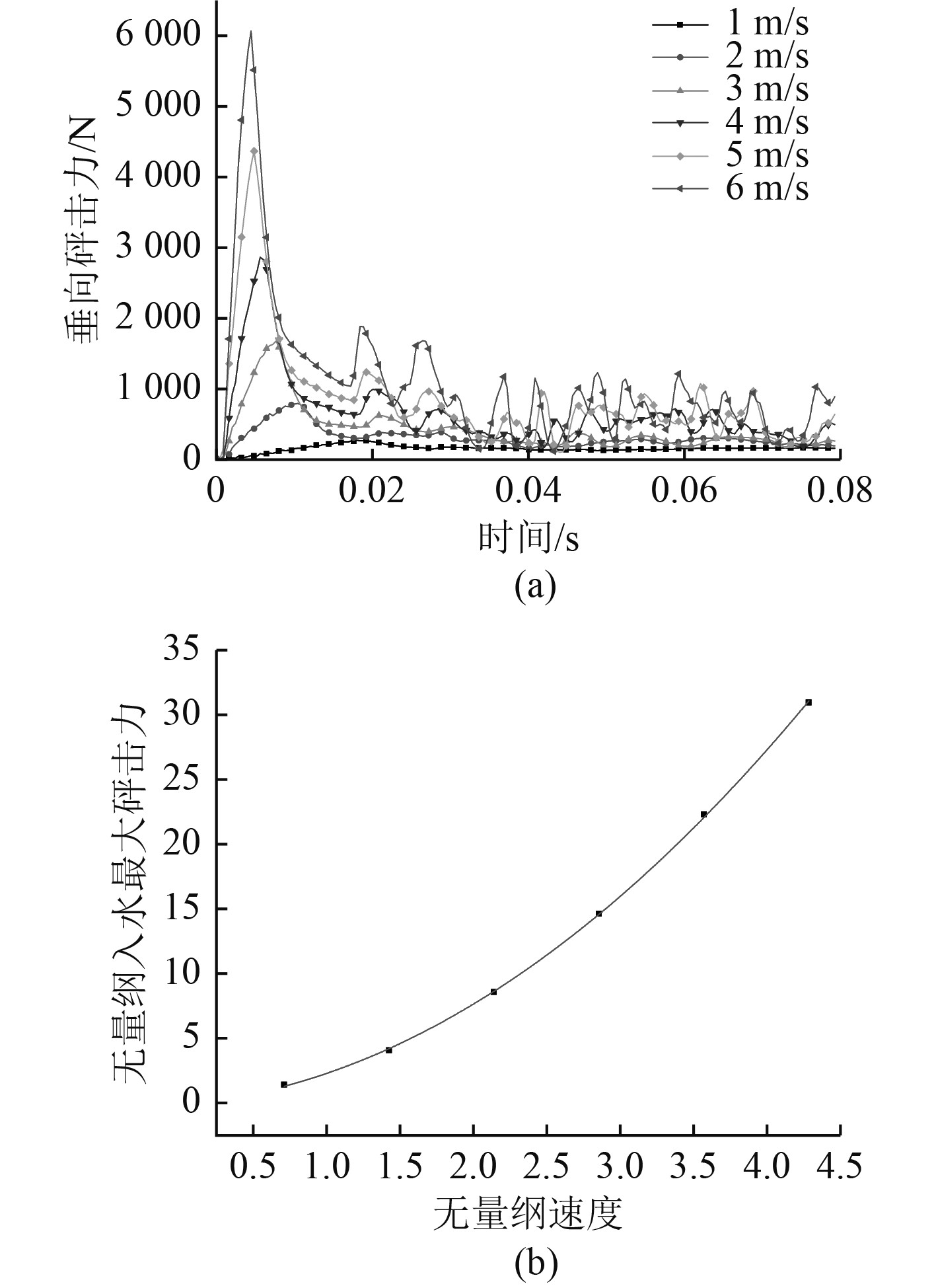
每个楔形体的计算结果如图9（a）所示。从图中可以看出，入水速度越大，砰击力在越短的时间内达到最大值，随着速度的增大，最大入水砰击力明显增大，速度从1 m/s增加到6 m/s时，最大砰击力增大了21.23倍。图9（b）为6种速度下的最大入水砰击力及其二次拟合曲线，曲线方程为：

$\overline F = 1.49{\overline v ^2} + 0.81\overline v - 0.10\text{。}$

(11)

其中：无量纲入水砰击力 $\overline F = F/(mg)$ ， $F$ 为入水砰击力， $m$ 为楔形体质量；无量纲入水速度 $\overline v = \sqrt {{v^2}/(2gL)}$ ， $v$ 为入水速度， $L$ 为楔形体顶边长度。可以看出入水砰击力和入水速度的二次方成正比

5 总结和展望

本文使用SPH方法研究了二维楔形体入水砰击问题，分析楔形体斜升角和入水速度对入水砰击力的影响。首先通过分析楔形体入水过程中的速度变化、砰击力变化和不同时刻压力分布，验证SPH方法在处理楔形体入水问题时，能够准确地计算楔形体受力和运动。随后进行楔形体入水实验并成功拍摄到了十分清晰的自由表面变形结果，将上述结果与SPH方法计算结果作对比，证明2种入水高度下，SPH模拟的自由表面变化十分接近实验结果，产生的射流也有一定程度的相似性，从而验证本方法计算自由表面变形的准确性。通过以上2个方面，验证了对于楔形体入水这种瞬时强相互作用过程，SPH方法有很好的适用性和准确性。

在上述研究的基础上，从最大砰击力和入水砰击时间上分析楔形体斜升角和入水速度对砰击过程的影响。从结果可以看出，改变这2种参数都会明显改变砰击过程，从拟合结果可以推断，最大砰击力与楔形体斜升角的三次方成正比，与入水速度的二次方成正比。

本文的主要创新点，一是使用合理的实验设置和拍摄手段，成功拍摄了楔形体入水过程中清晰的自由表面变化情况；二是给出了最大砰击力与斜升角和入水速度的定量关系。之后的研究将重点继续这两方面的工作，第一是实验覆盖更多的入水速度和斜升角并拍摄入水后期的自由表面变化，第二是计算更多不同入水速度和斜升角的情况，提高定量关系的准确性。