2. 中国船舶集团有限公司第七一四研究所,北京 100101;
3. 哈尔滨工程大学烟台研究院,山东 烟台 264000
2. The 714 Research Institute of CSSC, Beijing 100101, China;
3. Yantai Research Institute, Harbin Engineering University, Yantai 264000, China
水下航行器结构复杂,其主体结构中突出的部分如围壳和稳定翼等结构,均会导致主体结构表面压力场的连续性遭到破坏,进而在其尾流场中产生漩涡,并激发壳体产生共振。这些突出的部分大多为翼型或类翼型结构,此外螺旋桨桨叶虽然线型复杂,但其基本剖面也可视为沿半径方向参数变化的翼型。由此可见翼型结构流致振动对于水下航行器整体水动力噪声水平影响巨大,因此开展水下翼型结构流致振动研究对于水下航行器水动力噪声优化控制具有实际工程价值和理论研究价值。
水下航行器运动时,翼型结构表面与绕流场相互作用产生湍流边界层,湍流边界层内的脉动压力进而激励翼型结构产生流致振动,求解这类工程实际问题时,目前主要采用流固耦合计算方法。VayneA.Strawderman等[2-3]以统计学的观点给出了气流激励下平板结构流致振动响应的解析解法。魏建辉等[4]基于随机理论,计算求得结构表面的振动速度功率谱密度矩阵。胡世良等[5]采用Ansys Workbench平台中的system coupling模块来模拟流场与结构之间的强耦合关系。魏建辉等[6]分别计算了单层和双层圆柱壳在不同航速下的流激振动特性,对比计算了同一流速下2种壳体形式的振动特性,为壳体结构形式的优化选择提供了理论依据。
在脉动压力激励下,结构被激发的共振模态和声模态将在中高频段较为普遍,甚至还会产生彼此之间的随机迭加,从而使结构声振响应的空间分布更为均匀,峰值现象不再显著。在计算翼型结构的中高频流致振动问题时,采用流固耦合分析方法在设置时间步长和网格尺度两方面要求过高,存在较大的局限性,而统计能量分析方法在求解结构高频声振问题时具有较高的计算效率和计算精度,因此本文针对翼型结构流致振动问题,采用统计能量分析方法,建立翼型结构分析模型,开展在中高频段下翼梁间距、翼肋间距等对于结构流致振动特性的影响研究,旨在更好地揭示翼型流致振动规律。
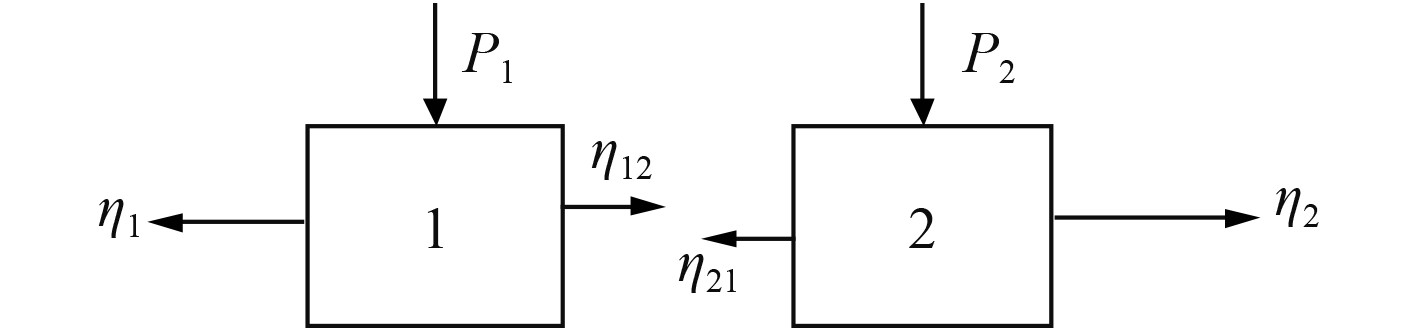
1 统计能量分析方法 1.1 基本原理统计能量分析方法着眼于统计学,将系统能量作为基本物理变量,计算研究声振系统发生振动时的平均能量。统计能量分析将复杂的声振系统划分为若干结构相对简单的子系统,将所有子系统的能量作为基本参数,建立各个子系统之间的能量平衡关系,图1为一耦合子系统的示意图。
|
图 1 耦合系统模型示意图 Fig. 1 Schematic diagram of the coupled system |
此时子系统能量平衡的表达式可写为:
| $\begin{split} & {P_1} = {E_1} + {\eta _1}\omega {E_1} + {\eta _{12}}\omega {E_{12}} - {\eta _{21}}\omega {E_2} \text{,}\\ & {P_2} = {E_2} + {\eta _2}\omega {E_1} + {\eta _{21}}\omega {E_1} - {\eta _{12}}\omega {E_2} \text{。} \end{split} $ | (1) |
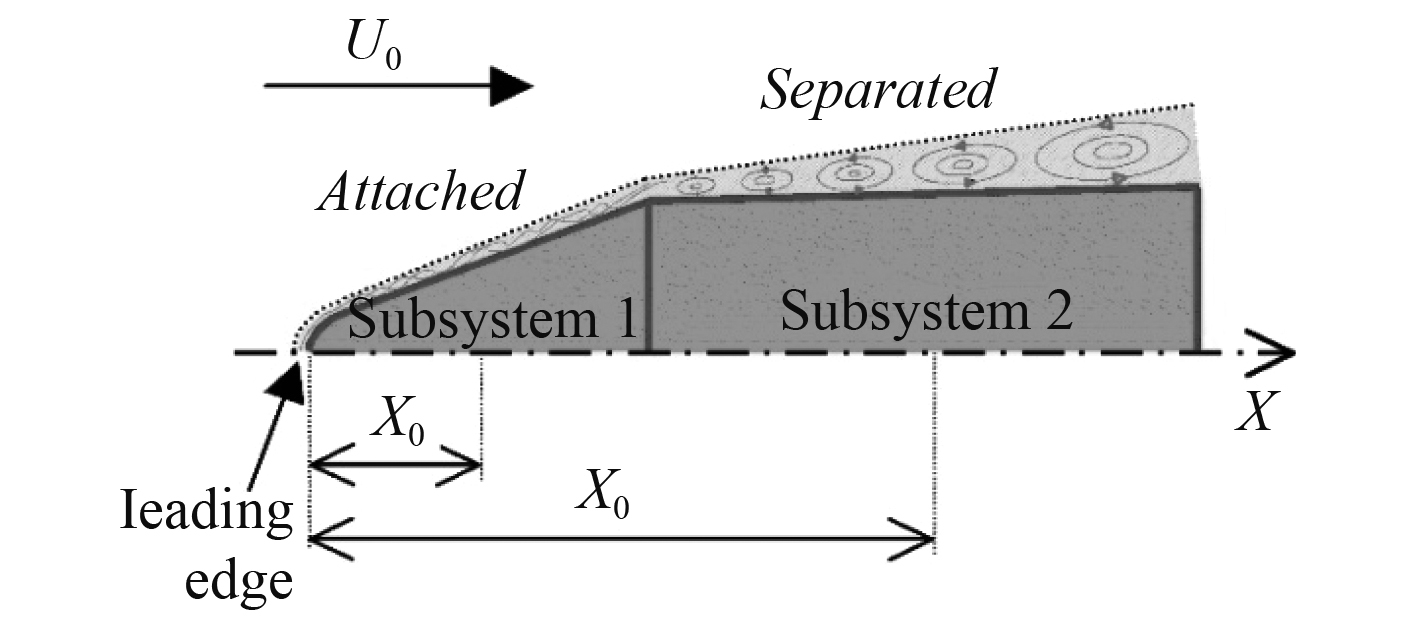
针对如图2所示的流致振动问题,一方面要基于统计能量分析基本原理,另一方面要确定湍流载荷输入。本文采用统计能量法分析研究流致振动问题时,采用Cockburn提出的功率谱密度函数计算方法确定湍流边界层压力载荷,其表达式如下:
|
图 2 流致振动统计能量分析模型 Fig. 2 Statistical energy analysis model for flow-induced vibration |
| ${S_{\rm{p}}}\left( f \right) = \dfrac{{P_{RMS}^2}}{{{f_0}{{\left( {1 + {{\left( {\dfrac{f}{{{f_0}}}} \right)}^A}} \right)}^B}}}\text{,}$ | (2) |
| $ \frac{{P}_{RMS}}{q}\!=\!\left\{\!\!\!\begin{array}{l}\dfrac{0.006}{1+0.14M{\rm{a}}^{2}}\;\;\;\;\;\;\;\;{\text{黏附状态}}\\ \min\left(0.26,\dfrac{0.041}{1+1.606M{\rm{a}}^{2}}\right)\;\;{\text{分离状态}}\end{array}\!\!\!\right\}\text{,}$ | (3) |
| $ q = \frac{1}{2}\rho U_0^2,\;{M_a} = \frac{{{U_0}}}{{{c_0}}},\;{f_0} = C\frac{{{U_0}}}{\delta }\text{,} $ | (4) |
| $ \delta = 0.37\frac{{{X_0}}}{{{R_e}^{0.2}}},\;{R_e} = \frac{{{U_0}{X_0}}}{\nu }\text{。} $ | (5) |
式中:U0为自由来流速度;Ρ为流体密度;ν为流体的运动学粘度;c0为声波在流体中传播的速度;X0为湍流边界层前缘到子系统中心的距离。黏附状态时系数A=0.9,B=2,C=0.346,分离状态时A=0.83,B=2.15,C=0.17。
1.3 关键计算参数1)模态密度
模态密度是指子系统在计算频带范围里单位频率内的结构模态数量,它表征了子系统贮存外界输入能量的能力,是统计能量分析方法的一个重要参数。表1给出了几种典型结构的模态密度估算方法。
|
|
表 1 典型子系统模态密度计算公式 Tab.1 Formula of modal density of typical subsystem |
2)耦合损耗因子
耦合损耗因子是表现2个相邻子系统之间耦合作用程度的一个参数。在工程实践中具有实用价值的结构均为各种型式的结构单元组合在一起,因而结构与结构之间的机械连接是最常见的耦合形式。由于工程实践中结构之间的连接形式、连接工艺数量众多,使得理论求解结构与结构间的耦合损耗因子难度十分大。目前统计能量分析中关于耦合损耗因子的理论是建立在弱耦合假设的前提下的,耦合损耗因子具体表达式如表2所示。
|
|
表 2 耦合损耗因子表达式 Tab.2 Coupling loss factor expression |
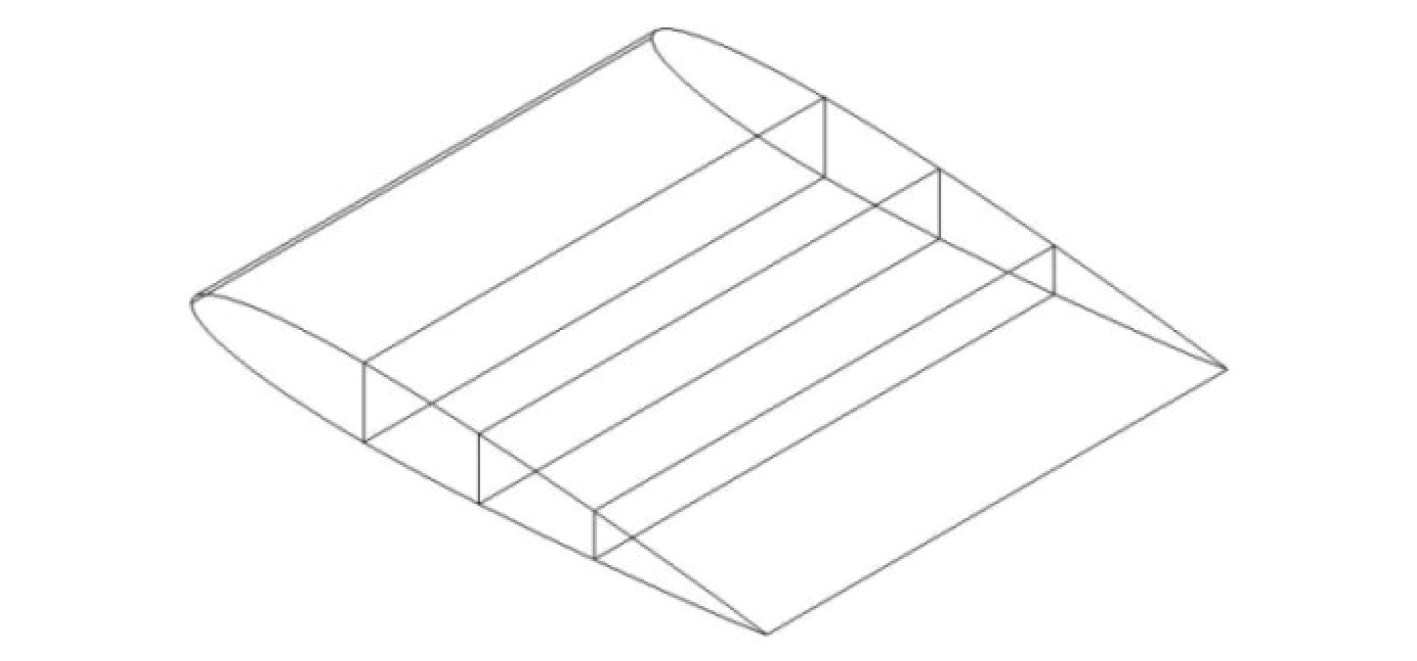
在原有翼型结构的基础上,于翼型结构内部增设加强翼梁,沿弦长方向,以中间翼梁为基准,分别在其两侧间距L为0.05 m,0.1 m,0.2 m和0.3 m处各设置一道加强翼梁,结构形式如图3所示。
|
图 3 翼梁加强结构示意图 Fig. 3 Schematic diagram of spar reinforcement structure |
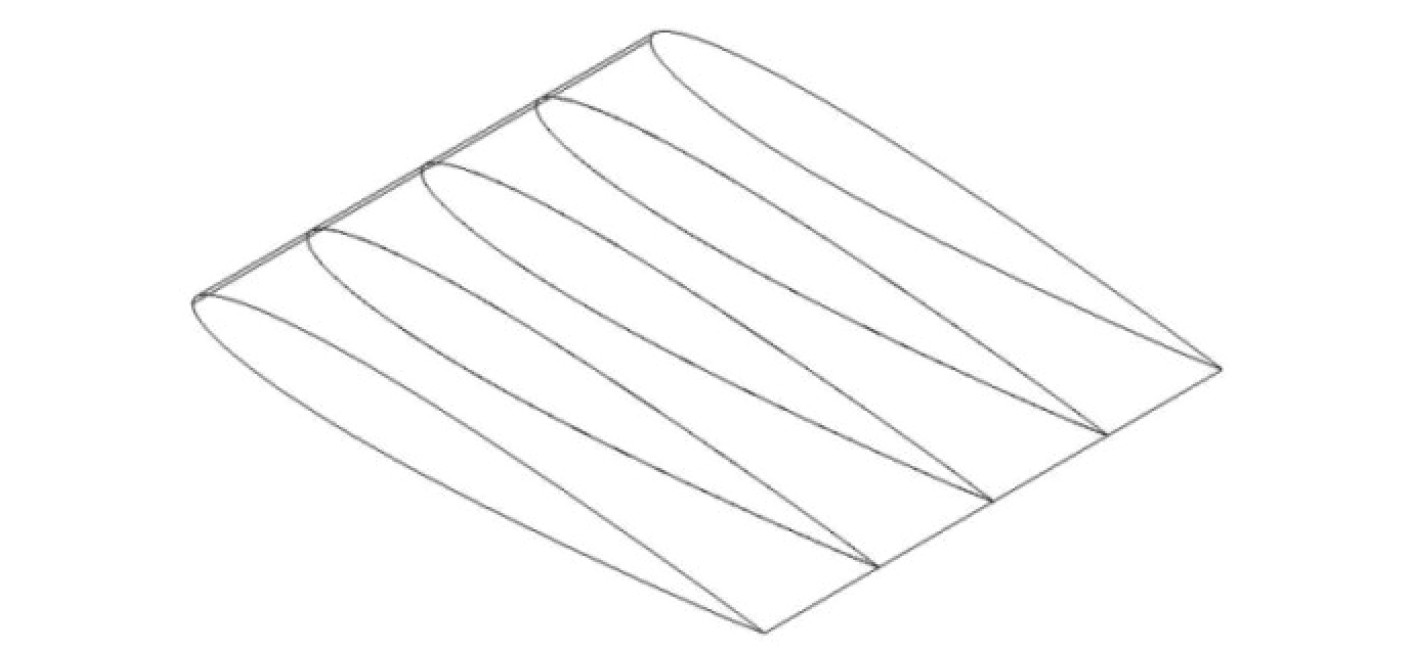
在原有翼型结构的基础上,于翼型结构内部增设加强翼梁,沿展长方向,以中间翼梁为基准,分别在其两侧间距D为0.05 m,0.1 m,0.2 m和0.3 m处各设置一道加强翼梁,结构形式如图4所示。
|
图 4 翼肋加强结构示意图 Fig. 4 Schematic diagram of rib reinforcement structure |
沿弦长方向将翼型蒙皮划分为n个板壳子系统,并在蒙皮子系统表面施加湍流边界层脉动压力载荷。自由来流速度为U0=5 m/s,迁移速度Uc=0.7×U0,脉动压力载荷采用上述的湍流边界层载荷计算方法进行估算,1/3Oct功率谱密度函数如图5所示。
|
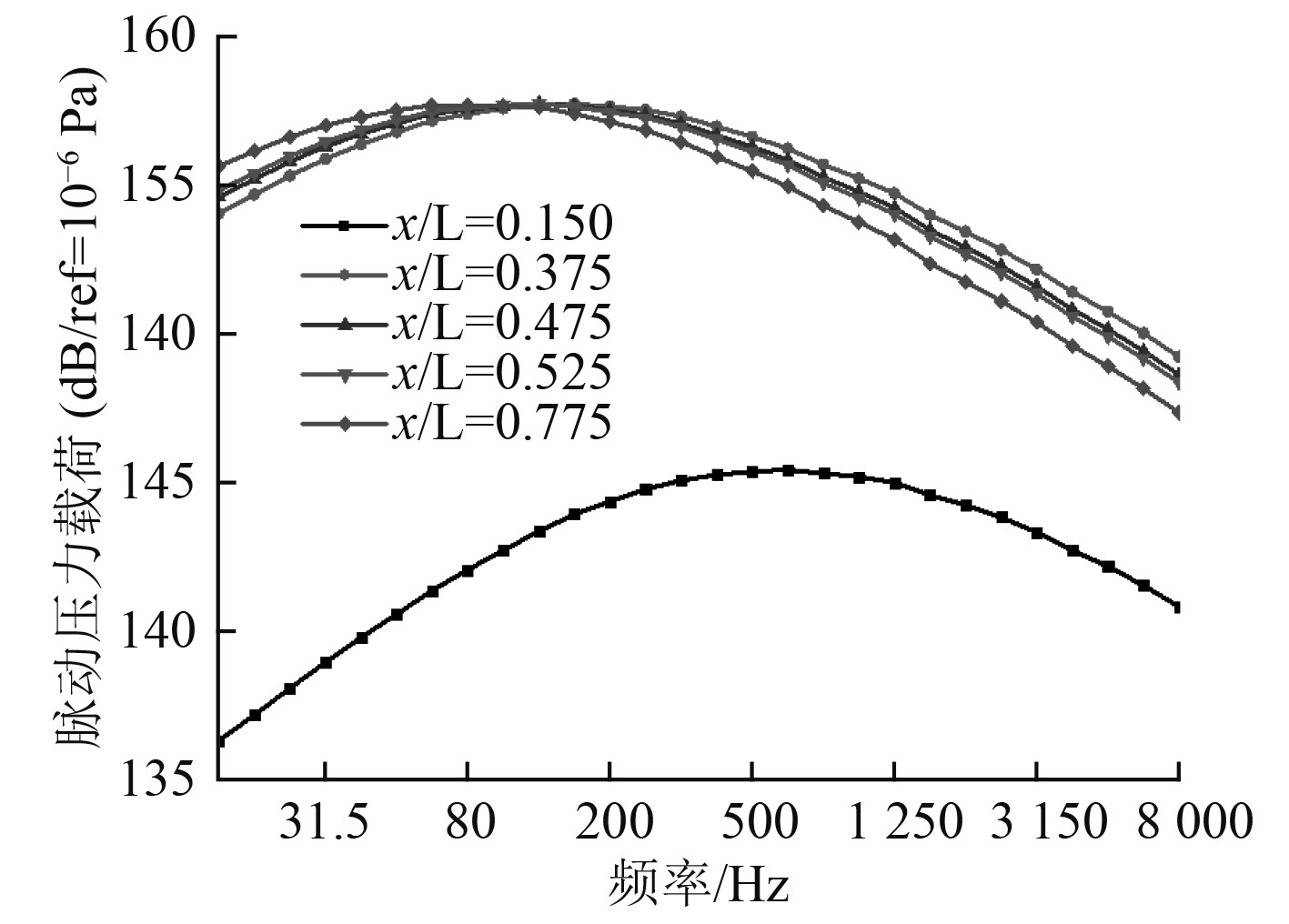
图 5 脉动压力功率谱密度函数曲线 Fig. 5 Pulsating pressure power spectral density function curve |
由图5功率谱密度函数曲线可知,沿弦长方向不同子系统上的脉动压力载荷均呈现先增后降的趋势。在200 Hz以内的低频段,越接近尾缘脉动压力载荷越大,在200 Hz~8 kHz的中高频段,越接近尾缘脉动压力载荷反而呈下降趋势。
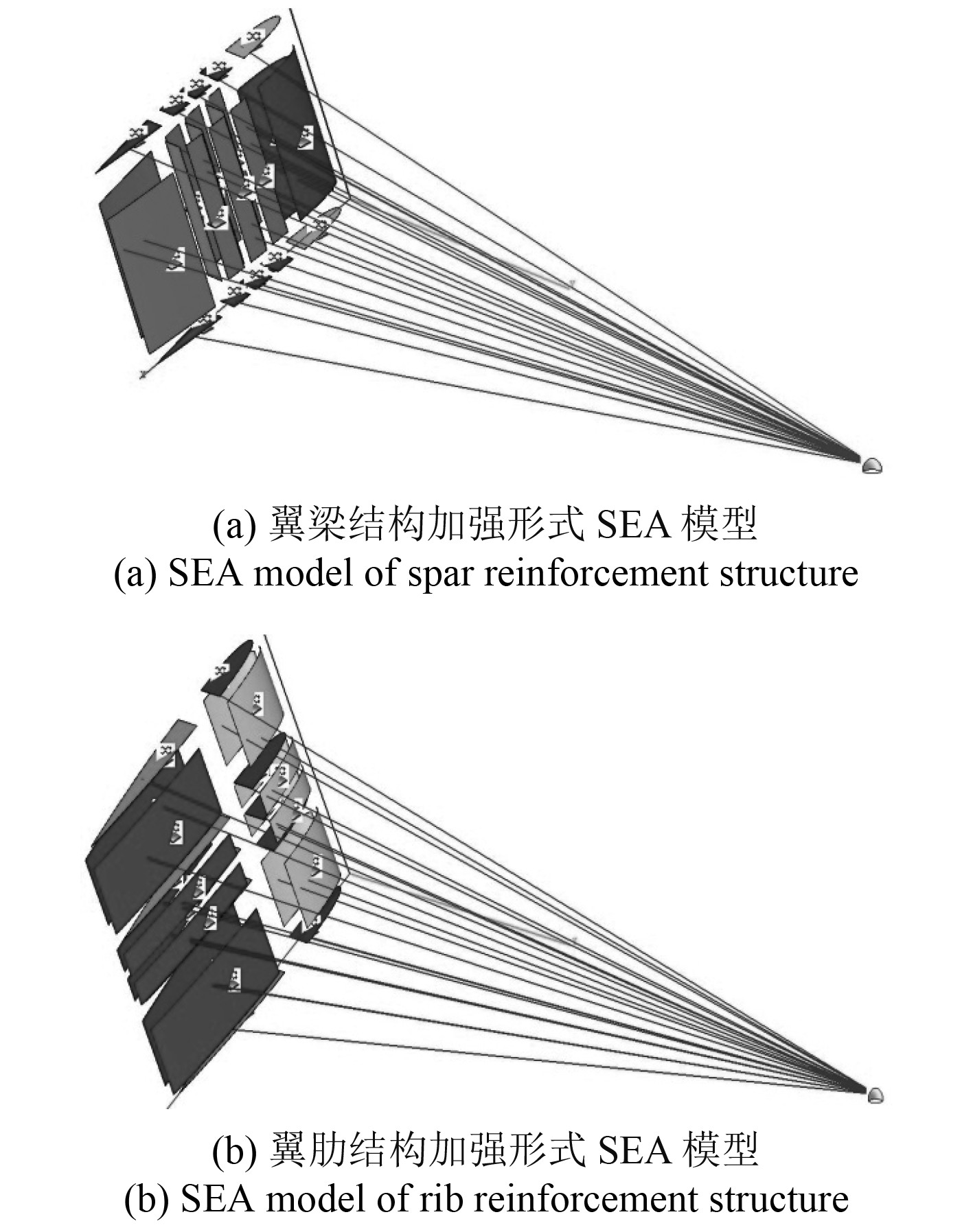
将上述所得脉动压力载荷加载至蒙皮子系统上后,2种不同翼型加强结构形式统计能量分析模型如图6所示。
|
图 6 翼型结构加强形式SEA模型 Fig. 6 SEA model of airfoil structure reinforced form |
本文采用尖锐随边NACA 0012型翼型,弦长1 m、展长0.8 m,自由来流速度为5 m/s。翼型结构SEA模型及模态密度如图7所示。
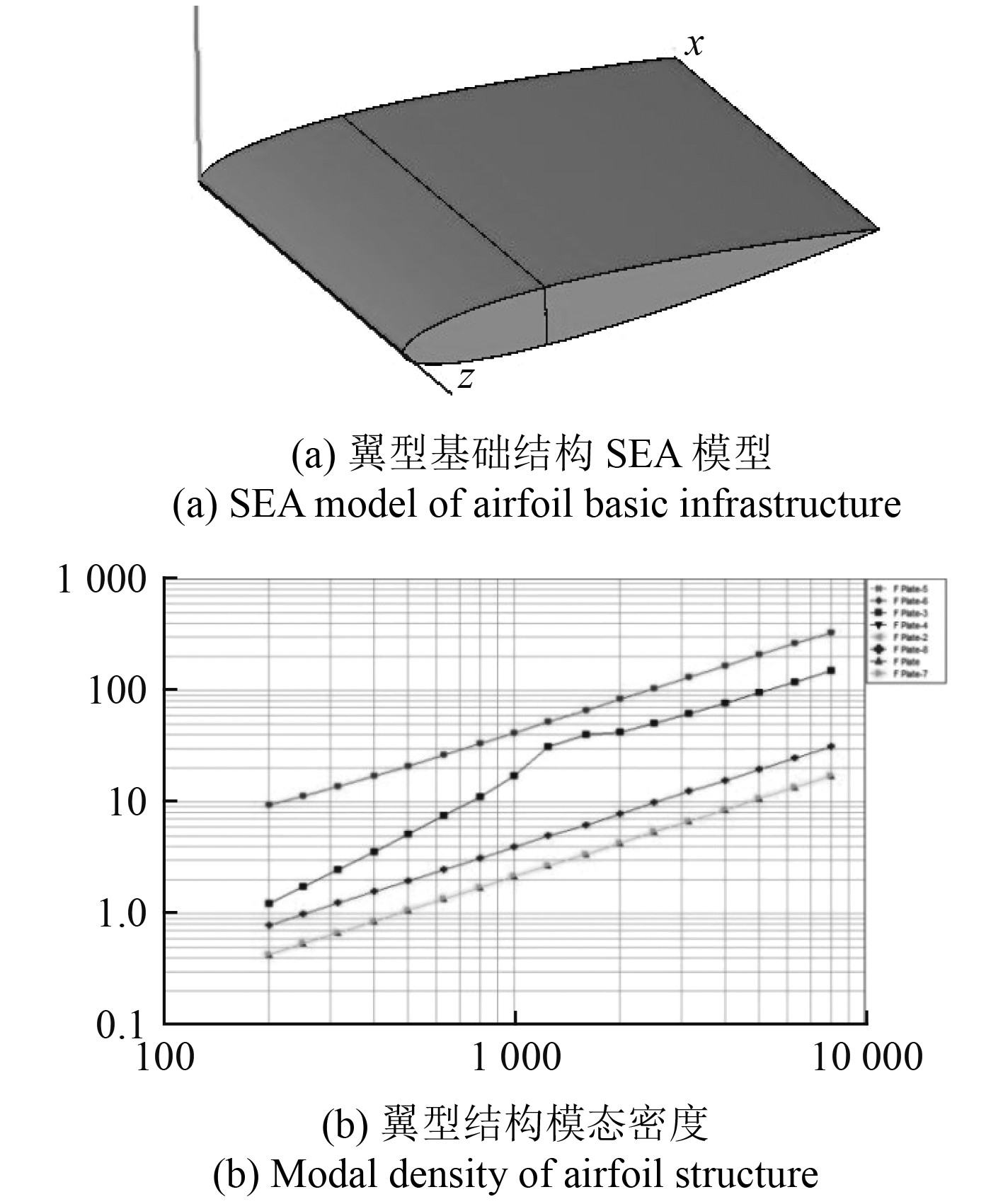
|
图 7 翼型基础结构SEA模型及模态密度 Fig. 7 SEA model and modal density of airfoil basic structure |
为保障SEA分析预报模型宽频分析的有效性,一般需保障各子系统在分析频带的模态数≥4,但对于形状及曲率变化较小的板架等子系统,其模态数可放宽至满足模态数≥1。由图7翼型结构模态密度图中可以看出,在200 Hz~8 kHz内,所有板子系统模态密度均大于1,因此,本文认为在200 Hz~8 kHz的中高频段内所计算出的结果是可信且可靠的。
3 加强形式对结构中高频流致振动的影响 3.1 翼梁间距对结构中高频流致振动的影响分别对L为0.05 m,0.1 m,0.2 m和0.3 m的不同翼梁加强结构进行数值模拟,计算频段为200 Hz~8 kHz,计算结果以振动加速度级的1/3Oct形式表现,5种结构形式的频响曲线对比如图8所示。
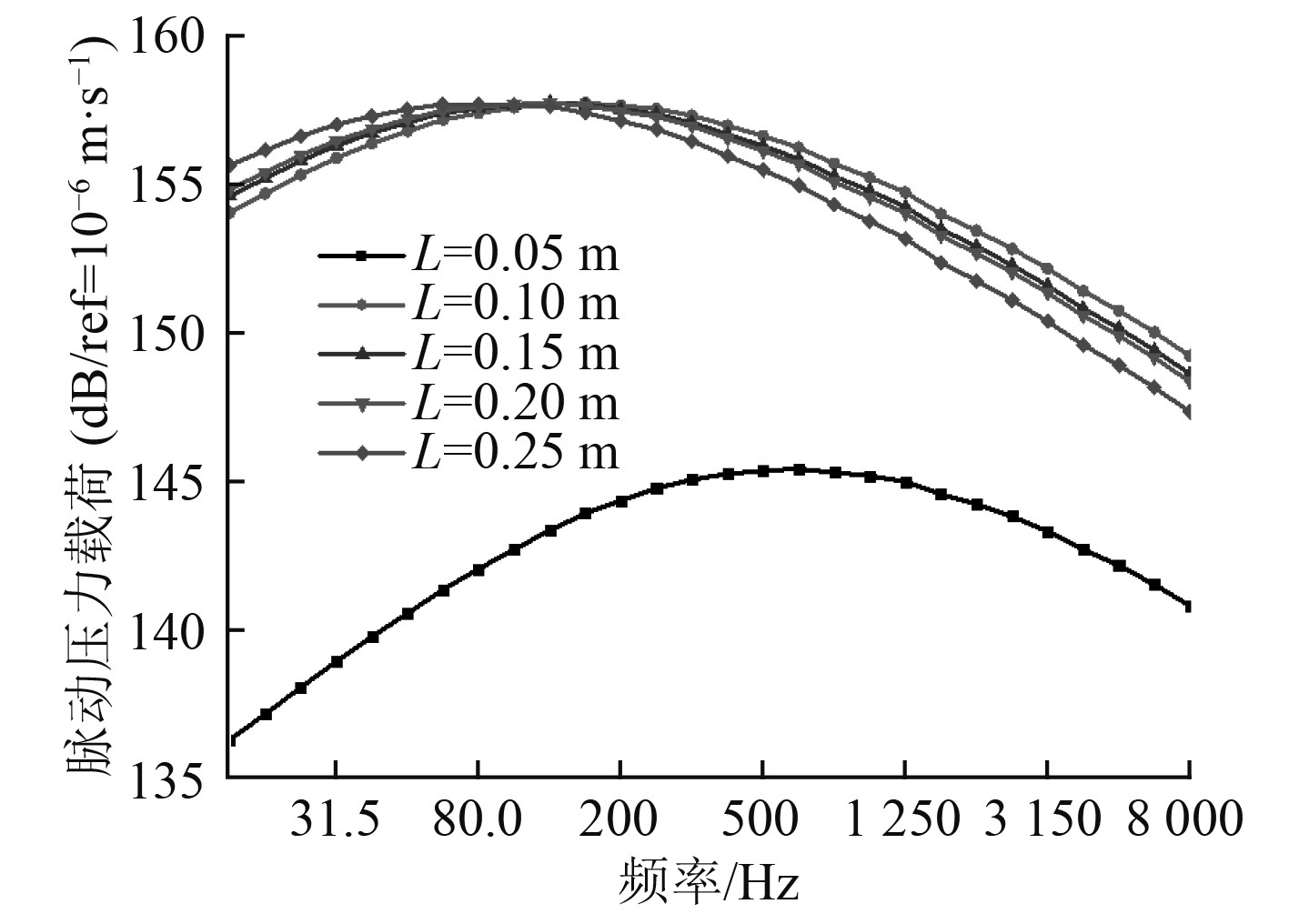
|
图 8 不同翼梁间距振动加速度级对比曲线 Fig. 8 Comparison curves of vibration acceleration level of different spar spacing |
由图8结果可知,翼型结构在中高频的流致振动响应呈现线性下降趋势,这与图5脉动压力的中高频频谱特性较为吻合,4种结构加强形式之间的振动加速度级差值均在3 dB以内。采用振动加速度总级的形式,整体性评价在中高频段内的4种不同翼梁布置间距下翼型结构的流致振动水平,得到计算结果如表3所示。
|
|
表 3 不同翼梁间距下翼型振动加速度总级 Tab.3 Vibration acceleration levels of airfoil under different spar spacing |
由表3可知,随着翼梁布置间距的增加,蒙皮子系统的振动加速度级逐渐增加,且翼梁间距的改变,对于翼型结构中高频流致振动响应的影响较为明显,无结构加强的翼型结构其振动加速度总级与采用加强翼型之间的差值均超过5 dB。由此可见,在中高频流体脉动压力载荷的作用下,翼型的流致振动响应会随翼梁布置间距的增加而增加。
3.2 翼肋间距对结构中高频流致振动的影响分别对D为0.05 m,0.1 m,0.2 m和0.3 m不同翼肋加强结构进行数值模拟,计算频段为200 Hz~8 kHz,计算结果以振动加速度级的1/3Oct形式表现,5种结构形式的蒙皮子系统振动加速度级频响对比曲线如图9所示。

|
图 9 不同翼肋间距振动加速度级对比曲线 Fig. 9 Comparison curves of vibration acceleration level of different wing rib spacing |
由图9可知,翼型结构在中高频的流致振动响应呈现线性下降趋势,与图3中脉动压力的中高频频谱特性相吻合,4种结构加强形式之间的振动加速度级差值不大。采用振动加速度总级的形式,整体性的评价在中高频段内的4种不同翼肋间距下翼型结构的流致振动水平,计算结果如表4所示。
|
|
表 4 不同翼肋间距振动加速度总级 Tab.4 Vibration acceleration levels of different wing rib spacing |
由表4可知,随着翼肋布置间距的增加,蒙皮子系统的振动加速度级逐渐减小,且翼梁间距的改变,对于翼型结构中高频流致振动响应的影响比较明显,无结构加强的翼型结构其振动加速度总级与采用加强翼型之间的差值均超过5 dB。由此可见,在中高频流体脉动压力载荷的作用下,翼型的流致振动响应会随翼肋布置间距的增加而减小。但与上节计算结果对比可知,翼肋降低翼型结构中高频流致振动响应的效果要略弱于翼梁。
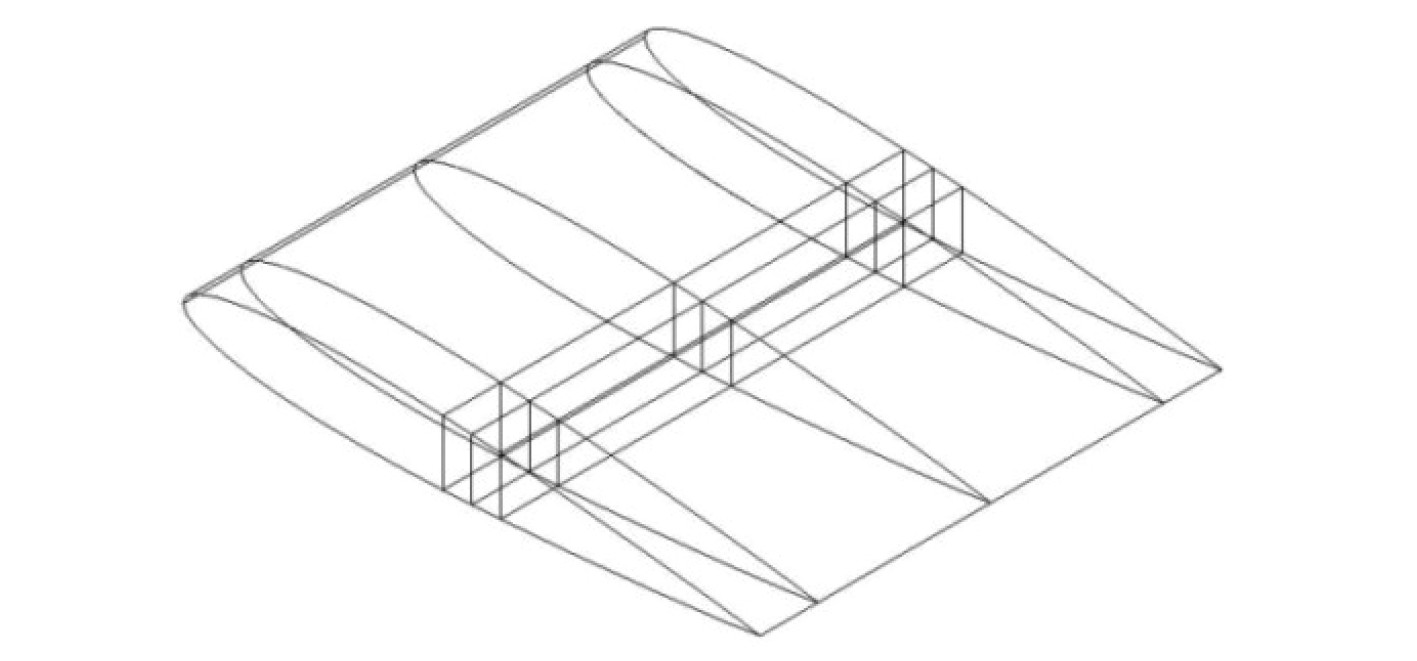
3.3 组合加强形式对结构中高频流致振动的影响结合以上内容可知,在原有基础翼型结构的基础上,以中间翼梁为基准,在其两侧间距为0.05 m处设置加强翼梁,或以中间翼肋为基准,在其两侧间距为0.3 m处设置加强翼肋,两者对翼型流致振动的影响都比较明显。综合考虑两者,在原有基础翼型结构的基础上,设置加强翼梁和加强翼肋,其结构形式如图10所示。
|
图 10 组合加强结构示意图 Fig. 10 Schematic diagram of combined reinforcement structure |
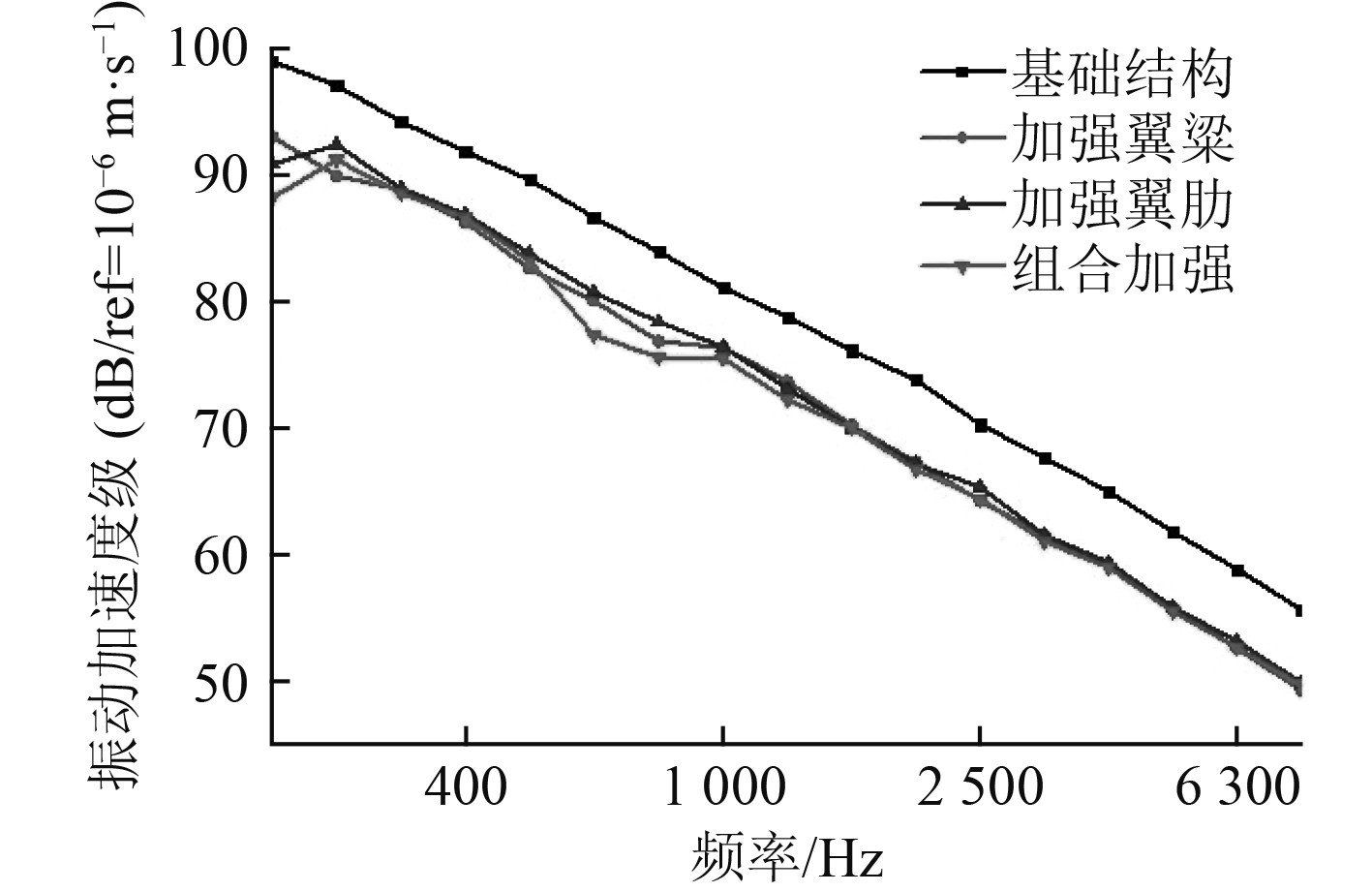
计算翼型在200 Hz~8 kHz频段下的振动加速度,以1/3Oct形式表现,基础翼型、加强翼梁、加强翼型与组合加强形式的蒙皮子系统振动加速度级频响对比曲线如图11所示。
|
图 11 不同加强形式振动加速度级对比曲线 Fig. 11 Comparison curves of vibration acceleration levels of different strengthening forms |
由图11可知,4种结构加强形式之间的振动加速度级差值不大。采用振动加速度总级的形式,整体性的评价在中高频段内的不同加强形式下翼型结构的流致振动水平,计算结果如表5所示。
|
|
表 5 不同加强形式振动加速度总级 Tab.5 Vibration acceleration levels of different strengthening forms |
由表5可知,不同加强形式对于翼型的流致振动响应均有显著的影响,翼梁结构其减振效果要略优于翼肋,但组合加强形式对于结构的流致振动影响更为明显,可在加强翼梁或加强翼肋的基础上再减少1 dB左右。
3 结 语本文基于统计能量分析方法建立NACA0012翼型SEA模型,探究了中高频段翼梁、翼肋间距等对结构流致振动特性的影响,给出了加强形式对翼型结构流致振动的影响规律。通过上述研究,可以得到如下主要结论:
1)随着翼梁和翼肋布置间距的增加,翼型结构湿表面振动加速度级呈下降趋势,且由于翼型结构在脉动压力载荷作用下以纵向弯曲振动为主,因此采用翼梁结构进行结构加强减振效果会更佳。
2)在中高频段下,翼梁和翼肋2种结构加强形式对于三维翼型结构流致振动特性的影响比较显著,且随着翼梁布置间距的增加,蒙皮子系统的平均振动加速度总级有小幅的增大,随着翼肋布置间距的增加,蒙皮子系统的平均振动加速度总级随之减小,但两者相比,翼梁结构其减振效果要略优于翼肋。
3)在中高频段下,加强翼梁,加强翼肋与组合加强形式均对翼型结构流致振动有较为显著的影响,但组合加强形式对翼型流致振动的影响较加强翼梁或加强翼肋更为明显。
| [1] |
董仁义, 吴崇健. 水下翼型水动力学与声学研究进展[J]. 中国舰船研究, 2008(3): 1-9. DOI:10.3969/j.issn.1673-3185.2008.03.001 |
| [2] |
STRAWDERMAN, WAYNE A. Turbulence-Induced Plate Vibrations: an Evaluation of Finite- and Infinite-Plate Models[J]. The Journal of the Acoustical Society of America, 1969, 46(5B): 1294. |
| [3] |
STRAWDERMAN W A, BRAND R S. Turbulent-Flow-Excited Vibration of a Simply Supported, Rectangular Flat Plate[J]. The Journal of the Acoustical Society of America, 1969, 45(1): 177-192. |
| [4] |
魏建辉, 陈美霞, 乔志, 等. 湍流激励下单双层圆柱壳振动特性对比[J]. 华中科技大学学报: 自然科学版, 2012, 40(8): 44-48. [8]. |
| [5] |
胡世良, 鲁传敬, 何友声. 平板流固耦合振动的数值分析[J]. 上海交通大学学报, 2013, 47(10): 1487-1493+1502. |
| [6] |
陈美霞, 魏建辉, 乔志, 等. 湍流激励下结构振动特性的半解析半数值算法研究[J]. 振动工程学报, 2011, 24(6): 689-695. DOI:10.3969/j.issn.1004-4523.2011.06.017 |
| [7] |
俞孟萨, 李东升. 统计能量法计算声呐自噪声的水动力噪声分量[J]. 船舶力学, 2004(1): 99-105. DOI:10.3969/j.issn.1007-7294.2004.01.013 |
| [8] |
何秦, 王禹, 王博涵, 等. 基于统计能量分析的船舶舱室噪声研究[J]. 舰船科学技术, 2020, 42(9): 18-23. |
| [9] |
COCKBURN J. A., ROBERTSON J. E.. Vibration response of spacecraft shrouds toin-flight fluctuating pressures[J]. Journal of Sound and Vibration, 1974, 33(4).
|
| [10] |
程广利, 朱石坚, 伍先俊. 统计能量分析方法及其损耗因子确定方法综述[J]. 船舶工程, 2004, 42(4): 10-15. DOI:10.3969/j.issn.1000-6982.2004.04.003 |
| [11] |
冯涛, 王晶. 统计能量法的原理及其在声学工程上的应用[J]. 北京工商大学学报(自然科学版), 2002(4): 25-27. |
 2021, Vol. 43
2021, Vol. 43
