2. 高新船舶与深海开发装备协同创新中心,上海 200400;
3. 船舶与海洋水动力湖北省重点实验室,湖北 武汉 430074;
4. 中国船舶及海洋工程设计研究院,上海 200011
2. Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration, Shanghai 200400, China;
3. Hubei Key Laboratory of Naval Architecture and Ocean Engineering Hydrodynamics, Wuhan 430074, China;
4. Marine Design and Research Institute of China, Shanghai 200011, China
船舶的水下辐射噪声主要包括了机械噪声、推进器噪声和水动力噪声,是船体结构及其周围流场耦合作用下产生的复杂过程,因此对其想要建立精确的声振动力学方程以获得解析解的难度很大,所以数值方法是目前较为有效且运用广泛的手段。在低频段,船舶的水下辐射噪声的主要成分为机械噪声。
在线性范围内,传统的机械噪声预报主要采用的是流固声耦合模型。首先将流体近似为不可压缩的理想介质,然后基于势流理论、结构动力学理论分别建立相应介质的动力学模型,在耦合界面建立连续条件后常将流体等效为附连水质量,求出结构的振动速度后,再单独基于边界元法进行声场分析。杨德庆等[1-4]基于Nastran和Sysnoise软件,采用结构有限元法耦合声学边界元法对某船舶在航行工况下的水下声辐射特性进行了分析,计算结果与实船测量对比吻合良好,为有限元法/边界元法应用于实船水下噪声预报提供了参考依据。该流程目前已较为成熟,在工程问题中应用较为广泛。
随着研究的深入,发展了基于声固耦合的分析模型。其基本思路是:考虑流体中的声波运动(理想声介质中主要是纵波),将流体处理为可压缩的声介质,基于Helmholtz理论、振动波理论分别建立声场模型、结构波模型,在耦合界面建立连续条件后将声介质的影响用声压(动载荷)作用在壳体上,进而进行耦合系统的声振性能分析。较多学者[5-6]采用结构有限元耦合声学有限元的声-固耦合算法对船舶在各种工况下的低频段水下辐射噪声进行了计算和分析。同时,基于声-固耦合动力学方程的直接声振耦合统一求解算法也逐步应用到工程实践当中。而在激励载荷施加的方式上,针对有些计算模型无法直接施加加速度激励的现状,Paraskevopoulos等[7]研究了大质量法的适用性;Kim等[8]针对单自由度和多自由度模型,对大质量法进行理论分析并给出了详细的推导过程。大质量法由于在有限元软件中可行性高,且可以进行线性、非线性分析因而相较于相对运动法更适用于结构多点激励分析,因此大质量法常被应用到将试验测得的振动信号转化为有限元软件所能直接施加的力激励中。
以上研究已经使声-固耦合理论和各种不同的有限元算法运用到船舶低频段水下辐射噪声的计算和分析中,但不同的有限元软件在载荷输入时往往存在不同的要求。本文基于直接声振耦合统一求解分析软件Virtual.Lab不能直接施加加速度激励的现状,在传统大质量法转化激励的基础上,提出将激励直接施加到设备质心处的简化大质量法,同时把机械噪声计算结果与基于传统大质量法、流固声方法的计算结果进行对比,验证提出的简化方法的有效性,为机械噪声预报时激励加载方式的选取提供参考。
1 机械噪声计算模型 1.1 船舶模型简介以某船为研究对象,根据船体的设计图纸,建立了全船的有限元模型,包括船体外板、各层甲板、舱壁等都用壳单元模拟;船底纵骨、各层甲板的纵骨和横梁、舱壁扶强材等都用梁单元模拟;船上各动力设备的基座用细化的壳单元模拟;设备用质量单元模拟。全船的有限元模型总长87.5 m,型宽12.5 m,型深7.5 m。单元数量为171599个,其中板壳单元有124071个,梁单元有47127个,质量单元有89个。船体结构材料弹性模量E=2.1×1011 Pa,泊松比
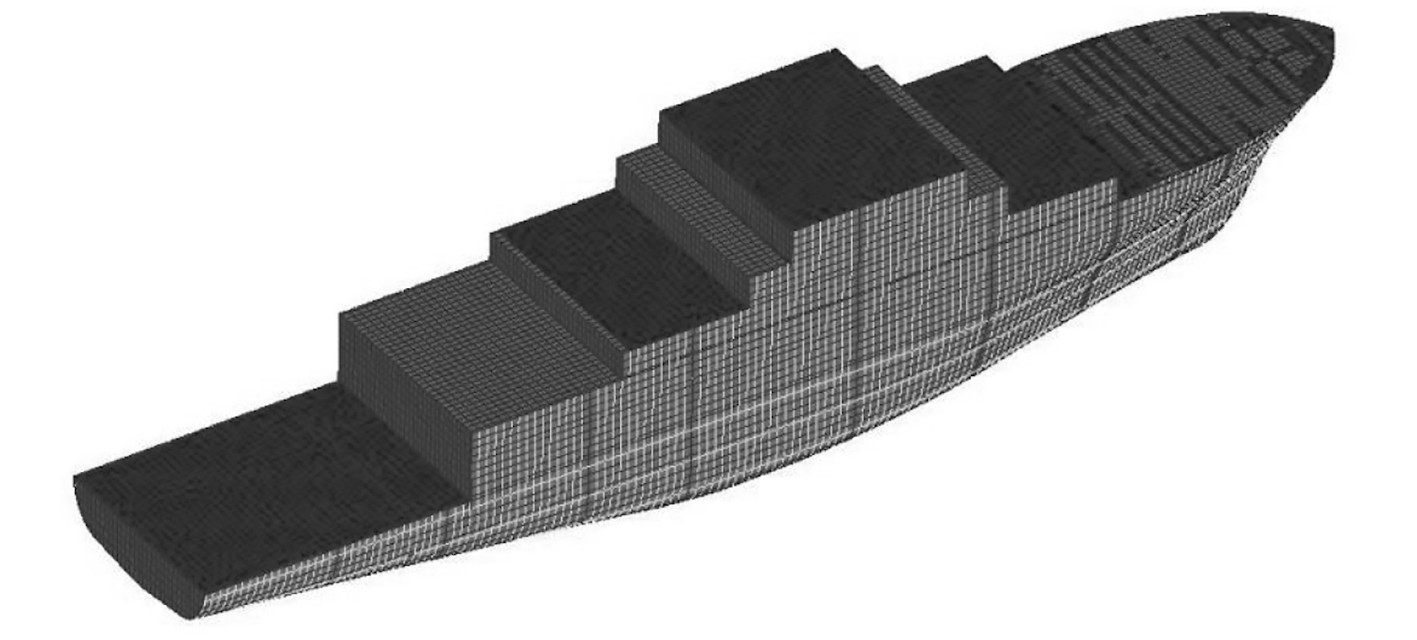
图1为本文采用的结构分析模型示意图。
|
图 1 船舶结构示意图 Fig. 1 Ship structure diagram |
在利用声学有限元法进行机械噪声数值预报时,流域模型尺寸的确定通常需要满足一定的条件,这便是涉及到了无限流域截断的问题。庞福振[9]提出不论流域模型如何截断,有限截断域流场都应至少满足以下的2个条件:
1)截断后的流域模型应确保流体与船舶结构的耦合效应。这便要求流场域需具有一最小尺度,该最小流域半径
| ${R_f} \text{≥} {\rm{max}}(D/2 + 0{\rm{.2}}\lambda ,2D)\text{。}$ | (1) |
式中:D为船体结构的最大直径;
2)截断后的流域模型应确保流域模型截断处的声传播不发生反射。此条件即是要求在流域模型截断后仍和无限域流场保障了声传播的特性。为满足这个条件,可在Virtual.Lab中对流域模型的自由液面节点组设置为声压为0的边界条件,并将附上AML属性。
根据以上截断流域的理论以及本文船舶的尺寸大小,实际流域由1个半圆柱和2个1/4的球组成。其中半圆柱宽度是70 m,长度是74 m,球半径为35 m。利用有限元软件Patran建立流域网格,再导入到Virtual.Lab中利用有关工具填充体网格到流域网格内部,并船体结构与流域模型的耦合面网格将赋予AML属性。其中流域网格的数量为33876个,填充的体网格数量为243170个。图2为本文船舶流域的有限元模型图。

|
图 2 流域的有限元模型图 Fig. 2 Finite element model of watershed |
根据本文所分析船舶的实际工作情况,在某航速工况下,此时开启的主要动力设备为图3所示的设备。该设备质量为16.75 t,用质量单元模拟,并用MPC多点约束与基座上方的弹簧单元连接,弹簧单元用以模拟基座上方与设备之间的隔振器。基座面板区域的细化网格大小为50 mm。图3即为某设备基座的有限元模型图。

|
图 3 某设备基座的有限元模型图 Fig. 3 Finite element model of a device base |
传统的机械噪声预报方法是基于流固声耦合模型,该方法将流体近似为不可压缩的理想介质,并在耦合界面即结构表面建立连续条件,将流体等效为附连水质量或者采用虚拟质量法考虑上流体的作用,后求出结构表面处的振动速度,最后基于边界元法进行声场分析。流固声法对结构振动和声场辐射的分步求解,降低机械噪声求解的规模,结合了有限元法及边界元法各自在求解时的优势。但是在船舶结构中低频机械噪声数值预报问题当中,求解范围通常需要覆盖20~400 Hz,且船体结构的湿表面网格数量较多,当采用边界元法进行声场分析时,将会因为以上2个问题大大增加计算规模,进而增加求解时间和求解成本。
基于声固耦合模型的Virtual.Lab中的声振耦合统一求解算法,它的简便在于可直接导入利用有限元软件建立的船体结构网格而不用计算附连水以及湿模态作为边界条件进行求解,较传统的流固声预报方法有较大的优势。但其不可采用直接加速度法作为输入,所以此时需要将加速度输入转化为力输入进行求解。
在实船试验或者台架测试时,动力设备基座面板上的振动位移、速度和加速度信号更加容易测得,而动力设备基座面板上的力信号往往不容易获取。因此,在进行机械噪声数值预报时,需要将给定的振动信号、速度和加速度信号转化为有限元软件能施加给结构的力激励。当前,基于加速度信号的载荷转化典型方法有相对运动法、大质量法、拉格朗日乘子法和惯性载荷法等等。其中大质量法由于在有限元软件中可行性高,且可以进行线性、非线性分析相较上法更适用于结构多点激励分析。
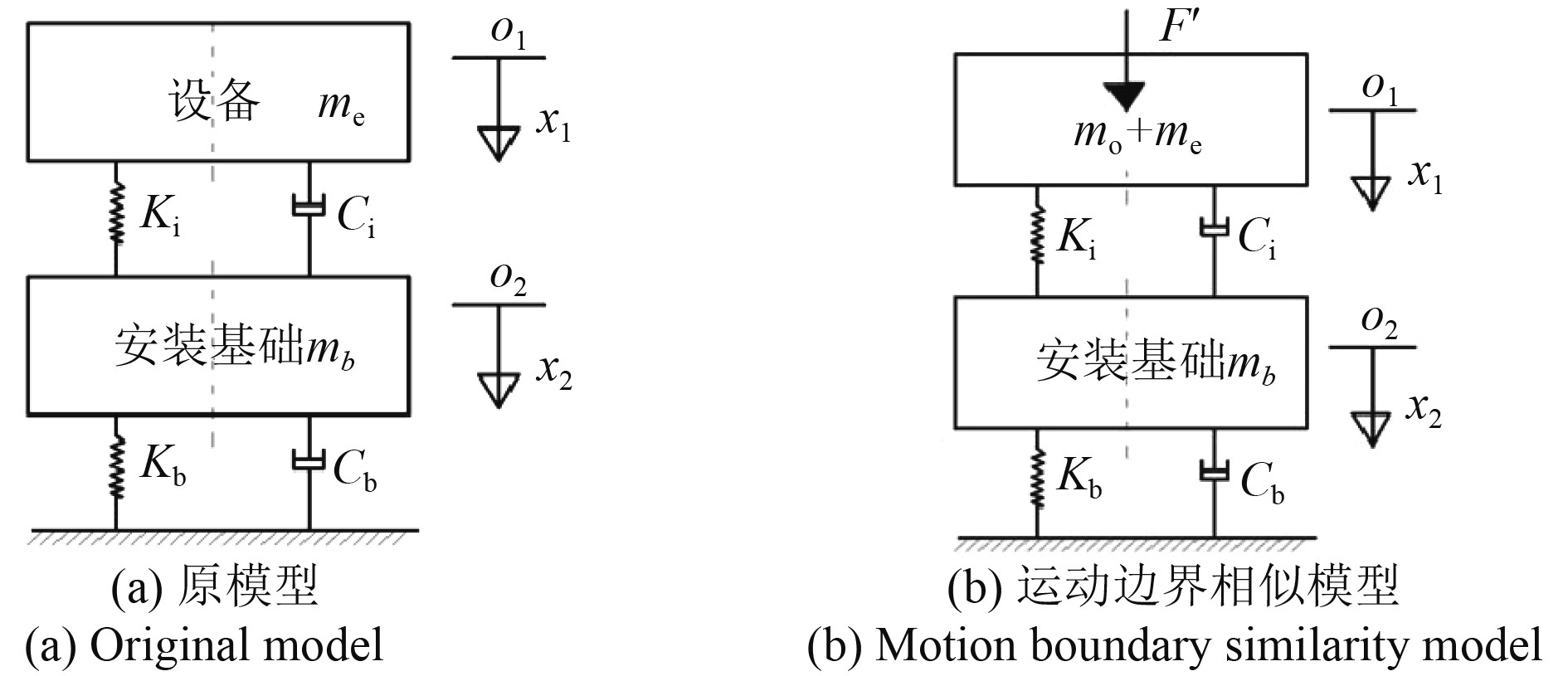
2.1 运动边界与力边界统一性根据结构的运动边界条件与力边界条件的统一性原理,运动边界条件可以和力边界条件相互转换。因此,对于确定了动力特性参数的振动系统,可采用相应的方法来变换结构的运动边界条件为相应的力边界条件。然而,在进行实船的机械噪声数值预报时,仅当已知台架试验测得的实船基座面板的加速度信号时,难以直接确定结构的力边界条件。
为了解决不确定的系统参数所带来的困难,可以构造一个具有相同原始结构运动边界的相似模型来得到原结构的振动响应。
当使用力学边界条件来表示某系统的运动时,可以将质量比设备质量大得多的刚体并联在原设备上(原设备质量为me,刚体质量为m0),并使
| $\begin{split} {F^{\prime} } =& \left( {{m_0} + {m_e}} \right){a_i} = \left( {{m_0} + {m_e}} \right){x_0}{\omega ^2}{e^{j(\omega t + \pi )}} = \\ &- \left( {{m_0} + {m_e}} \right){x_0}{\omega ^2}{e^{j\omega t}}\text{。}\end{split} $ | (2) |
由式(2)可得等效模型的运动[10]:
| $ {x_1} = {D_1}/D{e^{j\omega t}}\text{。} $ | (3) |
式中:
由于
| $\begin{split} {x_1} &=\\ &-{\frac{{\left[ {{k_b} + {k_i} - {m_b}{\omega ^2} + j\left( {{c_i} + {c_b}} \right)} \right]\omega \left( {{m_0} + {m_e}} \right){x_0}{\omega ^2}}}{{\left[ {{k_b} + {k_i} - {m_b}{\omega ^2} + j\left( {{c_i} + {c_b}} \right)} \right]\left[ {{k_i} - \left( {{m_0} + {m_e}} \right){\omega ^2} + j{c_j}\omega } \right] - {{\left( {{k_i} + j{c_i}\omega } \right)}^2}}}{e^{j\omega t}}} \approx \\ &{x_0}{e^{j\omega t}}\text{。}\\[-10pt] \end{split}$ | (4) |
可见,运动边界相似模型与原模型的运动是一致的,从而证明了运动边界相似法的有效性。
基于运动边界相似法,可以实现对运动边界和力边界的相互转换,但仍需要注意的是它成立的前提是大质量刚体的质量远远大于结构的质量,并且满足
因此,使用大质量法转化激励的实际做法就是在结构模型需要加载荷点处创建一个质量较大的质点单元,其质量通常为结构质量的103~106倍。然后该质量点处施加一个构成相似运动边界条件的力载荷,这便可以使基座面板处产生所需大小的加速度载荷,最终实现了加速度载荷的施加。简单地说,就是把加速度以力的加载形式施加给结构。
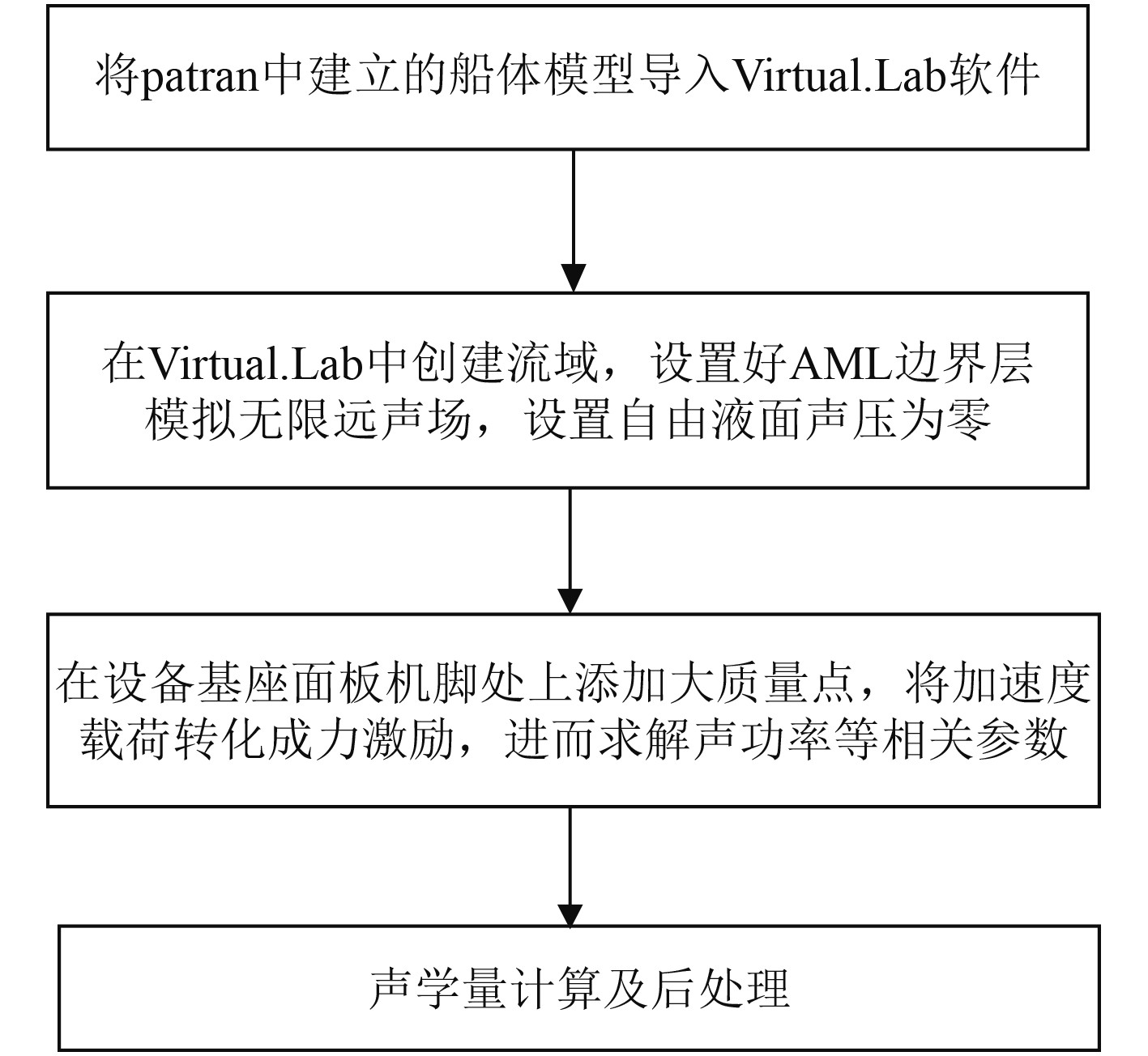
2.2 低频段机械噪声计算流程根据以上的介绍与分析,得到基于声-固耦合模型的声振耦合统一求解算法计算低频段机械噪声的流程,如图5所示。
|
图 5 基于声-固耦合模型的低频段机械噪声计算流程图 Fig. 5 Flow chart of low frequency mechanical noise calculation based on acoustic-solid coupling model |
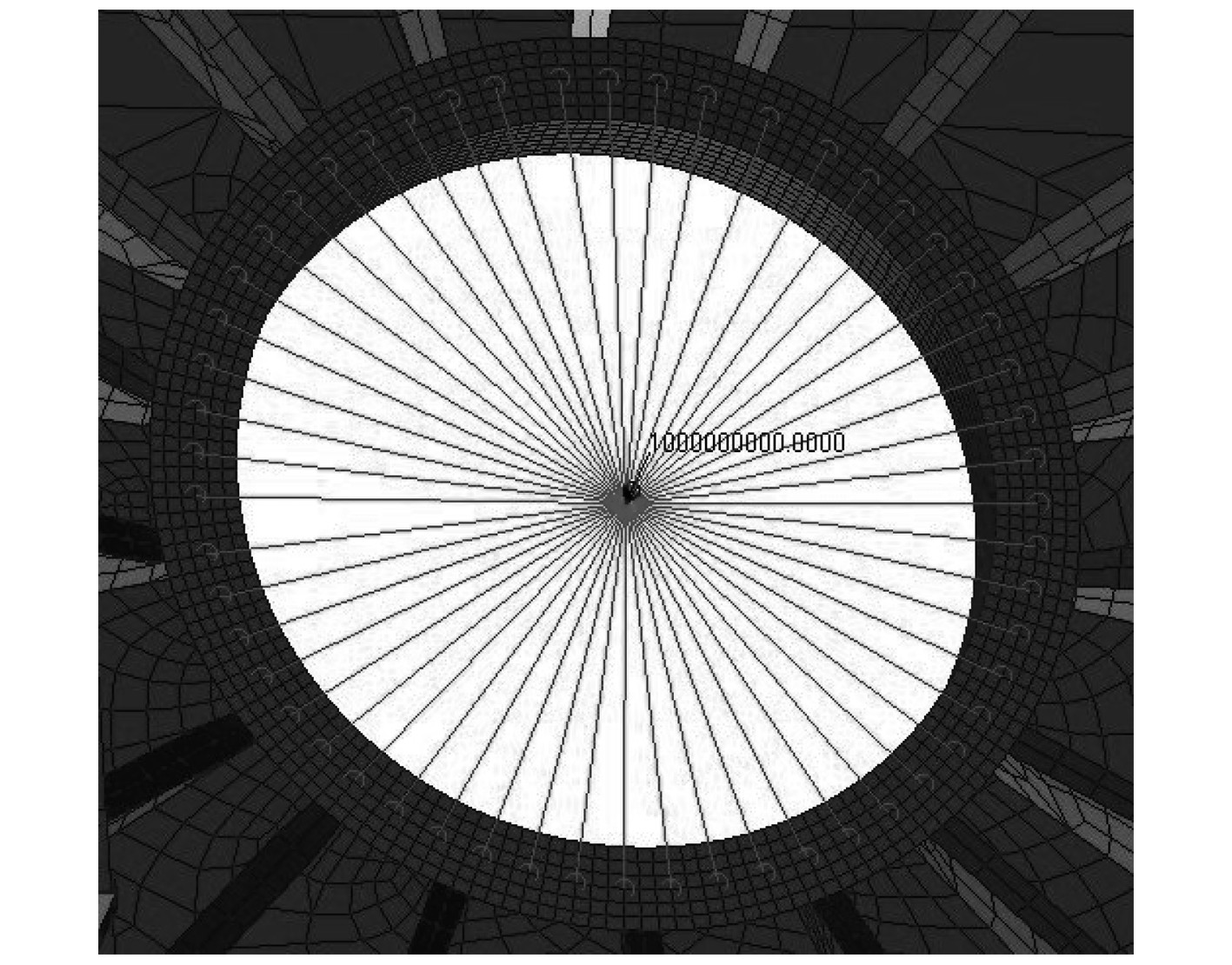
在对舰船结构进行数值仿真分析时,为了更能贴合实际工程中的真实情况,则需要在设备基座面板上每一个机脚处都附加上大质量以便保证基座面板上的动力输入。然而实际中,在进行质量较大的设备基座建模的时候,通常会存在基座面板上螺栓点过多的问题。此时若为了更好地模拟激励加载而采用上述的做法将大大增加建模的难度和时间。现提出一种简便方法,即只需要在设备质心处附加大质量,并施加对应的力激励,再用MPC多点约束方法将质量单元与设备安装位置(机脚)对应的船体结构的节点连接即可。图6和图7分别显示了传统的大质量法施加方式和简化的大质量法施加方式。根据本文船舶的实际情况,大质量的取值为109 t。

|
图 6 传统的大质量法施加方式 Fig. 6 Traditional application of large mass method |
|
图 7 简化的大质量法施加方式 Fig. 7 Simplified application of large mass method |
则在某航速工况下,选择开启设备为图3所示的动力设备,分别使用传统流固声数值模型即直接施加加速度激励并基于有限元软件Patran&Nastran和Sysnoise、声固耦合数值模型即施加传统大质量法和简化大质量法转化加速度激励为力激励并基于有限元软件Virtual.Lab计算该动力设备开启时的低频水下辐射噪声(18~220 Hz)。
图8为直接在质心处附加大质量(简化大质量法)、在设备基座上所有机脚螺栓处附加大质量(大质量法)以及直接加速度法(传统的流固声数值模型计算载荷输入)3种不同方式下,某推进器开启时距离激励点1000 m处远场半球包络面的辐射声功率级回推到距离声源1 m处的声压级的计算结果。
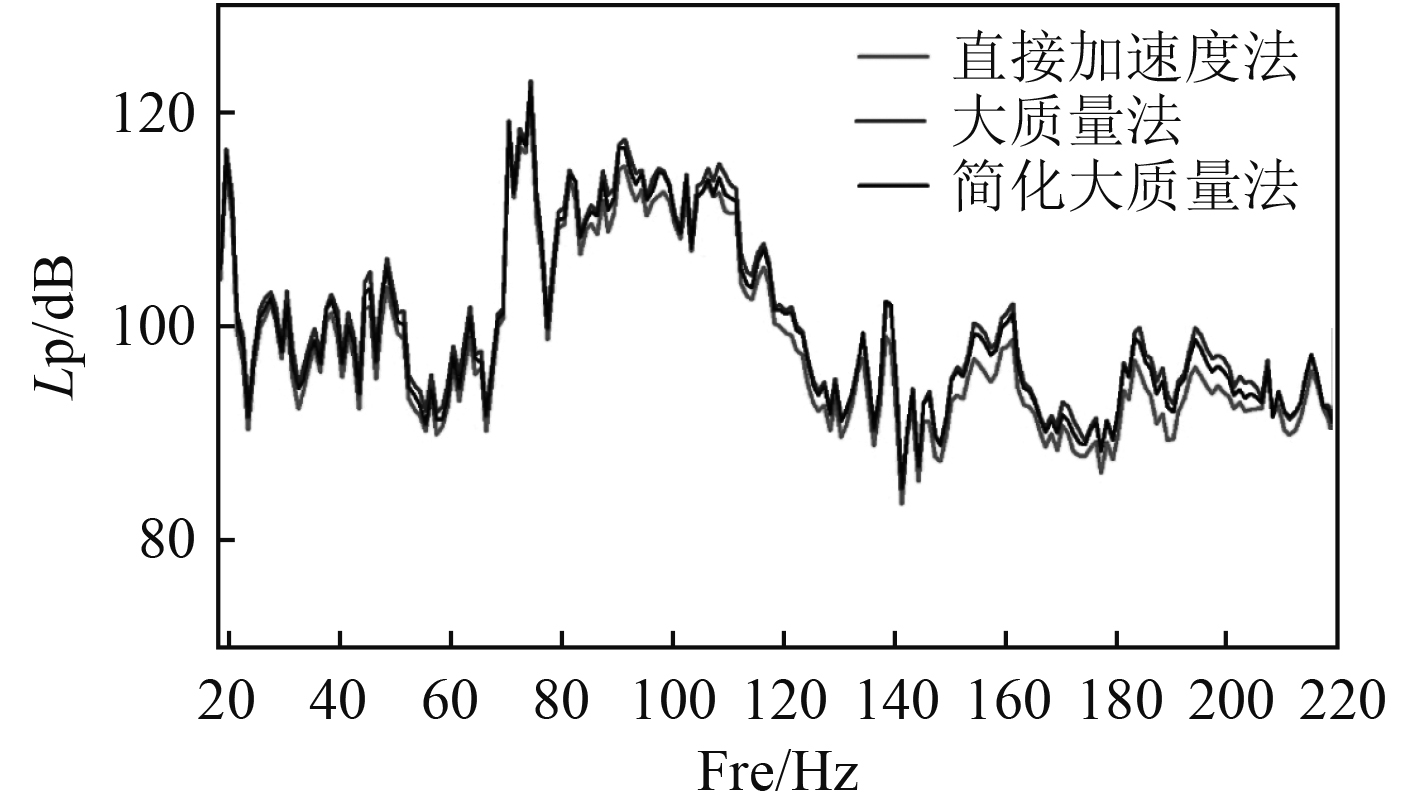
|
图 8 两种不同力激励施加方法时直翼推进器开启的辐射声压级曲线 Fig. 8 Radiation sound pressure level curve of a VSP when using two different excitation applied methods |
由图8可知,3种激励施加方式下的声压级曲线趋势有较好的一致性,且各个频点的声压级峰值基本吻合。为了更为直观地比较2种大质量法计算所得的仿真值的准确性,将声功率进行带宽(20~200 Hz)内合成,得到在质心处加激振力和在机脚(螺栓点)处加激振力的辐射声压总级分别为128.45 dB和128.72 dB,声压总级也较为接近。
4 结 语本文针对船舶的低频机械噪声数值计算问题,以某船舶为研究对象,比较了声固耦合数值模型与传统流固声数值模型在预报机械噪声时载荷输入存在的不同的要求。并基于结构有限元/声学自动匹配层(FEM/AML)声固耦合方法,提出了将激励直接施加到设备质心处的简化大质量法。在机械噪声预报结果中,运用大质量法施加加速度激励时,直接在设备质心处附加大质量与在设备基座面板上每一个机脚处都附加上大质量和传统的流固声数值模型运用的直接加速度法这3种施加方式下计算得到的辐射声压级曲线趋势有较好的一致性,且各个频点的声压级峰值基本吻合,从而验证了提出的简化大质量法的有效性。故在基于声固耦合数值模型预报船舶机械噪声时,可采用简化的大质量法将加速度激励转化为力激励,并作为输入直接施加到设备质心处。
| [1] |
杨德庆, 郑靖明, 王德禹, 等. 基于SYSNOISE软件的船舶振动声学数值计算[J]. 中国造船, 2002, 43(4): 32-38. YANG De-qing, ZHENG Jing-ming, WANG De-yu, et al. Numercial analysis of vibro-acoustic characters of ship with Sysnoise software[J]. Ship Building of China, 2002, 43(4): 32-38. DOI:10.3969/j.issn.1000-4882.2002.04.006 |
| [2] |
杨德庆, 王德禹, 刘洪林, 等. 某型艇近场噪声和自噪声数值计算[J]. 声学学报, 2003(5): 421-424. YANG De-qing, WANG De-yu, LIU Hong-lin, et al. Numerical analysis of acoustic characters in near field and self-noise of ship[J]. Acta Acustica, 2003(5): 421-424. DOI:10.3321/j.issn:0371-0025.2003.05.007 |
| [3] |
童宗鹏, 王国治. 舰船结构水下振动和声辐射特性研究[J]. 华东船舶工业学院学报, 2003(4): 18-22. |
| [4] |
邹春平, 陈端石, 华宏星. 船舶水下辐射噪声特性研究[J]. 船舶力学, 2004, 8(1): 113-124. ZOU Chun-ping, CHEN Duan-shi, HUA Hong-xing. Study on characteristics of ship underwater radiation noise[J]. Journal of Ship Mechanic, 2004, 8(1): 113-124. DOI:10.3969/j.issn.1007-7294.2004.01.015 |
| [5] |
邱中辉, 姚熊亮, 李卓, 等. 水下船舶低频段典型单机工况下声辐射特性研究[J]. 船舶, 2003(2): 45-49. |
| [6] |
薛彦卓, 李硕, 徐利刚, 等. 双体船结构水下中低频辐射噪声特性研究[J]. 中国造船, 2006(1): 94-102. XUE Yan-zhuo, LI Shuo, XU Li-gang, et al. Characteristics of low and middle frequency underwater noise from a catamaran[J]. Ship Building of China, 2006(1): 94-102. DOI:10.3969/j.issn.1000-4882.2006.01.015 |
| [7] |
PARASKEVOPOULOS E A, PANAGIOTOPOULOS C G, MANOLIS G D. Imposition of time-dependent boundary conditions in FEM formulations for elastodynamics: critical assessment of penalty-type methods[J]. Computational Mechanics, 2010, 45(2-3): 157-166. |
| [8] |
KIM Y W, JHUNG M J. A study on large mass method for dynamic problem of multiple degree-of-freedom system excited by ground acceleration time history[J]. Journal of Mechanical Science & Technology, 2014, 28(1): 25-41. |
| [9] |
庞福振. 船舶结构噪声截断模型数值预报方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2012: 20−21.
|
| [10] |
刘峰, 庞福振, 韩端锋, 等. 运动边界相似法及船舶结构动力分析应用[J]. 振动与冲击, 2014(20): 111-117. |
| [11] |
郭文杰, 李天匀, 朱翔, 等. 部分浸没圆柱壳声固耦合计算的半解析法研究[J]. 物理学报, 2018(8): 1-12. |
| [12] |
杨国栋, 李天匀, 朱翔, 等. 浸没圆柱壳低频自振频率计算中流固与声固耦合模型统一性分析[J]. 中国舰船研究, 2016(8): 87-92. |
 2021, Vol. 43
2021, Vol. 43