2. 中国舰船研究设计中心,湖北 武汉 430064
2. China Ship Development and Design Center, Wuhan 430064, China
船舶推进轴系具有扭转振动、纵向振动、回旋振动这三大振动问题[1],它们不仅严重影响推进轴系的正常运转,导致轴系零部件的异常磨损和疲劳破坏,还会激起尾部船体结构的异常振动,影响乘员舒适性和精密仪器可靠性,同时引起水下低频段的多频强线谱辐射噪声[2]。在推进轴系振动的计算中,纵向振动主要受推力轴承轴向动特性的影响,回旋振动主要受径向轴承支撑动特性的影响。所以,径向轴承和推力轴承的支撑动力学参数在推进轴系纵向和回旋振动的计算中有着显著影响[3],它们的准确获取对临界转速、传递特性、响应特性等动力学特性的准确计算至关重要。
船舶在海上航行时,当遇到战损、均衡系统故障、紧急机动等极端情况时,船体会发生倾斜(包括纵倾和横倾)。传统的转子动力学研究的对象主要是安装在地面基础上的旋转机械[4],研究时一般都首先假设支承的刚性足够大而且固定不动。然而,对于船体发生倾斜状态时的推进轴系—轴承系统而言,这种固定安装面的假设显然不符合实际。船舶的推进轴系-轴承系统是安装在船体结构上,船体结构的惯性质量远远大于推进轴系-轴承系统,当航行的船舶在外界激励作用下发生倾斜时,推进轴系-轴承系统也会随着船体同样发生倾斜。目前,针对船舶转子系统在船体发生极端倾斜状态下的动力学特性的研究工作非常少,公开资料有针对船上电机转子-轴承系统子在摇摆状态下的稳定性研究文献[5 – 6],但尚未发现针对推进轴系-轴承系统在船体倾斜尤其是极端倾斜状态下的研究报道。
因此,为弥补船舶推进轴系-轴承系统在船体发生倾斜状态下动特性研究的不足,本文以某船舶推进轴系的径向轴承和推力轴承为研究对象,对其在横倾和纵倾状态下的润滑动特性进行计算研究和影响分析。
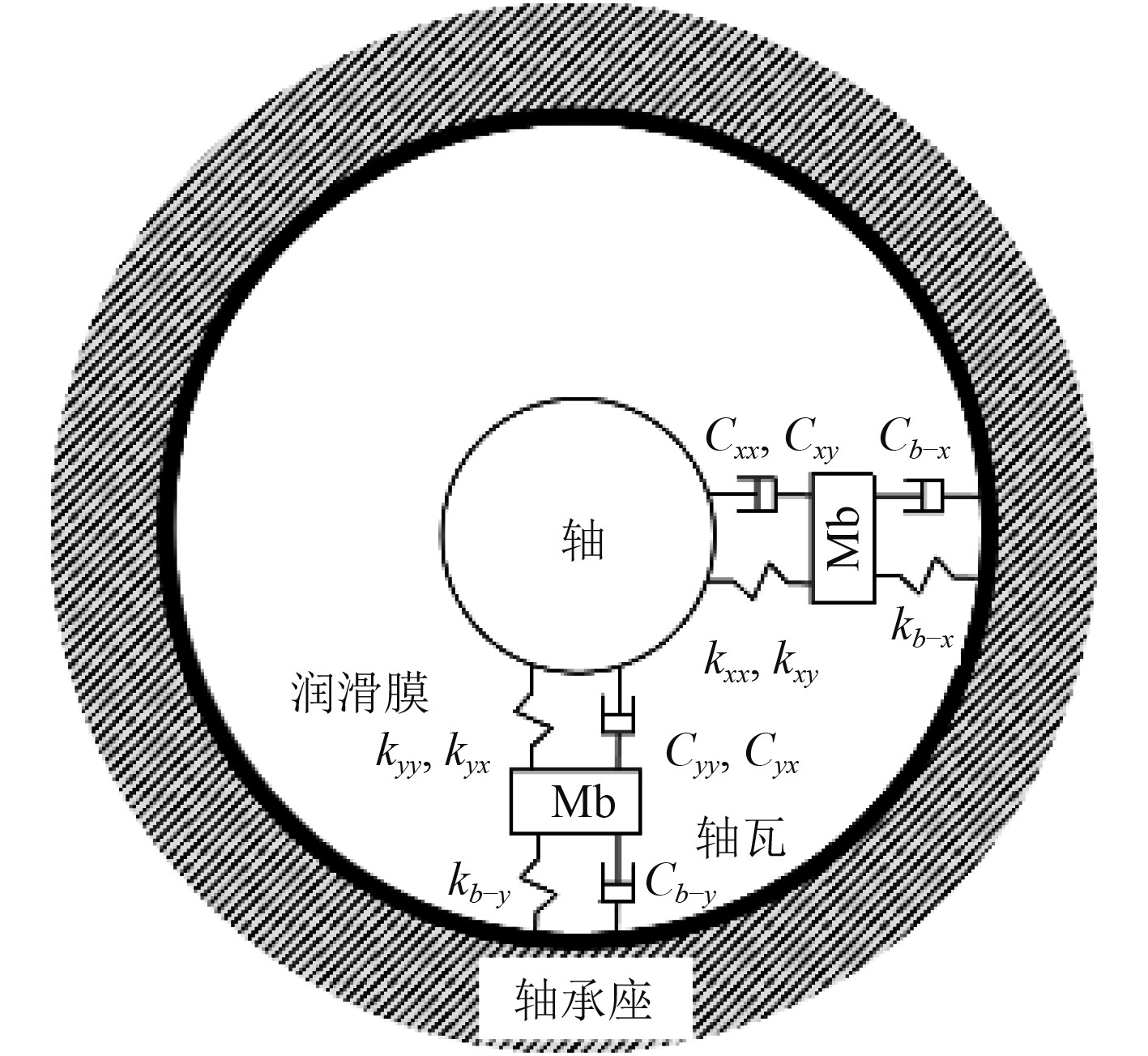
1 轴承润滑动特性计算方法 1.1 径向滑动轴承润滑方程船舶径向支撑滑动轴承的轴瓦与转轴轴颈之间采用流体动压润滑,两者之间可建立如图1所示的含有8个动力特性系数的质量-刚度-阻尼动力学模型。
|
图 1 滑动轴承的质量-刚度-阻尼动力学模型 Fig. 1 Mass-stiffness-damping dynamic model of plain bearing |
根据流体动力润滑理论[7],计算润滑膜动力学参数的关键就是对以下简化的雷诺方程进行求解:
| $\frac{\partial }{{\partial x}}\left( {{h^3}\frac{{\partial p}}{{\partial x}}} \right) + \frac{\partial }{{\partial y}}\left( {{h^3}\frac{{\partial p}}{{\partial y}}} \right) = 6\mu U\frac{{\partial h}}{{\partial x}}\text{。}$ | (1) |
式中:h为润滑膜厚度;p为润滑膜压力;µ为润滑介质动力粘度;U为轴颈表面速度。
轴颈旋转将润滑油带入收敛间隙而产生流体动压,润滑膜压力的合力与轴颈上的载荷相平衡,其平衡位置偏于一侧。轴心的平衡位置通过偏位角
| $h = c\left( {1 + \varepsilon \cos \varphi } \right)\text{,}$ | (2) |
将转轴平衡位置的偏心率和偏位角代入到雷诺方程中,采用有限差分法求解雷诺方程得到滑动轴承润滑膜压力分布,再积分求得2个相互正交的润滑膜合力,将润滑膜合力对4个正交的位移扰动项
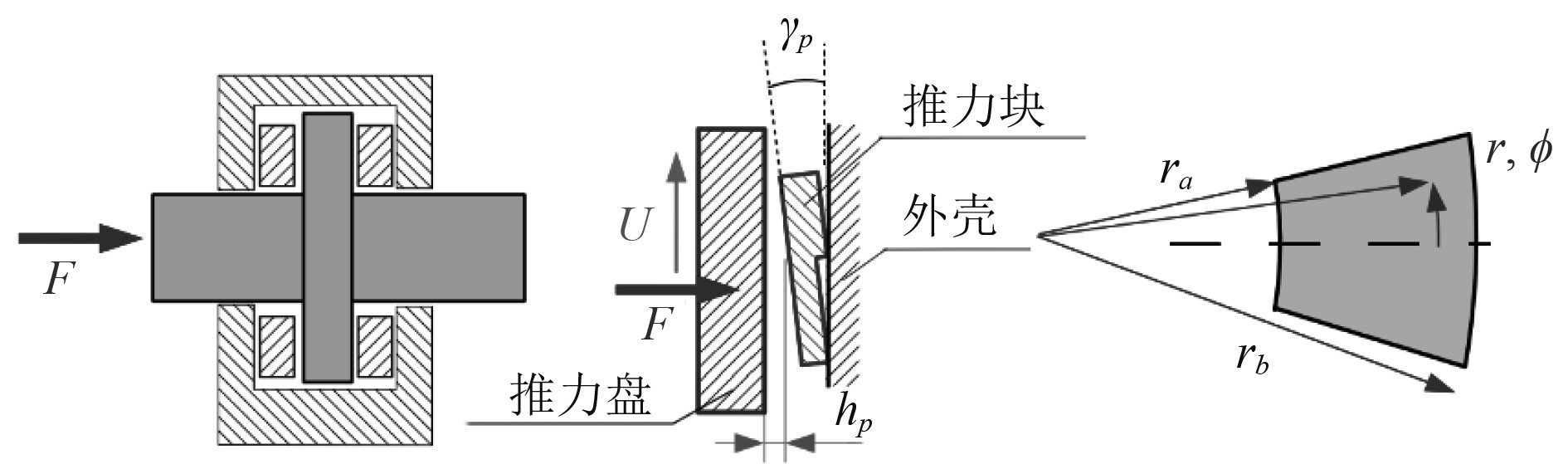
船舶轴系通常采用米歇尔型的流体动压滑动推力轴承,它由若干个支撑于边界的自调节可倾瓦推力块组成,推力块均匀布置于圆周上。推力轴法兰盘在推力的作用下与推力块接触,并在两者之间形成动压润滑油膜。米歇尔型推力轴承属于动压润滑轴承的一种,所以同样可以采用滑动轴承润滑雷诺方程进行动特性的计算。
|
图 2 米歇尔型推力轴承的结构形式 Fig. 2 Structure of Michelle type thrust bearing |
由于推力轴承各推力块的运动具有圆周对称的相对运动特点,因此只需求解一个推力块的油膜特性,即可得到推力轴承总的油膜特性。将二维雷诺方程写成极坐标形式,可得:
| $\frac{\partial }{{\partial r}}\left( {r{h^3}\frac{{\partial p}}{{\partial r}}} \right) + \frac{\partial }{{r\partial \phi }}\left( {{h^3}\frac{{\partial p}}{{\partial \phi }}} \right) = 6\eta r\omega \frac{{\partial h}}{{\partial \phi }}\text{。}$ | (3) |
式中:
| $h = {h_p} - r\sin \phi \tan {\gamma _p}\text{。}$ | (4) |
式中:
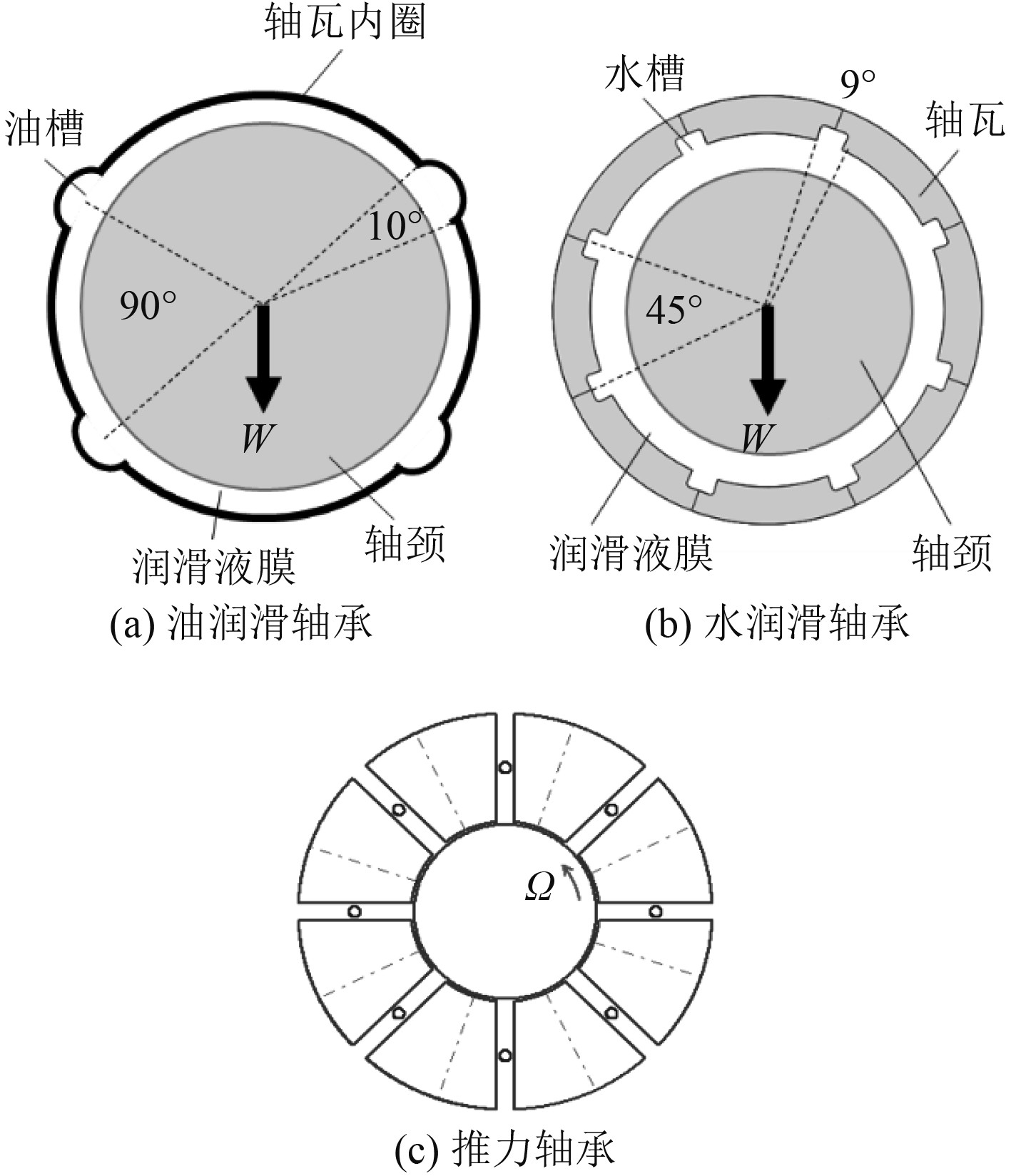
某船舶的推进轴系由油润滑径向轴承、水润滑径向轴承和推力轴承进行径向和轴向的支撑。其中,油润滑轴承为4油槽固定瓦白合金轴承,油槽在周向等距分布,每个油槽开角为10°;水润滑轴承为8水槽固定瓦赛龙轴承,水槽在周向等距分布,每个水槽开角为9°;推力轴承为米歇尔型滑动推力轴承,由8个合金推力块组成。支撑轴承的基本参数如表1和表2所示。
|
图 3 径向轴承和推力轴承结构示意图 Fig. 3 Structure of journal bearings and thrust bearing |
|
|
表 1 径向轴承参数 Tab.1 Parameters of journal bearings |
|
|
表 2 推力轴承参数 Tab.2 Parameters of thrust bearing |
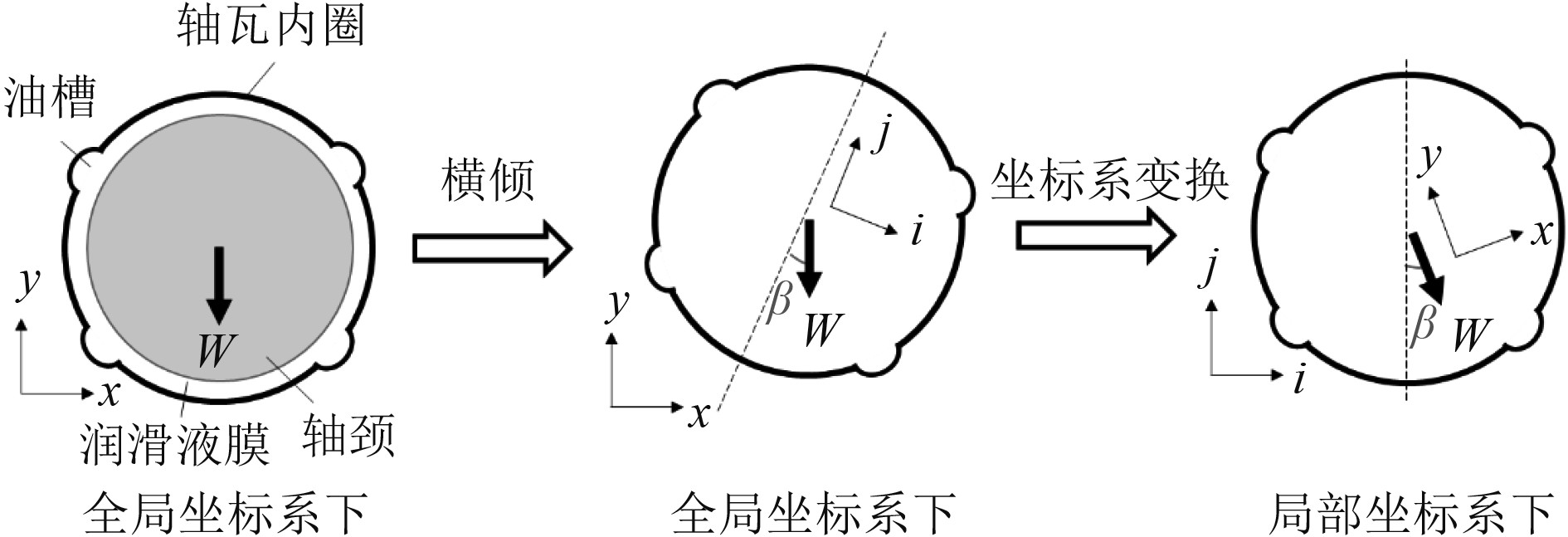
当以地球为固定坐标系进行观测时,横倾状态主要表现为轴承轴瓦的横倾,转轴是圆周对称的因而不受影响,而轴承载荷主要为重力载荷,其大小和方向不变,此时载荷有可能会作用在油槽或水槽等结构上。当以轴承为局部坐标系进行观测时,轴承的状态保持不变,此时载荷大小不变,作用方向随横倾角大小发生变化,如图4所示。
|
图 4 径向轴承横倾示意图 Fig. 4 Transversal inclination of the journal bearing |
目前在国内公开资料中尚未发现针对推进轴系-轴承系统在船体倾斜状态尤其是极端倾斜状态下的研究报道和相关标准或规定。因此,本文参考GJB150.23A-2009[8]中横倾和横摇试验量的规定,研究横倾对径向轴承动特性的影响。GJB150.23A-2009中的横倾考察极限角度范围±15°(应急设备±22.5°),本文按照横摇要求的最大角度范围进一步延伸至考察±45°范围的情况。同时定义横倾角度与转速方向一致为正,相反为负。
2.3 纵倾计算工况当纵倾角度较小时,其主要影响推力轴承的轴向推力载荷,对径向支撑轴承负荷的影响较小。同样参考GJB150.23A-2009中纵倾和纵摇试验量的规定,研究纵倾±10°对推力轴承动特性的影响。定义纵倾角
油润滑轴承的4个刚度系数随横倾角度变化、4个阻尼系数随横倾角度变化、最小油膜间隙和最大油膜压力随横倾角度变化、轴心偏心率及角度随横倾角度变化分布如图5~图8所示。随横倾角度变化的轴心位置如图9所示。
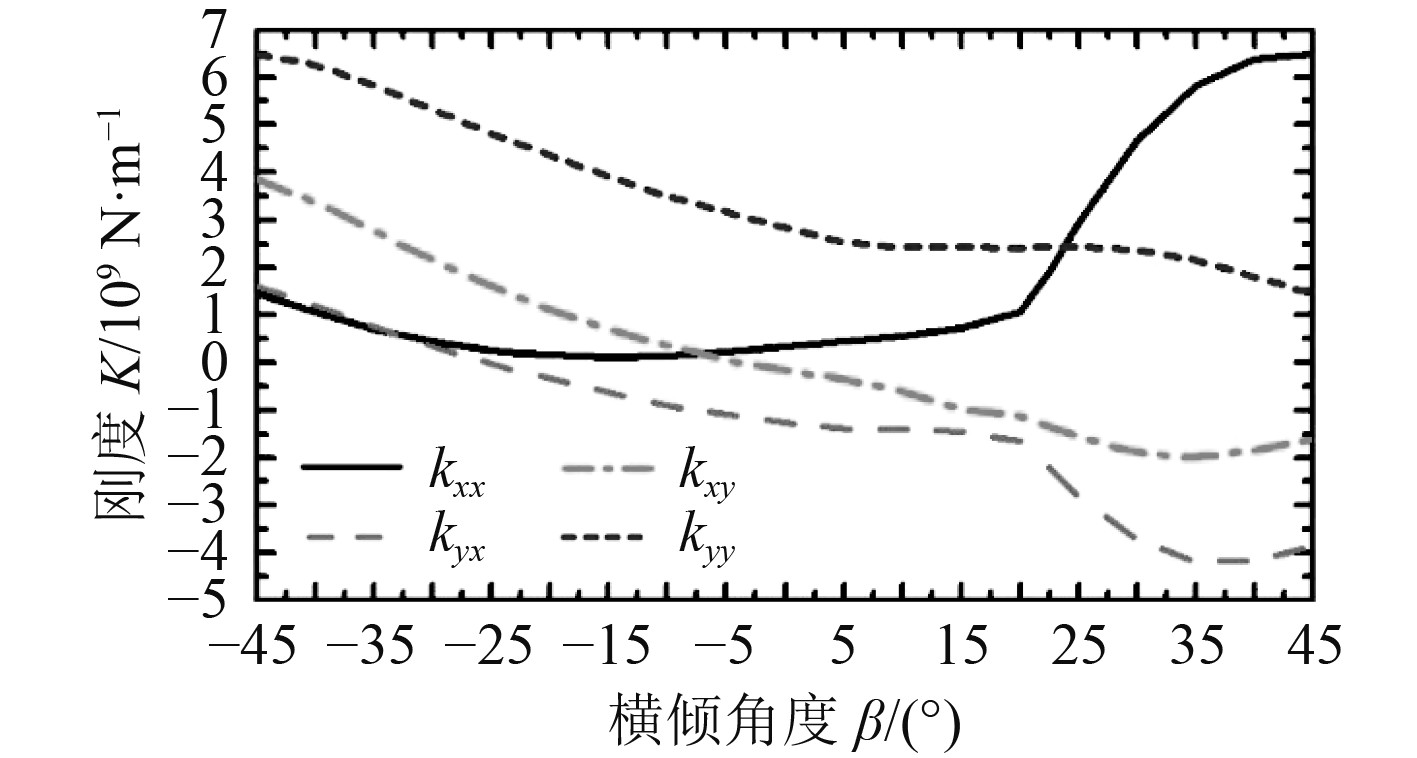
|
图 5 油润滑轴承刚度系数变化 Fig. 5 Stiffness coefficients of the oil lubricated bearing |
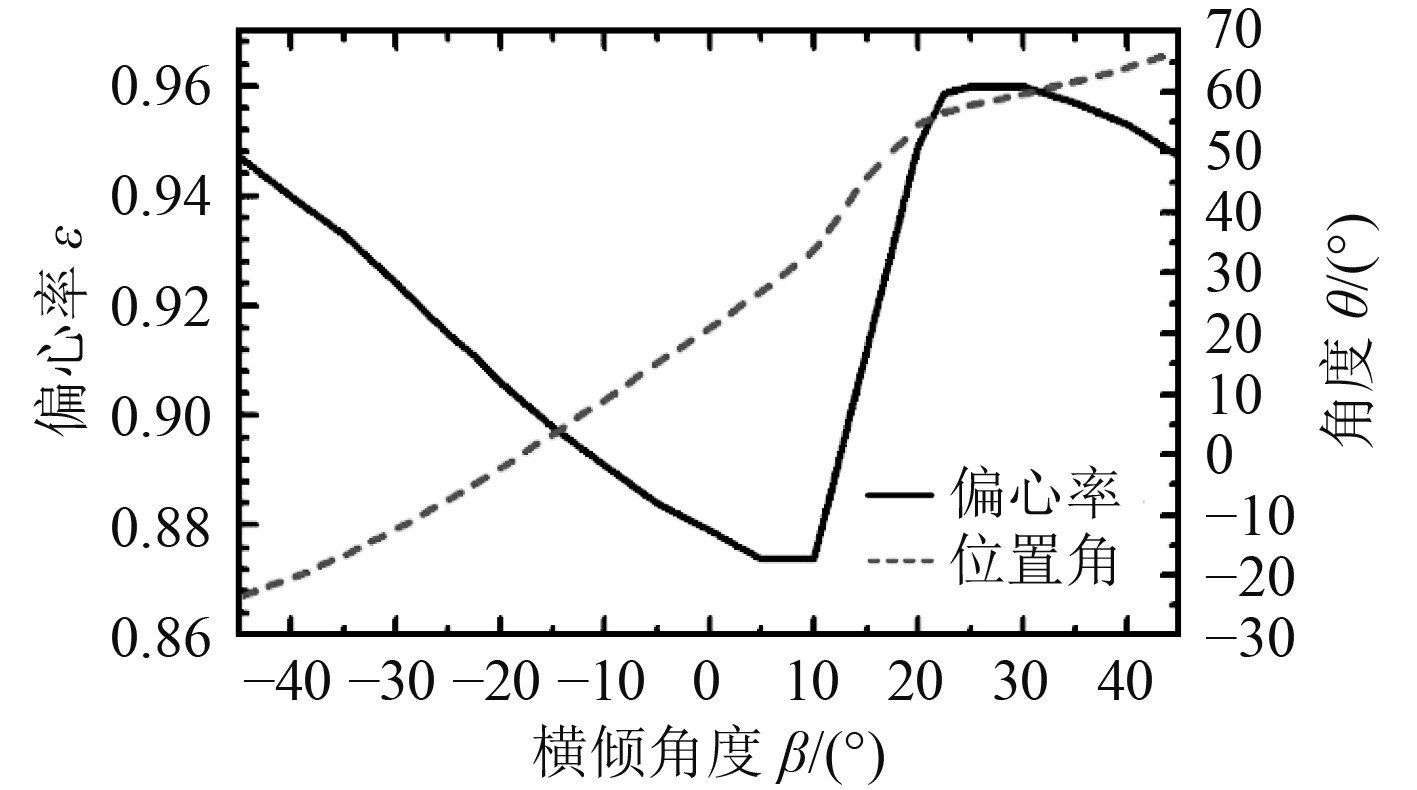
|
图 8 油润滑轴承轴心偏心率及角度变化 Fig. 8 Eccentricity and angle of the oil lubricated bearing |
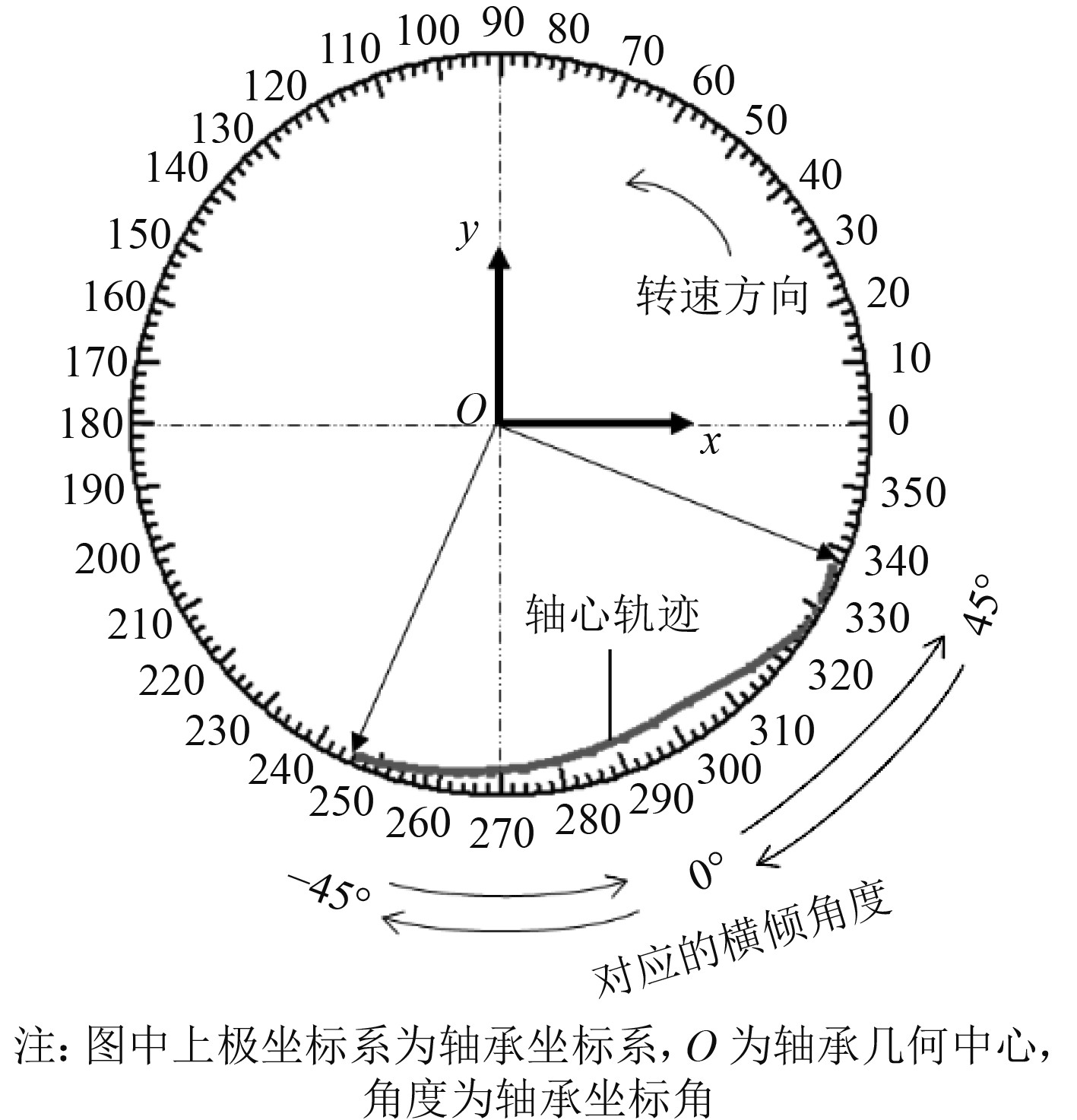
|
图 9 油润滑轴承随横倾角度变化的轴心位置图 Fig. 9 Axis position diagram of the oil lubricated bearing changing with the transversal inclination angles |
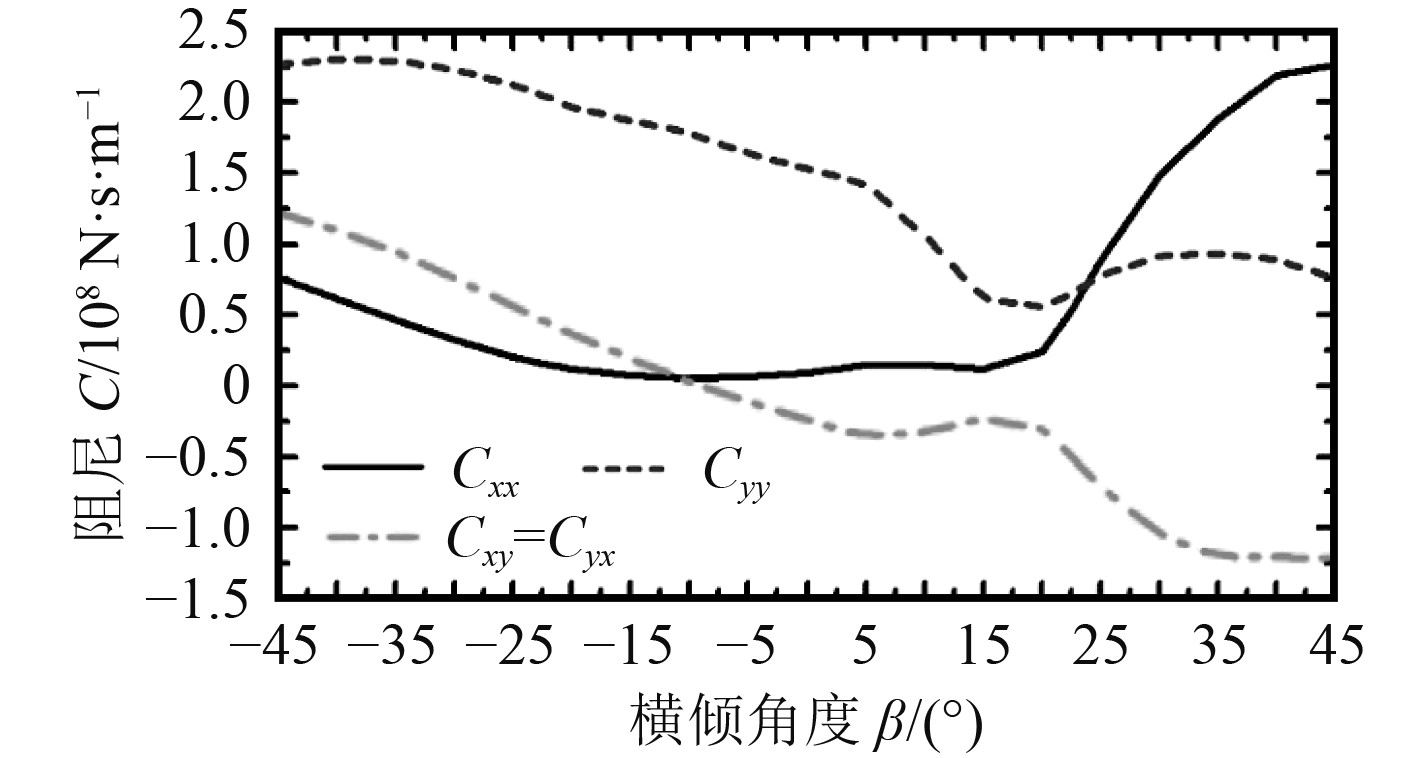
|
图 6 油润滑轴承阻尼系数变化 Fig. 6 Damping coefficients of the oil lubricated bearing |
|
图 7 油润滑轴承最小油膜厚度和最大油膜压力变化 Fig. 7 Minimum film thickness and maximum film pressure of the oil lubricated bearing |
水润滑轴承的4个刚度系数随横倾角度变化、4个阻尼系数随横倾角度变化、最小水膜厚度和最大水膜压力随横倾角度变化、轴心偏心率及角度随横倾角度变化分布如图10~图13所示。随横倾角度变化的轴心位置如图14所示。
|
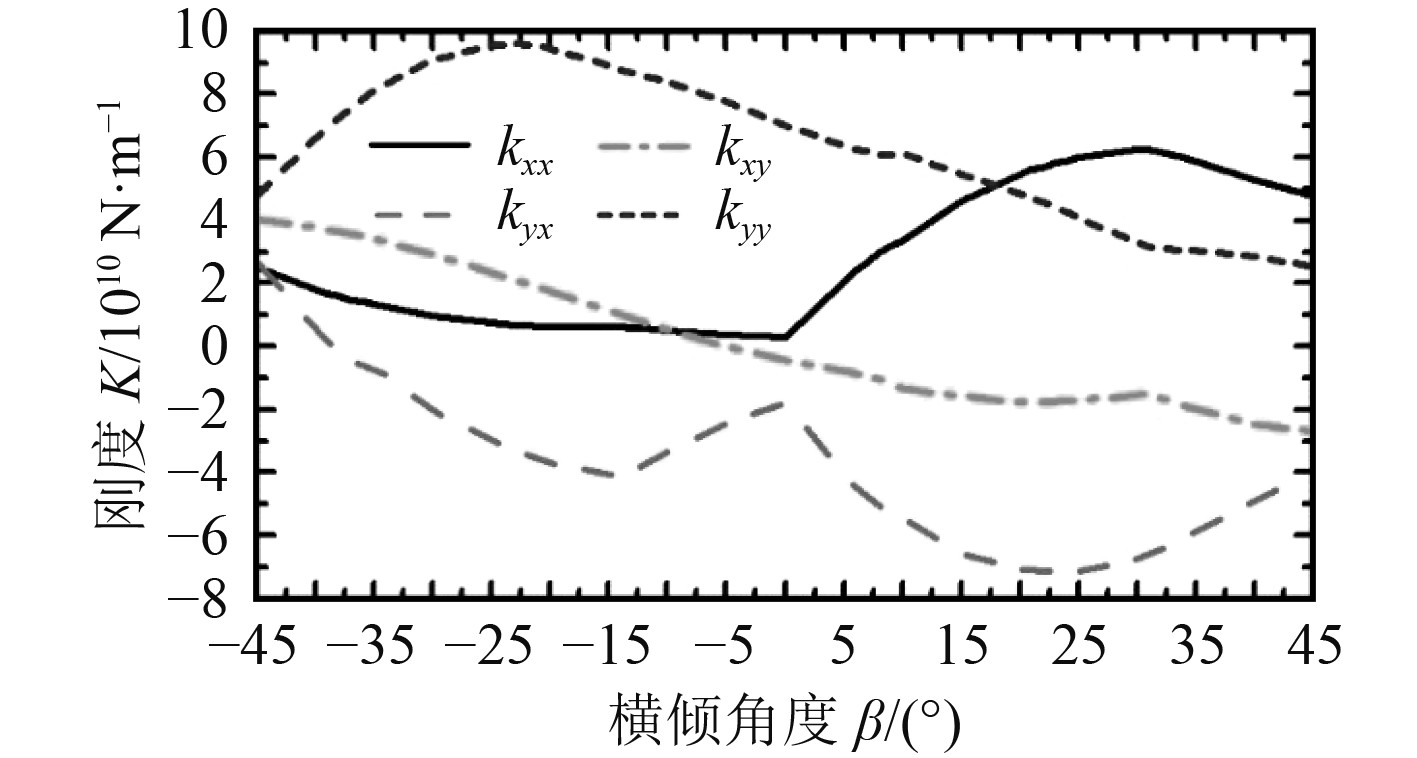
图 10 水润滑轴承刚度系数变化 Fig. 10 Stiffness coefficients of the water lubricated bearing |
|
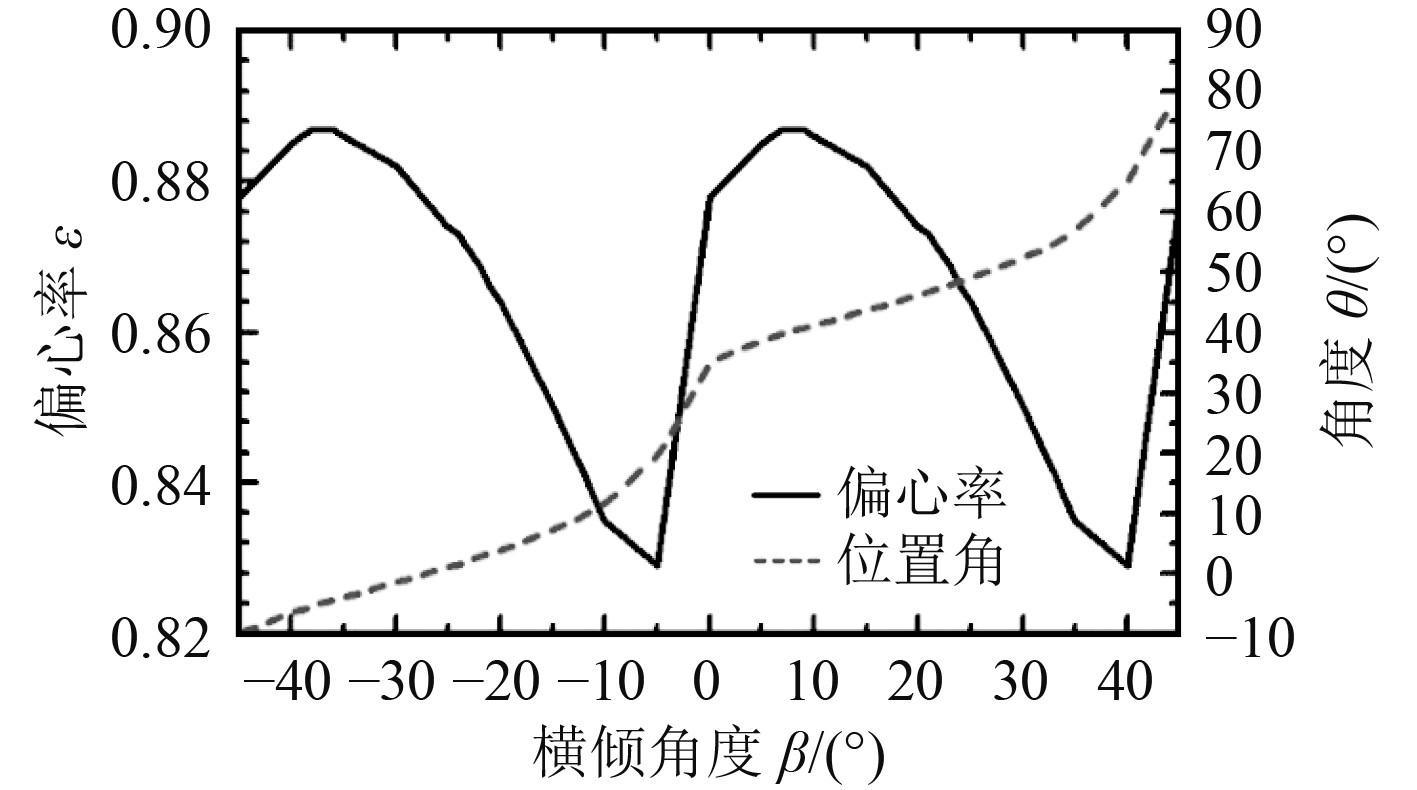
图 13 水润滑轴承轴心偏心率及位置角变化 Fig. 13 Eccentricity and angle of the water lubricated bearing |
|
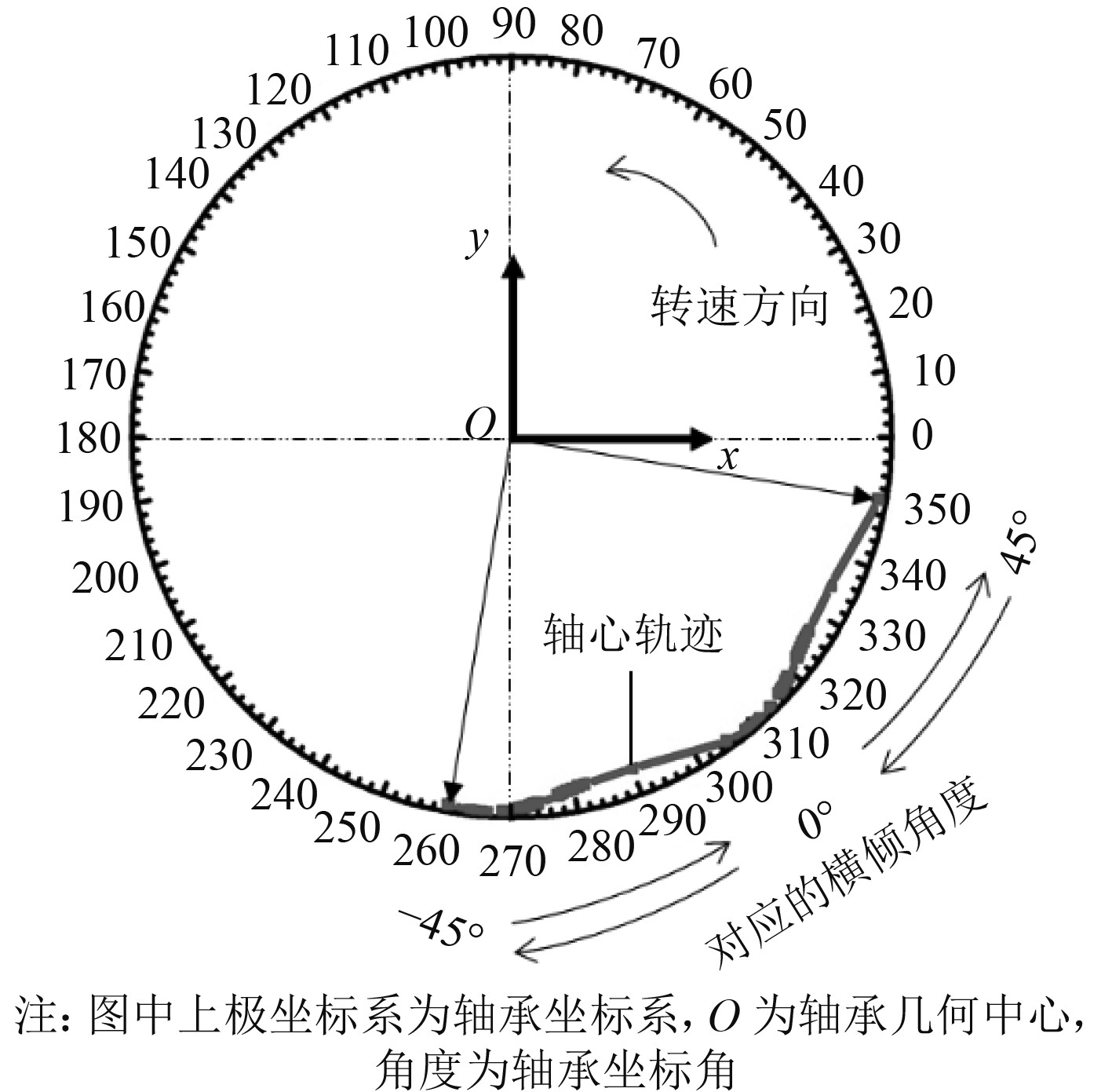
图 14 水润滑轴承随横倾角度变化的轴心位置图 Fig. 14 Axis position diagram of the water lubricated bearing changing with the transversal inclination angles |
|
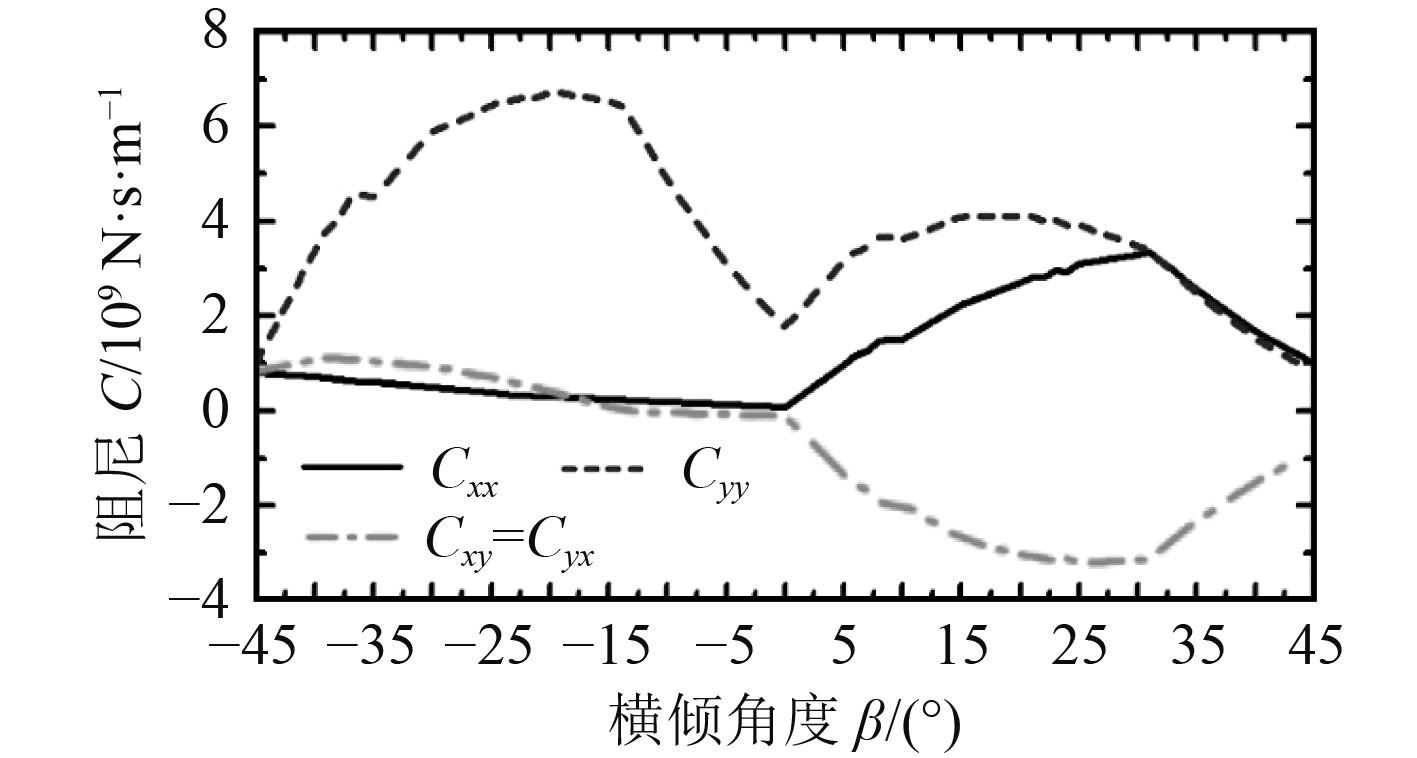
图 11 水润滑轴承阻尼系数变化 Fig. 11 Damping coefficients of the water lubricated bearing |

|
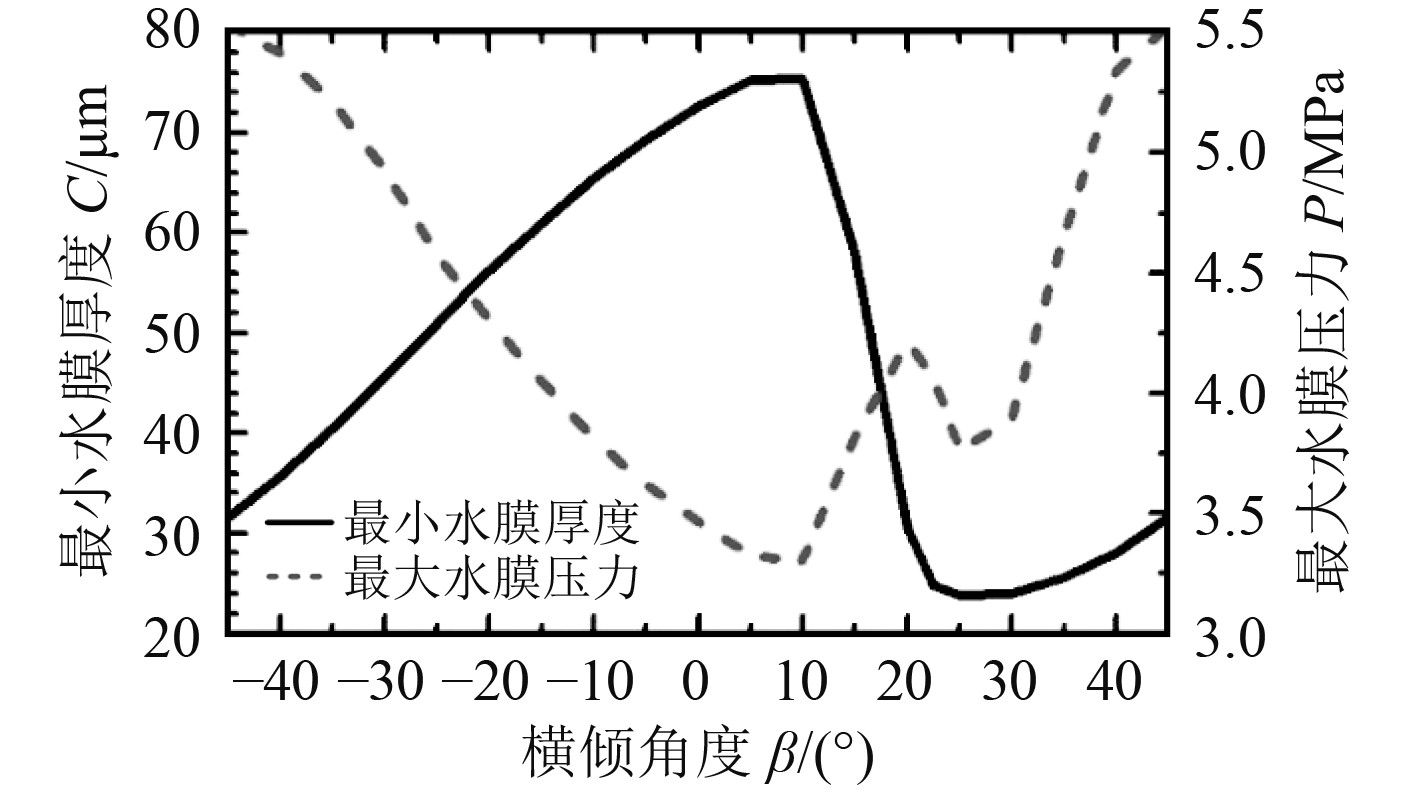
图 12 水润滑轴承最小水膜厚度和最大水膜压力变化 Fig. 12 Minimum film thickness and maximum film pressure of the water lubricated bearing |
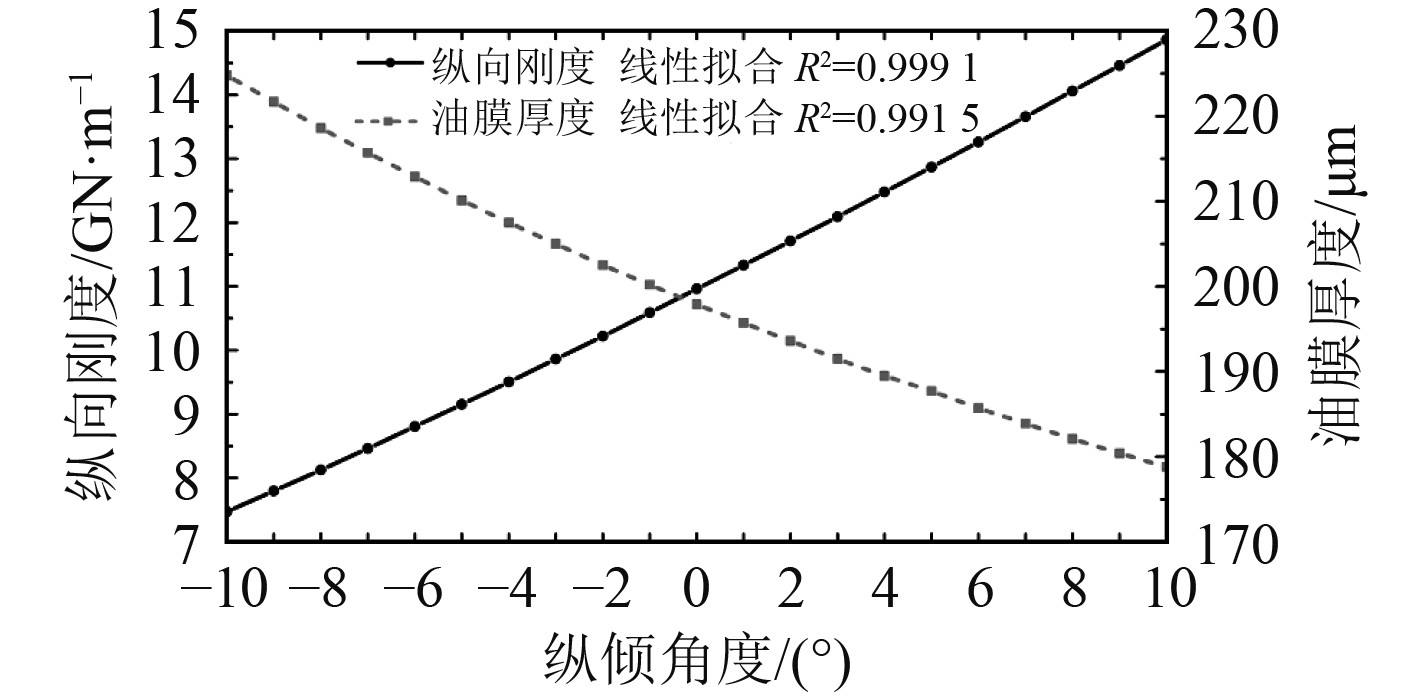
纵倾角度在–10°~10°范围内变化时,推力轴承纵向刚度和油膜厚度变化关系如图15所示。
|
图 15 推力轴承纵向刚度和油膜厚度随纵倾角度变化 Fig. 15 Longitudinal stiffness and oil film thickness of the thrust bearing changing with the longitudinal inclination angles |
本文以某船舶推进轴系为研究对象,针对其中各类径向轴承和推力轴承在纵倾和横倾状态下的润滑动特性问题进行计算研究,发现纵倾状态改变推力轴承的轴向载荷从而影响其轴向支撑动特性,横倾状态改变径向支撑轴承的载荷方向从而影响其径向支撑动特性,并得出了以下结论:
1)推力轴承纵向刚度和油膜厚度与承载推力/纵倾角度本应是非线性关系,但是当小角度(≤10°)纵倾时,一方面推力轴承纵向载荷的变化量可以近似为与纵倾角度相关的线性变化,另一方面纵向载荷的非线性增量相对于承载推力较小,在这两方面的综合影响下,推力轴承纵向刚度和油膜都厚度也可以近似与纵倾角度成线性关系。因此,在工程计算中,最少可以只计算2个纵倾角度工况下的推力轴承动特性参数,再线性外推出其他纵倾角度下的动特性参数。
2)油润滑和水润滑径向轴承在极限横倾范围内都表现为稳定润滑状态。
3)油润滑径向轴承在20°横倾角度处刚度和阻尼系数出现转折点,水润滑径向轴承在20°横倾角度处刚度和阻尼系数出现转折点。油润滑径向轴承的主刚度系数的值在109 N/m数量级,主阻尼系数的值在109 N.s/m数量级。水润滑径向轴承的值在1010 N/m数量级,主阻尼系数的值在109 N.s/m数量级。
4)在–45°~45°横倾范围内,油润滑径向轴承的最小油膜厚度在23.78~75.45 μm区间变化,轴颈和轴承处于完全流体动力润滑状态,而水润滑径向轴承的最小水膜厚度在3.4~5.1 μm区间变化,轴颈和轴承勉强处于流体动力润滑状态。
5)对于油润滑径向轴承,发生横倾时润滑承载区会跨越油槽,由侧瓦和下底瓦共同承载,横倾角度较大时甚至侧瓦的承载压力会大于下底瓦,油槽部分会阻断承载油膜的形成,在槽区丧失承载力。对于水润滑径向轴承,发生横倾时润滑承载区会跨越水槽,由相邻的2个瓦甚至3个瓦共同承载,甚至其它瓦的承载压力会大于下底瓦,同时水槽部分阻断了承载水膜的形成,在槽区丧失承载力。正因为横倾角度变化时承载区的移动会跨越水槽/油槽,所以轴承刚度系数、阻尼系数和轴心位置随横倾角会发生不连续变化。
6)对比油润滑轴承和水润滑轴承的计算结果可以看出,水润滑轴承在横倾状态下的不同表现是由其润滑介质属性和开槽特性耦合引起的:一方面水的动力粘度远小于油(相差几十倍),形成的水膜厚度很薄(与油膜厚度相差几十倍),水膜的承载力较差,提供支撑的润滑膜刚度较大;另一方面由于水的润滑属性(承载力)较差,所以需要多开轴向水槽改善润滑条件以防发生干摩擦,但水槽部分又阻断了水膜,在槽区丧失了承载力,进而影响了动力润滑状态下的支撑动特性。
| [1] |
周凌波, 段勇, 孙玉东, 等. 水面船舶推进轴系回旋振动研究综述[J]. 中国造船, 2017, 58(3): 233-244. DOI:10.3969/j.issn.1000-4882.2017.03.023 |
| [2] |
周凌波, 段勇, 孙玉东, 等. 多支点推进轴系回旋振动对艉部船体的激励特性研究[J]. 中国造船, 2018, 59(4): 105-114. DOI:10.3969/j.issn.1000-4882.2018.04.012 |
| [3] |
周凌波, 段勇, 吴江海. 船舶径向滑动轴承动力学参数分析[C]. 厦门: 中国钢结构协会海洋钢结构分会学术论文集, 2018: 257–267.
|
| [4] |
王正. 转动机械的转子动力学设计[M]. 北京: 清华大学出版社, 2015.
|
| [5] |
张磊, 裴世源, 徐华, 等. 摇摆工况下椭圆轴承转子系统动力学特性研究[J]. 机械设计与制造, 2018(7): 100-103. DOI:10.3969/j.issn.1001-3997.2018.07.029 |
| [6] |
张磊, 裴世源, 徐华. 摇摆工况下两种舰船转子轴承系统的安全性与稳定性研究[J]. 中国科学: 技术科学, 2018, 48(4): 369-381. |
| [7] |
张直明, 张言羊, 谢友柏, 等. 滑动轴承的流体动力润滑理论[M]. 北京: 高等教育出版社, 1986.
|
| [8] |
GJB 150.23A-2009. 军用装备实验室环境试验方法 第23部分: 倾斜和摇摆试验 [S].
|
 2021, Vol. 43
2021, Vol. 43
