0 引　言

水下无人航行器是未来海军战斗力的倍增器，可在浅水区或其他潜艇、水面舰无法进入的未知复杂水域执行水下威胁目标侦察、战术海洋学调查、监视预警、远程通信中继、攻击敌目标舰艇、诱骗等军事任务，也可应用于资源及地形探测、水下光缆等设施的维护及打捞等，在国家领海防御和海洋资源开发等方面将发挥日益重要的作用^[1]。攻击型水下无人航行器具备自主作战能力，将作战模式从平台级交战变为武器级交战，将以兵器攻防代替平台攻防，可大大降低人员的战损率。

潜艇、水下无人航行器等可采用基于主动探测的方位、距离法解算目标运动要素，但测量参数较多，水下主动探测方式的隐蔽性差。纯方位解算方法是一种从探测器观察到的加噪方位信息中估计目标运动要素的方法。纯方位法的特点是仅需要测量目标的方位值，测量参数少、算法比较简单、运算量较小，但解算时间长，收敛率低，但在航海、航空等领域中也可广泛采用基于被动探测的纯方位法解算目标运动要素^[2]。王艳艳等^[3]考虑到AUV机动性能，采用分段轨迹优化方法，AUV跟踪目标的初始阶段以定位的位置误差作为优化对象，提出一种基于短期预测的轨迹优化方法。董严红等^[4]分析了自导鱼雷纯方位攻击的使用过程，采用大样本仿真的方法，得出不同情况下鱼雷攻击提前角的最优解。舒象兰等^[5]提出一种基于匹配场处理思想改进的纯方位目标运动分析方法。

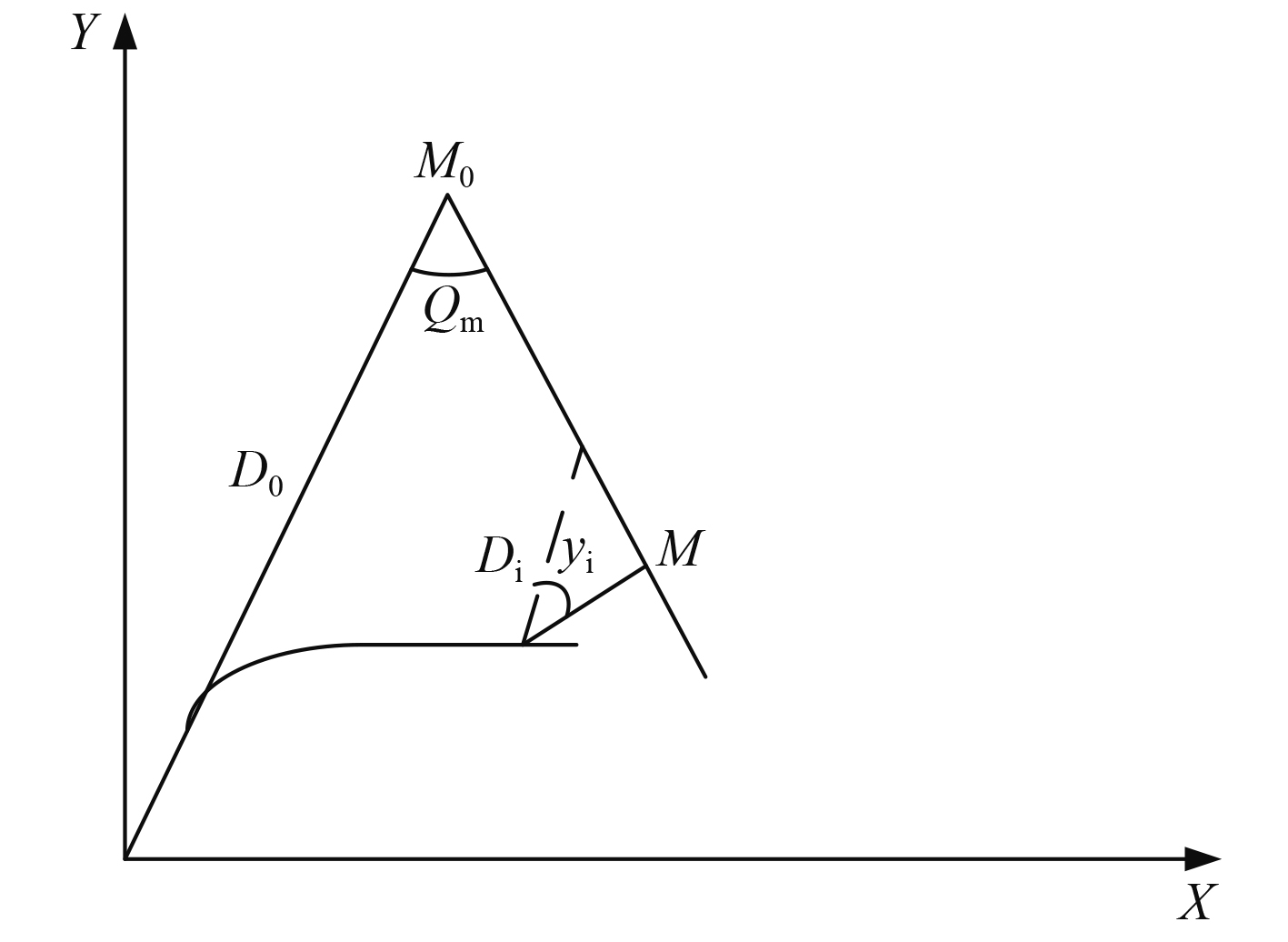
1 纯方位解算的传统算法 1.1 符号说明

${{{D}}_0}$ 为目标的初始距离； ${{{V}}_{{m}}}$ 为目标速度； ${{{Q}}_{{m}}}$ 为目标初始舷角； ${y_i}$ 为测量方位变化量（瞬时方位 ${f_i}$ 与初始方位 ${f_0}$ 的方位差）； $\overline {{{{y}}_i}}$ 为拟合推算方位变化量（拟合推算方位 ${f_i}$ 与初始方位 ${f_0}$ 的方位差）。

1.2 数学模型

在目标等速直航的条件下，由图1可得如下关系：

${\rm{tan}}{y_i} = \frac{{{t_i}{V_m}\sin {Q_m} - {J_{si}}}}{{{D_0} - {t_i}{V_m}\cos {Q_m} - {J_{ci}}}}\text{，}$

(1)

${J_{si}} = \int_0^{{t_i}} {{V_w}\sin ({C_w} - {f_0}){\rm{d}}t} \text{，}$

(2)

${J_{ci}} = \int_0^{{t_i}} {{V_w}\cos ({C_w} - {f_0}){\rm{d}}t}\text{，} $

(3)

令

$A = {D_0}\text{，}$

(4)

$B = {V_m}\sin ({Q_m})\text{，}$

(5)

$C = {V_m}\cos ({Q_m})\text{，}$

(6)

这时

$\left\{ {\begin{array}{*{20}{c}} {{V_m} = \sqrt {{B^2} + {C^2}} } \text{，}\\ {{Q_m} = t{g^{ - 1}}\dfrac{B}{C}} \text{，} \end{array}} \right.$

(7)

式（1）可变为

$tg{y_i} = \frac{{B{t_i} - {J_{si}}}}{{A - C{t_i} - {J_{ci}}}}\;\;\;{\rm{i}}=1,2\text{，}$

(8)

或等价的有

$ {J_{ci}}\sin {y_i} - {J_{si}}\cos {y_i} = A\sin {y_i} - B{t_i}\cos {y_i} - C{t_i}\sin {y_i} \text{。}$

(9)

之后，传统方法是基于式（8），使用最小二乘法解参数A，B，C，这时记

$X = \left( {\begin{array}{*{20}{c}} {\sin {y_1}}&{ - {t_1}\cos {y_1}}&{ - {t_1}\sin {y_1}} \\ {\sin {y_2}}&{ - {t_2}\cos {y_2}}&{ - {t_2}\sin {y_2}} \\ {\cdots}&{\cdots}&{\cdots} \\ {\sin {y_n}}&{ - {t_n}\cos {y_n}}&{ - {t_n}\sin {y_n}} \end{array}} \right)\text{，}$

(10)

$Y = \left( {\begin{array}{*{20}{c}} {{J_{c1}}\sin {y_1} - {J_{s1}}\cos {y_1}} \\ {{J_{C2}}\sin {y_2} - {J_{s2}}\cos {y_2}} \\ {\cdots} \\ {{J_{cn}}\sin {y_n} - {J_{sn}}\cos {y_n}} \end{array}} \right)\text{，}$

(11)

$\beta = {(A,B,C)'}\text{，}$

(12)

$\varepsilon = ({\varepsilon _1},{\varepsilon _2},\cdots,{\varepsilon _n})'\text{，}$

(13)

则有

${{Y}} = {{X}}\beta + \varepsilon \text{，}$

(14)

其中 $\varepsilon $ 为误差，未知参数 $\beta $ 可从如下正规方程解出

${{X'X}}\beta = {{X'Y}}\text{。}$

(15)

在目标和本舰等速直航的条件下，上述方程有无数的解，因此，为了得到有意义的解潜艇在测量过程中应适当机动。

传统解算方法认为解算空间是在无限的实数空间中进行，在无限空间上寻找方程的最优解，这给解算结果带来了许多不确定性，有时会造成方程的不收敛。

实际上，鱼雷攻击的目标运动要素的解算空间是有限的，将有限的连续空间范围离散化，就可以发现目标运动要素解的个数有限，在有限个目标运动要素的估计中，寻找估计方差最小的即为目标运动要素估计。

2 一种新的纯方位解算方法

设解算向量 $ {{X}}=({ D}_{0}, { V}_{m}, { Q}_{m}) \in {R^3}$ ，根据声呐测量特性及目标的运动特性， ${{X}}$ 应属于有限的3位实数空间。将三维实数空间离散化，可以得到有限个目标运动要素的实数解。

将 ${ D}_{0}, { V}_{m}, { Q}_{m}$ 分别划分为 $ {n}_{1}, {n}_{2}, {n}_{3}$ 个水平，水平间隔在解算误差允许的范围之内，离散化后可能的解算值应该有 ${n_1} \times {n_2} \times {n_3}$ 个，在 ${n_1} \times {n_2} \times {n_3}$ 个可能的解算值中，找出一个解 ${ D}_{0i}, { V}_{mi}, { Q}_{mi}$ 使得拟合值 $\overline {{y_i}} $ 与实际测量值 ${y_i}$ 之间的偏差平方和达到最小。

这种方法我们称为网格法，理论上可行，但是需要进行 ${n_1} \times {n_2} \times {n_3}$ 次计算，计算时间长，不适合工程上实时计算。

仔细分析，在解算空间中， ${ D}_{0}, { V}_{m}, { Q}_{m}$ 之间存在着很强的相关性，找出这种相关的关系：

$ {D}_{0}={f}_{1}({V}_{m}){\text{，}}$

(16)

$ {Q}_{m}={f}_{2}({V}_{m}){\text{，}}$

(17)

由此，解算值可以划分为 ${n_2}$ 个，其值分别是 $ ({f}_{1}({V}_{mi}), {V}_{mi}, {f}_{2}({V}_{mi}))$ ，在 ${n_2}$ 个解算值中推算观测值 ${y_i}$ 的拟合值 $\overline {{y_i}} $ 。使得 $\displaystyle\sum\limits_{i = 1}^n {|{y_i} - \overline {{y_i}|} }$ 达到最小。

现代潜艇中，被动测距声呐可以测目标距离，但误差较大，但是我们由此可以判定目标距离的最大最小范围 $ ({d}_{1}, {d}_{\rm{2}})$ ，将此范围划分成 $n$ 个水平，可以得到 $n$ 个初始距离的解，在 ${n}$ 个可能的解算值中，找出一个解 $ ({D}_{0k}, {V}_{mk}, {Q}_{mk})$ 使得拟合值 $\overline {{y_i}} $ 与实际测量值 ${y_i}$ 之间的偏差平方和达到最小。

对每个 ${D_{0j}}$ ，令

$B = {V_m}\sin ({Q_m})\text{，}$

(18)

$C = {V_m}\cos ({Q_m})\text{，}$

(19)

式（1）可变为：

$ {\rm{tan}}{y_i} = \frac{{B{t_i} - {J_{si}}}}{{{D_{0j}} - C{t_i} - {J_{ci}}}},\;\;{{i}}=1,2, \cdots {{n}}\text{，} $

(20)

或等价的有

$ {J_{ci}}\sin {y_i} - {J_{si}}\cos {y_i} = {D_{0j}}\sin {y_i} - B{t_i}\cos {y_i} - C{t_i}\sin {y_i} \text{。} $

(21)

之后，传统方法是基于式（21），使用最小二乘法解参数 $ A, {{B}}, {{C}}$ ，这时记

${{X}} = \left( {\begin{array}{*{20}{c}} { - {t_1}\cos {y_1}}&{ - {t_1}\sin {y_1}} \\ { - {t_2}\cos {y_2}}&{ - {t_2}\sin {y_2}} \\ {\cdots}&{\cdots} \\ { - {t_n}\cos {y_n}}&{ - {t_n}\sin {y_n}} \end{array}} \right)\text{，}$

(22)

${{Y}} = \left( {\begin{array}{*{20}{c}} {{J_{c1}}\sin {y_1} - {J_{s1}}\cos {y_1} - {D_{0j}}\sin {y_1}} \\ {{J_{C2}}\sin {y_2} - {J_{s2}}\cos {y_2} - {D_{0j}}\sin {y_2}} \\ {\cdots} \\ {{J_{cn}}\sin {y_n} - {J_{sn}}\cos {y_n} - {D_{0j}}\sin {y_n}} \end{array}} \right)\text{，}$

(23)

$\beta = {(B,C)'}\text{，}$

(24)

$\varepsilon = ({\varepsilon _1},{\varepsilon _2},\cdots,{\varepsilon _n})'\text{，}$

(25)

则有

${{Y}} = {{X}}\beta + \varepsilon \text{，}$

(26)

其中 $\varepsilon $ 为误差，未知参数 $\beta $ 可从如下正规方程解出：

${{X'X}}\beta = {{X'Y}}\text{，}$

(27)

根据式（26），解出 ${{V}}_{\rm{mj}}, {{Q}}_{\rm{mj}}$ 。

对每个采样时间 ${{{t}}_{\rm{i}}}$ ；

${J_{fsi}} = \int_0^{{t_i}} {{V_w}\sin ({C_w}){\rm{d}}t} \text{，}$

(28)

${J_{fci}} = \int_0^{{t_i}} {{V_w}\cos ({C_w}){\rm{d}}t} \text{，}$

(29)

$\begin{split} {D_{ji}} =& {\rm{(}}{({t_i}{V_{mj}}\sin ({C_m}) + {d_{0j}}\sin {f_0} - {J_{fsi}})^2} + \\ & {({t_i}{V_{mj}}\cos ({C_m}) + {d_{0j}}\cos {f_0} - {J_{fci}})^2}{{\rm{)}}^{1/2}} \text{，} \end{split} $

(30)

$\sin x = \frac{{{t_i}{V_{mj}}\sin ({C_m}) + {d_{0j}}\sin {f_0} - {J_{fsi}}}}{{{D_{ji}}}}\text{，}$

(31)

$\cos x = \frac{{{t_i}{V_m}\cos ({C_m}) + {d_{0j}}\cos {f_0} - {J_{fci}}}}{{{D_{ji}}}}\text{，}$

(32)

${\overline f _i} = t{g^{ - 1}}\dfrac{{\sin x}}{{\cos x}}\text{，}$

(33)

${\overline y _i} = {\overline f _i} - {f_0}\text{。}$

(34)

这种方法解算时间是传统的最小二乘滤波算法的 $n$ 倍，同时也要占用一定的存储空间，但在现代的计算机条件下这点存储量和解算时间是微不足道的。为了优化解算方法，可以在解算精度和解算时间上进行折中。

3 实　例

假设目标初始距离 ${D_0}$ = 90链，目标航速 ${V_{\rm{m}}}$ =22 kn，目标初始方位 ${Q_{m0}}$ =10°。

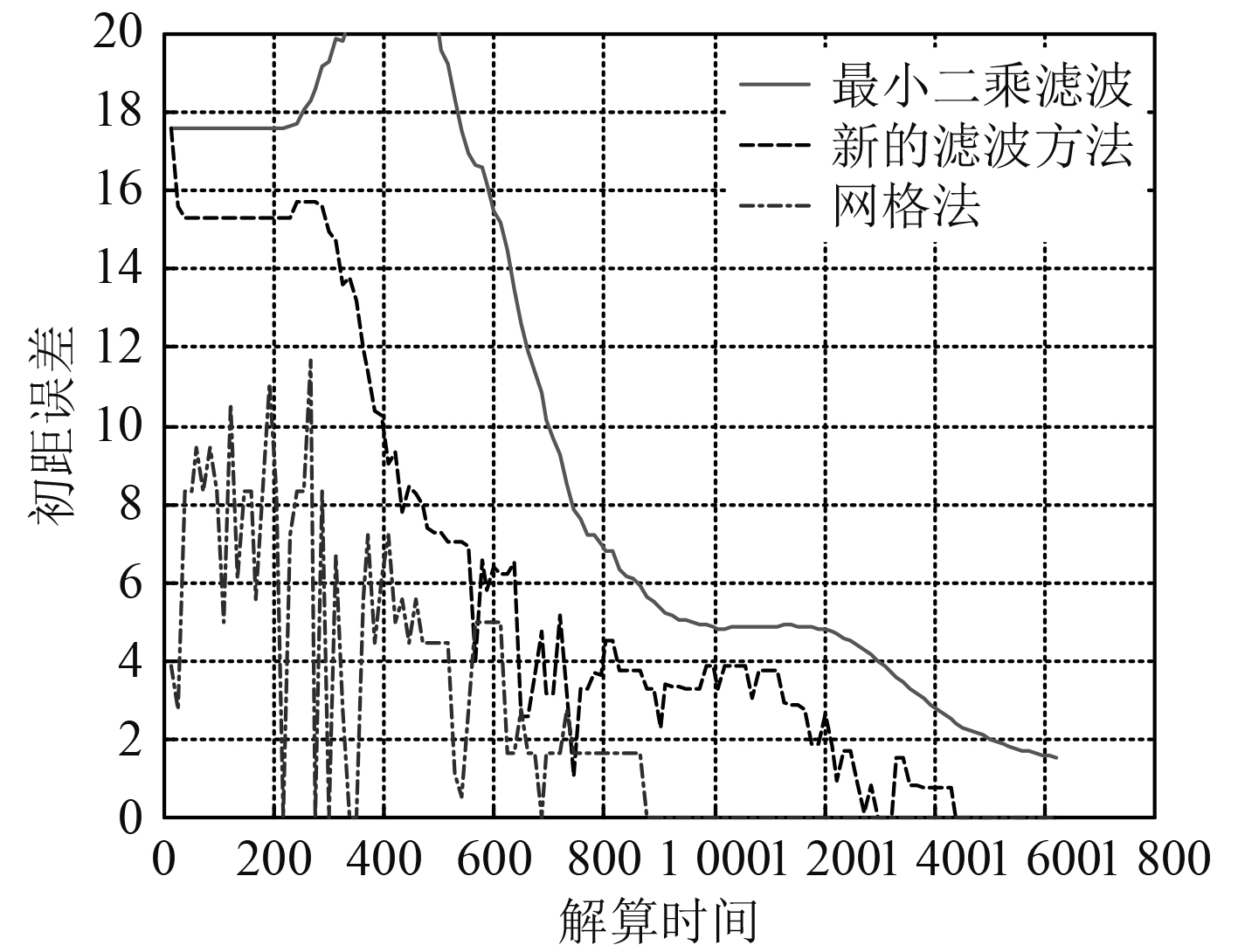
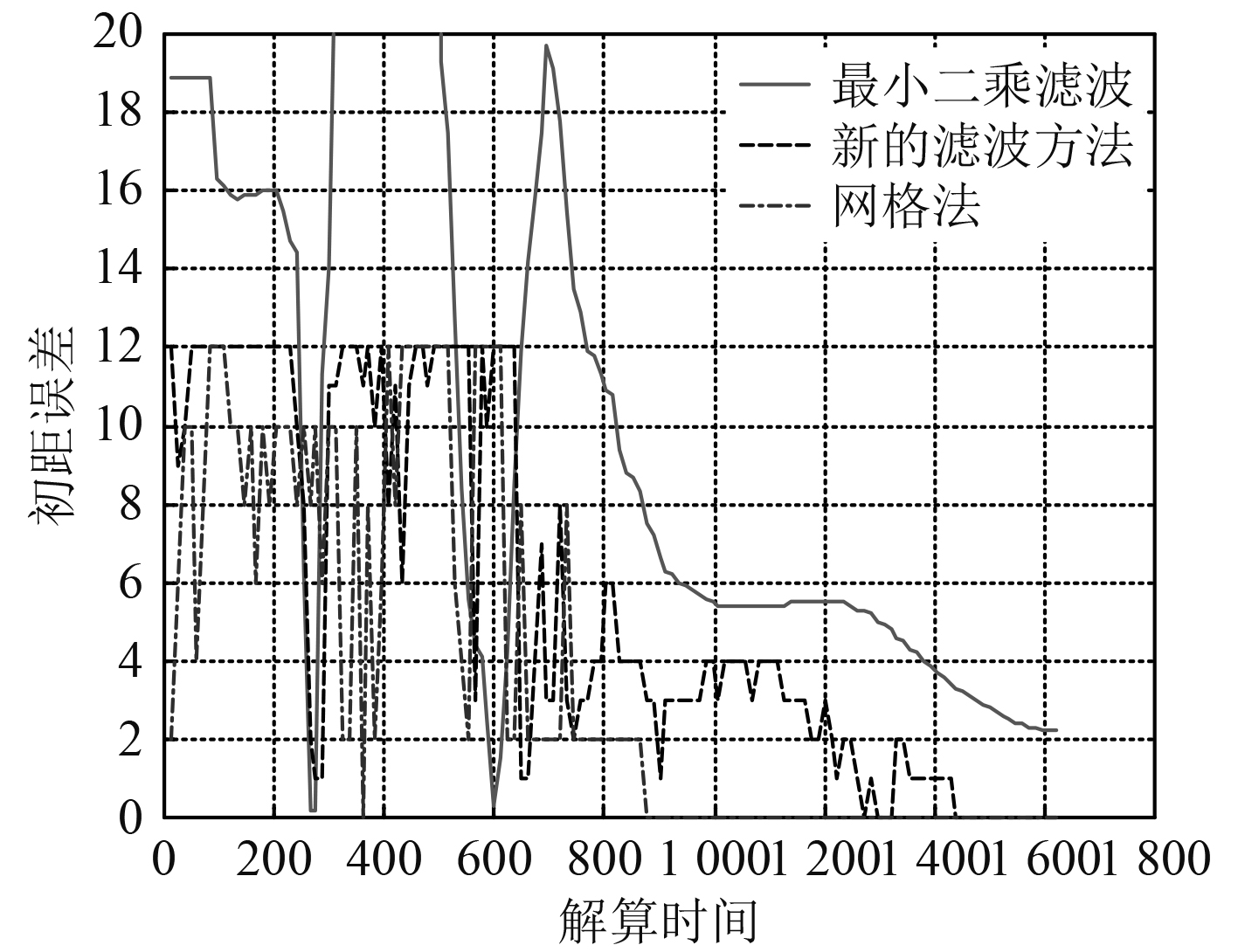
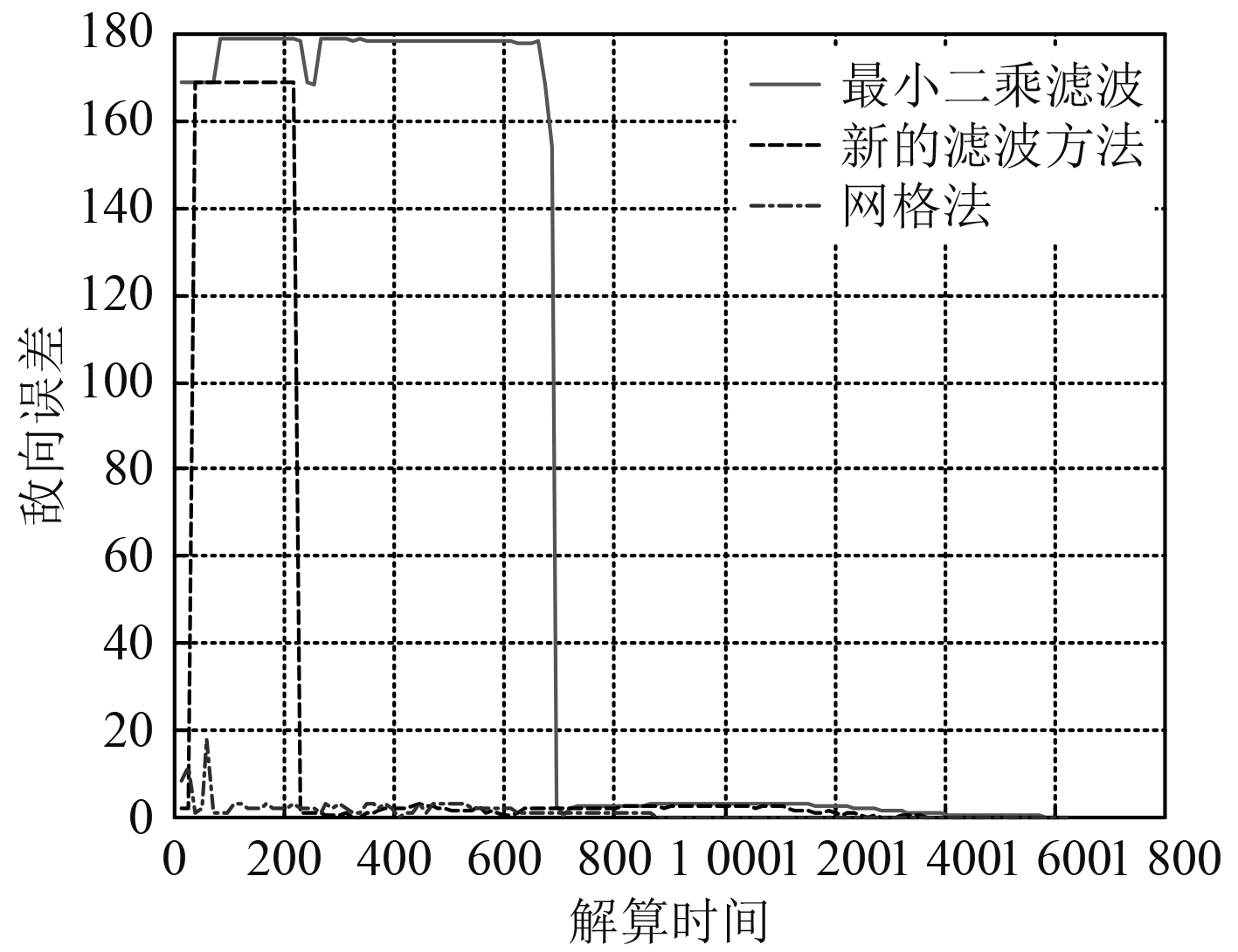
为了验证改进的滤波算法正确性与合理性，分别对传统的最小二乘滤波法、新的滤波算和网格法进行仿真计算，解算精度比较如图2～图4所示。结果表明，新的滤波算法在收敛时间和收敛精度上都优于传统的最小二乘滤波法，而网格法略优于新的滤波算法，但在滤波时间上占用的CPU时间太长，不适于实时滤波。

影响新的滤波算法的收敛精度的主要因素之一是测初始方位 ${f_0}$ 误差，如果 ${f_0}$ 误差很小，收敛精度高，如果 ${f_0}$ 误差大，影响估算的精度，造成滤波误差较大。

4 结　语

本文针对传统纯方位纯方位法解算目标运动要素时存在的解算时间长，收敛率低的问题，提出一种新的纯方位解算方法。根据案例计算结果可以看出，该滤波算法在收敛时间和收敛精度上都优于传统的最小二乘滤波法，而网格法略优于新的滤波算法，但在滤波时间上占用的CPU时间太长，不适于实时滤波。下一步将针对复杂态势下的解算情况开展深化研究，为水下无人航行器作战使用以及武器装备射击诸元计算的提供支撑。