本文水下机器人实体为中小型作业ROV,总体尺寸大约为0.82 m×0.68 m×0.50 m,配有2个密封舱,分别是电源舱与控制舱。动力系统为6个推进器,水平有4个,为矢量布置,2个垂推前后布置。作业系统为2关节机械臂。传感器配有深度计、高度计、加速度计、多普勒测速仪、摄像机、声呐等。
对ROV以及水池环境在仿真软件MuJoCo中进行建模,主要包括模型的尺度、形状、密度、重量等参数的设定。
1.1 水下机器人建模MuJoCo表示“多连接体动力学”。它由Emo Todorov为Roboti LLC开发。最初,它在华盛顿大学的运动控制实验室中使用,现在已被众多研究人员和开发人员所采用。其旨在促进机器人技术,生物力学,图形和动画以及其他需要快速而准确的仿真的领域的研究和开发,提供了速度,准确性和建模能力的独特组合。其为开源软件,通过把自己建立的模型导入其中,进行仿真演示、数据收集等工作。
ROV建模采用与真实比例1∶1进行建模,但因为ROV中有些部分难以精确绘制,会耗费大量时间,并且不是影响仿真结果的主要原因,故仿真模型只是尽可能逼近真实ROV,省略了缆,螺旋桨推进器和一些传感器、连接件设备。仿真模型见图1。

|
图 1 ROV上的传感器设备 Fig. 1 Sensor equipment on ROV |

|
图 2 MuJoCo中对ROV的建模 Fig. 2 ROV modeling in MuJoCo |
为了对仿真中的动力学计算进行讨论[1],定义需要用到的符号见表1。
|
|
表 1 动力学公式符号意义 Tab.1 Symbolic meaning of kinetic formula |
其中,仿真时刻要计算的不但有刚体平动,还有关节的转动,所以需要用到约束雅可比行列式。雅可比行列式建立关节坐标和约束坐标之间的数量关系。它将关节的运动矢量(速度和加速度)对应到约束坐标:关节速度
在连续时间内,所用的动力学方程为下式:
| $ M{\dot v}+c=\tau +{J}^{\rm{T}}f \text{,} $ | (1) |
关节空间惯性矩阵
| $ {\dot v}={M}^{-1}(\tau +{J}^{{\rm{T}}}f\rm{-c})\text{,} $ | (2) |
计算逆向动力学时,式(2)变为:
| $ \tau =M{\dot v}+c{-}{J}^{{\rm{T}}}f{\text{。}} $ | (3) |
为了使其计算速度可以适应仿真的频率,每个物体的形状被假定为等效惯性箱。盒子的每个正面(相对于线速度)面都沿其法线方向承受力。由于角速度,所有面也承受扭矩,该转矩是通过对表面积上旋转所产生的力进行积分获得的。用参数指定介质的粘度β和密度ρ,并适用于所有物体令v和ω表示与等效惯性盒对齐的线速度和角速度,而s表示盒大小的三维向量。
| $ {\text{密度力}}:\;{\rm{ - }}\frac{{\rm{1}}}{{\rm{2}}}\rho {s_j}{s_k}\left| {{v_i}} \right|{v_i}\text{,} $ | (4) |
| $ {\text{密度力矩}}:\;{\rm{ - }}\frac{{\rm{1}}}{{{\rm{64}}}}\rho {s_i}\left( {s_j^4 + s_k^4} \right)\left| {{\omega _i}} \right|{\omega _i}\text{,} $ | (5) |
上述计算式隐式地假设了高雷诺数,升阻比等于攻角的切线。
每个物体还承受与粘度成正比且与其线性和角速度相反的力和转矩。假设物体为低雷诺数的球体,当物体不为球体时直径d等于等效惯性盒尺寸的平均值。公式为:
| $ {\text{粘性力}}:\;{\rm{ - }}3\beta {\text{π}} dv \text{,} $ | (6) |
| $ {\text{粘性力矩}}:\;{\rm{ - }}\beta {\text{π}} {d^3}\omega \text{。} $ | (7) |
本文基于深度强化学习[2]进行水下机器人抓取控制的仿真实验,采用由简单到困难的仿真环境进行研究,针对各阶段分为4种仿真环境[3]。
1)目标初始位置固定,且位置已知
构造一个边长10 m的正方形水池,将对ROV建立的仿真模型放入其中,其初始高度为2 m。然后创建一个形状类似海参的模型放在池底,其位于ROV的前下方。ROV如同现实中一样,有5个自由度的运动,分别为前后左右的平移运动、上升下降、回转及纵倾运动。
ROV的仿真模型并没有手抓结构,所以对于ROV的最终目标是:在没有失去稳性的情况下,在局部趋近目标并且将机械臂末端距离目标足够近时其可以稳定的悬浮在目标上方。

|
图 3 环境1初始状态 Fig. 3 Environment 1 initial state |
需要说明的是:实体机械抓在操作时只有张开和闭合2个操作,并且在真实水池中抓取目标时,只要机械臂末端离目标足够近,并且ROV可以稳定住姿态,成功抓取的概率大于90%,所在只要达成仿真中的目标,就可以说完成了一次成功的抓取。对于足够近这个概念来讲,从经验上看其值小于0.1 m这个范围可以说是很苛刻了。而对于ROV稳定悬浮,在仿真设置的范围更加苛刻,其规定5个自由度的运动均小于0.03 m/s(或0.03 rad/s)。没有失去稳性是指ROV在运动的过程中,要保持其横倾与纵倾的角度不能过大,在抓取的时候要更加平衡,具体数值设定是在趋近目标的时候要保持倾角在40°以内,到抓取范围内要保持在25°以内。
2)目标初始位置随机,位置已知
相对于上面的仿真环境,在这次仿真训练中,使目标位置随机出现在ROV正下方4 m×4 m的正方形区域内,ROV可以在仿真中得到目标的位置信息。

|
图 4 环境4初始状态 Fig. 4 Environment 4 initial state |
3)目标位置信息接受不完全,且位置信息获取是基于对视觉识别的仿真
针对基于传统控制方法进行目标抓取可能出现的跟踪目标失败,或者提供错误信息,设计了这种目标初始位置随机,并且对于目标位置信息并不是完全准确的情况。在这次仿真中,有15%的概率,会不提供目标信息,有5%的概率会提供错误的信息。
4)多位置随机目标抓取,且位置信息获取是基于对视觉识别的仿真[4]
由于真实情况下,只有目标出现在摄像机视野中,才有机会得到目标的相对位置信息,所以设置ROV的摄像机视野,其范围大小与其高度和姿态相关,并且设置多个抓取目标,其初始位置随机分布。只有目标出现在摄像机视野内并且离视野中心最近,才会有80%的概率得到其相对位置信息,有15%几率没有检测到,有5%的几率返回错误的位置信息。这种情况与现实中抓取几乎完全相似。
2 近端策略优化算法策略梯度算法(VPG,Vanilla Policy Gradient)是近端策略优化算法的基础[8],其核心想法很简单,就是把可以得到更多奖励的动作概率增大,反之,减少奖励的动作概率,并且不停的迭代,直到达到最优的策略[8]。
下面使用
| $ J({{\text{π}} _\theta }) = \int_\tau {P(\tau |{{\text{π}}_\theta })} R(\tau )\text{,} $ | (8) |
所以
| $ {\nabla _\theta }J({{\text{π}} _\theta }) = \mathop E\limits_{\tau \sim {{\text{π}} _\theta }} \left[\sum\limits_{t = 0}^T {{\nabla _\theta }\log {{\text{π}} _\theta }({a_t}|{s_t})R(\tau )} \right], $ | (9) |
一般用优势函数来代替它是更好的选择,则公式变为:
| $ {\nabla _\theta }J({{\text{π}} _\theta }) = \mathop E\limits_{\tau \sim {{\text{π}} _\theta }} \left[\sum\limits_{t = 0}^T {{\nabla _\theta }\log {{\text{π}} _\theta }({a_t}|{s_t}){A^{{{\text{π}} _\theta }}}} ({s_t},{a_t})\right]{\text{。}} $ | (10) |
式中:
策略梯度算法是通过对表示策略好坏的
| $ {\theta _{k + 1}} = {\theta _k} + \alpha {\nabla _\theta }J({{\text{π}} _{{\theta _k}}})\text{。} $ | (11) |
近端策略优化(PPO,Proximal Policy Optimization)解决的问题[9-10,13]:如何在当前所采取策略下产生的数据,尽最大的可能更新到更好的策略,并且避免更新步幅过大,而导致运行新策略所得到的奖励大幅下降。PPO运用一些技巧,使更新所得到的新策略与旧策略足够接近,并且是一阶方法,这使得PPO方法易于实现,并且从经验上来看,其性能不错。
PPO-Clip在更新公式中没有KL-散度项[11-12],也没有任何约束。取而代之的是依靠对目标函数进行剪枝操作,来控制新旧策略之间的差距。
PPO-剪枝更新策略如下式:
| $ {\theta _{k + 1}} = \arg \mathop {\max }\limits_\theta \mathop E\limits_{s,a \sim {{\text{π}} _{{\theta _k}}}} [L(s,a,{\theta _k},\theta )]\text{。} $ | (12) |
通常取最大值操作都是用批量随机梯度下降来实现的。
式中:
| $\begin{split} &L(s,a,{\theta _k},\theta ) = \min \left(\frac{{{{\text{π}} _\theta }(a|s)}}{{{{\text{π}} _{{\theta _k}}}(a|s)}}{A^{{{\text{π}} _{{\theta _k}}}}}(s,a),\right.\\ &\left.clip([\frac{{{{\text{π}} _\theta }(a|s)}}{{{{\text{π}} _{{\theta _k}}}(a|s)}},1 - \varepsilon ,1 + \varepsilon ){A^{{{\text{π}} _{{\theta _k}}}}}(s,a)\right)\text{。}\end{split} $ | (13) |
式中:
式(13)很复杂,将其拆解为式(14)和式(15):
| $ L(\!s,a,{\theta _k},\theta \!)\! =\! \min \left(\!\frac{{{{\text{π}} _\theta }(a|s)}}{{{{\text{π}} _{{\theta _k}}}(a|s)}}{A^{{{\text{π}} _{{\theta _k}}}}}(s,a),g(\varepsilon ,{A^{{{\text{π}} _{{\theta _k}}}}}(s,a))\!\right)\!\text{,}\!\!\! $ | (14) |
| $ g(\varepsilon ,A) = \left\{ {\begin{array}{*{20}{c}} {(1 + \varepsilon )A} \text{,}\\ {(1 - \varepsilon )A} \text{,} \end{array}} \right.\begin{array}{*{20}{c}} {}&{\begin{array}{*{20}{c}} {A \geqslant 0} \text{,}\\ {A \leqslant 0} \text{。} \end{array}} \end{array} $ | (15) |
优势函数为正:假设对一状态-动作对(s,a)优势函数为正,在这种情况下公式变为:
| $ L(s,a,{\theta _k},\theta ) = \min \left(\left(\frac{{{{\text{π}} _\theta }(a|s)}}{{{{\text{π}} _{{\theta _k}}}(a|s)}},(1 + \varepsilon )\right.\right){A^{{{\text{π}} _{{\theta _k}}}}}(s,a)\text{。} $ | (16) |
因为优势函数为正,所以下一步更新会倾向增加采取相同动作的概率,从而使目标函数值增加。这时候取最小值操作就是设置一个增加此动作概率的极限值。一旦
出于同样的目的,当优势函数为负时,只需将上式的
以下算法所进行仿真环境为仿真环境1。
奖励函数的设定分为了以下的几种情况:
1)运动过程中失去了稳性,会有一个很大的负奖励,reward=−3000;
2)在机械臂离末端与目标相对较远,在0.18 m以上时,reward=−(10-dis_difference*500);
3)当机械臂离末端与目标相对较近,小于等于0.18 m时,reward=(0.18-distance)*30;
4)当两者距离小于0.18 m时,并且ROV各个维度的运动都小于0.03 m/s(或0.03 rad/s)s时,会有一个很大的正奖励,reward=3000。
其中dis_difference代表的是2次互动中机械臂距离目标远近的差异,因为2次互动间隔的时间很小,这个值不会很大,所以乘以一个系数,得到一个适合的量。Distance代表每一时刻机械臂离目标的距离。之所以以这个作为奖励函数,是希望在ROV离目标较远的情况下,可以快速移动到目标附近,当距离较近可以进行抓取时,ROV要稳定住。dis_difference不仅在距离上,还在时间上对训练过程中策略的选择产生了影响。
算法参数设置:训练轮次3000轮,每轮包括4000次与环境的互动,奖励折扣因子
深度神经网络结构为2个神经网络,分别用来训练策略与拟合值函数。其结构分别为:
1)策略网络
有2个隐藏层,每个隐藏层的神经元个数是64个,输入层神经元个数为22个神经元,其中包括各个维度运动以及2个关节的位置以及速度并且还包括机械手末端与目标的位置信息[5-6]。输出为控制ROV的5个自由度的力,与2个关节的角度,共7个输出。出于输出力有正有负的原因考虑,所以每层的激活函数都为tanh函数。
2)值函数网络
基本设置与策略网络相同,不过其输出层只有一个神经元作为输出[7]。
|
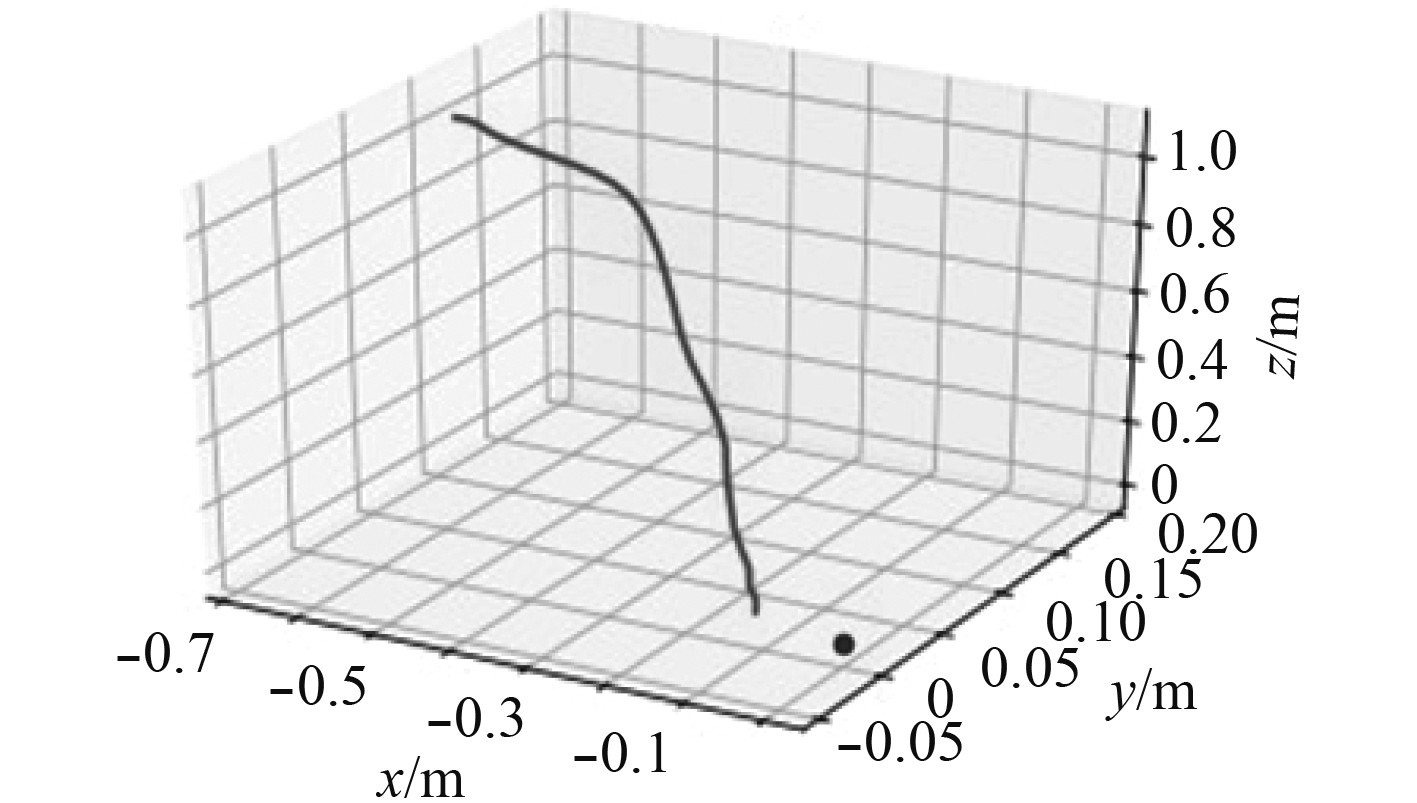
图 5 PPO算法机械臂末端抓取轨迹 Fig. 5 PPO algorithm manipulator end grab trajectory |
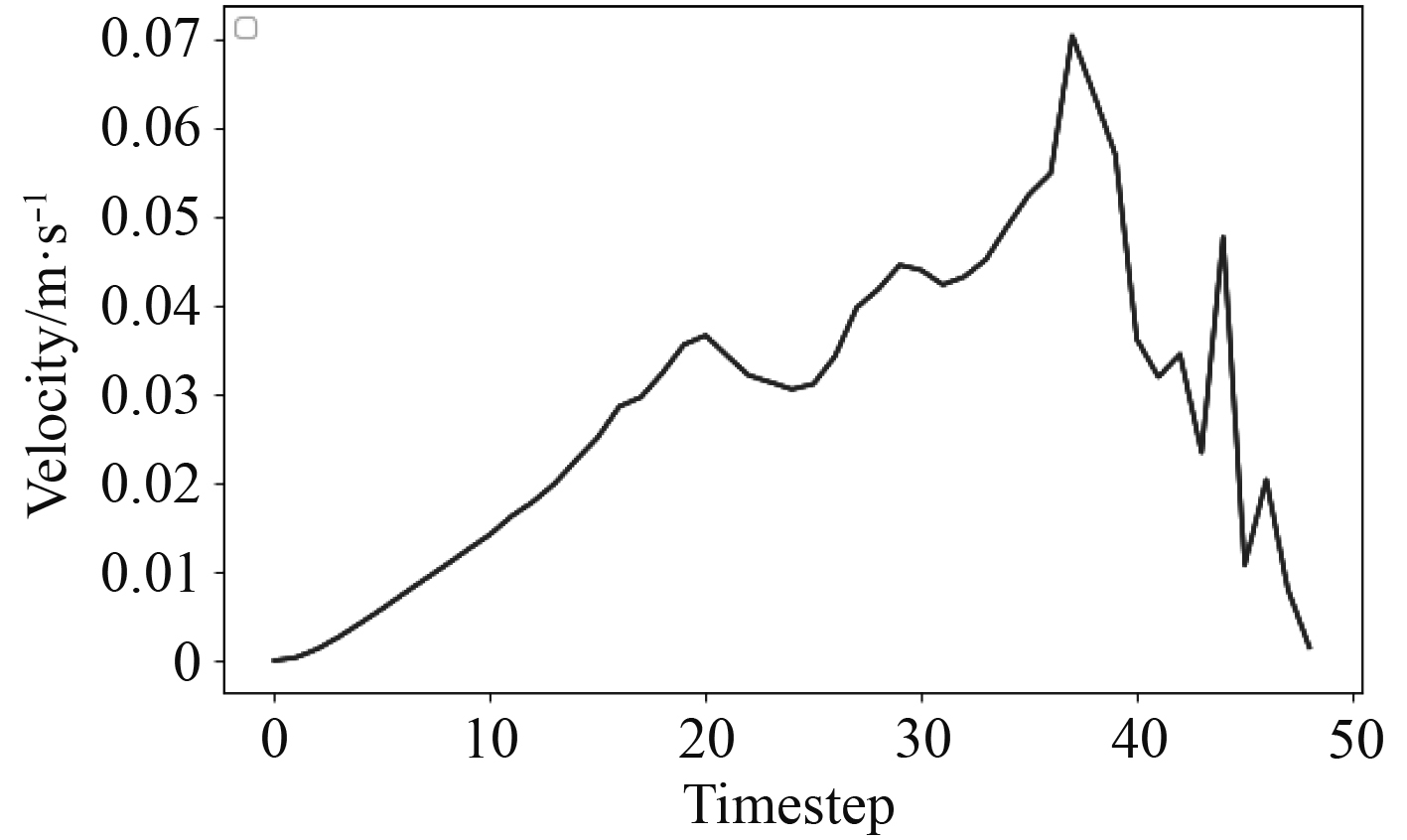
PPO算法完成任务在仿真中所需要的时间步数为49步,其速度曲线如图6所示。抓取过程中的平均速度为0.16 m/s,抓取成功率在99%以上。
|
图 6 PPO算法抓取过程中ROV速度曲线 Fig. 6 Velocity curve of ROV in the process of grasping with PPO algorithm |
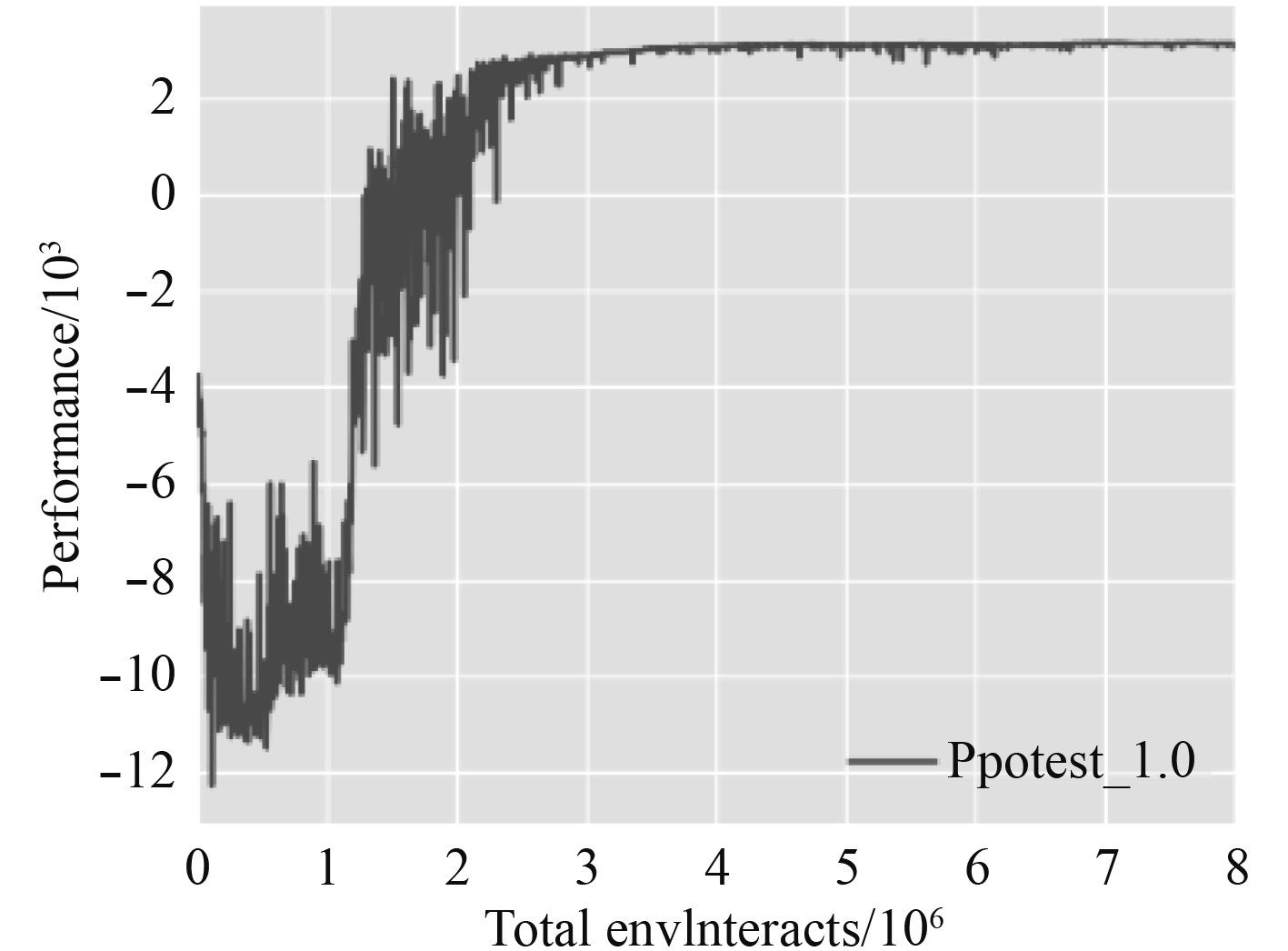
|
图 7 PPO算法收敛轨迹 Fig. 7 Convergence trajectory of PPO algorithm |

|
图 8 PPO算法训练后的仿真抓取过程 Fig. 8 Simulation process of PPO algorithm after training |
在使用PPO算法对这种环境进行训练仿真时,由于动作维度巨大,而且奖励稀疏,所以对算法进行改进[14-15]。
在PPO算法中使用的探索策略为对角高斯策略,对角高斯策略使用神经网络表示从状态与平均输出动作
用来进行探索的动作输出最终由下式得出,式中z为概率密度服从(0,1)的正态分布取值。
| $ a = {\mu _\theta }(s) + \sigma \odot z \text{,} $ | (17) |
对上式中的
| $ {\alpha }_{\theta }=M·\left(\frac{{\rm{log}}(\varepsilon +{\stackrel{\_}{D}}_{KL}(\theta \left|\right|{\theta }_{k}))}{{\rm{log}}\varepsilon }\right)\text{,} $ | (18) |
式中:M为动作最大取值范围的固定向量,
| $ a = {\mu _\theta }(s) + {\alpha _\theta } \odot z \text{。} $ | (19) |
这样虽然增加了需要收敛的时间,却使策略在探索的过程中可以遍历更大的区域,使其收敛到局部最优时可以快速跳出,寻找全局最优。
1)目标初始位置随机
仿真环境:对应仿真环境2。
参数设置:训练轮次3000轮,每轮包括9000次与环境的互动,奖励折扣因子
深度神经网络结构与上文相同。
奖励函数的设定分为了以下的几种情况:
①运动过程中失去了稳性,会有一个很大的负奖励,reward=−70000;
②在机械臂离末端与目标相对较远的时候,在0.18 m以上时,reward=−(10-dis_difference*500);
③当臂离末端与目标相对较近的时,小于等于0.18 m时,reward=(0.18-distance)*30;
④当两者距离小于0.18 m时,并且ROV各个维度的运动都小于0.03 m/s(或0.03 rad/s)时,会有一个很大的正奖励,reward=10000。
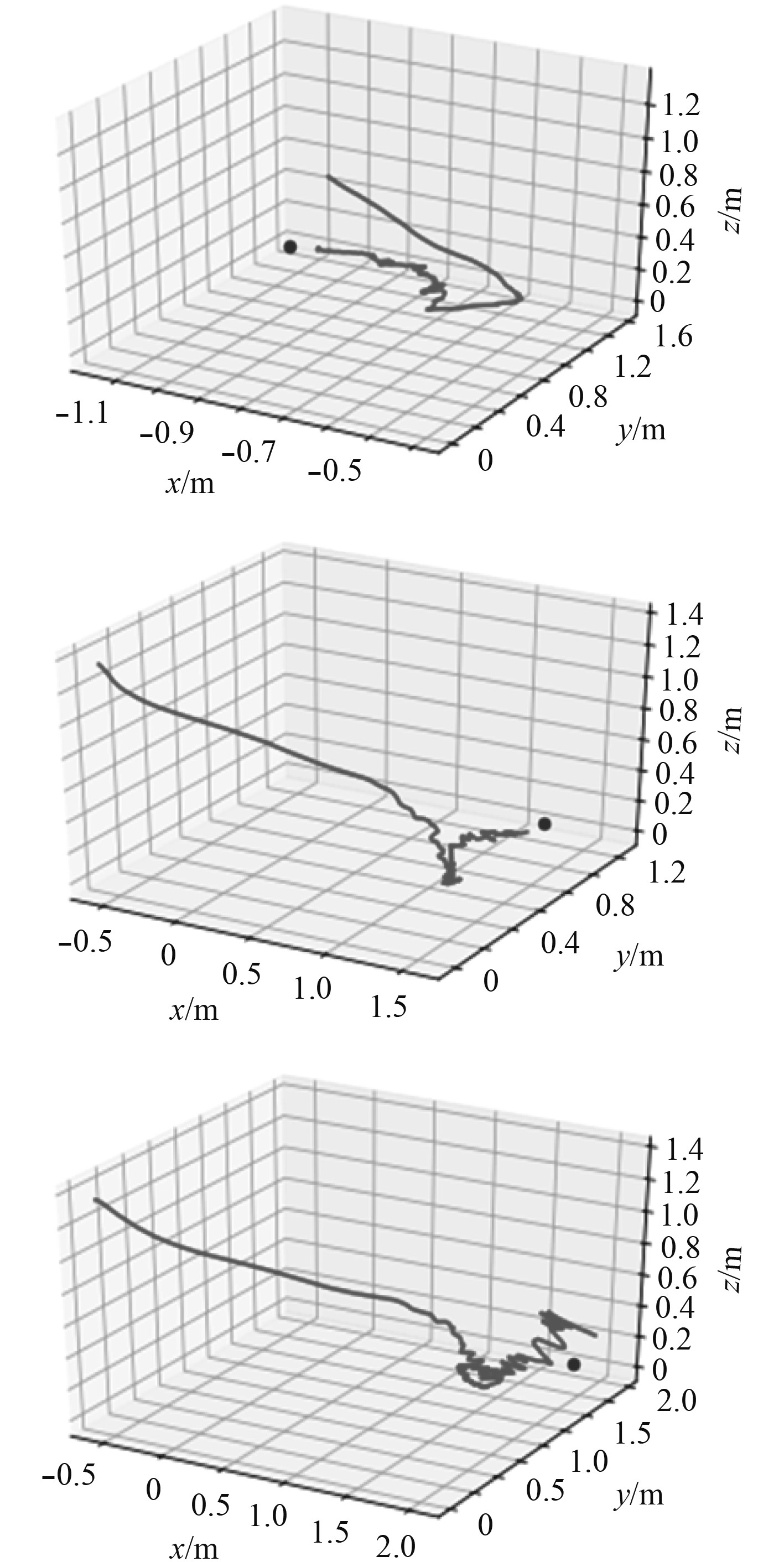
图9与图10分别为测试的ROV轨迹与训练所获总奖励的收敛曲线。
|
图 9 目标位置随机机械臂末端抓取轨迹 Fig. 9 Grab trajectory of robot arm with random target position |
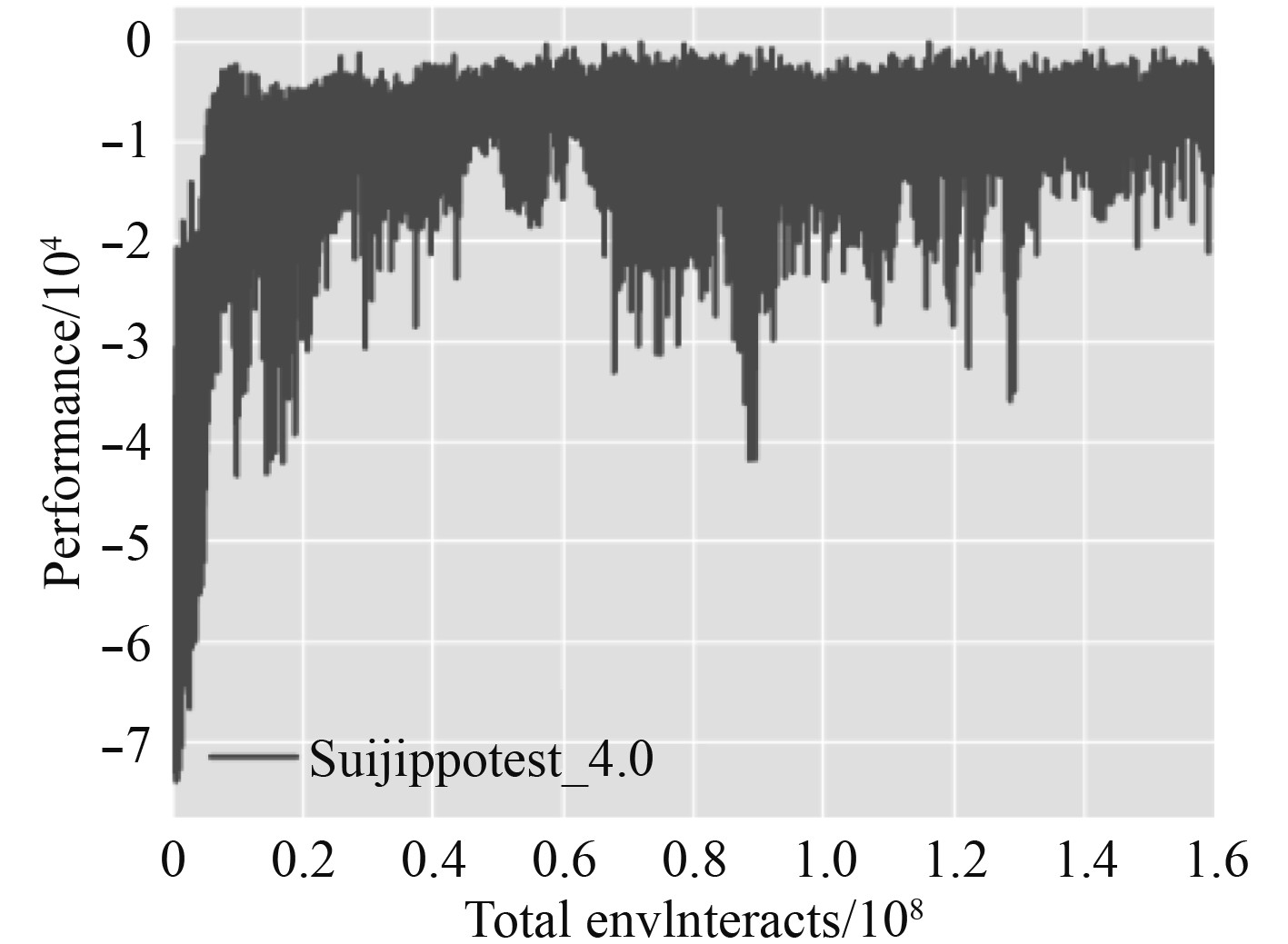
|
图 10 目标位置未知环境下训练的收敛曲线 Fig. 10 Convergence curve of training in unknown target location environment |
从图11可以看出ROV在趋近目标的过程中比较迅速的,其所走轨迹也近乎是最短的路线,但是在目标附近时为了满足抓取的要求会做许多调整,所以轨迹看起来会抖动比较多。综合来看,这一系列动作所用时间很短,平均只用200多次的与环境互动次数。
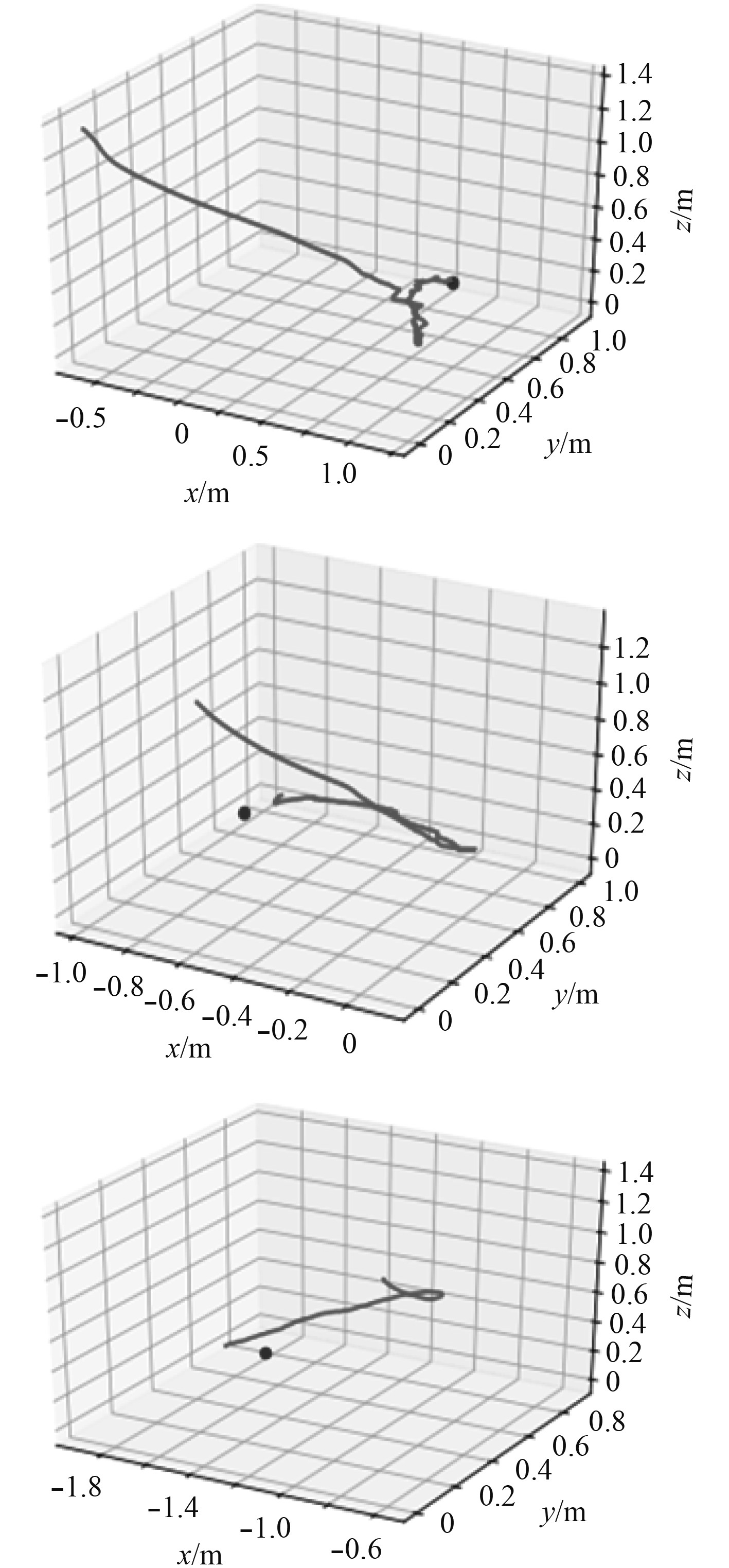
|
图 11 目标位置随机机械臂末端抓取轨迹 Fig. 11 Grab trajectory of random manipulator at target position |
2)目标位置信息接受不完全
仿真环境:对应仿真环境3。
利用对仿真环境2训练所得出的网络可以直接应用到这里,并取得不错的效果。
3)摄像机视野下多位置随机目标抓取
仿真环境:对应仿真环境4。
参数设置:训练轮次3000轮,每轮包括9000次与环境的互动,奖励折扣因子
奖励函数的设定分为以下几种情况:
1)运动过程中失去稳性,会有一个很大的负奖励,reward=−70000;
2)当目标出现在摄像机视野内奖励为:在机械臂离末端与目标相对较远,在0.18 m以上时,reward=−(10-dis_difference*500)+10,当机械臂离末端与目标相对较近,小于等于0.18 m时,reward=(0.18-distance)*30,当两者距离小于0.18 m,并且ROV各个维度的运动都小于0.03 m/s(或0.03 rad/s)时,会有一个很大的正奖励,reward=10000;
3)当目标没有出现在视野内时,reward=−5。

|
图 12 复杂环境仿真实验 Fig. 12 Complex environment simulation experiment |
在PPO改进算法训练后,利用训练好的网络模型作为控制器在所设置环境中执行抓取任务,任务中机械臂开始所处位置为(−0.0625,0,1.357),移动到分布在3 m×3 m的区域内6个随机目标中某一个所处位置,在仿真中所需要的时间步数为100~150步左右,其速度曲线如图13所示。抓取过程中的平均速度为0.2 m/s,抓取成功率在41%以上。
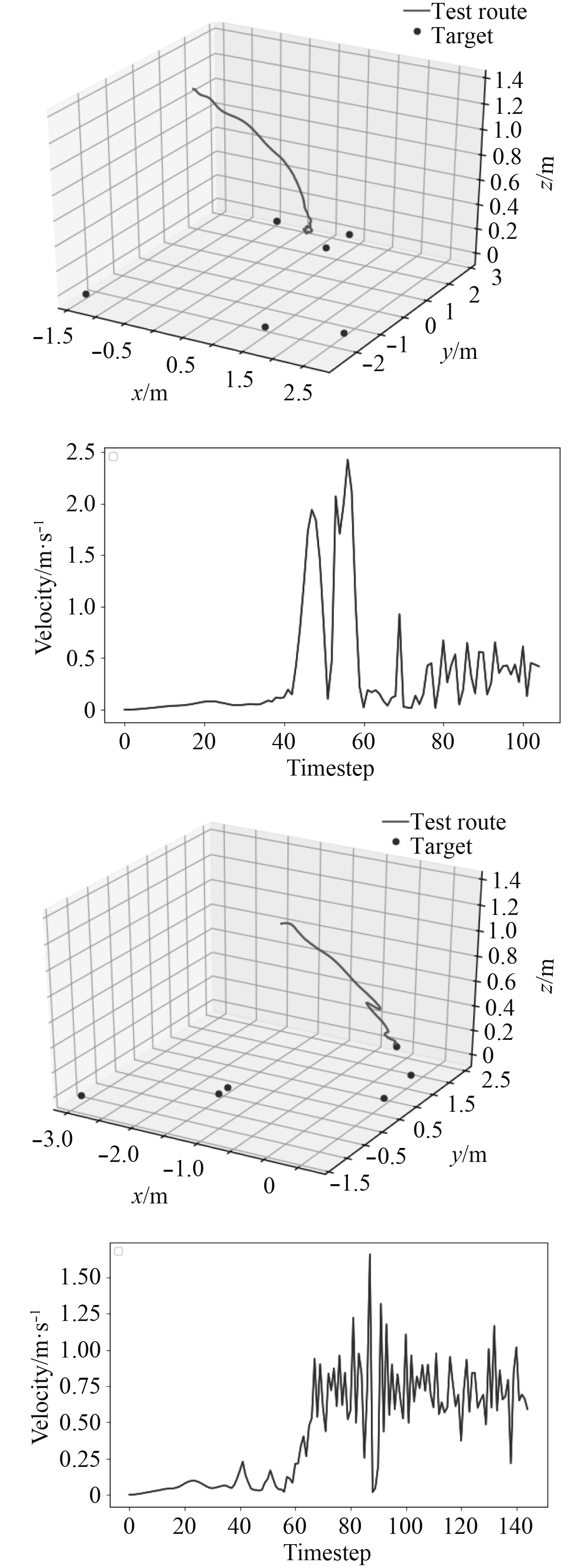
|
图 13 改进PPO算法机械臂末端抓取轨迹抓取过程速度 Fig. 13 The speed of manipulator end grasping trajectory based on improved PPO algorithm |
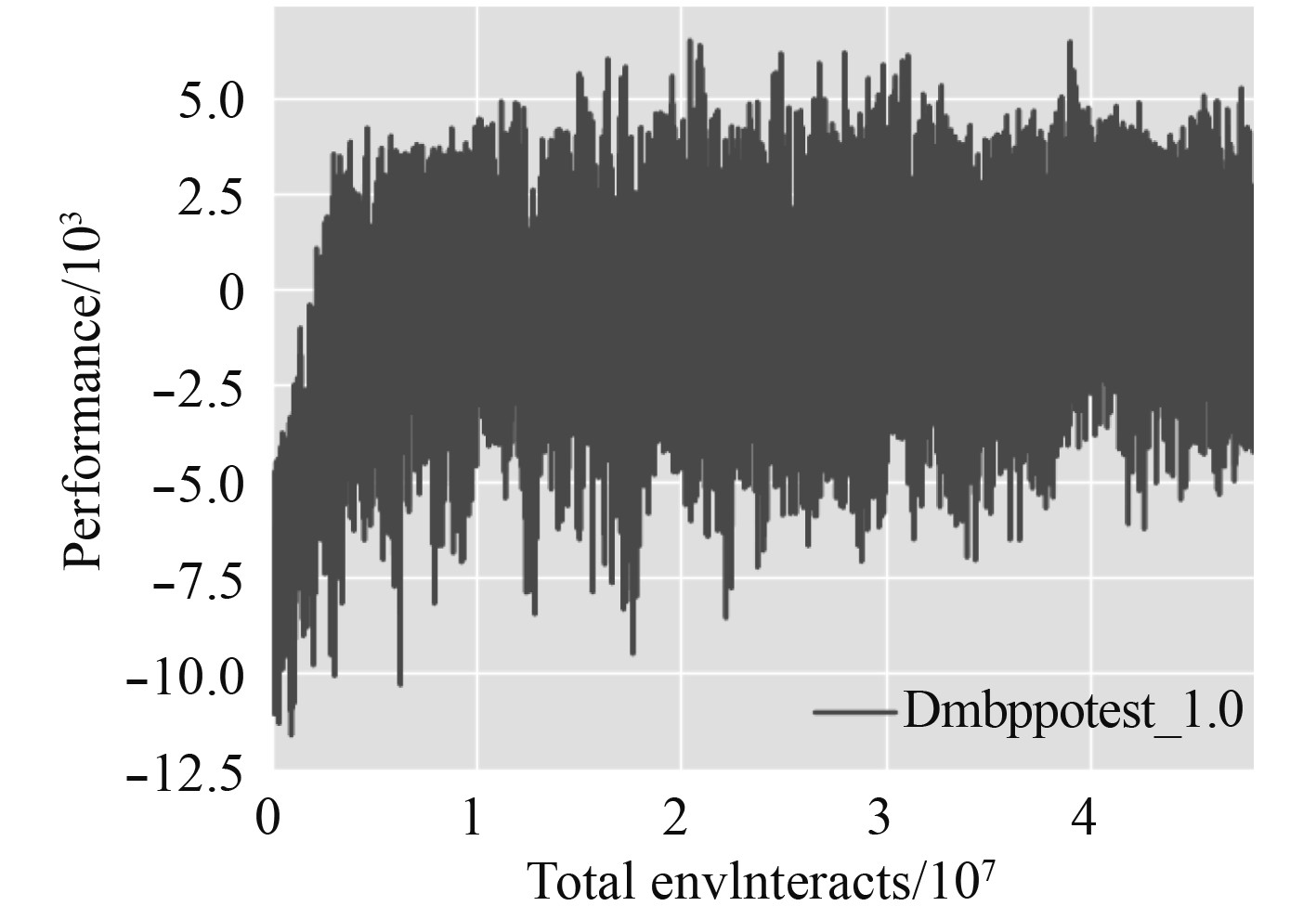
|
图 14 改进PPO算法收敛图 Fig. 14 Convergence diagram of improved PPO algorithm |
从收敛曲线可以看出,算法在改进后应对更为复杂的环境有较大的波动,但其最终成功抓取率优于修改之前,并且在相同的奖励函数下,奖励得分提高了53.1%,说明算法在收敛到局部最优值后可以跳出,继续搜索。
3 结 语表3是对不同抓取方式进行抓取测试的结果总结,其中需要说明的是学习类算法进行训练每次所采取的参数不同,但对最终结果影响很小,成功率为多次训练测试结果的平均水平。
|
|
表 3 抓取方法比较 Tab.3 Comparison of grabbing methods |
从表3比较得出结论:PPO算法在应对更复杂的环境时,抓取成功率大幅度降低。这是由于算法过早收敛,对一些情况探索不足。在对PPO算法利用散度关系进行修改,增加了探索的随机性,最终的抓取成功率有所提升。
| [1] |
ANITESCU M. 基于优化的非光滑多刚体动力学仿真[J]. 数学规划, 2006, 105(1): 113-143. ANITESCU M. Optimization-based simulation of nonsmooth rigid multibody dynamics[J]. Mathematical Programming, 2006, 105(1): 113-143. DOI:10.1007/s10107-005-0590-7 |
| [2] |
ABBEEL P, COATES A, NG A Y. 通过学徒学习自主直升机特技飞行[J]. 国际机器人研究杂志, 2010, 29(13): 1608-1639. DOI:10.1177/0278364910371999 |
| [3] |
ARGALL B D, CHERNOVA S, VELOSO M, 等. 机器人演示学习综述[J]. 机器人与自主系统, 2009, 57(5): 469-483. ARGALL B D, CHERNOVA S, VELOSO M, et al. A survey of robot learning from demonstration[J]. Robotics and Autonomous Systems, 2009, 57(5): 469-483. DOI:10.1016/j.robot.2008.10.024 |
| [4] |
RAHMATIZADEH R, ABOLGHASEMI P, BÖLÖNI, 等. 基于视觉的廉价机器人多任务操作的端到端学习演示[J]. 2017. RAHMATIZADEH R, ABOLGHASEMI P, BÖLÖNI, et al. Vision-Based Multi-Task manipulation for inexpensive robots using End-To-End learning from demonstration[J]. 2017. |
| [5] |
BENGIO Y, BENGIO S. 通过多层神经网络建模高维离散数据[C]//神经信息处理系统国际会议, 麻省理工学院出版社, 1999.
|
| [6] |
SUTSKEVER I, VINYALS O, LE Q V. 神经网络的序列到序列学习[J]. 神经信息处理系统进展, 2014. |
| [7] |
HOCHREITER, Sepp, SCHMIDHUBER, Jürgen. 长短期记忆网络[J]. 神经计算, 9(8): 1735-1780. . HOCHREITER, Sepp, SCHMIDHUBER, Jürgen. Long Short-Term Memory[J]. Neural Computation, 9(8): 1735-1780. |
| [8] |
Thomas, Philip S, Brunskill, Emma. 基于函数逼近和动作相关基线的强化学习策略梯度法[J]. arXiv:1706.06643, 2017.
|
| [9] |
YAN Duan, XI Chen, REIN Houthooft, 等. 连续控制的深度强化学习[C]//国际机器学习会议(ICML), JMLR. org 2016. YAN Duan, XI Chen, REIN Houthooft, et al. Benchmarking deep reinforcement learning for continuous control[C]// International Conference on Machine Learning (ICML), JMLR. org, 2016. |
| [10] |
SCHULMAN, John, LEVINE, Sergey, MORITZ, Philipp 等. 置信域策略优化[J]. 计算机科学, 2015, 1889-1897. SCHULMAN, John, LEVINE, Sergey, MORITZ, Philipp et al. Trust region policy optimization[J]. Computer Science, 2015, 1889-1897. |
| [11] |
BAXTER J, BARTLETT P L. 无限水平策略梯度估计[J]. 人工智能研究杂志, 2019, 15(1): 319-350. BAXTER J, BARTLETT P L. Infinite-Horizon Policy-Gradient estimation[J]. Journal of Artificial Intelligence Research, 2019, 15(1): 319-350. |
| [12] |
KAKADE, Sham and LANGFORD, John. 近似最优近似强化学习[J]. ICML, 2002(2): 267–274.
|
| [13] |
SCHULMAN, John, WOLSKI, Filip, DHARIWAL, Prafulla, 等. 近端策略优化算法[J]. arXiv: 1707.06347 202017年7月
|
| [14] |
SILVER D, LEVER G, HEESS N, 等. 确定性梯度策略算法[C]//2014.
|
| [15] |
FUJIMOTO, Scott, VAN HOOF, Herke, MEGER, David. 动作评判方法中函数逼近误差的处理[J]. 第35届机器学习国际会议论文集, PMLR 80: 1587-15962018.
|
 2020, Vol. 42
2020, Vol. 42
