水下机器人(Autonomous Underwater Vehicle, AUV)近年来在海洋工程领域发挥着越来越重要的作用,被广泛应用在水下设备安装监控、大范围海洋监测以及自然资源勘探等领域。由于水下机器人数学模型存在强耦合、强非线性、水动力学系数不确定以及不确定海流干扰等问题,为保证AUV在复杂环境下能够正常工作,迫切需要易用且稳定性与鲁棒性良好的运动控制方法[1-6]。
AUV的鲁棒控制方法是当前的研究热点之一,大量的工作主要集中在低自由度AUV的线性系统控制。B.Clement通过非线性补偿与卡尔曼滤波实现了AUV单自由度首向角的H∞鲁棒控制结构,对比传统PID控制具有低过冲、稳定快的优点[7]。Juan C. Cutipa-Luque在解耦的横移-首向2DOF AUV模型上应用H∞鲁棒控制策略,取得了较好的控制效果[8]。Wei Zhang等[9]提出插值型H∞鲁棒控制器,分别实现了速度、首向及深度控制器并给出了相应的实验结果,验证了控制器设计思路的有效性。AUV单自由度的鲁棒控制虽然易于单个控制过程实现,但是忽略了AUV实际上各自由度间的耦合,在实际应用上容易造成控制器设计逻辑复杂,控制环节无法有效平滑过渡以及控制器参数过多不便校准等问题。为解决AUV多自由度系统相互耦合、强非线性等问题,本文基于六自由度AUV工作点处的线性化方程,构建适用于鲁棒控制的不确定性模型,并据此设计方便实际应用的六自由度H∞鲁棒控制器,得到了对应的仿真结果。
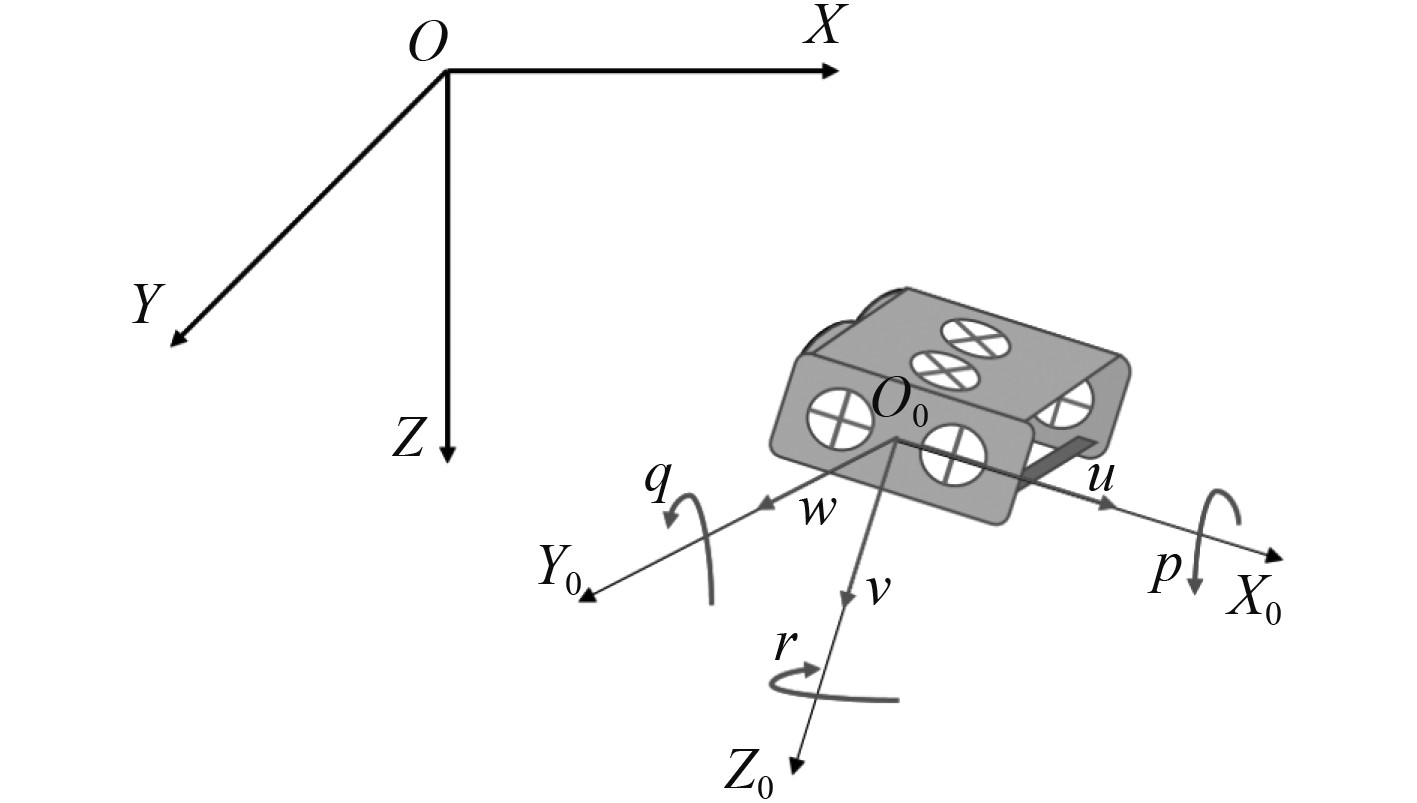
1 AUV六自由度非线性模型通过对AUV进行刚体运动及所受外力分析,可以得到AUV的动力学及运动学模型。为研究方便,本文采用Kambara外形AUV的模型进行仿真[10]。AUV的坐标系定义如图1所示,在此坐标系上,随体坐标系
| $ {{{\dot \eta }}_1} = {{{J}}_1}\left( {{{{\eta }}_2}} \right){{{v}}_1}{\text{,}} $ | (1) |
| ${{{\dot \eta }}_2} = {{{J}}_2}\left( {{{{\eta }}_2}} \right){{{v}}_2}{\text{。}} $ | (2) |
其中
|
图 1 AUV坐标系定义 Fig. 1 AUV coordinate system definition |
全驱动形式AUV的六自由度动力学模型可表示为:
| ${{{M}}_1}{\dot v_1} = - {{{C}}_1}\left( {{v_1}} \right){v_2} - {{{D}}_1}\left( {{v_1}} \right){v_1} - {g_1}\left( {{\eta _2}} \right) + {\tau _1}{\text{,}}$ | (3) |
| $ {{{M}}_2}{\dot v_2} \!=\! - {{{C}}_1}\left( {{v_1}} \right){v_1} \!-\! {C_2}\left( {{v_2}} \right){v_2} \!-\! {{{D}}_2}\left( {{v_2}} \right){v_2} \!-\! {g_2}\left( {{\eta _2}} \right) \!+\! {\tau _2}{\text{。}}\!\!\!\!\!\! $ | (4) |
其中:
令
| $ M= \left[\begin{array}{cc}{M}_{1}& O\\ O& {M}_{2}\end{array}\right]{\text{,}} $ | (5) |
| $ C\left( {{v}} \right) = \left[ {\begin{array}{*{20}{c}} O&{{C_1} \left( {{v_1} } \right)} \\ {{C_1} \left( {{v_1} } \right)}&{{C_2} \left( {{v_2} } \right)} \end{array}} \right]{\text{,}} $ | (6) |
| $ D\left( {{v}} \right) = \left[ {\begin{array}{*{20}{c}} {{D_1}\left( {{v_1}} \right)}&O \\ O&{{D_2}\left( {{v_2}} \right)} \end{array}} \right] {\text{,}} $ | (7) |
| $ g\left( {{\eta _2}} \right) = \left[ {\begin{array}{*{20}{c}} {{g_1}\left( {{\eta _2}} \right)} \\ {{g_2}\left( {{\eta _2}} \right)} \end{array}} \right]{\text{,}} $ | (8) |
则AUV六自由度方程可以简化为Fossen形式[11],且
| ${{M}}{\dot v}{\rm{ = }} - {{{C}}}\left( {v} \right){v} - {{D}}\left( {v} \right){v + }g\left( {{\eta _2}} \right) + {\tau }{\text{。}} $ | (9) |
本文所提出的六自由度AUV不确定性模型建立在AUV工作点处的线性化方程以及鲁棒控制中的加性不确定性模型之上,并最终在频域上对其进行描述,得到耦合性未丢失且方便处理的多自由度控制模型。
为便于处理,定义模型控制输入为
| $ {{C}}\left( {{v}} \right) \!=\! \left[\!\!\!\! {\begin{array}{*{20}{c}} 0\!\!&\!\!0\!\!&\!\!0\!\!&\!\!0\!\!&\!\!{{m_{33}}w}\!\!&\!\!{ - {m_{22}}v} \\ 0\!\!&\!\!0\!\!&\!\!0\!\!&\!\!{ - {m_{33}}w}\!\!&\!\!0\!\!&\!\!{{m_{11}}u} \\ 0\!\!&\!\!0\!\!&\!\!0\!\!&\!\!{{m_{22}}v}\!\!&\!\!{ - {m_{11}}u}\!\!&\!\!0 \\ 0\!\!&\!\!{{m_{33}}w}\!\!&\!\!{ - {m_{22}}v}\!\!&\!\!0\!\!&\!\!{{m_{66}}r}\!\!&\!\!{ - {m_{55}}q} \\ { - {m_{22}}v}\!\!&\!\!0\!\!&\!\!{{m_{11}}u}\!\!&\!\!{ - {m_{66}}r}\!\!&\!\!0\!\!&\!\!{{m_{44}}p} \\ {{m_{22}}v}\!\!&\!\!{ - {m_{11}}u}\!\!&\!\!0\!\!&\!\!{{m_{55}}q}\!\!&\!\!{ - {m_{44}}p}\!\!&\!\!0 \end{array}} \!\!\!\!\right]{\text{,}} $ | (10) |
| $ \begin{split} {{D}}\left( {{v}} \right) =& {\bf{diag}}\left(\!\! {\begin{array}{*{20}{c}} {{d_u}}&{{d_v}}&{{d_w}}&{{d_p}}&{{d_q}}&{{d_r}} \end{array}}\!\! \right) + \\ &{\bf{diag}}\left( \!\!{\begin{array}{*{20}{c}} {{d_{u1}}\left| u \right|}\!\!&\!\!{{d_{v1}}\left| v \right|}\!\!\!&\!\!\!{{d_{w1}}\left| w \right|}\!\!\!&\!\!\!{{d_{p1}}\left| p \right|}\!\!\!&\!\!\!{{d_{q1}}\left| q \right|}\!\!\!&\!\!\!{{d_{r1}}\left| r \right|} \end{array}} \!\!\right) =\\ & {{{D}}_l}\left( {{v}} \right) + {{{D}}_n}\left( {{v}} \right){\text{。}}\\[-15pt] \end{split} $ | (11) |
式中:
模型的线性化方程由文献[8]给出,在给定工作点
| $ {{v}_{{e}}} = {v}\left( t \right) - {{v}_{{0}}}\left( t \right){\text{,}} $ | (12) |
| $ {f_c}\left( {{v}} \right) = {{C}}\left( {{v}} \right){{v}}\left( t \right){\text{,}} $ | (13) |
| $ {f_d}\left( {{v}} \right) = {{{D}}_l}\left( {{v}} \right){{v}}\left( t \right){\text{,}} $ | (14) |
| $ {{{K}}_d} = \left\| {{{{D}}_n}\left( {{{{v}}_{\max }}} \right)} \right\|{\text{,}} $ | (15) |
则式(9)在
| $ {{M}}{{\dot v}_{{e}}} + {\left. {\frac{{\partial {f_c}\left( {v} \right)}}{{\partial {v}}}} \right|_{{{v}_{{0}}}}}{{v}_{{e}}} + {\left. {\frac{{\partial {f_d}\left( {v} \right)}}{{\partial {v}}}} \right|_{{{v}_{{0}}}}}{{v}_{{e}}} + {{{K}}_d}{{v}_{{e}}} = {{\tau }_{{e}}}{\text{。}} $ | (16) |
令
| $ M{{\dot v}_{{e}}} + {F_c}{{v}_{{e}}} + {F_d}{{v}_{{e}}} = {{\tau }_{{e}}}{\text{,}} $ | (17) |
式中:
| $\begin{split} &{{A}}=-{{{M}}}^{-1}\left({F}_{c}+{F}_{d}\right){\text{,}}\\ &{{B}} = {{{M}}^{ - 1}}{\text{,}}\\ &{{\dot v}_{{e}}} = {{A}}{{v}_{{e}}} + {{B}}{{\tau }_{{e}}}{\text{。}} \end{split} $ | (18) |
将非线性阻尼项
| $ M{{\dot v}_{{e}}} + {F_c}{{v}_{{e}}} + {F_d}{{v}_{{e}}} + {K_d}{{v}_{{e}}} = {{\tau }_{{e}}}{\text{,}} $ | (19) |
将
| $ {{\dot v}_{{e}}} = \left( {A + \Delta A} \right){{v}_{{e}}} + B{{\tau }_{{e}}}{\text{,}} $ | (20) |
将不确定性因素考虑为加性不确定性,则不确定性系统
| $ {G}_{0}\left(s\right)=G\left(s\right)+\Delta \left(s\right){W}_{d}\left(s\right) ,{\Vert \Delta \Vert }_{\infty }\leqslant 1 {\text{。}} $ | (21) |
其中
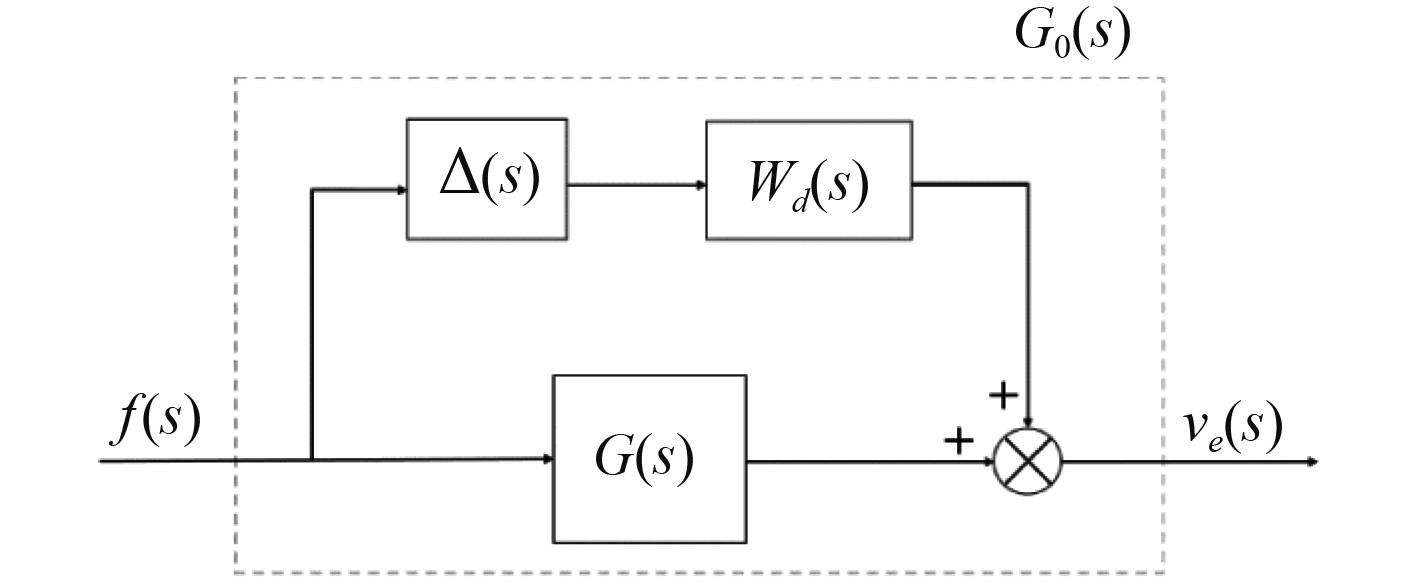
|
图 2 AUV加性摄动模型 Fig. 2 AUV additive perturbation model |
由于本系统为六自由度高阶系统,保持结果准确并且降低系统模型复杂性,可通过传递函数差值的频率响应得到满足要求的2阶加性摄动界函数
| $\left| {{G_0}\left( {j\omega } \right) - G\left( {j\omega } \right)} \right| = \left| {\Delta \left( s \right){W_d}\left( s \right)} \right| \leqslant \left| {{W_d}\left( s \right)} \right|{\text{,}}$ | (22) |
根据文献[10]中的六自由度非线性AUV模型,可得到在工作点
| $ \begin{split}&{{{F}}_c} = \\ &\left[\!\!\!\!\! {\begin{array}{*{20}{c}} 0\!\!\!\!\!&\!\!\!\!\!{ - 140.8{r_0}}\!\!\!\!\!&\!\!\!\!\!{140.8{q_0}}\!\!\!\!\!&\!\!\!\!\!0\!\!\!\!\!&\!\!\!\!\!{140.8{w_0}}\!\!\!\!\!&\!\!\!\!\!{ - 140.8{v_0}} \\ {175.4{r_0}}\!\!\!\!\!&\!\!\!\!\!0\!\!\!\!\!&\!\!\!\!\!{ - 140.8{p_0}}\!\!\!\!\!&\!\!\!\!\!{ - 140.8{w_0}}\!\!\!\!\!&\!\!\!\!\!0\!\!\!\!\!&\!\!\!\!\!{175.4{u_0}} \\ { - 175.4{q_0}}\!\!\!\!\!&\!\!\!\!\!{140.8{p_0}}\!\!\!\!\!&\!\!\!\!\!0\!\!\!\!\!&\!\!\!\!\!{140.8{v_0}}\!\!\!\!\!&\!\!\!\!\!{ - 175.4{u_0}}\!\!\!\!\!&\!\!\!\!\!0 \\ 0\!\!\!\!\!&\!\!\!\!\!0\!\!\!\!\!&\!\!\!\!\!0\!\!\!\!\!&\!\!\!\!\!0\!\!\!\!\!&\!\!\!\!\!{3.09{r_0}}\!\!\!\!\!&\!\!\!\!\!{3.09{q_0}} \\ {34.6{w_0}}\!\!\!\!\!&\!\!\!\!\!0\!\!\!\!\!&\!\!\!\!\!{34.6{u_0}}\!\!\!\!\!&\!\!\!\!\!{ - 1.99{r_0}}\!\!\!\!\!&\!\!\!\!\!0\!\!\!\!\!&\!\!\!\!\!{ - 1.99{p_0}} \\ { - 34.6{v_0}}\!\!\!\!\!&\!\!\!\!\!{ - 34.6{u_0}}\!\!\!\!\!&\!\!\!\!\!0\!\!\!\!\!&\!\!\!\!\!{ - 1.1{q_0}}\!\!\!\!\!&\!\!\!\!\!{ - 1.1{p_0}}\!\!\!\!\!&\!\!\!\!\!0 \end{array}} \!\!\!\!\!\right]{\text{,}} \end{split}$ | (23) |
| $ {{{F}}}_{d}=\left[\begin{array}{cccccc}120& 0& 0& 0& 0& 0\\ 0& 90& 0& 0& 0& 0\\ 0& 0& 150& 0& 0& 0\\ 0& 0& 0& 15& 0& 0\\ 0& 0& 0& 0& 15& 0\\ 0& 0& 0& 0& 0& 18\end{array}\right] {\text{。}} $ | (24) |
为不失一般性,在
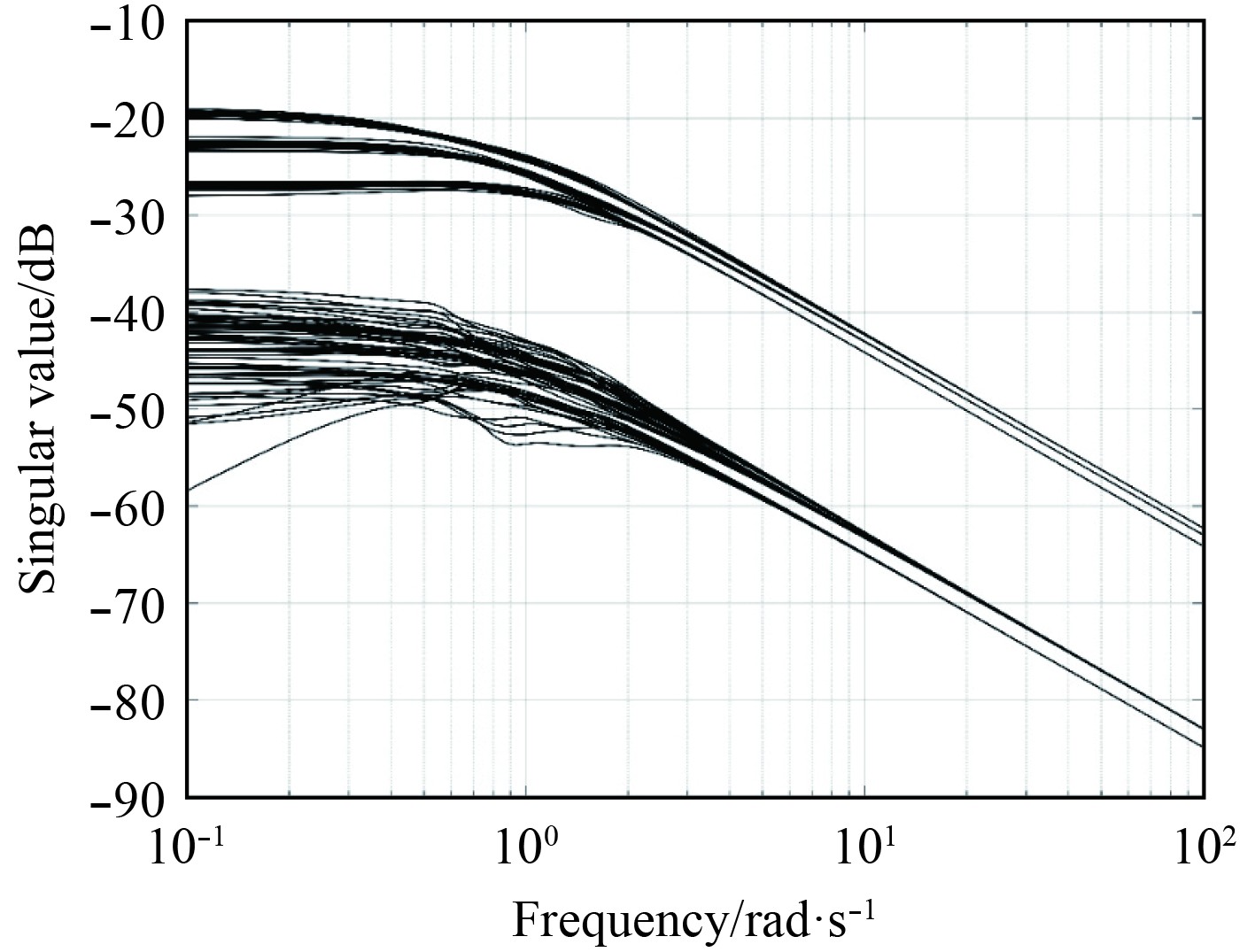
|
图 3 六自由度AUV不确定性系统奇异值 Fig. 3 Singular values of the six-DOF AUV uncertainty system |
本文采用回路成形设计方法得到六自由度AUV不确定性模型H∞控制器,设计时采用经典的闭环控制结构如图4所示。其中r为参考输入,d与n分别是输出扰动与传感器噪声,y为系统输出。
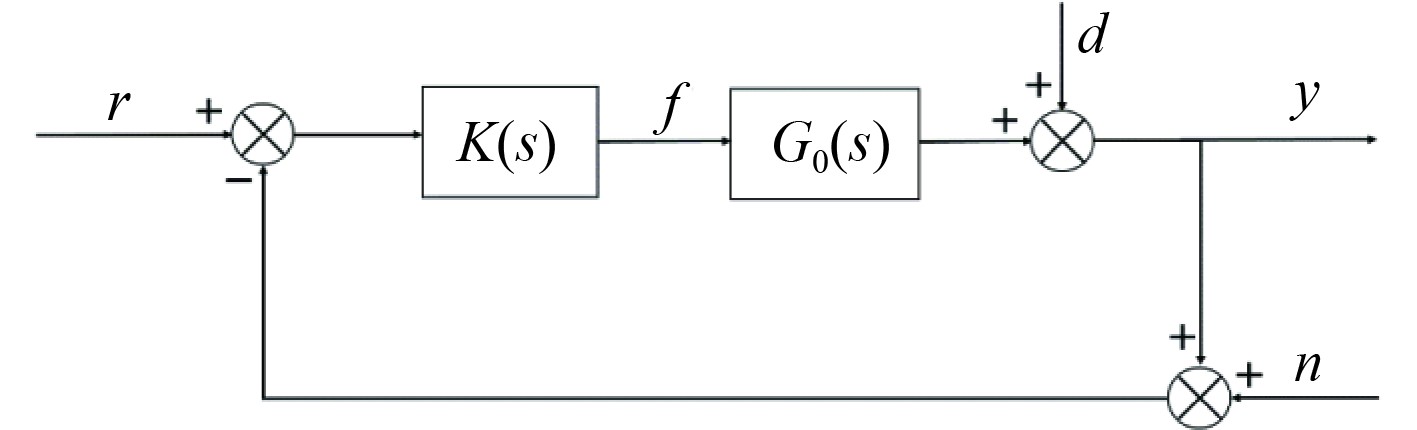
|
图 4 闭环控制结构图 Fig. 4 The closed-loop control structure |
开环传递传递函数
| $ y\left( s \right) = T\left( s \right)r\left( s \right) + S\left( s \right)d\left( s \right) - T\left( s \right)n\left( s \right) {\text{。}} $ | (25) |
得到的控制器
1)若系统有较强的抗干扰能力,应当使
2)若系统具有较强的噪声消除能力,应当使
3)若系统具有较强的信号跟踪能力,应当使
其中
1)在低频段范围使
2)在高频段范围使
满足条件的控制器由如下定理[13]确定:
定理 设
| $ \xi = \left\{ {\left. {\begin{array}{*{20}{c}} {C = \dfrac{{X + MQ}}{{Y - NQ}}} \end{array}} \right|Q \in \zeta } \right\}{\text{。}} $ |
其中
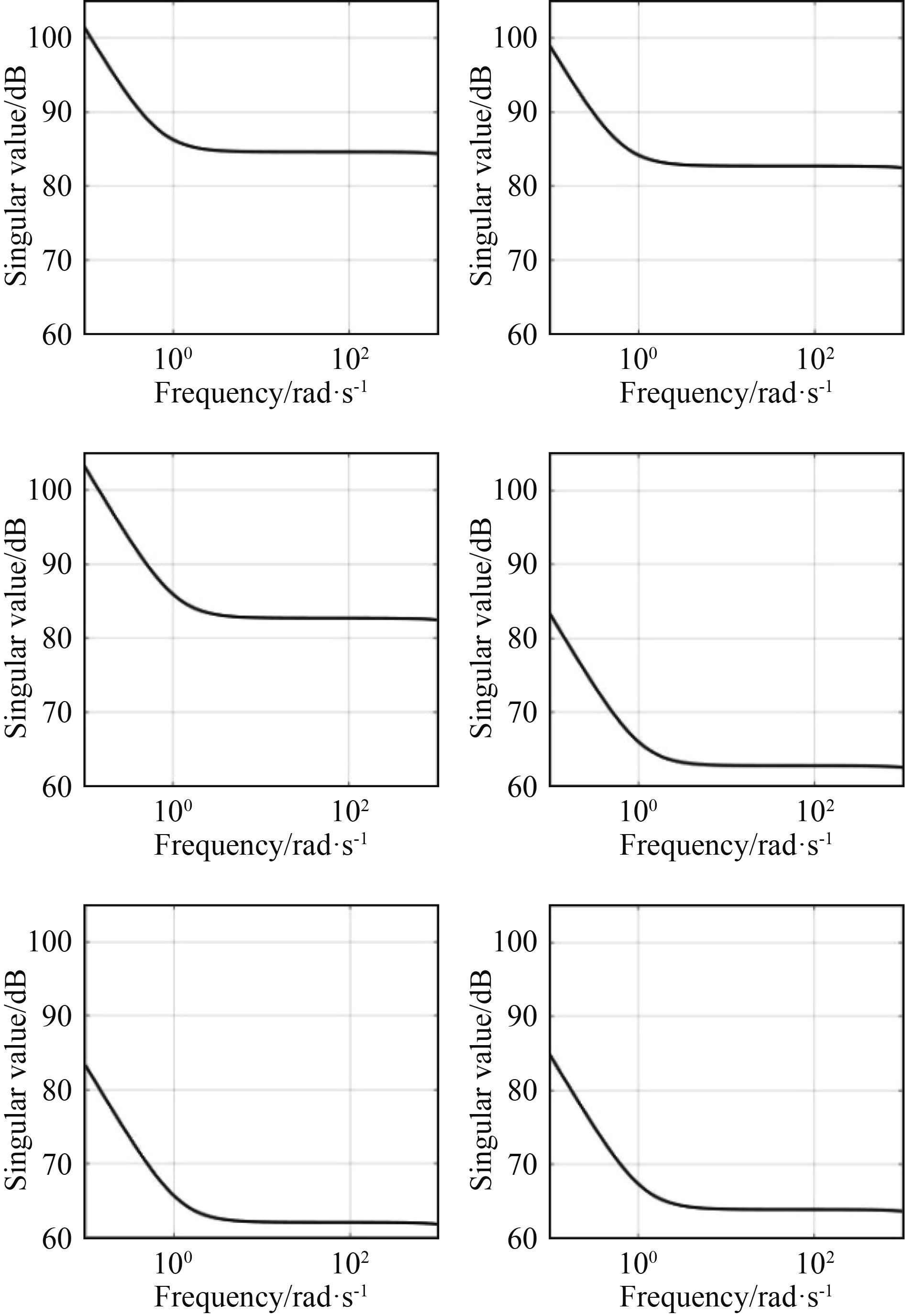
本文计算得到的控制器用于在
|
图 5 给定工作点处六自由度鲁棒控制器奇异值曲线 Fig. 5 The singular value curve of the 6-DOF robust controller at a given operating point |
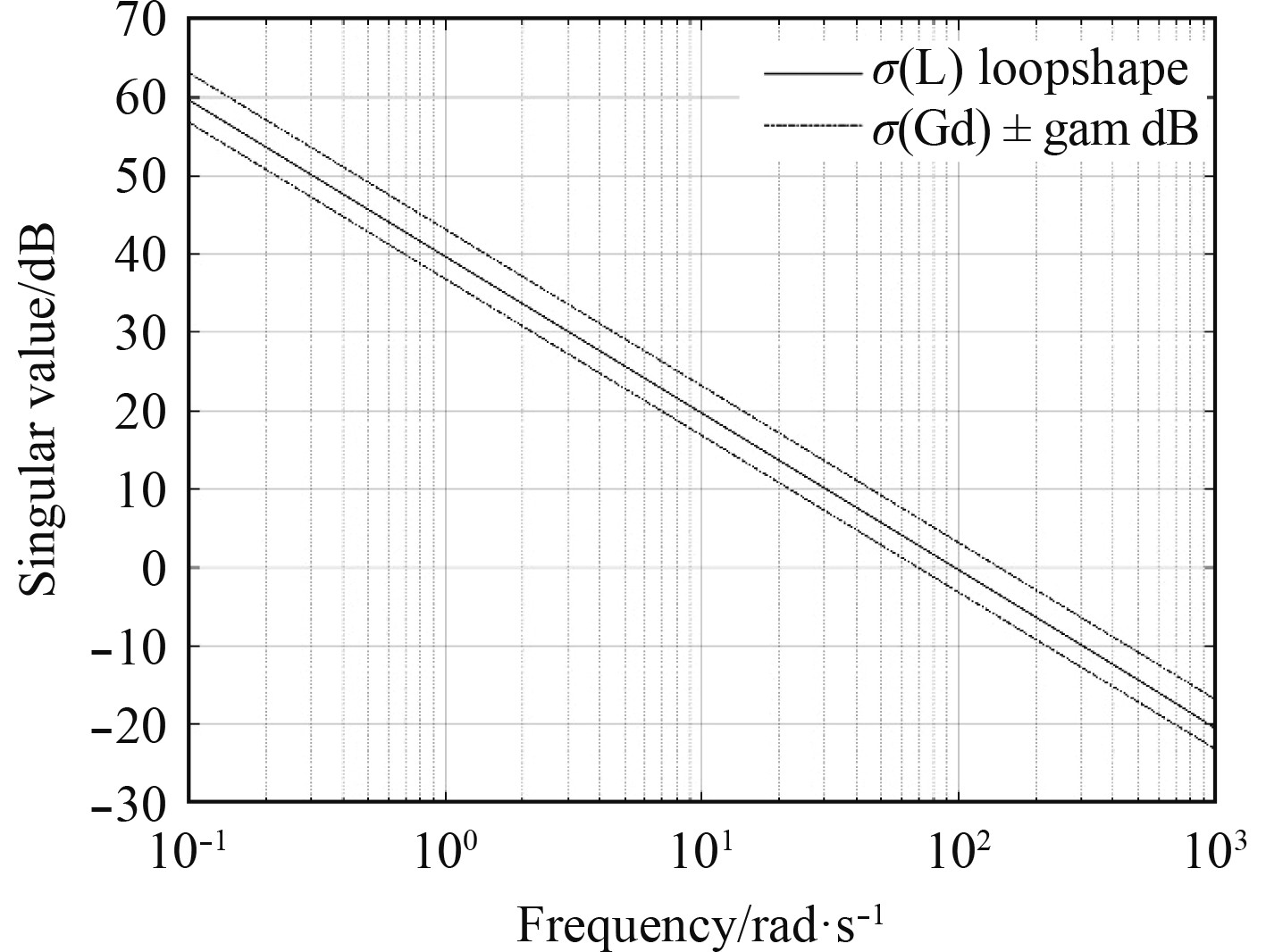
|
图 6 开环传递函数奇异值曲线 Fig. 6 Singular value curve of the open-loop transfer function |
将控制器作用于给定工作点
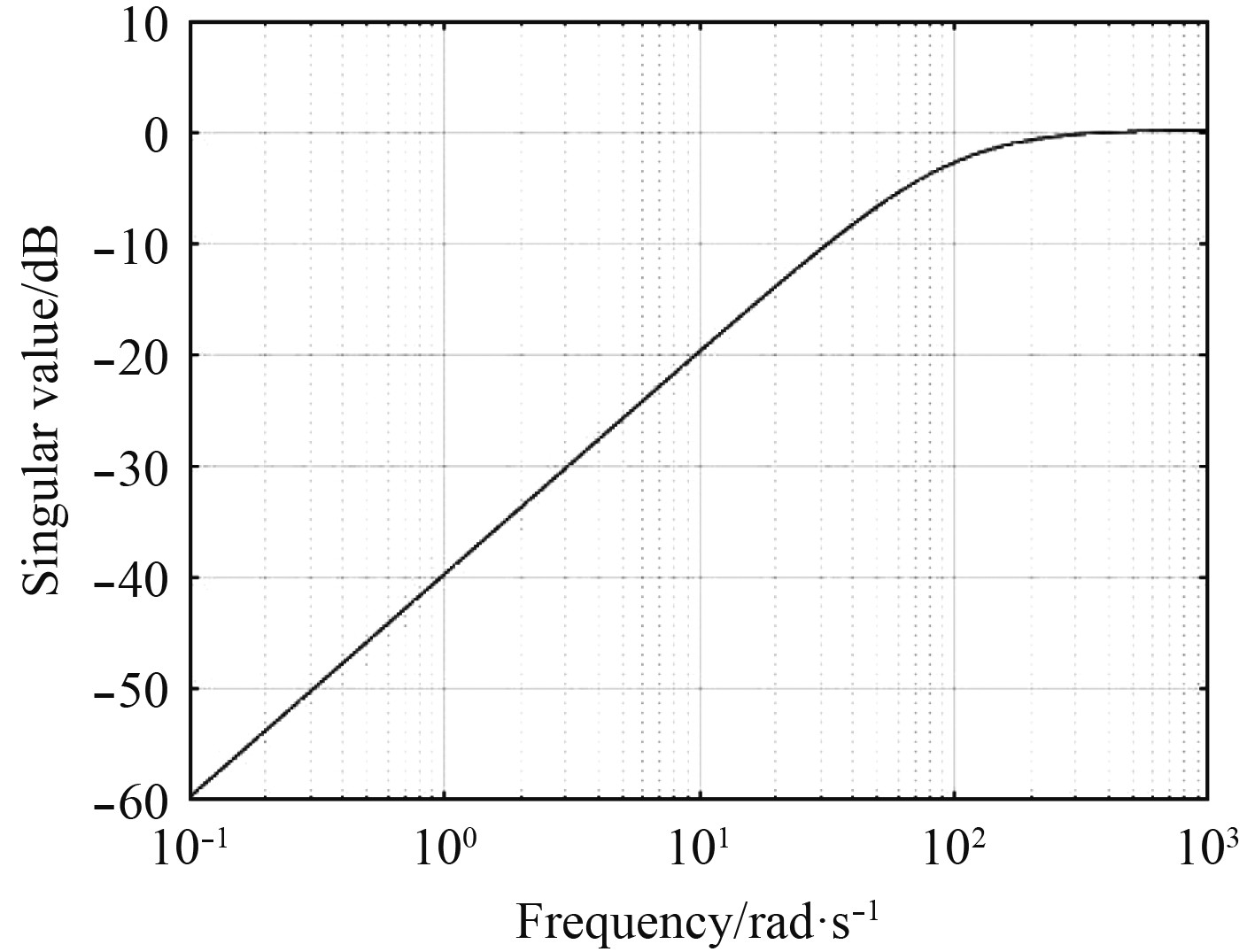
|
图 7 闭环系统的敏感函数曲线 Fig. 7 Sensitivity function curve of the closed-loop system |
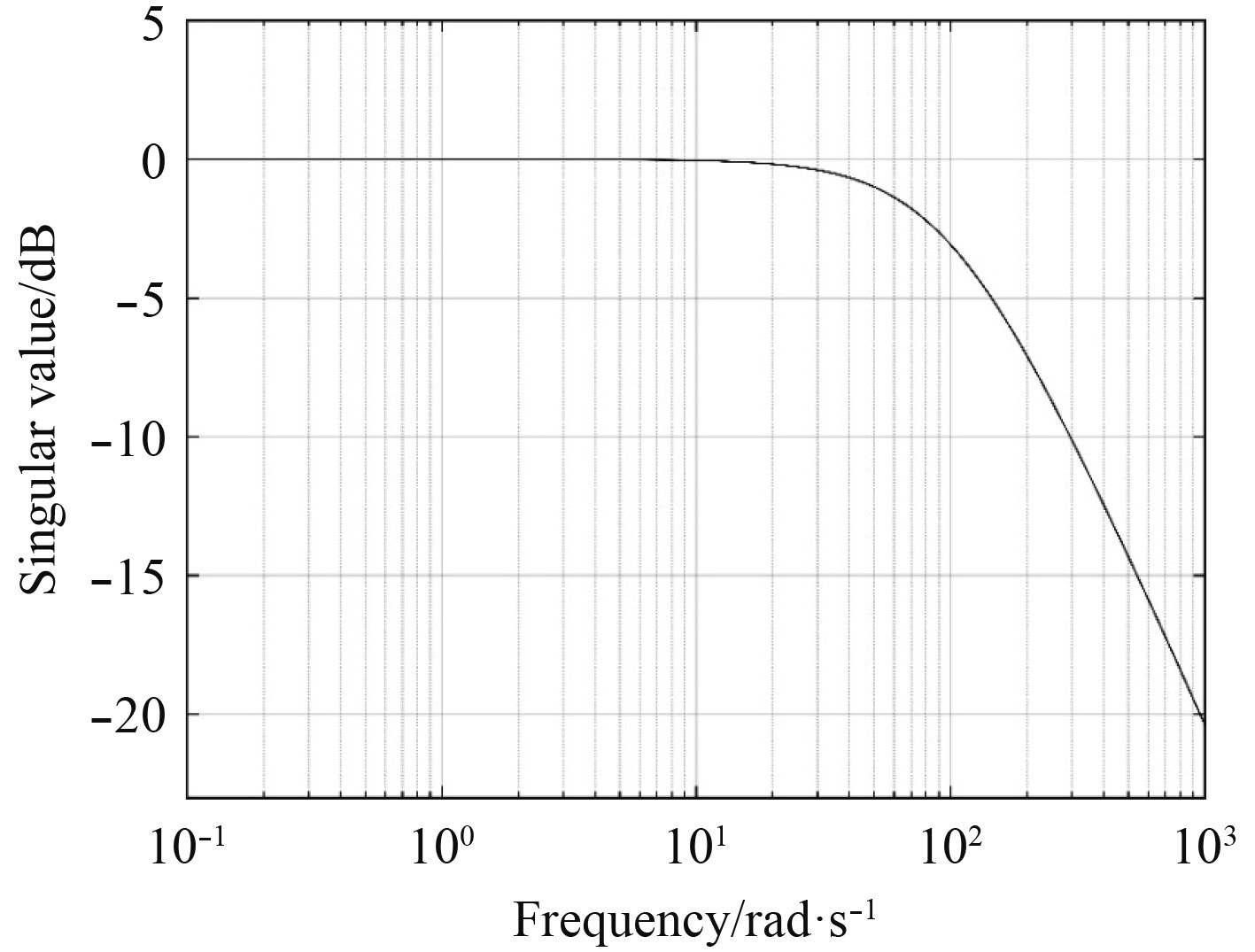
|
图 8 闭环系统的补敏感函数曲线 Fig. 8 Complementary sensitivity function curve of the closed-loop system |
图9~图11给出了闭环系统在工作点
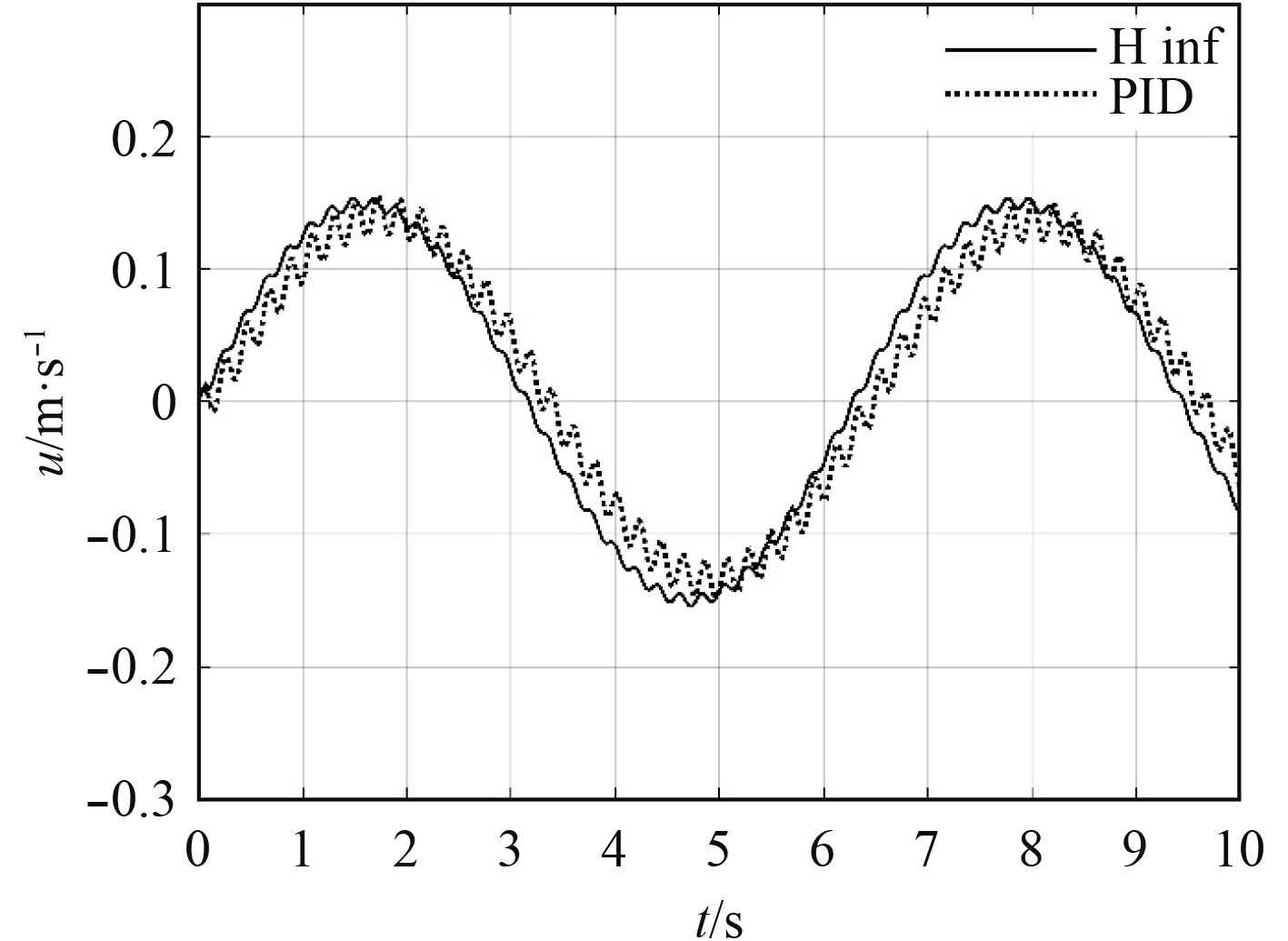
|
图 9 u方向对比响应曲线 Fig. 9 Response curve in u direction |
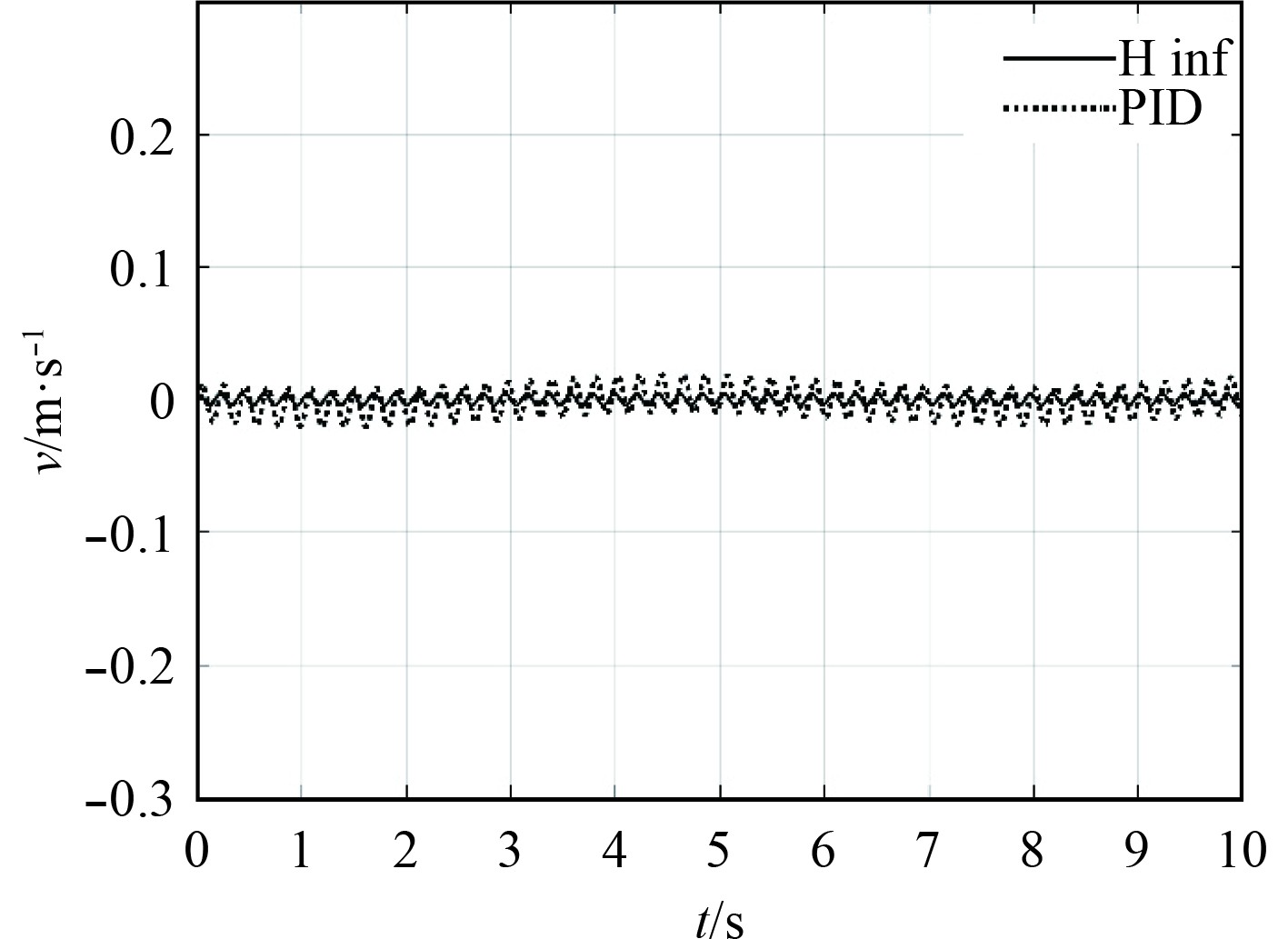
|
图 10 v方向对比响应响应曲线 Fig. 10 Response curve in v direction |
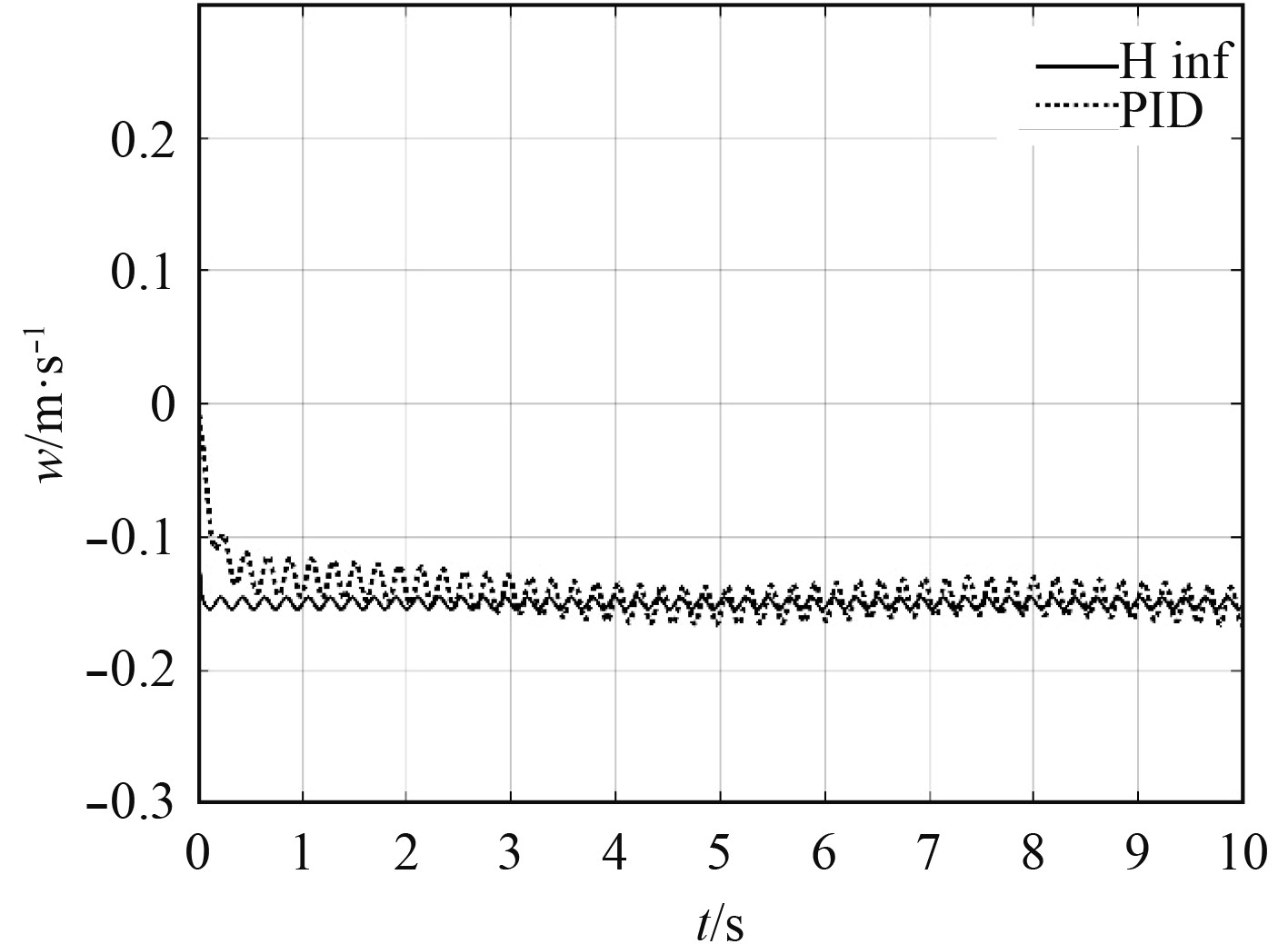
|
图 11 w方向对比响应响应曲线 Fig. 11 Response curve in w direction |
本文通过对自由度间相互耦合、强非线性的AUV模型在工作点附近进行了线性化,给出了该线性化模型的操作过程及结果,并据此建立了适合应用鲁棒控制方法的加性不确定性模型。使用回路成形方法得到了对应工作点的鲁棒控制器,对闭环系统的仿真试验取得了良好的控制效果,验证了回路成形方法设计的鲁棒控制器在多自由度AUV系统中使用的有效性,未来可以针对多个工作点的鲁棒控制器连续工作做进一步的研究。
| [1] |
边宇枢, 高志慧, 贠超. 6自由度水下机器人动力学分析与运动控制[J]. 机械工程学报, 2007(7): 87-92. DOI:10.3321/j.issn:0577-6686.2007.07.016 |
| [2] |
常涛, 张永林. 基于改进GA优化的水下机器人航向鲁棒控制[J]. 船舶工程, 2015, 37(9): 68-71. |
| [3] |
杨清, 宿浩, 唐功友, 等. 不确定AUV系统的鲁棒最优滑模控制[J]. 信息与控制, 2018, 47(2): 176-183. |
| [4] |
蒋云彪, 郭晨, 于浩淼. 自主水下航行器的鲁棒自适应姿态控制算法[J]. 计算机工程与应用, 2019, 55(17): 266-270. DOI:10.3778/j.issn.1002-8331.1804-0341 |
| [5] |
刘旌扬, 冯正平, 易宏, 等. 水下机器人H∞控制系统设计
[J]. 海洋工程, 2008, 26(3): 70-77. DOI:10.3969/j.issn.1005-9865.2008.03.012 |
| [6] |
熊华胜, 边信黔, 施小成. 自治水下机器人深度的鲁棒H_∞控制仿真[J]. 计算机仿真, 2007(3): 156-159. DOI:10.3969/j.issn.1006-9348.2007.03.042 |
| [7] |
CLEMENT B, Yang RUI, MANSOUR A, et al. A Modeling and Control approach for a cubic AUV[J]. IFAC PapersOnLine, 2016, 49(23): 279-284. DOI:10.1016/j.ifacol.2016.10.355 |
| [8] |
JUAN C. Cutipa-Luque, Décio Crisol Donha, João L. Dozzi Dantas, et al.. Robust control of an underactuated AUV[J]. IFAC Proceedings Volumes, 2012, 45(27): 138-143. DOI:10.3182/20120919-3-IT-2046.00024 |
| [9] |
Wei ZHANG, Yanbin TENG, Shilin WEI, et al. The robust H-infinity control of UUV with Riccati equation solution interpolation[J]. Ocean Engineering, 2018, 156: 252-262. DOI:10.1016/j.oceaneng.2018.02.004 |
| [10] |
LIU Shuyong, WANG Danwei, POH Engkee. Output feedback control design for station keeping of AUVs under shallow water wave disturbances[J]. International Journal of Robust and Nonlinear Control, 2009, 19: 1447-1470. DOI:10.1002/rnc.1387 |
| [11] |
THOR I. FOSSEN. Guidance and control of ocean vehicles. Wiley, 1994: 90 – 101.
|
| [12] |
ZHOU K M, DOYLE J C, GLOVER K. Robust and optimal control[M]. New Jersey: Prentice Hall, 1996.
|
| [13] |
苏宏业, 等. 鲁棒控制基础理论. 北京: 科学出版社, 2010: 63−69.
|
 2020, Vol. 42
2020, Vol. 42
