近几年自主水下航行器(AUV)在水下探测、作业领域扮演了越来越重要的作用,如水下巡查、海洋油气勘探、水下设备检修等。全驱动AUV在水下可以实现动力定位、控制灵活,因此在海洋工程领域得到了大量的应用。六自由度AUV是全驱动AUV常用的类型,其弹道跟踪是水下保持自主航行控制的一个关键问题,尤其是存在水下环境干扰以及AUV模型的不确定性时,控制系统在6-DOF的AUV弹道跟踪中面临着相当大的挑战。
预设性能控制是指将跟踪误差收敛到一个预先设定的一个任意小的区域内,同时在这个过程中可以保证一个较快的收敛速度以及可控的超调量满足预先设定的条件,同时满足瞬态性能以及稳定性的要求。文献[1]首次提出预设性能控制,阐述了预设性能控制的基本原理,证明了预设性能控制的稳定性及收敛性。文献[2-3]研究了欠驱动的AUV的三维路径跟踪问题。在没有任何AUV模型参数的先验知识情况下,设计了平滑控制方案,在洋流和波浪的外部干扰下也能保证预设性能跟踪。其控制特色在于控制方案中仅采用期望的轨迹而不使用其高阶导数,此外,在不将相应的测量值结合到控制信号中的情况下确保了欠驱动自由度的稳定性,从而简化了实现并提高了对测量噪声的鲁棒性。预设性能控制由于其优异的性能被广泛应用于各类航行器控制中[6-8]。
文献[9]介绍了滑模控制(SMC)是处理具有不确定性、扰动和有界外部干扰的非线性系统最有效方法之一。这主要是由于其对系统不确定性和外部干扰的强大鲁棒性。由于上述优点,SMC已被广泛应用于水下航行器的轨迹跟踪控制问题。文献[10]将滑模控制应用于航行器的路径追踪,然而这些SMC方法是基于线性滑模(LSM)设计的,它只能保证由于LSM的渐近收敛,无法获得有限时间误差收敛。
文献[11]提出的终端SMC(TSMC)旨在实现系统的有限时间收敛。终端滑模(TSM)是跟踪误差及其导数的非线性函数,可以实现有限时间收敛。与传统的SMC相比,TSMC可以提供更快的收敛速度、更好的干扰抑制能力和更好的抗不确定性的鲁棒性。然而,TSMC的主要缺点是它存在奇点问题。为了解决TSMC的奇异性问题,文献[12]提出了一些非奇异TSMC(NTSMC)方法,即通过结合新的非奇异TSM(NTSM)和不连续的达到定律,完全避免了奇点问题。
本文提出一种基于预设性能函数的用于AUV 六自由度路径跟踪控制。将预设性能控制与有限时间收敛的非奇异终端滑模控制结合起来,利用预设性能控制的瞬态性能以及稳定性能优势以及终端滑模的快速收敛性,实现了在AUV路径跟踪中快速的收敛速度,增强了干扰抑制能力和提升了抗不确定性的鲁棒性。
1 AUV动力学模型全驱动AUV在惯性坐标体系下运动学和动力学模型如下式:
| $\left\{ {\begin{array}{*{20}{l}} {\dot \eta = {{J}}(\eta )v} {\text{,}}\\ {{{M}}(v)\dot v{{C}}(v)v + {{D}}(v)v + g(\eta ) = \tau {\rm{ + }}{\tau _E}} {\text{。}} \end{array}} \right.$ | (1) |
其中:
有水流扰动下水下航行器的运动学模型为:
| $\dot \eta = {{J}}(\eta ){v_r}{\rm{ + }}{\nu _f}{\text{。}}$ | (2) |
式中:
假设1:水流速度是有界且慢变的,
假设2:
假设3:航行器未建模的变量为
控制系统的性能指标通常包括瞬态性能和稳态性能。目前在非线性控制领域,研究的成果主要侧重于系统稳态性能,对于系统控制中的瞬态性能研究不多。近年来,随着科技的不断发展,控制对象要求精度高、实时性强,因此对系统瞬态性能的研究逐渐受到研究者的关注,正是在这种背景下,预设性能控制应运而生,其为解决性能控制问题提供了一种全新的思路。希腊学者Bechlioulis于2008年首次提出了预设性能控制的概念,预设性能要求跟踪误差收敛到一个预先设定的任意小的区域内。同时,收敛速度和超调量满足预先设定的条件。由于这种方法是直接以提高系统的性能为目标,兼顾了稳态性能和瞬态性能。
传统的预设性能函数由文献[1]表述:
| $\rho = \left( {{\rho _0} - {\rho _\infty }} \right){e^{ - lt}} + {\rho _\infty }{\text{,}}$ | (3) |
变换后误差的上下限表示为:
| $ - \delta \rho (t) < e(t) < \rho (t){\text{,}} {\rm{ if }}\quad e(0) > 0{\text{,}}$ | (4) |
| $ - \rho (t) < e(t) < \delta \rho (t){\text{,}} {\rm{ if }}\quad e(0) < 0{\text{。}}$ | (5) |
其中:
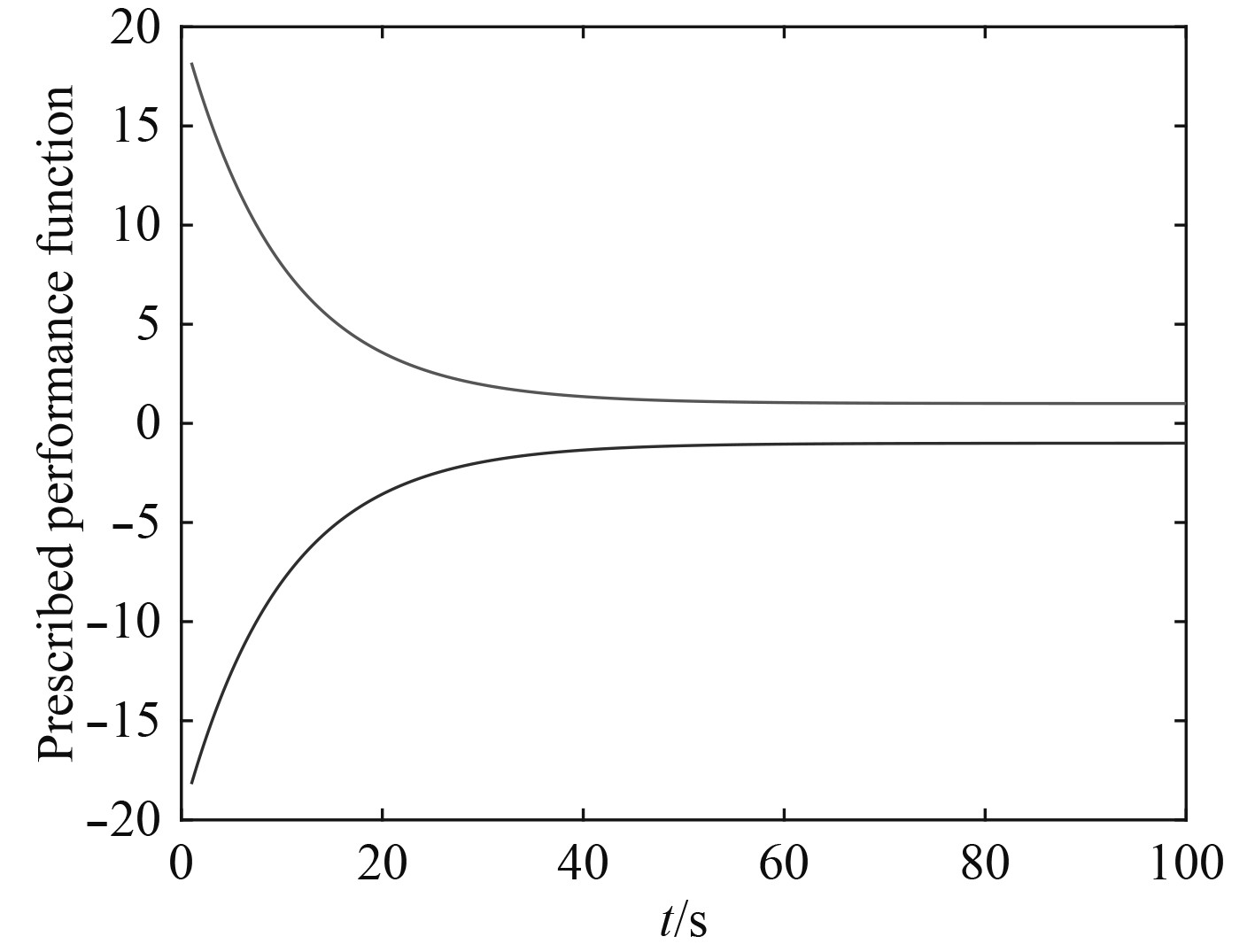
|
图 1 预设性能函数的模型示意 Fig. 1 The model of prescribed performance function |
| $e(t) = \rho (t)S(\varepsilon ){\text{,}}$ | (6) |
将式(6)变换得到:
| $S(\varepsilon ) = \frac{{\bar M{e^s} - M{e^{ - \varepsilon }}}}{{{e^\varepsilon } + {e^{ - \varepsilon }}}}{\text{,}}$ | (7) |
预设性能控制误差函数为:
| $\varepsilon = {S^{ - 1}}\left( {\frac{{e(t)}}{{\rho (t)}}} \right) = T\left( {\frac{{e(t)}}{{\rho (t)}}} \right) = \frac{1}{2}\ln \frac{{e/\rho + M}}{{\bar M - e/\rho }}{\text{。}}$ | (8) |
快速Terminal滑模控制可使系统状态在有限时间内收敛为0,突破了普通滑模控制在线性滑模面条件下状态渐近收敛的特点。系统的动态性能优于普通滑模控制相对于线性滑模控制。Terminal滑模控制无切换项可有效地消除抖振,快速Terminal滑模控制为滑动模态控制理论带来了新的发展方向。为了解决普通Terminal滑模控制的奇异问题,文献[12]提出了非奇异下Terminal滑模控制方法,该方法可很好地解决控制奇异问题。
利用有限时间收敛的非奇异终端滑模控制方法:
| $ s={e}+\beta {\dot {\left(e\right)}}_{}^{q/p}{\text{,}}$ | (9) |
其中
预设性能与终端滑模结合,给出控制率,模型中加入AUV未建模动力学模型以及定常的水流干扰。预设性能控制将滑模控制中的误差变化量
| $z = \ln \left( {\frac{{\dfrac{s}{\rho } - {m_{\min }}}}{{{m_{\max }} - \dfrac{s}{\rho }}}} \right){\text{。}}$ | (10) |
设计控制函数为:
| $ \tau ={{J}}^{-1}{{M}}\left(w+\ddot {{\eta }_{d}}-\dot {J}{\nu }_{r}\right)+{{C}}{\nu }_{r}+{{D}}{\nu }_{r}+g{\text{,}}$ | (11) |
其中,
| $ w=\frac{q\beta \left(\dot {s}-\dot {e}\right)}{p{(\dot {e})}^{\left(\frac{p-q}{q}\right)}}{\text{,}}$ | (12) |
| $ \dot {s}=\frac{-kz}{{z}_{c}\rho }{\left({m}_{\max}\rho -s\right)}^{2}+\dot {\frac{\rho s}{\rho }}{\text{,}}$ | (13) |
| ${z_c} = \left( {{m_{\max }} - {m_{\min }}} \right)/\left( {s/\rho - {m_{\min }}} \right)/\left( {{m_{\max }} - s/\rho } \right){\text{。}}$ | (14) |
预设性能控制要求设计的趋近律能使系统在任意初始状态下到达滑模面。基于Lyapunov稳定性理论,对式(10)稳定性进行证明。
设误差的能量函数为:
| $v = \frac{1}{2}{z^2}{\text{,}}$ | (15) |
误差的能量函数的导数表示为:
| $ \dot {v}=z\dot {z}{\text{,}}$ | (16) |
利用式(16)对
| $ \dot {z}=\frac{\dot {s}-{m}_{\max}\dot {\rho }}{s-{m}_{\max}\rho }-\frac{{m}_{\min}\dot {\rho }-\dot {s}}{{m}_{\min}\rho -s}{\text{,}}$ | (17) |
其中,
| $ \dot {s}=\dot {e}+\frac{p}{\beta q}\dot {e}\ddot {e}{\text{,}}$ | (18) |
其中,
| $ \ddot {e}=\ddot {\eta }-\ddot {{\eta }_{d}}=\dot {J}{\nu }_{r}+J\dot {{\nu }_{r}}+\dot {{\nu }_{f}}{\text{。}}$ | (19) |
将式(19)中的控制输出
| $ \dot {z}=-kz+{T}_{w}{\text{。}}$ | (20) |
其中,
| $\begin{split} {T}_{w}=&\left(\frac{p}{\beta q}{\dot {e}}^{\left(\frac{p}{q}-1\right)}\left(\dot {{\nu }_{f}}+J{M}^{\rm{-}1}{\tau }_{u}\right)\right)\times \\&\frac{{\left({m}_{\max}-{m}_{\min}\right)}^{2}}{\left(\frac{s}{\rho }-{m}_{\min}\right)\left({m}_{\max}-\frac{s}{\rho }\right)}{\text{。}}\end{split}$ | (21) |
因为存在假设1以及假设3,所以得到下式:
| $ \dot {{\nu }_{f}}+J{M}^{\rm{-}1}{\tau }_{u}\approx 0{\text{,}}$ | (22) |
| $ \dot {v}=z\dot {z}=-k{z}^{2} \leqslant 0{\text{。}}$ | (23) |
因此系统是渐进稳定的。
4 仿真模拟跟踪路径设计为:
| $\left\{ {\begin{array}{*{20}{c}} {x = Acos\left( {t/100} \right)}{\text{,}} \\ {y = Asin\left( {t/100} \right)} {\text{,}}\\ {z = - 100 + 0.04t}{\text{,}} \\ {\phi = 0}{\text{,}} \\ {\theta = 0} {\text{,}}\\ {\psi = pi/2 + 0.01t} {\text{。}} \end{array}} \right.$ | (24) |
航行器参数为:
| ${M_{RB}} = {\rm{diag}}\left\{ {\begin{array}{*{20}{c}} {117}&{117}&{117}&{10.7}&{11.8}&{13.4} \end{array}} \right\}{\text{,}}$ | (25) |
| ${M_{AM}} = {\rm{diag}}\left\{ {\begin{array}{*{20}{c}} {58.4}&{23.8}&{23.8}&{3.38}&{1.18}&{2.67} \end{array}} \right\}{\text{,}}$ | (26) |
| $D\left( \nu \right) = {\rm{diag}}\left\{ {\begin{array}{*{20}{l}} {120 + 90\left| u \right|}&{90 + 90\left| \upsilon \right|}&{150 + 120\left| w \right|}&\\{15 + 10\left| p \right|}& {15 + 12\left| q \right|}&{18 + 15\left| r \right|} \end{array}} \right\}{\text{。}}$ | (27) |
AUV质量为117 kg,浮力为1158 N;重心与浮心位置相同,浮心位置为
AUV系统未建模部分:
| $\left\{ {\begin{array}{*{20}{c}} {{t_{u1}}{\rm{ = }}1.2{\rm{ + }}0.3cos\left( {t/50} \right)} {\text{,}}\\ {{t_{u2}} = - 1.8{\rm{ + }}0.32cos\left( {t/50} \right)} {\text{,}}\\ {{t_{u3}} = 2.2 - 0.5cos\left( {t/50} \right)} {\text{,}}\\ {{t_{u4}} = - 0.1{\rm{ + }}0.2cos\left( {t/50} \right)} {\text{,}}\\ {{t_{u5}} = 0.2 - 0.2cos\left( {t/50} \right)} {\text{,}}\\ {{t_{u6}} = - 0.3{\rm{ + }}0.2cos\left( {t/50} \right)} {\text{。}} \end{array}} \right.$ | (28) |
定常水流速度:
| $\left\{ {\begin{array}{*{20}{c}} {{v_{f1}} = 0.1 + {\theta _1}} {\text{,}}\\ {{v_{f2}} = 0.2 + {\theta _2}} {\text{,}}\\ {{v_{f3}} = 0} {\text{,}}\\ {{v_{f4}} = 0} {\text{,}}\\ {{v_{f5}} = 0} {\text{,}}\\ {{v_{f6}} = 0} {\text{。}} \end{array}} \right.$ | (29) |
其中
AUV初始位置与速度设置为:
终端滑模函数的参数为:
图2为PPFNTSM算法跟踪路径的效果图,其中线1为AUV运动轨迹,线2为跟踪路径。
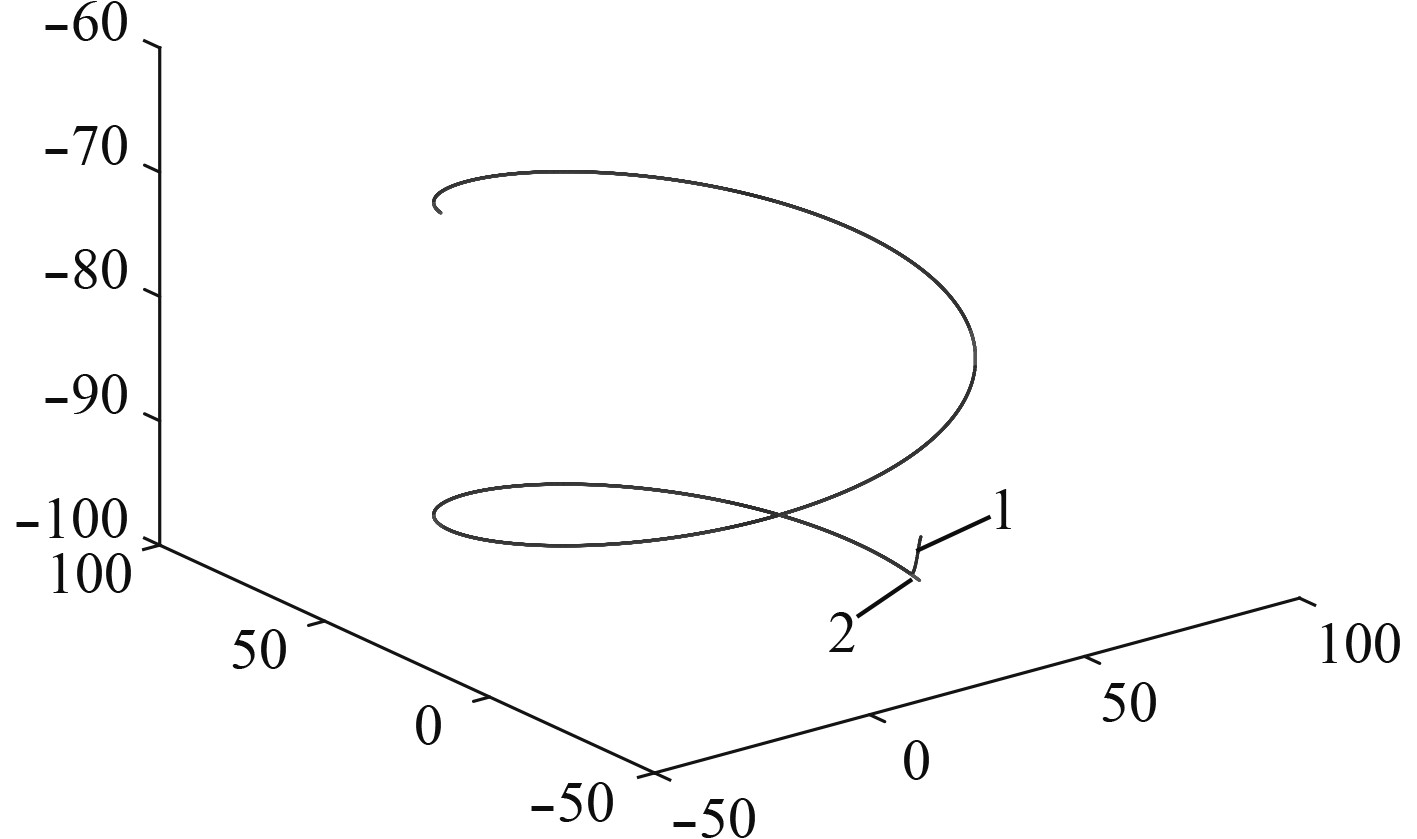
|
图 2 AUV运动轨迹及跟踪路径 Fig. 2 The AUV trajectory tracking |
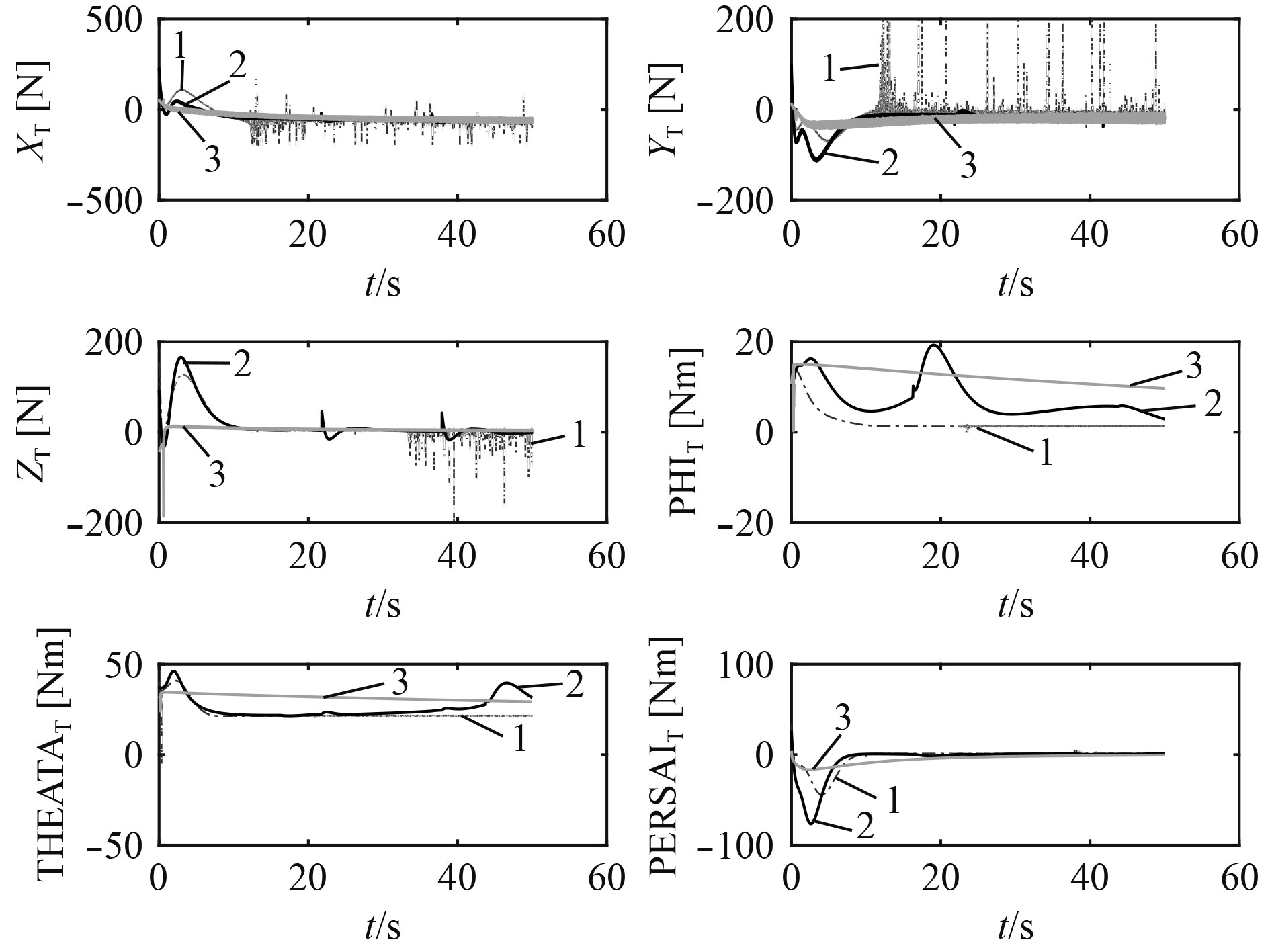
图3~图6为4种算法用于AUV控制的对比仿真,线1为预设性能与非奇异终端滑模结合控制(PPFNTSM),线2为预设性能与线性滑模结合控制(PPFSM),线3为非奇异终端滑模控制(NTSM)。
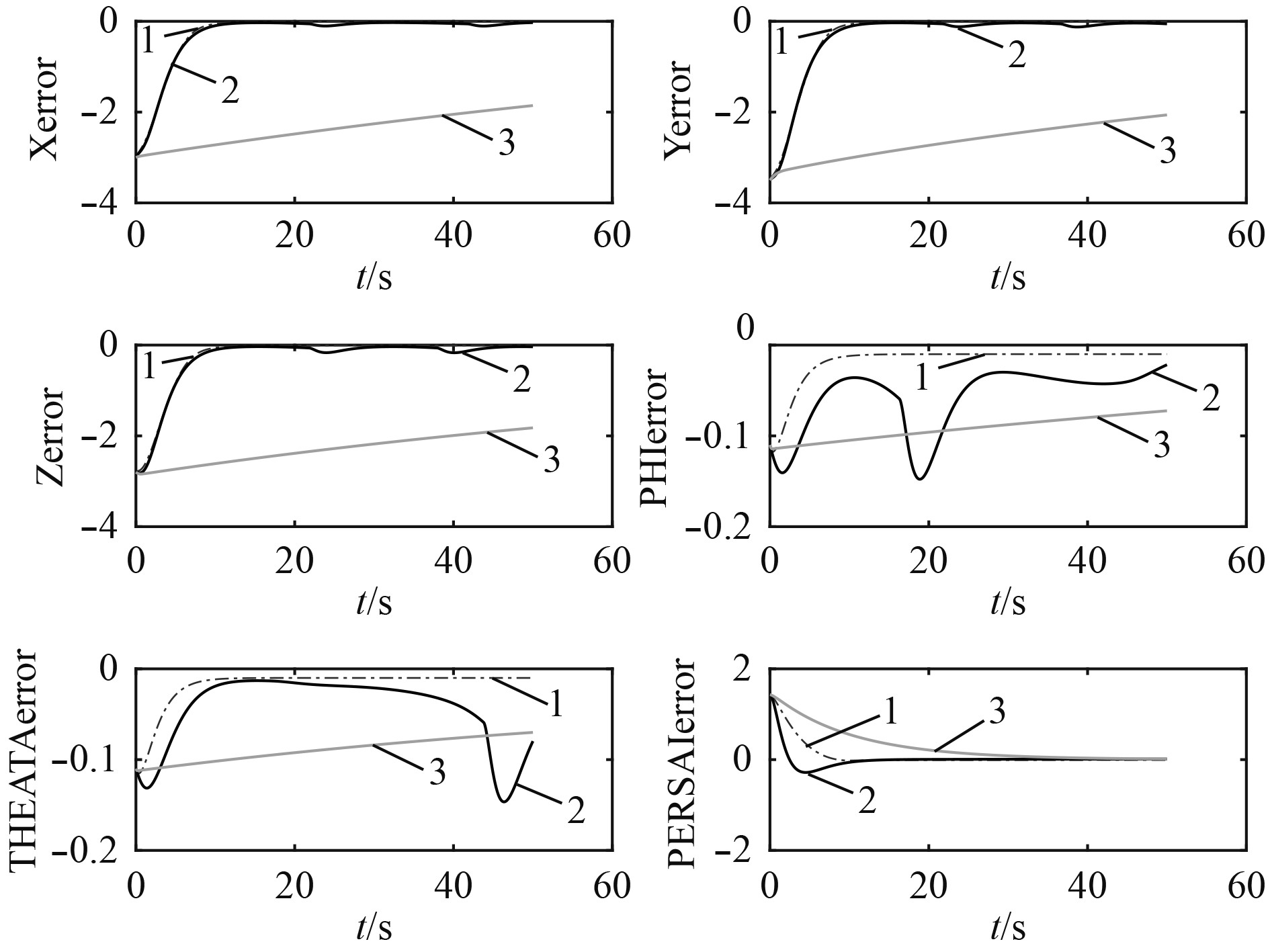
|
图 3 50 s位置误差收敛对比 Fig. 3 Comparison of 50s position error convergence |
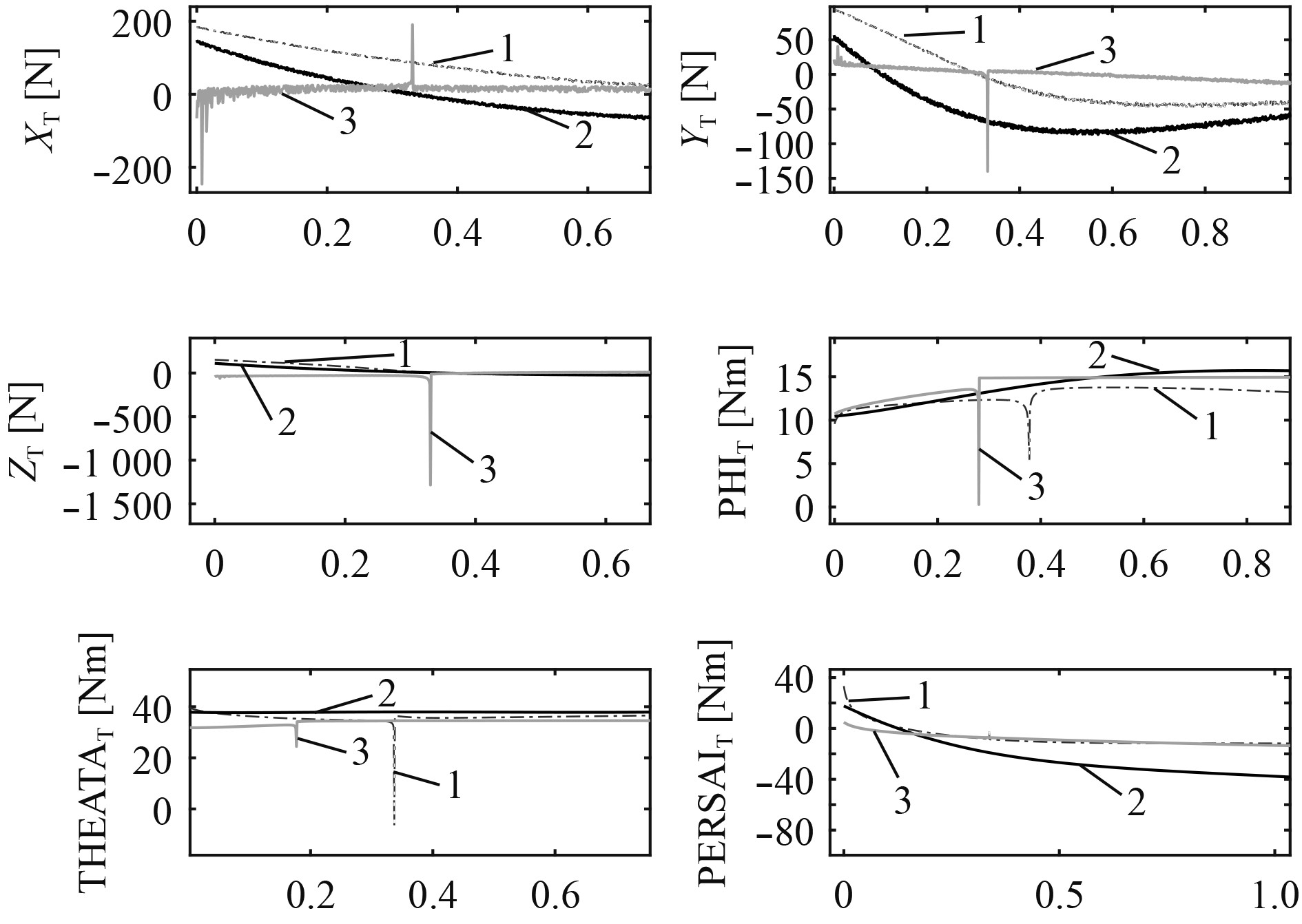
|
图 6 控制起始段推力输出对比 Fig. 6 Comparison of control thrust output in initial stage |
图3为3种算法的位置误差收敛图。在同样的反馈函数下,采用预设性能算法的收敛速度明显高于非奇异终端滑模控制,实现了快速控制。
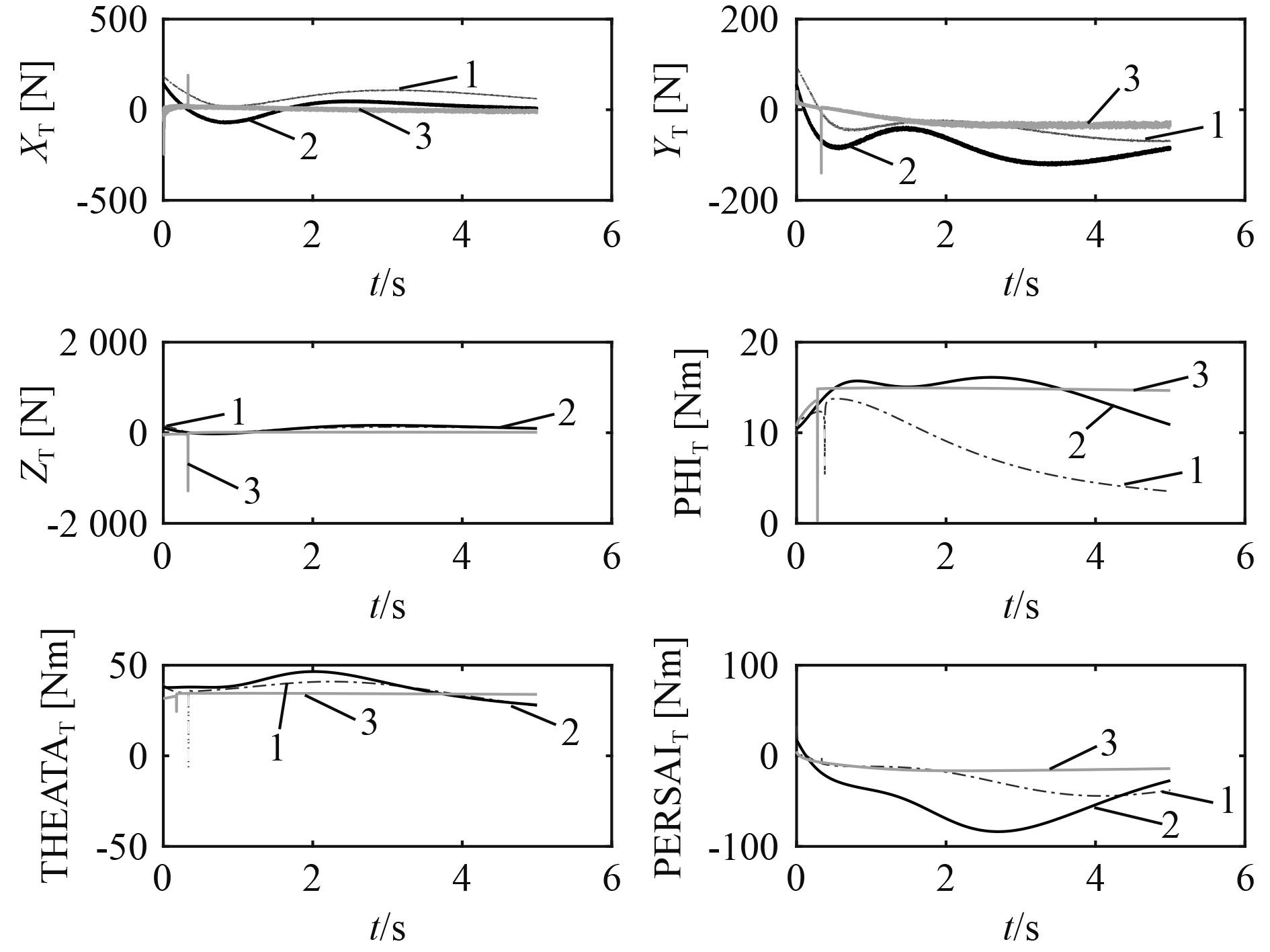
图4~图6为3种算法的控制推进器输出图。由图4可以看出,NTSM由于收敛速度最低,所以NTSM算法控制力输出很低。在控制的后期,由于水流的存在,NTSM算法的鲁棒性较差,产生了较大的推力波动。PPFSM算法的控制力波动最大,尤其是在控制初期产生了较大的超调以及控制方向的切换,在实际AUV控制过程中会产生很大的困难。PPFNTSM算法控制收敛速度最快,也最为平稳。
|
图 4 50 s控制推力输出对比 Fig. 4 Comparison of 50s thrust output |
|
图 5 5 s控制推力输出对比 Fig. 5 Comparison of 5s thrust output |
本文研究全驱动水下航行器的六维轨迹跟踪控制问题。将新型预设性能控制与有限时间收敛的非奇异终端滑模控制相结合,用于控制有海流扰动以及有未建模部分的航行器。利用预设性能控制提高了轨迹跟踪中的误差收敛速度,增加了控制系统鲁棒性。通过理论分析证明了系统的稳定性,再利用理论分析和数值模拟,验证了该控制算法的有效性。
| [1] |
BECHLIOULIS, C.P., ROVITHAKIS G.A... Robust adaptive control of feedback linearizable MIMO nonlinear systems with prescribed performance[J]. IEEE Transactions on Automatic Control, 2008, 53(9): 2090-2099. DOI:10.1109/TAC.2008.929402 |
| [2] |
BECHLIOULIS, C.P., K.J. KYRIAKOPOULOS. Robust prescribed performance tracking control for unknown underactuated torpedo-like AUVs[C]//2013 European Control Conference (ECC). 2013. IEEE.
|
| [3] |
BECHLIOULIS, C.P., et al.. Trajectory tracking with prescribed performance for underactuated underwater vehicles under model uncertainties and external disturbances[J]. IEEE Transactions on Control Systems Technology, 2017, 25(2): 429-440. DOI:10.1109/TCST.2016.2555247 |
| [4] |
HENG, L., et al.. Prescribed performance synchronization for fractional-order chaotic systems[J]. Chinese Physics B, 2015, 24(9): 090505. DOI:10.1088/1674-1056/24/9/090505 |
| [5] |
WANG, W., et al.. Prescribed performance consensus of uncertain nonlinear strict-feedback systems with unknown control directions[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2016, 46(9): 1279-1286. DOI:10.1109/TSMC.2015.2486751 |
| [6] |
基于SINS/DVL/GPS的AUV组合导航标定放大的研究及其误差分析[J]. 舰船电子工程, 2018, 38(6): 33–36.
|
| [7] |
基于生物启发神经网络的多AUV目标搜索[J]. 舰船电子工程 2019, 39 (3): 32–36
|
| [8] |
HE, S., et al.. Leader-follower formation control of USVs with prescribed performance and collision avoidance[J]. IEEE Transactions on Industrial Informatics, 2018. |
| [9] |
SLOTINE, J.-J.E., W. LI, Applied nonlinear control[J]. Prentice Hall Englewood Cliffs, NJ, 1991, 199.
|
| [10] |
CUI, R., ZHANG X, CUI D.. Adaptive sliding-mode attitude control for autonomous underwater vehicles with input nonlinearities[J]. Ocean Engineering, 2016, 123: 45-54. DOI:10.1016/j.oceaneng.2016.06.041 |
| [11] |
Zhihong, M, X.H. YU. Terminal sliding mode control of MIMO linear systems[C]//Proceedings of 35th IEEE Conference on Decision and Control. 1996, IEEE.
|
| [12] |
FENG, Y., X. Yu, Z. MAN.. Non-singular terminal sliding mode control of rigid manipulators[J]. Automatica, 2002, 38(12): 2159-2167. DOI:10.1016/S0005-1098(02)00147-4 |
 2020, Vol. 42
2020, Vol. 42
