AUV作为一种高度自动化水下自主航行装备,对海洋开发和探测有着重要的作用和意义。对AUV来说,自主航行控制作为其核心关键技术,是AUV真正实现自治的必要条件,因此也一直是备受关注的研究热点。对AUV自主航行控制技术来说,除基础的航向、深度和姿态控制外,跟踪预设的期望路径点航行是其非常重要和关键的功能。本文主要针对采用首、尾舵控制机构的AUV,研究其空间路径点的跟踪控制算法。
水下潜器的路径跟踪控制问题是近年来备受关注的热门课题,Do K.D[1]考虑了仅有4个推力器的AUV路径跟踪问题,结合Lyapunov直接法、反演方法以及参数映射等方法提出了一种AUV以定常轴向速度跟踪指定路径的方法。王银涛等[2]研究了AUV定常速度下的非时间参考路径跟踪问题,将跟踪控制问题分为导引和控制2个部分,导引部分基于视线导引原理输出AUV参考航向,控制部分构造了一种将航向控制器和路径跟踪控制器并行结合的混合型路径跟踪控制器。So-Ryeok Oh等[3]针对欠驱动船舶的路径点跟踪控制在视线导航法的基础上采用了基于状态空间形式的模型预测控制算法,并通过仿真验证了模型预测控制相较传统的PID控制算法具有更佳的控制效果。王宏健等[4]研究了欠驱动自主水下航行器的三维路径跟踪控制问题,针对基于虚拟向导建立的三维路径跟踪误差模型,采用滤波反步法设计跟踪控制器,增加了系统对噪声的鲁棒性。朱大奇等[5]针对水下机器人轨迹跟踪控制的速度跳变问题,提出一种基于生物启发神经动力学模型的自治水下机器人三维轨迹跟踪控制算法,基于水下机器人对算法进行了仿真实验。文献[6-7]提出了自适应区域跟踪控制方法,通过对AUV建模不确定性项进行在线辨识,使AUV能够从任意初始位姿收敛到目标区域,但在目标区域边界上出现容易出现震荡而难以收敛于目标区域中。文献[8]进一步地提出了一种PD神经滑模自适应区域跟踪控制方法,采用径向基函数神经网络对动力学模型中的未知项进行自适应估计,采用滑模控制项对神经网络逼近误差进行补偿。程相勤[9]针对欠驱动UUV的三维路径跟踪问题提出了一种离散滑模预测的控制方法,提高了欠驱动UUV在海流干扰情况下的空间曲线路径跟踪控制的精度并提升了控制系统的鲁棒性。
本文首先应用视线导航法和垂直面制导算法将路径点跟踪控制问题转化为航向、深度和纵倾的跟踪控制问题,再设计基于状态空间模型的模型预测控制算法使得AUV能收敛到期望航向、深度和纵倾达到预期的路径点跟踪控制效果。
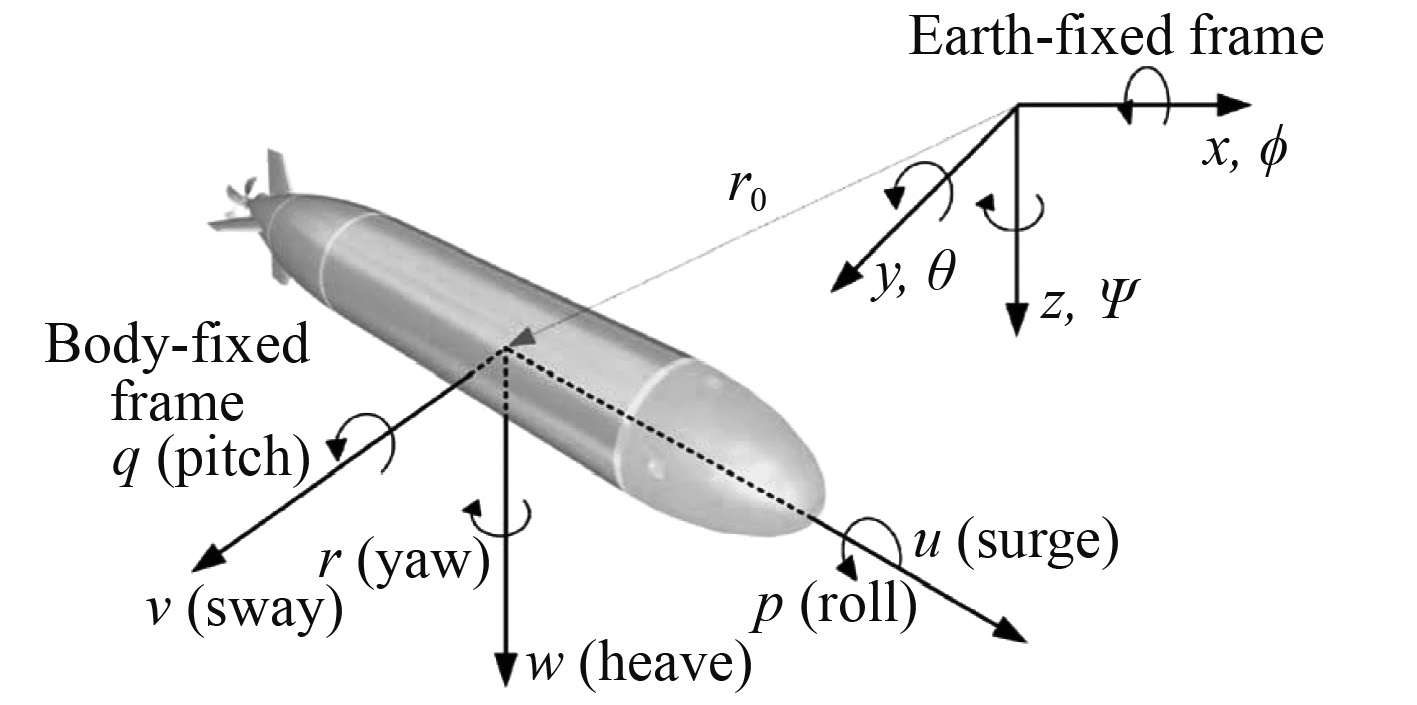
1 系统模型建立由于AUV在水下的航行是六自由度的空间运动,对于其六自由度的运动学以及动力学建模,可参考一般潜艇以及AUV(自主水下机器人)的建模方法。参考文献[10]中给出的AUV6空间运动坐标系,如图1所示。
|
图 1 AUV的运动坐标系以及固定坐标系 Fig. 1 Body-fixed frame and earth-fixed frame for AUV |
结合刚体动力学方程的矢量表达形式,可将AUV的动力学以及运动学方程[11]表示为:
| ${M}{\dot { {\nu}}} + {{C}}({{\nu }}){\nu} + {{D}}({\nu }){\nu} + {{g}}({\eta }) = {\tau} + {{g}_{0}} + {\omega }\text{,}$ | (1) |
| $\dot{ \eta} = {{J}}({\eta }){\nu }\text{。}$ | (2) |
式中:
| ${J}({\eta } ) = \left[ {\begin{array}{*{20}{c}} {{{J}_{1}}({\eta })}&{{{{0}}_{3 \times 3}}} \\ {{{{0}}_{3 \times 3}}}&{{{J}_{2}}({\eta })} \end{array}} \right]\text{。}$ | (3) |
| ${\begin{split}&{{{J}}_{{1}}}({{\eta }}) = \\& \left[\!\!\!\!\! {\begin{array}{*{20}{c}} {\cos \psi \cos \theta }\!\!&\!\!{ - \sin \psi \cos \phi + \cos \psi \sin \theta \sin \phi }\!\!&\!\!{\sin \psi \sin \phi + \cos \psi \sin \theta \cos \phi } \\ {\sin \psi \cos \theta }\!\!&\!\!{\cos \psi \cos \phi + \sin \psi \sin \theta \sin \phi }\!\!&\!\!{ - \cos \psi \sin \phi + \sin \psi \sin \theta \cos \phi } \\ { - \sin \theta }\!\!&\!\!{\cos \theta \sin \phi }\!\!&\!\!{\cos \theta \cos \phi } \end{array}}\!\!\!\!\! \right]\text{,}\end{split}}$ | (4) |
| ${{{J}}_{{2}}}({{\eta }}) = \left[ {\begin{array}{*{20}{c}} 1&{\sin \phi \tan \theta }&{\cos \phi \tan \theta } \\ 0&{\cos \phi }&{ - \sin \phi } \\ 0&{\sin \phi /\cos \theta }&{\cos \phi /\cos \theta } \end{array}} \right]\text{。}$ | (5) |
针对水下潜器的路径跟踪问题的误差建模主要有2种思路,一种是在Serret-frenet坐标系下建立误差模型,另一种为运用导航视线法将跟踪误差模型简化为简单的航速控制、航向控制以及纵倾控制问题,目前水平面视线导航法已经应用得相当成熟,其原理如图2所示。要驱使AUV收敛到由水平面离散路径点

|
图 2 直线航迹段视线导航法示意图 Fig. 2 Body-fixed frame and earth-fixed frame for AUV |
垂直面航迹制导算法如果采用视线导航算法将垂直面位置偏差解算为指令纵倾的会造成以下问题:1)AUV垂直面内航行对纵倾角有一定限制,采用视线导航法进行解算将造成部分参数难以调整。2)AUV在进行垂直面机动控制的过程中,深度速率的控制必须同时考虑垂向速度和纵倾,采用视线导航法解算指令纵倾角而忽略垂向速度,将引起较大的航迹控制偏差。因此,本文通过分析AUV垂直面运动特性以及仿真验证等方法,采用指令深度速率、指令深度以及指令纵倾三者结合的方式作为垂直面的航迹跟踪控制算法。
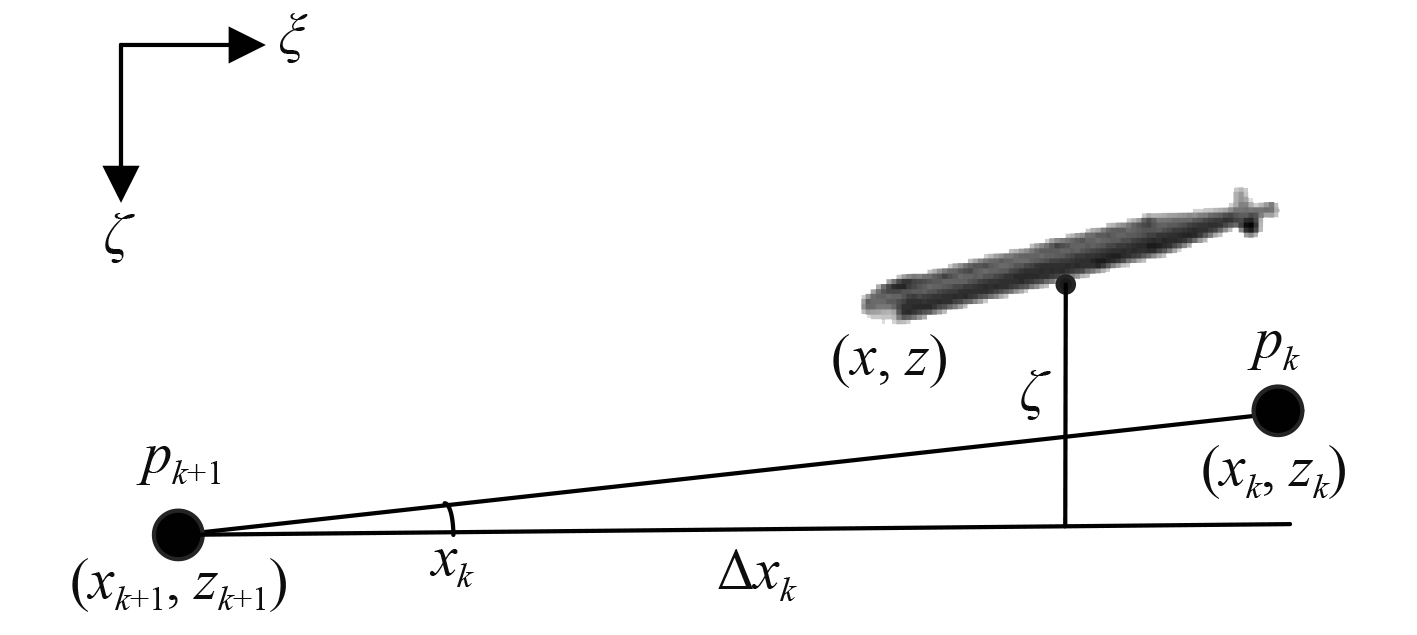
其中指令深度与指令纵倾的解算方法如图3所示。当前时刻的指令深度为AUV当前位置点在航迹线上的投影点的垂直位置,其解算方法为:
|
图 3 垂直面指令深度、指令纵倾、指令深度速率解算方法 Fig. 3 Calculation method of vertical plane command depth,command trim ,command depth rate |
| ${\zeta ^*} = \frac{{{z_{k + 1}} - {z_k}}}{{{x_{k + 1}} - {x_k}}}({x_{k + 1}} - \Delta {x_k}) + {z_{k + 1}}\text{,}$ | (6) |
式中:
| ${\dot \zeta ^*} = \frac{{{z_{k + 1}} - {z_k}}}{{{x_{k + 1}} - {x_k}}}*V\text{。}$ | (7) |
模型预测控制(Model Predictive Control, MPC)是20世纪70年代发展起来的一类控制算法,算法采用多步预测、滚动优化以及反馈校正等控制策略,使得模型预测控制具有控制效果好、鲁棒性强且对模型精确性要求较低等优点,同时可以考虑到执行机构的约束性。预测控制算法另一个明显的优势便是可以将各类约束条件加入到控制过程当中使得控制系统更具有安全性[12],因此基于以上几点考虑,本文设计一种基于状态空间模型的预测控制算法用于AUV深度控制算法。
3.1 线性化模型由于AUV的非线性模型十分复杂,不宜直接作为控制器设计的模型,故需将AUV的六自由度非线性模型简化成线性模型以便于控制器的设计。本文考虑路径点跟踪控制问题,并假定AUV的纵向速度
| $\begin{split} & \left[\!\!\! {\begin{array}{*{20}{c}} {\dot w} \\ {\dot q} \\ {\dot \theta } \\ {\dot \zeta } \end{array}} \!\!\!\right] = \left[\!\!\! {\begin{array}{*{20}{c}} {{a_{11}}}&{{a_{12}}}&{{a_{13}}}&0 \\ {{a_{21}}}&{{a_{22}}}&{{a_{23}}}&0 \\ 0&1&0&0 \\ 1&0&{ - u}&0 \end{array}} \!\!\!\right]\left[\!\! {\begin{array}{*{20}{c}} w \\ q \\ \theta \\ \zeta \end{array}} \!\!\!\right] + \left[\!\!\! {\begin{array}{*{20}{c}} {{b_{11}}}&{{b_{12}}} \\ {{b_{21}}}&{{b_{22}}} \\ 0&0 \\ 0&0 \end{array}} \!\!\!\right] \left[\!\!\! {\begin{array}{*{20}{c}} {{\delta _b}} \\ {{\delta _s}} \end{array}} \!\!\!\right] \text{,} \\ & \left[\!\! {\begin{array}{*{20}{c}} \theta \\ \zeta \end{array}} \!\!\!\right] = \left[\!\!\! {\begin{array}{*{20}{c}} 0&0&1&0 \\ 0&0&0&1 \end{array}} \!\!\!\right]\left[\!\!\! {\begin{array}{*{20}{c}} w \\ q \\ \theta \\ \zeta \end{array}} \!\!\!\right] \text{,} \end{split} $ | (8) |
即
| $\begin{split} & {\dot{ x}} = {{Ax}} + {{Bu}}\text{,} \\ &y = {{Cx}} \text{。} \end{split} $ | (9) |
再将其转换为离散时间的线性状态空间模型:
| $\begin{split} &{{x}}(k + 1) = {{{A}}_{{d}}}{{x}}(k) + {{{B}}_{{d}}}{{u}}(k)\text{,} \\ & y(k) = {{{C}}_{{d}}}{{x}}(k) \text{。} \end{split} $ | (10) |
其中,
| $\left\{ {\begin{array}{*{20}{l}} {\left[\!\!\! {\begin{array}{*{20}{c}} {{{x}}(k + 1)} \\ {{{u}}(k)} \end{array}}\!\!\! \right] = \left[\!\!\! {\begin{array}{*{20}{c}} {{{{A}}_{{d}}}}&{{{{B}}_{{d}}}} \\ {{0}}&{{I}} \end{array}} \!\!\!\right]\left[\!\!\! {\begin{array}{*{20}{c}} {{{x}}(k)} \\ {{{u}}(k - 1)} \end{array}} \!\!\!\right] + \left[\!\!\! {\begin{array}{*{20}{c}} B \\ I \end{array}} \!\!\!\right]\Delta {{u}}(k)}\text{,} \\ {y(k) = \left[\!\!\! {\begin{array}{*{20}{c}} {{{{C}}_{{d}}}}&{{0}} \end{array}} \!\!\!\right]\left[\!\!\! {\begin{array}{*{20}{c}} {{{x}}(k)} \\ {{{u}}(k - 1)} \end{array}} \!\!\!\right]} \text{,} \\[-25pt] \end{array}} \right.$ | (11) |
令
| $\left\{ {\begin{array}{*{20}{l}} {{{z}}(k + 1) = {{{A}}_{{o}}}z(k) + {{{B}}_{{o}}}\Delta {{u}}(k)} \text{,}\\ {{{y}}(k) = {{{C}}_{{o}}}{{z}}(k)} \text{。} \end{array}} \right.$ | (12) |
不考虑测量噪声对状态量的影响,即整个状态向量是可测的,得
| $\begin{gathered} {{{\vec{ z}}}_k} = {P_x}z(k) + {H_x}\Delta {{{\vec{ u}}}_k} \text{,} \\ {{{\vec{ y}}}_k} = Pz(k) + H\Delta {{{\vec{ u}}}_k} \text{。} \\ \end{gathered} $ | (13) |
其中:
| ${\vec {{z}}_k} = \left[\!\!\! {\begin{array}{*{20}{c}} {z(k + 1|k)} \\ \vdots \\ {z(k + {N_c}|k)} \\ {z(k + {N_c} + 1|k)} \\ \vdots \\ {z(k + {N_y}|k)} \end{array}} \!\!\!\right],\; {{{P}}_{{x}}} = \left[\!\!\! {\begin{array}{*{20}{c}} {{{{A}}_{{o}}}} \\ \vdots \\ {{{{A}}_{{o}}}^{{N_c}}} \\ {{{{A}}_{{o}}}^{{N_{c + 1}}}} \\ \vdots \\ {{{{A}}_{{o}}}^{{N_y}}} \end{array}}\!\!\! \right] \text{,}$ |
| $\Delta {{\vec{ u}}_k} = \left[\!\!\! {\begin{array}{*{20}{c}} {\Delta {{u}}(k)} \\ \vdots \\ {\Delta {{u}}(k + {N_c} - 1|k)} \\ 0 \\ \vdots \\ 0 \end{array}}\!\!\! \right],\;{{\vec{ y}}_k} = \left[\!\!\! {\begin{array}{*{20}{c}} {y(k + 1|k)} \\ \vdots \\ {y(k + {N_c}|k)} \\ {y(k + {N_c} + 1|k)} \\ \vdots \\ {y(k + {N_y}|k)} \end{array}}\!\!\! \right]\text{,}$ |
| $ { \begin{aligned}{{{H}}_{{x}}} \! = \left[\!\!\!\! {\begin{array}{*{20}{c}} {{{{B}}_{{o}}}}\!\!\!&\!\!\!0\!\!\!&\!\!\!0\!\!\!&\!\!\! \cdots \!\!\!&\!\!\!{{{{0}}_{({N_y} - {N_c}) \times 1}}} \\ \vdots \!\!\!&\!\!\! \vdots \!\!\!&\!\!\! \vdots \!\!\!&\!\!\! \vdots \!\!\!&\!\!\! \vdots \\ {{{{A}}_{{o}}}^{{N_c} - 1}{{{B}}_{{o}}}}\!\!\!&\!\!\!{{{{A}}_{{o}}}^{{N_c} - 2}{{{B}}_{{o}}}}\!\!\!&\!\!\! \cdots \!\!\!&\!\!\!{{{{B}}_{{o}}}}\!\!\!&\!\!\!{{{{0}}_{({N_y} - {N_c}) \times 1}}} \\ {{{{A}}_{{o}}}^{{N_c}}{{{B}}_{{o}}}}\!\!\!&\!\!\!{{{{A}}_{{o}}}^{{N_c} - 1}{{{B}}_{{o}}}}\!\!\!&\!\!\! \cdots \!\!\!&\!\!\!{{{{A}}_{{o}}}{{{B}}_{{o}}}}\!\!\!&\!\!\!{{{{0}}_{({N_y} - {N_c}) \times 1}}} \\ \vdots \!\!\!&\!\!\! \vdots \!\!\!&\!\!\! \vdots \!\!\!&\!\!\! \vdots \!\!\!&\!\!\! \vdots \\ {{{{A}}_{{o}}}^{{N_y} - 1}{{{B}}_{{o}}}}\!\!\!&\!\!\!{{{{A}}_{{o}}}^{{N_y} - 2}{{{B}}_{{o}}}}\!\!\!&\!\!\! \cdots \!\!\!&\!\!\!{{{{A}}_{{o}}}^{{N_y} - {N_c}}{{{B}}_{{o}}}}\!\!\!&\!\!\!{{{{0}}_{({N_y} - {N_c}) \times 1}}} \end{array}}\!\!\!\! \right]\end{aligned}}\text{,} $ |
将性能指标函数定义为:
| ${J_k}(\Delta {{\vec{ u}}_k}) = \sum\limits_{j = 1}^{{N_y}} {\left\| {y(k + j|k) - {{r}}} \right\|_{{{Q}}(j)}^2} + \sum\limits_{j = 1}^{{N_c} - 1} {\left\| {\Delta u(k + j|k) - {{r}}} \right\|_{{{R}}(j)}^2}\text{,} $ | (14) |
写成向量形式为:
| ${J_k} = \left\| {{{{\vec{ y}}}_k} - {{r}}} \right\|_{{Q}}^2 + \left\| {\Delta {{{\vec{ u}}}_k}} \right\|_{{R}}^2\text{。}$ | (15) |
其中
对于AUV的路径跟踪控制问题而言,由于执行器的物理约束,转首力矩的大小受到一定的限制,也即控制输入量需满足一定的约束条件,也即
| $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{U} \leqslant {{u}}(k) \leqslant \bar U\text{,}$ | (16) |
其中
| $\begin{split} & \mathop {\min }\limits_{\Delta {{U}}(k)} {J_k} = \left\| {{{{\vec{ y}}}_k} - r} \right\|_Q^2 + \left\| {\Delta {{{\vec{ u}}}_k}} \right\|_R^2 \text{,}\\ & {\rm{s.t.}}\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{U} \leqslant {{u}}(k) \leqslant \bar U \text{。} \end{split} $ | (17) |
将式(13)代入式(15)并展开得到下式:
| $\begin{split} {J_k} =& {({{P}}{{\xi }}(k) - {{r}})^{\rm{T}}}{{Q}}({{P}}{{\xi }}(k) - {{r}}) + 2{({{P}}{{\xi }}(k) - {{r}})^{\rm{T}}}{{QH}}\Delta {{\vec{ u}}_k} + \\&\Delta {{\vec{ u}}_k}^{\rm{T}}({{{H}}^{\rm{T}}}{{QH}} + {{R}})\Delta {{\vec{ u}}_k} \text{。} \\[-10pt] \end{split}$ | (18) |
式中等号右边第1项为确定值,与优化无关,在计算时可只考虑后2项的影响,并将后2项写成标准的二次型形式,同时将输入量的约束写成向量形式,则可将式(16)写成新的标准二次型约束优化问题,得到:
| $\begin{split} & \mathop {\min }\limits_{\Delta {{U}}(k)} {J_k} = \Delta {{{\vec{ u}}}_k}^{\rm{T}}{{S}}\Delta {{{\vec{ u}}}_k} + 2{{{f}}^{\rm{T}}}\Delta {{{\vec{ u}}}_k} \text{,} \\ & {\rm{s.t.}}{{W}}\Delta {{{\vec{ u}}}_k} \leqslant U \text{。} \\ \end{split} $ | (19) |
其中
| $\Delta {u_{opt}}(k) = \left[ {\begin{array}{*{20}{c}} {{{{I}}_{{N_c}}}}&{{0}}& \cdots &{{0}} \end{array}} \right]\Delta {{{U}}_{opt}}(k)\text{,}$ | (20) |
则当前时刻的控制器最优输出值为上一时刻的控制器输出值加上当前时刻的控制器增量值,即
| ${u_{opt}}(k) = u(k - 1) + \Delta {u_{opt}}(k)\text{。}$ | (21) |
在此基础上进行滚动优化便可得出整个控制过程的最优控制输入。
4 仿真示例本文采用Matlab/Simulink仿真工具,首先设定空间离散路径点,并由AUV实时位置信息,采用水平面视线导航算法和垂直面制导算法推算出动态的期望航向角、期望深度、期望纵倾、或深度速率,再由MPC控制器解算出期望控制输入量
设定控制机构需满足的约束条件为
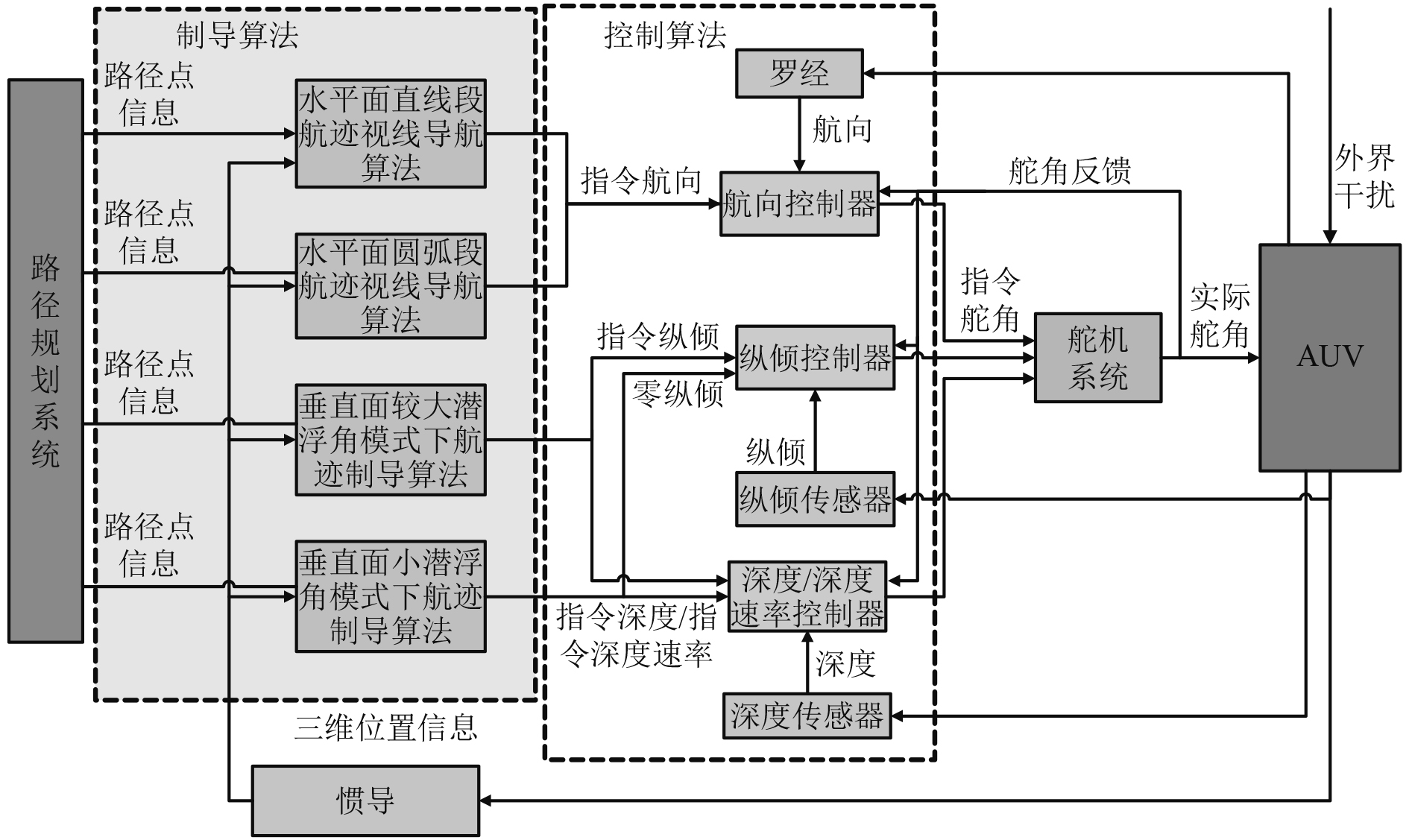
|
图 4 路径点跟踪控制原理框图 Fig. 4 Block diagram of waypoint tracking control principle |
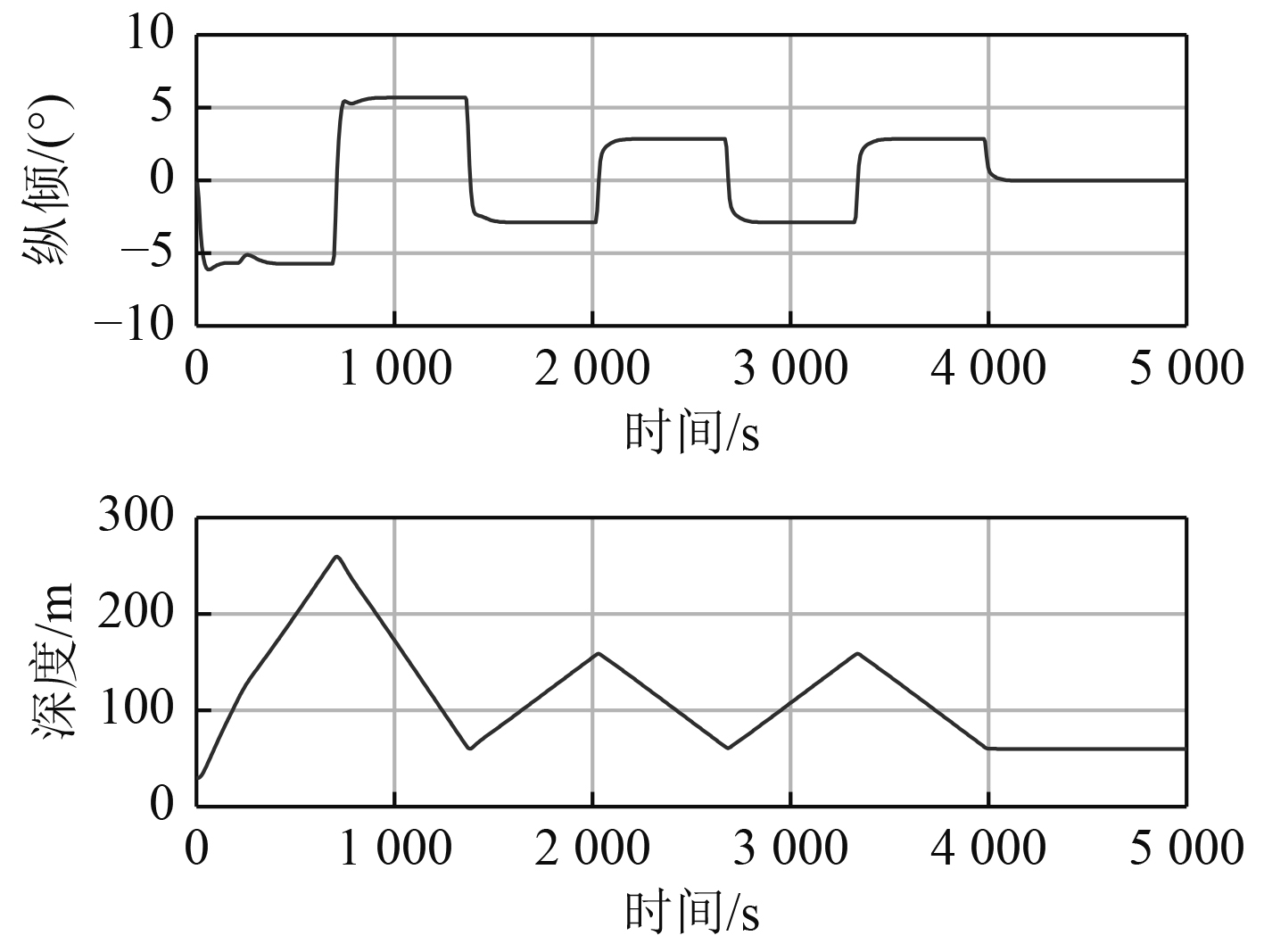
可知,AUV能实现垂直面的路径点跟踪。图5为路径跟踪过程中的纵倾和深度曲线,AUV与设定路径的垂直距离误差仿真结果如图6所示。
|
图 5 垂直面路径点跟踪曲线 Fig. 5 The curve of way-point following with current |
|
图 6 纵倾和深度曲线 Fig. 6 The curve of trim and depth |
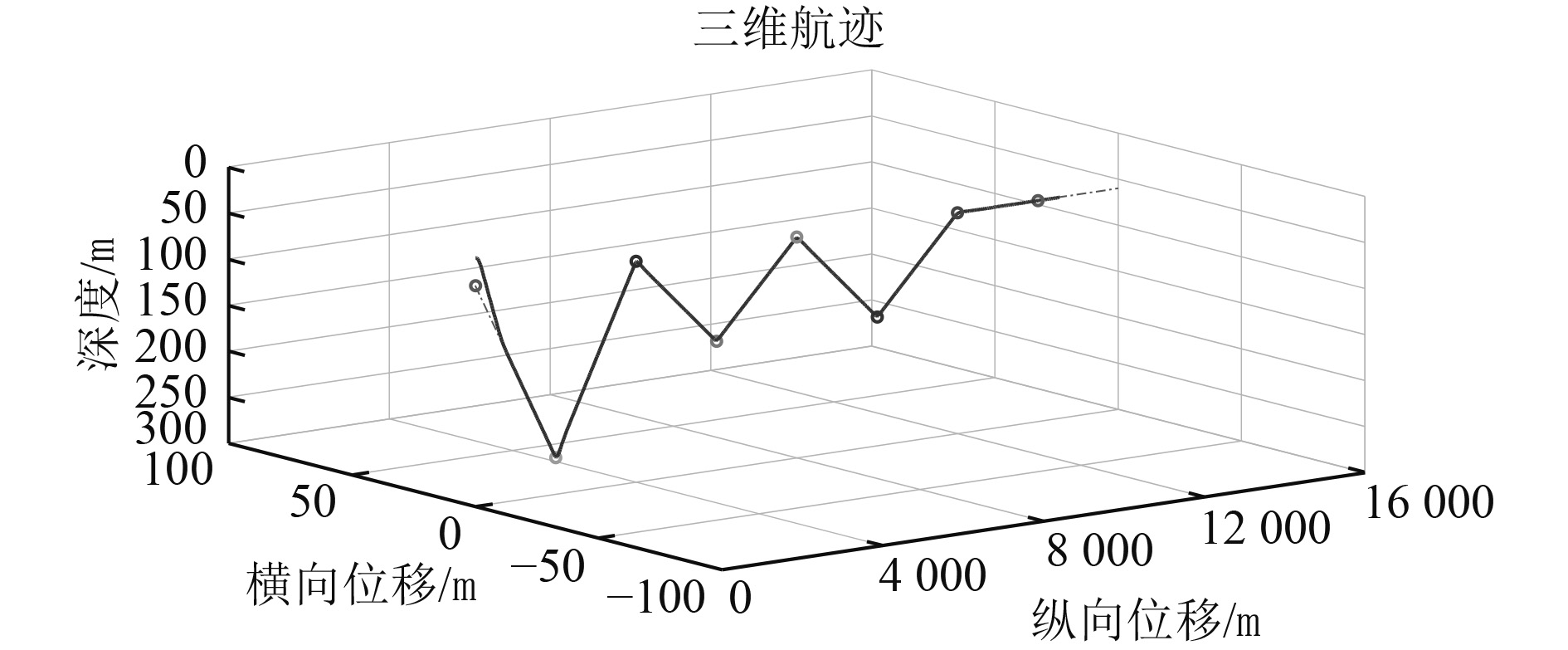
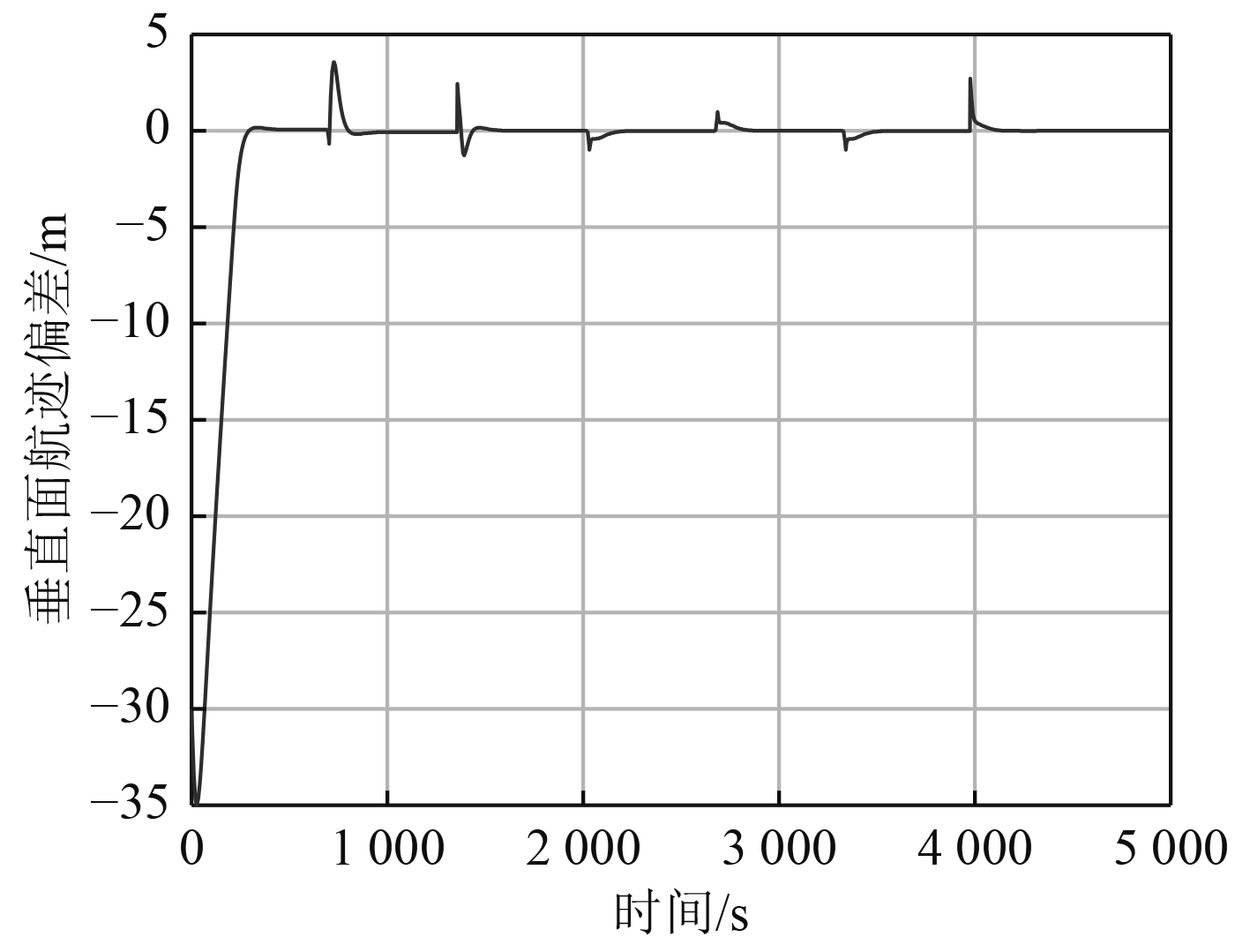
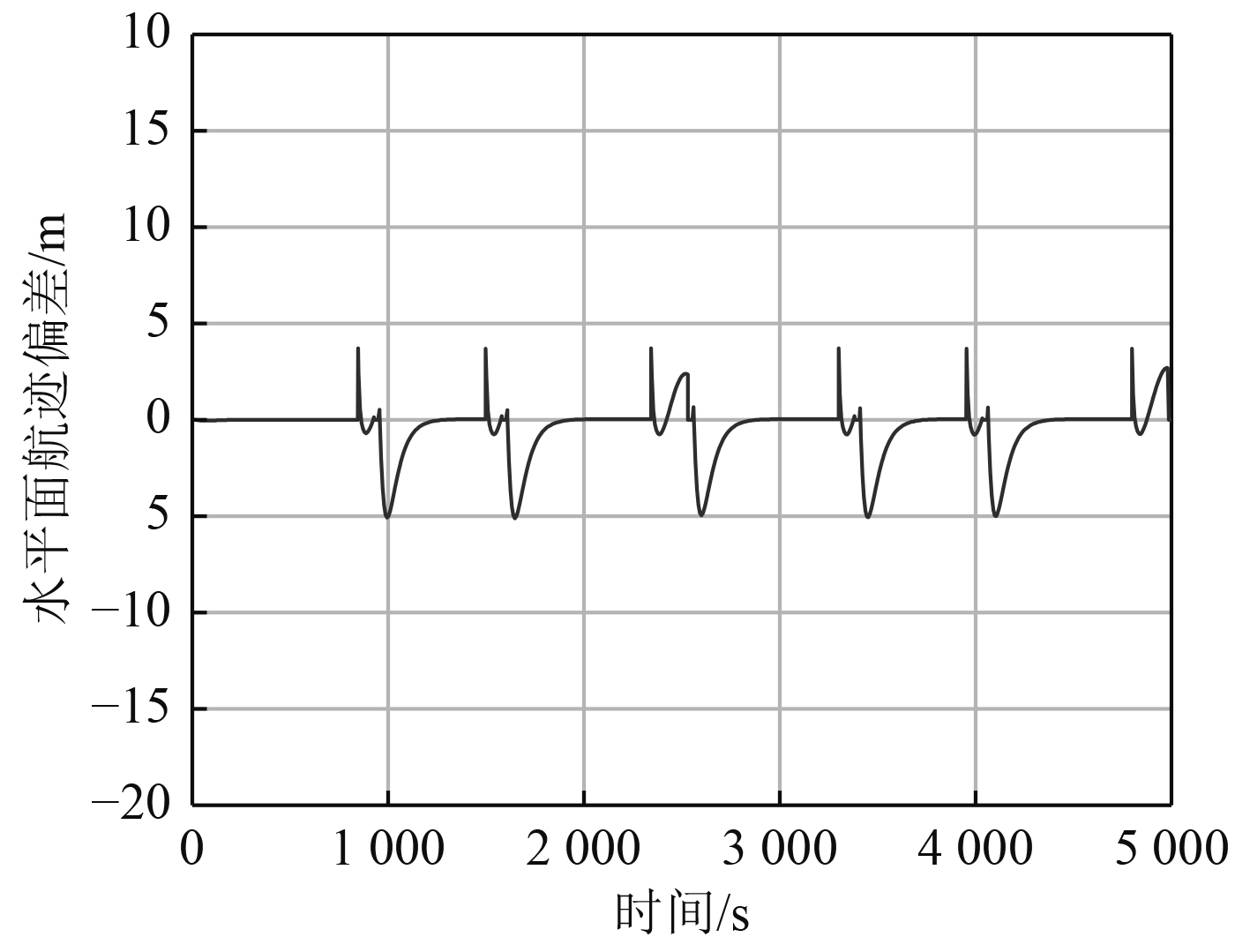
仿真算例2为空间路径点跟踪控制,空间路径点序列为[0 0 60],[2000 2000 140],[2000 4000 60],[0 6000 140],[−2000 4000 60],[−2000 2000 140],[0 0 60] m,路径跟踪效果如图7所示。图8和图9分别为水平面和垂直面的航迹偏差。
|
图 7 垂直距离偏差曲线 Fig. 7 The curve of vertical distance deviation |

|
图 8 空间路径点跟踪曲线 Fig. 8 The curve of spatial way-point following with current |
|
图 9 水平面航迹偏差曲线 Fig. 9 The curve of horizontal plane tracking error |

|
图 10 垂直面航迹偏差曲线 Fig. 10 The curve of vertical plane horizontal plane tracking error |
本文针对AUV的空间路径点跟踪控制问题,采用水平面视线导航法计算AUV指令航向,采用垂直面制导算法计算AUV的垂直面指令深度、指令纵倾和指令深度速率,采用模型预测控制算法用于AUV的航向和深度控制。仿真结果表明,空间航迹控制算法能达到较高的控制精度,采用的指令深度+指令纵倾+指令深度速率的控制方法能使AUV尽快的航行至指令轨迹并跟踪垂直面航迹,分析航迹偏差曲线,可发现只有在航迹切换过程中才有明显的航迹偏差出现,且垂直面切换时潜浮角的改变越小,也即垂直面航迹越平坦时,航迹控制的精度也越高,对应的航迹切换过程中的航迹偏差也越小。
| [1] |
DO K D, JIANG Z P. Robust and adaptive path following for underactuated autonomous vehicles[J]. Ocean Engineering, 2004, 31(16): 1967-1997. DOI:10.1016/j.oceaneng.2004.04.006 |
| [2] |
王银涛, 郑美云, 严卫生. 一种新的AUV路径跟踪控制方法[J]. 西北工业大学学报, 2009, 27(4): 517-521. WANG Yintao, ZHENG Meiyun, YAN Weisheng. A new AUV path tracking control method[J]. Journal of Northwestern Polytechnical University, 2009, 27(4): 517-521. DOI:10.3969/j.issn.1000-2758.2009.04.017 |
| [3] |
SO-RYEOK Oh, JING Sun. Path following of underactuated marine surface vessels using line-of-sight based model predictive control[J]. Ocean Engineering, 2010, 37: 289-295. DOI:10.1016/j.oceaneng.2009.10.004 |
| [4] |
王宏健, 陈子印, 贾鹤鸣, 等. 基于滤波反步法的欠驱动AUV三维路径规划跟踪控制[J]. 自动化学报, 2015, 41(3): 631-645. WANG Hongjian, CHEN Zijian, JIA Heming, et al. Three-dimensional path-following control of underactuated autonomous underwater vehicle with command filtered backstepping[J]. ACTA Automatica Sinica, 2015, 41(3): 631-645. |
| [5] |
朱大奇, 张光磊, 李蓉. 生物启发AUV三维轨迹跟踪控制算法[J]. 智能系统学报, 2014(2): 58-63. |
| [6] |
LI X, HOU S P, CHEAH C C. Adaptive region tracking control for autonomous underwater vehicle[C]. IEEE International Conference on Control, Robotics and Vision, 2010.
|
| [7] |
ISMAIL Z H, DUNNIGAN M W. A region boundary-based control scheme for an autonomous underwater vehicle[J]. Ocean Engineering, 2011, 38(11): 2270-2280. |
| [8] |
张铭钧, 褚振忠. 自主式水下机器人自适应区域跟踪控制[J]. 机械工程学报, 2014, 50(2019): 50-57. ZHANG Mingjun, CHU Zhenzhong. Adaptive region tracking control for autonomous underwater vehicle[J]. Journal of Mechanical Engineering, 2014, 50(2019): 50-57. |
| [9] |
程相勤. 基于滑模理论的欠驱动UUV空间曲线路径跟踪控制[D]. 哈尔滨: 哈尔滨工程大学, 2010: 78−79. CHENG X Q. Spatial curvilinear path following of underactuated UUV based on sliding mode theory [D]. Harbin: Harbin Engineering University, 2010: 78−79. |
| [10] |
T. I. Fossen, Guidance and Control of Ocean Vehicles[M]. Chicester: John Wiley & Sons, 1994.
|
| [11] |
边信黔, 付明玉, 王元慧. 船舶动力定位[M]. 北京: 科学出版社, 2011.
|
| [12] |
龚建伟, 姜岩, 徐威. 无人驾驶车辆模型预测控制[M]. 北京: 北京理工大学出版社, 2014.
|
| [13] |
邹涛, 丁宝仓, 张端. 模型预测控制工程应用导论[M]. 北京: 化学工业出版社, 2010.
|
 2020, Vol. 42
2020, Vol. 42
