2. 海装装备保障大队,北京 100841
2. Equipment Maintenance Team of Navy, Beijing 100841, China
水下无人航行器是一种集环境感知、动态决策与规划、行为控制及能源适配等功能的复杂无人系统,同时还可以作为水下运动载体实现对物体设备的承载,主要通过远程控制或自主操作完成特定任务,具有无人化、隐蔽性、智能化的突出优点,是执行海洋环境观测、水中目标探测、海底目标搜探等任务的重要装备[1 – 2]。UUV的动态控位,是指UUV基于动力定位技术,通过UUV自身的各个执行机构如舵、推进器等,使其能够抵御浪、流等水下环境干扰的影响,从而在预设位置处自动保持位姿[3]。UUV动态控位技术主要应用于定点悬停、机动、航迹保持等3个方面。
在统一的通信架构基础上,多艘UUV构成的UUV集群,通过智能控制算法,实现多个作业单元的协同控制,包括协同航行、协同探测、协同通信、协同导航定位等,通过链网增效实现作业效率的倍增。不完全相同于单体UUV的低能耗动态控位,主从式UUV集群在协同观探测时对于其中单体UUV的动态控位能力有着不同的要求。主从式UUV集群由一个主UUV及多个从UUV构成,从UUV跟随主UUV完成作业,其中从UUV以主UUV的各项运动状态信息作为控制及决策系统的输入及判断条件。本文考虑的UUV集群为同构UUV集群,即主UUV及各从UUV的功能及负载均无差别,在相同工况下其自身的动态控位能力也是相同的。UUV集群协同作业(探测)时的动态控位过程[4],即是UUV集群在某一预设区域依照战术阵型进行展开占位后,对非合作方或未知身份的目标进行观测及探测,并保持阵型、坚守战术阵地的过程。主从式UUV集群协同观探测任务的想定如图1所示[12]。

|
图 1 主从式UUV集群协同观探测的任务想定示意图 Fig. 1 Task scenario of master-slave UUV group cooperative observation detection |
本文所研究的主从式UUV集群低能耗动态优化控制问题,是基于单体UUV的动态控位能力,通过多UUV的有机聚合,使多个UUV能够以较低的功耗,最大化保持群体预设阵型并尽可能持久地完成协同作业(例如探测等)任务[5]。从集群的阵型保持角度考虑,主UUV作为集群的定位及通信“标杆”,其运动状态、通信状态及机动位置都应尽可能地保持稳定各从UUV在定位点附近做小范围机动运动[6],并遵守阵型保持的安全距离、通信距离、阵型要素等约束条件,在保持阵型的同时以较低的功耗完成动态控位任务。因此,面向协同探测任务的UUV集群需要具备较低的UUV动车频次、较长的UUV待机时长以及UUV集群在区域内阵型保持的能力。因此,本文结合任务约束、通信能力约束、安全距离约束等,分别对其进行位姿保持需求分析。针对面向协同任务阵型保持的UUV,设计了低能耗动态控位方法及策略。
1 基于协同探测任务的UUV集群动态控位需求针对UUV集群的协同探测任务,工程上有一字形阵型、三角形阵型和矩形阵型3种典型阵型。针对面向协同作业的UUV低能耗动态控位,本文以协同探测为例,提出UUV集群的群员在各自的控位区域内可以低速机动的形式进行小范围运动,允许个体在受到缓慢的随机扰动后以较小的偏差偏离阵位点使阵型产生微小的畸变,但该偏差应存在上限,以约束各群员UUV不得超出阵型构型保持的最大可偏移范围,从而使整体探测阵型保持不变。
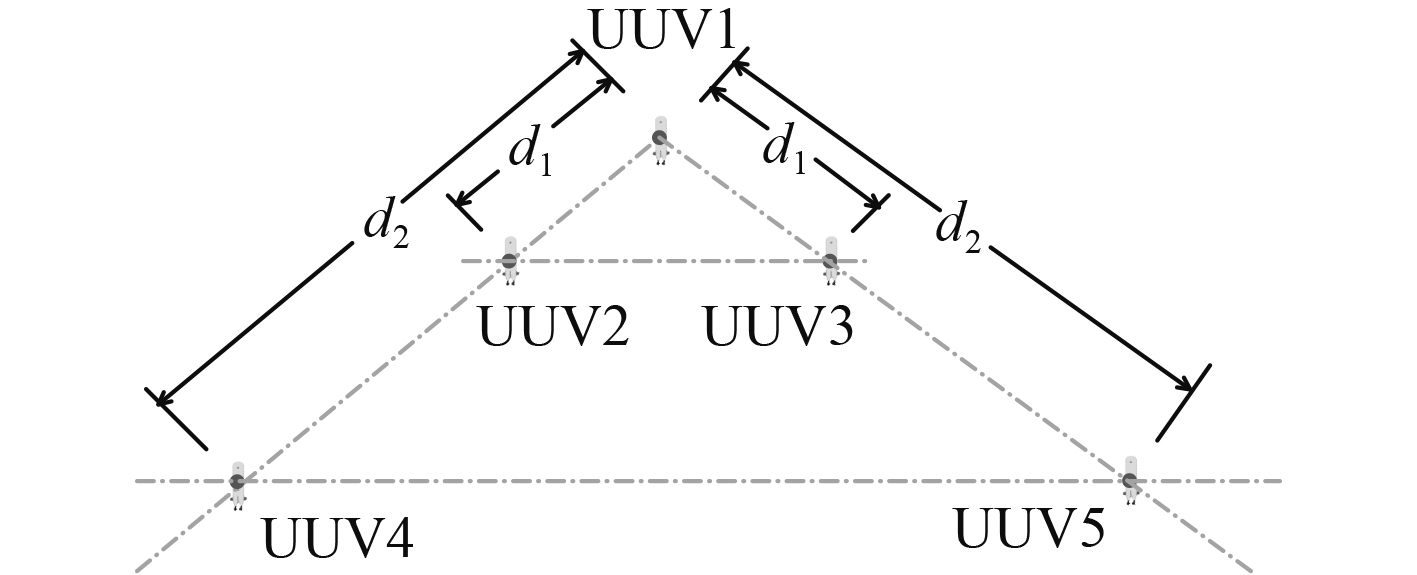
为便于理解,本文选用5艘UUV进行UUV动态控位时的位姿保持需求分析,其中UUV1为主UUV,设定以UUV1的目标定位点为整个阵型的中心,UUV2~UUV5均为从UUV,其目标定位点对称地分布在UUV1的两侧。记UUV2和UUV3的目标定位点距离UUV1的目标定位点距离为
| ${d_2} \geqslant 2{d_1} \text{。}$ | (1) |
UUV2,UUV3和UUV4,UUV5分别与UUV1具有相同大小的垂直距离。在本文的研究中,各UUV的目标定位点一经设定即不再变化,设定UUV群员的间距由集群中心向外逐步扩大或等间距[12]。
|
图 2 UUV集群三角形阵型示意图 Fig. 2 Triangle formation of UUV group |
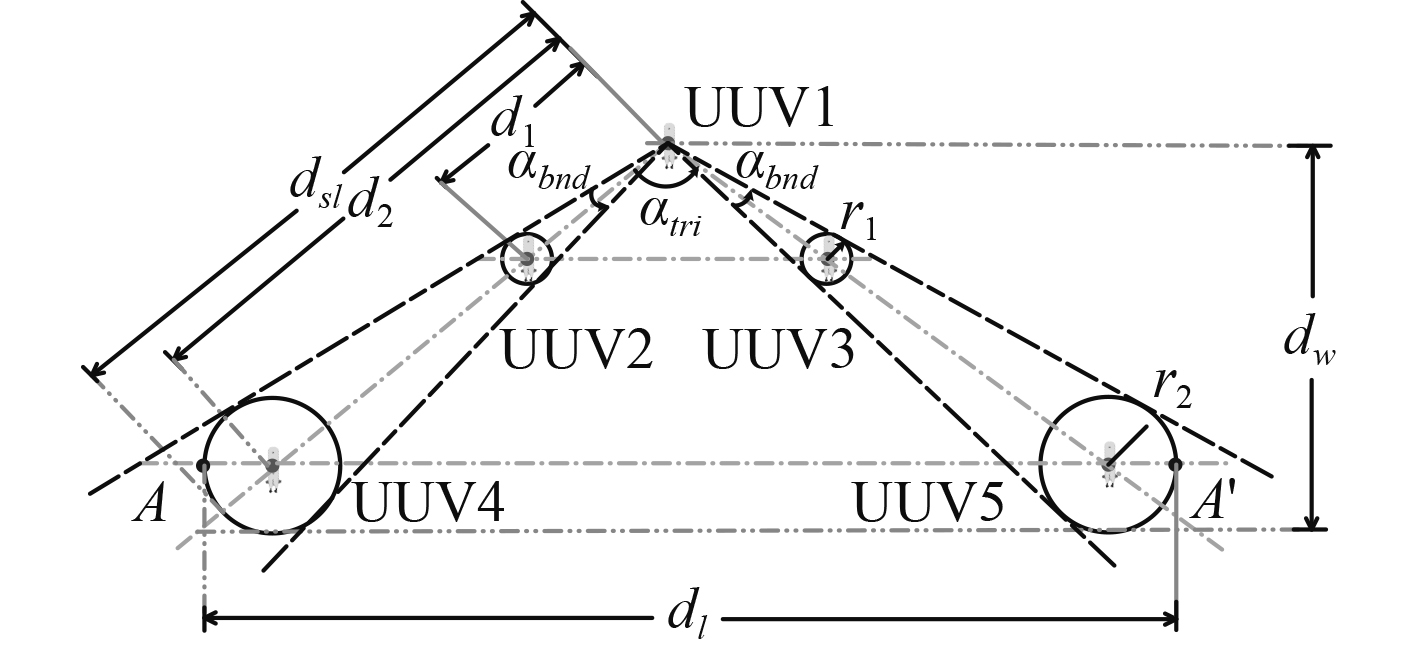
如图3所示,在三角形阵型下,从UUV机动范围允许的最大边界是具有固定半径的圆形区域。
|
图 3 UUV集群三角形阵型示意图 Fig. 3 Triangle formation of UUV group |
记三角形阵型左右两侧机动带的开角为
| ${\alpha _{bnd}} \leqslant 30^\circ \text{。}$ | (2) |
本文对三角形阵型进行描述时,主要选取宽度、长度、开角、边长4个要素。记UUV2和UUV3的最大机动半径为
| $\begin{array}{l} {r_1} = {d_1} \times \tan \left(\displaystyle\frac{{{\alpha _{bnd}}}}{2}\right) \text{,}\\ {r_2} = {d_2} \times \tan \left(\displaystyle\frac{{{\alpha _{bnd}}}}{2}\right) \text{,} \\ \mathop {}\nolimits_{}^{} \mathop {}\nolimits_{}^{} \mathop {}\nolimits_{}^{}\;\;\;\;\;\;\;\; \cdots\cdots \\ {r_n} = {d_n} \times \tan \left(\displaystyle\frac{{{\alpha _{bnd}}}}{2}\right) \text{。}\\ \end{array} $ | (3) |
其中,
| ${d_{sl}} = {d_2} + r \text{。}$ | (4) |
图3所示的阵型最大长度为
| ${d_l} = 2 \times {d_2} \times \sin \left(\frac{{{\alpha _{tri}}}}{2}\right) + 2{r_2} \text{,}$ | (5) |
| ${d_w} = {d_2} \times \cos \left(\frac{{{\alpha _{tri}}}}{2}\right) + {r_2} \text{。}$ | (6) |
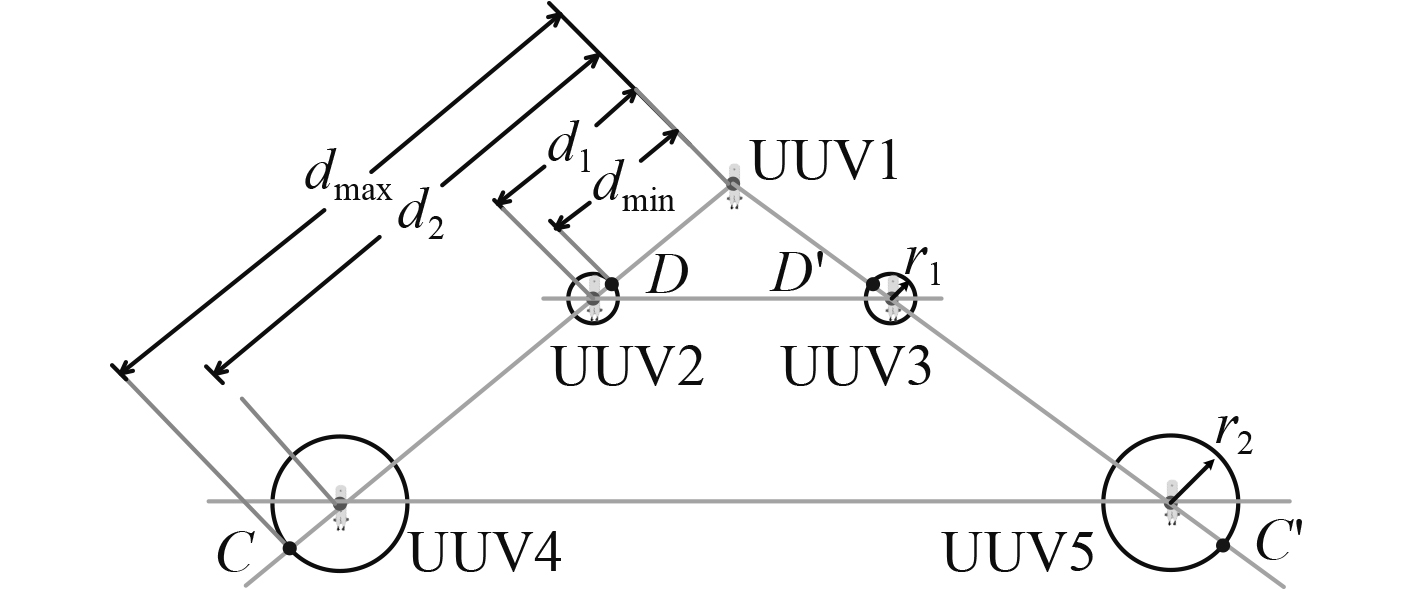
引入针对主从式UUV集群的安全距离约束及通信距离约束。同样地,设
根据图4及上文描述可知:
|
图 4 UUV集群三角形阵型示意图 Fig. 4 Triangle formation of UUV group |
| ${d_{\min }} = {d_1} - {r_{\rm{1}}} \text{,}$ | (7) |
| ${d_{\max }} = {d_{sl}} = {d_2} + {r_2} \text{,}$ | (8) |
针对三角形阵型考虑UUV集群协同探测时的安全距离约束及通信距离约束,与前文所述同理可得:主UUV与从UUV间的最短距离
| ${d_2} + {r_2} \leqslant {l_c} \text{,}$ | (9) |
| ${d_1} - {r_{\rm{1}}} \geqslant {l_s} \text{。}$ | (10) |
上述内容主要描述了主从式UUV 集群在协同探测阵型呈三角形阵型时的动态控位目标点位置及从UUV的最大可机动范围半径约束分析。此外,在姿态保持方面,三角形阵型与横一字形阵型时的需求相同,即主UUV在精确控位的同时,严格保持预设的首向不变,各从UUV也需要保持各自的首向,以使集群阵型更加明晰,利于协同探测任务的完成。
2 UUV集群动态控位策略主从式UUV集群在执行协同探测任务时,既需要保持在阵地部署的探测阵型,又需要以较少的功耗完成该任务[7],因此本文设计了面向主从式UUV集群阵型保持的低能耗动态控位策略,提出了基于布谷鸟寻优的全局最优推力规划方法。通过设计合理的主从式UUV集群阵型保持的低能耗动态控位策略,使各单体UUV降低工作期间的功耗,以此能够在携载电源设备不变的条件下,尽可能延长其执行协同探测任务的时长,提升任务的质量。
本文最终要实现的效果有以下3条:
1)主从式UUV集群能够大体保持观预测的探测阵型;
2)各UUV实现单点的动态控位功能;
3)在各UUV进行动态控位控制时,其耗能能够尽量减少。
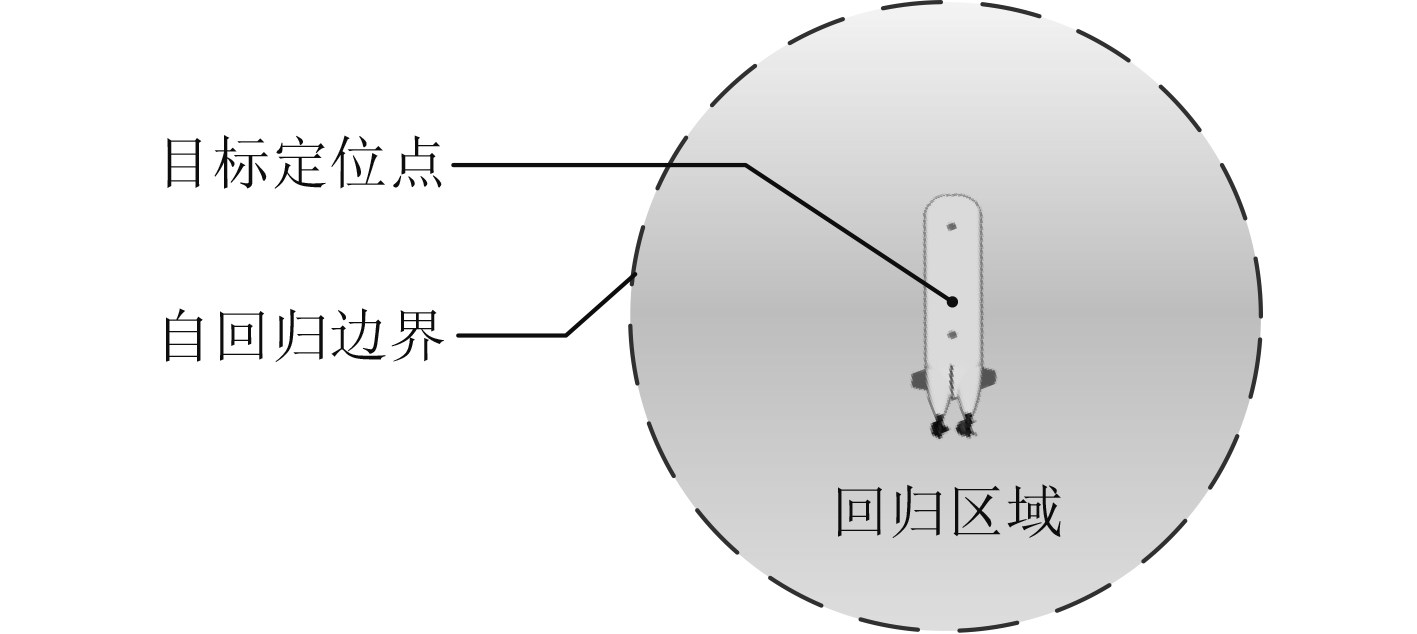
本文面向主从式UUV集群阵型保持的低能耗动态控位策略,为主从式UUV集群中的每个从UUV划定3个不同级别的工作区域。在集群具体观探测阵型部署、阵地选择、通信距离及安全距离的共同约束下,确定各UUV的目标定位点,该点一经设定即不再变化。
|
图 5 主从式UUV集群中从UUV工作区域划分示意图 Fig. 5 Working area division of slave UUV in master-slave UUV group |
以各从UUV的目标定位点为圆心,以UUV的动态控位能力为约束限制条件,UUV工作区域半径
布谷鸟算法利用鸟群个体在集群中对信息的共享及更新,以及借此实现群体在搜寻食物过程中运动由散乱无序化向有序演变的过程,从而获得待求解问题的最优解。
3.1 UUV动态控位过程中优化目标函数的确立UUV动态控位过程中的优化目标函数主要考虑UUV的运动消耗及机械损耗两部分,其中运动消耗包括UUV从当前点到目标定位点的直线距离运动做功
| ${f_{\rm{1}}}{\rm{ = }}E{\rm{(v) = }}{E_m} + {E_c} \text{,}$ | (11) |
| ${f_2} = kT(v) \text{,}$ | (12) |
其中:
|
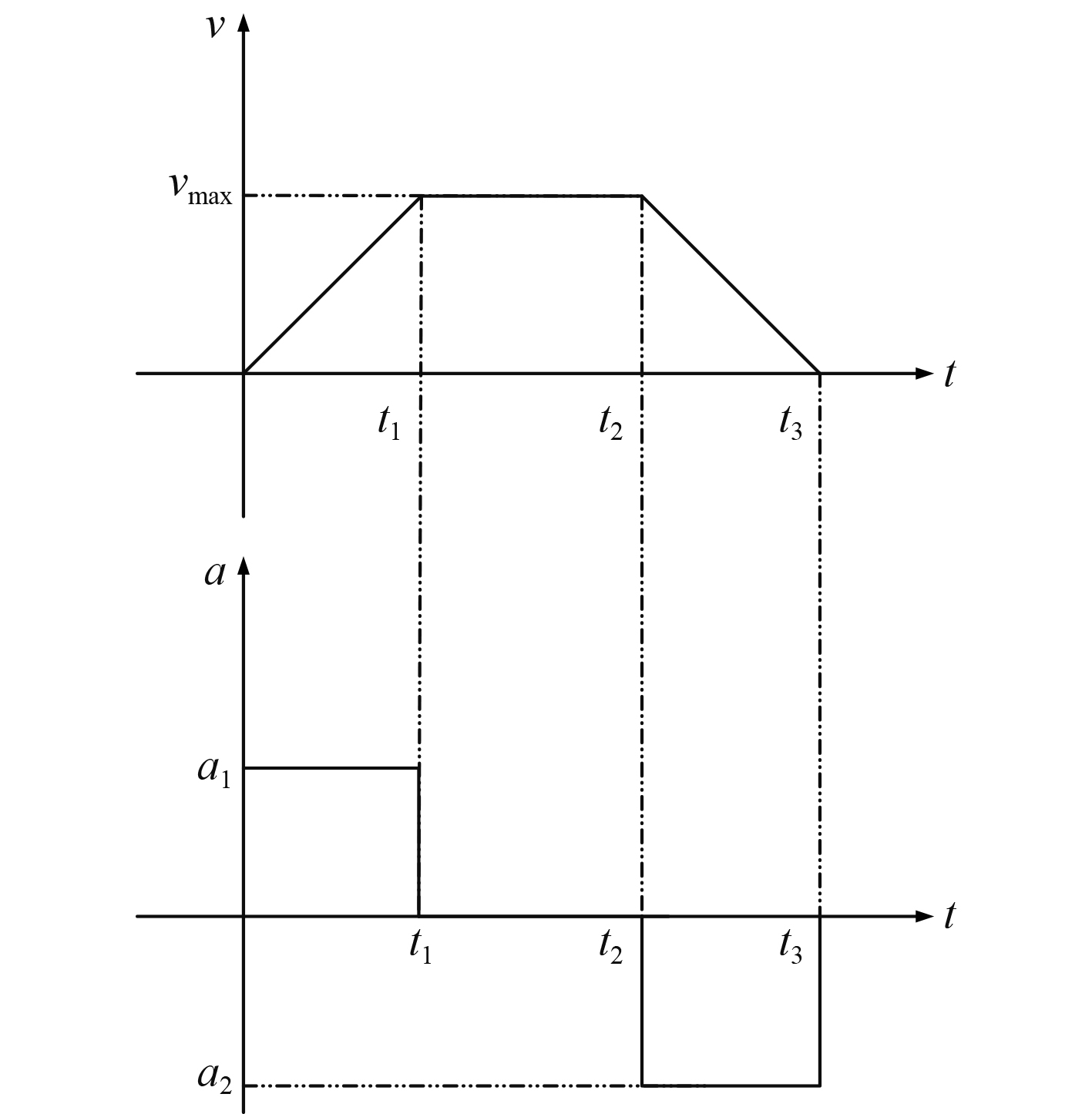
图 6 基于布谷鸟寻优的UUV推力规划方案示意图 Fig. 6 Schematic diagram of UUV thrust planning scheme based on Cuckoo algorithm |
为使UUV的运动规划方案尽可能地与实际贴合且能尽量少地避免UUV加速度的频繁变化,设该方案主要分为如图6所示的匀加速-匀速-匀减速3段。设定UUV到达目标定位点时速度即减为0,由此从理论上避免超调冲击。UUV克服海流做功
| $\begin{split} {f_1} = \displaystyle\frac{1}{2}mv_{\max }^2 + \displaystyle\frac{1}{2}\rho {C_X}({\alpha _c}){A_{TS}}V_c^2 \cdot {s_x} +\\ \;\;\;\displaystyle\frac{1}{2}\rho {C_Y}({\alpha _c}){A_{LS}}V_c^2 \cdot {s_y} \text{,}\end{split}$ | (13) |
| ${f_2} = k{t_3} \text{。}$ | (14) |
式中:
|
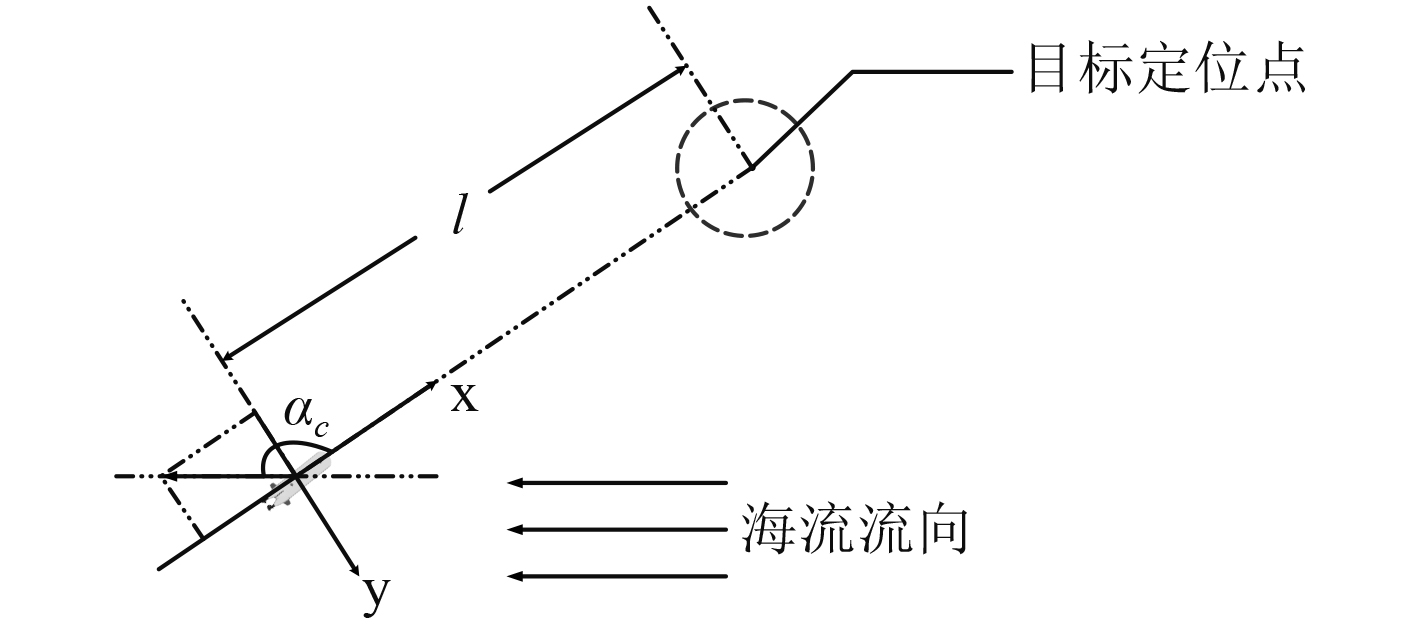
图 7 UUV海流流向角示意图 Fig. 7 Flow direction angle of UUV current |
根据前文设定,UUV抵近目标点的过程中运动的总距离即为UUV初始位置距目标定位点的距离
| $\left\{ {\begin{array}{*{20}{l}} {\left| {{a_1}} \right| \leqslant {a_{\max }}} \text{,}\\ {\left| {{a_2}} \right| \leqslant {a_{\max }}} \text{,}\\ {0 \leqslant {t_1} \leqslant {t_2} \leqslant {t_3}} \text{,}\\ {{a_1}{t_1} = - {a_2}({t_3} - {t_2})} \text{,}\\ {\displaystyle\int_0^{{t_1}} {{a_1}t{\rm{d}}t + \int_{{t_1}}^{{t_2}} {v{\rm{d}}t + \int_{{t_2}}^{{t_3}} {{a_2}t{\rm{d}}t = l} } } } \text{。} \end{array}} \right.$ | (15) |
根据上述内容,通过权重系数将2个优化子函数转换成本文的待优化单目标函数为:
| $J = {\tau _1}{f_1}{\rm{ + }}{\tau _{\rm{2}}}{f_{\rm{2}}}\text{,}$ | (16) |
根据约束条件进行化简,得到最终的优化目标函数:
| $\begin{array}{l} J = {\tau _1} \cdot \displaystyle\frac{1}{2}m{a_1}^2{t_1}^2{\rm{ + }}{\tau _1} \cdot \frac{1}{2}\rho {C_X}({\alpha _c}){A_{TS}}V_c^2 \cdot (l{\rm{ - }}{V_c}{t_3}\cos {\alpha _c}){\rm{ + }} \\ \;\;\;\;\;\; {\tau _1} \cdot \displaystyle\frac{1}{2}\rho {C_Y}({\alpha _c}){A_{LS}}V_c^2 \cdot ({V_c}{t_3}\sin {\alpha _c}){\rm{ + }}{\tau _2} \cdot k{t_3} \text{。} \\[-15pt] \end{array} $ | (17) |
其中,
基于布谷鸟寻优的最优运动规划主要解决UUV的速度、加速度及时间的最优分配问题,从而使UUV在该阶段的运动在满足约束条件的同时具有最优的能量消耗。布谷鸟寻优算法是一种模拟布谷鸟智能行为的仿生优化算法[14-16],利用布谷鸟特殊的繁殖方式和Lévy~
1)在搜索空间中随机产生10组满足安全约束的初始鸟窝。
2)根据以能耗为评价指标的目标函数
3)利用更新其他鸟窝的位置,然后测试更新后得到的新鸟窝位置,并与上一代鸟窝位置进行对比,选取对应的鸟窝位置中测试值较好的位置并将其保留至下一步运算。
| $x_i^{t + 1} = x_i^t + \alpha s \otimes H\left( {{p_a} - \varepsilon } \right) \otimes \left( {x_j^t - x_k^t} \right)\text{,}$ | (18) |
其中,
| $x_i^{t + 1} = x_i^t + \alpha L\left( {s,\lambda } \right)\text{。}$ | (19) |
其中,
4)随机产生一个服从均匀分布的
5)判断
根据上述布谷鸟优化过程,可以得到基于能耗最小的,UUV在距离目标定位点较远距离时,速度及加速度的最优规划方案。根据上述关于加速度的最优规划方案,可推知UUV在各阶段受到的合外力大小,则再结合已知的环境信息及力的分解与合成原理,可求得相应阶段的UUV推力规划方案。
4 算法仿真分析对各典型阵型下的UUV位姿保持需求分析,根据UUV携载通信设备的通信能力、动态控位能力以及UUV间安全距离,设定本节仿真试验中各从UUV的刚性守位区半径为30 m,柔性守位区半径为20 m。对UUV集群的三角形阵型保持能力进行仿真试验验证。设定目标阵型为三角形,其中主UUV位于阵型的几何中心处,始终进行精确控位,UUV集群的目标航向为70°。海流流速为1 m/s,流向为北偏东45°,如图8所示。各UUV的初始位置为随机生成的各自柔性守位区内某一点,仿真结果如图9所示。

|
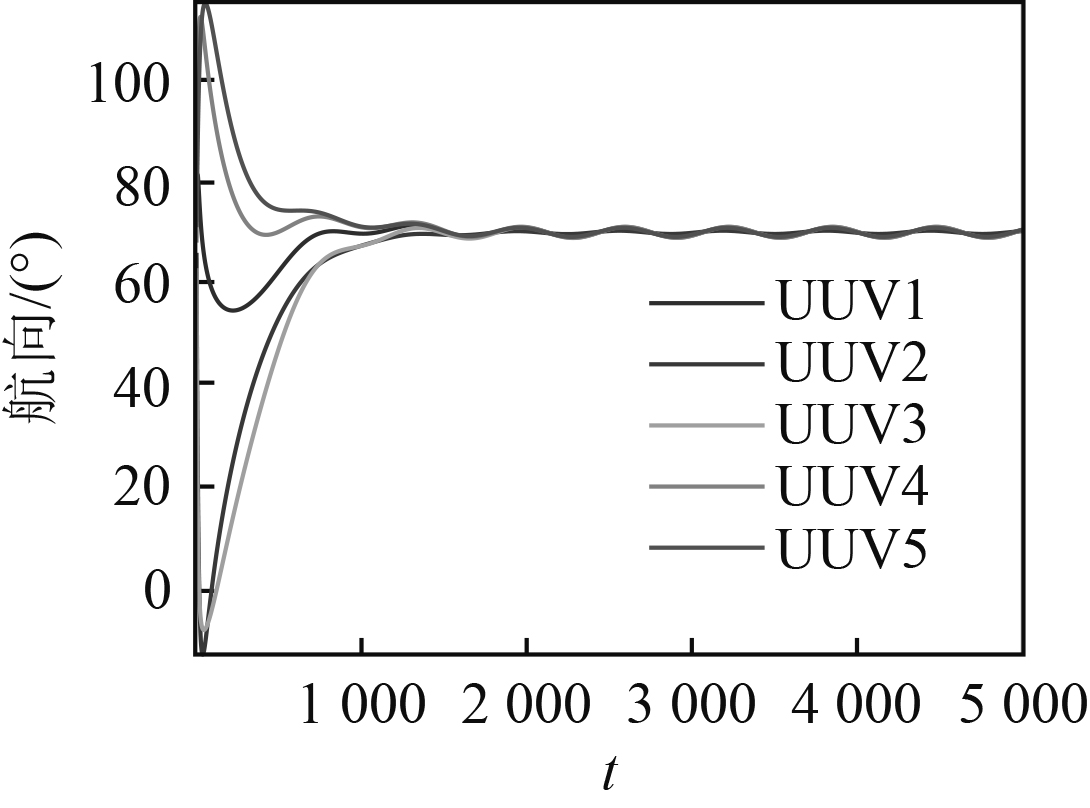
图 8 UUV集群三角形阵型保持过程的航向变化曲线 Fig. 8 Simulation diagram of UUV group triangle formation keeping |
|
图 9 UUV集群三角形阵型保持仿真图 Fig. 9 Course variation curve of UUV group triangle formation keeping process |
根据图9可知,对于初始航向及初始位置均不相同的UUV集群,当其目标阵型为三角形阵型时,各从UUV能够在海流的干扰下,通过本文设计的低能耗动态控位策略及控制方法,将自身位置始终保持在刚性守位区以内。结合UUV集群三角形阵型位姿保持需求分析,观察航向变化曲线可知,各UUV具备精确控制航向并保持目标航向的能力,即认为该控制策略及方法下的各UUV群员具备在目标定位区域保持自身位姿、目标阵位及目标航向的能力,即认为该UUV集群整体具备三角形阵型保持的能力。
5 结 语本文针对UUV集群在控位过程中存在的推进器动车频繁的问题,从环境约束、任务需求、测量信息处理、动态控位策略及方法设计几方面进行了研究。对主从式UUV集群在协同观探测过程中的动态控位问题进行描述建模,以三角形阵型为例,进行UUV的位姿保持需求分析。结合UUV集群的通信约束、安全约束、阵型保持约束等,设计了UUV集群的低能耗动态控位策略。当UUV处于刚性守位区以外时,建立UUV动态控位过程的能耗指标函数,设计一种基于布谷鸟寻优的全局最优运动规划方法,使UUV在水平面内距离目标定位点不同远近时均有一套相应的以能耗最优为目标的控制方案,并通过仿真试验验证该方案的合理性。
| [1] |
肖玉杰, 邱志明, 石章松. UUV国内外研究现状及若干关键问题综述[J]. 电光与控制, 2014, 21(2): 46-49, 89. DOI:10.3969/j.issn.1671-637X.2014.02.011 |
| [2] |
陈强. 水下无人航行器[M].北京: 国防工业出版社, 2014.
|
| [3] |
MORTEN Breivik, STIG Kvaal, PER Østby. From Eureka to K-Pos: Dynamic positioning as a highly successful and important marine control technology[J]. IFAC PapersOnLine, 2015, 48(16). |
| [4] |
朱光文. 我国海洋监测技术研究和开发的现状和未来发展[J]. 海洋技术学报, 2002, 21(2): 27-32. |
| [5] |
VINCENZO C, HASNES G. Reducing power demand and spikes in dynamic positioning: A model predictive control approach[C]. Oceans, 2015: 1–5.
|
| [6] |
ZHANG G, CAI Y, ZHANG W. Robust neural control for dynamic positioning ships with the Optimum-Seeking guidance[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2016, 1-10. |
| [7] |
曾舒婷. 低能耗长航时水下机器人方案的探究[J]. 机器人技术与应用, 2015(2): 33-36. DOI:10.3969/j.issn.1004-6437.2015.02.007 |
| [8] |
曹建春, 李聪. 推力分配优化算法在船舶动态控制中的应用研究[J]. 舰船科学技术, 2017, 39(6): 43-45. DOI:10.3404/j.issn.1672-7619.2017.06.009 |
| [9] |
余婷婷. 布谷鸟优化算法在船舶动力定位模拟器推力系统中的应用[J]. 舰船科学技术, 2018, 40(4): 58-60. DOI:10.3404/j.issn.1672-7649.2018.04.012 |
| [10] |
刘贵杰, 刘鹏, 穆为磊, 等. 采用能耗最优改进蚁群算法的自治水下机器人路径优化[J]. 西安交通大学学报, 2016, 50(10): 93-98. DOI:10.7652/xjtuxb201610014 |
| [11] |
高志伟, 代学武, 郑志达. 基于运动控制和频域分析的移动机器人能耗最优轨迹规划[J/OL]. 自动化学报: 1-12[2019-10-18]. https://doi.org/10.16383/j.aas.c180399.
|
| [12] |
陈冬. 面向协同观探测的UUV绿色动态控位方法研究[D].哈尔滨: 哈尔滨工程大学, 2020.
|
| [13] |
DENG J. Optimal algorithm for ship energy consumption based on dynamic distribution[J]. Ship Science and Technology, 2018, 40(22): 23-25. |
| [14] |
Xin-She YANG, Suash DEB. Cuckoo Search via Lévy flights[C]// 2009 World Congress on Nature & Biologically Inspired Computing (NaBIC). IEEE, 2009.
|
| [15] |
郭兆新. 布谷鸟搜索算法研究及其在AUV路径规划中的应用[D].哈尔滨: 哈尔滨工程大学, 2014.
|
| [16] |
YANG, Xin-She, DEB, Suash. Cuckoo search: recent advances and applications[J]. Neural Computing & Applications, 24(1): 169−174.
|
| [17] |
YANG X S, DEB S. Cuckoo Search: State-of-the-Art and Opportunities[C]// 2018.
|
| [18] |
EHSAN Teymourian, VAHID Kayvanfar, GH. M. Komaki. Enhanced intelligent water drops and cuckoo search algorithms for solving the capacitated vehicle routing problem[J]. Information Sciences, 2016, 334–335: 354-378. |
| [19] |
OUAARAB A, AHIOD B, YANG X S. Random-key cuckoo search for the travelling salesman problem[M]. 2015.
|
 2020, Vol. 42
2020, Vol. 42
