目前,水下航行器的动力主要由螺旋桨提供,其中导管螺旋桨具有推力大、效率高等特点,被广泛应用到水下航行器中。国内外对导管螺旋桨的敞水性能已经有了相当多的研究,导管螺旋桨桨叶的螺距比[1]、桨叶与导管的间隙[2]、导管的形状[3]都会对螺旋桨的性能产生影响,从而影响航行器的运动。槽道螺旋桨主要用于海洋船舶上,作为转向的辅助设备,可提供良好的操纵性。槽道螺旋桨的性能跟槽道的长度、横向流速的大小以及方向有很大的关系[4]。目前,对于流线型水下航行器的槽道螺旋桨数值计算研究不是很多。Alistair Palmer [5]通过水池实验来验证AUV不同航速和不同航向角时槽道螺旋桨的性能,发现不同航速和航向角对槽道螺旋桨的推力有明显的影响。谷海涛等[6]通过数值计算分析了槽道螺旋桨的大小和位置对水下机器人航行阻力大小的影响,对AUV的设计和优化有很大的参考价值。
本文以一种流线型高速ROV的结构外型为基础,使用计算流体力学软件Fluent对导管螺旋桨的水动力特性进行计算仿真,得到导管螺旋桨推力、扭矩及效率曲线,并与图谱曲线对比验证,证明了数值仿真的可行性。选取航行器上一个槽道螺旋桨,对其进行计算仿真。在无航速时,对槽道螺旋桨在不同转速下进行数值仿真模拟,得到桨叶在不同转速下产生的推力大小;在槽道螺旋桨一定转速下,航行器不同航速时,进行数值仿真模拟,得到槽道螺旋桨的性能曲线和压力云图。通过压力云图,可以直观地看到航行器表面的流场状况。最后通过流线型高速ROV受到的阻力与螺旋桨推力的对比,验证了流线型高速ROV设计的可行性。
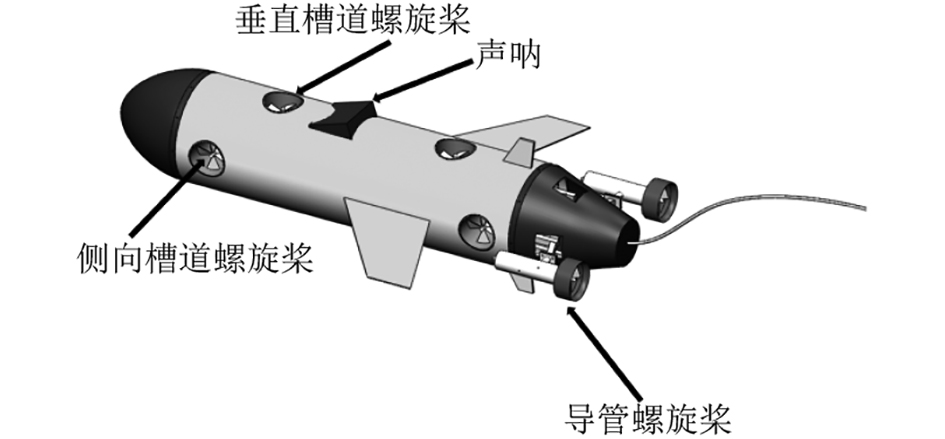
图1为流线型高速ROV的外观结构图,其长为1.7 m,外径为0.35 m,通过一根脐带电缆从母船供电以及通信,设计最大航速为5 kn。由2个No.37+Ka4-70导管螺旋桨作为主推,2个槽道螺旋桨作为侧向运动推进器,2个槽道螺旋桨作为垂直运动推进器。
|
图 1 流线型高速ROV的外观结构 Fig. 1 The structure of streamline high speed ROV |
本文研究的螺旋桨周围的流场可假设为恒定不可压缩的,因此根据物理守恒定律,包括质量守恒和动量守恒定律,不可压缩流体的控制方程如下:
| $ \frac{\partial {u}_{i}}{\partial {x}_{i}}=0{\text{,}} $ | (1) |
| $\begin{split} \frac{\partial {u}_{i}}{\partial t}+\frac{\partial \left({u}_{i}{u}_{j}\right)}{\partial t}=&-\frac{1}{\rho }\frac{\partial p}{\partial {x}_{i}}+{g}_{i}+\\&\mu \frac{\partial }{\partial {x}_{j}}\left(\frac{\partial {u}_{i}}{\partial {x}_{j}}+\frac{\partial {u}_{j}}{\partial {x}_{i}}\right)-\frac{\partial }{\partial {x}_{j}}\overline{{u}_{i}^{'}{u}_{j}^{'}}{\text{。}} \end{split}$ | (2) |
式中:ui,uj为速度分量时均值,i,j=1,2,3;xi,xj为坐标的3个分量(i,j=1,2,3);p为压力;ρ为流体密度;μ为流体运动的黏性系数;t为时间;gi为重力加速度分量。
1.2 湍流模型选取由于方程(2)是不封闭的,需引入湍流模型。在本文的计算中,选用常用的包含湍流动能k和能量扩散ε的RNG k-ε湍流模型,其表达形式如下:
| $ \rho \frac{{\rm{d}}k}{{\rm{d}}t}=\frac{\partial }{\partial {x}_{i}}\left[\left(\mu +\frac{{\mu }_{t}}{{\sigma }_{k}}\right)\frac{\partial k}{\partial {x}_{i}}\right]+{G}_{k}+{G}_{b}-\rho \varepsilon -{Y}_{M}{\text{,}} $ | (3) |
| $\begin{split} \rho \frac{{\rm{d}}\varepsilon }{{\rm{d}}t}=&\frac{\partial }{\partial {x}_{i}}\left[\left(\mu +\frac{{\mu }_{t}}{{\sigma }_{k}}\right)\frac{\partial \varepsilon }{\partial {x}_{i}}\right]+\\&{C}_{{1g}}\frac{\varepsilon }{k}\left({G}_{k}+ {C}_{{3g}}{G}_{b}\right)+{C}_{\rm{2g}}\rho \frac{{\varepsilon }^{2}}{k} {\text{。}}\end{split}$ | (4) |
式中:Gk表示由层流速度梯度而产生的湍动能项;Gb为由浮力产生的湍动能项;YM表示在可压缩流动中,湍流膨胀对总的耗散率的贡献项;ρ为流体密度;μ为流体运动的黏性系数;μt为湍流粘性系数,μt=ρCμk;C1g,C2g,C3g为常量。
2 导管螺旋桨的敞水性能验证 2.1 几何模型的建立考虑到流线型高速ROV的大小以及对推进器性能的要求,本文选取No.19A+Ka4-70导管螺旋桨作为其主推进器。首先将螺旋桨的曲面型值利用空间坐标变换公式[7]转换成三维数值点,再将这些点导入到三维设计软件Solid-Works中,利用Solid-Works得到完整的导管螺旋桨几何模型。图2为导管螺旋桨几何模型,螺旋桨直径为150 mm,螺距比为1.2,盘面比为0.7。

|
图 2 导管螺旋桨三维模型 Fig. 2 Modeling of the thruster |
为了得到螺旋桨周围流场较为真实的数据,同时为提高计算效率,采用混合网格方式,将螺旋桨的计算流域划分为3个区域,以便对不同区域进行网格加密。计算域V1是直径为6倍导管直径的圆形区域,其入流段长度为3倍导管直径,出流段长度为5倍导管直径,此区域采用结构化网格进行划分。计算域V2是网格加密区域,采用非结构网格进行划分,其直径为1.5倍导管直径的圆形区域,长度为2倍导管直径。计算域V3是转动区域,用来模拟螺旋桨的转动,采用非结构网格进行划分。图3为计算流域图。

|
图 3 计算流域 Fig. 3 Graph of calculation field |
由于导管螺旋桨桨叶曲面形状复杂,因而在螺旋桨附近计算域设立加密区域,采用非结构网格进行划分。同时为了减小计算量,在V1区域采用结构化网格进行划分。2个网格之间通过设置interface连接。螺旋桨的旋转采取旋转坐标体系MRF进行模拟,设置为绕轴以角速度n=1600 r/min旋转。通过设置不同大小的网格进行比较,最终确定了总数目为160万的网格数可得理想的收敛结果。图4为网格划分图。

|
图 4 网格划分图 Fig. 4 Grids of calculation domain |
对于导管螺旋桨,桨叶在转动时,由于叶面两边的压差不同,会在桨叶上产生一定的推力。对于导管,其前后也会产生压力差,增大导管螺旋桨的推力。图5给出了不同进速下导管螺旋桨的敞水性能,并与图谱进行对比。其中螺旋桨的推力系数KTp、转矩系数KQ、导管的推力系数KTd、导管螺旋桨总推力系数KT= KTp+KTd、导管螺旋桨效率η0、进速系数J定义表示为:

|
图 5 导管螺旋桨敞水曲线图 Fig. 5 Open water curves of ducted propeller |
| $ {K}_{{Tp}}=\frac{{T}_{p}}{\rho {n}^{2}{D}^{4}} {\text{,}}$ | (5) |
| $ {K}_{\rm{Td}}=\frac{{T}_{d}}{\rho {n}^{2}{D}^{4}} {\text{,}}$ | (6) |
| $ {K}_{\rm{Q}}=\frac{Q}{\rho {n}^{2}{D}^{5}}{\text{,}} $ | (7) |
| $ {{\rm{\eta}} }_{0}=\frac{{K}_{T}}{{K}_{Q}}\frac{J}{2{\text{π}} }{\text{,}} $ | (8) |
| $ J=\frac{{V}_{A}}{nD}{\text{。}} $ | (9) |
式中:Tp为螺旋桨的推力;Q为螺旋桨的转矩;Td为导管的推力;n为转速;D为螺旋桨的直径;ρ为流体的密度;VA为进速。从图5可以看出,对于No.19A+Ka4-70型螺旋桨,本文中CFD模拟的计算值与图谱值吻合较好。
3 槽道螺旋桨的性能验证 3.1 计算模型及设置为了简化计算,本文只保留流线型高速ROV的主体部分,忽略掉附属物影响,并且只单独对一个槽道螺旋桨进行性能验证。选取前端侧向推进器作为仿真对象,螺旋桨中心距前导流罩长X=100 mm,如图6所示。槽道螺旋桨仍然使用Ka4-70浆叶,直径D=110 mm,螺距比为1.2,浆叶数为4,盘面比为0.7。

|
图 6 槽道螺旋桨计算模型 Fig. 6 Modeling of channel thrusters |
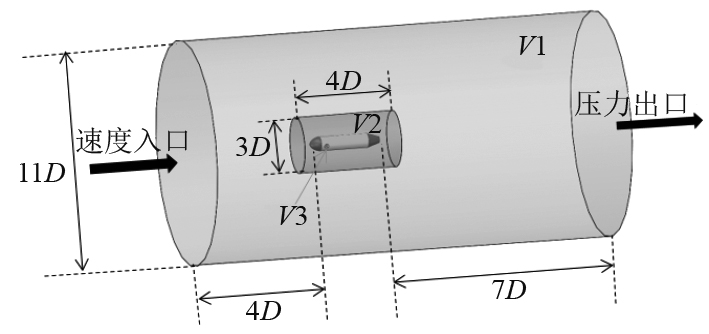
流体域采用混合网格方式建立,共分为3个区域。如图7所示,最外区域V1是直径为11D圆形区域,入流段长度为4D,出流段长度为7D,该区域采用结构网格形式划分。过渡区域V2是直径为3D圆形区域,长度为4D,该区域采用非结构网格形式划分。最内区域V3的直径为1.01D,该区域采用非结构网格形式划分,采取滑移网格模式作为旋转区域,模拟螺旋桨的旋转。
|
图 7 槽道螺旋桨计算区域 Fig. 7 Calculation field of channel thrusters |
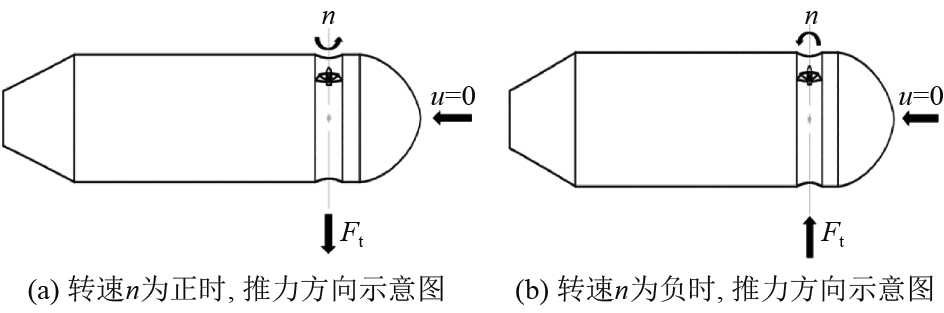
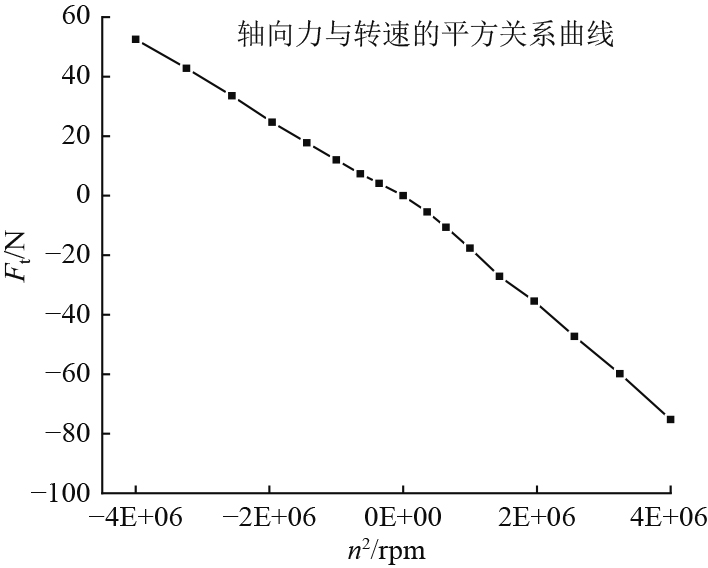
当流线型高速ROV的航速u为0时,将螺旋桨设置不同的转速。转速范围设置为0~2 000 r/min,不同转向下螺旋桨对应的推力方向如图8所示。通过Fluent仿真计算,得到航速u为0时,螺旋桨的轴向推力Ft与转速n平方的关系,如图9所示。由图可知,总推力的大小与转速的平方成正比。同时也可看出螺旋桨正转时,推力的线性曲线斜率要比逆转时大,这是因为螺旋桨的构造以及桨叶的位置决定的。
|
图 8 不同方向转速时,推力示意图 Fig. 8 Diagram of thrust direction when speed n is different |
|
图 9 螺旋桨的轴向推力曲线 Fig. 9 Curve of axial thrust in channel propeller |
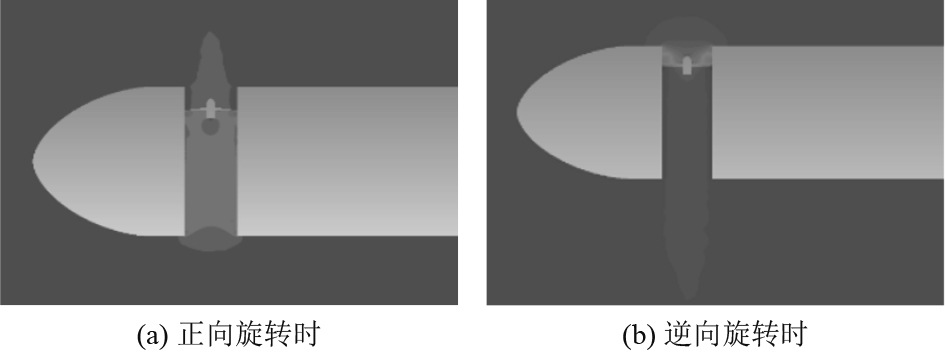
螺旋桨转速为1000 r/min和–1000 r/min时,其表面的压力云图如图10所示。由图可得,当螺旋桨正转时,在桨叶上表面产生低压区,在桨叶下表面产生高压区,使得螺旋桨表面产生压力差,从而形成推力。
|
图 10 压力云图 Fig. 10 Contours of static pressure at different turn |
当流线型高速ROV向前运动时,设置推进器为正向旋转,转速n=2 000 r/min。改变航速u的大小,通过仿真计算得到不同航速时,流线型高速ROV受到的推力和扭矩大小,并转换成无量纲量推力比Kf、扭矩比Kn和速度比η[8]。
| $ {K}_{f}=\frac{{T}_{c}(u,n)}{{T}_{c}(0,n)}{\text{,}} $ | (10) |
| $ {K}_{n}=\frac{{N}_{T}(u,n)}{{N}_{T}(0,n)}{\text{,}} $ | (11) |
| $ {\eta }=\frac{{u}}{{{u}}_{{j}}}=\frac{{u}}{\sqrt{\dfrac{{{T}}_{{c}}\left(0,{n}\right)}{{\rho }{A}}}}{\text{。}} $ | (12) |
式中:Tc(u,n)和NT(u,n)为不同航速时,一定转速下,水下航行器的横向推力和扭矩;Tc(0,n)和NT(0,n)是航速为0时,一定转速下,水下航行器的横向推力和扭矩;u是航速;uj是航速为0时,不同转速下槽道出口的速度。
将计算得到的值,根据公式转化为无量纲值,并做推力比Kf、扭矩比Kn与速度比η对应的曲线,如图11所示。可看出,随着航行器航速的增加,槽道推进器的推力迅速减小。当速度比达到1.5时,推力比只有0.16。当速度比继续增加时,推力比小幅度增加,但是比值仍然小于0.2。扭矩比也有同样的变化,当速度比达到1.3时,扭矩比达到最小,然后缓慢增加。

|
图 11 不同航速时槽道螺旋桨的推力比和扭矩比与速度比的关系 Fig. 11 Contours of static pressure at different turn |
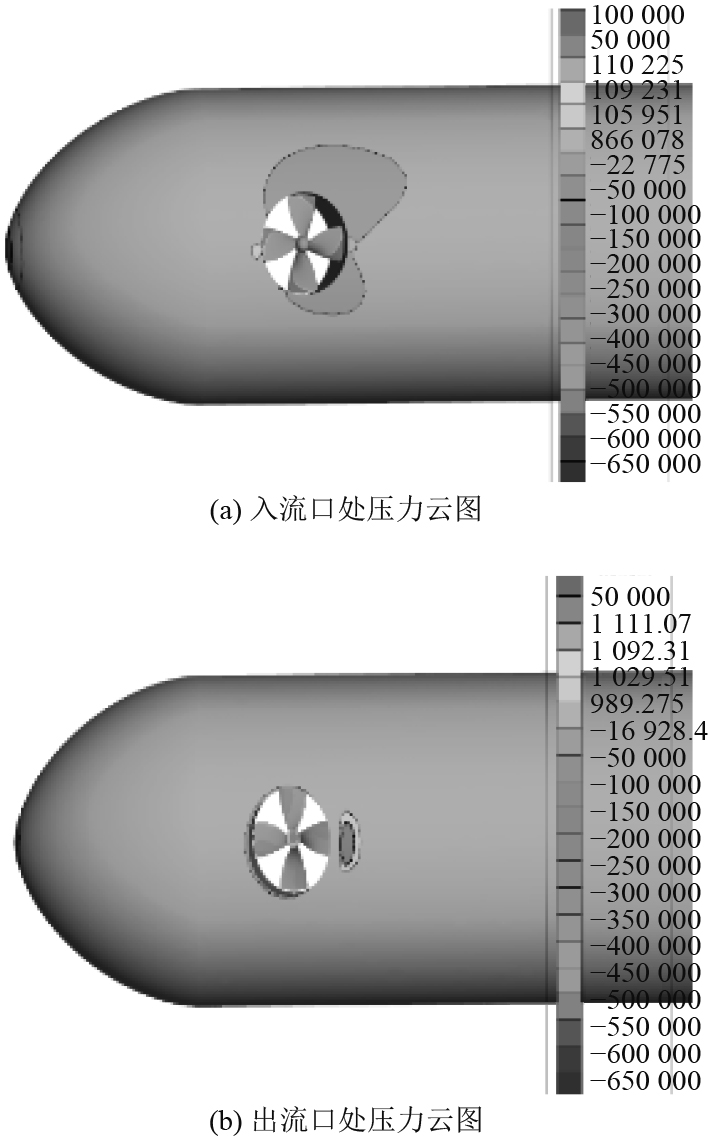
图12和图13分别为流线型高速ROV航速为2 kn和4 kn时,其表面的压力云图。从图可以明显看出,保持螺旋桨转速不变,当航速逐渐增大时,出流口附近表面的压力明显减小,而入流口附近则增大。这样在航行器表面产生一个与推进器推力相反的压力,导致横向推力明显减小。
|
图 12 航速2 kn时表面压力云图 Fig. 12 Contours of static pressure at surface when the vehicle speed is 2 kn |

|
图 13 航速4 kn时表面压力云图 Fig. 13 Contours of static pressure at surface when the vehicle speed is 4 kn |
水下航行器在运动时,主要受到摩擦阻力和粘压阻力的影响。随着航速的增加,其受到的总阻力会逐渐增大。为了实现流线型ROV的高速航行,需要螺旋桨提供足够的推力。该流线型高速ROV通过2个平行的导管螺旋桨提供直航时的推力,2个平行的横向槽道螺旋桨提供横向运动时的推力,2个平行的垂直槽道螺旋桨提供垂直运动时的推力。本文通过数值仿真计算,得到流线型高速ROV直航速度u为1~6 kn时受到的纵向(x轴)阻力值Fx,横向运动速度uy为0.5~2 kn时受到的横向(y轴)阻力值Fy,垂直运动速度uz为0.5~2 kn时受到的垂直方向(z轴)阻力值Fz。
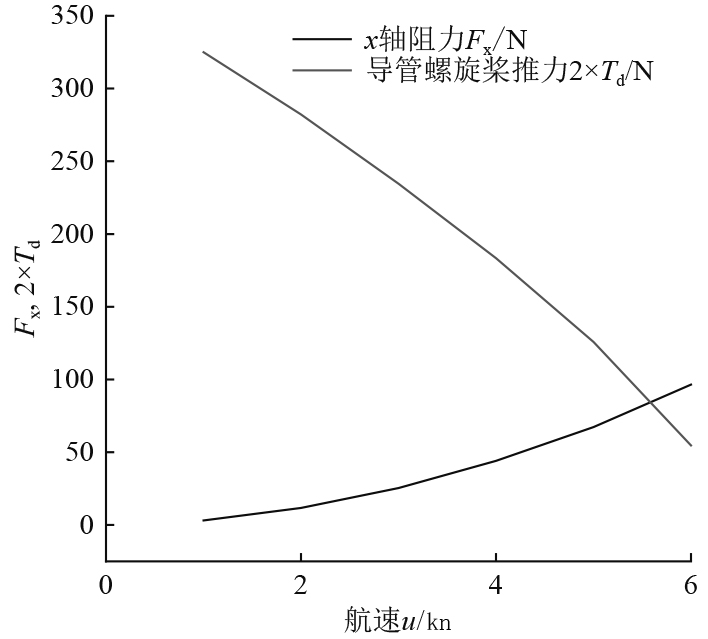
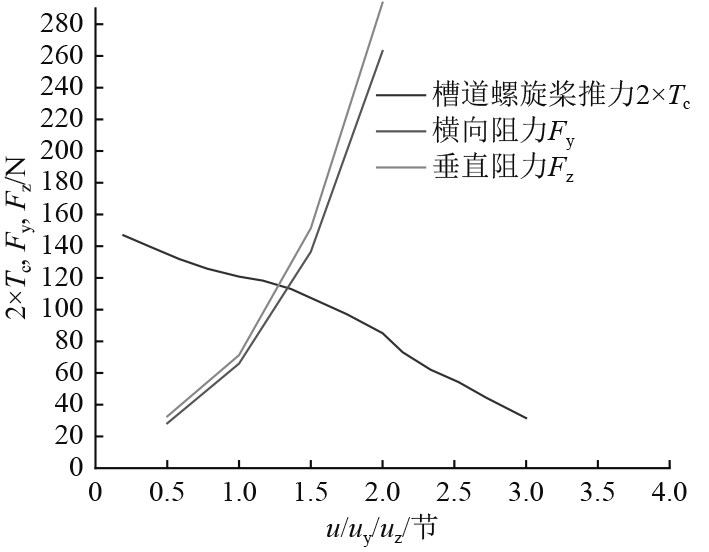
图14为不同航速u时,纵向阻力值Fx与导管螺旋桨推力值Td的曲线图。可以看出,随着航速的增加,流线型高速ROV受到的阻力逐渐增大,同时导管螺旋桨的推力逐渐减小。当航速超过5.6 kn时,2个导管螺旋桨所提供的推力则不能满足流线型高速ROV受到的阻力。图15为不同直航速度时2个槽道螺旋桨的推力值曲线、不同横向运动速度时受到的横向阻力值曲线以及不同垂直运动速度时垂直方向受到的阻力值曲线对比。从图中可以得出流线型高速ROV不同直航速度时,槽道螺旋桨的推力可使得流线型高速ROV横向和垂直运动的最大速度。
|
图 14 不同航速时阻力值Fx与导管螺旋桨推力值Td曲线 Fig. 14 Curves of resistance value Fx and thrust value Td at different vehicle speed |
|
图 15 不同航速时,阻力值Fy,Fz以及槽道螺旋桨推力值Tc的曲线 Fig. 15 Curves of resistance value Fy,Fz and thrust value Tc at different vehicle speed |
1)对No.37+Ka4-70导管螺旋桨进行数值模拟计算,将结果和图谱对比表明,仿真值和实际图谱值误差在5%~15%之内。使用Fluent软件可以较为真实地预报螺旋桨的敞水性能,验证了数值仿真的可行性。
2)无航速时,对单独一个槽道螺旋桨仿真模拟,得到了桨叶在不同转速下产生的推力大小,其大小与转速的平方满足线性关系,并且正向旋转时的系数要比负向旋转时大。保持桨叶转速不变,对水下航行器不同航速时槽道螺旋桨的仿真模拟,得到了槽道螺旋桨的推力比和扭矩比与速度比对应的关系,可发现当速度比到达1.5时,槽道螺旋桨的效率达到最小。通过压力云图可以直观地看到,当航速逐渐增大时,在航行器表面会产生负向压力,导致螺旋桨的效率减小。
3)通过水下航行器受到的阻力与螺旋桨推力的对比,本文的流线型高速ROV直航时,可以达到5 kn的设计速度。当直航速度在3 kn以内时,槽道螺旋桨产生的推力可以满足流线型高速ROV以0.5 kn以上的速度做横向和垂向运动。
| [1] |
王国强, 盛振邦. 船舶推进[M]. 北京: 国防工业出版社, 1985.
|
| [2] |
丁一文. 水下潜器系统中导管螺旋桨水动力性能及其梢涡变化对桨叶推力特性的影响[D]. 广州: 华南理工大学, 2018. DING Yi-wen, Hydrodynamic performance of duct propeller and influence of tip vortex variation on thrust characteristics of propeller blades in underwater submersible system[D]. Guangzhou: South China University of Technology, 2018. |
| [3] |
吴家鸣, 廖贯宇, 赖宇锋, 等. 导管剖面设计对导管螺旋桨水动力特性的影响[J]. 舰船科学与技术, 2017, 39(11): 38-43. WU Jia-ming, LIAO Guan-yu, LAI Yu-feng, et al. The influence of duct profile design on hydrodynamic characteristics of ducted propeller[J]. Ship Science and Technology, 2017, 39(11): 38-43. |
| [4] |
刘辉, 代燚, 冯榆坤, 等. 船舶艏侧推器推力减缩试验与数值计算研究[J]. 中国造船, 2017, 58(4): 1-13. LIU Hui, DAI Yi, FENG Yu-kun, et al. Experimental measurement and numerical simulation of thrust reduction for bow thruster[J]. Shipbuilding of China, 2017, 58(4): 1-13. DOI:10.3969/j.issn.1000-4882.2017.04.001 |
| [5] |
SAUNDERS A. , NAHON M.. The effect of forward vehicle velocity on through-body AUV tunnel thruster performance[C]. Proceedings of Oceans 2002 Conference, MTS/IEEE, Biloxi, MI, USA.
|
| [6] |
谷海涛, 林扬, 胡志强. 带槽道桨水下机器人阻力特性的数值分析[J]. 微计算机信息, 2007, 23(5-2): 227-229. GU Hai-tao, LIN Yang, HU Zhi-qiang. Numerical analysis on the resistance of autonomous underwater vehicle with tunnel thruster[J]. Microcomputer Information, 2007, 23(5-2): 227-229. |
| [7] |
姚震球, 高慧, 杨春蕾. 螺旋桨三维建模与水动力数值分析[J]. 船舶工程, 2008, 30(6): 23-26. YAO Zhen-qiu, GAO Hui, YANG Chun-lei. 3D modeling and numerical analysis for hydrodynamic force of propeller[J]. Ship Engineering, 2008, 30(6): 23-26. DOI:10.3969/j.issn.1000-6982.2008.06.007 |
| [8] |
ALISTAIR Palmer, GRANT E. Hearn, PETER Stevenson. Experimental testing of an autonomous underwater vehicle with tunnel thrusters[C]. First International Symposium on Marine Propulsors. June 2009.
|
 2020, Vol. 42
2020, Vol. 42
