伴随着相关技术的快速发展,水下无人艇(UUV)多被用于布雷排雷、侦察等军事用途以及勘探资源、沉船打捞、水下电缆铺设等民事用途[1]。UUV具备超高的隐蔽能力,有较强的续航力、作战和突击能力等诸多优势,但其自我保护力不强,水下联络较困难,不易实现双向、及时、远距离的通信,且容易受环境影响,掌握敌方情况比较困难。水面无人艇(USV)可承担环境监测、监视侦察、远程打击、搜捕、水文地理勘察、远程通信等任务,但USV在水面作业目标大,容易被发现,防御能力弱,且易较大遭到海面风浪的影响。无论是UUV还是USV,都有一定的局限性[2-3],因此,为了更好发挥各自的优势,实现两者的有效结合,发展一种以水下航行为主、可兼顾水面航态的UUV已经势在必行,深入研究该型UUV的快速性、操纵性和功能性显得尤为重要。多学科设计优化一般用在比较复杂工程系统和子系统,并且统筹各系统的彼此相关要素[4],因为设计过程中,关系到多个学科范围,进行UUV的综合优化是无人艇设计的主要部分[5]。因此本文基于团队自编多学科综合优化软件,并进行了必要的改进,经过多种优化算法进行计算分析,得出了优良的计算结果,体现了优化软件的准确性和可靠性,该计算结果为新艇型的开发设计提供了有效的数据支撑和参考依据[6-7]。
1 无人艇优化设计数学模型 1.1 主艇体设计预计把UUV的主艇体分成首部、平行中体和尾部型线部分。其设计艇型的首段为半椭圆,尾段是一段圆锥体,可以适当与平行中体流线型过渡,平行中体可以适当增大长度。为能同时起到兼顾水面的效果,可搭载一种可伸缩支柱平台,在其上部搭载天线、传感器等一些装置,更高效的监测水面与水下,如图1所示。
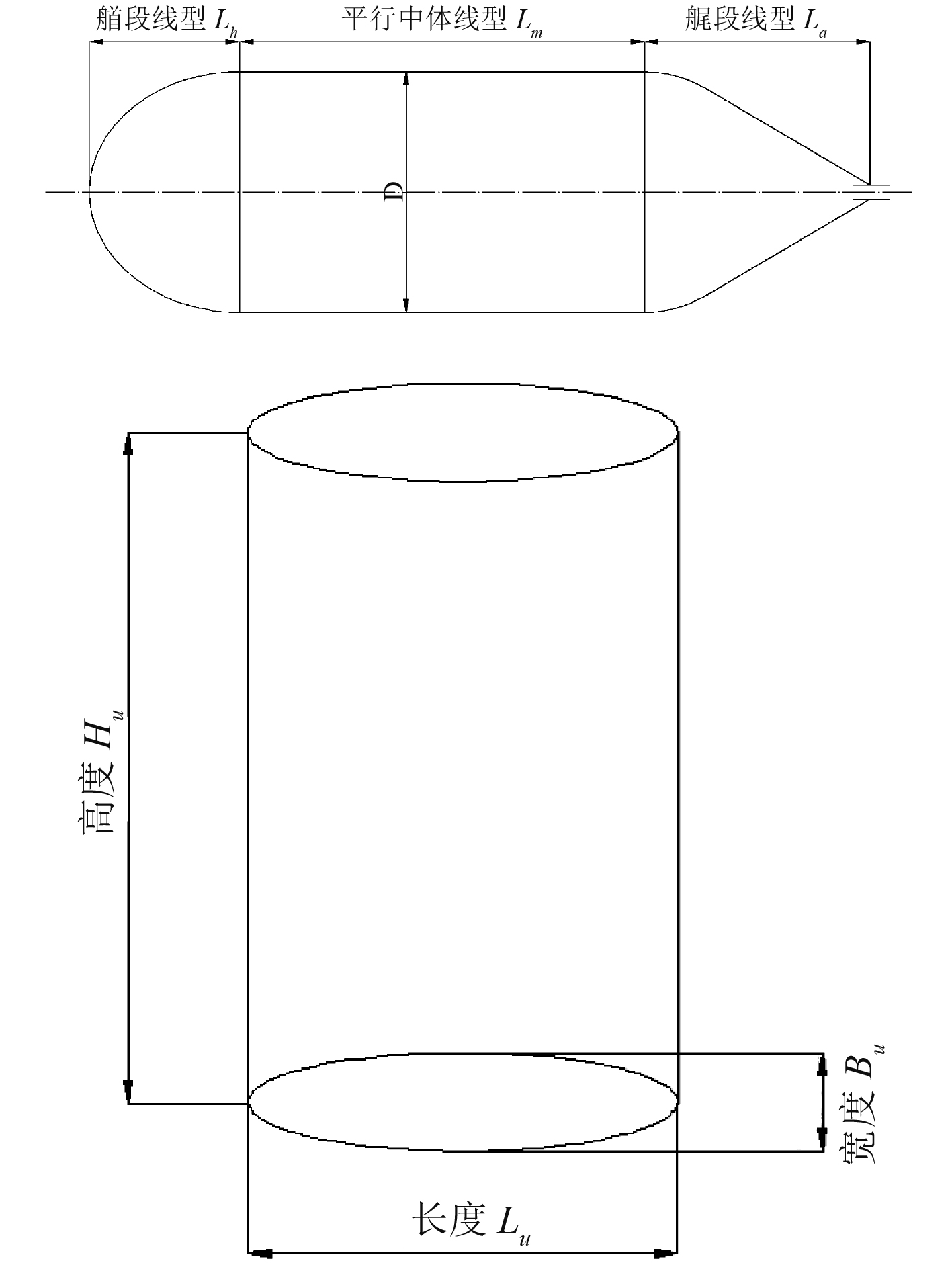
|
图 1 主体和柱体基本型线图 Fig. 1 Basic profile of main body and column |
在深入研究多种回转体形状几何特征基础上,阻力性能AUTOSUB型回转型深潜器阻力性能相对较佳[8]。本文初步设计主艇体艇型参考AUTOSUB型,对其进行改进,以更好起到对水面航态的兼顾性目的。
1.2 优化数学模型 1.2.1 设计变量24个设计变量:首段
1)快速性子目标函数
参考并选择海军系数公式:
| ${f_1}(X) = {C_{sp}}\left( x \right) = \frac{{{\Delta ^{2/3}} \cdot {V_s}^2}}{{{R_t}/{\eta _0} \cdot {\eta _H} \cdot {\eta _R} \cdot {\eta _S}}}{\text{。}}$ | (1) |
本文水下无人航行器以水下航行为主,忽略兴波阻力的影响,总阻力为:
| ${R_t} = {R_f} + {R_{pv}} + {R_{ap}} = \frac{1}{2}\rho {V_S}^2S\left( {{C_f} + {C_{pv}} + {C_{ap}}} \right){\text{。}}$ | (2) |
2)操纵性子目标函数
UUV的航行可从水平面和垂直面运动两方面探讨,共选择水平面稳定性横准数、相对回转半径、升速率3个指标构成操纵性的目标函数,即
| ${f_2}\left( X \right) = {C^{'{\beta _1}}} \cdot {\left( {1/{C_{RS}}} \right)^{{\beta _2}}} \cdot V_\chi ^{'{\beta _3}}{\text{,}}$ | (3) |
根据相关经验,无因次稳定性横准数和升速率越大则结果更优,相对回转半径越小则结果更优,式中
其中水平面稳定性横准数
| $C = {Y_v}{N_r} - {N_v}({Y_r} - m{u_1}){\text{,}}$ | (4) |
无因次稳定性衡准数
| $C' = C/\frac{1}{4}{\rho ^2}{L^6}{V^2} = {Y_v}^\prime {N_r}^\prime - {N_v}^\prime ({Y_r}^\prime - m'){\text{,}}$ | (5) |
相对回转半径
| ${C_{RS}} = \frac{{{R_S}}}{L} = \frac{1}{{r_s^{'}}} = \frac{1}{{{K^{'}}\delta }} = \frac{{N_v^{'}\left( {{m^{'}} - Y_r^{'}} \right) + N_r^{'}Y_v^{'}}}{{N_v^{'}Y_\delta ^{'} - N_\delta ^{'}Y_v^{'}}} \cdot \frac{1}{\delta }{\text{,}}$ | (6) |
升速率
| $\frac{{\partial {V_{{x^{'}}}}}}{{\partial {\delta _h}}} = - \frac{{{V^3}}}{{{m^{'}}gh}}\Bigg[\frac{{M_{{\delta _h}}^{'}}}{{Z_{{\delta _h}}^{'}}} - \frac{{M_w^{'}}}{{Z_w^{'}}} - \frac{{M_\theta ^{'}}}{{Z_w^{'}}}\Bigg]Z_{{\delta _h}}^{'}{\text{,}}$ | (7) |
其中潜伏角为:
| $_{}\chi = - \frac{1}{{M_\theta ^{'}}}Z_{{\delta _s}}^{'} \cdot l_{cs}^{'}{\text{。}}$ | (8) |
3)功能性子目标函数
在监测功能的优化设计过程中,内部因素以及外部因素都会对其有一定影响,对各项数据进行一系列的市场调研,进行模糊评判多个变量特征,因为这些特征符号不一,而且不在一个量级,因此在构造特征函数时,需要将其进行统一标准。通过模糊理论,并按照这些特征项的本质含义和实践统计,得出每一项具有实际意义的隶属度值,构造隶属度函数。对其综合评判并且进行响应面公式拟合得出各项系数,进而得出目标函数如下:
| $\begin{split} {f_3}(X) =&Y = {\rm{0.266}} + {\rm{0.190}}{{X}_{\rm{1}}} + {\rm{0.237}}{{X}_{\rm{2}}} +\\ &{\rm{0.063}}{{X}_{\rm{3}}} + {\rm{0.317}}{{X}_{\rm{4}}} - {\rm{0.405}}{{X}_{\rm{5}}} + {\rm{0.0293}}{{V}_s}{\text{。}}\end{split}$ | (9) |
显然,目标函数值
4)总目标函数
| $F(X) = {f_1}{(X)^{{\varepsilon _1}}}*{f_2}{(X)^{{\varepsilon _2}}}*{f_3}{(X)^{{\varepsilon _3}}}{\text{,}}$ | (10) |
式中:
1)浮性约束
无人艇优化计算后得到的排水体积,与设计的主艇体和支柱体的排水体积之和一致:
| $\nabla = {\nabla _1} + {\nabla _2}{\text{。}}$ | (11) |
2)推力阻力平衡约束
螺旋桨有效推力与所受到阻力一致:
| ${N_p}{K_T}\rho {N^2}D_P^4(1 - t) = {R_t}{\text{。}}$ | (12) |
3)转矩平衡约束
螺旋桨通过轴系收到的转矩与螺旋桨受到的水动力矩一致:
| $\frac{{{\eta _R}{\eta _s}{P_s}}}{{2\text{π} N}} = {K_Q}\rho {N^2}D_p^5{\text{。}}$ | (13) |
4)定深直线航行平衡纵倾角约束
能够使UUV在水中一定深度直航稳定运动时,纵倾角不大于10°。
5)定深直线航行平衡舵角约束
UUV在水中一定深度直航时,不排除外流场不稳定等因素的干扰,促使必须转尾舵的舵角来恢复平衡,一般这个舵角不超过在±5°。
2 优化算法及综合优化计算分析 2.1 优化算法 2.1.1 遗传算法遗传算法(GA)其主要原理是借鉴并根据大自然的物种进化的原则,精选出一种最佳解决方案的过程[9-10]。按照“物竞天择、适者生存”的原理,将最优值的求解过程表示成个体的适者生存过程,并通过选择、交叉、变异等使个体群逐代进化,输出为全局最优解。
2.1.2 混沌算法混沌优化算法(CA)是一种新的优化算法,具有非线性、遍历性、随机性等特点。一个混沌变量具有几个方面的特点:随机性;遍历性,混沌变量可以不重复历经空间内所有状态;规律性。
2.1.3 粒子群算法粒子群算法(PSO)是借鉴鸟类觅食现象而提出的一种新型优化算法,其特点具有易实现、收敛快、精度高等[11-14]。粒子群算法流程图如图2所示。
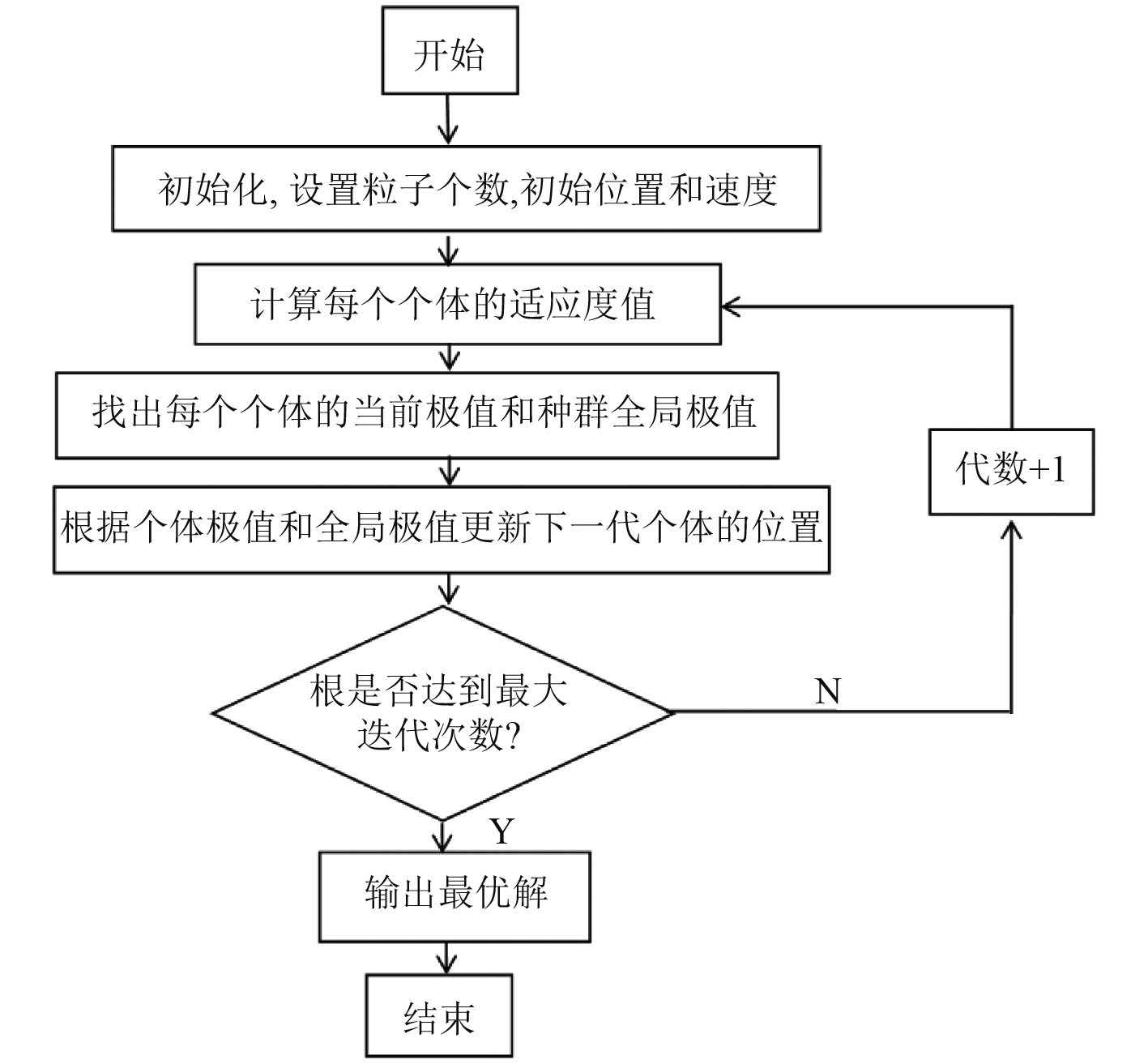
|
图 2 PSO算法的基本流程图 Fig. 2 Flow chart of PSO algorithm |
本文的快速性、操纵性和功能特性3个系统的初始权重设定如表1所示。采用遗传、混沌和粒子群3种算法进行计算。
|
|
表 1 各优化系统初始权重设置 Tab.1 Set the initial weights of the optimization system |
主要的数据如下设定:选取遗传代数为1000~6000,进化权重设成0.5,种群规模设成400,分别进行多次计算,选取各代数的最好结果,如表2所示。
|
|
表 2 不同计算次数的计算结果 Tab.2 The calculation results of different calculation number |
由表2计算结果可以得出,约束条件均在99%以上。遗传代数对目标函数值的影响如图3所示。
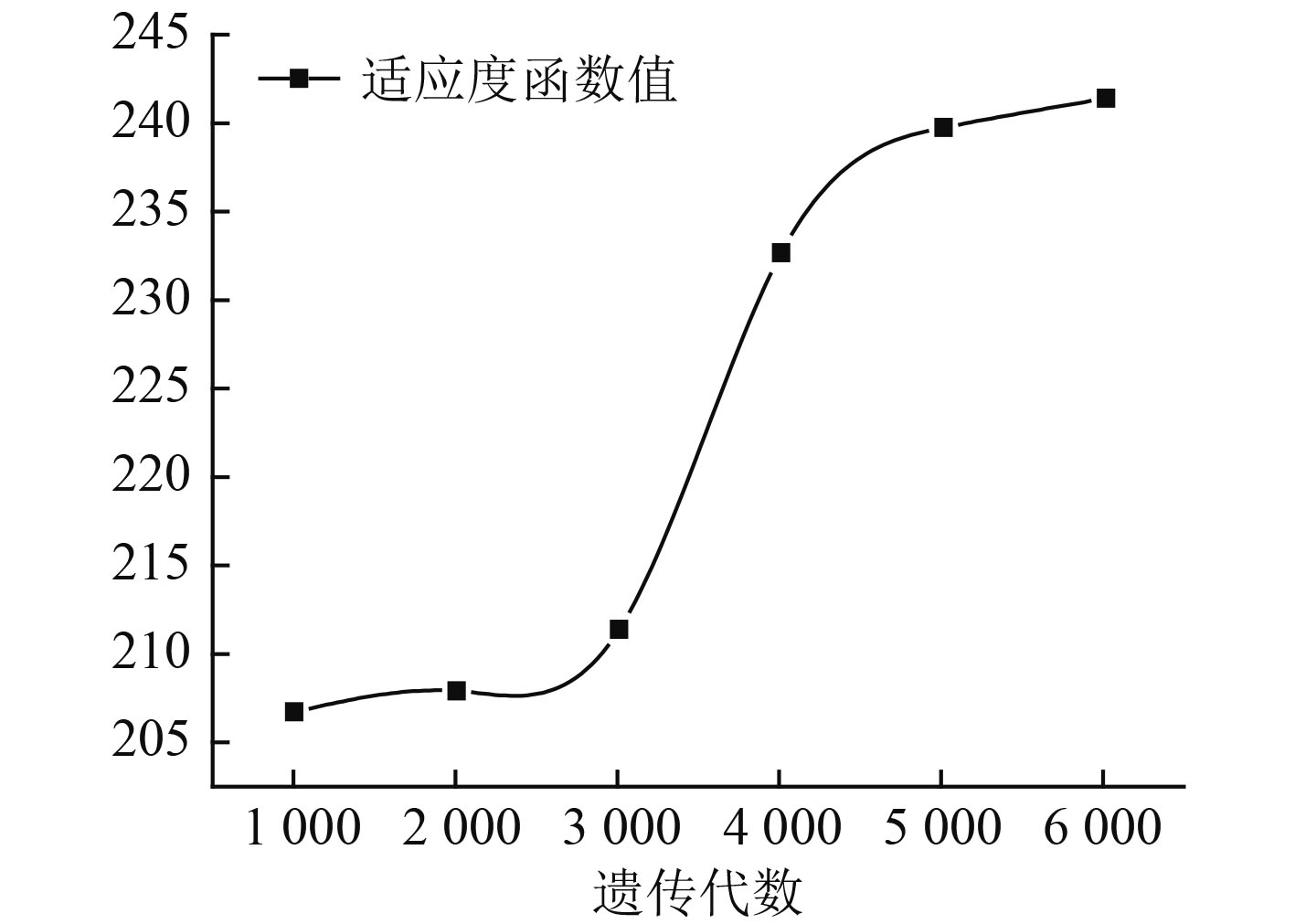
|
图 3 适应度函数值随遗传代数的变化曲线 Fig. 3 Change curve of fitness function value with genetic algebra |
由图3可以看出,遗传次数比较小的时候,函数值也相对较低,随着遗传代数的增加,其相应的适应度函数值也进行了正向的变化,并在一定程度上增加较快,最终到达了一个稳定的程度,增加缓慢,仅有小幅的波动。由此得出,遗传次数达到5000代时,其相对应的适应度函数值趋于稳定,所计算的结果相对较优。
2.2.2 混沌算法优化计算本文在对混沌算法进行优化计算时,主要讨论的是在混沌算法中优化代数对目标函数值的影响情况,如表3所示。
|
|
表 3 混沌算法不同迭代次数优化结果 Tab.3 The calculation results of different optimization algebra of chaos algorithm |
由表3计算结果可以得出,约束条件均在99%以上。
由图4可以看出,伴随着混沌计算代数的增大,适应度函数值也表现出增大的趋势,波动也相对较大。对比遗传算法计算结果,可以看出,混沌算法的函数值普遍小一些,即采用混沌算法相对遗传算法优化计算效果较差。
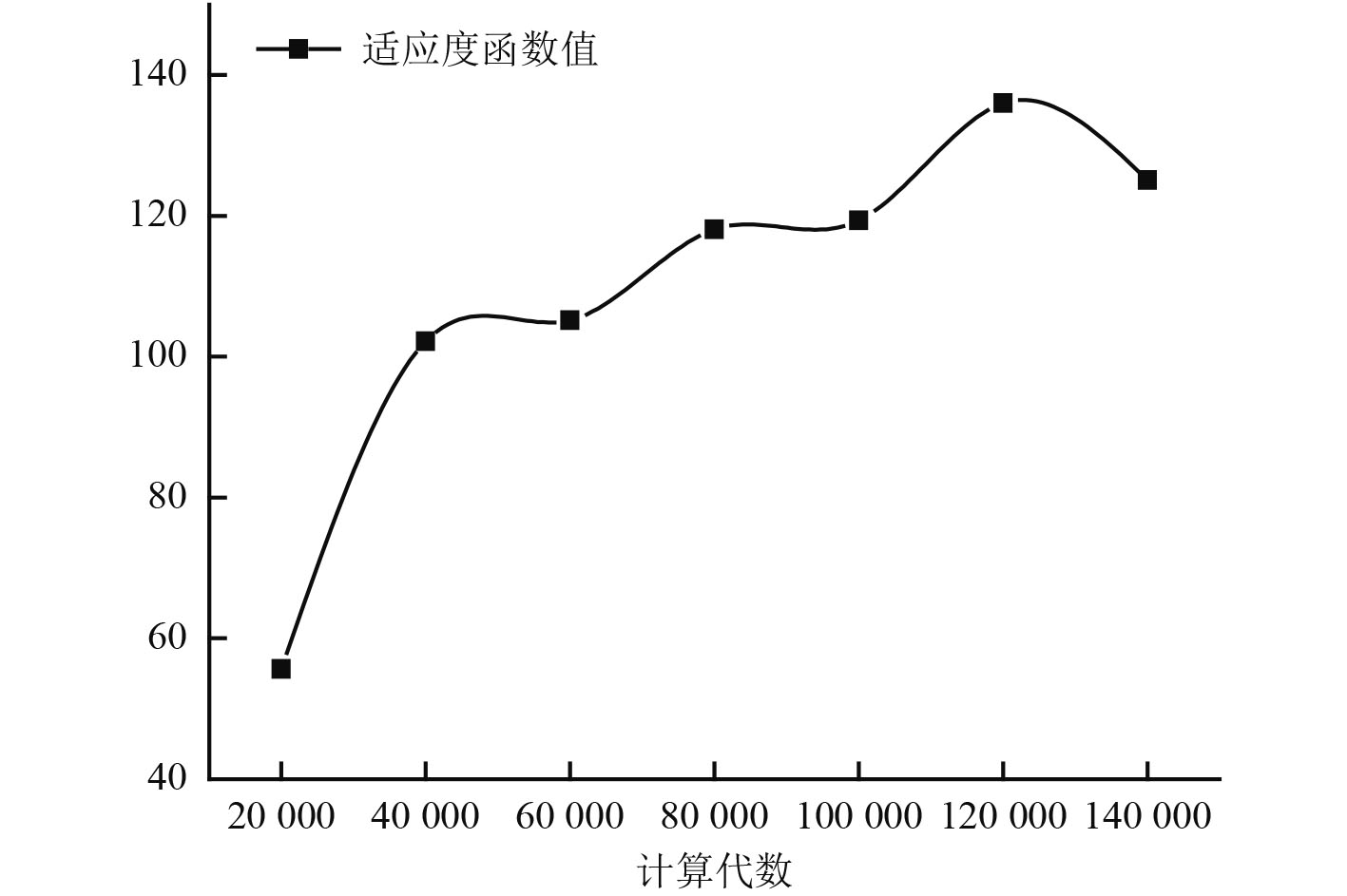
|
图 4 适应度函数值随计算代数的变化曲线 Fig. 4 Change curve of fitness function value with calculation algebra |
主要数据设定如下:种群规模400,最大粒子飞行速度与区间概率0.15,变权重0.9~0.4,选取6组优化代数进行计算,计算结果汇总如表4所示。
|
|
表 4 粒子群算法不同优化代数的计算结果 Tab.4 The calculation results of different optimization algebra of PSO algorithm |
由表4可以看出,所计算的数据值都相对较好,而且符合约束。
如图5所示,在计算到较大的代数时,适应度函数值表现出更加稳定,增加缓慢,或有细微的变化波动。由此得出,优化次数达到5000代时,目标函数值趋于稳定,所计算的结果相对较优。
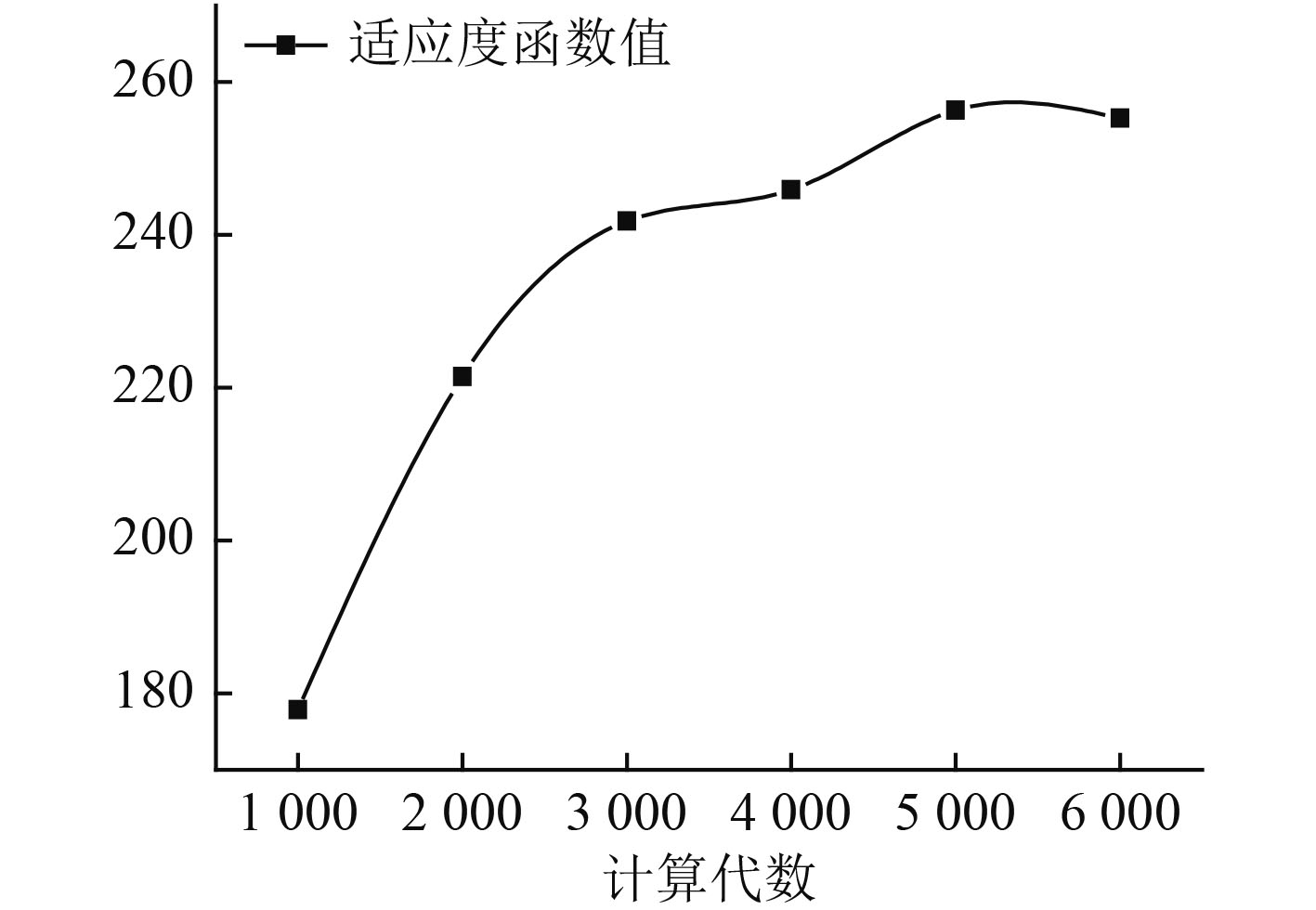
|
图 5 适应度函数值随计算代数的变化曲线 Fig. 5 Variation curve of fitness function value with calculation algebra |
根据上述几种计算的结果不难看出,根据粒子群算法算出来的数据明显更好,更符合要求,最终数据如表5所示。
|
|
表 5 最佳优化的设计变量结果 Tab.5 The best optimized results of design variables |
本文针对一种水下无人艇,设计一种支柱平台对传统艇型进行改进,使之能有效兼顾水面航态,结合快速性、操纵性、功能特性,构造总目标函数、约束条件以及惩罚函数,建立该型UUV的综合优化数学模型,分别使用遗传算法、混沌算法和粒子群算法不同计算代数进行了该型UUV的运算,从计算结果可以得出:
1)混沌算法计算结果的适应度函数值相对其他2个算法较低,虽然遗传与粒子群算法计算结果更接近,但整体还是粒子群算法所计算的更优,相对更稳定;
2)随着计算次数的增加,3种计算方法所计算的结果都呈现正向增加的变化趋势,且当计算次数到达5000时,适应度函数一般达到最大值,并满足约束条件;
3)相比其他2种优化方法,使用粒子群算法得出的浮性约束、力的约束和转矩约束的值多在99.9%以上,惩罚值更易达到1,更易满足约束;
4)功能方面的结果提供了一个更优的参考值,可以更好选择一个适合实际需求的功能设备,有效避免成本的过高与资源的浪费。
本文对传统回转体进行了改进,并对改进后的回转体进行综合优化。其相对优势一是可有效提高稳定性,二是在工程实际应用尤其是军事应用中可在主体与支柱内安装可靠的升降装置,使之对水面航态具有一定的兼顾性,具有更高的可靠性和操作性。
| [1] |
陈鹏. 水下无人艇结构力学特性和性能综合优化初步研究[D]. 镇江: 江苏科技大学, 2013. CHEN Peng. A preliminary study on the comprehensive optimization of mechanical properties and properties of underwater unmanned craft [D]. Zhenjiang: Jiangsu University of Science and Technology, 2013. |
| [2] |
邹启杰. 基于多目标决策的USV系统可变自主实现机制研究[D].哈尔滨: 哈尔滨工程大学, 2014. QI jie Zou. Research on variable autonomous realization mechanism of USV system based on multi-objective decision-making [D]. Harbin: Harbin Engineering University, 2014. |
| [3] |
魏子凡, 井升平, 杨松林. 基于改进遗传算法的新型水面无人艇性能综合优化分析[J]. 江苏科技大学学报(自然科学版), 2017, 31(1): 6-11. |
| [4] |
尹星月, 闫旭, 刘欣, 等. 基于改进遗传算法的无功优化[J]. 东北电力大学学报, 2014, 34(3): 48-53. YIN Xingyue, YAN Xu, LIU Xin, et al. reactive power optimization based on improved genetic algorithm[J]. Journal of Northeast University of Electric Power, 2014, 34(3): 48-53. DOI:10.3969/j.issn.1005-2992.2014.03.010 |
| [5] |
俞强. 深海无人智能潜水器力学性能和能源系统综合优化方法研究[D]. 镇江: 江苏科技大学, 2014.
|
| [6] |
Ch en, Sh un, Frouws, Ko os, Van De Voorde, Ed dy. Simulation-based optimization of ship design for dry bulk vessels[J]. Maritime Economics & Logistics, 2011, 13(2). |
| [7] |
ZAKERDOOST H, GHASSEMI H. A multi-level optimization technique based on fuel consumption and energy index in early-stage ship design[J]. Structural & Multidisciplinary Optimization, 2018. |
| [8] |
苏玉民, 庞永杰. 潜艇原理[M]. 哈尔滨: 哈尔滨工程大学出版社, 2004.
|
| [9] |
DANIELE Peri. Hybridization of the imperialist competitive algorithm and local search with application to ship design optimization[J]. Computers & Industrial Engineering, 2019, 137. |
| [10] |
李素素, 王锡淮. 基于粒子群优化的船舶电力系统经济环境调度[J]. 船电技术, 2019, 39(11): 27-30. DOI:10.3969/j.issn.1003-4862.2019.11.007 |
| [11] |
赵翱东, 壮而行. 基于蚁群算法的船舶调度优化研究[J]. 舰船科学技术, 2019, 41(6): 7-9. ZHAO Aodong, ZHUANG Erxing. A Study on Ship Scheduling Optimization Based on Ant Colony Algorithm[J]. Ship Science and Technology, 2019, 41(6): 7-9. |
| [12] |
薛敏, 徐海成, 王硕. 基于粒子群优化算法的无人艇路径规划[J]. 中国科技信息, 2018(24): 69-70. DOI:10.3969/j.issn.1001-8972.2018.24.025 |
| [13] |
李嘉宁, 刘峰, 姚竞争, 等. 无人潜水器主体多学科多目标设计优化[J]. 哈尔滨工程大学学报, 2019, 40(4): 858-864. LI Jianing, LIU Feng, YAO Jingzheng, et al. Optimization of Multidisciplinary Multi-objective Design of Unmanned Submersible Subject[J]. Journal of Harbin Engineering University, 2019, 40(4): 858-864. |
| [14] |
刘曼. 一种水面无人艇艇型优化及远程设计系统初步研究[D]. 2018.
|
 2020, Vol. 42
2020, Vol. 42
