射击精度是考核航炮射击性能的一项重要指标,除了内外弹道因素对航炮射击精度有影响外,航炮炮口的振动也是重要的影响环节,有时可能是首要影响环节[1]。本文基于有限元理论对航炮身管和炮口夹箍等易变形的构件进行模态分析并得到身管和炮口夹箍的模态中性文件。在此基础上,利用多体动力学理论在动力学仿真软件ADAMS中构建航炮的刚柔耦合动力学虚拟样机模型,分析了不同射速下航炮连发射击时炮口的动态响应[2]。
1 刚柔耦合模型的建立在进行航炮炮口振动规律的研究时,把与炮口扰动关系紧密、易变形的身管、炮口夹箍作为柔性体,把其他变形量小、与炮口振动无关的构件处理成刚体,利用有限元理论在Ansys中对其柔性体构件建立模态中性文件[3],利用多体动力学理论在动力学仿真软件ADAMS中建立刚柔耦合模型[4-5],进行仿真计算,得到航炮自动机连续射击时炮口的振动规律。
在ADAMS中,分别以刚体质心的笛卡尔坐标、能够反映刚体位移的广义欧拉角以及欧拉角作为物体坐标系的广义坐标:
| ${Q_i} = \left[ {x,y,z,\psi ,\theta ,\varphi } \right]_i^{\rm{T}}\text{,}$ |
| $Q = {\left[ {q_i^{\rm{T}},\Lambda ,q_n^{\rm{T}}} \right]^{\rm{T}}}\text{。}$ |
系统的动力学方程采用拉格朗日算法:
| $\frac{{\rm d}}{{{\rm d}t}}{\left( {\frac{{\partial T}}{{\partial q}}} \right)^{\rm{T}}} - {\left( {\frac{{\partial T}}{{\partial q}}} \right)^{\rm{T}}} + \varphi _q^{\rm{T}}\rho + \theta _q^{\rm{T}}\mu = Q\text{,}$ |
全约束方程为:
| $\varphi \left( {q,t} \right) = 0\text{,}$ |
欠约束方程为:
| $\theta \left( {q,\mathop q\limits^ \bullet ,t} \right) = 0\text{。}$ |
式中:T,Q分别为系统的动能和广义力列阵;q,ρ,μ分别为系统广义坐标列阵,完全约束拉式列阵和不完全约束拉式列阵[6]。
约束多体动力学方程如下:
| $F\left( {q,\mathop {q,}\limits^ \bullet \mathop {q,}\limits^{ \bullet \bullet } \lambda ,t} \right) = { M}\left( {q,t} \right)\mathop q\limits^{ \bullet \bullet } + { {\varphi}} _q^{\rm T}\left( {q,t} \right)\lambda - f\left( {q,\mathop q\limits^ \bullet ,t} \right) = 0\text{,}$ |
| ${ {\varphi}} \left( {q,t} \right) = 0\text{,}$ |
| $\left\{ {\begin{array}{*{20}{c}} {{ {\varphi}} \left( {q,\mathop q\limits^ \bullet ,t} \right) = {{ {\varphi}} _q}\left( {q,t} \right) - v\left( {q,t} \right) = 0}\text{,} \\ {v = - {{ {\varphi}} _i}\left( {q,t} \right)} \text{,} \end{array}} \right.$ |
| $\left\{ {\begin{array}{*{20}{c}} {{ {\varphi}} \left( {q,\mathop q\limits^ \bullet ,\mathop q\limits^{ \bullet \bullet } ,t} \right) = {{ {\varphi}} _q}\left( {q,t} \right)\mathop q\limits^{ \bullet \bullet } }\text{,} \\ { - \eta \left( {q,\mathop q\limits^ \bullet ,t} \right) = 0} \text{,}\\ {\eta = - {{\left( {{\varphi _q}\mathop q\limits^ \bullet } \right)}_q}\mathop q\limits^ \bullet - 2{\varphi _{qt}}\mathop q\limits^ \bullet - {\varphi _n}} \text{。} \end{array}} \right.$ |
式中:
通过上述方程,分别给出了ADAMS中的坐标定义、动力学方程以及多体动力学各参数之间的函数相关量,因此可利用ADAMS软件对模型的运动参数和力参数进行求解[8]。
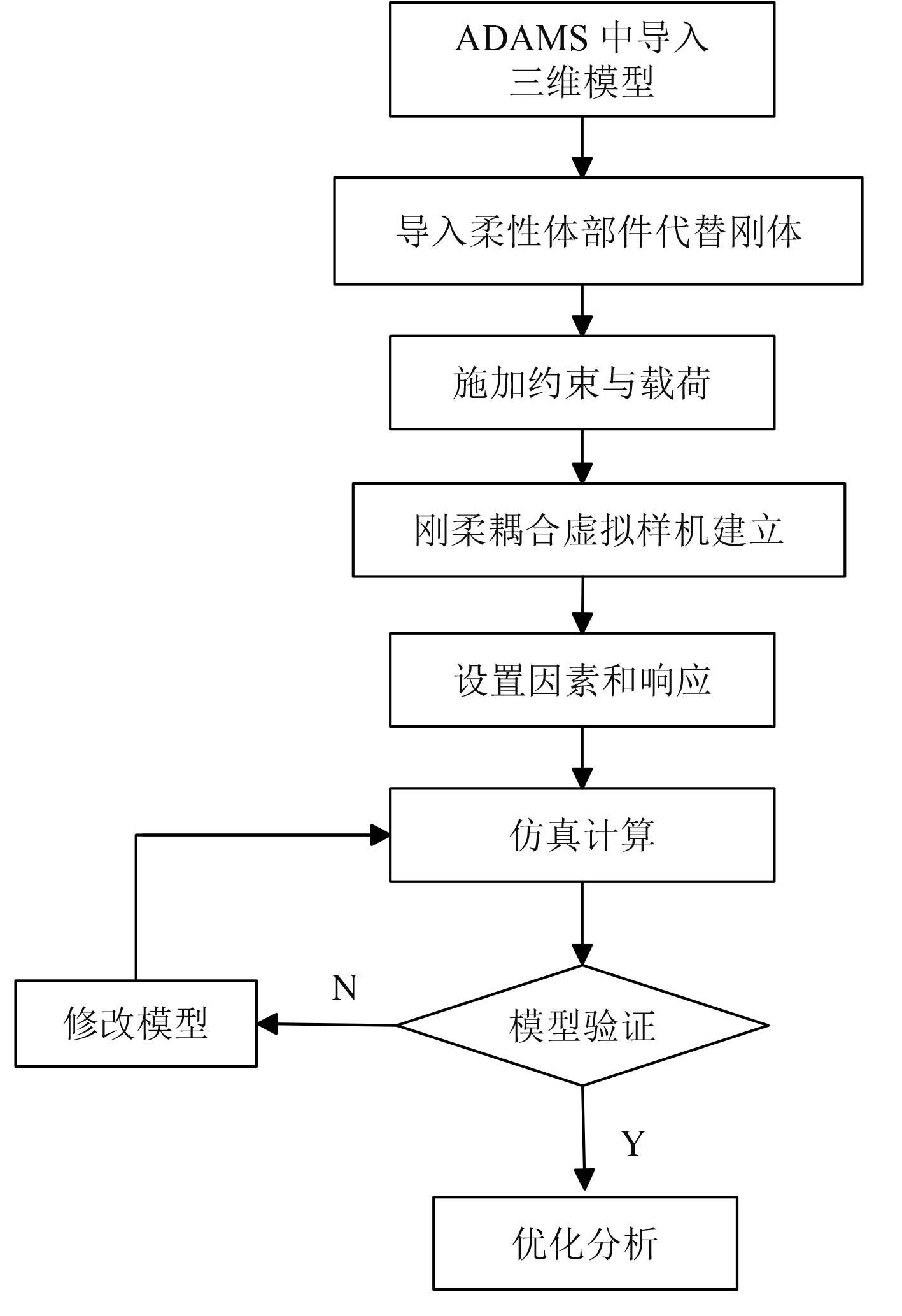
ADAMS建立刚柔耦合虚拟样机模型的流程如图1所示。
|
图 1 ADAMS中刚柔耦合建模流程 Fig. 1 Modelling flow charts of rigid-flexible coupling in ADAMS |
航炮射击过程中,身管和炮口夹箍的弹性变形对射击精度的影响不容忽视,因此本文主要对身管和炮口夹箍这两个构件建立柔性体,在刚柔耦合模型中采用模态法来描述柔性体的变形。
1.1 柔性体-身管的模态计算与刚性区域的建立为了方便与其他的刚体或柔性体建立连接关系、载荷、接触或者约束,在柔性体建模时需要建立可与外界进行信息交换的刚性节点[9]。
在Ansys中计算得到的柔性体-身管的各阶模态,身管、炮口夹箍的材料为钢,其密度为
在身管和炮口夹箍的有限元模型中,利用有限元理论计算得到身管和炮口夹箍各阶模态的固有频率。目的在于:一方面得到身管-炮口夹箍组件各阶模态的固有频率,与自动机的射频进行比较,观察在射击过程中是否发生共振,来验证身管结构设计的合理性;一方面得到身管-炮口夹箍组件各阶模态的振型,为后续结构的改进提供理论依据[10]。
身管主要与炮口夹箍、炮尾、前后衬套连接,因此有4个界面节点(即刚性节点)。柔性身管利用固定副实现刚性节点与刚性炮尾、刚性衬套以及柔性炮口夹箍的连接,保证了载荷(炮膛合力)均布分在身管后端面的每个节点上。其他柔性构件的连接也采用上述方式,由于建立刚性节点的方法相同。柔性体身管在Ansys中的刚性区域建立如图2所示。

|
图 2 Ansys下身管刚性区域 Fig. 2 Rigid region of gun tube in Ansys |
计算身管-炮口夹箍组件的模态时,根据航炮自动机的实际支撑方式对其添加约束,身管-炮口夹箍组件的约束方式为后端面固定,其约束方式如图3所示:

|
图 3 身管-炮口夹箍组件的约束方式 Fig. 3 Restraint mode of gun tube-muzzle clamp |
表1列出了身管-炮口夹箍组件的前4阶固有频率、振型。身管-炮口夹箍组件的振型图如图4所示。
|
|
表 1 身管-炮口夹箍1~4阶模态的频率与振型 Tab.1 4 extended modal frequency and shape of gun tube - muzzle clamp |

|
图 4 身管-炮口夹箍前4阶振型 Fig. 4 4 extended modal shape of gun tube - muzzle clamp |
通过分析可以得出以下结论:
1)身管-炮口夹箍的第1阶和第3阶模态以弯曲振型为主,第2阶和第4阶模态以扭转为主。
2)航炮自动机的射速为3000发/分,振动频率为50 Hz,由表1得到该身管-炮口夹箍组件的前4阶模态振动频率范围为98–333 Hz。因此在正常射击工况下,该结构各阶频率远离了载荷激励频率,其本体不会出现共振情况,其他频率皆分布在高频段,这说明了身管-炮口夹箍频率结构设计的合理性。
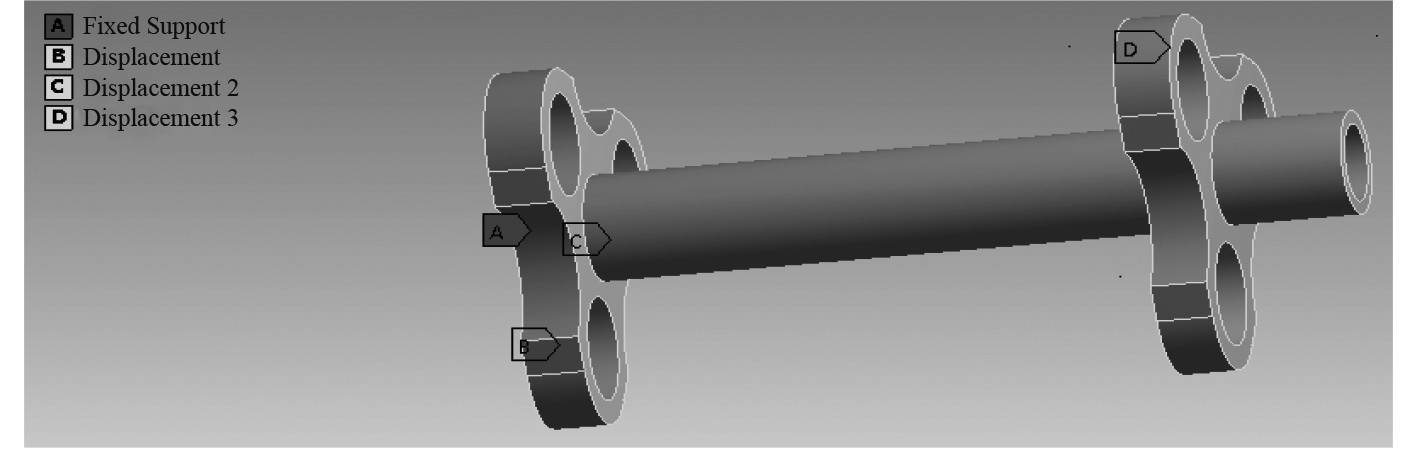
1.2 炮口夹箍的模态计算与刚性区域建立利用Ansys计算得到炮口夹箍在约束状态下前6阶模态的固有频率,约束方式为一端固定,与身管接触的孔为径向方向位移约束,约束方式如图5所示。
|
图 5 炮口夹箍组件的约束方式 Fig. 5 Restraint mode of muzzle clamp |
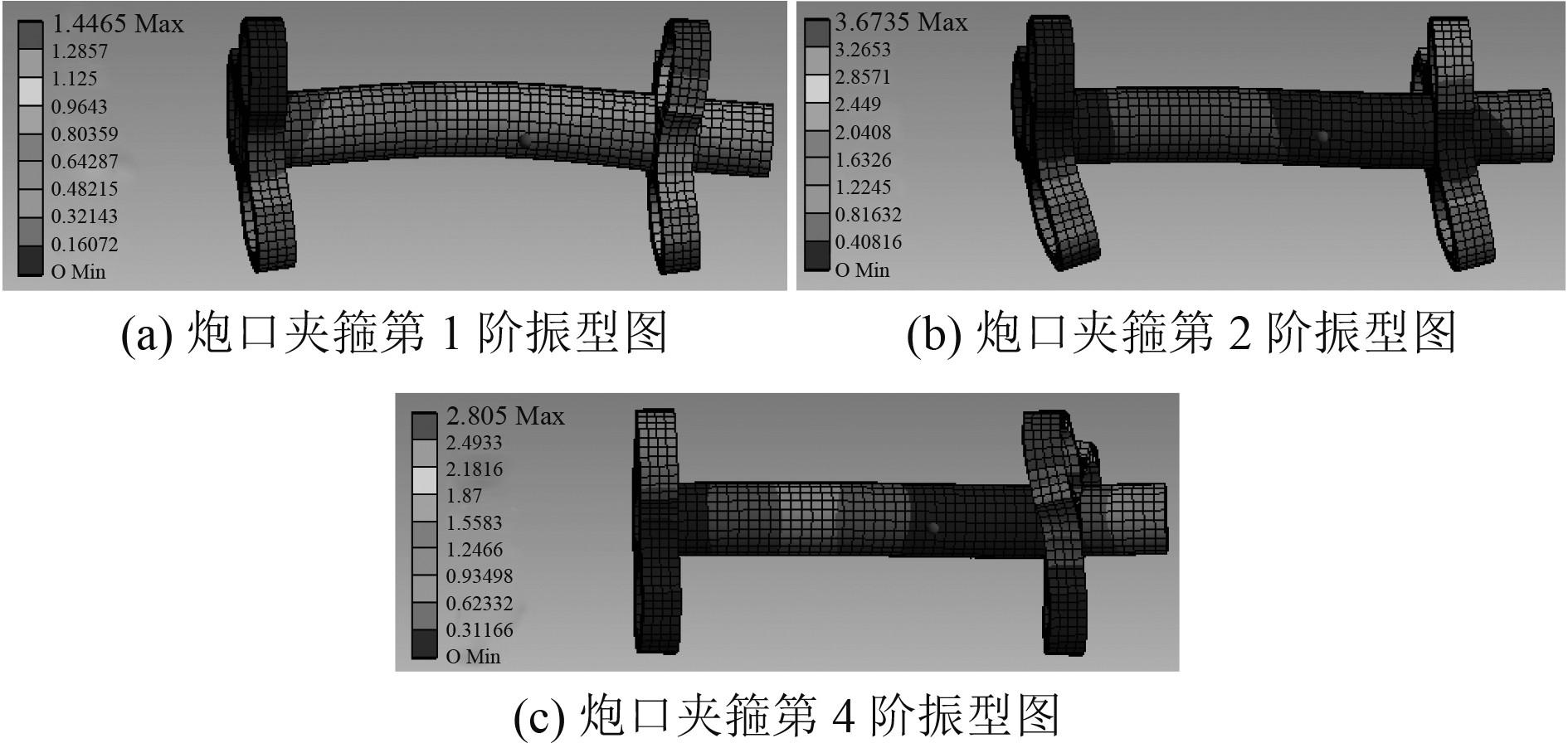
炮口夹箍前6阶模态的固有频率如表2所示,振型图如图6所示(频率相同的振型已整合)。
|
|
表 2 炮口夹箍1~6阶频率与振型 Tab.2 6 extended modal frequency and shape of muzzle clamp |
|
图 6 炮口夹箍各阶振型 Fig. 6 Modal shapes of muzzle clamp |
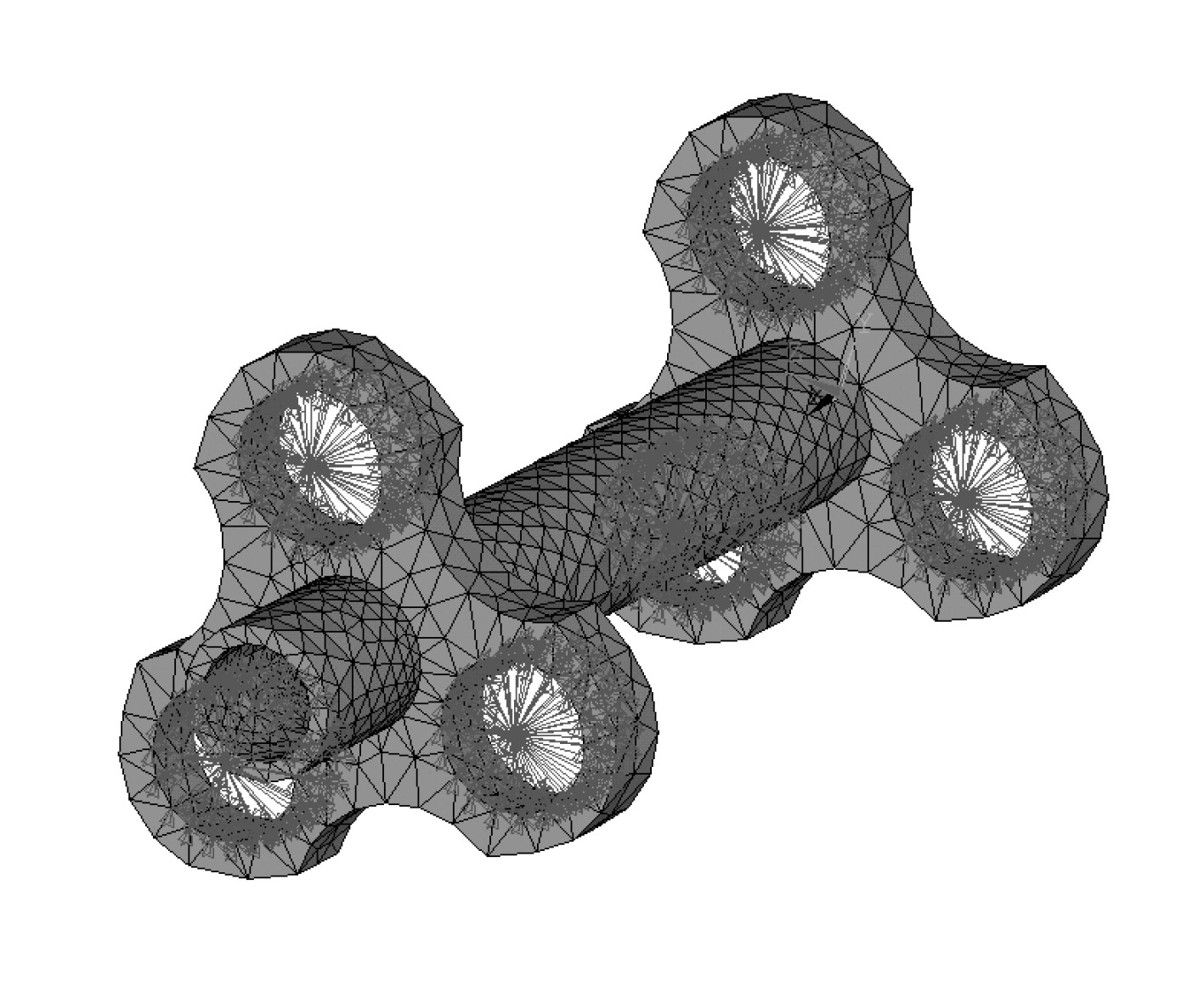
炮口夹箍有6个界面节点(即刚性节点)分别与3根身管相连。柔性体炮口夹箍在Ansys中的刚性区域如图7所示。
|
图 7 炮口夹箍刚性区域的建立 Fig. 7 Establishment of muzzle clamp rigid region |
通过以上分析可以得出结论:炮口夹箍在约束状态下的前3阶振动频率远远大于载荷激励频率,说明了炮口夹箍结构设计的合理性。
2 航炮刚柔耦合虚拟样机的建立将建立好的柔性体(身管和炮口夹箍)导入动力学仿真软件ADAMS中,建立航炮虚拟样机模型。刚体与柔体的约束一般都可以直接用ADAMS中的常用约束副来完成,可以通过约束柔性体上的刚性节点和刚体上的marker点实现的。刚体与柔体的接触在ADAMS中一般选择flexible-solid接触来实现。
自动机刚柔耦合虚拟样机中刚体和柔性体约束如表3所示,得到自动机刚柔耦合虚拟样机模型如图8所示。
|
|
表 3 刚体和柔性体约束列表 Tab.3 Constraint list of rigid body and flexible body |

|
图 8 自动机刚柔耦合虚拟样机模型 Fig. 8 Virtual prototype model of rigid-flexible coupling of automaton |
根据建立的自动机刚柔耦合虚拟样机,分析不同射速下炮口的横向振动位移和纵向振动位移,得出炮口振动随自动机射速的变化规律,为提高航炮的射击精度提供理论支持。由于刚柔耦合模型约束关系复杂、计算量大,故选择航炮理论射速周边的射速进行计算。选择航炮射速5000发/分、6000发/分、7000发/分的计算结果进行讨论。
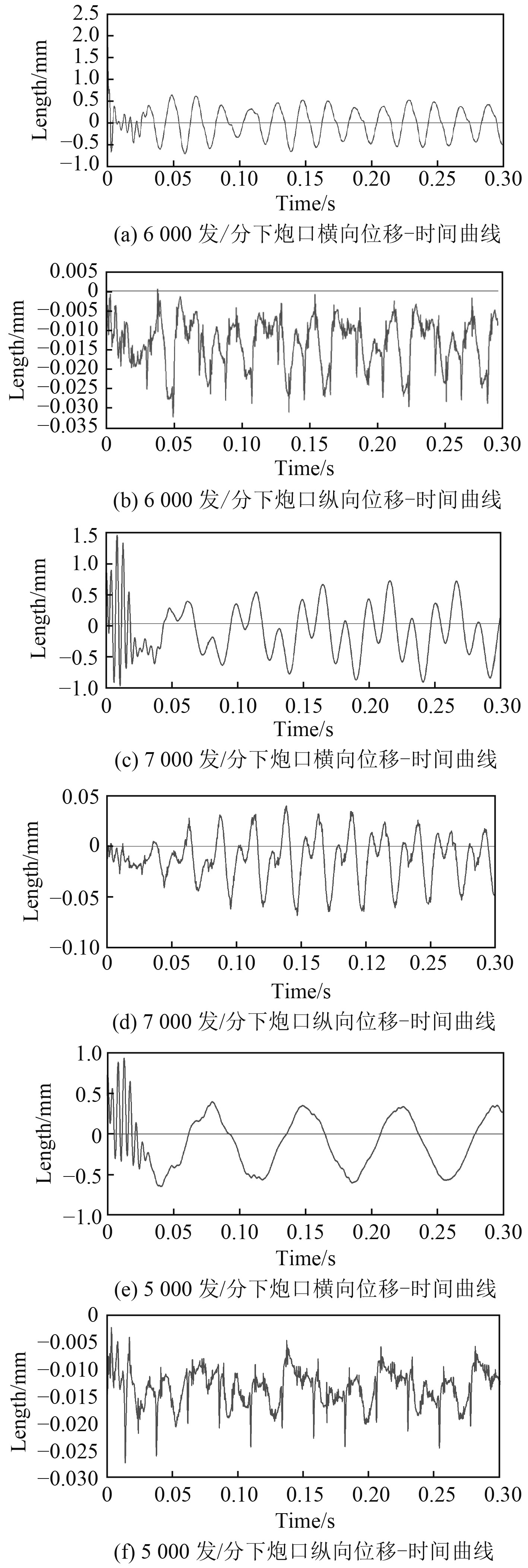
|
图 9 不同射速下炮口横向/纵向位移-时间曲线 Fig. 9 Transverse/longitudinal displacement-time curves of the muzzle at different firing rate |
|
|
表 4 稳定射击状态下炮口位移 Tab.4 Muzzle displacement under stable firing rate |
自动机稳定射击状态下,炮口纵向振动位移最大值随射速的提高明显增加,从5000发/分到6000发/分,其纵向振动位移的最大值增加了约60%;从6000发/分到7000发/分,其纵向振动位移的最大值增加了约70%。自动机稳定射击状态下,炮口的横向位移值同样随射速的提高出现明显增加,从5000发/分到6000发/分,炮口横向位移的最大值增加了约1.2倍,但其位移值较小可以忽略;从6000发/分到7000发/分,其横向位移的最大值增加了约3倍,虽然横向位移量较小以至于可以忽略,但随着射速的继续增加,其横向位移最大值达到不可忽略的程度,将会对航炮的射击精度造成影响。
4 结 语本文运用有限元理论对影响炮口振动的柔性体构件建立模态中性文件和其对应的刚性区域。在动力学仿真软件中得到自动机刚柔耦合虚拟样机模型并进行仿真计算,得到航炮在不同射速下炮口振动位移的变化规律,为航炮射击精度的研究和飞机总体的设计提供理论依据。
| [1] |
徐诚, 王亚平. 火炮与自动武器动力学[M]. 北京: 北京理工大大学出版社, 2006.
|
| [2] |
郭小炜. 刚柔耦合系统的动力学建模与响应分析[D]. 重庆: 重庆大学. 2016.
|
| [3] |
王娟. 基于虚拟样机技术的航炮系统动力学仿真研究[D]. 西安: 西北工业大学. 2004.
|
| [4] |
郭振锋, 金国光, 畅博彦, 等. 刚-柔性机械臂动力学建模及其动力学特性研究[J]. 天津工业大学学报, 2013, 32(1): 70-74. |
| [5] |
王欣, 杜汉平, 滕儒民. 基于刚柔耦合的履带起重机虚拟样机建模技术[J]. 中国工程机械学报, 2007, 5(1): 26-31. |
| [6] |
刘银虎, 缪炳祺. 多体动力学仿真软件ADAMS理论基础及其功能分析[J]. 电子与封装, 2005, 5(4): 25-28. |
| [7] |
陈立平. 机械系统动力学分析及ADAMS应用教程[M]. 北京: 清华大学出版社, 2005.
|
| [8] |
谢文献, 滕腾, 柴德民. 基于ADAMS的水力式油管切割工具多体动力学研究[J]. 石油机械, 2019, 47(2): 86-90. |
| [9] |
刘雷. 弹丸-身管耦合系统动力学模型[J]. 振动与冲击, 2007, 26(6): 121-124. |
| [10] |
王德石, 史跃东. 火炮振动分析与多体系统模型研究[J]. 动力学与控制学报, 2012, 10(4): 303-323. |
 2020, Vol. 42
2020, Vol. 42
