2. 河南省水下智能装备重点实验室,河南 郑州 450015
2. Henan Key Laboratory of Underwater Intelligence Equipment, Zhengzhou 450015, China
燃气-蒸汽式弹射动力系统具有内弹道稳定、能量可调节、系统简单、维护方便等优点,被广泛应用于国内外各类导弹发射装置[1],其主要工作原理是由燃气发生器产生高温高压燃气,当燃气流经冷却器时与冷却水进行混合,一方面降低了高温燃气的温度,同时形成燃气-水蒸气混合气体在筒底建立压力,推动导弹出筒[2]。如何实现大范围、稳定的能量调节控制,直接地影响到导弹发射内弹道性能稳定性,对于适应现代战争实战化需要,提高导弹武器系统的适用性、快速反应能力及生存能力至关重要[3]。
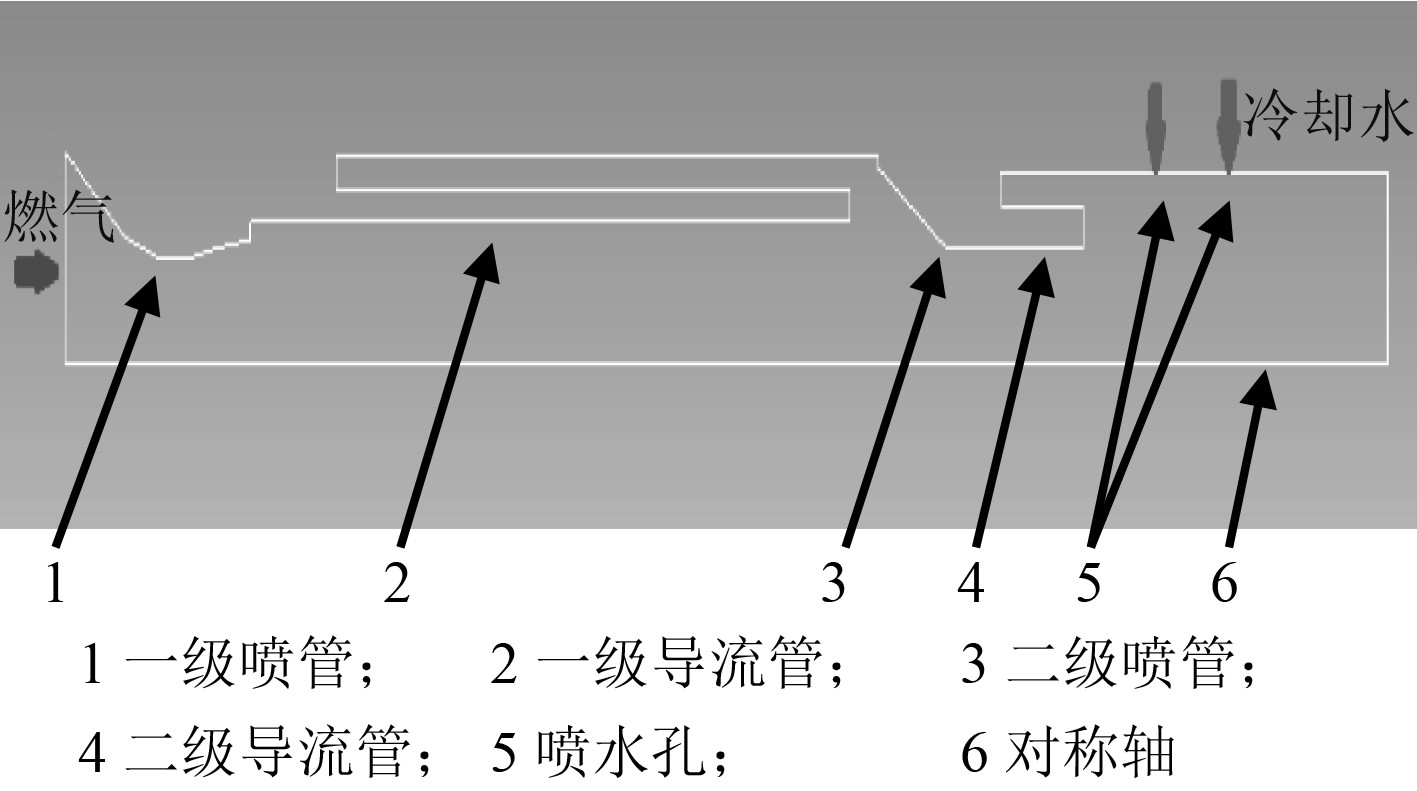
某型燃气-蒸汽式弹射动力系统通过冷却器的结构设计实现能量的调节,其内通道二维轴对称结构如图1所示,燃气发生器的高温高压燃气经由一级喷管、一级导流管后分流,少部分进入水室,产生水室压力;另一部分经二级喷管、二级导流管之后进入喷水区,气流在进入喷水区扩张后压力降低,形成水室-喷水区之间显著的压力差,通过喷水压差将水室内冷却水喷入内通道,冷却水蒸发雾化形成燃气流的能量控制。在这个过程中,保持稳定的喷水压差的稳定是实现能量稳定调节的基础。为了得到需要的喷水压差,应合理控制一二级喷管喉径尺寸。在长期的工程实践中,形成了一套成熟的一二级喷管喉径匹配设计方法,使得在动力系统工作过程中可以根据需要实现喷水量的有效控制。
|
图 1 某型燃气-蒸汽式动力系统内通道二维结构示意图 Fig. 1 The two dimensional structure of inner passage of a gas steam power system |
在实际过程中发现,为得到所需要的、稳定的喷水压差,除了需要匹配一二级喷管喉径尺寸,还应合理控制二级喉道的长度。研究表明,适当延长二级喉道即设置二级导流管有利于喷水压差的稳定。然而,二级喉道的长度是如何影响喷水压差的,怎样设置二级导流管长度更有利于保持喷水压差的稳定,在以往的研究中未曾阐述。二级喉道出口存在着复杂的气液混合流动与蒸发过程,难以通过传统理论推导的方法实现精确的计算与控制。
近年来,计算流体力学发展迅速,越来越多地应用于燃气-蒸汽式气液两相流的数值模拟。芮守祯等[4]对超声速气液两相流场不同孔径、喷水压差及水气质量比进行了数值模拟,分析了各种工况下液滴蒸发情况及其对气相流场和能量输出的影响;刘伯伟等[5]研究了汽化效应对燃气蒸汽气液两相流场的影响,并使用试验结果验证了数值模型的可靠性;胡晓磊等[6]使用数值方法研究了喷水对冷却器流场的影响,研究结果表明喷水降低了冷却器出口的温度及压力,并会对气流产生阻滞作用。
本文采用计算流体力学的方法对燃气-蒸汽式动力系统内流场进行研究,对比分析了不同二级导流管出口距第一排喷水孔的距离与二级导流管直径的比值(以下简称二级导流管特征值)对喷水压差及喷水区压力的影响,得出有利于实现喷水压差稳定的特征值范围,并对特征值范围边界及推荐的特征值结构进行了试验验证。
1 仿真分析 1.1 基本假设本文对燃气-蒸汽式弹射动力系统内通道进行仿真计算,对内通道流场进行了适当的简化。由于燃气分流进入水室的燃气量较小,对进入喷水区的燃气及喷水区压力影响较小,因此假设该部分燃气从内通道流出,从而减少水室部分计算区域,节省计算资源。
1.2 控制方程本次仿真计算采用文献[7]推荐的VOF多相流模型描述内通道气液混合流动,该模型控制方程如下[8]:
连续性方程
| $\frac{{\partial \left( {{\alpha _q}{\rho _q}} \right)}}{{\partial t}} + \nabla \left( {{\alpha _q}{\rho _q}{u_j}} \right) = 0\text{,}$ | (1) |
| $\sum\limits_{q = 1}^n {{\alpha _q} = 1} \text{,}$ | (2) |
动量守恒方程
| $\frac{\partial }{{\partial t}}\left( {\rho {u_i}} \right) + \nabla \cdot \left( {\rho {u_i}{u_i}} \right) = - \nabla p + \nabla \cdot [\mu \left( {\nabla {u_i} + \nabla {u_j}} \right)] + \rho \overrightarrow g + \overrightarrow F \text{,}$ | (3) |
能量守恒方程
| $\frac{\partial }{{\partial t}}\left( {\rho E} \right) + \nabla \cdot \left( {{u_i}(\rho E + p)} \right) = \nabla \cdot \left( {{k_{eff}}\nabla T} \right) + {S_h}\text{,}$ | (4) |
| $E = \frac{{\sum\limits_{q = 1}^n {{\alpha _q}{\rho _q}{E_q}} }}{{\sum\limits_{q = 1}^n {{\alpha _q}{\rho _q}} }}\text{。}$ | (5) |
其中:p,q为不同的相;
气相包括初始状态下内通道的空气以及高温高压燃气,使用文献[9]推荐的输运模型描述气相不同组分之间的混合;采用文献[10]推荐的RNG k-ε湍流模型描述湍流流动。输运模型、湍流模型控制方程及参数见Fluent帮助手册[8]。
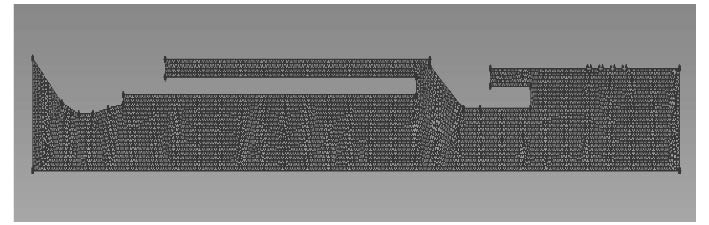
1.3 网格划分及边界条件使用Ansys ICEM软件对二维轴对称模型进行自适应网格划分,网格类型为三角形网格。对该结构共划分了3种网格结构进行计算,总数分别是10 568,17 445及25603个,仿真结果表明当网格总数为17445及25603时局部参数没有明显差异。为了节省计算时间,本次仿真选用总数为17445的网格结构,如图2所示。
|
图 2 网格划分示意图 Fig. 2 The meshing diagram |
仿真采用非稳态计算方式,计算中一级喷管入口边界条件设定为压力入口,全部为燃气,并设置为理想气体,燃气温度设置为燃气发生器装药定压燃温3000 K,燃气压力使用燃气发生器设计压力曲线,燃气速度设为0 m/s;
冷却水入口采用质量流率入口边界条件,冷却水量采用理论计算喷水量,并使用自定义函数UDF分段函数描述。出口都采用压力出口,对称轴设置为对称轴边界条件,其余设置为壁面,壁温设为常温300 K。
初始时刻计算域内喷水孔区域为预加水,其余部分全部为空气,压力为常压。仿真计算由Ansys Fluent 18.2完成。
1.4 仿真结果及分析 1.4.1 动力系统内通道流场仿真图3为不同时刻动力系统内通道马赫数分布示意图,从图中可以看出燃气-蒸汽式弹射动力系统内通道一、二级喷管喉径之间确实形成了激波,气流经一级喷管加速后,在分流处扩张并在二级喉道内形成音速流动,这与设计参数一致,也从侧面验证了本次仿真的准确性。在二级喉道出口气流再次扩张加速,最高速度达到3 Ma以上,同时在喷水区形成明显的激波,激波的位置相对固定,不同时刻没有明显的变化。

|
图 3 特征值0.5结构下动力系统内通道0.15 s(a)、0.25 s(b)、0.35 s(c)马赫数Ma分布示意图 Fig. 3 The schematic diagram of distribution of Mach number of 0.15 s (a), 0.25 s (b), and 0.35 s (c) in the inner passage of power system under the structure of eigenvalue 0.5 |
从图3还可以看出,该结构中激波的位置与喷水孔区域较近,这会直接地影响到喷水区压力及喷水压差,因此有必要对不同特征值下喷水区激波与喷水孔相对位置及喷水孔附近区域的压力分布进行研究。
1.4.2 不同特征值下内通道流动状态的对比选择特征值为0.5,0.25,0.15的动力系统内通道结构进行建模,保持其他结构及边界条件不变,计算内通道流场分布形态。图4为相同时刻(0.15 s)不同特征值下内通道马赫数分布示意图,从图中可以看出不同特征值下流场状态基本一致,随着特征值的减小,二级导流管越来越长,喷水区激波的位置越来越向下游偏移。当激波越偏向下游,二级导流管出口位置越接近第一排喷水孔,当特征值0.15时,二级导流管出口扩张处高速气流与喷水孔非常接近,这会对喷水压差造成一定的影响,因此还需对3种特征值喷水区压力进行对比分析。

|
图 4 特征值0.5(a)、0.25(b)、0.15(c)结构下相同时刻(0.15 s)内通道马赫数Ma分布示意图 Fig. 4 The schematic diagram of distribution of channel Mach number at the same moment (0.15 s) under the structure of characteristic values 0.5 (a), 0.25 (b), 0.15 (c) |
图5为相同时刻下(0.25 s)不同特征值0.5,0.25,0.15的动力系统内通道压力分布示意图,从图中可以看出,不同特征值下内通道压力呈现的基本形态较为一致,一级喷管内的压力最高,二级喷管与二级导流管内气流呈现音速流动,喷水区压力相对较低,难以显示出该区域压力变化规律;不同特征值对燃气上游区域的压力影响较小。

|
图 5 特征值0.5(a)、0.25(b)、0.15(c)结构下相同时刻(0.25 s)内通道压力分布示意图 Fig. 5 The schematic diagram of channel pressure distribution at the same moment (0.25 s) under the structure of characteristic values 0.5 (a), 0.25 (b), and 0.15 (c) |
将不同特征值0.5,0.25,0.15下内通道喷水区压力分布云图放大进行对比,如图6所示。从图中可以看出,特征值为0.5时,激波位置与喷水孔位置较为接近,使得喷水孔附近区域压力呈现不规则形状;特征值为0.25时,喷水孔附近区域压力较为均匀,对喷水压差稳定相较为有利;特征值为0.15时,激波位置距喷水孔较远。从图中还可以看出第一排喷水孔附近区域压力收到了气流的影响,使得该区域压力明显低于其余三排喷水孔压力。为了保持喷水压差的稳定,应尽量避免这种情况的发生。

|
图 6 特征值0.5(a)、0.25(b)、0.15(c)结构下相同时刻(0.25 s)喷水区压力分布示意图 Fig. 6 The schematic diagram of the pressure distribution in the spray area at the same moment (0.25 s) under the structure of characteristic values 0.5 (a), 0.25 (b) and 0.15 (c) |
因此,特征值过大过小都不利于保持喷水压差的稳定,特征值过大会使得激波正处于喷水区,影响喷水区压力稳定性。而特征值过小则会使二级导流管出口到喷水孔距离过近,扩张气流会影响到第一排喷水孔附近的压力,也不利于喷水压差的稳定。经过仿真研究,本文推荐的特征值范围为0.2~0.35。
2 试验验证仿真结果表明,当特征值取值在0.2~0.35之间时,喷水区压力不会受到激波与气流的影响,喷水压差会更加稳定。对仿真结果进行试验验证,保持动力系统其他结构不变,选择不同二级导流管特征值,取特征值范围内特征值0.25,范围外特征值0.5,各进行3次试验,并对比其对喷水压差的影响。试验结果喷水压差系数曲线如图7和图8所示。
|
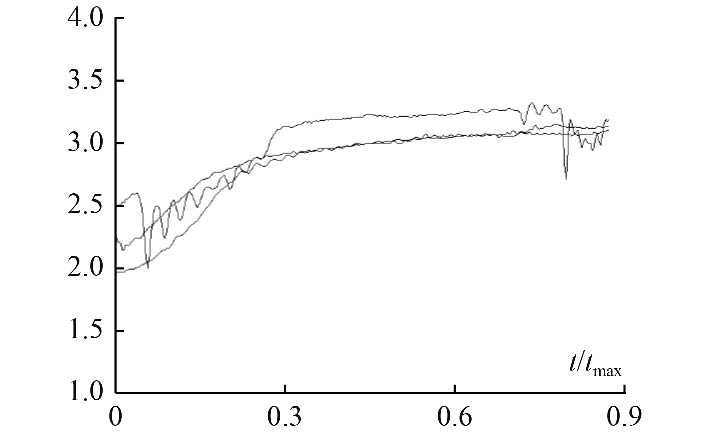
图 7 特征值0.5结构下喷水压差系数示意图 Fig. 7 The schematic diagram of the spray pressure difference coefficient under the structure of characteristic value 0.5 |
|
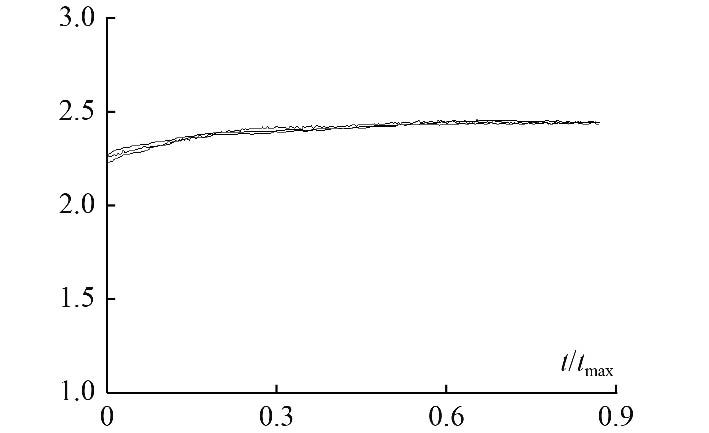
图 8 特征值0.25结构下喷水压差变化曲线 Fig. 8 The variation curve of water spray pressure difference under the structure of characteristic value 0.25 |
图7为特征值0.5时喷水压差曲线变化示意图,从图中可以看出,3次试验喷水压差曲线重复性较差,其中1次试验与其他2次曲线明显不同,并且出现明显的震荡现象。结合仿真结果进行分析,该结构下喷水压差受到激波影响较大,激波的波动影响到了喷水区压力及喷水压差的稳定性,这会对冷却水喷水量及内弹道性能产生一定的影响。
图8为特征值为0.25时3次试验喷水压差曲线示意图,从图中可以看出,特征值0.25喷水压差曲线相对于特征值0.5更为平滑,并且3次试验结果重复性较好,未出现上下震荡的情况,说明该结构下冷却器工作更稳定,有利于喷水压差及内弹道的稳定控制。
3 结 语本文使用计算流体力学方法对某型燃气-蒸汽式弹射动力系统喷水压差规律进行研究,对比不同特征值对冷却器内通道及喷水区压力分布的影响,并进行了相关特征值结构的试验验证。
研究结果表明,二级导流管特征值过大或者过小都不利于弹射动力系统喷水压差的稳定性。特征值过大,激波位置处于喷水区,会直接影响喷水区的压力与喷水压差;而特征值过小,扩张气流会影响到第一排喷水孔附近的压力,也会影响喷水压差系数的稳定。采用推荐的特征值可以更加有利于喷水压差的稳定性,推荐的特征值范围为0.2~0.35。研究结果为燃气-蒸汽式弹射动力系统的结构设计提供理论依据。
| [1] |
李咸海, 王俊杰. 潜地导弹发射动力系统[M]. 哈尔滨: 哈尔滨工程大学出版社, 2000.
|
| [2] |
赵险峰, 王俊杰. 潜地弹道导弹发射系统内弹道学[M]. 哈尔滨: 哈尔滨工程大学出版社, 2001.
|
| [3] |
倪火才. 潜地弹道导弹发射装置构造[M]. 哈尔滨: 哈尔滨工程大学出版社, 1998.
|
| [4] |
芮守祯, 邢玉明, 梁材. 高温高压超声速气液两相流场数值模拟[J]. 航空动力学报, 2011, 26(5): 991-996. |
| [5] |
刘伯伟, 姜毅. 气化效应对燃气蒸汽式弹射气液两相流场的影响[J]. 固体火箭技术, 2014, 37(2): 156-160. |
| [6] |
胡晓磊, 乐贵高, 马大为, 等. 喷水对冷却器流场影响数值研究[J]. 计算机仿真, 2015, 32(1): 117-121. |
| [7] |
王汉平, 吴菊华. 基于CFD的潜射导弹筒口压力场预测[J]. 弹道学报, 2008, 20(4): 73-87. |
| [8] |
Inc B F. Fluent User's Guide[C]//Fluent Incorporated, Lebanon NH, 2010.
|
| [9] |
颜凤, 史少岩, 姜毅. 燃气蒸汽式弹射内弹道研究[J]. 舰船科学技术, 2017, 39(3): 118-122. |
| [10] |
李仁凤, 乐贵高, 马大为, 等. 结构参数对燃气-蒸汽弹射载荷和弹道影响[J]. 上海交通大学学报, 2016, 50(11): 1789-1794. |
 2020, Vol. 42
2020, Vol. 42
